1. Introduction
The study of harmonic oscillators, the connection between which is realized through coordinates and momenta, is a current direction in modern physics. Interest in this area is driven by a wide range of applications where models of such systems find application: from quantum optics [
1,
2,
3] and nonlinear physics [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13] to molecular chemistry [
14,
15,
16] and biophysics [
17,
18,
19]. Physical models of coupled harmonic oscillators have been successfully used in various studies, including the Lee model in quantum field theory [
5,
6,
7]. A similar Hamiltonian is used in biophysics to explain the processes occurring during photosynthesis [
17,
18,
19,
20]. It has long been known that in quantum optics, such phenomena as frequency conversion, parametric amplification, and Raman and Brillouin scattering can be described using the coupled harmonic oscillator model [
21,
22,
23]. In modern studies of coupled quantum harmonic oscillators, the main emphasis is on their quantum entanglement, which forms a separate direction for research in quantum physics. Quantum communication protocols, in particular quantum cryptography [
24], quantum dense coding [
25], quantum computational algorithms [
26], and quantum-state teleportation [
27,
28], can be interpreted using entangled states. This is due to the fact that such oscillators adequately model real physical systems, such as thermal vibrations of coupled atoms, photons in resonators, optomechanical cooling, ions in ion traps, linear beam splitters and others [
3,
29,
30,
31,
32,
33,
34]. Moreover, coupled harmonic oscillators are one of the key models for studying quantum decoherence (see, e.g., [
13,
35]).
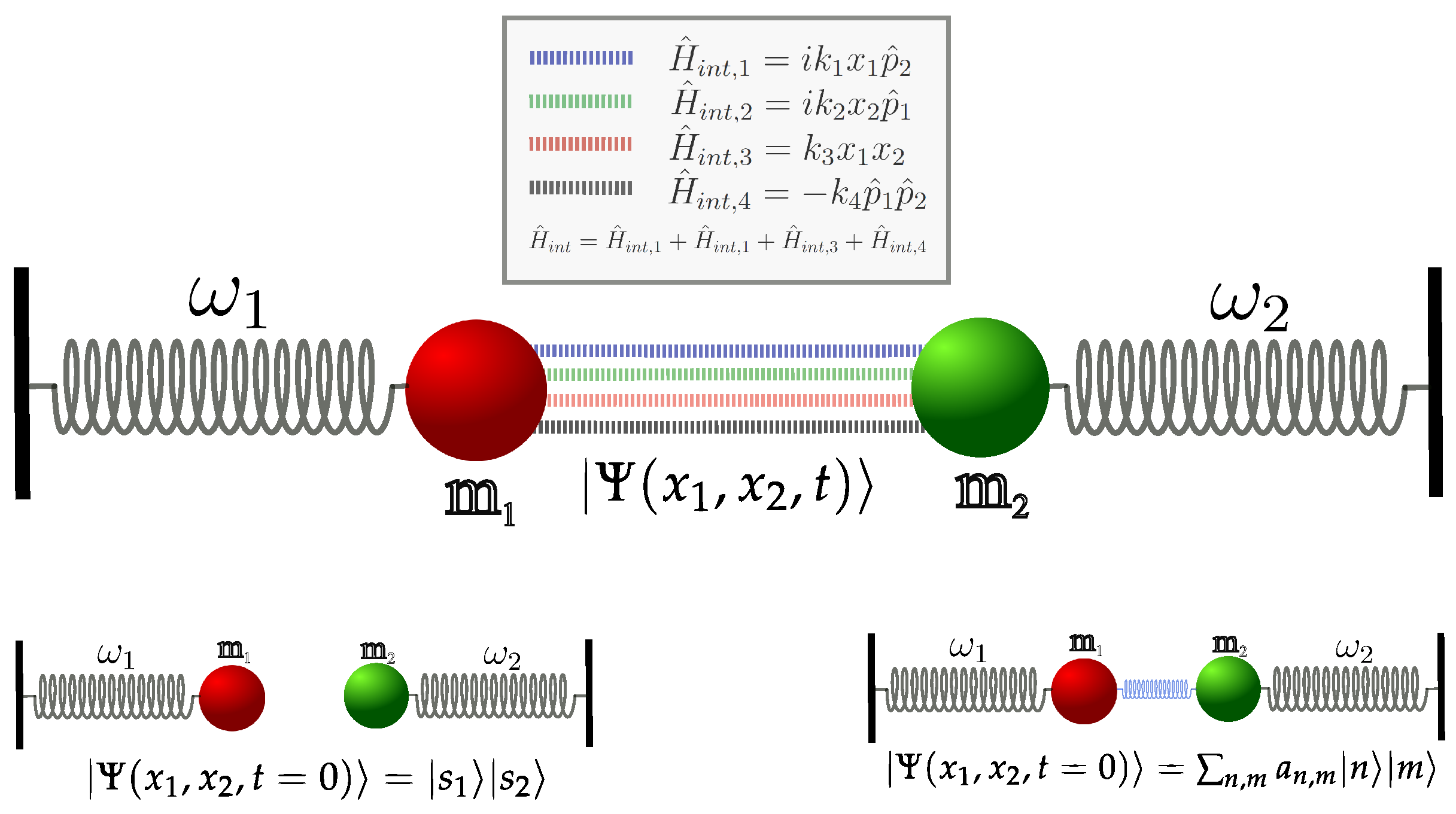
Thus, many systems can be represented as quantum harmonic oscillators coupled in coordinates and momenta with a Hamiltonian in the form
where
(
) is the momentum operator;
are the mass and frequency of oscillator
i, respectively; coefficients
determine the coupled between two oscillators with the interaction energy
. Often, in quantum optics, Equation (
1) can be seen through the operators of particle creation
and annihilation
; in this case, the Hamiltonian will be
where
are some constants (below, we will show the connection between these constants and the constants in Equation (
1)).
The solution of the Schrödinger equation
in general form is currently unknown, taking into account arbitrary initial states, which can be factorized and can be in the Fock state
or non-factorizable, i.e., being in a superposition
; see
Figure 1. There are only some special cases of this solution, where the quantum entanglement of such oscillators is also studied. For example, in the works [
9,
33,
36,
37], the solution and quantum entanglement of such a system were obtained for
, and in the work [
38], a solution was found for
. In the works [
39,
40,
41], the solution for
was studied. Various special cases can be found in the works [
1,
2,
3] (see also the references of these works).
It is well known that to study the quantum entanglement of a two-component system, it is necessary not only to find a solution
of the Schrödinger equation with the Hamiltonian (
1), but also to find the decomposition of this solution into Schmidt modes. By the Schmidt theorem [
42,
43], the wave function
of two interacting systems can be expanded as
, where
is the pure state of the first system, and
is the pure state of the second system, where
is the Schmidt mode. To calculate entanglement, one can use various measures of it; for example, the Schmidt parameter [
42,
43]
or the von Neumann entropy [
37,
44]
. We also add that in this paper we study quantum entanglement for a dynamic system where the non-stationary Schrödinger equation is solved. This means that at the initial time
, the system of oscillators was in the initial state
, but the considered connection arises at
in the system as a result of some process (depending on the problem under study), as a result of which the dynamics of the system appear.
As a result, a solution to the non-stationary Schrödinger equation was found in the analytical form and it was shown that this solution depends on only two parameters, which include all the quantities of the system under consideration. This solution made it possible to find the Schmidt mode and calculate the quantum entanglement of the system under study depending on the initial conditions. It was shown that quantum entanglement depends only on one coefficient for the initial Fock states of the oscillator, and depends on two parameters and for arbitrary initial states. These two parameters and include the entire set of variables of the system under consideration.
2. Solution of the Non-Stationary Schrödinger Equation for Arbitrary Initial States
Let us consider the non-stationary Schrödinger equation
with the Hamiltonian (
1). We choose the initial conditions in the general form, i.e.,
, which defines a superposition of the Fock states (with
) for the 1st and 2nd oscillators, respectively. For now, we will not define the summation
(this will be carried out below) and will assume that it can be any. We add that the initial condition can be represented in a different form using the Schmidt expansion, i.e.,
, where
and
are some states for the first (system
A) and second (system
B) oscillators, and
N is the Schmidt rank, which is defined as
. However, the Schmidt decomposition cannot be used directly, since the states
and
are not defined. For example, the simplest version of the initial conditions is
, where
and
are the quantum numbers of the first and second oscillators before the interaction, in this case
, and all other coefficients are zero.
Next, to solve Equation (
1) it is convenient to move to dimensionless variables; to achieve this, we need to replace
, we get
If we introduce the well-known annihilation operators
and creation
, then we obtain Equation (
2), where
The solution of differential equations of this type has not been presented in the literature before, except for the recent works [
45,
46,
47], where a method for their solution was proposed. Traditionally, such equations are solved by diagonalizing the Hamiltonian (
3) by changing variables, as, for example, in [
9,
33,
36]. In [
38], a method was developed to diagonalize the Hamiltonian in the presence of only one of the coefficients
using a unitary transformation, avoiding the change of variables. To solve Equation (
3), we combine these two approaches. The first step to diagonalize the Hamiltonian (
3) is a change of variables:
where
and
are unknown coefficients. Then, in the second step, a unitary transformation is applied to the Hamiltonian depending on the variables
(i.e.,
):
, where
. That is, the wave function
corresponds to the Hamiltonian
under the conditions
and
, where
E is the energy eigenvalue. As a unitary operator
, we choose
Ref. [
38], where
and
are also unknown coefficients. Let us add that the physical meaning of this operator and the unitary transformation is the transition to a new frame of reference. As a result, we obtain the Hamiltonian
in analytical form, containing four unknown coefficients:
. From Equation (
3), we know four coefficients:
. By composing a system of fourth-order equations and equating the coefficients of the non-diagonalizable variables to zero, we can bring the Hamiltonian
to a diagonal form.
During diagonalization, it is assumed that the oscillators are weakly coupled, i.e., the coupling energies
are significantly less than the energies of the oscillators themselves
. This assumption allows, firstly, to obtain an analytical solution; secondly, it corresponds to most physical systems, where if this condition is violated, the coupling becomes nonlinear, and, thirdly (as will be shown below), it ensures the conservation of quantum numbers before and after the interaction, which in the case of photons means the conservation of their total number in the system. Here, we have described a solution strategy for bringing the Hamiltonian Equation (
3) to diagonal form; the main solution is presented in
Appendix A. As a result, accurate to the phase, which can be ignored, we obtain the solution
where
are Jacobi polynomials and the condition
is satisfied, i.e., the total number of quantum numbers in the system is conserved. States
and
(
are Hermite polynomials,
are known normalization coefficients for a linear oscillator) are states of oscillators in a state without interaction. The coefficients
R and
in Equation (
5) are defined
In general, Equation (
5) does not decompose into Schmidt modes, since the initial state of the oscillators is correlated. It can be seen that if we choose the initial states in the form
, where
, i.e., where the total number of quantum numbers is conserved, then Equation (
5) can be easily decomposed into Schmidt modes in the form
where
is the Schmidt mode (
). Let us add that the expansion of the initial state in the form
is the most correct from a physical point of view. Indeed, if our system is isolated and the initial state
was formed as a result of the evolution of this system from a state without connections at all previous moments of time, i.e.,
, where
is the evolution operator (defined in the
Appendix A), and the operator
(where
for
) specifies the evolution of the system after the rupture of connections after the evolution of
. As a result, we can obtain
where
is a inessential phase that does not affect the probabilities. As a result, the coefficient
in the Equation (
7) will be
. So
determines the probability of detecting the system in the states
and
. Thus,
determines the probability of detecting the system in states
and
and is the Schmidt mode for the initial state of the system in the form
. It is evident that the entire dependence in the wave function is reduced to two variables:
R and
. The properties of the obtained expressions are such that when calculating
the dependence on
disappears for the initial condition
and the entire dependence is reduced to only one parameter
R. This case corresponds to the coefficient
(
is the Kronecker delta) for
. Since quantum entanglement is calculated via the Schmidt mode
, quantum entanglement depends only on
R for this initial condition. This remarkable result allows one to analyze probability and quantum entanglement quite simply. In addition, it is clear that
is a certain parameter characterizing the degree of interaction of two oscillators. The physical meaning of the parameter
R depends on what physical system is described by the Equation (
1). For example, the case
corresponds to the interaction of a two-mode electromagnetic field in a waveguide beam splitter, and the coefficient
R is the reflection coefficient [
33,
36,
37]. It is clear that this coefficient
R depends on time
t, which is easy to understand, since the interaction time of photons in the beam splitter is determined by its thickness, and therefore depends on the interaction time. In the general case, this coefficient
R characterizes the interaction of two systems, each of which in a free state is described by the Hamiltonians
and
, i.e., free oscillators.
The parameter
, expressed in terms of the interaction parameters
(when representing the Hamiltonian in the form of Equation (
2)), takes the form
. Although the parameters
and
are missing in this formula, this is not an error. This simplification arises from the assumption that
. In this situation, the quantum numbers (and, equivalently, the number of particles) remain unchanged during the interaction, which is a mathematically rigorous result. The conservation of quantum numbers implies that interaction occurs only through combinations of creation and annihilation operators of the form
or
. This means that the annihilation operator of the first oscillator is compensated by the creation operator of the second oscillator, and vice versa, maintaining the stability of quantum states. It is interesting to note that, given
, the operators corresponding to the coefficients
and
(namely,
and
) are operators of higher orders of smallness compared to the operators
and
, even if the parameters
themselves have comparable values.
The presented results are consistent with previously known special cases, such as those in [
9,
33,
36,
37], where the case
was considered. This corresponds to the quantum entanglement of photons propagating along two modes in a waveguide beam splitter, as well as to the photon statistics at the output ports of both waveguide and other types of beam splitters [
33,
34]. The case
studied in [
38] describes a different physical situation: the interaction between a single-mode electromagnetic field and an electron in a magnetic field, which is equivalent to placing an electron at Landau levels in an optical resonator. The works [
39,
40,
41] investigated the interesting case
, which under certain conditions can model frequency converters, parametric amplifiers, and Raman and Mandelstam–Brillouin scattering processes. Recent studies [
45] have shown the possibility of quantum entanglement of photons on free electrons for modeling, for which, within the framework of the considered approach, although small compared to the energy of the oscillators
, non-zero values of the coefficients
are required. Similarly, this model can describe the interaction of photons with a two-mode electromagnetic field and electrons, both free and bound, which is confirmed by the fact that Equation (
1) is part of the general Hamiltonian. In addition, one can imagine a model of mechanical nanoharmonic oscillators linearly coupled to each other through various types of interaction. Thus, the considered model covers a wide range of physical phenomena, both already realized and promising for future research. In general, coupled harmonic oscillators are fundamental models used to describe many physical systems, e.g., [
1,
2,
3] (and the references cited therein).
An analysis of Equation (
6) shows that for
and
the frequency
vanishes, which in turn leads to the absence of interaction (
). This result is important because it demonstrates that, despite the presence of coupling, the interaction can be compensated by different terms of
. This means that by changing the parameters
, one can control the interaction of oscillators, up to its suppression, while maintaining the coupling between them, i.e., the coupling parameters can remain non-zero. Equation (
6) also indicates that significant dynamics of the system are observed under the condition
, i.e., the frequencies
and
should be close enough, given that we are considering the case
.
3. Quantum Entanglement of Oscillators
Let us consider quantum entanglement based on two measures, the Schmidt parameter
[
42,
43] and the von Neumann entropy
[
37,
44]. To calculate these measures of quantum entanglement, we must directly use Equation (
5) with
. To calculate quantum entanglement, we must determine the initial conditions of the system under consideration. Let us choose two variants: the first is the most widely used case in quantum optics
(where
), and the second case is the equiprobable distribution of states
. In the first case, as was said earlier,
does not depend on the phase
, but only on the coefficient
R, and the second case depends on the phase
. Here, we present only some special cases in analytical form for quantum entanglement for the first case
and
and the second case for
. As an example, we present:
- ❑
For
at
and
where the maximum quantum entanglement will be
at
and
.
- ❑
For
at
and
- ❑
For
at
and
where the maximum quantum entanglement will be
at
and
.
- ❑
For
at
and
where the maximum quantum entanglement will be
at
and
.
- ❍
For
and
at
where the maximum quantum entanglement will be (for
)
- ❍
For
and
at
(similarly for
and
)
where the maximum quantum entanglement will be (for
)
- ❍
For
and
at
where the maximum quantum entanglement will be
for
and
for
.
The quantum entanglement of some particular cases can be found in general form, for example, for the initial state
. Using the results of [
33] for the initial state
, we obtain
where
2 is Gaussian hypergeometric function. Also, analyzing the Equation (
15), you can obtain the maximum of this function at
. With this value of
, one can obtain a simpler expression for quantum entanglement
This can also be found from parameter
K in Equation (
16) for large values of the quantum number
s, where we obtain
. It can be seen that in this case quantum entanglement is unlimited from above.
There is also another important case, when
and
. In this case, Holland–Burnett (HB) [
48] states are realized. It is well known that this wave function is of great interest in various fields of physics, for example, in quantum metrology [
49,
50]. In this case, we obtain
where
is the gamma function, and
4 is the generalized hypergeometric function. It should be added that the Equation (
17) has a fairly simple approximation for sufficiently large
s; we obtain it in the form
.
Let us add that for the case , the maximum entanglement is realized at and . This means that for these values of R, the wave function at any time t is equal to the wave function at the initial time. Since at the initial time the state of the system is maximally close to a chaotic distribution (since the probability of detecting each of the states is equally probable ), the entropy of the system will be maximum, and entropy is a measure of entanglement.
Below are the results of calculations for the initial state
(where
), quantum entanglement for the von Neumann entropy
and the Schmidt parameter
K depending on the parameter
and the dimensionless quantity
for studying the dynamics of the system; see
Figure 2 and
Figure 3.
The analysis of the presented figures (
Figure 2 and
Figure 3) and Equations (
12)–(
17) allows us to conclude the following. An increase in the quantum numbers
and
leads to an increase in quantum entanglement. For a fixed sum
, the entanglement value changes insignificantly, but when analyzing additional figures we can say that the entanglement reaches its maximum possible value at
for certain values of the parameter
R. Quantum entanglement exhibits symmetry with respect to the point
, i.e., the entanglement values coincide for
and
. We add that the symmetry of quantum entanglement with respect to
can be explained if
R is defined as the reflection coefficient. As a result, if we deviate
R from
by
in the direction of decrease, i.e.,
, then the number of states that will pass from one oscillator to another will be the same as if we deviate
R by
in the direction of increase, i.e.,
. In other words, the oscillators exchange energy equally at
. The same exchange of states with respect to
yields the same statistics, which defines quantum entanglement. The dependence of entanglement on
R is oscillatory in nature, and the number of oscillations increases with an increase in the sum
.
In addition, the graphs demonstrate the oscillatory dynamics of quantum entanglement. This is explained by the exchange of energy between two coupled oscillators, which leads to oscillations of various physical characteristics. In the absence of coupling (), this phenomenon is similar to the pendulum effect, which is also applicable in this situation. It is interesting to note that the period of these oscillations is equal to when . In the general case, the period depends on the value of . It is important to note that the minimum level of entanglement corresponds to the smallest quantum numbers, i.e., (no entanglement), and the maximum level is determined by the maximum value of the sum .
We also present figures of quantum entanglement for the Schmidt parameter
K in the case of initial conditions in the form
. The results are presented in
Figure 4.
From
Figure 4, it is evident that quantum entanglement will always be maximal at
and
for the reason explained above in the analysis of Equations (
8)–(
11). Also evident is the tendency for quantum entanglement to decrease at
and
. We add that with increasing quantum number
N, the dependence of entanglement on
R and
for
will be close to
Figure 4.
It should be noted that for , there is a significant dependence of entanglement on the phase, whereas for (where ) there is no such dependence. The dependence of the probability on the phase and, as a consequence, entanglement for all , except , is easily explained due to the superposition of the initial states . Indeed, each term of the superposition is analogous to the sum , and when squaring the absolute value, when calculating a physically measurable quantity, the phase is preserved for .