Objective Framework for Bayesian Inference in Multicomponent Pareto Stress–Strength Model Under an Adaptive Progressive Type-II Censoring Scheme
Abstract
1. Introduction
- Insurance: estimating the probability that a specified number of policyholders can withstand financial losses, thereby ensuring the stability of an insurance pool.
- Finance: assessing the resilience of financial institutions by modeling the possibility that a sufficient subset can withstand extreme market fluctuations.
- Climate risk assessment: estimating the probability that an adequate number of geographic regions can withstand large-scale natural disasters without triggering systemic collapse.
- Healthcare systems: determining whether a sufficient number of hospitals or intensive care units can absorb patient surges during public health crises, thereby maintaining overall system functionality.
2. Model Description
2.1. Pareto Distribution
2.2. Adaptive Progressive Type-II Censoring Scheme
- Case 1:
- -
- If the vth failure occurs before time T, the experiment follows the conventional PT-II CS, terminating at .
- Case 2:
- -
- If the vth failure occurs after time T, it prevents the removal of surviving units by modifying the scheme so that , where D denotes the number of observed failures up to time T, provided that .
- -
- All remaining units are withdrawn immediately upon the occurrence of the vth failure, and the experiment is terminated.
- : The ith APT-II censored strength sample, .
- : The removal scheme for the ith APT-II censored strength sample, .
- : The APT-II censored stress sample.
- : The removal scheme for the APT-II censored stress sample.
- : The predetermined time threshold for the strength sample.
- : The predetermined time threshold for the stress sample.
- : A vector containing the number of observations recorded up to time for each strength sample, where denotes the number of observations recorded up to time in the ith APT-II censored strength sample.
- : The number of observations recorded up to time in the APT-II censored stress sample.
- Then, under the APT-II CS, strength and stress samples for the multicomponent system can be written asrespectively. For the sake of notational simplicity, we adopt the simplified forms and throughout the remainder of this study.
3. Likelihood-Based Approach
4. Objective Bayesian Approach
4.1. Reference Prior with Partial Information
4.2. Posterior Analysis
- (1)
- Draw a MCMC sample from the marginal posterior density function (14), using the NUTS algorithm.
- (2)
- Draw a MCMC sample for from .
- (3)
- Draw a MCMC sample from .
- (4)
- Compute .
- (5)
- Repeat times.
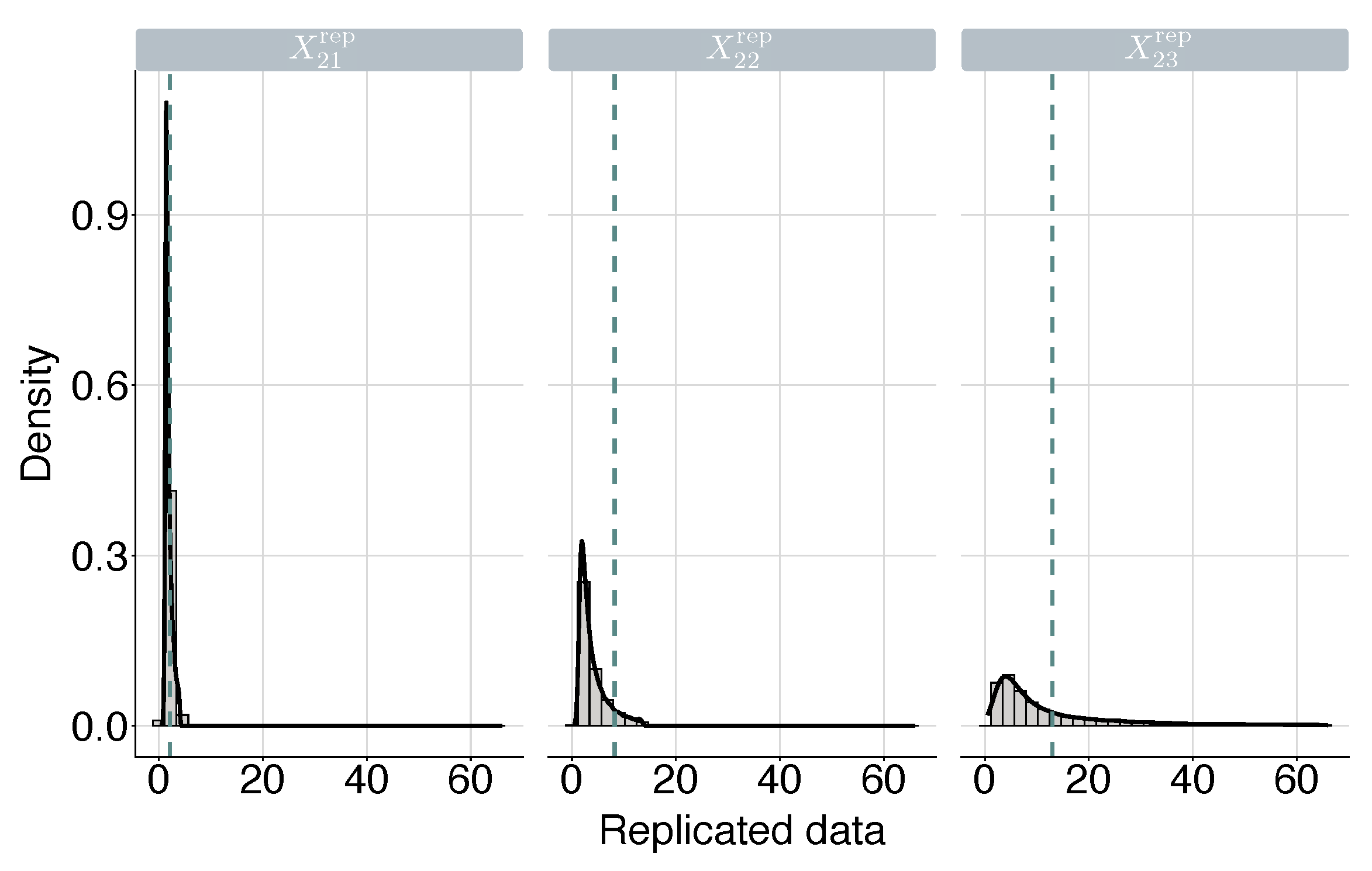
4.3. Posterior Predictive Checking
5. Application
5.1. Simulation Study
- (1)
- Generate an ordinary PT-II censored sample with the CS from the algorithm of Balakrishnan and Sandhu [17] as follows:
- (a)
- Generate k independent realizations from the standard uniform distribution.
- (b)
- Compute for .
- (c)
- Compute for .
- (d)
- Compute for , which is a PT-II censored sample for the strength variable from the Pareto distribution with the CDF (2) in a single component system.
- (2)
- Determine the value of satisfying .
- (3)
- Generate the first order statistics from a truncated distribution with sample size , where denotes the PDF of the strength variable.
- (4)
- Substitute with the first order statistics obtained in (3).
- In a similar manner, multicomponent APT-II censored samples are generated by considering m-out-of- systems coupled with k-out-of- components. The APT-II censored sample for the stress variable is also generated using the algorithm of Ng et al. [6].
5.2. Software Failure Time Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhattacharyya, G.K.; Johnson, R.A. Estimation of reliability in a multicomponent stress-strength model. J. Am. Stat. Assoc. 1974, 69, 966–970. [Google Scholar] [CrossRef]
- Wang, L.; Wu, K.; Tripathi, Y.M.; Lodhi, C. Reliability analysis of multicomponent stress-strength reliability from a bathtub-shaped distribution. J. Appl. Stat. 2022, 49, 122–142. [Google Scholar] [CrossRef] [PubMed]
- Lio, Y.; Tsai, T.R.; Wang, L.; Cecilio Tejada, I.P. Inferences of the multicomponent stress-strength reliability for Burr XII distributions. Mathematics 2022, 10, 2478. [Google Scholar] [CrossRef]
- Jha, M.K.; Dey, S.; Alotaibi, R.; Alomani, G.; Tripathi, Y.M. Multicomponent stress-strength reliability estimation based on unit generalized exponential distribution. Ain Shams Eng. J. 2022, 13, 101627. [Google Scholar] [CrossRef]
- Jana, N.; Bera, S. Interval estimation of multicomponent stress-strength reliability based on inverse Weibull distribution. Math. Comput. Simul. 2022, 191, 95–119. [Google Scholar] [CrossRef]
- Ng, H.K.T.; Kundu, D.; Chan, P.S. Statistical analysis of exponential lifetimes under an adaptive Type-II progressive censoring scheme. Nav. Res. Logist. 2009, 56, 687–698. [Google Scholar] [CrossRef]
- Chen, S.; Gui, W. Statistical analysis of a lifetime distribution with a bathtub-shaped failure rate function under adaptive progressive Type-II censoring. Mathematics 2020, 8, 670. [Google Scholar] [CrossRef]
- Ateya, S.F.; Amein, M.M.; Mohammed, H.S. Prediction under an adaptive progressive Type-II censoring scheme for Burr Type-XII distribution. Commun. Stat.-Theory Methods 2022, 51, 4029–4041. [Google Scholar] [CrossRef]
- Dutta, S.; Dey, S.; Kayal, S. Bayesian survival analysis of logistic exponential distribution for adaptive progressive Type-II censored data. Comput. Stat. 2024, 39, 2109–2155. [Google Scholar] [CrossRef]
- Azhad, Q.J.; Arshad, M.; Khandelwal, N. Statistical inference of reliability in multicomponent stress strength model for Pareto distribution based on upper record values. Int. J. Model. Simul. 2022, 42, 319–334. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Sun, D.; Berger, J.O. Reference priors with partial information. Biometrika 1998, 85, 55–71. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Duane, S.; Kennedy, A.D.; Pendleton, B.J.; Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 1987, 195, 216–222. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Balakrishnan, N.; Sandhu, R.A. A simple simulational algorithm for generating progressive Type-II censored samples. Am. Stat. 1995, 49, 229–230. [Google Scholar] [CrossRef]
- Stan Development Team. RStan: The R Interface to Stan, R Package Version 2.32.3. 2023. Available online: https://mc-stan.org/ (accessed on 15 December 2022).
- Musa, J.D. Software Reliability Data; Technical Report; Data and Analysis Center for Software, Rome Air Development Center: Rome, NY, USA, 1979. [Google Scholar]
- Kayal, T.; Tripathi, Y.M.; Dey, S.; Wu, S.J. On estimating the reliability in a multicomponent stress-strength model based on Chen distribution. Commun. Stat.-Theory Methods 2020, 49, 2429–2447. [Google Scholar] [CrossRef]
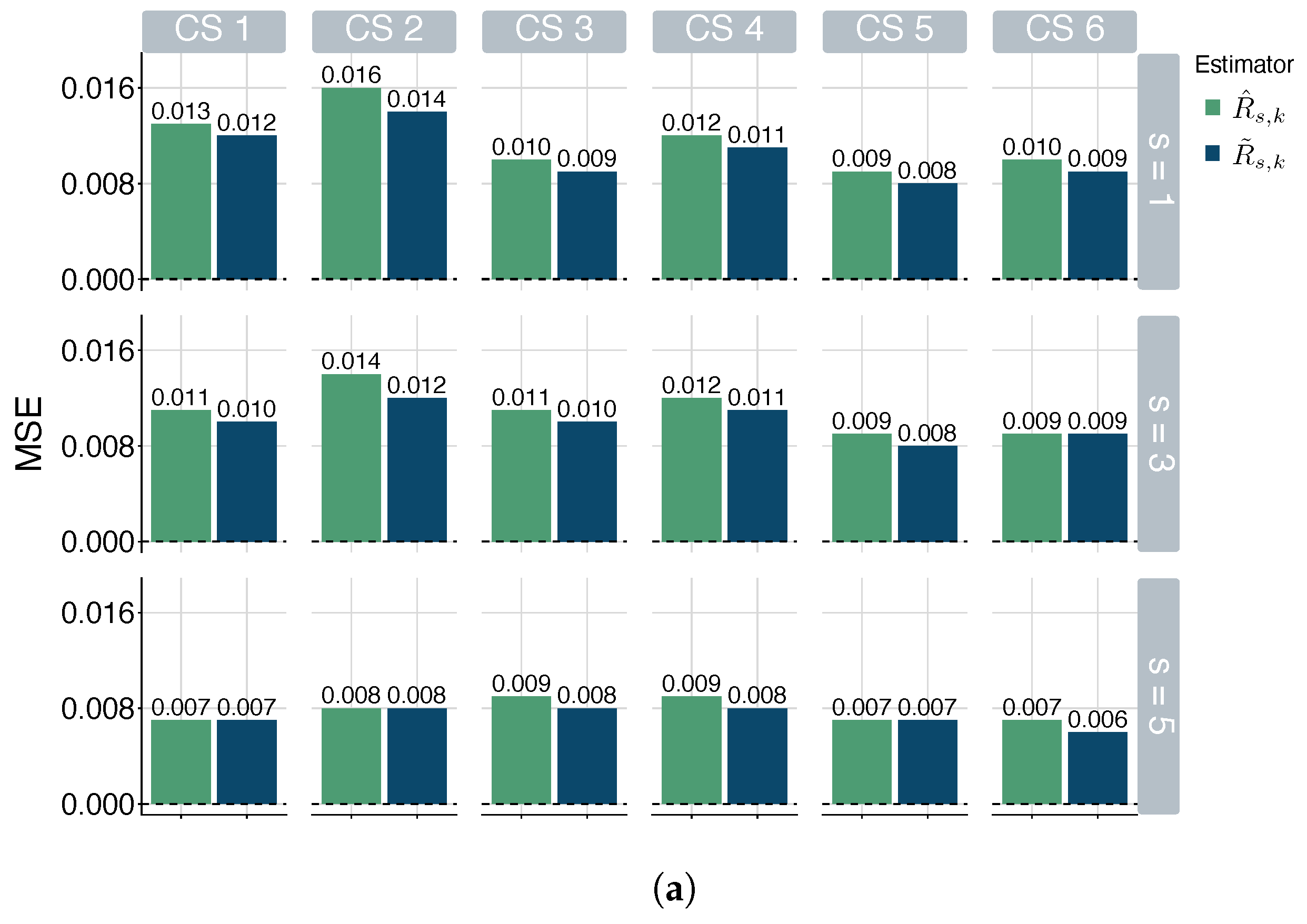
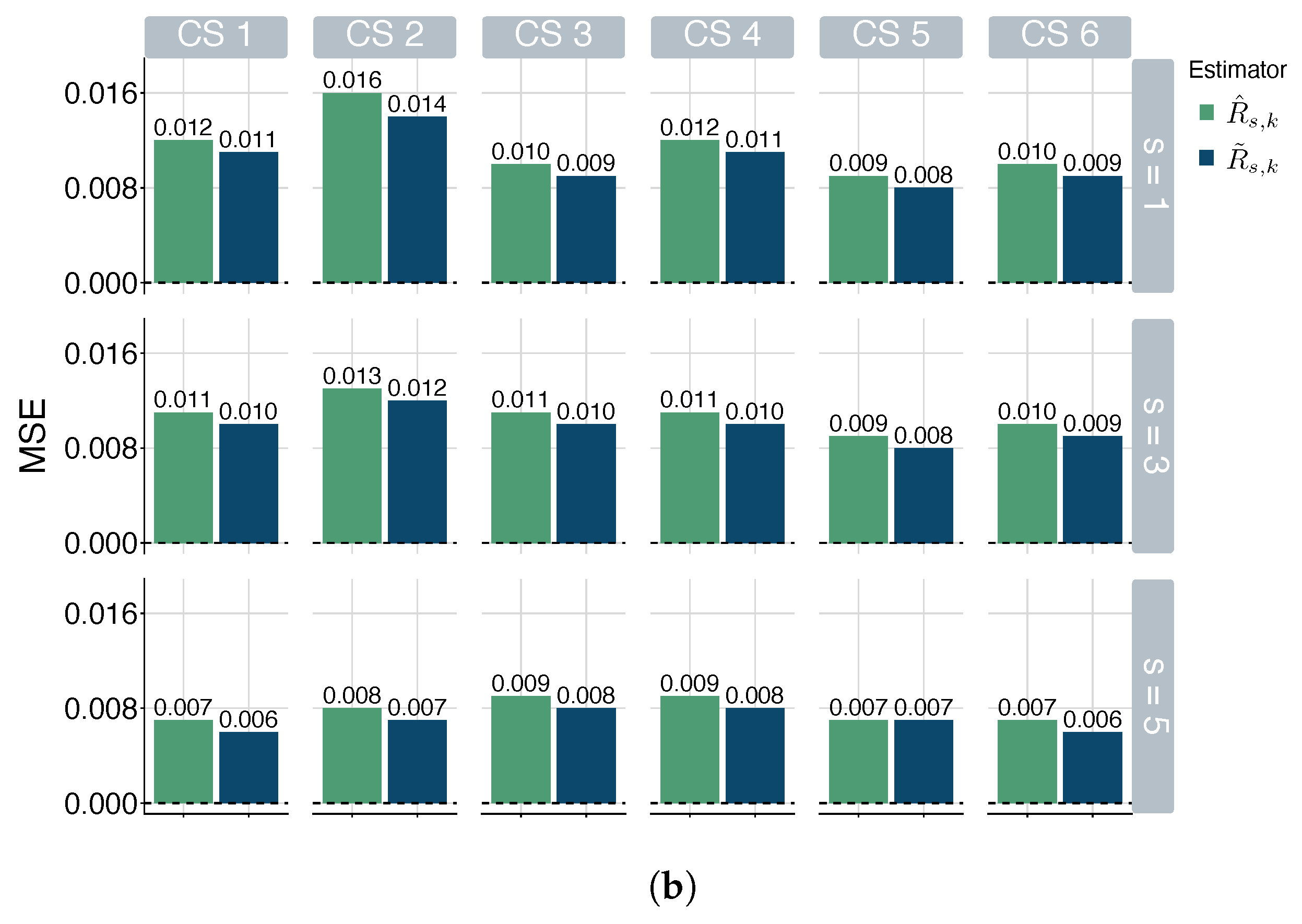
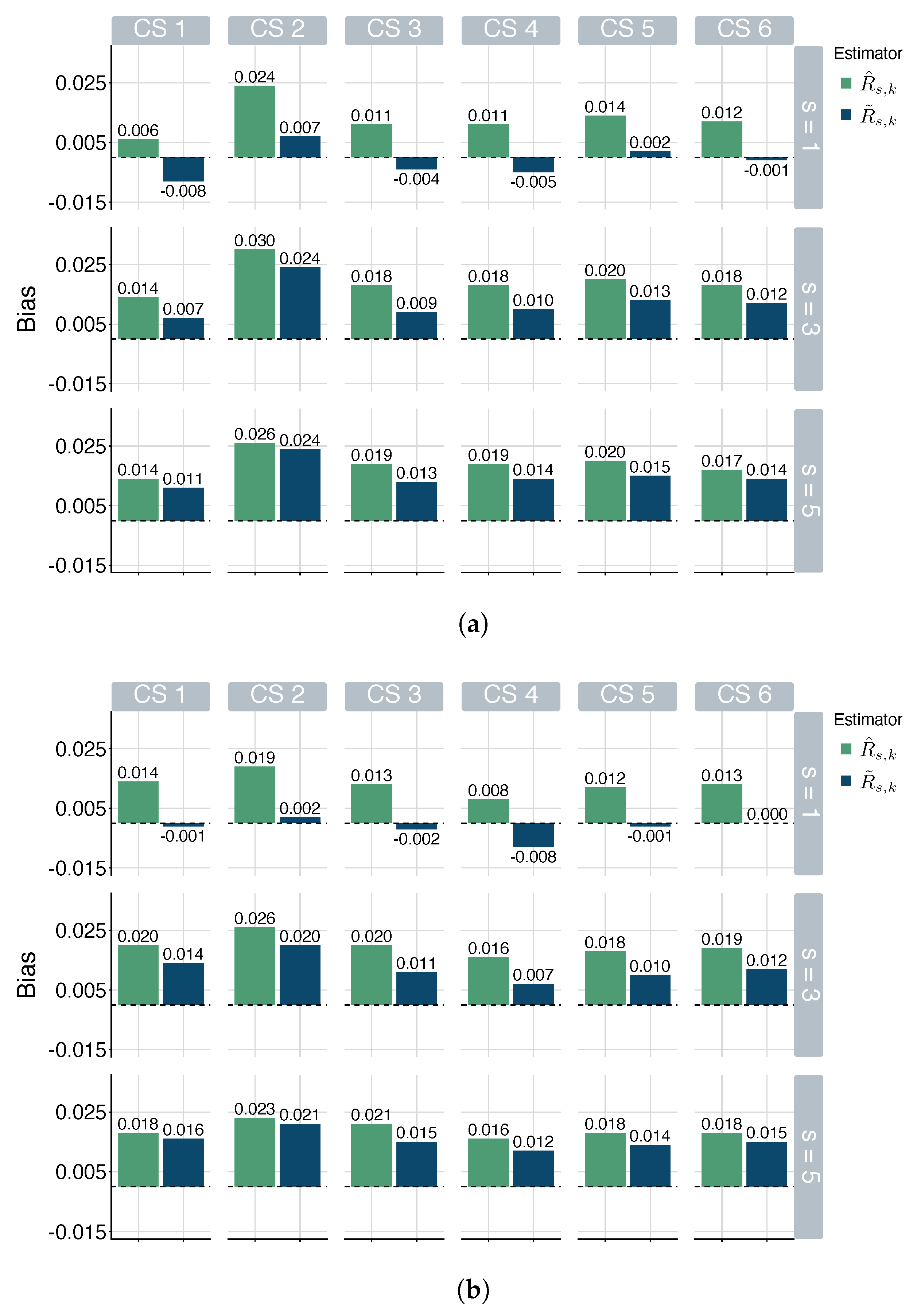
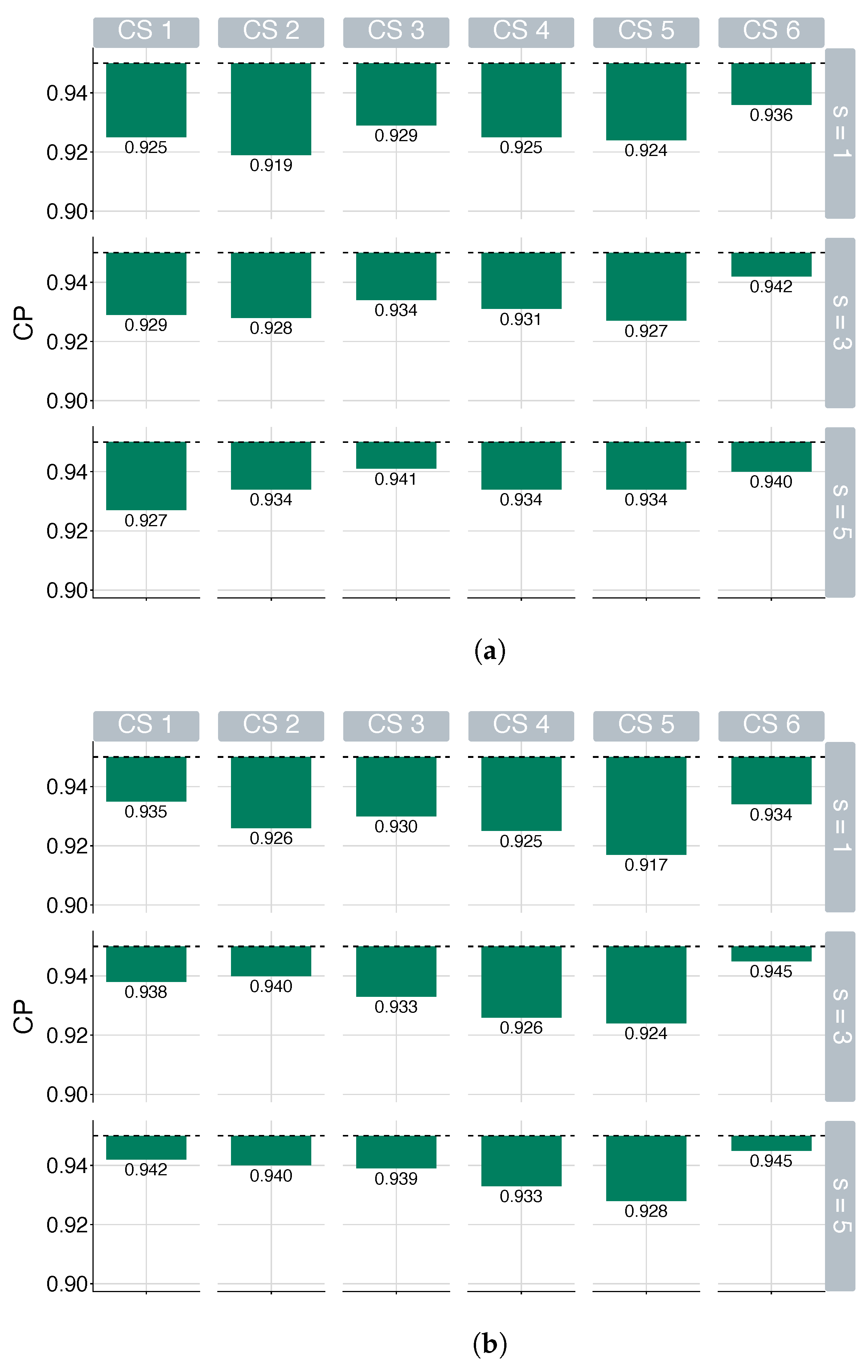









| Pattern | CS | k | m | ||||
| Pattern 1 | 1 | 20 | 20 | 12 | 10 | ||
| 2 | 10 | 8 | |||||
| 3 | 30 | 20 | 20 | 12 | |||
| 4 | 16 | 10 | |||||
| 5 | 30 | 30 | 18 | 14 | |||
| 6 | 14 | 12 | |||||
| Pattern 2 | 1 | 20 | 20 | 12 | 10 | ||
| 2 | 10 | 8 | |||||
| 3 | 30 | 20 | 20 | 12 | |||
| 4 | 16 | 10 | |||||
| 5 | 30 | 30 | 18 | 14 | |||
| 6 | 14 | 12 |
| Likelihood-Based Approach | Proposed Bayesian Approach | |||||||
| HPD CrI | ||||||||
| 1.350 | 0.388 | 0.860 | 0.915 | 1.235 | 0.362 | 0.763 | 0.852 | (0.563, 0.999) |
| Mean | 0.596 | 0.385 | 0.633 | 0.545 |
| SD | 0.722 | 0.428 | 0.793 | 0.511 |
| 32.38 | 104.30 | 109.49 | 107.12 | 102.49 | 109.48 | 107.48 | 77.73 | 109.52 | 109.52 | 78.65 | 109.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, Y.E.; Kim, Y.; Seo, J.-I. Objective Framework for Bayesian Inference in Multicomponent Pareto Stress–Strength Model Under an Adaptive Progressive Type-II Censoring Scheme. Mathematics 2025, 13, 1379. https://doi.org/10.3390/math13091379
Jeon YE, Kim Y, Seo J-I. Objective Framework for Bayesian Inference in Multicomponent Pareto Stress–Strength Model Under an Adaptive Progressive Type-II Censoring Scheme. Mathematics. 2025; 13(9):1379. https://doi.org/10.3390/math13091379
Chicago/Turabian StyleJeon, Young Eun, Yongku Kim, and Jung-In Seo. 2025. "Objective Framework for Bayesian Inference in Multicomponent Pareto Stress–Strength Model Under an Adaptive Progressive Type-II Censoring Scheme" Mathematics 13, no. 9: 1379. https://doi.org/10.3390/math13091379
APA StyleJeon, Y. E., Kim, Y., & Seo, J.-I. (2025). Objective Framework for Bayesian Inference in Multicomponent Pareto Stress–Strength Model Under an Adaptive Progressive Type-II Censoring Scheme. Mathematics, 13(9), 1379. https://doi.org/10.3390/math13091379






