A Modified Nonlinear Lorentz Model for Third-Order Optical Nonlinearity
Abstract
1. Introduction
2. Models
2.1. The Kerr Model
2.2. The Duffing Model
2.3. The Nonlinear Lorentz Model
2.4. Modified Nonlinear Lorentz Model
3. Results
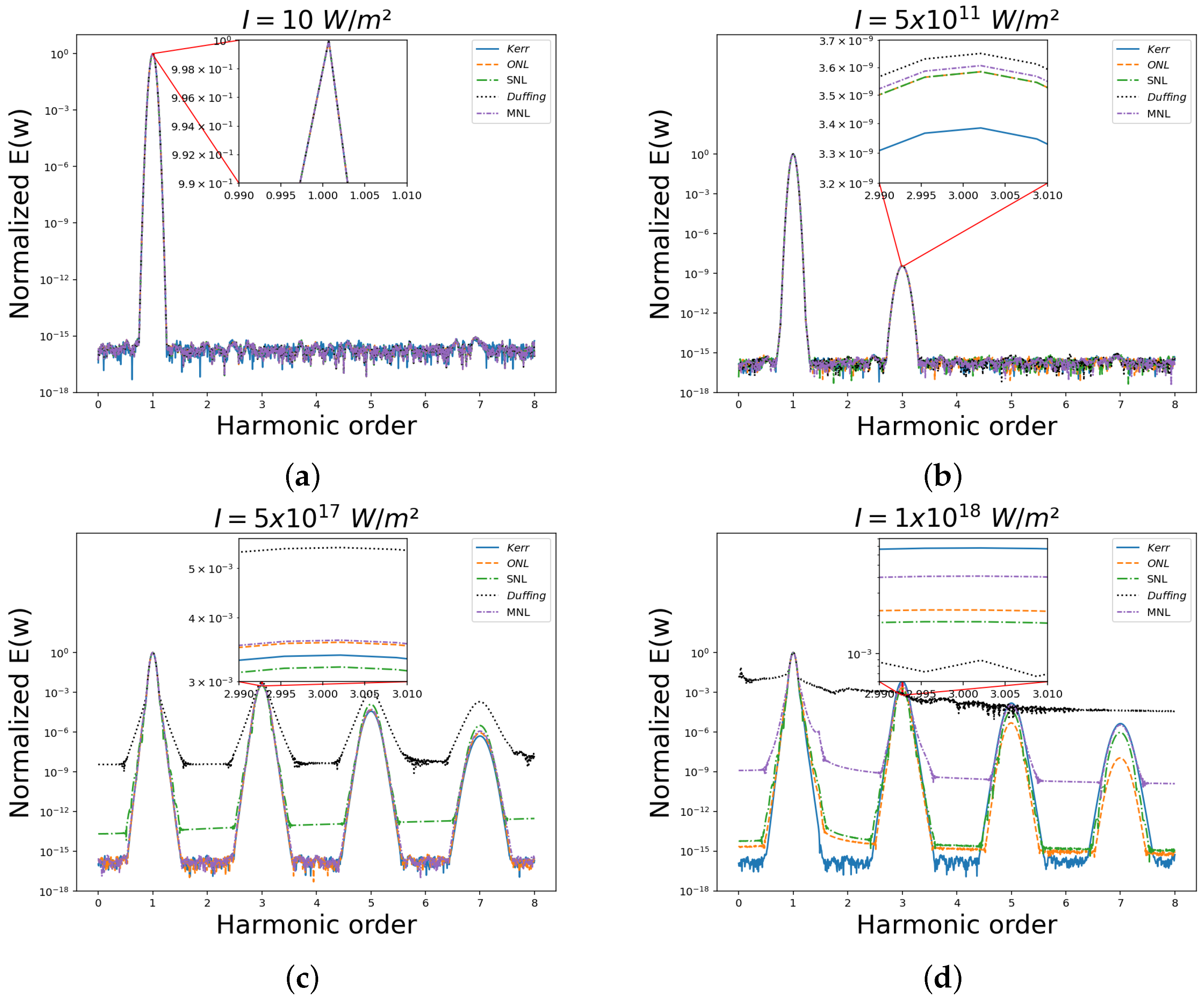
3.1. Comparison Under Different Light Intensities
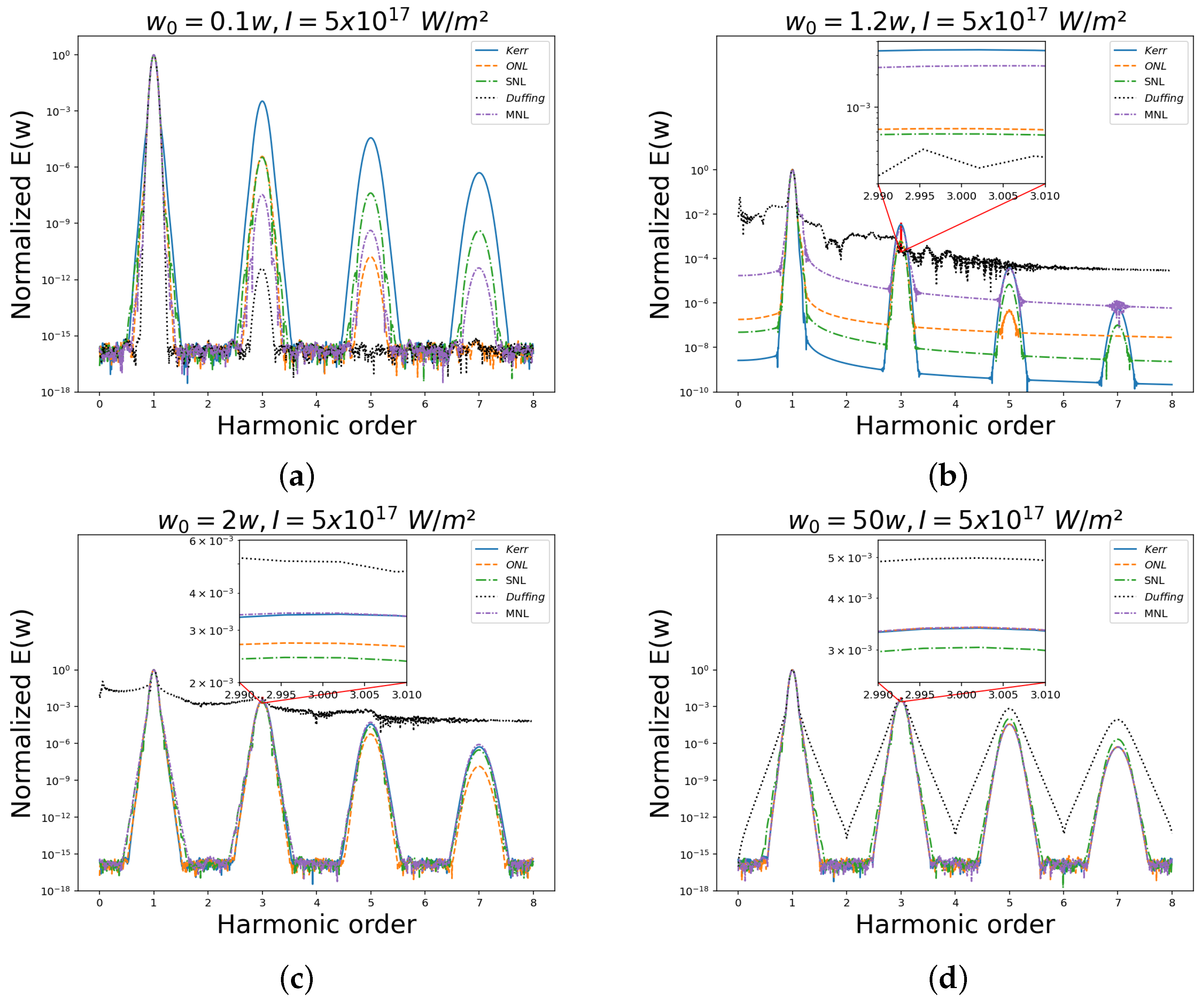
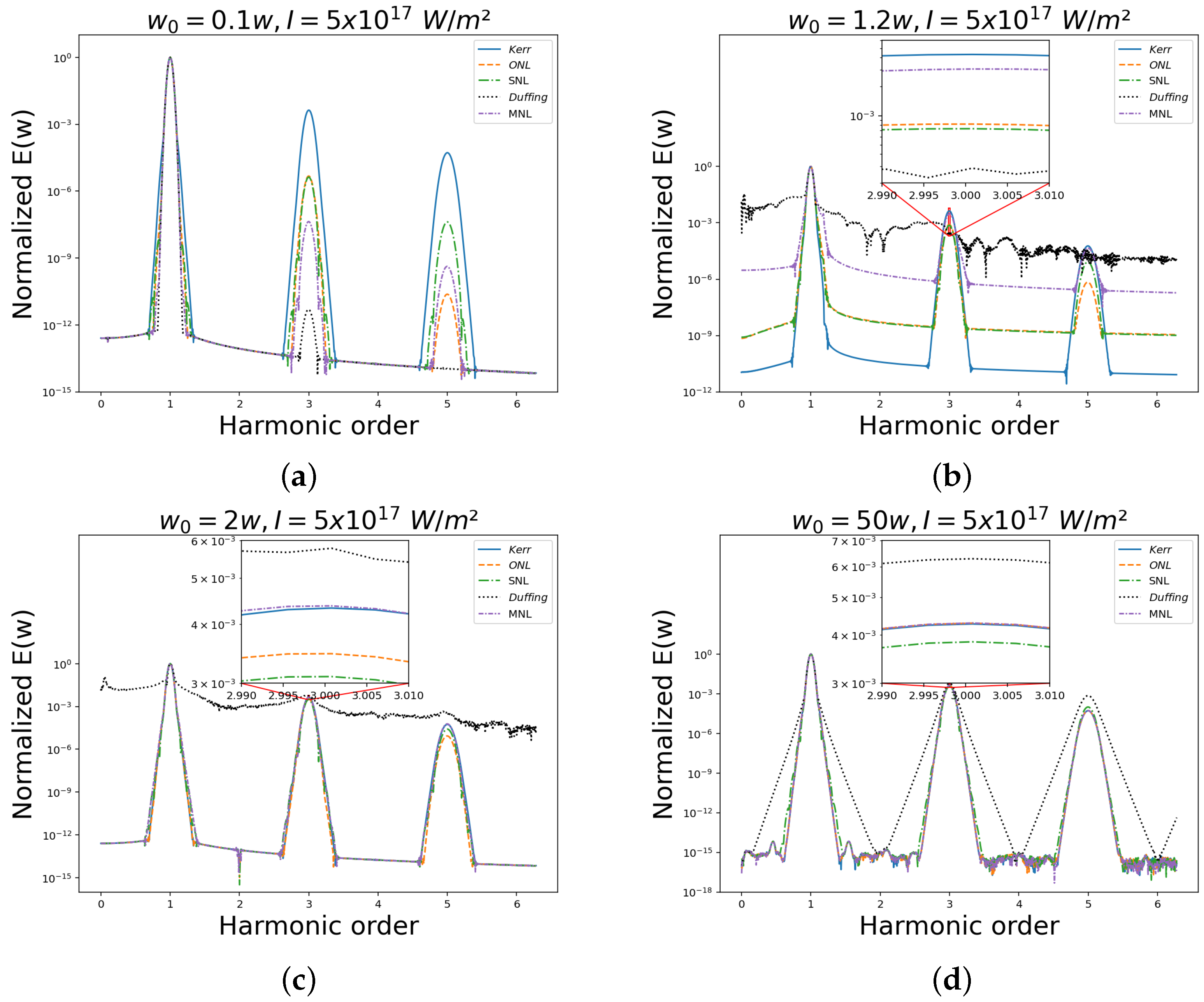
3.2. Comparison Under Different Ratios Between Wave Frequency and Resonant Frequency
3.3. Quantitative Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Q.; Huang, Z.; Sun, Y.; Triki, H.; Liu, W.; Biswas, A. Collision dynamics of three-solitons in an optical communication system with third-order dispersion and nonlinearity. Nonlinear Dyn. 2023, 111, 5757–5765. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear fiber optics. In Nonlinear Science at the Dawn of the 21st Century; Springer: Berlin/Heidelberg, Germany, 2000; pp. 195–211. [Google Scholar]
- Zhou, Y.; Lin, X.; Xu, Z.; Lu, Z.; Huang, Y.; Luo, Z.; Chi, N. Beyond 600Gbps Optical Interconnect Utilizing Wavelength Division Multiplexed Visible Light Laser Communication. Chin. Opt. Lett. 2025, 23. [Google Scholar]
- Ma, P.; Yao, T.; Liu, W.; Pan, Z.; Chen, Y.; Yang, H.; Chen, Z.; Wang, Z.; Zhou, P.; Chen, J. A 7-kW narrow-linewidth fiber amplifier assisted by optimizing the refractive index of the large-mode-area active fiber. High Power Laser Sci. Eng. 2024, 12, e67. [Google Scholar] [CrossRef]
- Xu, Z.; Lin, X.; Luo, Z.; Lin, Q.; Zhang, J.; Wang, G.; Wang, X.; Jiang, F.; Li, Z.; Shi, J.; et al. Flexible 2 × 2 multiple access visible light communication system based on an integrated parallel GaN/InGaN micro-photodetector array module. Photonics Res. 2024, 12, 793–803. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Boyd, R.W.; Gaeta, A.L.; Giese, E. Nonlinear optics. In Springer Handbook of Atomic, Molecular, and Optical Physics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1097–1110. [Google Scholar]
- Stegeman, G.I.; Stegeman, R.A. Nonlinear Optics: Phenomena, Materials and Devices; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 78. [Google Scholar]
- Goorjian, P.M.; Taflove, A.; Joseph, R.M.; Hagness, S.C. Computational modeling of femtosecond optical solitons from Maxwell’s equations. IEEE J. Quantum Electron. 1992, 28, 2416–2422. [Google Scholar] [CrossRef]
- Fujii, M.; Tahara, M.; Sakagami, I.; Freude, W.; Russer, P. High-order FDTD and auxiliary differential equation formulation of optical pulse propagation in 2-D Kerr and Raman nonlinear dispersive media. IEEE J. Quantum Electron. 2004, 40, 175–182. [Google Scholar] [CrossRef]
- Li, C.; Miao, P. Single-frame statistical gating in a speckle pattern generated by the dynamic scattering in disordered medium. Appl. Phys. Lett. 2025, 126, 043701. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, F.; Gu, Y.; Zhang, Y.; Cui, C.; Liu, J.; Qiu, Z.; Wang, P. Optimization of 3D reconstruction of granular systems based on refractive index matching scanning. Opt. Laser Technol. 2025, 186, 112662. [Google Scholar] [CrossRef]
- Brzozowski, L.; Sargent, E.H. Optical signal processing using nonlinear distributed feedback structures. IEEE J. Quantum Electron. 2000, 36, 550–555. [Google Scholar] [CrossRef]
- Maimistov, A.I.; Caputo, J.G. Propagation of extremely short pulses in nonresonant media: The total Maxwell–Duffing model. Phys. D Nonlinear Phenom. 2004, 189, 107–114. [Google Scholar] [CrossRef]
- Kazantseva, E.V.; Maimistov, A.I.; Caputo, J.G. Reduced Maxwell-Duffing description of extremely short pulses in nonresonant media. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 71, 056622. [Google Scholar] [CrossRef] [PubMed]
- Scalora, M.; Vincenti, M.A.; de Ceglia, D.; Cojocaru, C.; Grande, M.; Haus, J. Nonlinear Duffing oscillator model for third harmonic generation. JOSA B 2015, 32, 2129–2138. [Google Scholar] [CrossRef]
- Varin, C.; Emms, R.; Bart, G.; Fennel, T.; Brabec, T. Explicit formulation of second and third order optical nonlinearity in the FDTD framework. Comput. Phys. Commun. 2018, 222, 70–83. [Google Scholar] [CrossRef]
- Varin, C.; Bart, G.; Fennel, T.; Brabec, T. Nonlinear Lorentz model for the description of nonlinear optical dispersion in nanophotonics simulations. Opt. Mater. Express 2019, 9, 771–778. [Google Scholar] [CrossRef]
- Varin, C.; Bart, G.; Emms, R.; Brabec, T. Saturable Lorentz model for fully explicit three-dimensional modeling of nonlinear optics. Opt. Express 2015, 23, 2686–2695. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Yu, A.; Hu, M.; Wang, Q.; Pang, C.; Xiong, H.; Cheng, Y.; Qi, J. Non-interleaved shared-aperture full-stokes metalens via prior-knowledge-driven inverse design. Adv. Mater. 2025, 37, 2408978. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C.; Piket-May, M. Computational electromagnetics: The finite-difference time-domain method. Electr. Eng. Handb. 2005, 3, 15. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Xie, G.; Hou, G.; Xu, K.; Niu, K.; Feng, N.; Li, Y.; Huang, Z.; Elsherbeni, A.Z. Extension of FLOD-FDTD method for multiterm modified Lorentz model. IEEE Trans. Antennas Propag. 2023, 71, 8830–8840. [Google Scholar] [CrossRef]
- Gordon, D.F.; Helle, M.H.; Peñano, J.R. Fully explicit nonlinear optics model in a particle-in-cell framework. J. Comput. Phys. 2013, 250, 388–402. [Google Scholar] [CrossRef]
- Janyani, V.; Vukovic, A.; Paul, J.D.; Sewell, P.; Benson, T.M. Time domain simulation in photonics: A comparison of nonlinear dispersive polarisation models. Opt. Quantum Electron. 2005, 37, 3–24. [Google Scholar] [CrossRef]
- Conti, C.; Di Falco, A.; Assanto, G. Optical parametric oscillations in isotropic photonic crystals. Opt. Express 2004, 12, 823–828. [Google Scholar] [CrossRef] [PubMed]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press, Inc.: Orlando, FL, USA, 2008. [Google Scholar]
- Shen, Y.R. Principles of Nonlinear Optics; Wiley-Interscience: New York, NY, USA, 1984. [Google Scholar]
- Deinega, A.; John, S. Effective optical response of silicon to sunlight in the finite-difference time-domain method. Opt. Lett. 2011, 37, 112–114. [Google Scholar] [CrossRef] [PubMed]
- Prokopidis, K.P.; Zografopoulos, D.C. An ADI-FDTD formulation with modified Lorentz dispersion for the study of plasmonic structures. IEEE Photonics Technol. Lett. 2014, 26, 2267–2270. [Google Scholar] [CrossRef]
- Choi, H.; Baek, J.W.; Jung, K.Y. Comprehensive study on numerical aspects of modified Lorentz model-based dispersive FDTD formulations. IEEE Trans. Antennas Propag. 2019, 67, 7643–7648. [Google Scholar] [CrossRef]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]


| 0.1 | 0.9989 | 0.9989 | 1.0000 | 0.9999 |
| 0.2 | 0.9955 | 0.9955 | 1.0000 | 0.9998 |
| 0.3 | 0.9899 | 0.9899 | 0.9999 | 0.9990 |
| 0.4 | 0.9819 | 0.9819 | 0.9999 | 0.9966 |
| 0.5 | 0.9715 | 0.9715 | 0.9989 | 0.9905 |
| 0.6 | 0.9584 | 0.9584 | 0.9926 | 0.9765 |
| 0.7 | 0.9425 | 0.9425 | 0.9489 | 0.9444 |
| 0.8 | 0.9235 | 0.9235 | 0.5650 | 0.8622 |
| 1.2 | 0.8100 | 0.8100 | 5.8903 | 0.3667 |
| 1.3 | 0.7691 | 0.7691 | 2.4483 | 0.4299 |
| 1.4 | 0.7219 | 0.7219 | 1.3904 | 0.4296 |
| 1.5 | 0.6671 | 0.6671 | 0.9551 | 0.3989 |
| 1.6 | 0.6030 | 0.6030 | 0.7635 | 0.3471 |
| 1.7 | 0.5277 | 0.5277 | 0.6956 | 0.2765 |
| 1.8 | 0.4383 | 0.4383 | 0.7053 | 0.1865 |
| 1.9 | 0.3313 | 0.3313 | 0.7743 | 0.0741 |
| 2.0 | 0.2014 | 0.2014 | 0.8974 | 0.0658 |
| 4.0 | 1.2886 | 1.2886 | 1.7786 | 1.4415 |
| 5.0 | 0.5634 | 0.5634 | 0.7675 | 0.6286 |
| 6.0 | 0.3338 | 0.3338 | 0.4516 | 0.3720 |
| 7.0 | 0.2253 | 0.2253 | 0.3036 | 0.2508 |
| 8.0 | 0.1638 | 0.1638 | 0.2202 | 0.1823 |
| 9.0 | 0.1251 | 0.1251 | 0.1679 | 0.1392 |
| 10.0 | 0.0990 | 0.0990 | 0.1327 | 0.1101 |
| 15.0 | 0.0417 | 0.0417 | 0.0558 | 0.0464 |
| 20.0 | 0.0230 | 0.0230 | 0.0308 | 0.0256 |
| 50.0 | 0.0036 | 0.0036 | 0.0048 | 0.0040 |
| 0.1 | 0.9989 | 0.9990 | 1.0000 | 0.9999 |
| 0.2 | 0.9955 | 0.9960 | 1.0000 | 0.9998 |
| 0.3 | 0.9899 | 0.9910 | 0.9999 | 0.9991 |
| 0.4 | 0.9819 | 0.9838 | 0.9999 | 0.9970 |
| 0.5 | 0.9714 | 0.9744 | 0.9990 | 0.9917 |
| 0.6 | 0.9583 | 0.9627 | 0.9930 | 0.9797 |
| 0.7 | 0.9424 | 0.9485 | 0.9587 | 0.9532 |
| 0.8 | 0.9235 | 0.9316 | 0.7976 | 0.8897 |
| 1.2 | 0.8101 | 0.8300 | 0.9186 | 0.2869 |
| 1.3 | 0.7692 | 0.7935 | 0.8603 | 0.3997 |
| 1.4 | 0.7220 | 0.7512 | 0.7801 | 0.4191 |
| 1.5 | 0.6670 | 0.6445 | 0.7362 | 0.4001 |
| 1.6 | 0.6029 | 0.6447 | 0.6227 | 0.3576 |
| 1.7 | 0.5275 | 0.5773 | 0.4164 | 0.2962 |
| 1.8 | 0.4382 | 0.4973 | 0.2306 | 0.2164 |
| 1.9 | 0.3312 | 0.4016 | 0.0689 | 0.1162 |
| 2.0 | 0.2013 | 0.2854 | 0.4649 | 0.0082 |
| 4.0 | 1.2871 | 1.0467 | 5.8617 | 1.5992 |
| 5.0 | 0.5638 | 0.4011 | 1.9172 | 0.6737 |
| 6.0 | 0.3342 | 0.1943 | 1.3949 | 0.3963 |
| 7.0 | 0.2259 | 0.0971 | 1.0964 | 0.2664 |
| 8.0 | 0.1645 | 0.0421 | 0.9276 | 0.1933 |
| 9.0 | 0.1258 | 0.0075 | 0.8090 | 0.1476 |
| 10.0 | 0.0997 | 0.0159 | 0.7337 | 0.1167 |
| 15.0 | 0.0424 | 0.0672 | 0.5747 | 0.0495 |
| 20.0 | 0.0238 | 0.0839 | 0.5251 | 0.0276 |
| 50.0 | 0.0044 | 0.1013 | 0.4745 | 0.0050 |
| 0.1 | 0.9989 | 0.9989 | 1.0000 | 0.9999 |
| 0.2 | 0.9955 | 0.9955 | 1.0000 | 0.9998 |
| 0.3 | 0.9899 | 0.9899 | 0.9999 | 0.9990 |
| 0.4 | 0.9819 | 0.9819 | 0.9999 | 0.9965 |
| 0.5 | 0.9714 | 0.9714 | 0.9989 | 0.9905 |
| 0.6 | 0.9583 | 0.9583 | 0.9926 | 0.9765 |
| 0.7 | 0.9424 | 0.9424 | 0.9487 | 0.9444 |
| 0.8 | 0.9234 | 0.9234 | 0.5652 | 0.8626 |
| 1.2 | 0.8095 | 0.8095 | 5.7950 | 0.3704 |
| 1.3 | 0.7688 | 0.7688 | 2.4258 | 0.4312 |
| 1.4 | 0.7215 | 0.7215 | 1.3817 | 0.4301 |
| 1.5 | 0.6666 | 0.6666 | 0.9510 | 0.3989 |
| 1.6 | 0.6024 | 0.6024 | 0.7615 | 0.3468 |
| 1.7 | 0.5269 | 0.5269 | 0.6947 | 0.2760 |
| 1.8 | 0.4374 | 0.4374 | 0.7052 | 0.1856 |
| 1.9 | 0.3301 | 0.3301 | 0.7749 | 0.0729 |
| 2.0 | 0.1998 | 0.1998 | 0.8988 | 0.0674 |
| 4.0 | 1.2853 | 1.2853 | 1.7739 | 1.4377 |
| 5.0 | 0.5624 | 0.5624 | 0.7661 | 0.6275 |
| 6.0 | 0.3333 | 0.3333 | 0.4509 | 0.3714 |
| 7.0 | 0.2250 | 0.2250 | 0.3032 | 0.2505 |
| 8.0 | 0.1636 | 0.1636 | 0.2199 | 0.1821 |
| 9.0 | 0.1250 | 0.1250 | 0.1677 | 0.1391 |
| 10.0 | 0.0989 | 0.0989 | 0.1325 | 0.1100 |
| 15.0 | 0.0417 | 0.0417 | 0.0557 | 0.0463 |
| 20.0 | 0.0230 | 0.0230 | 0.0307 | 0.0256 |
| 50.0 | 0.0036 | 0.0036 | 0.0048 | 0.0040 |
| 0.1 | 0.9989 | 0.9990 | 1.0000 | 0.9999 |
| 0.2 | 0.9955 | 0.9960 | 1.0000 | 0.9998 |
| 0.3 | 0.9899 | 0.9909 | 0.9999 | 0.9991 |
| 0.4 | 0.9819 | 0.9838 | 0.9999 | 0.9969 |
| 0.5 | 0.9714 | 0.9744 | 0.9990 | 0.9916 |
| 0.6 | 0.9582 | 0.9626 | 0.9930 | 0.9797 |
| 0.7 | 0.9423 | 0.9484 | 0.9584 | 0.9532 |
| 0.8 | 0.9234 | 0.9315 | 0.7948 | 0.8895 |
| 1.2 | 0.8097 | 0.8297 | 0.9353 | 0.2939 |
| 1.3 | 0.7687 | 0.7930 | 0.8551 | 0.4012 |
| 1.4 | 0.7213 | 0.7506 | 0.7636 | 0.4191 |
| 1.5 | 0.6662 | 0.7013 | 0.6650 | 0.3995 |
| 1.6 | 0.6018 | 0.6437 | 0.6181 | 0.3566 |
| 1.7 | 0.5262 | 0.5761 | 0.5209 | 0.2949 |
| 1.8 | 0.4365 | 0.4959 | 0.2521 | 0.2147 |
| 1.9 | 0.3291 | 0.3998 | 0.0562 | 0.1140 |
| 2.0 | 0.1987 | 0.2831 | 0.2918 | 0.0108 |
| 4.0 | 1.2812 | 1.0417 | 5.4571 | 1.5870 |
| 5.0 | 0.5626 | 0.4000 | 1.8499 | 0.6718 |
| 6.0 | 0.3338 | 0.1944 | 1.4749 | 0.3953 |
| 7.0 | 0.2258 | 0.0974 | 1.0808 | 0.2660 |
| 8.0 | 0.1646 | 0.0425 | 0.9181 | 0.1933 |
| 9.0 | 0.1260 | 0.0079 | 0.8019 | 0.1476 |
| 10.0 | 0.1000 | 0.0154 | 0.7292 | 0.1169 |
| 15.0 | 0.0428 | 0.0666 | 0.5719 | 0.0498 |
| 20.0 | 0.0242 | 0.0833 | 0.5229 | 0.0280 |
| 50.0 | 0.0048 | 0.1007 | 0.4729 | 0.0054 |
| (W/) | ||||
|---|---|---|---|---|
| 0.2013 | 0.2014 | 0.8976 | 0.0659 | |
| 0.2014 | 0.2014 | 0.8974 | 0.0658 | |
| 0.2014 | 0.2014 | 0.8974 | 0.0658 | |
| 0.2014 | 0.2014 | 0.8974 | 0.0658 | |
| 0.2014 | 0.2014 | 0.8974 | 0.0658 | |
| 0.2014 | 0.2014 | 0.8975 | 0.0658 | |
| 0.2014 | 0.2015 | 0.8978 | 0.0657 | |
| 0.2014 | 0.2023 | 0.9012 | 0.0651 | |
| 0.2014 | 0.2106 | 0.9373 | 0.0594 | |
| 0.2013 | 0.2854 | 0.4649 | 0.0082 | |
| 0.2012 | 0.3544 | 0.6051 | 0.0383 |
| (W/) | ||||
|---|---|---|---|---|
| 0.1862 | 0.1862 | 0.9205 | 0.0830 | |
| 0.1984 | 0.1984 | 0.9010 | 0.0690 | |
| 0.1996 | 0.1996 | 0.8991 | 0.0676 | |
| 0.1998 | 0.1998 | 0.8988 | 0.0674 | |
| 0.1998 | 0.1998 | 0.8989 | 0.0674 | |
| 0.1998 | 0.1998 | 0.8989 | 0.0674 | |
| 0.1998 | 0.1999 | 0.8992 | 0.0674 | |
| 0.1998 | 0.2007 | 0.9026 | 0.0668 | |
| 0.1997 | 0.2089 | 0.9387 | 0.0612 | |
| 0.1987 | 0.2831 | 0.2918 | 0.0108 | |
| 0.1976 | 0.3517 | 0.6664 | 0.0349 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Liu, J. A Modified Nonlinear Lorentz Model for Third-Order Optical Nonlinearity. Mathematics 2025, 13, 1354. https://doi.org/10.3390/math13081354
Xia Y, Liu J. A Modified Nonlinear Lorentz Model for Third-Order Optical Nonlinearity. Mathematics. 2025; 13(8):1354. https://doi.org/10.3390/math13081354
Chicago/Turabian StyleXia, Yao, and Jinjie Liu. 2025. "A Modified Nonlinear Lorentz Model for Third-Order Optical Nonlinearity" Mathematics 13, no. 8: 1354. https://doi.org/10.3390/math13081354
APA StyleXia, Y., & Liu, J. (2025). A Modified Nonlinear Lorentz Model for Third-Order Optical Nonlinearity. Mathematics, 13(8), 1354. https://doi.org/10.3390/math13081354





