Abstract
This paper presents a comprehensive time-series analysis framework leveraging the Temporal Fusion Transformer (TFT) architecture to address the challenge of multi-horizon forecasting in complex ecological systems, specifically focusing on global fishery resources. Using global fishery data spanning 70 years (1950–2020), enhanced with key climate indicators, we develop a methodology for predicting time-dependent patterns across three-year, five-year, and extended seven-year horizons. Our approach integrates static metadata with temporal features, including historical catch and climate data, through a specialized architecture incorporating variable selection networks, multi-head attention mechanisms, and bidirectional encoding layers. A comparative analysis demonstrates the TFT model’s robust performance against traditional methods (ARIMA), standard deep learning models (MLP, LSTM), and contemporary architectures (TCN, XGBoost). While competitive across different horizons, TFT excels in the 7-year forecast, achieving a mean absolute percentage error (MAPE) of 13.7%, outperforming the next best model (LSTM, 15.1%). Through a sensitivity analysis, we identify the optimal temporal granularity and historical context length for maximizing prediction accuracy. The variable selection component reveals differential weighting, with recent market observations (past 1-year catch: 31%) and climate signals (ONI index: 15%, SST anomaly: 10%) playing significant roles. A species-specific analysis uncovers variations in predictability patterns. Ablation experiments quantify the contributions of the architectural components. The proposed methodology offers practical applications for resource management and theoretical insights into modeling temporal dependencies in complex ecological data.
Keywords:
time-series analysis; multi-horizon forecasting; Temporal Fusion Transformer; feature importance; sequential data; network interpretability MSC:
68T07
1. Introduction
The accurate forecasting of global fish catch is a critical challenge for ensuring food security, maintaining marine ecological balance, and informing economic policies on fisheries [1,2,3]. With the increasing threats of overfishing and climate change, sustainable fisheries management has become an urgent priority [4]. Effective resource allocation, policy planning, and catch quota adjustments rely on robust forecasting models that can predict fishery trends over various time scales, including short-term (e.g., three years), medium-term (e.g., five years), and longer-term (e.g., seven years) horizons [5]. However, achieving high-precision predictions remains complex due to the dynamic nature of marine ecosystems, market fluctuations, policy interventions, and the significant influence of external environmental drivers like climate variability [6].
Traditional time-series forecasting methods, such as AutoRegressive Integrated Moving Average (ARIMA) and Seasonal ARIMA, have been used for fish catch prediction [7]. While useful for linear trends, they struggle to integrate multiple external factors (like climate data) and capture complex non-linear dependencies [8]. Moreover, they often require extensive manual feature engineering and assumptions, limiting their adaptability [9].
Deep learning models, particularly Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) networks, have shown promise [10,11]. However, their effectiveness can be limited in multi-horizon forecasting: they may struggle with very long sequences, and often lack inherent interpretability, hindering expert insights into the domain [12]. Other advanced techniques like Temporal Convolutional Networks (TCNs) [13] and gradient boosting machines like XGBoost offer alternative powerful approaches but may face challenges in seamlessly integrating diverse input types (static, dynamic observed, dynamic known) or providing built-in temporal interpretation mechanisms suited for complex time-series interactions.
Recently, Temporal Fusion Transformer (TFT) has emerged as a state-of-the-art deep learning framework specifically designed for multi-step forecasting with high interpretability [14,15,16]. TFT combines recurrent layers with self-attention, enabling it to capture both local and long-range temporal dependencies. Crucially, it incorporates mechanisms to handle various input types (static metadata, past time series, known future inputs) and provides built-in variable selection and attention-based interpretability [17,18]. Despite its potential, systematic application and rigorous evaluation of TFT, especially integrating key climate drivers and assessing performance over extended forecast horizons, for global fish catch forecasting remain limited.
This study aims to bridge this gap by developing and evaluating a TFT-based forecasting model using historical fish catch data (1950–2020) from the Sea Around Usdataset augmented with climate indicators (annual ONI index and global SST anomalies). Specifically, we seek to achieve the following: First, construct a TFT model capable of predicting global fish catch trends over three-year, five-year, and seven-year horizons, leveraging historical catch, static attributes, and climate data. Next, comprehensively compare TFT’s performance against a wide range of benchmarks, including ARIMA, Multi-layer Perceptron (MLP), LSTM, TCN, and XGBoost, evaluating predictive accuracy across all horizons. Then, utilize TFT’s built-in interpretability tools to analyze key factors influencing fish catch fluctuations, including the relative importance of historical catch versus climate signals.
The primary contributions of this work are as follows:
- We propose and validate a TFT-based approach for short-to-long-term (3, 5, and 7 years) global fish catch forecasting, demonstrating its ability to effectively integrate historical trends, static identifiers, and crucial climate variability data while maintaining explainability.
- We fine-tune the TFT architecture for the specific characteristics of the Sea Around Us dataset enriched with climate information.
- We systematically benchmark TFT against five diverse established models (ARIMA, MLP, LSTM, TCN, XGBoost), showcasing its advantages, particularly in its robustness for longer forecasting horizons and its capacity to leverage external climate drivers.
By leveraging state-of-the-art deep learning techniques and incorporating essential environmental context, this study provides an interpretable and high-accuracy forecasting framework, offering valuable insights for sustainable fisheries management, especially for medium-to-longer-term planning horizons.
2. Related Work
The prediction of fishery catch volume is a critical area of research that intersects with marine resource management, economic planning, and environmental sustainability. Over the years, various modeling approaches have been employed to forecast fishery yields, ranging from traditional statistical methods to advanced deep learning architectures [19,20]. Each class of models offers unique advantages and limitations, particularly in handling non-linearity, incorporating external variables, and enabling multi-step forecasting. This section provides an overview of the primary methodologies employed in fishery catch forecasting, including traditional statistical approaches, biologically and economically driven models, and recent advancements in deep learning-based time-series forecasting.
2.1. Traditional Statistical Models for Fishery Forecasting
Historically, statistical models have played a dominant role in time-series forecasting due to their mathematical rigor, interpretability, and relatively low computational cost. Some of the most widely used statistical approaches for fishery forecasting include AutoRegressive Integrated Moving Average (ARIMA), Seasonal ARIMA (SARIMA), and Vector AutoRegression (VAR) [21,22]. These models primarily focus on capturing trends, seasonality, and autocorrelation in historical catch data as shown in Table 1.
However, their effectiveness is constrained by several limitations. First, these models rely on strong stationarity assumptions, requiring pre-processing techniques such as differencing and detrending to stabilize time series. Second, they struggle to integrate multiple exogenous variables, which are crucial in fisheries forecasting due to the influence of environmental and economic factors such as sea surface temperature, El Niño–Southern Oscillation (ENSO) events, and fishing regulations [23]. Finally, traditional statistical models generally underperform in long-horizon forecasting because they rely on extrapolating patterns from historical data without the ability to model complex temporal dependencies dynamically [24].

Table 1.
Comparison of traditional statistical models for fishery forecasting.
Table 1.
Comparison of traditional statistical models for fishery forecasting.
| Model | Strengths | Limitations | Typical Use Cases |
|---|---|---|---|
| ARIMA [25] | Effective for short-term univariate forecasting | Assumes stationarity; limited ability to model exogenous factors | Monthly or annual fish catch trends based on historical data |
| SARIMA [26] | Captures seasonality better than ARIMA | Requires manual parameter tuning; computationally expensive for large datasets | Forecasting seasonal fishery yields, e.g., quarterly catch predictions |
| VAR [27] | Models interdependencies between multiple time series | Requires large datasets; less effective for non-linear dependencies | Analyzing interactions between fish stock levels and environmental variables |
2.2. Biological and Economic Models for Fishery Forecasting
In addition to statistical methods, fisheries forecasting has been approached through biologically and economically driven models. Biomass-based models, such as the Schaefer surplus production model and age-structured models, are commonly used to estimate stock dynamics based on recruitment, growth, and mortality rates [28]. Economic models, on the other hand, incorporate market demand, price elasticity, and trade policies to project future fishery yields [29].
Despite their theoretical rigor, these models exhibit significant shortcomings when applied to large-scale historical datasets. Many biological models assume equilibrium conditions and fail to account for abrupt changes caused by environmental fluctuations or regulatory interventions. Economic models, while useful for price and demand forecasting, are often inadequate for predicting actual fish catch volumes due to the unpredictable nature of ecological variables [30].
2.3. Deep Learning Approaches for Time-Series Forecasting in Fisheries
Recent advances in deep learning have introduced powerful alternatives to traditional time-series forecasting methods, particularly for handling complex temporal dependencies and multi-source data integration.
Recurrent neural network (RNN)-based architectures, such as LSTM and GRU networks, have demonstrated promising results in short-term and mid-term fishery forecasting [31,32]. These models excel at capturing sequential dependencies and non-linear patterns in fishery datasets. However, they suffer from issues such as vanishing gradients over long sequences and limited interpretability, making them less ideal for multi-horizon forecasting where explainability is crucial.
Transformer-based models, which leverage attention mechanisms, have recently gained traction for time-series forecasting [33,34,35]. Models such as the Informer and Autoformer architectures have proven effective in large-scale, long-sequence forecasting due to their ability to dynamically focus on relevant historical patterns while handling sparse data efficiently [36]. TFT, in particular, has emerged as a state-of-the-art deep learning model for multi-horizon forecasting [37]. Unlike traditional transformers, TFT incorporates additional interpretability features such as variable selection networks and self-attention mechanisms, enabling it to identify key drivers of fishery fluctuations while maintaining high predictive accuracy.
2.4. Application of the Sea Around Us Dataset in Fisheries Management
The Sea Around Us dataset [38] is one of the most comprehensive sources of historical fish catch data, covering global, national, and species-specific records from 1950 onwards. The dataset includes detailed information on exclusive economic zones (EEZs), large marine ecosystems (LMEs), taxonomic classifications, and fishing gear types, making it a valuable resource for both retrospective analysis and forecasting applications [39].
Previous studies utilizing this dataset have predominantly focused on historical trend analysis and time-series retrospection rather than predictive modeling. Most research efforts have aimed at reconstructing total global catch estimates, assessing the impact of illegal and unreported fishing, and analyzing long-term sustainability trends [40]. However, the application of deep learning models, particularly TFT, for multi-horizon forecasting using this dataset remains relatively unexplored. This study aims to fill this gap by leveraging the Sea Around Us data to develop a scalable, interpretable forecasting framework for short-term fisheries prediction. By integrating state-of-the-art deep learning methodologies with high-quality fishery datasets, this research contributes to the growing field of fisheries management, providing insights that can support sustainable fishing practices, quota regulations, and economic policy decisions.
3. Data and Task Definition
3.1. Data Source
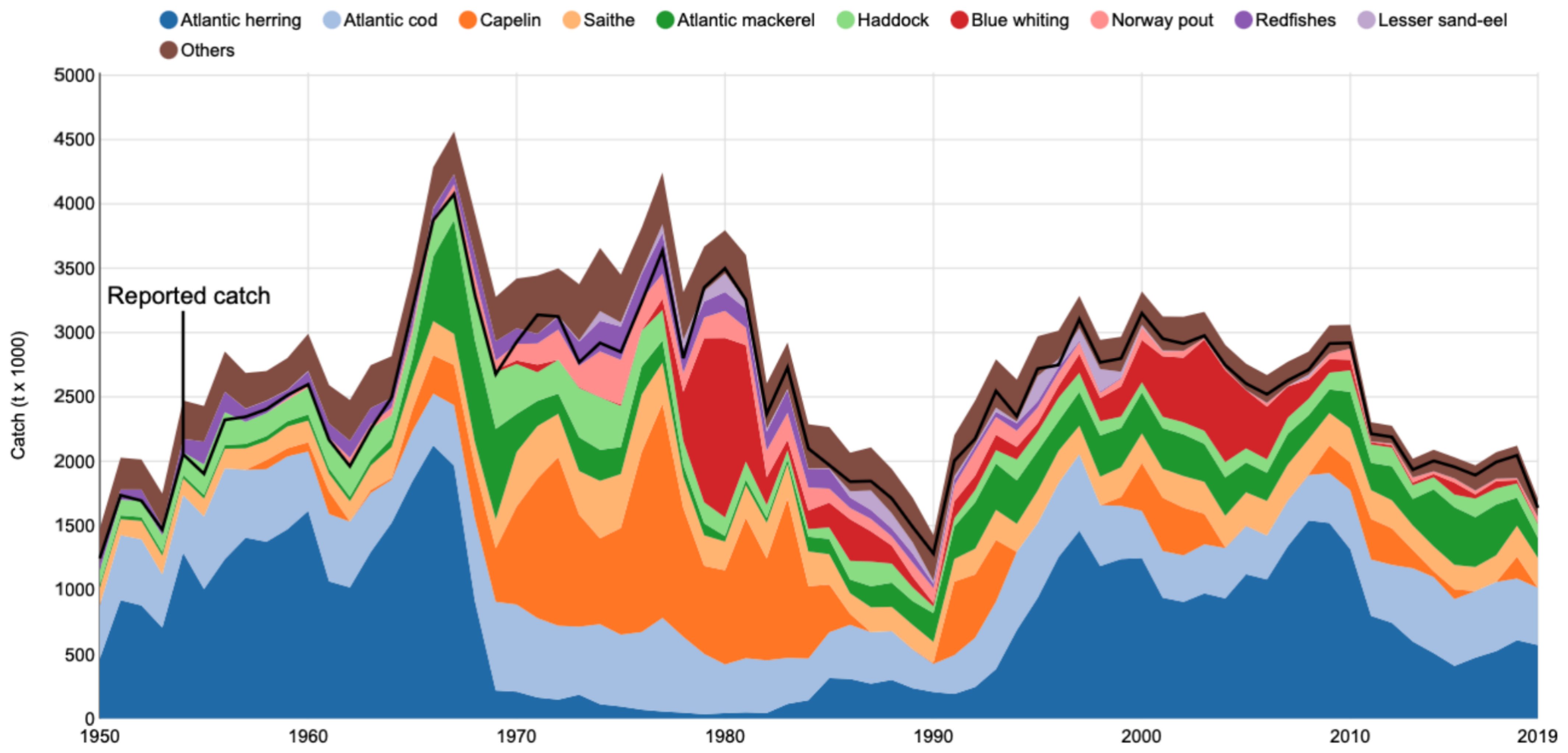
The primary dataset used in this study is obtained from the Sea Around Us platform [38], providing reconstructed fish catch estimates from 1950 to 2020. It covers various regions, exclusive economic zones, and species groups. For this study, we have selectively chosen data from the top 10 fishing nations based on their total reported catch volume over the past two decades (Table 2). Additionally, we focus on 10 major commercially significant species groups, ensuring the dataset remains representative yet computationally manageable. An example subset of the data for Norway is shown in Figure 1.

Table 2.
Statistical summary of selected fishing nations.
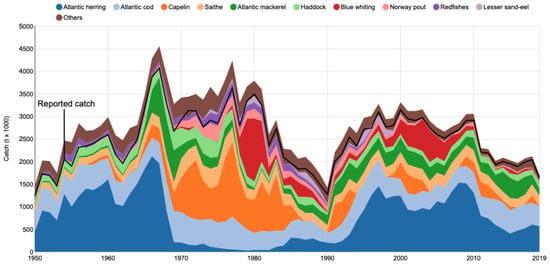
Figure 1.
Examples of Norway fishing catch data.
The selected dataset consists of approximately 3.2 million records, with annual fish catch values reported in metric tons. Each record includes attributes like country of origin, species group classification, fishing gear type, and commercial sector classification, as shown in Table 3. To enhance the predictive power by incorporating crucial environmental context, we augmented this dataset with two key annual climate indicators:

Table 3.
Summary of the dataset features used in modeling.
- Annual Oceanic Niño Index (ONI): Derived from the monthly ONI data provided by the NOAA Climate Prediction Center (CPC) [41], the ONI, based on a 3-month running mean of SST anomalies in the Niño 3.4 region (5° N–5° S, 120°–170° W), is a primary indicator for monitoring El Niño and La Niña events. We calculated the annual average ONI for each year from 1950 to 2020.
- Annual global mean sea surface temperature (SST) anomaly: This is calculated from the monthly NOAA Extended Reconstructed Sea Surface Temperature (ERSST) v5 dataset [42]. This dataset provides global gridded SST data back to 1854. We computed the global average SST anomaly for each month relative to a 1971–2000 baseline and then averaged these monthly anomalies to obtain an annual value for 1950–2020.
These climate indicators were integrated into the dataset, aligning them by year with the corresponding fish catch records.
Preprocessing steps were implemented, including aggregation, normalization of numerical features (including catch volume and climate indicators, using standardization based on training set statistics), and categorical encoding of static attributes. Missing values in historical records were handled using interpolation or zero-padding. The dataset was structured globally and for specific species groups.
3.2. Prediction Task
The objective is to develop a forecasting model capable of predicting global and species-specific fish catch volumes over multiple time horizons using historical data including catch history and climate indicators. The prediction task is framed as a multi-horizon forecasting problem, where the model utilizes past fishery data to estimate cumulative catch over three-year, five-year, and seven-year periods.
The target variable for prediction is the cumulative fish catch over predefined forecasting horizons. Given historical data up to year t, the model is required to predict the total catch for the subsequent periods: to (3-year forecast), to (5-year forecast), and to (7-year forecast). For example, when trained on data up to 2010, the model generates predictions for the cumulative catch from 2011 to 2013, 2011 to 2015, and 2011 to 2017. This approach captures short-term fluctuations, medium-term trends, and allows for longer-term strategic assessment.
The dataset is partitioned into three subsets to facilitate training, validation, and testing:
- Training set (1950–2010): Used to learn temporal patterns and model parameters.
- Validation set (2011–2015): Used for hyperparameter tuning and early stopping.
- Test set (2016–2020): Used for final evaluation of forecasting performance on unseen data.
For evaluating the 7-year forecast performance on the test set (ending in 2020), predictions starting in 2016, 2017, etc., are assessed based on the available actual data up to 2020. Specifically, the error for a 7-year forecast initiated in year (where ) is calculated over the available future steps .
3.3. Feature Engineering
To ensure the model captures essential temporal dependencies and explanatory factors, the dataset is structured into feature categories suitable for TFT:
- Static covariates: Categorical attributes that remain constant over time for each entity (time series), including the country identifier and species group classification. These are processed using embedding layers to learn meaningful representations.
- Past observed inputs: Time-dependent features observed up to the current time step t. This includes the historical fish catch volumes (target variable history) and the historical climate indicators (annual ONI, annual global SST anomaly) spanning a rolling window of 20 years (i.e., from to t).
- Future known inputs: Time-related attributes known for the entire forecast horizon ( to , where is 3, 5, or 7). In this study, this primarily includes the relative time index (e.g., 1 for the first forecast step, 2 for the second, etc.) and potentially the calendar year embedding if deemed known.
This structuring allows TFT to leverage different types of information appropriately during the encoding and decoding phases.
3.4. Evaluation Metrics
To systematically assess the performance of the forecasting models, multiple standard error metrics are employed:
- Root mean squared error (RMSE): Measures the square root of the average squared differences between predicted () and actual () values. It penalizes larger errors more heavily.
- Mean absolute error (MAE): Measures the average absolute differences between predicted and actual values, providing a linear score of the error magnitude.
- Mean absolute percentage error (MAPE): Measures the average absolute percentage difference relative to the actual value. It is scale-independent but sensitive to zero or near-zero actual values (which are avoided here due to log-transformation or handling).
Lower values for all metrics indicate better predictive accuracy. These metrics are calculated separately for the 3-year, 5-year, and 7-year cumulative forecast horizons on the test set.
4. Methodology
4.1. Temporal Fusion Transformer for Fishery Forecasting
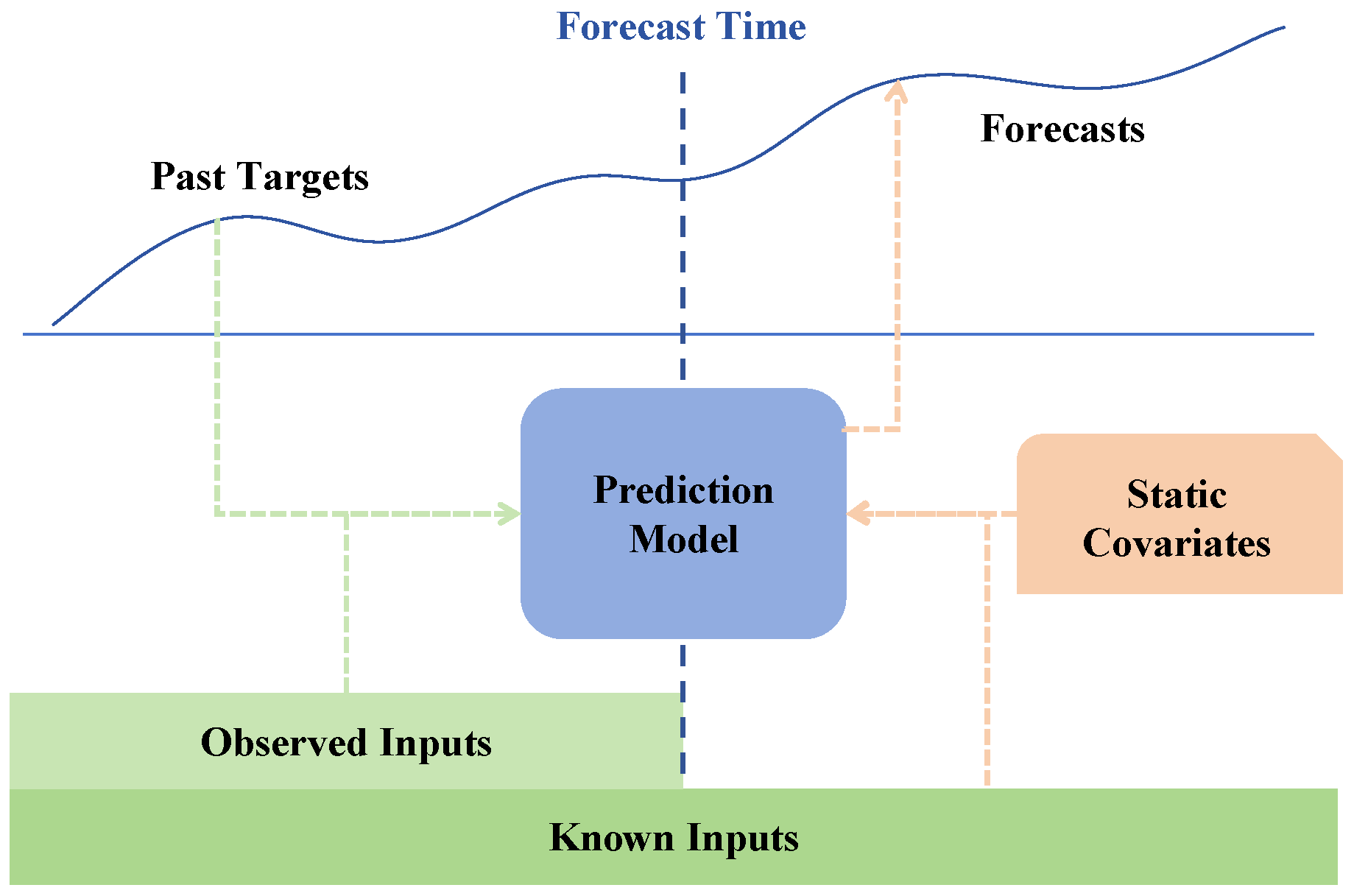
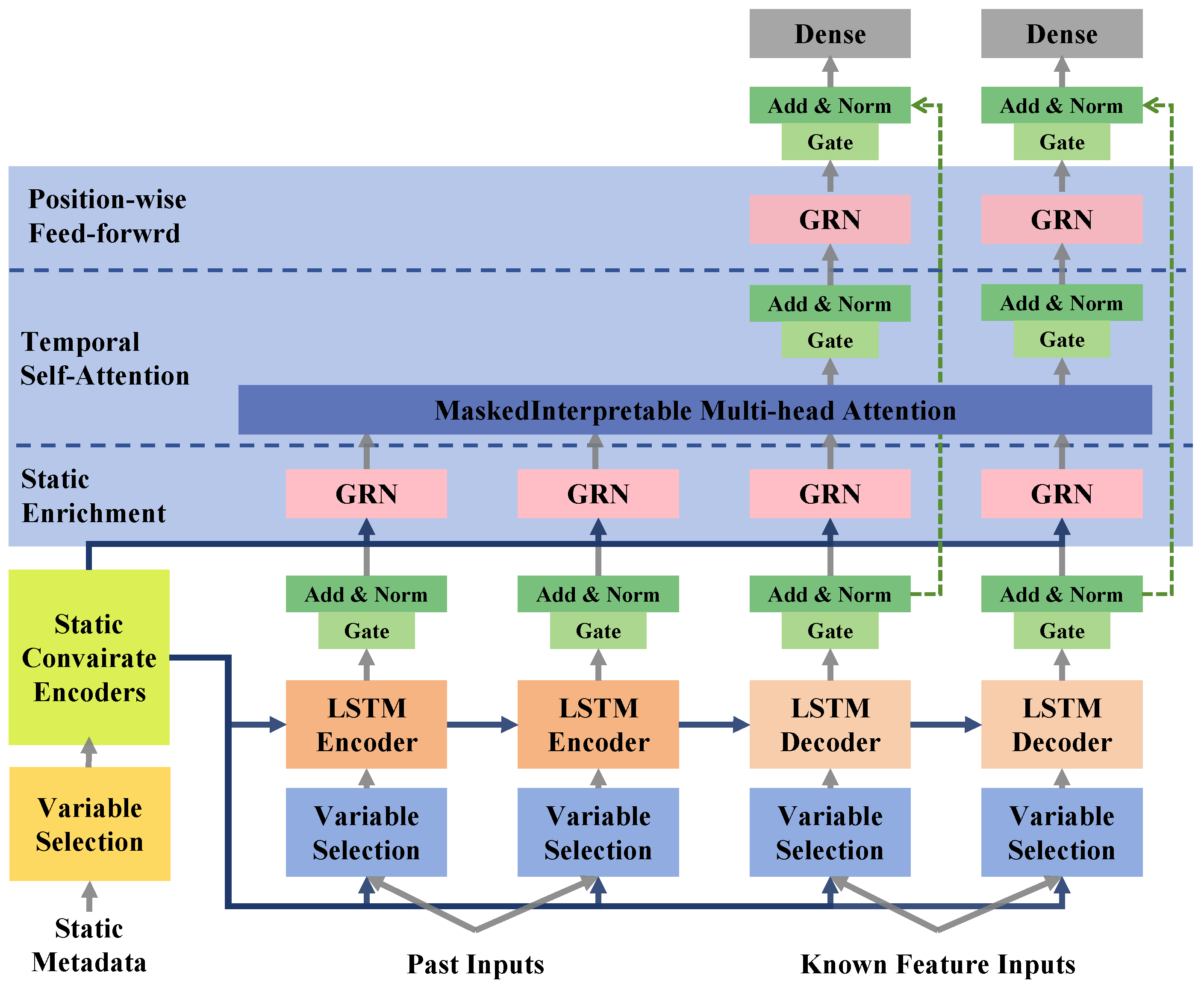
The forecasting model in this study is based on TFT [14], a state-of-the-art deep learning architecture designed specifically for multi-horizon time-series forecasting. Unlike traditional autoregressive models such as ARIMA and deep learning-based recurrent neural networks, which often struggle with long-range dependencies and multi-source feature integration, TFT effectively captures both local and long-term temporal patterns while offering interpretable insights into feature importance, as shown in Figure 2. This makes it particularly well suited for modeling fishery catch trends, which exhibit non-linear seasonal variations and long-term shifts influenced by environmental and regulatory factors, as shown in Figure 3.
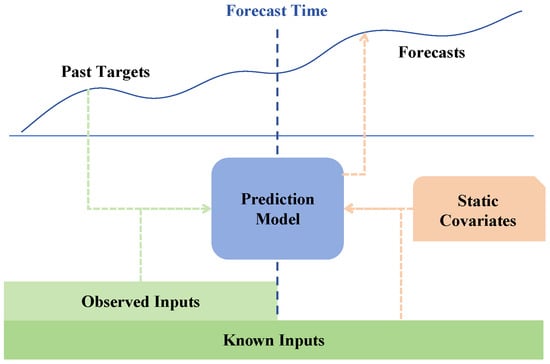
Figure 2.
Illustration of multi-horizon forecasting.
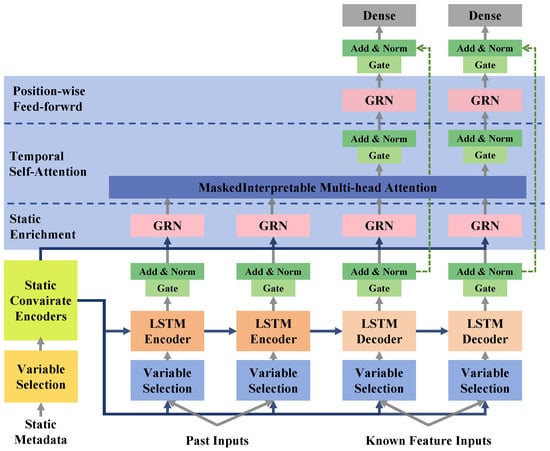
Figure 3.
Illustration of Temporal Fusion Transformer model architecture.
Given a historical time series of observed fishery catches spanning T years, along with known future covariates for a forecasting horizon , the objective is to predict the target sequence . Mathematically, the forecasting process is represented as
where s represents static covariates such as country identifiers and species classifications. The TFT processes these inputs through a series of specialized network modules that enhance predictive performance while preserving interpretability.
The first key component of TFT is the variable selection network, which dynamically assigns importance weights to input features at each time step, enabling the model to filter out irrelevant information and reduce noise. Given an input vector at time step t, the importance score for each feature is computed as
where and b are learnable parameters. The selected features are then propagated to the main processing layers.
The core temporal modeling is handled by an LSTM-based encoder–decoder module. The encoder compresses historical fishery catch data into a latent representation by sequentially updating a hidden state through the recurrence relation
where denotes a non-linear activation function such as the hyperbolic tangent. The decoder then reconstructs future values by leveraging these encoded states and the known future covariates.
To capture long-term dependencies, TFT incorporates an interpretable multi-head attention layer. This module allows the model to focus on different past time steps when making predictions for future values. The attention scores are computed as
where , and V represent the query, key, and value matrices, respectively, and is a scaling factor. This mechanism ensures that the model learns significant historical patterns that influence future trends.
TFT also integrates static covariate encoders to transform categorical features, such as country and species IDs, into dense embeddings. These embeddings are then incorporated into the temporal processing layers to contextualize predictions. Additionally, gating mechanisms and skip connections are employed throughout the network to prevent overfitting by allowing selective information flow through different layers. The gating function is defined as
where z acts as a dynamic filter that determines how much information from previous layers should be retained.
4.2. Adaptation of TFT for Fishery Catch Prediction
The TFT model is adapted to predict global fishery catch by structuring its inputs and outputs according to the dataset characteristics. The input sequence length (look-back window) is set to 20 years, allowing the capture of long-term trends in both catch and climate patterns. Zero-padding handles records with fewer than 20 years of history. The forecasting task involves predicting cumulative catch for three-year, five-year, and seven-year horizons.
The input features are categorized as described in Section 3.3:
- Past observed inputs include the sequence of normalized annual fish catch volumes and the sequences of normalized annual ONI and annual global SST anomaly over the preceding 20 years.
- Future known inputs primarily consist of the relative time indices for the forecast steps (1 to 3, 1 to 5, or 1 to 7).
- Static attributes are the embedded country and species group identifiers.
The model produces quantile predictions for each future time step (, …, ). For point forecasts (used in RMSE, MAE, MAPE evaluation), the median prediction (quantile ) is used. The cumulative forecast for a horizon H (where ) is computed by summing the median point forecasts for the individual steps within that horizon:
4.3. Loss Function and Evaluation Metrics
The primary loss function used to train TFT is the mean squared error (MSE), which minimizes the squared differences between predicted and actual cumulative fishery catch values. Additionally, the root mean squared error (RMSE) is employed as a performance metric to provide a more interpretable measure of the prediction error magnitude.
To account for uncertainty in forecasting, the model is also trained using the quantile loss function at the 50th and 90th percentiles. The quantile loss is defined as
where denotes the quantile level, such as for median estimation or for upper-bound predictions.
5. Experiments
5.1. Data Preparation and Preprocessing
The dataset, sourced from Sea Around Us and augmented with annual ONI and global SST anomaly data, covers global fishery catch records from 1950 to 2020. Preprocessing involved handling missing values (linear interpolation or zero-padding), aggregating data where necessary, and feature scaling. Numerical features, including the target variable (fish catch volume) and the climate indicators (ONI, SST anomaly), were transformed using to reduce skewness and then standardized by subtracting the mean and dividing by the standard deviation, with parameters derived solely from the training set (1950–2010). Categorical features (country, species) were encoded. The data were structured for input into the time-series models, with temporal partitioning into training (1950–2010), validation (2011–2015), and test (2016–2020) sets.
5.2. Baseline Models for Comparison
To rigorously evaluate the TFT model’s effectiveness, five diverse baseline methods were implemented and evaluated on the same dataset:
- ARIMA (Autoregressive Integrated Moving Average): Where applicable, exogenous climate variables (ONI, SST) were included, effectively creating an ARIMAX model. Models were fitted independently for each country–species time series.
- MLP (Multi-layer Perceptron): A feedforward neural network with two hidden layers (ReLU activation) using a flattened sequence of the past 20 years of catch and climate data as input features to directly predict the cumulative catch for each horizon (3, 5, 7 years).
- LSTM (Long Short-Term Memory) network: A standard two-layer LSTM network processing sequences of the past 20 years of catch and climate data to forecast future steps, from which cumulative values were derived.
- TCN (Temporal Convolutional Network): Implemented using stacked dilated causal convolutional layers to capture temporal dependencies from the 20-year input sequences of catch and climate data.
- XGBoost: An optimized gradient boosting decision tree model. Input features included lagged values of catch and climate data, rolling window statistics, and encoded static features.
The primary model evaluated was the Temporal Fusion Transformer (TFT) [14], configured as described in Section 4 to leverage static, past observed (catch, ONI, SST), and future known (time index) inputs.
5.3. Hyperparameter Configuration and Training Strategy
The model hyperparameters were tuned based on performance (minimizing RMSE on the 5-year forecast) on the validation set (2011–2015). Key parameters for TFT included the follwing: hidden state size of 64; two attention heads; dropout rate of 0.2; and batch size of 128. For the LSTM and TCN, hidden layer sizes/filter numbers and layer counts were tuned. For the MLP, the hidden layer dimensions were optimized. For XGBoost, parameters like tree depth, number of estimators, and learning rate were tuned using grid search or randomized search. All neural network models (TFT, LSTM, TCN, MLP) were trained using the Adam optimizer with an initial learning rate of 0.001 and employed the quantile loss (quantiles: 0.1, 0.5, 0.9). Training proceeded for a maximum of 100 epochs, utilizing early stopping with a patience of 10 epochs based on validation loss to prevent overfitting. Each model was trained and evaluated three times using different random seeds to ensure robustness of the results; the average performance across these runs is reported.
6. Results and Analysis
This section presents an empirical evaluation of the Temporal Fusion Transformer model against the selected baselines across different forecasting horizons (3, 5, and 7 years). All models were trained and evaluated using the dataset enriched with historical catch data and the annual ONI and global SST anomaly climate indicators.
6.1. Overall Prediction Accuracy
The comparative forecasting performance of all evaluated models on the test set (2016–2020) is detailed in Table 4. The results across the RMSE, MAE, and MAPE metrics reveal that while performance varies by horizon and metric, the Temporal Fusion Transformer consistently demonstrates robust and often superior accuracy, particularly for the extended 7-year forecast.

Table 4.
Overall prediction performance comparison.
For the 7-year horizon, TFT achieves the lowest error across all metrics, recording an RMSE of 2.18, MAE of 1.71, and MAPE of 13.7%. This marks a clear advantage over the next best models at this horizon, LSTM (MAPE 15.1%) and TCN (MAPE 15.4%). The relative MAPE improvement of TFT over LSTM at 7 years is approximately 9.3%. This superior long-term performance underscores TFT’s capability in capturing enduring temporal dependencies potentially modulated by multi-year climate cycles present in the input data.
At the 5-year horizon, TFT also leads in overall performance, achieving the lowest RMSE (1.94), MAE (1.49), and MAPE (12.0%). For the 3-year horizon, the competition is closer; while LSTM achieves a slightly lower MAPE (9.6% vs. TFT’s 9.7%), TFT secures the best RMSE (1.60) and MAE (1.22), indicating high accuracy even in the shorter term.
When compared against the strong non-recurrent baselines, TFT maintains its lead. Its 7-year MAPE of 13.7% is considerably better than XGBoost’s 16.5% and TCN’s 15.4%. This suggests that TFT’s architecture, specifically designed for multi-horizon forecasting with heterogeneous inputs and attention mechanisms, effectively leverages the combined information from catch history, climate signals, and static attributes more efficiently than these alternative approaches for this specific task.
As expected, the traditional ARIMA model and the simpler MLP architecture exhibit significantly higher errors, especially as the forecast horizon lengthens. This reflects their inherent limitations in modeling the complex non-linear dynamics and diverse data types characterizing global fisheries.
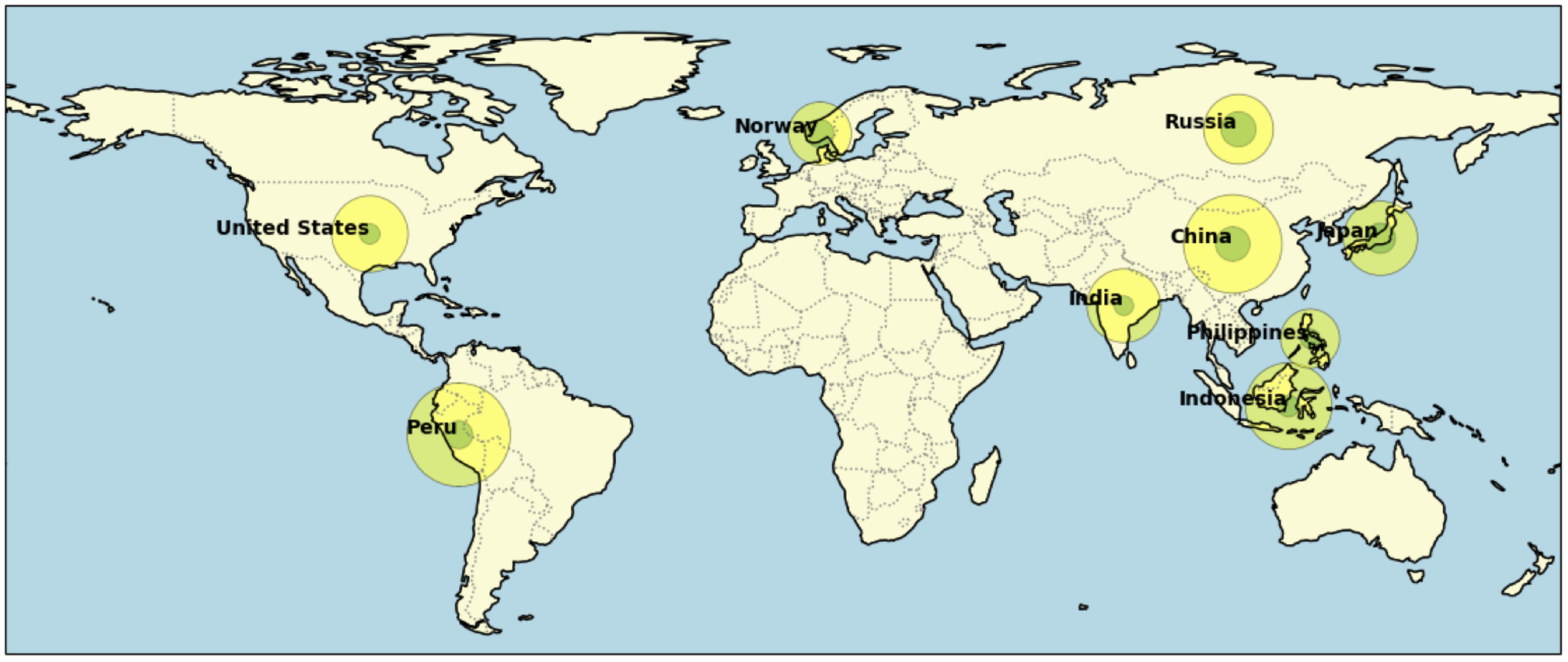
Figure 4 provides a visualization of the spatial distribution of prediction errors derived from the TFT model’s 5-year forecasts. It highlights geographical variations in predictability, with larger errors often coinciding with regions known for highly variable fish stocks or those particularly sensitive to large-scale climate events.
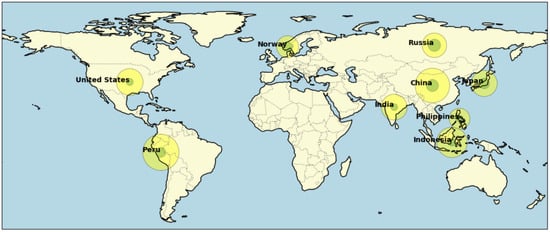
Figure 4.
Global prediction error visualization based on the TFT model’s 5-year forecast. Yellow circles demonstrate total fish catch; green circles demonstrate the prediction error.
6.2. Prediction Performance at Species Level
Table 5 illustrates the TFT model’s forecasting accuracy for ten commercially important fish species across the 3-, 5-, and 7-year horizons. The results highlight substantial heterogeneity in predictability among different species groups. This variation likely stems from a combination of factors, including species-specific life history traits, differing sensitivities to environmental fluctuations captured by the ONI and SST inputs, varying fishing pressures, and data quality differences.

Table 5.
TFT model prediction performance for 10 common fish species.
For instance, Atlantic herring maintains relatively high predictability, exhibiting the lowest 7-year MAPE among the group at 10.8%. This suggests its population dynamics within the studied period might be more stable or better explained by the model’s input features. Conversely, cephalopods consistently show higher prediction errors, reaching a 7-year MAPE of 14.2%. This aligns with the known rapid turnover and high sensitivity of many cephalopod populations to oceanographic conditions, making them inherently more challenging to forecast accurately, even with climate data included. Other species like anchovy and cod also show relatively higher errors over longer horizons, possibly linked to recruitment variability and strong ENSO influences (for anchovy) or complex stock dynamics and historical fishing impacts (for cod).
6.3. Model Interpretation and Feature Importance
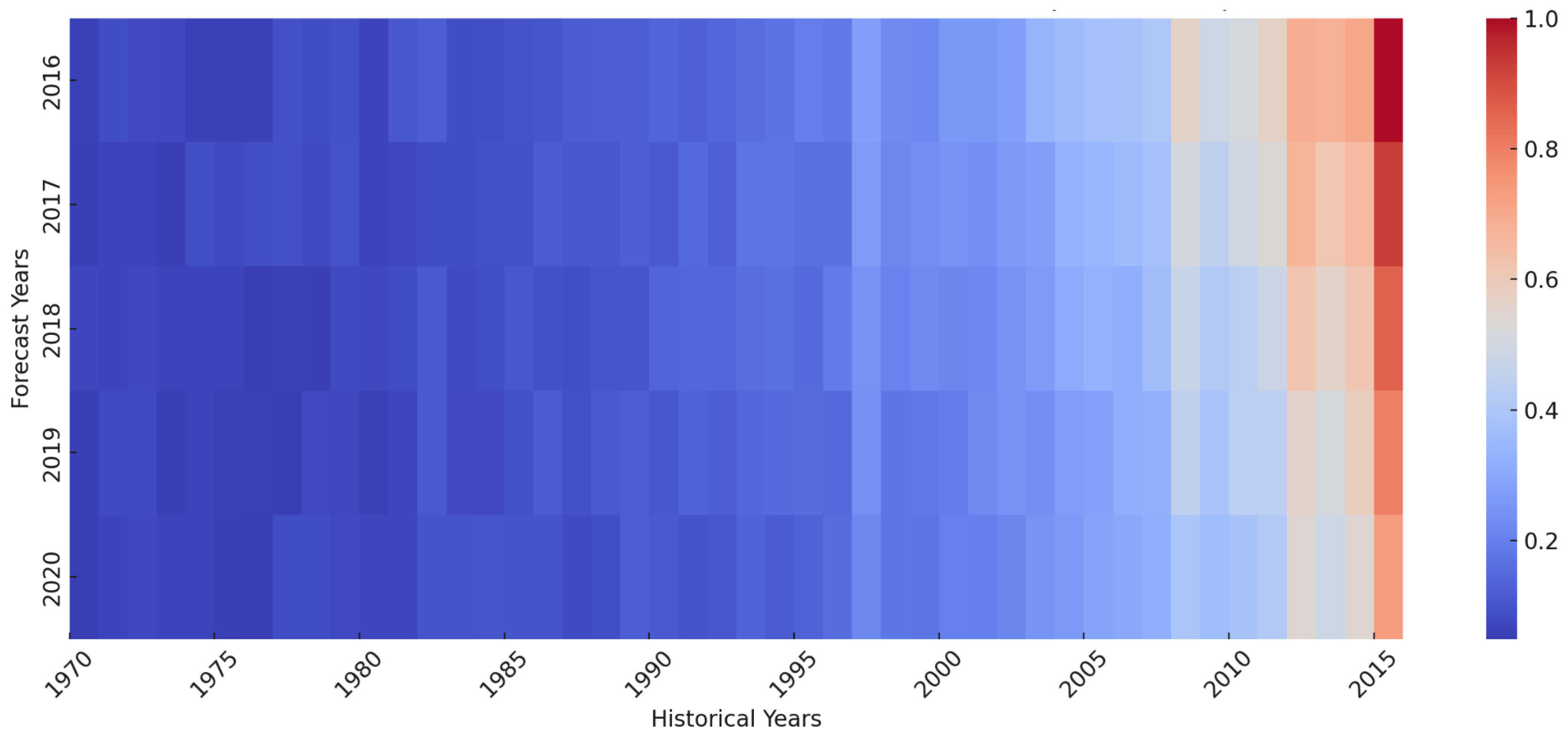
Understanding the key drivers behind the forecasts is essential. TFT’s variable selection network (VSN) provides quantitative insights by assigning importance scores to each input feature, averaged over time steps and forecast horizons, as shown in Figure 5.
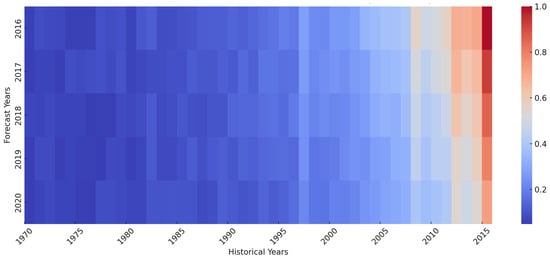
Figure 5.
TFT model attention distribution over historical data.
Table 6 displays the feature importance ranking from the trained TFT model. As anticipated, the most recent historical catch volume (past 1-year fish catch) remains the most influential feature, with an importance score of 0.31, reflecting the strong autoregressive nature of fisheries data. However, the integrated climate indicators demonstrate substantial predictive power. The annual ONI Index ranks as the third most important feature with a score of 0.15, confirming the substantial influence of ENSO patterns on global fisheries, as captured by the model. The annual global SST anomaly also contributes notably, ranking fifth with a score of 0.10.

Table 6.
Feature importance ranking from TFT variable selection network.
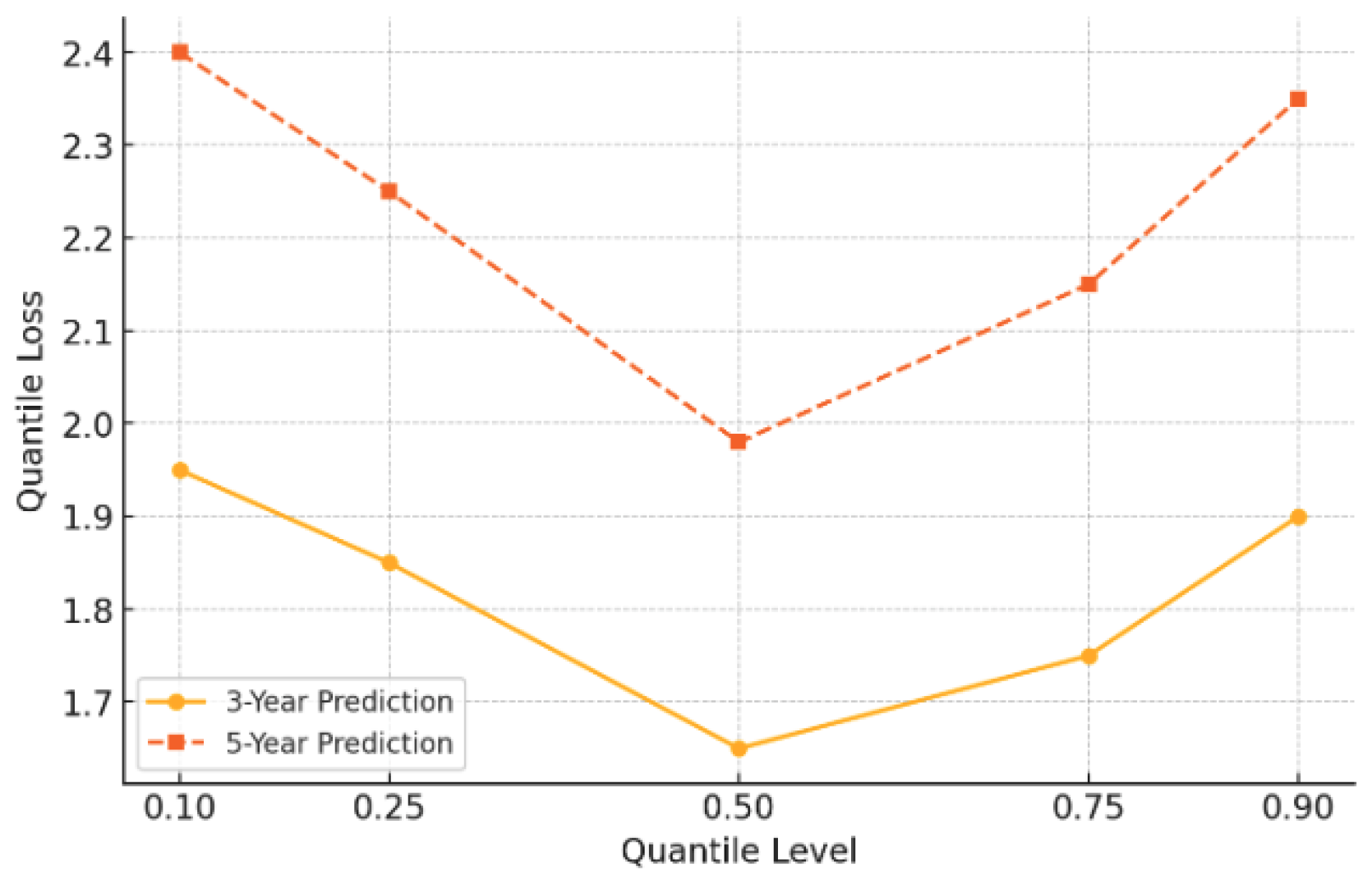
Together, these two climate variables account for 25% of the total feature importance, clearly demonstrating their value in complementing the information derived purely from historical catch trends (1-year and 3-year average catch combine for 46% importance). Temporal context (year embedding, 12%) and static attributes differentiating entities (country ID, 9%; species group ID, 8%) also contribute meaningfully. This analysis quantitatively validates the benefit of incorporating environmental context into the forecasting model, allowing it to capture dynamics beyond simple historical extrapolation, as shown in Figure 6.
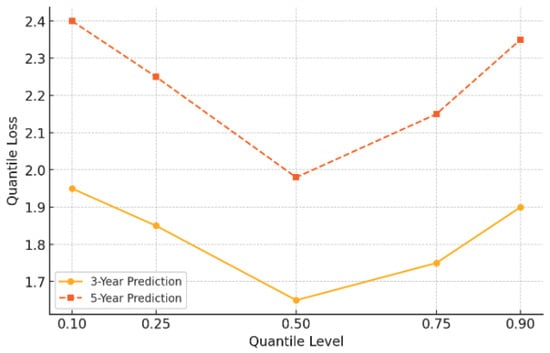
Figure 6.
Quantile loss across different prediction horizons.
6.4. Ablation Study
To dissect the contribution of different architectural components within the TFT model, an ablation study was performed. Key modules were systematically removed, and the model was retrained and evaluated. The results, shown in Table 7, quantify the impact of each component on the forecasting accuracy across the three horizons.

Table 7.
Ablation study results for the TFT model.
The most substantial performance degradation occurs when temporal covariates are removed (7-year RMSE increases by 0.32 from 2.18 to 2.50). This component group includes the time index and, crucially, the ONI and SST climate variables, highlighting the vital role of incorporating both sequential context and external environmental drivers for effective prediction. The exclusion of static embeddings (country, species identifiers) also significantly impacts performance (7-year RMSE rises to 2.38), confirming that entity-specific information provides essential context for the model.
Omitting the multi-head attention mechanism or the variable selection network leads to smaller, yet consistent, performance degradation. For example, removing attention increases the 7-year RMSE to 2.27. This indicates that while the core temporal processing (LSTM layers) and context integration (static/temporal covariates) are paramount, the attention mechanism effectively helps the model focus on relevant long-range historical patterns, and variable selection aids in filtering input features, both contributing positively to the final accuracy.
6.5. Sensitivity Analysis
Two sensitivity analyses were conducted on the final TFT model configuration to examine its robustness concerning the temporal granularity of the input data and the length of the historical input sequence (look-back window).
Table 8 shows the impact of aggregating the input data annually, quarterly, or monthly. The results show that quarterly aggregation yields slightly superior performance compared to annual aggregation across most metrics and horizons, achieving a 7-year RMSE of 2.14 versus 2.18 for annual data. This suggests that capturing some sub-annual dynamics offers a small benefit. However, using monthly data significantly degrades performance (7-year RMSE 2.42), likely because the increased noise outweighs any potential signal gain at this aggregation level for multi-year forecasting.

Table 8.
Impact of temporal granularity on TFT model’s performance.
Table 9 assesses the impact of varying the input sequence length from 5 to 25 years. The analysis confirms that employing a 20-year look-back window provides the optimal balance for prediction accuracy, yielding the lowest errors across the board (7-year RMSE: 2.18). Using substantially shorter histories (5 or 10 years) markedly reduces performance, demonstrating the importance of capturing long-term dependencies and historical context, which includes multi-year climate patterns. Extending the history to 25 years provides no further significant improvement, indicating diminishing returns from incorporating data beyond two decades for predicting up to 7 years ahead in this context.

Table 9.
Sensitivity Analysis on Input Sequence Length for TFT Model.
7. Conclusions
This study presented a comprehensive framework and empirical evaluation of the Temporal Fusion Transformer for multi-horizon global fish catch forecasting, demonstrating its effectiveness when integrating historical catch data with key climate indicators. By leveraging the extensive Sea Around Us database augmented with environmental context, the TFT model successfully predicted fishery trends over three-year, five-year, and notably, extended seven-year horizons.
Our experiments showed that TFT consistently delivered highly accurate predictions. It outperformed a diverse set of benchmark models including ARIMA, MLP, LSTM, TCN, and XGBoost, particularly on the challenging 7-year forecast horizon, where it achieved the lowest error (MAPE of 13.7%). This result highlights TFT’s superior capability in handling long-range dependencies and effectively fusing heterogeneous information sources compared to other architectures.
The model’s built-in interpretability provided valuable insights, quantifying the significant predictive power of the incorporated climate signals. The ENSO indicator and global SST anomaly collectively accounted for 25% of the feature importance, confirming their crucial role alongside historical catch trends in driving forecast outcomes. Ablation studies further validated the importance of both temporal context and static entity information, while sensitivity analyses confirmed the choice of quarterly aggregation and a 20-year look-back window as near-optimal for this application.
Despite the promising results, limitations remain. The use of global climate indices, while informative, might mask important regional environmental variations impacting specific fisheries. The study focused only on ONI and SST, neglecting other potential climate modes or ecological drivers (e.g., primary productivity, ocean currents). Furthermore, the evaluation of the 7-year forecast was necessarily limited by the available data endpoint (2020).
Future research should aim to incorporate higher-resolution regional climate and oceanographic data to potentially improve predictions for specific stocks. Exploring additional environmental drivers and socio-economic factors could further enhance model realism. Applying this framework to specific fishery management scenarios, such as evaluating adaptive quota setting under different climate projections, would demonstrate its practical utility. Overall, this research underscores the potential of advanced, interpretable deep learning models like TFT, when appropriately contextualized with environmental data, to significantly improve our ability to forecast complex ecological systems like global fisheries over meaningful short-to-long-term planning horizons relevant for sustainable management.
Author Contributions
Conceptualization, J.S. and P.H.; methodology, P.Q.; software, P.Q.; validation, J.S., P.Q., and P.H.; formal analysis, P.Q.; investigation, J.S.; data curation, P.Q.; writing—original draft preparation, J.S.; writing—review and editing, P.H. and R.Z.; visualization, J.S.; supervision, P.H. and R.Z.; project administration, P.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable, as this study did not involve humans.
Data Availability Statement
The historical fish catch data presented in this study are openly available from the Sea Around Us database at https://www.seaaroundus.org/ (accessed on 31 March 2025). The Oceanic Niño Index data are available from the NOAA Climate Prediction Center at https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 31 March 2025). The Extended Reconstructed Sea Surface Temperature v5 data are available from the NOAA National Centers for Environmental Information at https://www.ncei.noaa.gov/products/extended-reconstructed-sst (accessed on 31 March 2025). The processed dataset and analysis code used in this study are available upon reasonable request from the corresponding author.
Acknowledgments
The authors would like to thank the Sea Around Us project for providing comprehensive fisheries data. We also thank the NOAA Climate Prediction Center and the NOAA National Centers for Environmental Information for making the ONI and ERSSTv5 climate data publicly available. The authors also thank their colleagues at Beijing Technology and Business University for their valuable suggestions and support throughout this research. The authors would also like to express their gratitude to the anonymous reviewers for their valuable feedback, which proved instrumental in enhancing the quality of the final version of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jennings, S.; Stentiford, G.D.; Leocadio, A.M.; Jeffery, K.R.; Metcalfe, J.D.; Katsiadaki, I.; Auchterlonie, N.A.; Mangi, S.C.; Pinnegar, J.K.; Ellis, T.; et al. Aquatic food security: Insights into challenges and solutions from an analysis of interactions between fisheries, aquaculture, food safety, human health, fish and human welfare, economy and environment. Fish Fish. 2016, 17, 893–938. [Google Scholar] [CrossRef]
- Mandal, A.; Ghosh, A.R. Role of artificial intelligence (AI) in fish growth and health status monitoring: A review on sustainable aquaculture. Aquac. Int. 2024, 32, 2791–2820. [Google Scholar] [CrossRef]
- Tang, C.; Ji, J.; Lin, Q.; Zhou, Y. Evolutionary neural architecture design of liquid state machine for image classification. In Proceedings of the ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 91–95. [Google Scholar]
- Lam, V.W.; Allison, E.H.; Bell, J.D.; Blythe, J.; Cheung, W.W.; Frölicher, T.L.; Gasalla, M.A.; Sumaila, U.R. Climate change, tropical fisheries and prospects for sustainable development. Nat. Rev. Earth Environ. 2020, 1, 440–454. [Google Scholar] [CrossRef]
- Hobday, A.J.; Spillman, C.M.; Paige Eveson, J.; Hartog, J.R. Seasonal forecasting for decision support in marine fisheries and aquaculture. Fish. Oceanogr. 2016, 25, 45–56. [Google Scholar] [CrossRef]
- Gambín, Á.F.; Angelats, E.; González, J.S.; Miozzo, M.; Dini, P. Sustainable marine ecosystems: Deep learning for water quality assessment and forecasting. IEEE Access 2021, 9, 121344–121365. [Google Scholar] [CrossRef]
- Anuja, A.; Yadav, V.; Bharti, V.; Kumar, N. Trends in marine fish production in Tamil Nadu using regression and autoregressive integrated moving average (ARIMA) model. J. Appl. Nat. Sci. 2017, 9, 653–657. [Google Scholar] [CrossRef]
- Chen, J.; Cui, Y.; Zhang, X.; Yang, J.; Zhou, M. Temporal Convolutional Network for Carbon Tax Projection: A Data-Driven Approach. Appl. Sci. 2024, 14, 9213. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, D.; Zhang, Y.; Zhao, G.; Xie, Y.; Jiang, H. Advancements and Challenges in Deep Learning-Driven Marine Data Assimilation: A Comprehensive Review. Comput. Res. Prog. Appl. Sci. Eng 2023, 9, 1–17. [Google Scholar] [CrossRef]
- Farah, S.; Humaira, N.; Aneela, Z.; Steffen, E. Short-term multi-hour ahead country-wide wind power prediction for Germany using gated recurrent unit deep learning. Renew. Sustain. Energy Rev. 2022, 167, 112700. [Google Scholar] [CrossRef]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent neural networks: A comprehensive review of architectures, variants, and applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, M.; Li, T.; Wang, H.; Li, C. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks for action segmentation and detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Fayer, G.; Lima, L.; Miranda, F.; Santos, J.; Campos, R.; Bignoto, V.; Andrade, M.; Moraes, M.; Ribeiro, C.; Capriles, P.; et al. A temporal fusion transformer deep learning model for long-term streamflow forecasting: A case study in the funil reservoir, Southeast Brazil. Knowl.-Based Eng. Sci. 2023, 4, 73–88. [Google Scholar]
- Jitha, P.; Vijaya, M. Temporal fusion transformer: A deep learning approach for modeling and forecasting river water quality index. Int. J. Intell. Syst. Appl. Eng. 2023, 11, 277–293. [Google Scholar]
- Joseph, S.; Jo, A.A.; Raj, E.D. Improving Time Series Forecasting Accuracy with Transformers: A Comprehensive Analysis with Explainability. In Proceedings of the 2024 Third International Conference on Electrical, Electronics, Information and Communication Technologies (ICEEICT), Tamil Nadu, India, 24–26 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–7. [Google Scholar]
- Rühmann, S.; Leible, S.; Lewandowski, T. Interpretable Bike-Sharing Activity Prediction with a Temporal Fusion Transformer to Unveil Influential Factors: A Case Study in Hamburg, Germany. Sustainability 2024, 16, 3230. [Google Scholar] [CrossRef]
- Kaur, G.; Adhikari, N.; Krishnapriya, S.; Wawale, S.G.; Malik, R.; Zamani, A.S.; Perez-Falcon, J.; Osei-Owusu, J. Recent advancements in deep learning frameworks for precision fish farming opportunities, challenges, and applications. J. Food Qual. 2023, 2023, 4399512. [Google Scholar] [CrossRef]
- Gladju, J.; Kamalam, B.S.; Kanagaraj, A. Applications of data mining and machine learning framework in aquaculture and fisheries: A review. Smart Agric. Technol. 2022, 2, 100061. [Google Scholar] [CrossRef]
- Raman, R.; Mohanty, S.; Bhatta, K.; Karna, S.; Sahoo, A.; Mohanty, B.; Das, B. Time series forecasting model for fisheries in Chilika lagoon (a Ramsar site, 1981), Odisha, India: A case study. Wetl. Ecol. Manag. 2018, 26, 677–687. [Google Scholar] [CrossRef]
- Raman, R.K.; Das, B.K. Forecasting shrimp and fish catch in chilika lake over time series analysis. In Time Series Analysis-Data, Methods, and Applications; IntechOpen: London, UK, 2019. [Google Scholar]
- Bakit, J.; Álvarez, G.; Díaz, P.A.; Uribe, E.; Sfeir, R.; Villasante, S.; Bas, T.G.; Lira, G.; Pérez, H.; Hurtado, A.; et al. Disentangling environmental, economic, and technological factors driving scallop (Argopecten purpuratus) aquaculture in Chile. Fishes 2022, 7, 380. [Google Scholar] [CrossRef]
- Livieris, I.E. A novel forecasting strategy for improving the performance of deep learning models. Expert Syst. Appl. 2023, 230, 120632. [Google Scholar] [CrossRef]
- Ho, S.L.; Xie, M. The use of ARIMA models for reliability forecasting and analysis. Comput. Ind. Eng. 1998, 35, 213–216. [Google Scholar] [CrossRef]
- Dubey, A.K.; Kumar, A.; García-Díaz, V.; Sharma, A.K.; Kanhaiya, K. Study and analysis of SARIMA and LSTM in forecasting time series data. Sustain. Energy Technol. Assess. 2021, 47, 101474. [Google Scholar]
- Qin, D. Rise of VAR modelling approach. J. Econ. Surv. 2011, 25, 156–174. [Google Scholar] [CrossRef]
- Maunder, M.N.; Thorson, J.T. Modeling temporal variation in recruitment in fisheries stock assessment: A review of theory and practice. Fish. Res. 2019, 217, 71–86. [Google Scholar] [CrossRef]
- Msangi, S.; Kobayashi, M.; Batka, M.; Vannuccini, S.; Dey, M.M.; Anderson, J.L.; Kelleher, K.; Singh, K.; Brummet, R. Fish to 2030: Prospects for Fisheries and Aquaculture; World Bank Group: Washington, DC, USA, 2013. [Google Scholar]
- Patterson, K.; Cook, R.; Darby, C.; Gavaris, S.; Kell, L.; Lewy, P.; Mesnil, B.; Punt, A.; Restrepo, V.; Skagen, D.W.; et al. Estimating uncertainty in fish stock assessment and forecasting. Fish Fish. 2001, 2, 125–157. [Google Scholar] [CrossRef]
- Kheimi, M.; Almadani, M.; Zounemat-Kermani, M. Stochastic (S[ARIMA]), shallow (NARnet, NAR-GMDH, OS-ELM), and deep learning (LSTM, Stacked-LSTM, CNN-GRU) models, application to river flow forecasting. Acta Geophys. 2024, 72, 2679–2693. [Google Scholar] [CrossRef]
- Zhao, Q.; Peng, S.; Wang, J.; Li, S.; Hou, Z.; Zhong, G. Applications of deep learning in physical oceanography: A comprehensive review. Front. Mar. Sci. 2024, 11, 1396322. [Google Scholar] [CrossRef]
- Zhang, Z.; Meng, L.; Gu, Y. SageFormer: Series-Aware Framework for Long-Term Multivariate Time Series Forecasting. IEEE Internet Things J. 2024, 11, 18435–18448. [Google Scholar] [CrossRef]
- Tang, C.; Song, S.; Ji, J.; Tang, Y.; Tang, Z.; Todo, Y. A cuckoo search algorithm with scale-free population topology. Expert Syst. Appl. 2022, 188, 116049. [Google Scholar] [CrossRef]
- Song, Z.; Tang, C.; Song, S.; Tang, Y.; Li, J.; Ji, J. A complex network-based firefly algorithm for numerical optimization and time series forecasting. Appl. Soft Comput. 2023, 137, 110158. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W. Deep Time Series Forecasting Models: A Comprehensive Survey. Mathematics 2024, 12, 1504. [Google Scholar] [CrossRef]
- Wang, S.; Lin, Y.; Jia, Y.; Sun, J.; Yang, Z. Unveiling the multi-dimensional spatio-temporal fusion transformer (MDSTFT): A revolutionary deep learning framework for enhanced multi-variate time series forecasting. IEEE Access 2024, 12, 115895–115904. [Google Scholar] [CrossRef]
- Sea Around Us. Sea Around Us. Fish. Cent. Res. Rep. 2020, 28, 9. [Google Scholar]
- Schwing, F.B. Modern technologies and integrated observing systems are “instrumental” to fisheries oceanography: A brief history of ocean data collection. Fish. Oceanogr. 2023, 32, 28–69. [Google Scholar] [CrossRef]
- Temple, A.J.; Skerritt, D.J.; Howarth, P.E.; Pearce, J.; Mangi, S.C. Illegal, unregulated and unreported fishing impacts: A systematic review of evidence and proposed future agenda. Mar. Policy 2022, 139, 105033. [Google Scholar] [CrossRef]
- Western Regional Climate Center; Hydrometeorological Prediction Center; Environmental Modeling Center. National Oceanic and Atmospheric Administration (NOAA). 2003. Available online: https://www.noaa.gov/ (accessed on 31 March 2025).
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.M. NOAA Extended Reconstructed Sea Surface Temperature (ERSST), Version 5; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).