Oscillation Criteria for Delay Difference Equations with Continuous Time, Piecewise Linear Delay Functions, and Oscillatory Coefficients
Abstract
1. Introduction
2. The New Oscillation Criteria
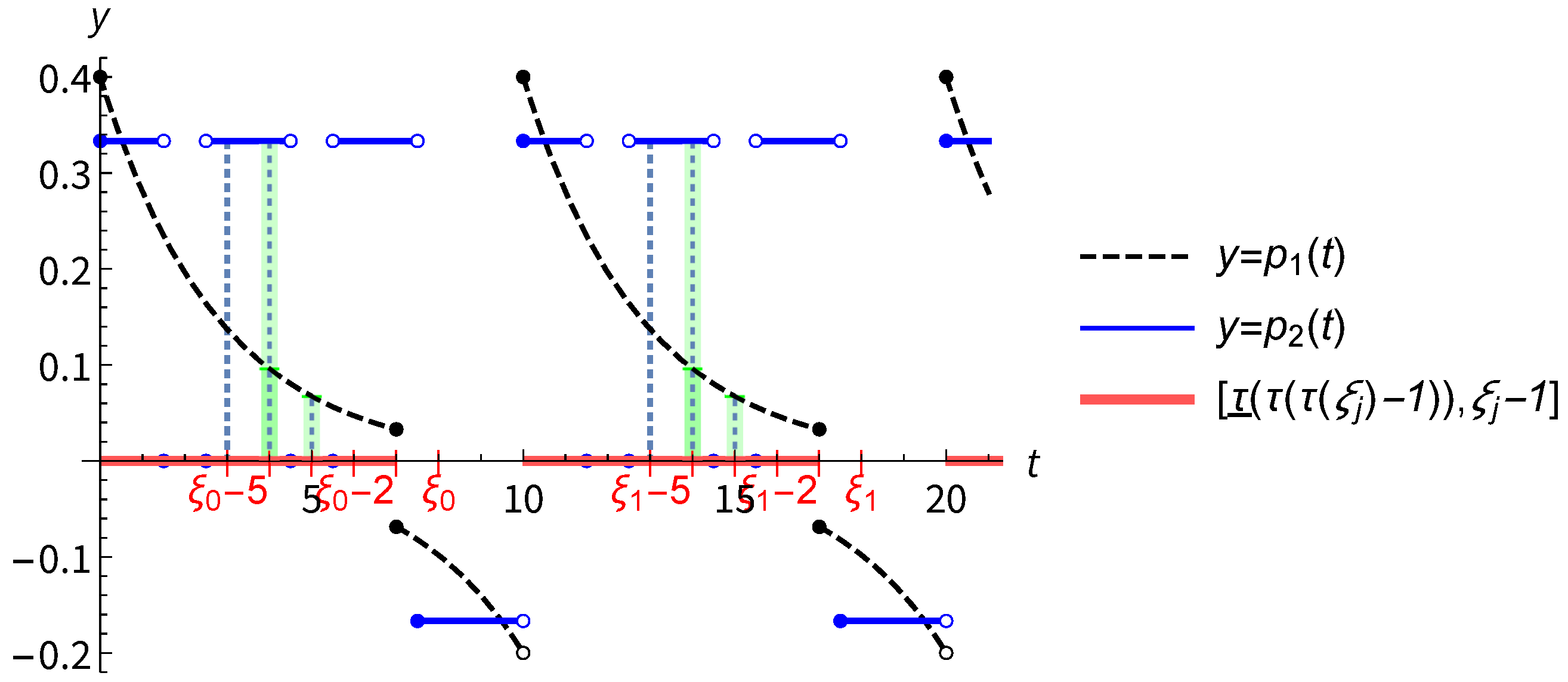
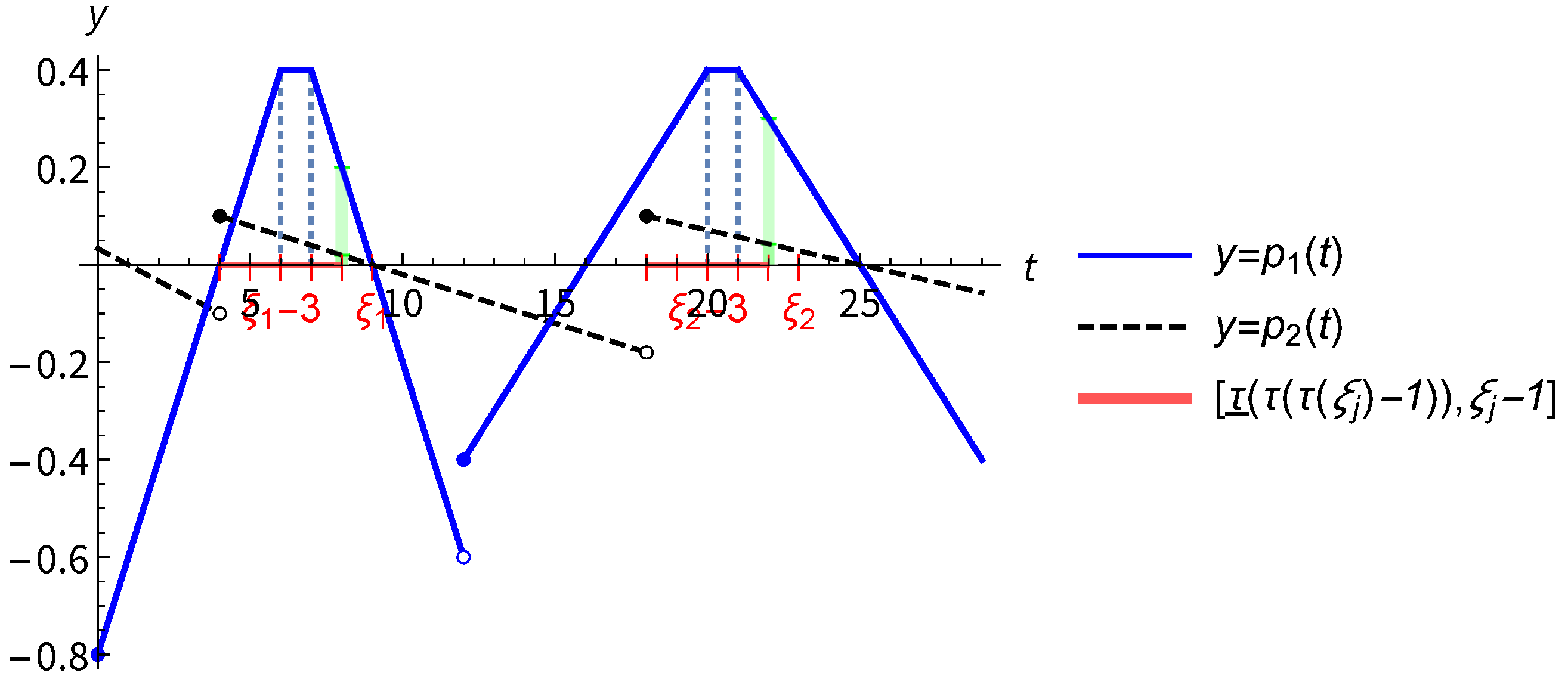
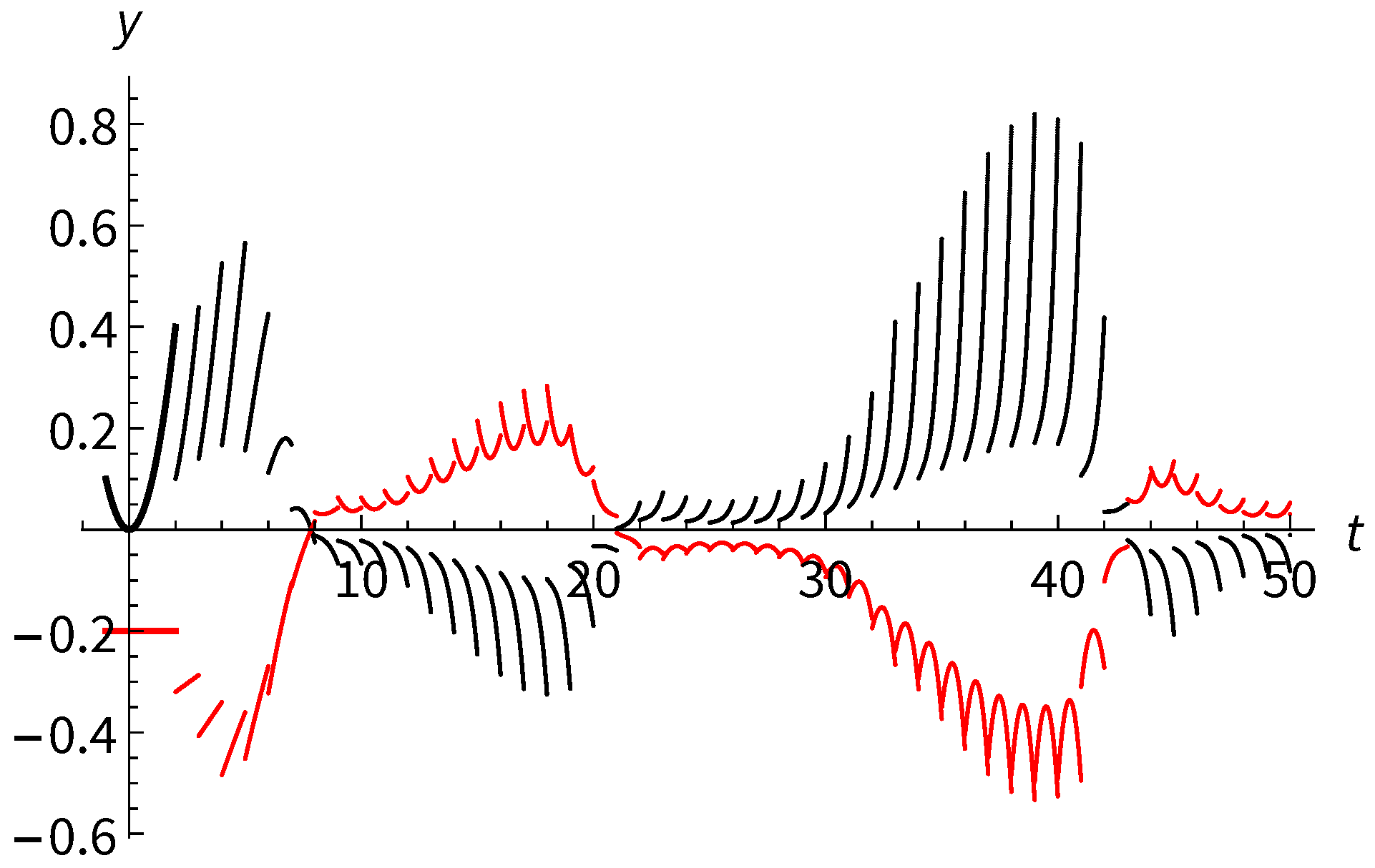
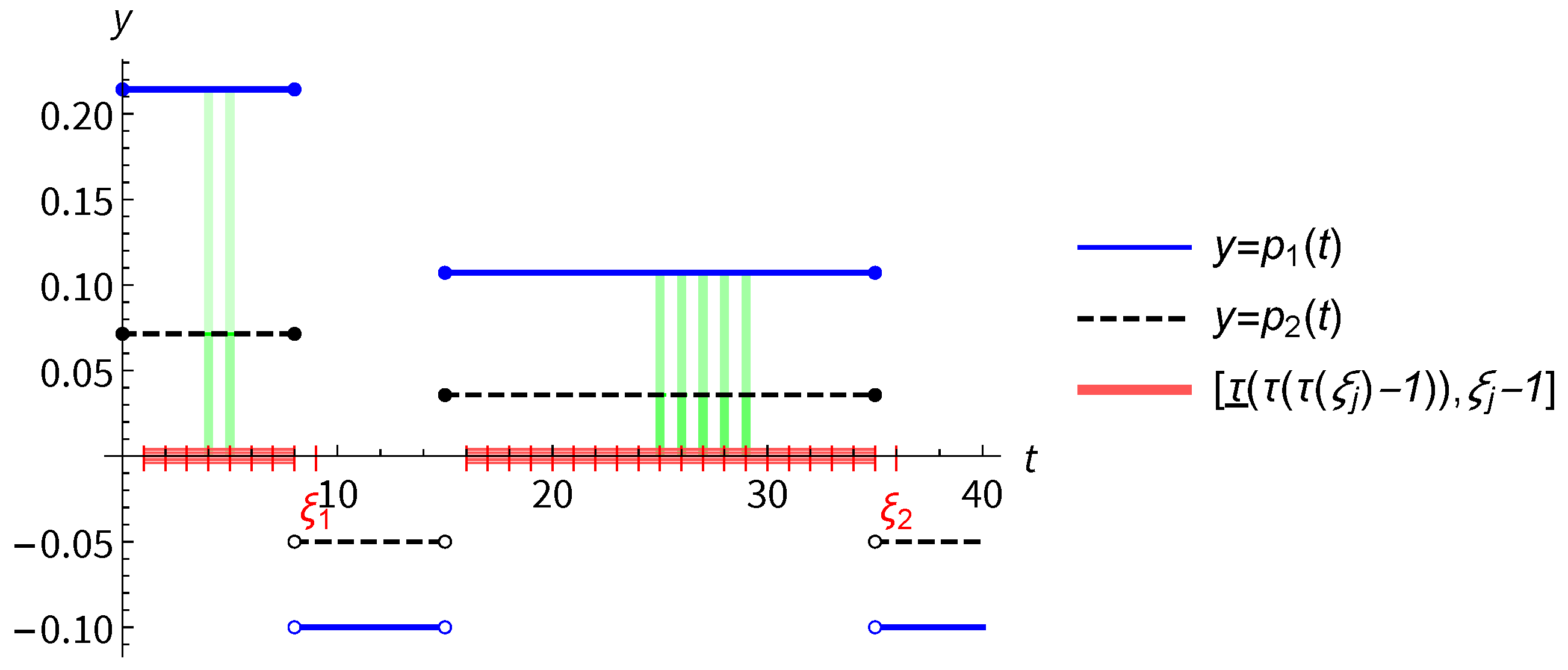
3. Examples and Comparisons
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharkovsky, A.N.; Maistrenko, Y.L.T.; Romanenko, E.Y. Difference Equations and Their Applications; Ser. Mathematics and Its Applications 250; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar] [CrossRef]
- Romanenko, O. Continuous-time difference equations and distributed chaos modelling. Math. Lett. 2022, 8, 11–21. [Google Scholar] [CrossRef]
- Sharkovsky, A.N. Chaos from a time-delayed Chua’s circuit. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 1993, 40, 781–783. [Google Scholar] [CrossRef]
- Braverman, E.; Johnson, W.T. On oscillation of difference equations with continuous time and variable delays. Appl. Math. Comput. 2019, 355, 449–457. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Péics, H.; Rožnjik, A. Oscillations in difference equations with continuous time caused by several deviating arguments. Filomat 2020, 34, 2693–2704. [Google Scholar] [CrossRef]
- Karpuz, B.; Öcalan, Ö. Discrete approach on oscillation of difference equations with continuous variable. Adv. Dyn. Syst. Appl. 2008, 3, 283–290. [Google Scholar]
- Ladas, G.; Pakula, L.; Wang, Z. Necessary and sufficient conditions for the oscillation of difference equations. Panam. Math. J. 1992, 2, 17–26. [Google Scholar]
- Zhang, B.G.; Yan, J.; Choi, S.K. Oscillation for difference equations with continuous variable. Comput. Math. Appl. 1998, 36, 11–18. [Google Scholar] [CrossRef]
- Nowakowska, W.; Werbowski, J. Conditions for the oscillation of solutions of iterative equations. Abstr. Appl. Anal. 2004, 2004, 543–550. [Google Scholar] [CrossRef]
- Shen, J.; Stavroulakis, I.P. An oscillation criteria for second order functional equations. Acta Math. Sci. Ser. B Eng. Ed. 2002, 22, 56–62. [Google Scholar] [CrossRef]
- Zhang, B.G.; Choi, S.K. Oscillation and nonoscillation of a class of functional equations. Math. Nachr. 2001, 227, 159–169. [Google Scholar] [CrossRef]
- Attia, E.; El-Matary, B. New explicit oscillation criteria for first-order differential equations with several non-monotone delays. Mathematics 2023, 11, 64. [Google Scholar] [CrossRef]
- Braverman, E.; Karpuz, B. On oscillation of differential and difference equations with non-monotone delays. Appl. Math. Comput. 2011, 218, 3880–3887. [Google Scholar] [CrossRef]
- Kiliç, N.; Öcalan, Ö. A new oscillation result for nonlinear differential equations with nonmonotone delay. Miskolc Math. Notes 2023, 24, 841–851. [Google Scholar] [CrossRef]
- Fukagai, N.; Kusano, T. Oscillation theory of first order functional differential equations with deviating arguments. Ann. Mat. Pura Appl. 1984, 136, 95–117. [Google Scholar] [CrossRef]
- Tang, X. Oscillation of first order delay differential equations with oscillating coefficients. Appl. Math. J. Chin. Univ. Ser. B 2000, 15, 252–258. [Google Scholar] [CrossRef]
- Attia, E.R.; Alotaibi, S.M.; Chatzarakis, G.E. New oscillation criteria for first-order difference equations with several not necessarily monotonic delays. J. Appl. Math. Comput. 2024, 70, 1915–1936. [Google Scholar] [CrossRef]
- Koplatadze, R.; Khachidze, N. Oscillation criteria for difference equations with several retarded arguments. J. Math. Sci. 2020, 246, 384–393. [Google Scholar] [CrossRef]
- Berezansky, L.; Chatzarakis, G.E.; Domoshnitsky, A.; Stavroulakis, I.P. Oscillations of difference equations with several oscillating coefficients. Abstr. Appl. Anal. 2014, 2014, 392097. [Google Scholar] [CrossRef]
- Yan, W.; Yan, J. Comparison and oscillation results for delay difference equations with oscillating coefficients. Int. J. Math. Math. Sci. 1996, 19, 171–176. [Google Scholar] [CrossRef]
- Yu, J.S.; Tang, X.H. Sufficient conditions for the oscillation of linear delay difference equations with oscillating coefficients. J. Math. Anal. Appl. 2000, 250, 735–742. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Péics, H.; Rožnjik, A. Oscillations of deviating difference equations with continuous time and oscillatory coefficients. J. Differ. Equ. Appl. 2023, 29, 682–700. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzarakis, G.E.; Péics, H.; Rožnjik, A. Oscillation Criteria for Delay Difference Equations with Continuous Time, Piecewise Linear Delay Functions, and Oscillatory Coefficients. Mathematics 2025, 13, 1325. https://doi.org/10.3390/math13081325
Chatzarakis GE, Péics H, Rožnjik A. Oscillation Criteria for Delay Difference Equations with Continuous Time, Piecewise Linear Delay Functions, and Oscillatory Coefficients. Mathematics. 2025; 13(8):1325. https://doi.org/10.3390/math13081325
Chicago/Turabian StyleChatzarakis, George E., Hajnalka Péics, and Andrea Rožnjik. 2025. "Oscillation Criteria for Delay Difference Equations with Continuous Time, Piecewise Linear Delay Functions, and Oscillatory Coefficients" Mathematics 13, no. 8: 1325. https://doi.org/10.3390/math13081325
APA StyleChatzarakis, G. E., Péics, H., & Rožnjik, A. (2025). Oscillation Criteria for Delay Difference Equations with Continuous Time, Piecewise Linear Delay Functions, and Oscillatory Coefficients. Mathematics, 13(8), 1325. https://doi.org/10.3390/math13081325






