Price Decisions in a Two-Server Queue Considering Customer Retrial Behavior: Profit-Driven Versus Social-Driven
Abstract
1. Introduction and Literature Review
1.1. Motivation
1.2. Literature Review
2. Introduction
3. Analysis of Customers’ Equilibrium Behavior and Optimal Price
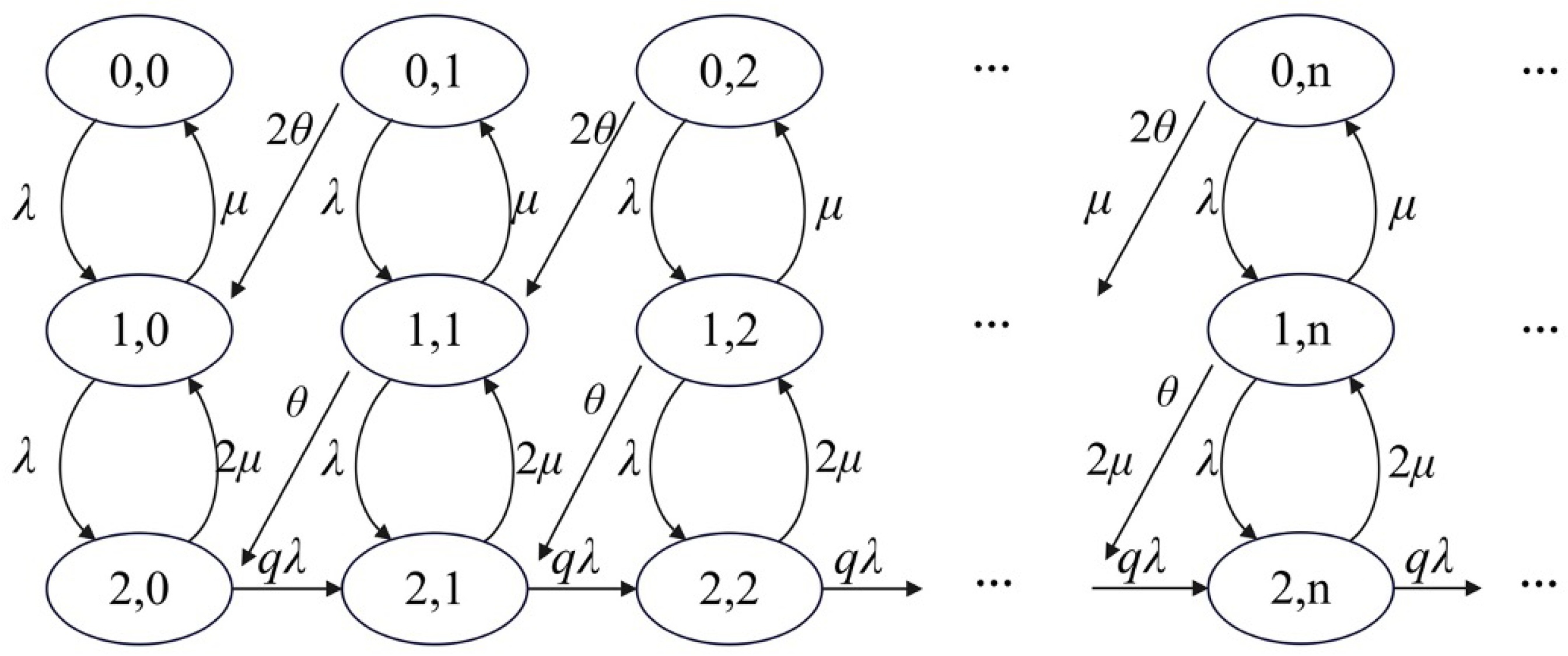
3.1. The Unobservable Case
3.1.1. Profit-Maximizing Price in the Unobservable Case
3.1.2. Welfare-Maximizing Price in the Unobservable Case
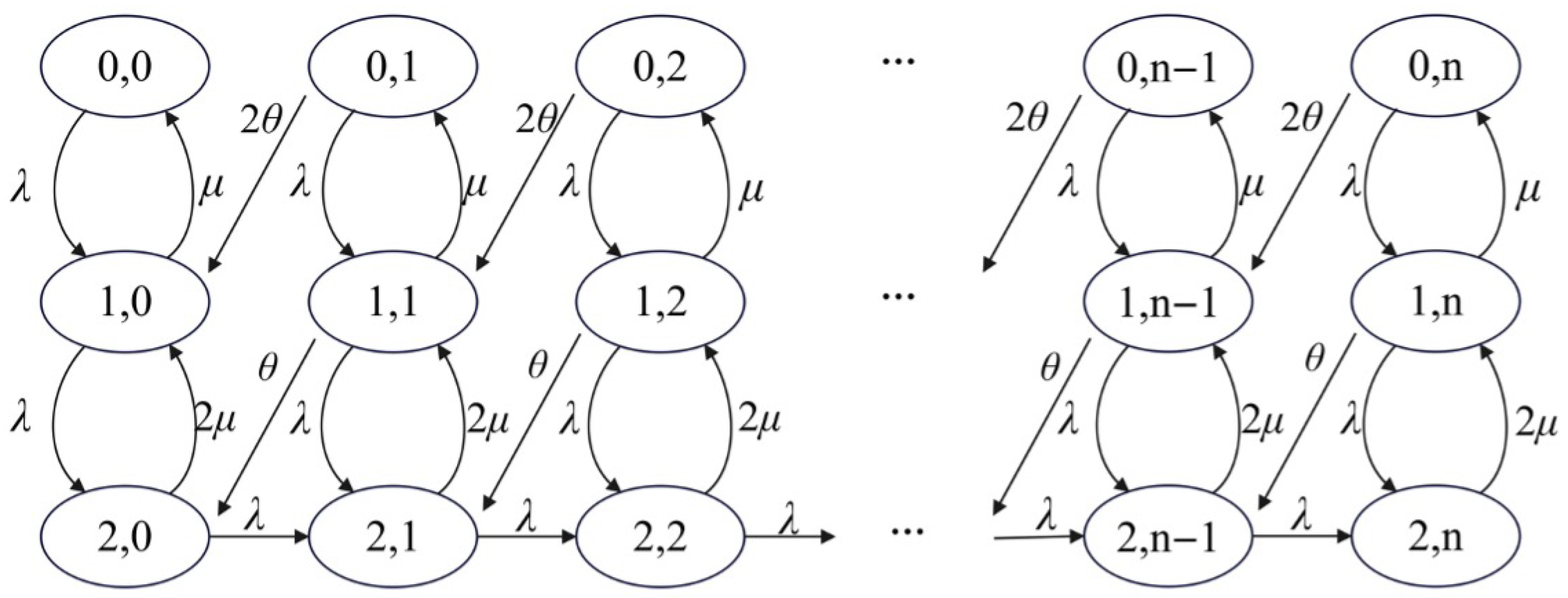
3.2. The Observable Case
3.2.1. Profit-Maximizing Price in the Observable Case
3.2.2. Welfare-Maximizing Price in the Observable Case
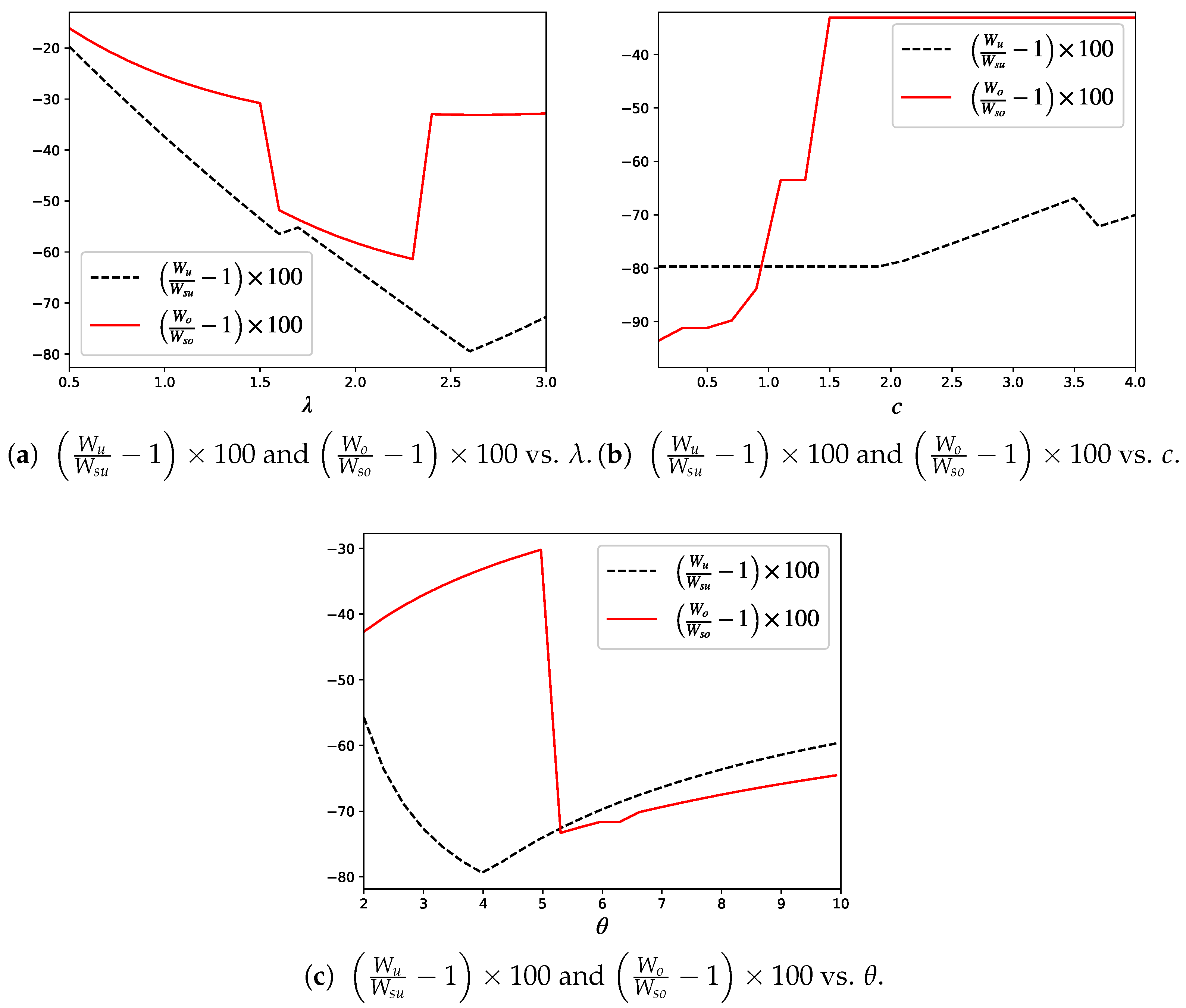
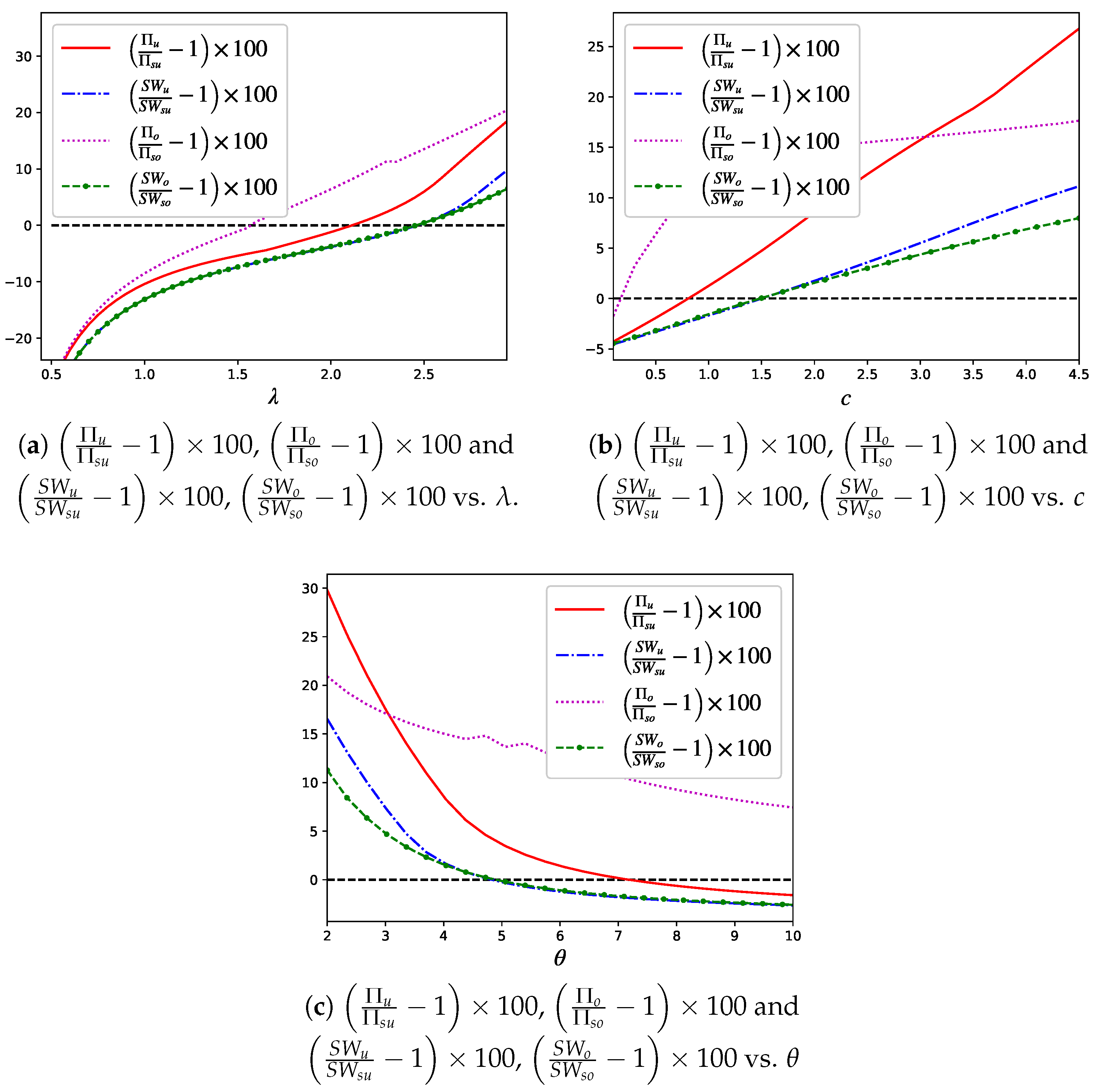
4. Numerical Results
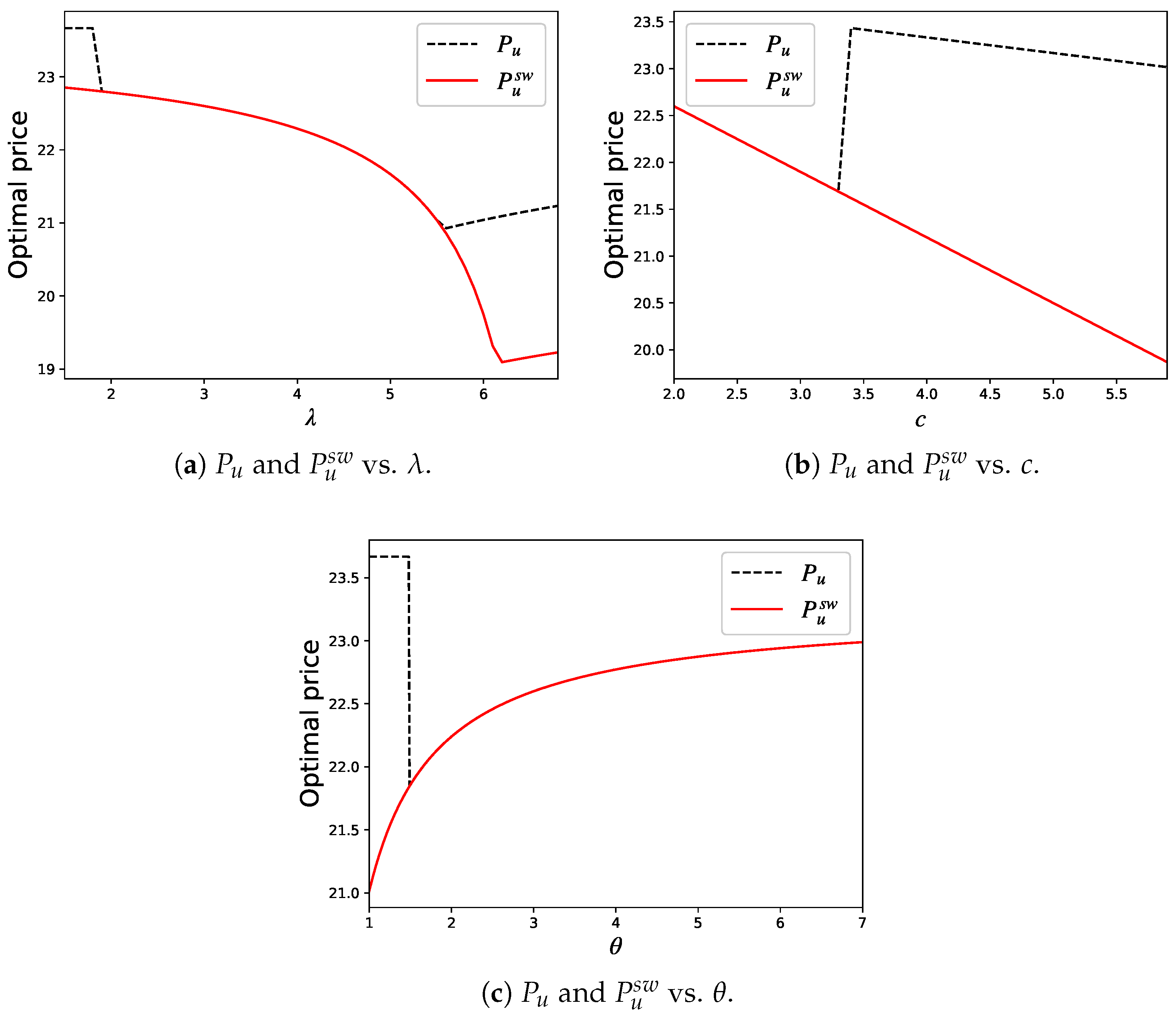
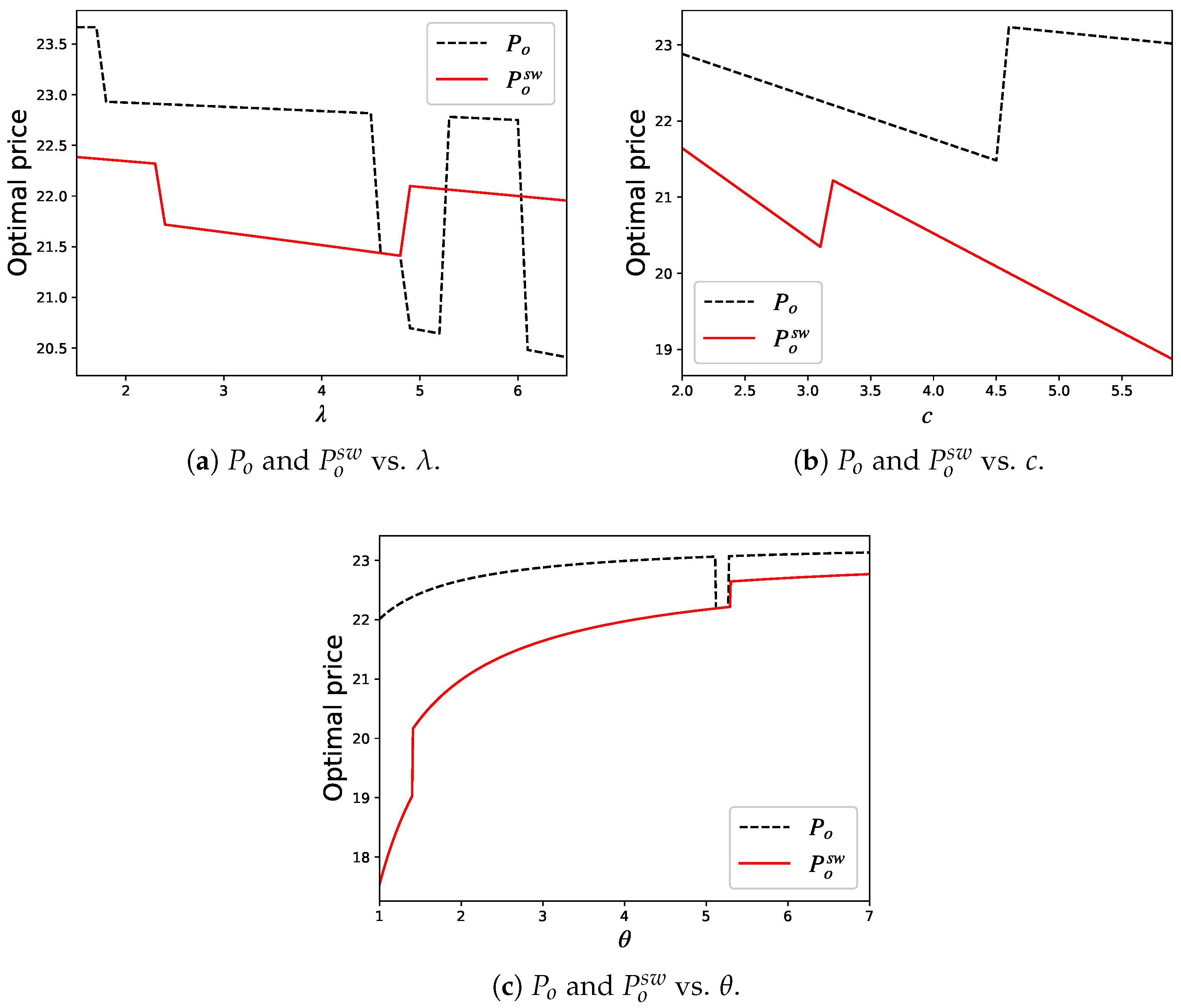
4.1. Sensitivity Analysis
4.2. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- If , then . If , then .
- If , then . If , then .
- If , then . If , then .
References
- Lai, C.; Kasim, E.; Muhammadhaji, A. Dynamic Analysis of a Standby System with Retrial Strategies and Multiple Working Vacations. Mathematics 2024, 12, 3999. [Google Scholar] [CrossRef]
- Samanta, S.K.; Rashmi, K.M. Analytical and computational aspects of a batch arrival retrial queue with a constant retrial policy. In Quality Technology & Quantitative Management; Taylor & Francis: Abingdon-on-Thames, UK, 2025; pp. 1–28. [Google Scholar]
- Aissani, A. An MX/G/1 energetic retrial queue with vacations and control. IMA J. Manag. Math. 2011, 21, 13–32. [Google Scholar] [CrossRef]
- Tapiero, C.S. Energy consumption and environmental pollution: A stochastic model. IMA J. Manag. Math. 2009, 20, 263–273. [Google Scholar] [CrossRef]
- Dimitriou, I. A single server retrial queue with event-dependent arrival rates. Ann. Oper. Res. 2023, 331, 1053–1088. [Google Scholar] [CrossRef]
- Artalejo, J.R.; Gómez-Corral, A. Retrial Queueing Systems: A Computational Approach; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Falin, G.; Templeton, J.G. Retrial Queues; CRC Press: Boca Raton, FL, USA, 1977. [Google Scholar]
- Economou, A.; Kanta, S. Equilibrium customer strategies and social–profit maximization in the single-server constant retrial queue. Nav. Res. Log. 2011, 58, 107–122. [Google Scholar] [CrossRef]
- Cui, S.; Su, X.; Veeraraghavan, S. A model of rational retrials in queues. Oper. Res. 2019, 67, 1699–1718. [Google Scholar] [CrossRef]
- Armony, M.; Maglaras, C. Contact centers with a call-back option and real-time delay information. Oper. Res. 2004, 52, 527–545. [Google Scholar] [CrossRef]
- Tang, Y.; Guo, P.; Wang, Y. Equilibrium queueing strategies of two types of customers in a two-server queue. Oper. Res. Lett. 2018, 46, 99–102. [Google Scholar] [CrossRef]
- Naor, P. The regulation of queue size by levying tolls. Econometrica 1969, 37, 15–24. [Google Scholar] [CrossRef]
- Edelson, N.M.; Hilderbrand, D.K. Congestion tolls for Poisson queuing processes. Econometrica 1975, 43, 81–92. [Google Scholar] [CrossRef]
- Hassin, R.; Haviv, M. To Queue or Not to Queue: Equilibrium Behavior in Queueing Systems; Springer Science and Business Media: Berlin, Germany, 2003. [Google Scholar]
- Hassin, R. Rational Queueing; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hassin, R.; Haviv, M. Equilibrium strategies and the value of information in a two line queueing system with threshold jockeying. Stoch. Model. 1994, 10, 415–435. [Google Scholar] [CrossRef]
- Hassin, R. On the advantage of being the first server. Manage. Sci. 1996, 42, 618–623. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Z. The impact of line-sitting on a two-server queueing system. Eur. J. Oper. Res. 2023, 74, 748–761. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, W.; Hsu, V.N.; Guo, P. On the benefit of privatization in a mixed duopoly service system. Manag. Sci. 2023, 69, 1486–1499. [Google Scholar] [CrossRef]
- Cattani, K.; Schmidt, G.M. The pooling principle. Informs Trans. Edu. 2005, 5, 17–24. [Google Scholar] [CrossRef]
- Yechiali. Customers’ optimal joining rules for the GI/M/s queue. Manag. Sci. 1972, 18, 434–443. [Google Scholar]
- Wang, J.; Zhang, Y.; Zhang, Z.G. Strategic joining in an M/M/K queue with asynchronous and synchronous multiple vacations. J. Oper. Res. Soc. 2021, 72, 161–179. [Google Scholar] [CrossRef]
- Kulkarni, V.G. On queueing systems by retrials. J. Appl. Probab. 1983, 20, 380–389. [Google Scholar] [CrossRef]
- Elcan, A. Optimal customer return rate for an M/M/1 queueing system with retrials. Probab. Eng. Inform. Sci. 1994, 8, 521–539. [Google Scholar] [CrossRef]
- Hassin, R.; Haviv, M. On optimal and equilibrium retrial rates in a queueing system. Probab. Eng. Inform. Sci. 1994, 10, 223–227. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, F. Strategic joining in M/M/1 retrial queues. Eur. J. Oper. Res. 2013, 230, 76–87. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Information heterogeneity in a retrial queue: Throughput and social welfare maximization. Queueing Syst. 2019, 92, 131–172. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Managing retrial queueing systems with boundedly rational customers. J. Oper. Res. Soc. 2023, 74, 748–761. [Google Scholar] [CrossRef]
- Armony, M.; Plambeck, E.; Seshadri, S. Sensitivity of optimal capacity to customer impatience in an unobservable M/M/S queue (Why you shouldn’t shout at the DMV). Manuf. Serv. Oper. Manag. 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Hanukov, G. Improving efficiency of service systems by performing a part of the service without the customer’s presence. Eur. J. Oper. Res. 2022, 302, 606–620. [Google Scholar] [CrossRef]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Courier Corporation: Chelmsford, MA, USA, 1994. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, X.; Yu, M.; Yang, Y. Price Decisions in a Two-Server Queue Considering Customer Retrial Behavior: Profit-Driven Versus Social-Driven. Mathematics 2025, 13, 1310. https://doi.org/10.3390/math13081310
Cai X, Yu M, Yang Y. Price Decisions in a Two-Server Queue Considering Customer Retrial Behavior: Profit-Driven Versus Social-Driven. Mathematics. 2025; 13(8):1310. https://doi.org/10.3390/math13081310
Chicago/Turabian StyleCai, Xiaoli, Miaomiao Yu, and Yunling Yang. 2025. "Price Decisions in a Two-Server Queue Considering Customer Retrial Behavior: Profit-Driven Versus Social-Driven" Mathematics 13, no. 8: 1310. https://doi.org/10.3390/math13081310
APA StyleCai, X., Yu, M., & Yang, Y. (2025). Price Decisions in a Two-Server Queue Considering Customer Retrial Behavior: Profit-Driven Versus Social-Driven. Mathematics, 13(8), 1310. https://doi.org/10.3390/math13081310




