Application of Integrable Systems in Carbon Price Determination
Abstract
1. Introduction
2. Sample Selection and Data Analysis
2.1. Sample Selection
2.2. Carbon Emission Rights Futures Data Processing
2.2.1. Descriptive Statistical Analysis of Yield Series
2.2.2. Return to Baseline
2.2.3. Conduction Mechanism Test
2.3. Data Analysis
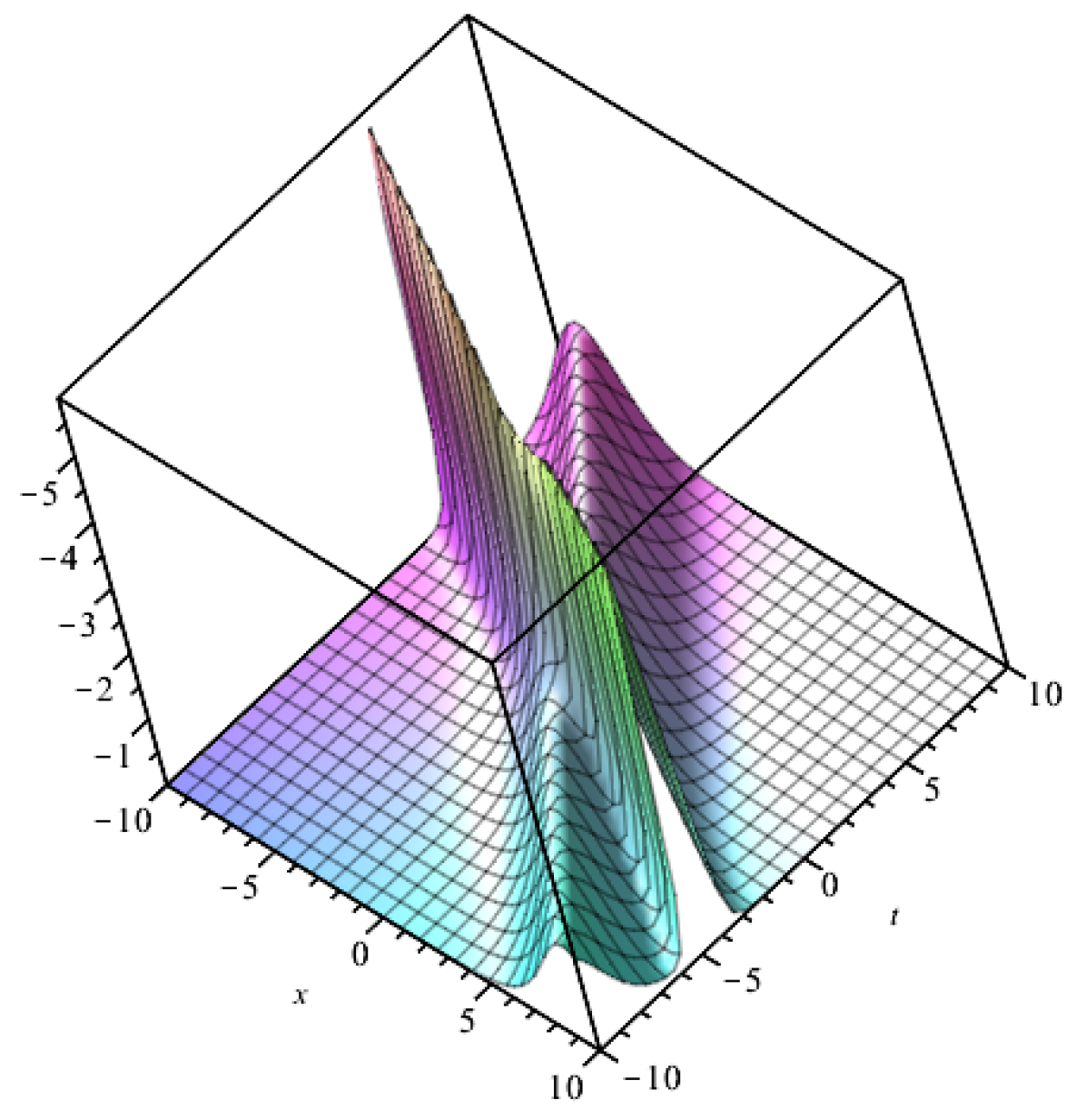
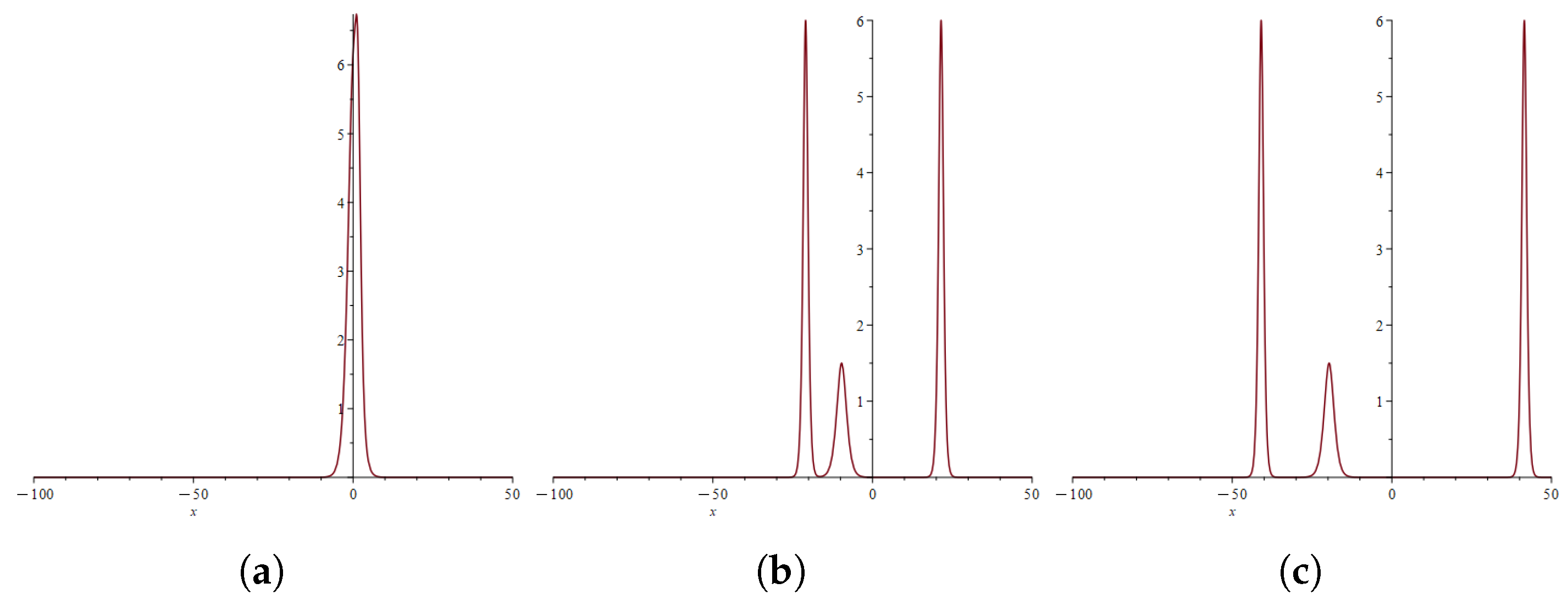
3. Tests of the Nature of Carbon Price Solitons
3.1. Bell Polynomial Theory and Hirota Bilinear Forms
3.2. Verification of System Productability
3.3. Verification of the Soliton Solution of the System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Bai, E. The Regime Complexes for Global Climate Governance. Sustainability 2023, 15, 9077. [Google Scholar] [CrossRef]
- Wang, A.L. Regulating domestic carbon outsourcing: The case of China and climate change. UCLA L. Rev. 2013, 61, 2018. [Google Scholar]
- Fokas, A.S. Integrable nonlinear evolution equations in three spatial dimensions. Proc. R. Soc. A 2022, 478, 20220074. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.M.; Yu, J.P.; Ma, W.X.; Khalique, C.M.; Sun, Y.L. Dynamic analysis of lump solutions based on the dimensionally reduced generalized Hirota bilinear KP-Boussinesq equation. Mod. Phys. Lett. B 2023, 37, 2250203. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, M.; Liu, S.; Li, C.; Wang, X. Bäcklund transformation, Lax pair, infinite conservation laws and exact solutions to a generalized (2+1)-dimensional equation. Int. J. Mod. Phys. B 2022, 36, 2250146. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Ganie, A.H.; Mahnashi, A.M.; Shah, R. Perturbed Gerdjikov–Ivanov equation: Soliton solutions via Backlund transformation. Optik 2024, 298, 171576. [Google Scholar] [CrossRef]
- Liu, Z.; Madhavan, V.; Tegmark, M. Machine learning conservation laws from differential equations. Phys. Rev. E 2022, 106, 045307. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.; Xu, L.; Sun, Y.; Liang, Z.; Lu, E.; Li, Y. Development of a cleaning fan for a rice combine harvester using computational fluid dynamics and response surface methodology to optimise outlet airflow distribution. Biosyst. Eng. 2020, 192, 232–244. [Google Scholar] [CrossRef]
- Tang, P.; Li, H.; Issaka, Z.; Chen, C. Impact forces on the drive spoon of a large cannon irrigation sprinkler: Simple theory, cfd numerical simulation and validation. Biosyst. Eng. 2017, 159, 1–9. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, H.; Chen, C.; Xiang, Q. Calculation and verification of formula for the range of sprinklers based on jet breakup length. Int. J. Agric. Biol. Eng. 2018, 11, 49–57. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Kang, W.; Lin, H.; Adade, S.; Wang, Z.; Ouyang, Q.; Chen, Q. Advanced sensing of volatile organic compounds in the fermentation of kombucha tea extract enabled by nano-colorimetric sensor array based on density functional theory. Food Chem. 2023, 405, 134193. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Q.; Belwal, T.; Lin, X.; Luo, Z. Insights into chemometric algorithms for quality attributes and hazards detection in foodstuffs using raman/surface enhanced raman spectroscopy. Compr. Rev. Food Sci. Food Saf. 2021, 20, 2476–2507. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Mi, J.; Zeng, Y.; Wei, W. Bilinear Integrable soliton solutions and carbon emission rights pricing. Int. J. Low-Carbon Technol. 2023, 18, 131–143. [Google Scholar] [CrossRef]
- Dash, R.; Dash, P.K. An evolutionary hybrid Fuzzy Computationally Efficient EGARCH model for volatility prediction. Appl. Soft Comput. 2016, 45, 40–60. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, S. Research on pricing of carbon options based on GARCH and BS model. J. Appl. Sci. Eng. Innov. 2019, 6, 109–116. [Google Scholar]
- Stoev, S.; Taqqu, M.S.; Park, C.; Marron, J.S. On the wavelet spectrum diagnostic for Hurst parameter estimation in the analysis of Internet traffic. Comput. Netw. 2005, 48, 423–445. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Jaiswal, S.; Jaiswal, T. Review on machine learning techniques for stock-market forecasting. Artif. Intell. Evol. 2020, 1, 34–47. [Google Scholar] [CrossRef]
- Tapkın, S.; Çevik, A.; Uşar, Ü. Accumulated strain prediction of polypropylene modified marshall specimens in repeated creep test using artificial neural networks. Expert Syst. Appl. 2009, 36, 11186–11197. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, K.; Yang, H.; Li, Y. Generalised (2+1)-dimensional super MKdV hierarchy for integrable systems in soliton theory. East Asian J. Appl. Math. 2015, 5, 256–272. [Google Scholar] [CrossRef]
- Jiang, J.; Li, W.; Cai, X.; Wang, Q. Empirical study of recent Chinese stock market. Phys. Stat. Mech. Its Appl. 2009, 388, 1893–1907. [Google Scholar] [CrossRef]
- Lou, S.Y.; Jia, M. From one to infinity: Symmetries of integrable systems. J. High Energy Phys. 2024, 2024, 1–10. [Google Scholar] [CrossRef]
- Xu, G.; Li, Z. Symbolic computation of the Painlevé test for nonlinear partial differential equations using Maple. Comput. Phys. Commun. 2004, 161, 65–75. [Google Scholar] [CrossRef]
- Wang, C. Lump solution and integrability for the associated Hirota bilinear equation. Nonlinear Dyn. 2017, 87, 2635–2642. [Google Scholar] [CrossRef]
- Yan, S.; Li, C. Explicit solutions from Darboux transformation for the two-component nonlocal Hirota and Maxwell-Bloch system. Int. J. Geom. Methods Mod. Phys. 2023, 20, 2350062. [Google Scholar] [CrossRef]
- Gaillard, P. Degenerate Riemann theta functions, Fredholm and wronskian representations of the solutions to the KdV equation and the degenerate rational case. J. Geom. Phys. 2021, 161, 104059. [Google Scholar] [CrossRef]
- Dong, P.; Ma, Z.Y.; Fei, J.X.; Cao, W. The shifted parity and delayed time-reversal symmetry-breaking solutions for the (1 + 1)-dimensional Alice-Bob Boussinesq equation. Front. Phys. 2023, 11, 1137999. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhang, Y.; Tang, Y.; Tu, J. Hirota bilinear equations with linear subspaces of solutions. Appl. Math. Comput. 2012, 218, 7174–7183. [Google Scholar] [CrossRef]
- Léger, F.; Li, W. Hopf-Cole transformation via generalized Schrödinger bridge problem. J. Differ. Equ. 2021, 274, 788–827. [Google Scholar] [CrossRef]
- Nolte, B.; SchäFer, I.; Ehrlich, J.; Ochmann, M.; Marburg, R.B.A.S. Numerical methods for wave scattering phenomena by means of different boundary integral formulations. J. Comput. Acoust. 2007, 15, 495–529. [Google Scholar] [CrossRef]





| Variant | −1 | −2 |
|---|---|---|
| Innovation | Innovation | |
| Region × Post | 0.045 *** | - |
| −0.017 | ||
| Region × Year2021 | - | 0.005 |
| −0.023 | ||
| Region × Year2022 | - | 0.001 |
| −0.024 | ||
| Region × Year2023 | - | 0.048 *** |
| −0.022 | ||
| Control variable | Yes | Yes |
| Year fixed | Yes | Yes |
| City × industry fixed | Yes | Yes |
| Constant term (math.) | −4.217 *** | −4.158 *** |
| −0.377 | −0.38 | |
| Sample size | 144,936 | 144,936 |
| R2 | 0.897 | 0.897 |
| Variant | (1) | (2) | Variant | (3) | Variant | (4) |
|---|---|---|---|---|---|---|
| Inn. 1 | Inn. 2 | Inn. | Inn. | |||
| Bullish prices | 2.496 (0.133) | 1.931 (0.083) | Trend price 1 | 1.365 (0.067) | Product price 1 | 0.216 (0.013) |
| Bearish prices | 0.575 (0.128) | 0.533 (0.049) | Trend price 2 | 0.443 (0.007) | Product price 2 | 0.226 (0.003) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Chen, W.; Zhang, C. Application of Integrable Systems in Carbon Price Determination. Mathematics 2025, 13, 1304. https://doi.org/10.3390/math13081304
Yang X, Chen W, Zhang C. Application of Integrable Systems in Carbon Price Determination. Mathematics. 2025; 13(8):1304. https://doi.org/10.3390/math13081304
Chicago/Turabian StyleYang, Xiyan, Wenxia Chen, and Chaosheng Zhang. 2025. "Application of Integrable Systems in Carbon Price Determination" Mathematics 13, no. 8: 1304. https://doi.org/10.3390/math13081304
APA StyleYang, X., Chen, W., & Zhang, C. (2025). Application of Integrable Systems in Carbon Price Determination. Mathematics, 13(8), 1304. https://doi.org/10.3390/math13081304





