Abstract
This article investigates the boundary value problem for an extended stationary system of Nernst–Planck–Poisson equations, corresponding to a mathematical model of the influence of changes in the equilibrium coefficient on the transport of ions of a binary salt in the diffusion layer. Dimensionless variables were introduced using characteristic parameter values. As a result, a dimensionless boundary value problem was obtained, which is singularly perturbed, containing a small parameter in the derivative of the Poisson equation and, additionally, another regular small parameter. A similarity theory was developed: trivial and non-trivial similarity criteria and their physical meaning were determined, which allowed for the identification of general properties of the solutions. A numerical investigation of the boundary value problem was conducted using the finite element method. With an increase in the initial solution concentration, the value of the small parameter entering singularly decreases, reaching values on the order of 10−12 and below, leading to computational difficulties that prevent a comprehensive analysis of the influence of changes in the equilibrium coefficient on salt ion transport. In this regard, an analytical solution to the problem was constructed, based on dividing the solution domain into several subdomains (regions of electroneutrality, extended space charge region, quasi-equilibrium region, recombination region, intermediate layer), in each of which the problem is solved differently, followed by matching these solutions. Verification of the analytical solution was carried out by comparing it with the numerical solution. The advantage of the obtained analytical solution is the possibility of a comprehensive analysis of the influence of the dissociation/recombination reaction of water molecules on salt ion transport over a wide range of real changes in the concentration and composition of the electrolyte solution and other input parameters. This boundary value problem serves as a benchmark for constructing asymptotic solutions for other singularly perturbed boundary value problems in membrane electrochemistry.
Keywords:
boundary value problems; extended system of Nernst–Planck–Poisson equations; analytical solution; singularly perturbed problems; method of matched asymptotic expansions MSC:
35Q92
1. Introduction
This article investigates the boundary value problem for an extended system of stationary Nernst–Planck–Poisson (NPP) equations [1,2,3,4], describing the transport of ions of a binary salt in the diffusion layer, taking into account the influence of space charge on changes in the equilibrium coefficient. It is known that in strong electric fields the equilibrium coefficient of equilibrium/recombination of water molecules can increase many times. For bipolar ion-exchange membranes, Timashev S.F. and others [5] based on Onsager’s idea suggested an empirical formula, from which it follows that the equilibrium coefficient exponentially depends on the stability of the external field of external action. There are some considerations [3] in favor of using a linear dependence on the space charge density instead of the exponential dependence of the equilibrium coefficient on the electric field strength. For bipolar membranes, due to the Boltzmann–Debye equation, this is equivalent to an exponential dependence on the electric field strength. It is easy to show that the same is preserved in the quasi-equilibrium region of the space charge in the diffusion layer of the ion-exchange membrane. However, at overlimiting current densities in the diffusion layer of monopolar membranes of the extended region of the space charge [6], it can be shown that in the extended space charge region, the equilibrium coefficient will depend almost linearly on the electric field strength. A similar solution of the boundary value problem, obtained by us, in the extended region of space charge, shows that along with the dependence of the equilibrium coefficient on the voltage, the key role is played by the dependence on the initial concentration of the electrolyte solution. Namely, at high solution concentrations of the order of 1 mol/m3 and higher, the effect of the change in the equilibrium coefficient on the transfer of salt ions is not significant and can be ignored, but at lower concentrations it must be taken into account. This allows for a more accurate description of ion transport processes in electromembrane systems (EMS) and makes the model more universal and applicable to a wide range of parameters. Moreover, in previous studies, numerical methods were generally used to solve boundary value problems in membrane electrochemistry in diffusion layers, nonlinear processes in porous electrodes, electrochemical phenomena in microfluidic systems, etc. [7,8,9,10,11,12]. Numerical methods for solving boundary value problems for the Nernst–Planck–Poisson system are currently a pressing and complex problem. For example, in [13], numerical schemes are proposed that can unconditionally ensure conservation of mass, initial energy dissipation, and the existence of positive numerical solutions.
The transition to dimensionless variables using characteristic parameter values shows that the boundary value problem is singularly perturbed, containing two small parameters, one of which is in the derivative of the Poisson equation, leading to computational difficulties at small parameter values in numerical solutions and the need for special methods [13,14,15]. In this regard, obtaining analytical solutions is of great importance. The main problem of the analytical solution lies in the fact that different physical processes dominate in different regions of the diffusion layer [16,17]. In this article, we estimate the characteristic quantities used to make the transition to a dimensionless form and obtain trivial and nontrivial similarity criteria. We have determined their physical meaning, defined the regions of change, and clarified the main properties of the solution to the boundary value problem. We have performed a numerical analysis of the boundary value problem and shown that the diffusion layer has a complex structure; namely, it is divided into six intervals where different processes dominate, and therefore, in each of them, the solution to the boundary value problem behaves differently. In this article, to construct an analytical solution to the boundary value problem, we divide the solution region into a number of subregions (regions of electroneutrality, region of extended space charge, quasi-equilibrium region, recombination region, intermediate layer), in each of which the boundary value problem is solved in its own way, and then these solutions are merged. The analytical solution is verified by comparing it with the numerical solution. The advantage of the analytical solution we obtained is the possibility of a comprehensive analysis of the effect of the dissociation/recombination reaction of water molecules on the transport of salt ions over a wide range of real changes in the concentration and composition of the electrolyte solution and other input parameters. Thus, the model we propose and its analytical solution represent a significant step forward in understanding the processes of ion transport in EMS, taking into account the effect of the dissociation/recombination reaction of water molecules and solving boundary value problems for the extended system of NPP equations. The mathematical model we propose and the analytical method for its study are the standard for other singularly perturbed boundary value problems in membrane electrochemistry. It demonstrates how complex physicochemical processes, such as the dissociation and recombination of water molecules [18], can be taken into account within a single mathematical formulation. This opens up new possibilities for constructing asymptotic solutions for other problems related to ion transport in EMS, when numerical methods become ineffective.
2. Mathematical Model of the Influence of the Dependence of the Dissociation Coefficient on the Space Charge Value on the Stationary Transport of Salt Ions in the Diffusion Layer
The dissociation of water at interphase boundaries and changes in the equilibrium coefficient are important for understanding the processes occurring in ion transport using ion-exchange membranes. The increase in the rate coefficient of water molecule dissociation at interphase boundaries (membrane/solution or membrane/membrane) can have several causes, as indicated in [19]. In this work, the influence of the electric field on the equilibrium coefficient of the water molecule dissociation/recombination reaction is investigated.
According to the concepts developed by Timashev S.F. and Sheldeshov N.V. et al. [5,20,21] for bipolar membranes, the current density of ions generated in the membrane system is determined by an empirical formula where the equilibrium coefficient depends exponentially on the external electric field strength [9]. In electrodialysis systems with monopolar membranes, few studies have been devoted to studying this dependence [22,23].
There are several considerations suggesting that, unlike the studies mentioned above, in systems with monopolar membranes, changes in the equilibrium coefficient can be associated not only with the magnitude of the electric field strength but also with the magnitude of the space charge. For the first time, the dependence of ion fluxes on the magnitude of the space charge was mentioned in the work of Nikonenko V.V. et al. [23].
Consider the water molecule dissociation/recombination reaction equation:
where is the equilibrium constant, and and are the dissociation and recombination coefficients, respectively, is the concentration of water in the solution and ions, and is fluxes of ions. Assume that depends on the space charge . Expanding , or, what is the same , in a Taylor series with respect to and limiting ourselves to the first approximation, we obtain the empirical formula: , where is a constant that must be determined, for example, from experimental data, considering it as a fitting parameter. We transform this formula to a convenient form by multiplying by ; then
Let us denote and , where ( is a dimensionless quantity, and, accordingly, has the dimension of concentration); then, we obtain
Thus, we obtain only one, dimensionless fitting parameter , which has a clear and simple physical meaning, which consists in the influence of the magnitude of the space charge on the increase in the rate of dissociation of water molecules. In addition, the function depends linearly on the values of the ion concentrations at each point, which allows us to study its change in different parts of the diffusion layer [24] and find analytical solutions.
2.1. System of Equations
Stationary transport of salt ions for a 1:1 electrolyte in a diffusion layer at a cation-exchange membrane (CEM), taking into account the space charge and the dissociation/recombination reaction, taking into account the dependence of the dissociation coefficient on the value of the space charge, is described by the following extended system of NPP equations:
Here, (1) is the material balance equations, (2) is the Nernst–Planck equations for the flows of potassium or sodium ions (), chlorine (), hydrogen () and hydroxyl (), (3) is the Poisson equation for the electric field potential, where , (4) is the formula describing the reaction of dissociation/recombination of water molecules, where , and (5) is the current flow equation, which means that the current density flowing through the cross-section of the desalination channel is determined by the ion flow, that is, it is the Faraday current density, is the permittivity of the solution, is the Faraday number, is the universal gas constant, is the absolute temperature, is the potential, is the electric field strength, , , —is the concentration, flux, diffusion coefficient of the i-th ion, m3/(s mol) is the recombination rate constant, s−1 is the dissociation rate constant of water molecules, and mol2/m6 is the equilibrium coefficient (ionic product of water).
Remark 1.
As follows from Equations (1), (4) and (5), the relations , and are valid, where are constant unknown partial currents for salt ions and dissociation products of water molecules.
2.2. Boundary Conditions
At :
The concentration values are considered to be known and given in (6)–(8). Condition (8) means that the solution away from the cation-exchange membrane is acidified.
At :
The concentration of cations (11) on the membrane surface is determined by its exchange capacity, and the membrane is considered to be ideally selective (12). It is believed that, in the surface layer of the cation-exchange membrane, there is a less intense generation of than in the anion-exchange membrane; therefore, the concentration of ions is significantly less than the concentration of cations, and they pass through the membrane freely (13) and no longer participate in the transport processes. In this case, a flow of ions is injected into the solution from the surface of the cation-exchange membrane and this flow is specified by condition (14). In this study, the potential drop (10), (15) is specified and the current density is found using Formula (5).
3. Trivial and Non-Trivial Similarity Criteria
3.1. Characteristic Quantities and Transition to Dimensionless Form
Let us take the initial concentration of the solution as a characteristic concentration, and the actual values are in the range . Let us consider the thickness of the diffusion layer , which has the order of [25], as a characteristic length. Let us denote —the diffusion coefficient of the electrolyte, for example, (NaCl), (); —the thermal potential () [2].
Let us introduce the limiting diffusion current according to the formula [26] .
Let us take as . Let us estimate the value , which depends on the initial concentration , for example, at , we obtain .
Let us move on to dimensionless quantities using the following formulas:
Then, we obtain the boundary value problem in dimensionless form:
The boundary conditions are as follows:
At :
At :
3.2. Physical Meaning of Similarity Criteria
The boundary value problem contains the following parameters , which are trivial similarity criteria. Let us determine the physical meaning of these parameters and estimate their values at characteristic values of the input parameters of the problem.
- (1)
- Let us consider the parameter .
Let us find out the physical meaning of this parameter. To do this, we write it in the form
where is the Debye length.
Thus, the parameter is the doubled square of the ratio of the Debye length to the width of the diffusion layer , i.e., is the dimensionless Debye length (the thickness of the quasi-equilibrium region of the space charge).
The estimate shows that . As can be seen from the value , it can be taken as a small parameter, and with an increase in the initial concentration of the solution , its value decreases.
- (2)
- Let us consider the parameter .
The estimate shows that it varies within . So, for example, for mol/m3, we have .
It is clear that can be considered a small parameter, independent of , and with an increase in the initial concentration of the solution , it decreases rapidly.
However, if the width of the diffusion layer is fixed, then there is a relationship between them (see below).
- (3)
- Consider the parameter
—a universal constant independent of the initial concentration, potential jump, etc. To clarify the physical meaning of this parameter, we transform it as follows:
where is the width of the recombination region. For example, for mol/m3, we have lr = 2.70798 · 10−8 m.
Thus, the parameter is the square of the ratio of the Debye length to the width of the recombination region . The value of the constant shows that the recombination region is approximately 3.5 times smaller than the quasi-equilibrium region of the space charge.
- (4)
- Let the width of the diffusion layer be fixed; then, we have the following non-trivial similarity criterion , where is a dimensionless parameter.
In addition, .
With , it follows that with an increase in the initial concentration of the solution , the influence of the dissociation/recombination reaction on the transfer of salt ions rapidly decreases.
4. Analysis of Numerical Solution and Algorithm of Analytical Solution
We have developed a special program “Program for computer modeling of changes in the rate constant of dissociation and recombination of water molecules in the diffusion layer” № 2024688199 in the Comsol MPh 6.2 environment, with the help of which we carried out a numerical study of the boundary value problem using the finite element method. This software product is designed to calculate the mathematical model (1)–(15) and allows to describe with high accuracy the processes occurring in the diffusion layer of ion-exchange membranes, taking into account the reactions of dissociation and recombination of water molecules. This program provides a more adequate idea of the behavior of salt ions under steady-state transfer conditions, which can be used to develop new materials and technologies for ion-exchange membranes with improved characteristics, with increased selectivity, strength and resistance to various effects. The functionality of the program includes the input of initial data, calculation of the mathematical model and visualization of the results on graphs, surfaces and video, in comparison with the analytical solution.
An analysis of the numerical solution shows that the diffusion layer can be conditionally divided into six intervals by five points: —the center of the recombination region ; —the center of the intermediate region between the region of electroneutrality and the region of extended space charge , where the space charge has a local maximum; —the left boundary of the quasi-equilibrium region of space charge (Figure 1).
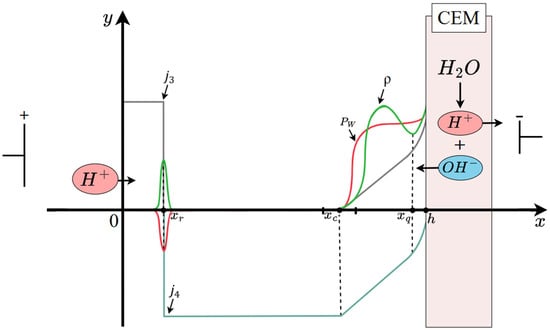
Figure 1.
Diagram of the structure of the diffusion layer in a cation-exchange membrane (CEM). Not to scale.
In the region , the equilibrium is shifted (the solution is acidified) due to the generation of ions (see the boundary condition). In this region, there are practically no ions (the concentration of these ions is significantly less than the concentration of ions). The concentration of cations and anions is equal with high accuracy, even if they are artificially set unequal at ; this inequality is compensated for on the artificially arising boundary layer. In the region , the value of the space charge is sufficiently small, and as a first approximation, it can be assumed that the condition of local electroneutrality is satisfied in it (Figure 2).
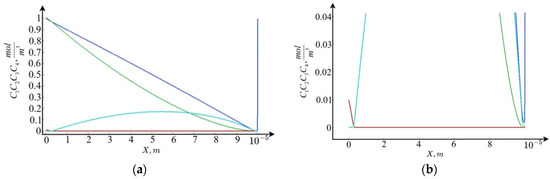
Figure 2.
Concentration graphs. Blue— concentration graph; green—; red—; light blue—: (a) general view; (b) enlargement.
On the segment , there is a recombination of hydrogen ions that come from the depth of the solution towards the cation-exchange membrane with hydroxyl ions that arise in the space charge region (SCR) of the cation-exchange membrane. In this region, the recombination of and ions dominates over the dissociation reaction of water molecules, so we will call this region the recombination region. On the interval , the condition of local electroneutrality is violated, that is, this space charge region and the interval is an extended space charge region that occurs at currents above the limiting value, is an intermediate layer between the electroneutrality region and the extended SCR, and the interval is a quasi-equilibrium space charge region. On each interval, the solution is sought in its own way, and then they are merged, that is, the constants included in the solution are determined and the boundaries of the intervals are specified. Let us note some properties of the solutions. From the numerical analysis (Figure 2) and asymptotic estimates, it follows that the cation concentration changes linearly on the interval , then slowly decreases to the point , and then, exponentially increasing, satisfies the boundary condition at the point . The anion concentration decreases linearly on the interval , and then becomes practically equal to zero. The ion concentration decreases linearly on the interval , and then the concentration value is practically equal to zero up to the point , after which it begins to grow, reaching a local maximum at the point , and then decreases. The ion concentration on the interval is practically equal to zero, then this concentration begins to grow, reaching its maximum at some internal point , and then the concentration on the interval becomes practically equal to zero.
5. Analytical Solution
For the convenience of the analytical solution, we write a dimensionless boundary value problem, omitting the index “u” for simplicity of notation:
At :
At :
The system of equations contains two small parameters and , and the parameter enters the equations singularly, i.e., as a coefficient at the derivative, and the parameter is regular [27]; therefore, the system of equations is simultaneously singularly and regularly perturbed.
General idea of the solution.
For the analytical solution, as follows from the results of the numerical solution, it is necessary to divide the diffusion layer into six sublayers (areas of electroneutrality, area of extended space charge, quasi-equilibrium area, area of recombination, intermediate layer), in each of which a certain physical process, different from the others, dominates. For example, in the recombination area, the recombination of H+ and OH− ions dominates over the dissociation of water molecules. The extended area of space charge arises from the overlimit current density and occupies a small but finite part of the diffusion layer, and in the remaining part, the condition of local electroneutrality is fulfilled. The intermediate layer is needed to merge the solutions of the area of electroneutrality and the extended area of space charge.
Thus, we divide the initial segment into six intervals:
In each interval, the system of equations is simplified in its own way and a general solution is found. The constants of integration and the boundaries of the intervals are found from the condition of matching the solutions at the boundaries of the intervals.
In the intervals , , in the first approximation, the condition of electroneutrality and equilibrium is satisfied; therefore, we obtain the equations:
where the flows are constant, and in , we have , and in , on the contrary, .
The general solutions of these equations are found quite simply and therefore omitted here.
5.1. Analytical Solution in the Recombination Region
In the recombination region, the equilibrium is disturbed. In the first approximation, the condition of local electroneutrality is satisfied; however, in this interval , unlike in the interval .
From asymptotic estimates, numerical solution and physical considerations, the following assumptions are valid:
- (1)
- The width of the recombination region is small (i.e., is small), since the recombination coefficient is quite large;
- (2)
- Recombination prevails over dissociation, i.e., , in , and in .
Using these assumptions, the system of Equations (16)–(19) is simplified:
From this system, after a number of transformations, we obtain the equation for :
Remark 2.
If we formally put in Equation (24) , we obtain the equation , whence, taking into account , we obtain and . That is, the assumptions used for the solution in the interval . Similarly, if we put , we get . That is, the assumptions used for the solution in the interval . This allows us to merge solutions in all three intervals.
- (1)
- Let us find a solution in the interval
Taking into account , since the concentration of hydroxyl ions decreases to almost zero after recombination with hydrogen ions, we get a linear non-homogeneous equation of the second order:
After a series of transformations, we get an approximate analytical solution:
where is the constant of integration.
Let us find the value at the point . The first term, regardless of , should be close to zero. If we take , where , where is an arbitrary constant, we get that by choosing we can ensure proximity to with any degree of . Note that .
- (2)
- Let us find the solution in the interval
Similarly to item (1), we find the solution in the interval , using the equation :
where is the constant of integration.
To merge the solutions and , the condition of continuity and smoothness of the function at the point is used, which gives a system of equations that uniquely determines :
- (3)
- Making calculations similar to (1) and (2), it is easy to find and show that the relation is satisfied in the entire recombination region. In addition, from the solutions given above, it follows that the width of the recombination region is of the order of .
5.2. Analytical Solution in the Extended RPR
We present the solution in the extended region of space charge . As follows from the analysis of the numerical solution in this region and the asymptotic estimates [17], dissociation dominates over recombination, and slowly decreases, and is of the order of (Figure 3).
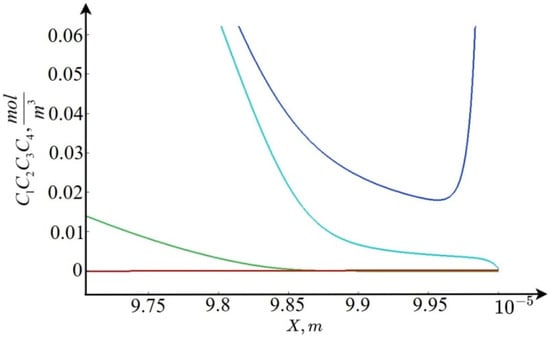
Figure 3.
Graphs of concentrations in the extended space charge region: blue is the concentration of cations, light blue is the concentration of , green is the concentration of anions, and red is the concentration of ions.
Using these relations, the original system of equations in the extended space charge region can be simplified:
An approximate solution to the system (25)–(28) depends on the relationship and , which is determined by the value . For small , we have , and for large , on the contrary , and for some , we obtain .
- (1)
- Let , then discarding the second term on the right-hand side of Equation (28), we obtain the expression for the flows
From this formula, it is clear that the effect of changing the equilibrium coefficient at in the extended region of space charge on the flows and, accordingly, the distribution of the concentration and electric field strength is insignificant, and the flows themselves increase linearly (see Figure 4).
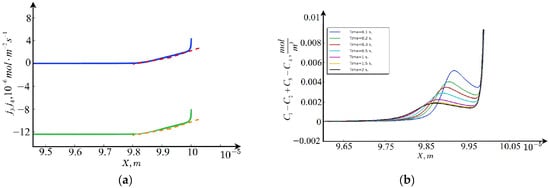
Figure 4.
(a)—graphs of (blue line) and (green line) calculated numerically (solid line) and analytically (dashed line); (b)—graphs of space charge for different t. Numerical and analytical data coincide with 99% accuracy.
For an analytical solution, we derive an equation for the electric field strength independent of the remaining unknowns.
The system of equations has a first integral
From Equations (26) and (27), we have the relation
Substituting into which the first integral and the value , we obtain the equation:
Using asymptotic estimates, it can be shown that the left-hand side of the equation in the extended region of the space charge is small compared to the remaining terms of the equation. As a result, to find the electric field strength, we obtain the equation
which has one isolated positive solution, using which, we find the remaining functions from the solution of linear Equations (26) and (27).
- (2)
- Let ,
Using Equations (25) and (28), we obtain the relationship and ; namely, from one equation, we express and substitute into the other, and integrating which, we obtain
, where is the integration constant. Let us write this equation using the electric field strength as:
where we can see the linear dependence of the and flows on the electric field strength in the extended space charge region.
Substitute into Equation (27), and after a series of transformations, we obtain the first integral of the system
where is the integration constant.
Using the first equation and the first integral, we obtain an equation for that does not contain other unknown functions:
Asymptotic evaluation of the terms of this equation shows that the term on the left-hand side of the equation is small compared to the remaining terms, so the equation can be used to calculate the potential:
This equation is solved analytically by introducing the parameter [28]. After determining , the remaining unknown functions are also found analytically from the solution of the linear Equations (26) and (27).
5.3. Analytical Solution in a Quasi-Equilibrium SCR on the Segment
In the case where the equilibrium coefficient does not depend on the space charge in this region, the flows of hydrogen and hydroxyl ions increase linearly, i.e., dissociation occurs with the maximum possible constant rate. However, when it depends on the space charge, the flows of hydrogen and hydroxyl ions increase with an exponential rate, i.e., the second Wien effect comes into play and the rate of dissociation of water molecules increases by many orders of magnitude.
From the analysis of the numerical solution it follows that this region is a quasi-equilibrium region of space charge, and , exponentially increases , , has a local maximum, and exponentially decreases to zero, , . In addition, and increase with the rate of the exponential.
Taking these assumptions into account, we obtain the following system of equations:
Integrating (30) from point to arbitrary point , we obtain
where , and, accordingly, we have
Thus, in a quasi-equilibrium SCR, the equilibrium coefficient exponentially depends on the electric field strength .
It is easy to verify that the system of Equations (30)–(33) has an analytical solution:
From this solution, it follows that the thickness of the quasi-equilibrium region is of the order of , i.e., the same as the width of the recombination region. This confirms the conclusions obtained using the similarity theory in Section 2.2.
6. Conclusions
A mathematical model of stationary transfer of a binary electrolyte in electromembrane systems is constructed taking into account the dissociation/recombination reaction and changes in the equilibrium coefficient. A similarity theory of the transfer process in the diffusion layer of a cation-exchange membrane has been developed. Using trivial similarity criteria, it has been shown that the size of the recombination region is of the same order of magnitude as the quasi-equilibrium region of the space charge. A non-trivial similarity criterion has been found and the contribution of the dissociation/recombination reaction of water molecules to the transfer of salt ions in the diffusion layer has been clarified. It has been shown that, assuming that the thickness of the diffusion layer remains constant, the effect of the dissociation/recombination reaction of water molecules decreases with increasing initial concentration of the solution and, conversely, increases with decreasing initial concentration at a quadratic rate. The similarity theory constructed above is of great importance for engineering calculations and for scaling experimental results. With increasing initial concentration of the solution, the value of the small parameter entering singularly decreases and reaches values of the order of 10−12 or less, which leads to computational difficulties that do not allow an exhaustive analysis of the effect of changes in the equilibrium constant on the transport of salt ions. In this regard, an analytical solution to the problem has been constructed, based on the division of the solution, which was divided into a number of subregions (electroneutrality regions, extended space charge region, quasi-equilibrium region, recombination region, intermediate layer), in each of which the problem was solved in its own way, and then these solutions were merged. The analytical solution was verified by comparison with the numerical solution, which shows a match with 99% accuracy. The advantage of the obtained analytical solution is the possibility of an exhaustive analysis of the effect of the dissociation/recombination reaction of water molecules on the transfer of salt ions over a wide range of real changes in the concentration and composition of the electrolyte solution and other input parameters. For example, it was shown that the dependence of the equilibrium coefficient on the space charge leads to a linear dependence on the electric field strength in the extended space charge region and an exponential dependence on the electric field strength in the quasi-equilibrium space charge region. This is a non-trivial generalization of the assumption of an exponential dependence of the equilibrium coefficient on the electric field strength for bipolar ion-exchange membranes to the case of monopolar membranes. The boundary value problem solved in this work is a reference for constructing asymptotic solutions for other singularly perturbed boundary value problems of membrane electrochemistry.
Author Contributions
Conceptualization, N.C. and M.U.; methodology, E.K.; software, R.N.; validation, A.K., N.C. and M.U.; formal analysis, E.K.; investigation, R.N.; resources, A.K.; data curation, N.C.; writing—original draft preparation, M.U.; writing—review and editing, E.K.; visualization, R.N.; supervision, M.U.; project administration, E.K.; funding acquisition, A.K., N.C. and M.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, research project No. 24-19-00648, https://rscf.ru/project/24-19-00648/ (accessed on 13 April 2025). Open Access funding was provided by the Open Access Publication Fund of the RheinMain University of Applied Sciences, https://ror.org/0378gm372 (accessed on 12 March 2025).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; John Wiley and Sons Inc.: New York, NY, USA, 1994; 416p. [Google Scholar]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems; John Wiley & Sons, Inc.: Hoboken, NJ, Canada, 2004; 672p. [Google Scholar]
- Kovalenko, S.; Kirillova, E.; Chekanov, V.; Uzdenova, A.; Urtenov, M. Analytical Solutions and Computer Modeling of a Boundary Value Problem for a Nonstationary System of Nernst–Planck–Poisson Equations in a Diffusion Layer. Mathematics 2024, 12, 4040. [Google Scholar] [CrossRef]
- Ding, J.; Zhou, S. Second-order, positive, and unconditional energy dissipative scheme for modified Poisson–Nernst–Planck equations. J. Comput. Phys. 2024, 510, 113094. [Google Scholar] [CrossRef]
- Sheldeshov, N.V.; Zabolotsky, V.I.; Kovalev, N.V.; Karpenko, T.V. Electrochemical Characteristics of Heterogeneous Bipolar Membranes and Electromembrane Process of Recovery of Nitric Acid and Sodium Hydroxide from Sodium Nitrate Solution. Sep. Purif. Technol. 2020, 241, 116648. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotic slip of the second kind and instability in concentration polarization at electrodialysis membranes. Math. Model. Numer. Anal. 2000, 34, 263–281. [Google Scholar] [CrossRef]
- Yaroshchuk, A. Non-stationary ion transport through charged membranes: A numerical solution. J. Membr. Sci. 2000, 167, 1–17. [Google Scholar]
- Nikonenko, V.V.; Pismenskaya, N.D.; Belova, E.I.; Sistat, P.; Huguet, P.; Pourcelly, G. Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis. Adv. Colloid Interface Sci. 2010, 160, 101–123. [Google Scholar] [CrossRef] [PubMed]
- Biesheuvel, P.M.; Bazant, M.Z. Nonlinear dynamics of capacitive charging and desalination by porous electrodes. Phys. Rev. E 2010, 81, 031502. [Google Scholar] [CrossRef]
- Kim, S.J.; Han, J. Self-assembled monolayers for electrokinetic phenomena in microfluidics. Lab A Chip 2008, 8, 1163–1170. [Google Scholar]
- Kornyshev, A.A. Double-layer in ionic liquids: Paradigm change? J. Phys. Chem. B 2007, 111, 5545–5557. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena: Theory and microfluidic applications. Phys. Rev. Lett. 2004, 92, 066101. [Google Scholar] [CrossRef]
- Liu, C.; Wang, C.; Wise, S.M.; Yue, X.; Zhou, S. A positivity-preserving, energy stable and convergent numerical scheme for the Poisson-Nernst-Planck system. Math. Comp. 2021, 90, 2071–2106. [Google Scholar] [CrossRef]
- Kumar, M.; Parul. Methods for solving singular perturbation problems arising in science and engineering. Math. Comput. Model. 2011, 54, 556–575. [Google Scholar] [CrossRef]
- Shiromani, R.; Shanthi, V.; Ramos, H. Numerical Treatment of a Two-Parameter Singularly Perturbed Elliptic Problem with Discontinuous Convection and Source Terms. Differ. Equ. Dyn. Syst. 2025, 33, 303–331. [Google Scholar] [CrossRef]
- Kumar, M.H.; Saini, S. Various Numerical Methods for Singularly Perturbed Boundary Value Problems. Am. J. Appl. Math. Stat. 2014, 2, 129–142. [Google Scholar] [CrossRef][Green Version]
- Illingworth, T.C.; Golosnoy, I.O. Numerical solutions of diffusion-controlled moving boundary problems which conserve solute. J. Comput. Phys. 2005, 209, 207–225. [Google Scholar] [CrossRef]
- Martín, J.; Rodríguez-Mateos, F.; Company, R. Analytic solution of mixed problems for thegeneralized diffusion equation with delay. Math. Comput. Model. 2004, 40, 361–369. [Google Scholar] [CrossRef]
- Krol, J.J.; Wessling, M.; Strathmann, H. Concentration polarization with monopolar ion exchange membranes: Current-voltage curves and water dissociation. J. Membr. Sci. 1999, 162, 145–154. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef]
- Zholkovskij, E.K.; Masliyah, J.H. Electrokinetic phenomena in concentrated suspensions: Theory and experiment. Adv. Colloid Interface Sci. 2004, 112, 59–83. [Google Scholar]
- Manzanares, J.A.; Murphy, W.D. Electrokinetic phenomena in porous membranes: From ion transport to energy conversion. J. Membr. Sci. 2003, 212, 1–15. [Google Scholar]
- Nikonenko, V.V.; Pis’menskaya, N.D.; Volodina, E.I. Rate of Generation of Ions H+ and OH− at the Ion-Exchange Membrane/Dilute Solution Interface as a Function of the Current Density. Russ. J. Electrochem. 2005, 41, 1205. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications; Wiley: New York, NY, USA, 2000; 864p. [Google Scholar]
- Urtenov, M.K.; Kovalenko, A.V.; Sukhinov, A.I.; Chubyr, N.O.; Gudza, V.A. Model and numerical experiment for calculating the theoretical current-voltage characteristic in electro-membrane systems. IOP Conf. Ser. Mater. Sci. Eng. 2019, 680, 012030. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Theoretical Analysis of the Effect of Ion Concentration in Solution Bulk and at Membrane Surface on the Mass Transfer at Overlimiting Currents. Russ. J. Electrochem. 2017, 53, 1254–1265. [Google Scholar] [CrossRef]
- Vasil’eva, A.B.; Butuzov, V.F. Singularly Perturbed Equations in Critical Cases; Moscow University: Moscow, Russia, 1978; p. 106. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems, 8th ed.; Wiley: New York, NY, USA, 2004; 625p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).