Multi-Vehicle Collision Avoidance by Vehicle Longitudinal Control Based on Optimal Collision Distance Estimation
Abstract
1. Introduction
- Estimation of collision points on vehicle surfaces for collision avoidance.
- Identification and estimation of optimal collision points for multiple vehicles.
- Comparative experimental validation of collision avoidance systems based on estimated collision points.
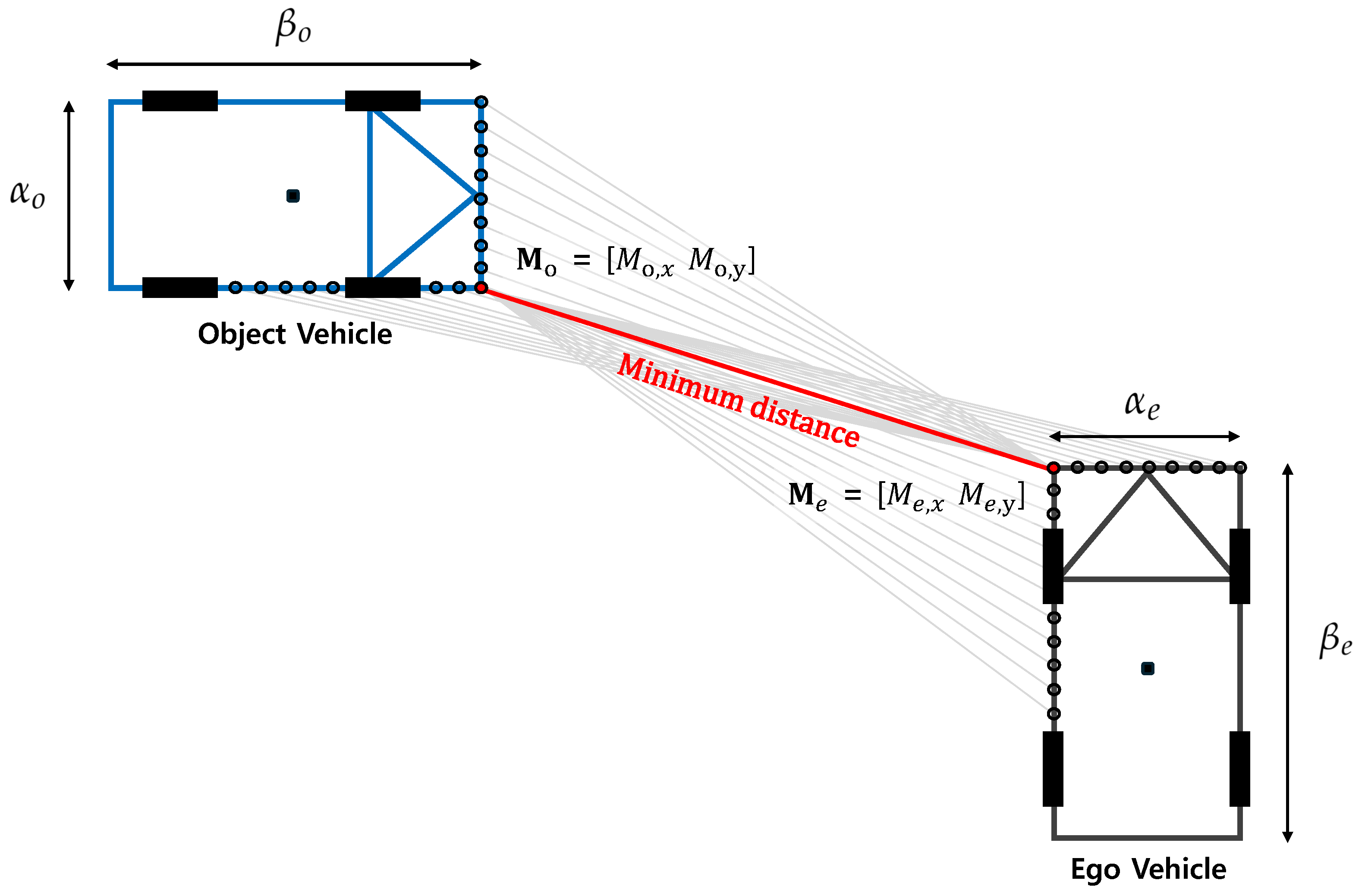
2. Vehicle Collision Point Estimation
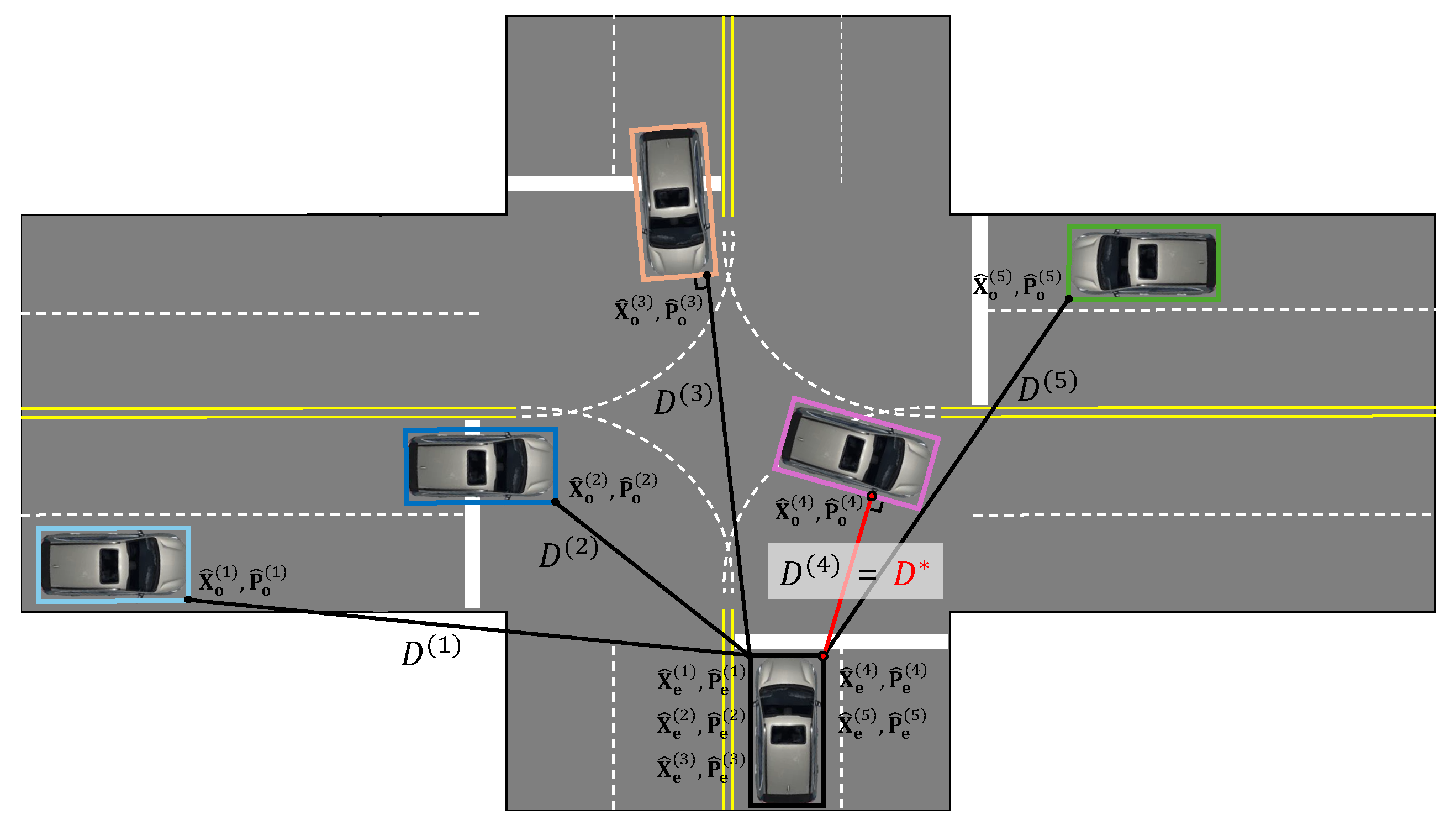
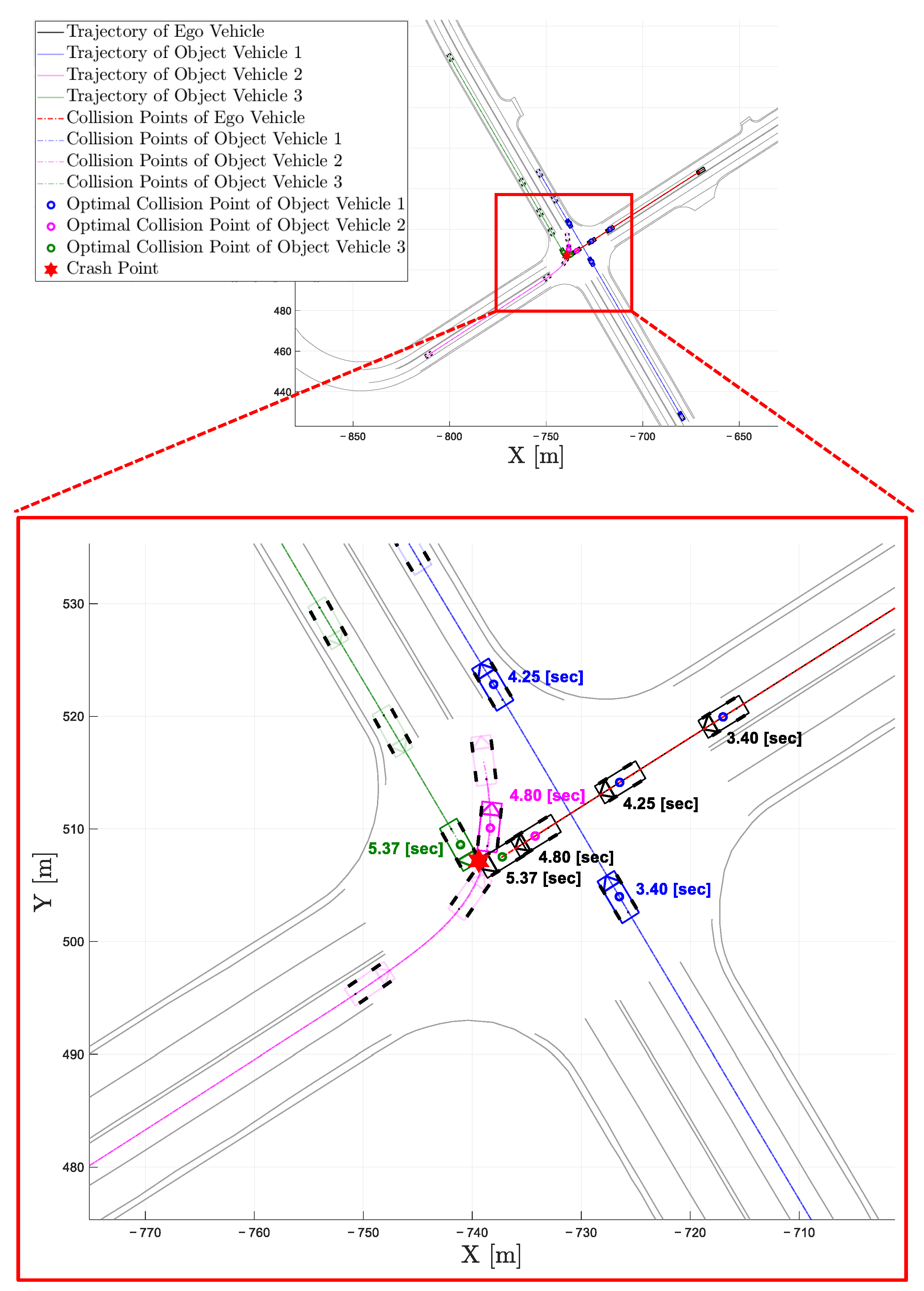
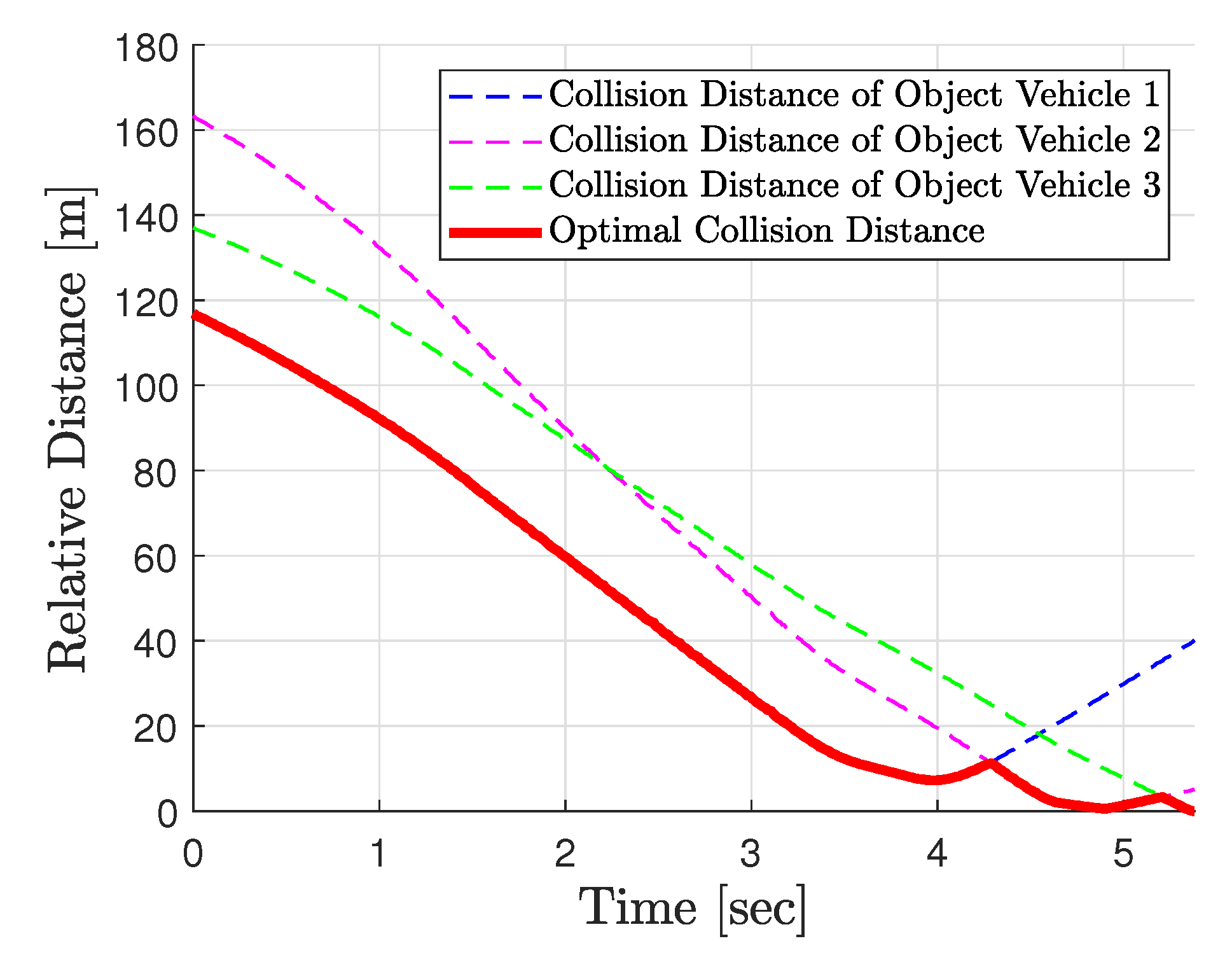
3. Multi-Vehicle Collision Point Identification
4. Optimal Longitudinal Control with Time Gap
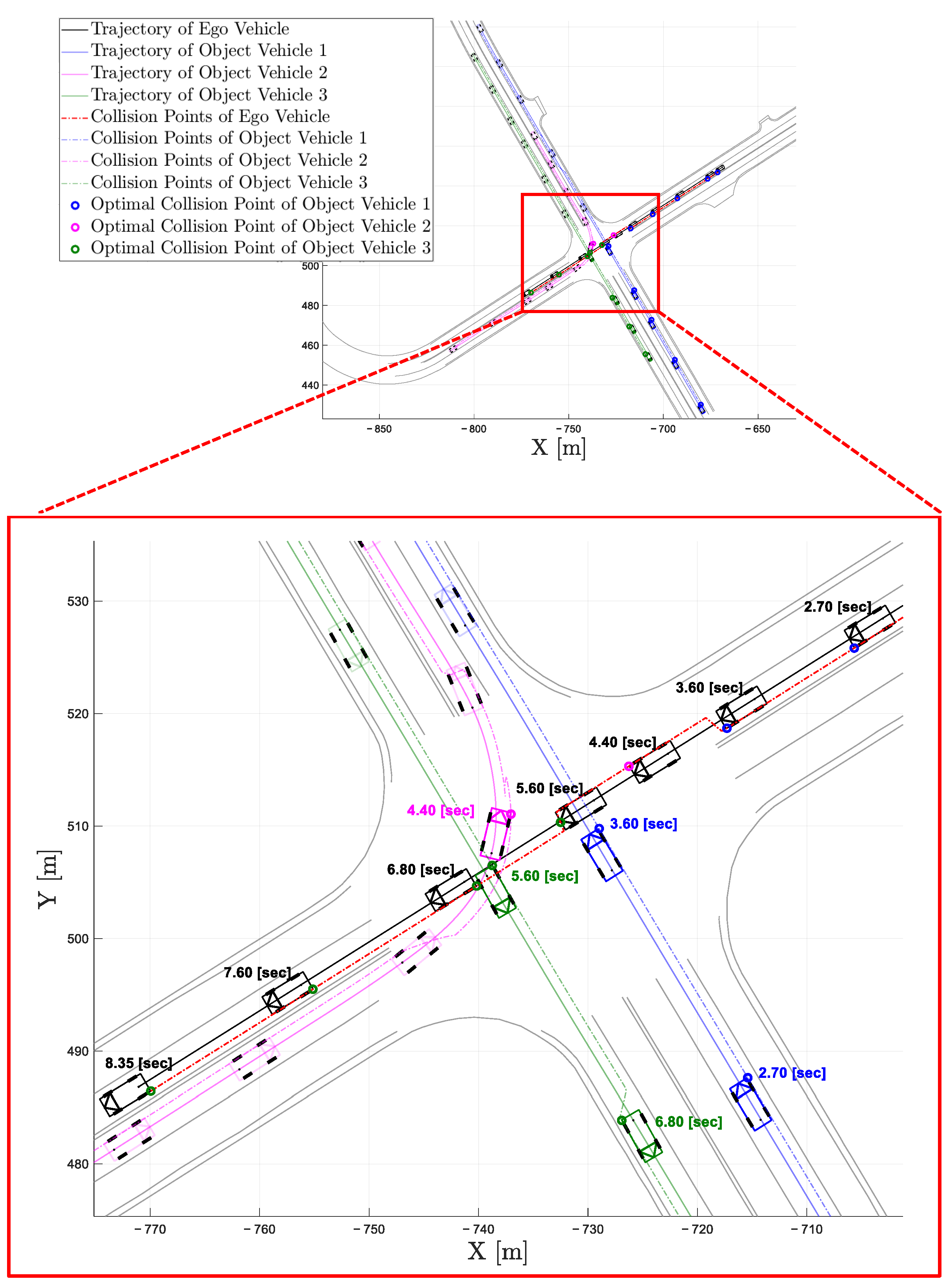
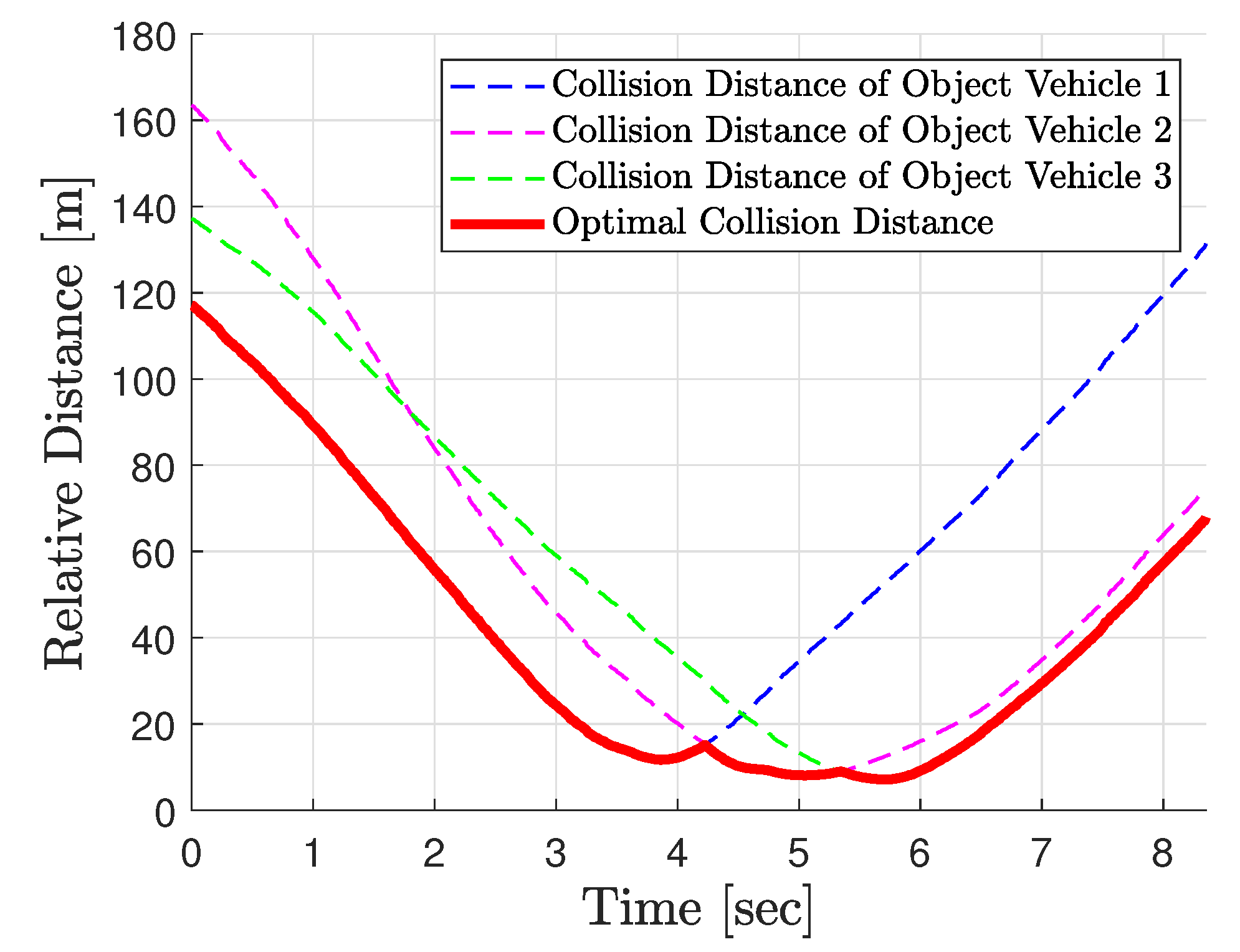
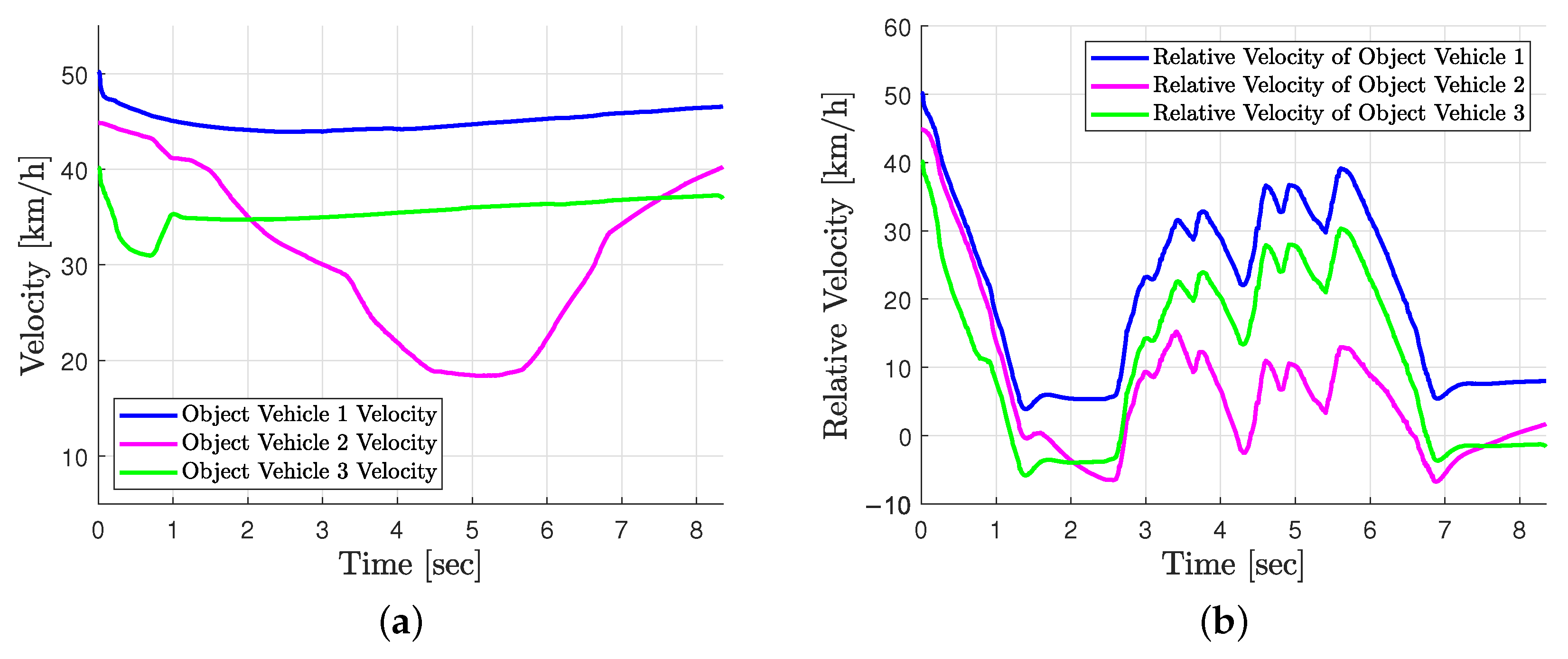
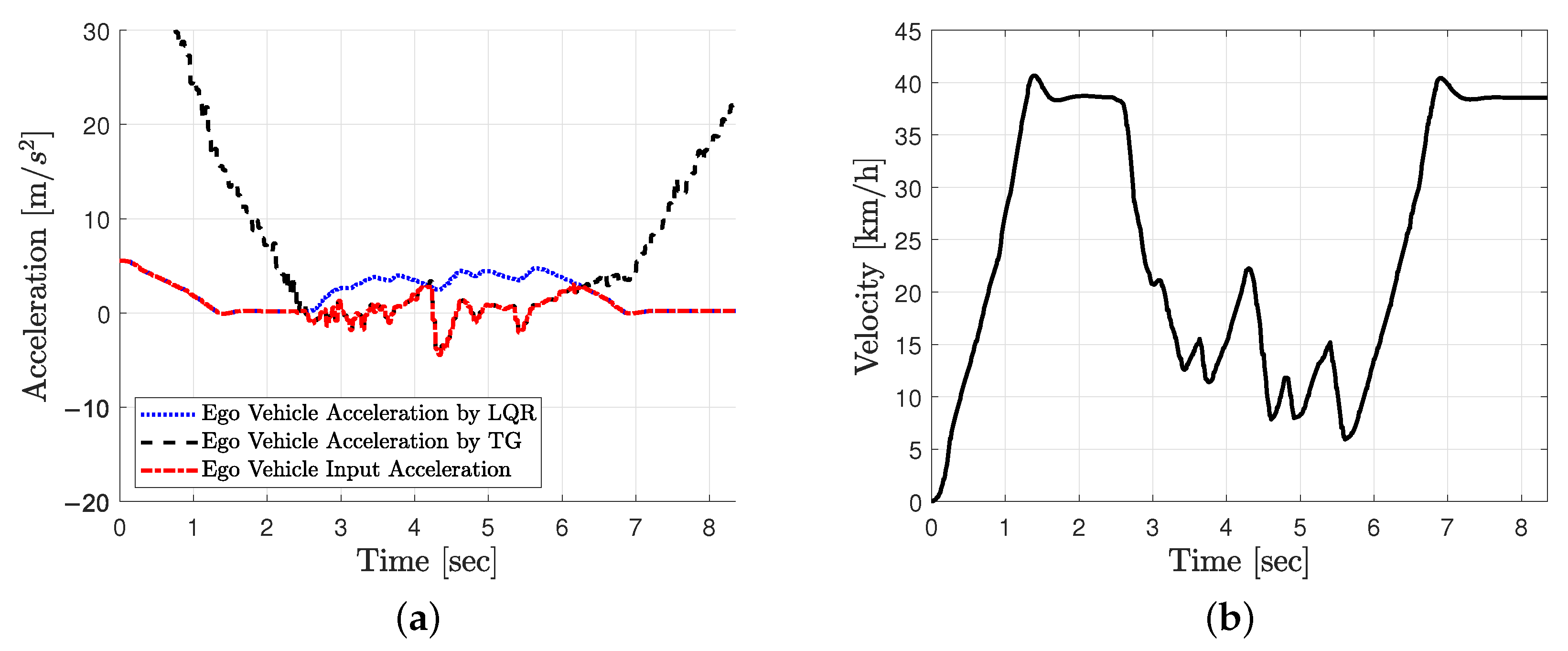
5. Experiment
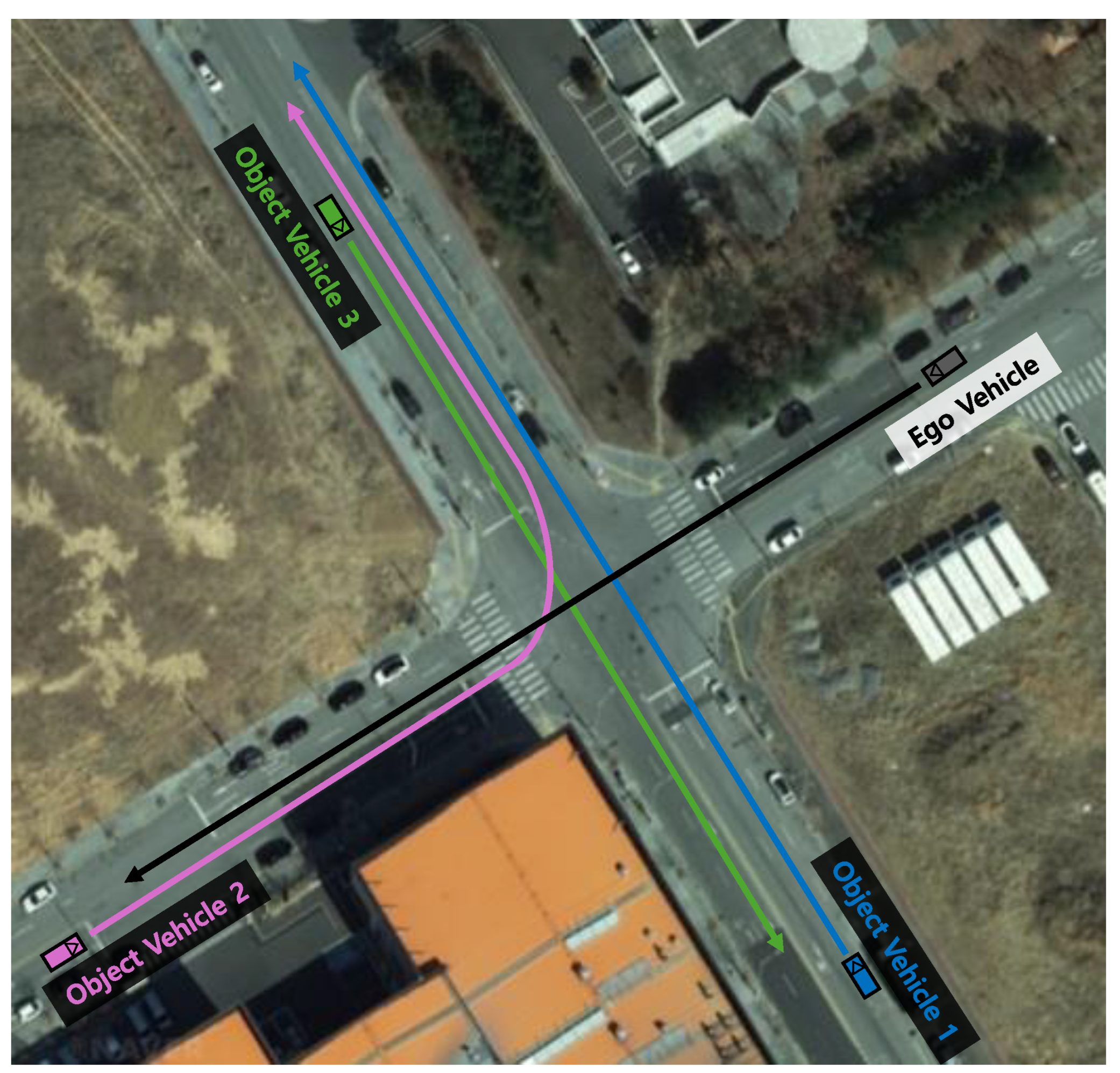
5.1. Experimental Setup
5.2. Scenario-Based Simulation
5.3. Test Result
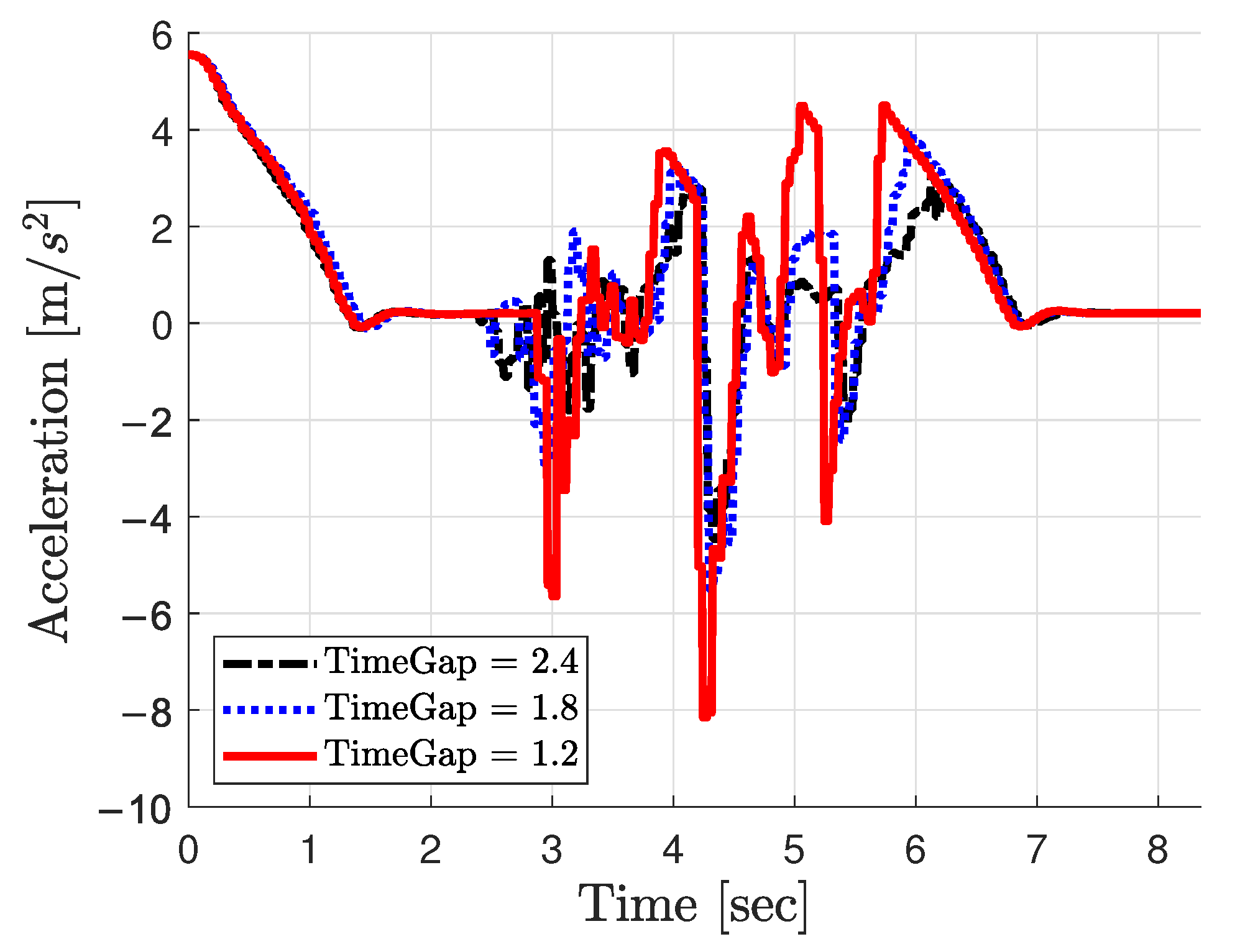
5.4. Experiment Varying Time-Gap Parameter
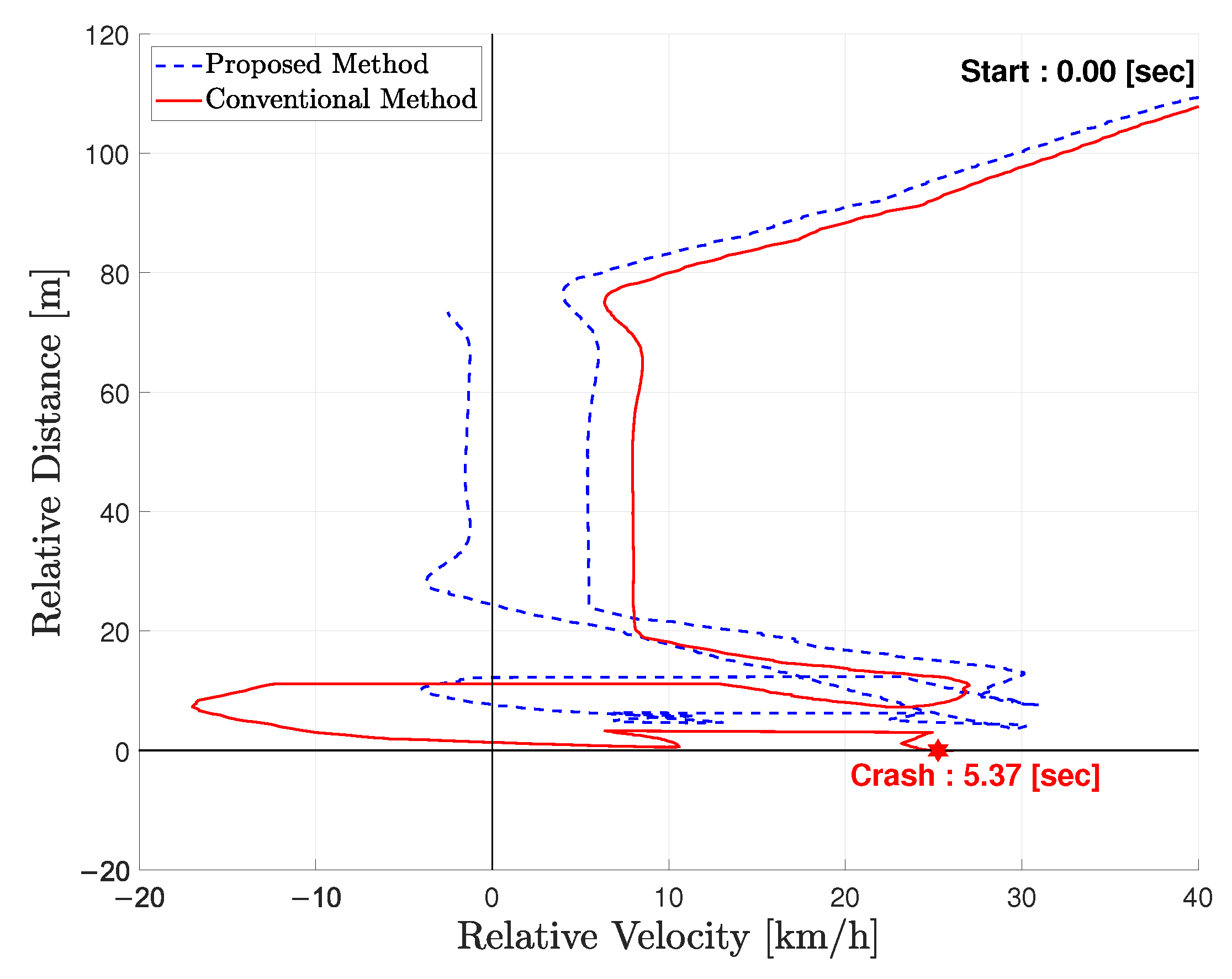
5.5. Comparison Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, Y.; Li, C.; Yu, F.R.; Luan, T.H.; Zhang, Y. A Survey of Driving Safety with Sensing, Vehicular Communications, and Artificial Intelligence-Based Collision Avoidance. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6142–6163. [Google Scholar] [CrossRef]
- Choi, W.Y.; Lee, S.H.; Chung, C.C. On-Road Object Collision Point Estimation by Radar Sensor Data Fusion. IEEE Trans. Intell. Trans. Syst. 2021, 23, 14753–14763. [Google Scholar] [CrossRef]
- Altendorfer, R.; Wilkmann, C. A new approach to estimate the collision probability for automotive applications. Automatica 2021, 127, 109497. [Google Scholar] [CrossRef]
- Choi, W.Y.; Yang, J.H.; Chung, C.C. Data-Driven Object Vehicle Estimation by Radar Accuracy Modeling with Weighted Interpolation. Sensors 2021, 21, 2317. [Google Scholar] [CrossRef]
- Lee, H.; Kang, C.M.; Kim, W.; Choi, W.Y.; Chung, C.C. Predictive risk assessment using cooperation concept for collision avoidance of side crash in autonomous lane change systems. In Proceedings of the 2017 17th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 18–21 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 47–52. [Google Scholar]
- Kim, J.; Kum, D. CollisionRrisk Assessment Algorithm via Lane-Based Probabilistic Motion Prediction of Surrounding Vehicles. IEEE Trans. Intell. Trans. Syst. 2017, 19, 2965–2976. [Google Scholar] [CrossRef]
- Li, G.; Yang, Y.; Zhang, T.; Qu, X.; Cao, D.; Cheng, B.; Li, K. Risk assessment based collision avoidance decision-making for autonomous vehicles in multi-scenarios. Transp. Res. Part C Emerg. Technol. 2021, 122, 102820. [Google Scholar] [CrossRef]
- Ma, Y.; Dong, F.; Yin, B.; Lou, Y. Real-time risk assessment model for multi-vehicle interaction of connected and autonomous vehicles in weaving area based on risk potential field. Phys. A Stat. Mech. Its Appl. 2023, 620, 128725. [Google Scholar] [CrossRef]
- Noh, S. Decision-Making Framework for Autonomous Driving at Road Intersections: Safeguarding Against Collision, Overly Conservative Behavior, and Violation Vehicles. IEEE Trans. Ind. Electron. 2018, 66, 3275–3286. [Google Scholar] [CrossRef]
- Katrakazas, C.; Quddus, M.; Chen, W.H. A new integrated collision risk assessment methodology for autonomous vehicles. Accid. Anal. Prev. 2019, 127, 61–79. [Google Scholar] [CrossRef]
- He, X.; Liu, Y.; Lv, C.; Ji, X.; Liu, Y. Emergency steering control of autonomous vehicle for collision avoidance and stabilisation. Veh. Syst. Dyn. 2019, 57, 1163–1187. [Google Scholar] [CrossRef]
- Zou, Z.; Chen, K.; Shi, Z.; Guo, Y.; Ye, J. Object Detection in 20 Years: A Survey. Proc. IEEE 2023, 111, 257–276. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Y.; Zhang, S.; Ogai, H. Deep 3D Object Detection Networks Using LiDAR Data: A Review. IEEE Sens. J. 2020, 21, 1152–1171. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, P.; Xu, Z.; Min, H.; Yu, H. Fusion of 3D LIDAR and Camera Data for Object Detection in Autonomous Vehicle Applications. IEEE Sens. J. 2020, 20, 4901–4913. [Google Scholar] [CrossRef]
- Ghasemieh, A.; Kashef, R. 3D object detection for autonomous driving: Methods, models, sensors, data, and challenges. Transp. Eng. 2022, 8, 100115. [Google Scholar] [CrossRef]
- Lee, S.H.; Choi, W.Y. Enhancing Object Estimation by Camera-LiDAR Sensor Fusion Using IMM-KF with Error Characteristics in Autonomous Robot Systems. IEEE Access 2024, 12, 197247–197258. [Google Scholar] [CrossRef]
- Ravindran, R.; Santora, M.J.; Jamali, M.M. Multi-Object Detection and Tracking, Based on DNN, for Autonomous Vehicles: A Review. IEEE Sens. J. 2020, 21, 5668–5677. [Google Scholar] [CrossRef]
- Feng, D.; Haase-Schütz, C.; Rosenbaum, L.; Hertlein, H.; Glaeser, C.; Timm, F.; Wiesbeck, W.; Dietmayer, K. Deep Multi-Modal Object Detection and Semantic Segmentation for Autonomous Driving: Datasets, Methods, and Challenges. IEEE Trans. Intell. Trans. Syst. 2020, 22, 1341–1360. [Google Scholar] [CrossRef]
- Watta, P.; Zhang, X.; Murphey, Y.L. Vehicle Position and Context Detection Using V2V Communication. IEEE Trans. Intell. Veh. 2020, 6, 634–648. [Google Scholar] [CrossRef]
- Li, Y.; Ma, D.; An, Z.; Wang, Z.; Zhong, Y.; Chen, S.; Feng, C. V2X-Sim: Multi-Agent Collaborative Perception Dataset and Benchmark for Autonomous Driving. IEEE Robot. Autom. Lett. 2022, 7, 10914–10921. [Google Scholar] [CrossRef]
- Lin, F.; Wang, K.; Zhao, Y.; Wang, S. Integrated Avoid Collision Control of Autonomous Vehicle Based on Trajectory Re-Planning and V2V Information Interaction. Sensors 2020, 20, 1079. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Guo, H.Q.; Chen, Z.G.; Song, P. Longitudinal Collision Avoidance and Lateral Stability Adaptive Control System Based on MPC of Autonomous Vehicles. IEEE Trans. Intell. Trans. Syst. 2019, 21, 2376–2385. [Google Scholar] [CrossRef]
- Cao, Y.; Fang, X. Optimized-Weighted-Speedy Q-Learning Algorithm for Multi-UGV in Static Environment Path Planning under Anti-Collision Cooperation Mechanism. Mathematics 2023, 11, 2476. [Google Scholar] [CrossRef]
- Zheng, L.; Zeng, P.; Yang, W.; Li, Y.; Zhan, Z. Bézier curve-based trajectory planning for autonomous vehicles with collision avoidance. IET Intell. Transp. Syst. 2020, 14, 1882–1891. [Google Scholar] [CrossRef]
- Ammour, M.; Orjuela, R.; Basset, M. A MPC Combined Decision Making and Trajectory Planning for Autonomous Vehicle Collision Avoidance. IEEE Trans. Intell. Trans. Syst. 2022, 23, 24805–24817. [Google Scholar] [CrossRef]
- Fu, T.; Nguyen, H.H.; Findeisen, R. Guaranteed Collision Avoidance for Autonomous Vehicles Fusing Model Predictive Control and Data Driven Reachability Analysis. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 2286–2291. [Google Scholar]
- Hajiloo, R.; Abroshan, M.; Khajepour, A.; Kasaiezadeh, A.; Chen, S.K. Integrated Steering and Differential Braking for Emergency Collision Avoidance in Autonomous Vehicles. IEEE Trans. Intell. Trans. Syst. 2020, 22, 3167–3178. [Google Scholar] [CrossRef]
- Cui, Q.; Ding, R.; Wu, X.; Zhou, B. A new strategy for rear-end collision avoidance via autonomous steering and differential braking in highway driving. Veh. Syst. Dyn. 2020, 58, 955–986. [Google Scholar] [CrossRef]
- Choi, W.Y.; Lee, S.H.; Chung, C.C. Horizonwise Model-Predictive Control with Application to Autonomous Driving Vehicle. IEEE Trans. Ind. Informatics 2021, 18, 6940–6949. [Google Scholar] [CrossRef]
- Choi, W.Y.; Lee, S.H.; Chung, C.C. Robust Vehicular Lane-Tracking Control with a Winding Road Disturbance Compensator. IEEE Trans. Ind. Informatics 2020, 17, 6125–6133. [Google Scholar] [CrossRef]
- Khayatian, M.; Mehrabian, M.; Andert, E.; Dedinsky, R.; Choudhary, S.; Lou, Y.; Shirvastava, A. A Survey on Intersection Management of Connected Autonomous Vehicles. ACM Trans. Cyber-Phys. Syst. 2020, 4, 1–27. [Google Scholar] [CrossRef]
- Shu, K.; Yu, H.; Chen, X.; Li, S.; Chen, L.; Wang, Q.; Li, L.; Cao, D. Autonomous Driving at Intersections: A Behavior-Oriented Critical-Turning-Point Approach for Decision Making. IEEE/ASME Trans. Mechatronics 2021, 27, 234–244. [Google Scholar] [CrossRef]
- Song, W.; Yang, Y.; Fu, M.; Qiu, F.; Wang, M. Real-Time Obstacles Detection and Status Classification for Collision Warning in a Vehicle Active Safety System. IEEE Trans. Intell. Trans. Syst. 2017, 19, 758–773. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, P.; Lu, G. Cooperative autonomous traffic organization method for connected automated vehicles in multi-intersection road networks. Transp. Res. Part C Emerg. Technol. 2020, 111, 458–476. [Google Scholar] [CrossRef]
- Fu, Y.; Li, C.; Luan, T.H.; Zhang, Y.; Mao, G. Infrastructure-cooperative algorithm for effective intersection collision avoidance. Transp. Res. Part C Emerg. Technol. 2018, 89, 188–204. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Yan, X.; Li, X.; Duan, K.; Xue, Q. Using a V2V-and V2I-based collision warning system to improve vehicle interaction at unsignalized intersections. J. Saf. Res. 2022, 83, 282–293. [Google Scholar] [CrossRef]
- Li, G.; Lin, S.; Li, S.; Qu, X. Learning automated driving in complex intersection scenarios based on camera sensors: A deep reinforcement learning approach. IEEE Sens. J. 2022, 22, 4687–4696. [Google Scholar] [CrossRef]
- Wang, B.; Gong, X.; Wang, Y.; Lyu, P.; Liang, S. Coordination for connected and autonomous vehicles at unsignalized intersections: An iterative learning-based collision-free motion planning method. IEEE Internet Things J. 2023, 11, 5439–5454. [Google Scholar] [CrossRef]
- Jin, X.; Yang, H.; He, X.; Liu, G.; Yan, Z.; Wang, Q. Robust LiDAR-Based Vehicle Detection for On-Road Autonomous Driving. Remote Sens. 2023, 15, 3160. [Google Scholar] [CrossRef]
- Edelsbrunner, H. Algorithms in Combinatorial Geometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987; Volume 10. [Google Scholar]
- Grewal, M.S. Kalman Filtering; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Choi, W.Y.; Chung, C.C. Optimizing Look-Ahead Distance for Vehicle Lateral Control: A Controller-Adaptive Approach. IEEE Trans. Intell. Veh. 2024. [Google Scholar] [CrossRef]
- Gdey, K.L.; Choi, W.Y. Optimized Super-Twisting Sliding Mode Control with Parameter Estimation for Autonomous Vehicle Longitudinal Motion on Downhill Road. Appl. Sci. 2025, 15, 981. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- ISO 26262; Road Vehicles—Functional Safety. International Organization for Standardization: Geneva, Switzerland, 2018.


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.H.; Lee, Y.; Son, Y.S.; Choi, W.Y. Multi-Vehicle Collision Avoidance by Vehicle Longitudinal Control Based on Optimal Collision Distance Estimation. Mathematics 2025, 13, 1283. https://doi.org/10.3390/math13081283
Lee JH, Lee Y, Son YS, Choi WY. Multi-Vehicle Collision Avoidance by Vehicle Longitudinal Control Based on Optimal Collision Distance Estimation. Mathematics. 2025; 13(8):1283. https://doi.org/10.3390/math13081283
Chicago/Turabian StyleLee, Joon Ho, Youngok Lee, Young Seop Son, and Woo Young Choi. 2025. "Multi-Vehicle Collision Avoidance by Vehicle Longitudinal Control Based on Optimal Collision Distance Estimation" Mathematics 13, no. 8: 1283. https://doi.org/10.3390/math13081283
APA StyleLee, J. H., Lee, Y., Son, Y. S., & Choi, W. Y. (2025). Multi-Vehicle Collision Avoidance by Vehicle Longitudinal Control Based on Optimal Collision Distance Estimation. Mathematics, 13(8), 1283. https://doi.org/10.3390/math13081283






