1. Introduction
We consider a boundary-value problem for the
n-dimensional Laplace equation with
:
where
is the smooth boundary of a bounded domain
.
Notice that the complex number
can be written as
with
, such that
. It is known that in terms of
z and
, the 2D Laplace equation can be written as
such that the general solution is given by
where
F and
G are any differentiable functions.
In a domain
, a complex-valued function
is said to be
analytic if it has a derivative at every point in
. A complex function
is analytic if and only if
which are well-known Cauchy–Riemann equations [
1]. As a consequence of Equation (
6),
;
and
are harmonic functions for the 2D Laplace equation.
In the complex form, the Cauchy–Riemann equations can be merged into a single equation:
If
and
are 2D harmonic functions, then it is easy to prove that
are both the solutions of Equation (
6);
and
are potential functions for
u and
v, automatically satisfying the Cauchy–Riemann equations.
The single variable analytic function can be extended to multivariate analytic function [
2,
3]. Let
be a function defined on
. If
is analytic for each
in the above sense, then
is an
m-dimensional analytic function. Let
be open, and
a
function. Write
with
, and define for
:
Then, we have the result that
f is analytic on
if and only if
for
. Equation (
12) comprises
m-dimensional Cauchy–Riemann equations. Considering the mapping
, the underlying space of the multivariate analytic function theory is the even-dimensional real space
(or
).
The issue of how to extend the general solution (
5) for the
n-dimensional Laplace equation is interesting, especially for
. Moreover, the problem of constructing the analytic function theory and the Cauchy–Riemann equations is a challenging task, if
n is not an even number.
If n is an even number, the multivariate complex function theory can be applied to construct the analytic function with . If n is an odd number, can the single-complex-variable analytic function theory be applied to construct the analytic function and the harmonic function in the space ? This problem is not yet fully taken into account and addressed in the literature.
In the literature, the four-component
in the 3D elliptic system was set up by Moisil and Teodorescu [
4]:
It can be observed that
are harmonic functions in the 3D space, and so Equation (
13) is a generalization of the Cauchy–Riemann equations, which is the Moisil–Teodorescu system [
5,
6,
7,
8]. Motivated by this work, there are many different extensions of the Moisil–Teodorescu system based on the theories of quaternion and hypercomplex [
9,
10,
11,
12,
13,
14,
15].
For the 3D Laplace equation, a typical analytic process to derive the series solutions in different coordinates’ systems are (i) using the method of separation of variables; (ii) deriving ordinary differential equations (ODEs), which are generally constructed with varying coefficients, like as the Bessel equation and the Legendre equation; (iii) solving the corresponding Sturm–Liouville problem to determine the eigenfunctions and eigenvalues; and finally, (iv) determining the expanding coefficients to match the specified boundary conditions.
In such a traditional method, we may encounter the difficulty that the solution bases are some special functions, which are not the elementary functions. The analytic process would become tedious when the dimension of the Laplace equation is raised. To overcome these difficulties, we will propose a novel method to transform the multi-dimensional Laplace equation to a second-order ODE with a constant coefficient, which can greatly simplify the work to seek the analytic solutions and derive a powerful method with the elementary functions or the compositions of elementary functions as the bases for the series solutions. We will construct new projective-type particular solutions, which are based on the 2D general solutions in Equation (
5) derived from the conventional complex analytic function theory, for the
n-dimensional Laplace equation, and demonstrate a new aspect of the analytic functions and the Cauchy–Riemann equations for the
n-dimensional Laplace equation.
In addition to the Trefftz method [
16,
17,
18], the method of fundamental solutions (MFS) can be used to solve the Laplace equation as a boundary-type meshless method. The MFS has been applied to solve a lot of boundary-value problems of the Laplace equation [
19,
20,
21,
22,
23,
24]. We are going to apply the analytic function theory to derive some useful bases for solving the 2D and 3D Laplace equations.
In the traditional method for solving the 3D Laplace equation, we may encounter the difficulty that the solution bases are certain special functions, such as the spherical harmonic functions, the Bessel functions, and the modified Bessel functions, which need extra computations of these functions. The motivation of the present study is that we will derive very simple bases for the 3D Laplace equation, which consist of the elementary functions, such as the cosine function, sine function, cosine hyperbolic function, sine hyperbolic function, and exponential function. In doing so, we can overcome the difficulty of traditional methods. However, the present method is limited to the linear PDEs with constant coefficients.
Let us consider the
n-dimensional second-order linear PDEs with constant coefficients:
where
is an
symmetric matrix. In the characteristic theory of second-order linear PDEs, the characteristic form [
25,
26]
is crucial, where
with
is the characteristic vector to satisfy the equation
.
The novelties involved in the paper are as follows:
The new projective solutions of 2D, 3D, and n-dimensional Laplace equations are evaluated for the first time in the literature.
A new concept of projective variable is introduced, such that we can transform the Laplace equations to the second-order ODEs with the leading term multiplied by the squared norm of the characteristic vector, which must be a complex form to satisfy the null equation.
For the n-dimensional Laplace equation, its analytic function theory and the generalized Cauchy–Riemann equations are established using the projection technique and the complex analytic function theory; we provide an alternative way from the multivariate analytic function theory to construct the analytic function with a single complex variable and not limited to an even dimension.
In terms of analytic functions as the bases, a powerful numerical technique is created to solve the 2D and 3D Laplace equations.
Owing to its simple bases, the projective solutions method (PSM) outperforms the conventional methods.
Numerical experiments verify the accuracy and efficiency of the PSM by using the Trefftz-type bases derived from the analytic functions.
We outline the contents sequentially.
Section 2 is devoted to a new approach of the 2D Laplace equation by transforming it to a second-order ODE with a constant coefficient preceding to the second-order derivative term, whose value must be zero to satisfy the Laplace equation, such that the characteristic vector must have a complex form. In
Section 3, we introduce a new projective variable for the 3D Laplace equation, and different bases in the Cartesian coordinates, cylindrical coordinates, and spherical coordinates are established. The 3D analytic function theory and the projective-type particular solutions are developed in
Section 4. The analytic function theory for Equation (
1) is developed in
Section 5, where the Cauchy–Riemann equations and multi-dimensional analytic functions are generalized. The Trefftz-type bases are constructed in
Section 6, and the numerical tests of the 3D Laplace equation are carried out in
Section 7. Finally, the conclusions are given in
Section 8.
2. New Projective Solutions of the 2D Laplace Equation
Before embarking on the theory to present the analysis of the 3D Laplace equation, a schematic flow diagram is added to clarify the process of the proposed method in
Figure 1.
We first construct a new projective solution of Equation (
1) with
by introducing a new variable:
where the imaginary pair
satisfy
We will name the vector a characteristic vector, no matter whether it is real or complex. Hereby, w is a projective variable, because it is obtained by projecting the field point onto .
Theorem 1. If w is given by Equation (16), and Equation (17) is satisfied, thenis a projective-type particular solution satisfying Equation (1) with , where is a twice-differentiable function of w. Proof of Theorem 1. It follows from Equation (
16) that
and from Equations (
18) and (
19) that
where
is supposed to be a twice-differentiable function of
w. Inserting them into Equation (
1) with
yields
If Equation (
17) is satisfied, then Equation (
1) with
is proven. Since
v can be any twice-differentiable function of
w,
is a particular solution of Equation (
1) with
. □
It is of the utmost importance that the 2D Laplace equation is transformed to a second-order ODE in Equation (
21) with a constant coefficient
preceding
. For Equation (
21), if we take
, we can also derive the Laplace equation
. However, only a linear solution is obtained, which is not interesting. Therefore, for satisfying
, we must take
rather than
, and thus
can be an arbitrary differentiable function of
w. Equations (
16)–(
18) form a particular solution of the 2D Laplace equation. Chen et al. [
27] proposed the method of particular solutions for solving the PDEs without considering the homogeneous solution.
Like
z in Equation (
3), which can be viewed as the projection of the field point
onto
,
w in Equation (
16) is a generalization of
z;
w is obtained by projecting
onto
. Therefore,
w is called a projective variable. A function
is called a projective solution if it satisfies the following ODE:
Correspondingly, if
is given by Equation (
18), then
, where
is a particular projective solution of the 2D Laplace equation.
We consider different situations of Equation (
17).
- (A)
We take
and then
by Equation (
17), and
w in Equation (
16) is presented in the polar coordinates by
where
and
. Since
v can be any twice-differentiable function of
w, we can take
, such that
Taking the real and imaginary parts of
u generates the 2D Trefftz bases in the polar coordinates:
If we take
, then
are the fundamental solution and angular solution of the 2D Laplace equation.
and
are, respectively, the real and imaginary parts of
.
In the polar coordinates
, the 2D Laplace equation can be written as
Both
and
are particular solutions of Equation (
27). Because
is a polar angle, we call
an angular solution of the 2D Laplace equation.
- (B)
Alternatively, we can take
and then
in view of Equation (
17). By means of Equation (
16), we have
If we take
, we can derive
which are rudimentary solutions of Equation (
1) with
. In terms of the basic functions cosh, sinh, cos, and sin, we can express the solution of the 2D Laplace equation by
where
is the highest order of
k.
3. New Projective Solutions of the 3D Laplace Equation
We extend the above results to the 3D Laplace equation by introducing the following projective variable:
where the triplet
satisfies
Theorem 2. For the 3D Laplace equation, if the w given by Equations (31) and (32) is satisfied, thenis a projective-type particular solution. Proof of Theorem 2. It follows from Equation (
31) that
and from Equations (
33) and (
34) that
Inserting them into the left-hand side of Equation (
1) with
yields
If Equation (
32) is satisfied, then we can prove that
given by Equation (
33) satisfies Equation (
1) with
. □
By the same token, for Equation (
36) only a linear solution is obtained if we take
. Therefore, for satisfying the 3D Laplace equation
, we must take
, and thus
can be arbitrary twice-differentiable function of
w.
Because
w in Equation (
31) is obtained by projecting
onto
, we call it a projective variable. A function
is called a projective solution if it satisfies the following ODE:
Correspondingly, if
is given by Equation (
33), then
, where
is a particular projective solution of the 3D Laplace equation.
We discuss Equation (
32) by considering different cases.
- (A)
First, we take
and then by Equation (
32),
which is satisfied by
where
is a fictitious angle. In the Cartesian coordinates, we have
By taking
, we can generate the following bases:
Thus, the solution
of the 3D Laplace equation in the Cartesian coordinates can be presented by
- (B)
We take
and then, by Equation (
32),
which can be satisfied by
In the cylindrical coordinates,
and
can generate the following bases:
If we take
,
generates the following bases:
They are all the projective solutions of the 3D Laplace equation in the cylindrical coordinates. Thus, we can express the solution of
in the cylindrical coordinates
by
- (C)
If we take , and ,
generates the following bases:
Thus, we can express the solution
of 3D Laplace equation by
- (D)
In Equation (
49), if
r is replaced by
and
z replaced by
, we can express the solution of
in the spherical coordinates
by
Ku et al. [
18] employed the multiple-scale Trefftz method to solve the 3D Laplace equation in the cylindrical coordinates
with 18 independent bases involving the Bessel functions and the modified Bessel functions. Equation (
49) is simpler than that used in [
18]. However, the bases in Equations (
42), (
49), and (
53) are still too complex. In
Section 6, we will derive the so-called Trefftz-type bases, which are more compact.
4. Analytic Function and Projective-Type Particular Solutions of the 3D Laplace Equation
Because of Equation (
32), among
there is at least one element being a complex number. If we take
, then it follows from Equations (
32) and (
31) that
where
w is a complex variable, and
is a complex conjugate of
w.
Theorem 3. For the 3D Laplace equation, if w and are given by Equation (55), and Equation (54) is satisfied, thenis a projective-type particular solution of Equation (1) with , where F and G are differentiable functions. Proof of Theorem 3. By means of Equation (
55), we have
Summing the results, we can obtain
If Equation (
54) is satisfied, then we have
Hence, Equation (
56) is proven. □
Equation (
59) is an extension of Equation (
4) from the 2D Laplace equation to the 3D Laplace equation. To prove the following result, we recast Equation (
55) to a complex form:
where
and
z are, respectively, the real and imaginary parts of
w in Equation (
60). Here, we must take
and
to be real values, such that
is a real variable. In general, we take
and
, where
is an angle and
is a planar direction.
Notice that the single complex variable
w in Equation (
60) will be used to construct the analytic function, which is different from the multivariate analytic function theory, by using
m complex variables
.
Theorem 4. Let be a complex variable, where and . For the 3D Laplace equation, is an analytic function if and only if Further, and are harmonic functions in the 3D space: Proof of Theorem 4. By means of Equation (
61), we have
Summing the last two equations and using
renders
Thus, we have a 2D like Laplace equation:
According to Equation (
6), we have the following Cauchy–Riemann equations:
Multiplying the first one in Equation (
65) by
, the second one in Equation (
65) by
, summing the results and using Equation (
61), leads to
where
is a 2D gradient operator. This equation provides a rule how the operator
works, which is a directional derivative of
u along the direction
. Similarly, we can obtain
Inserting Equations (
70) and (
71) into Equation (
69), we can derive Equations (
62) and (
63).
Next, we prove Equation (
64). Using Equations (
63), (
70) and (
71), and differentiating Equation (
62) with respect to
yields
which by Equation (
67) leads to the first one in Equation (
64). Similarly, differentiating Equation (
63) with respect to
yields
which leads to the second one in Equation (
64). □
The 2D potential functions for the 2D Laplace equation as shown in Equations (
8) and (
9) can be extended to the 3D potential functions for the 3D Laplace equation. If
and
are harmonic functions, then
are both the solutions of the system (
62) and (
63);
and
are potential functions for
u and
v automatically satisfying the Cauchy–Riemann Equations (
62) and (
63).
Upon comparing the analytic function in Theorem 4 to the multivariate analytic function mentioned in
Section 1, the differences are that
is still a single-complex-variable analytic function, and is different from
in the multivariate analytic function; the underlying space in Theorem 4 is
, not
in the multivariate analytic function theory; Equations (
62) and (
63) are generalized Cauchy–Riemann equations, which are different from Equation (
12).
It is interesting that we have proved the generalized Cauchy–Riemann Equations (
62) and (
63) in
for the 3D Laplace equation. Recalling the Moisil–Teodorescu system in Equation (
13) as the generalized Cauchy–Riemann equations in
, it needs four equations and four harmonic functions
of
in
. From the algebraic point of view, the presented theory in Theorem 4, using two equations and two harmonic functions
and
, is more compact than the theory of the Moisil–Teodorescu system [
4].
Theorem 5. For the 3D Laplace equation, the projective-type particular solution iswhere , are differentiable functions and Proof of Theorem 5. For , the result was proven in Theorem 3. Then, we change the variable to and , whose solutions can be derived similarly. □
It is interesting that Equation (
76) bears certain similarity to Equation (
5). It is a novel projective-type particular solution of the 3D Laplace equation.
As a demonstration of Theorem 4, we take a simple analytic function:
such that
and
are obvious. By
it is easy to verify the first Cauchy–Riemann equation in Equation (
62). Then, by
we can verify the second Cauchy–Riemann equation in Equation (
63).
5. Analytic Function and Generalized Cauchy–Riemann Equations
Let us extend Theorem 4 to an
n-dimensional Laplace equation with
. Let
be the Cartesian coordinates, where
, and we take
where
is an
-dimensional direction and ∇ is an
-dimensional gradient operator.
Notice that the single complex variable
w in Equation (
81) will be used to construct the analytic function, which is different from the multivariate analytic function theory by using
m complex variables
.
Theorem 6. Let be a complex variable, where , , and . For the n-dimensional Laplace equation with , is an analytic function if and only if Moreover, and , satisfyingare harmonic functions in the n-dimensional space. Proof of Theorem 6. By means of Equation (
80), we have
Summing these equations yields
Thus, we obtain a 2D-like Laplace equation:
According to Equation (
6), the corresponding Cauchy–Riemann equations are
With the aid of Equation (
82), we can derive Equation (
83).
Take the operator
to the second one in Equation (
83),
Take the operator
to the first one in Equation (
83),
which by Equation (
82) changes to
The summation of Equations (
88) and (
90) leads to
hence, by Equation (
86), we prove
.
Acting the operator
on the first one in Equation (
83) generates
Take the operator
to the second one in Equation (
83),
which by Equation (
82) changes to
The summation of Equations (
91) and (
93) leads to
This ends the proof. □
Theorem 7. The analytic function for the n-dimensional Laplace equation satisfieswhere with , , and . Proof of Theorem 7. Because of Equation (
82), the Cauchy–Riemann equations in Equation (
83) can be written as those in Equation (
87), which are sufficient and necessary conditions for
to be analytic.
By the chain rule, we have
Multiplying Equation (
95) by
i and summing it to Equation (
96) results in
Inserting
into the second one in Equation (
94) leads to
which with the aid of Equation (
87) implies
With the aid of Equations (
97) and (
99), Equation (
94) is proven. □
Equation (
94) is an extension of Equation (
7). Theorem 7 is interesting in that any differentiable function
is an analytic function, where
and
satisfy the
n-dimensional Laplace equation. The
n-dimensional analytic function theory bears a certain similarity to the analytic function theory for complex function. However, the two-dimensional complex function theory is extended here to the
n-dimensional complex function theory.
Upon comparing the analytic function in Theorems 6 and 7 to the multivariate analytic function mentioned in
Section 1, the differences are that
is still a single-complex-variable analytic function, and is different from
in the multivariate analytic function; the underlying space in Theorems 6 and 7 is
, not
in the multivariate analytic function theory; Equation (
83) is a generalized Cauchy–Riemann equation, which is different from Equation (
12). Equation (
94) holds for the analytic function with a single complex variable, which is not like Equation (
12) that holds for
m complex variables
. Notice that the presented analytic function theory can be applied to any dimensional space with
, not limited to the even-dimensional space. They are totally different theories about the analytic function.
Notice that in terms of a linear operator, Equation (
83) can be expressed as
Thus, we can derive
which indicates that
u and
v are harmonic functions. Indeed, the system (
100) is an extension of the Moisil–Teodorescu system to the
n-dimensional setting. However, we only need two functions
u and
v, rather than the four functions
,
,
, and
in Equation (
13).
An operator
is said to be a Dirac operator if
and its conjugate
satisfy Equation (
102); that is
Our approach to the Dirac operator is simpler than the Moisil–Teodorescu system [
4,
5] in terms of saving algebraic manipulations.
6. Trefftz-Type Bases
Before embarking on the numerical experiments of 3D Laplace equation, we extend Equation (
25) from the 2D Trefftz bases to the Trefftz-type bases in 3D. For the analytic function as explored in Theorem 5, we can express
generated from Equation (
79) by
where
These can be carried out similarly for
and
. Consequently, we can expand
for the solution of 3D Laplace equation by the following Trefftz-type bases:
where
Instead of using Equation (
49), which is too complicated, we consider
w in the cylindrical coordinates:
Now, we can expand
by the Trefftz-type bases in the cylindrical coordinates:
which is much simpler than Equation (
49). Notice that for the problem in the cylindrical coordinates, we can add the following terms
in Equation (
107) to enhance the accuracy.
The classical approach of linear PDEs is usually using the method of separation variables to build up the Trefftz bases. When the linear PDEs are more complex than the Laplace equation and with dimension greater than two
, there exist no simple ways to set up the Trefftz bases. The projective solutions method proposed here is very useful to construct the particular solutions of the projective type for many linear PDEs with
and with constant coefficients; it can help us to derive the Trefftz bases in terms of elementary functions, which are more simpler than the method by using the special functions as the bases [
18] for solving the 3D Laplace equation in the cylindrical coordinate system.
7. Numerical Experiments
Now, we are in a good position to compare the different types of the bases used in the solution of 3D Laplace equation. Let
. We assess the errors of
by the maximum error (ME) and root-mean-square error (RMSE):
where
denotes the exact solution and
the numerical solution, and
is the number of tested points.
Example 1. We consider the following exact solution [28]:with the following boundary shape:where We impose the Dirichlet boundary condition for this problem, where
collocated points are used to satisfy the boundary condition. By using the Cartesian bases in Equation (
42), we take
and
with
unknown coefficients. The resulting linear system is scaled by
, such that all the column norms of the coefficient matrix of the linear system are equal to
[
29]. The dimension of the coefficient matrix is
, and we apply the conjugate gradient method (CGM) to solve the resulting normal system with a convergence criterion
. We test the accuracy at 2500 points in the domain. It does not converge within 10,000 steps and the maximum error (ME) in the entire domain is ME =
and the root-mean-square error (RMSE) is RMSE =
. The numerical and exact solutions are compared on the curve of
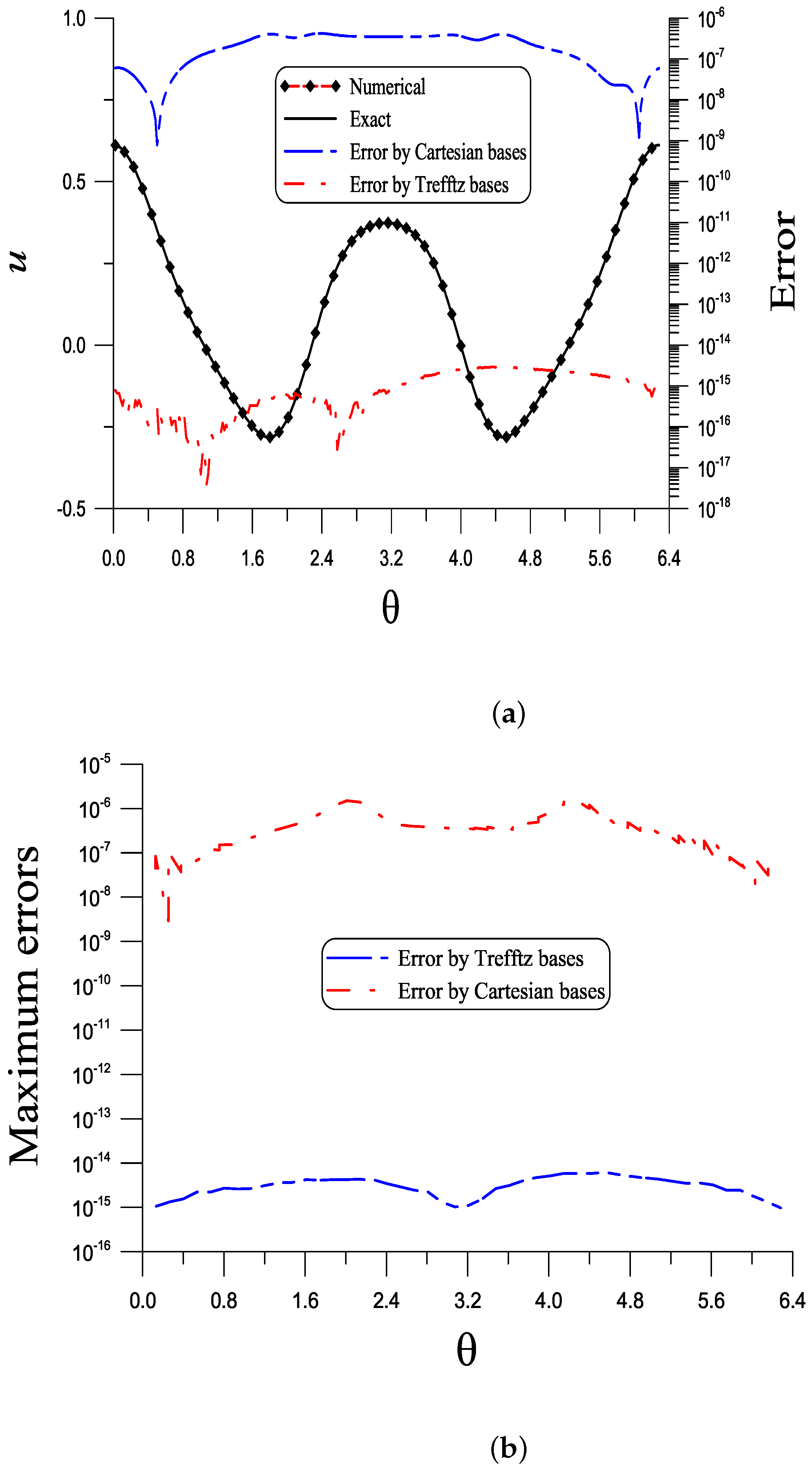
, on which the maximum error is
, as shown in
Figure 2a by a dashed–dotted line.
Under Equation (
107) with
and
and
unknown coefficients, the Trefftz-type basis is convergent with 9 steps, and ME =
and RMSE =
are obtained. The local error on the above curve and the maximum error in the entire domain are shown in
Figure 2a,b. It can be seen that the Trefftz-type basis is convergent fast and very accurate.
Figure 3 plots the error of numerical solution using the Trefftz bases over the plane
. It can be seen that the absolute error of
u in the entire domain is of the order
.
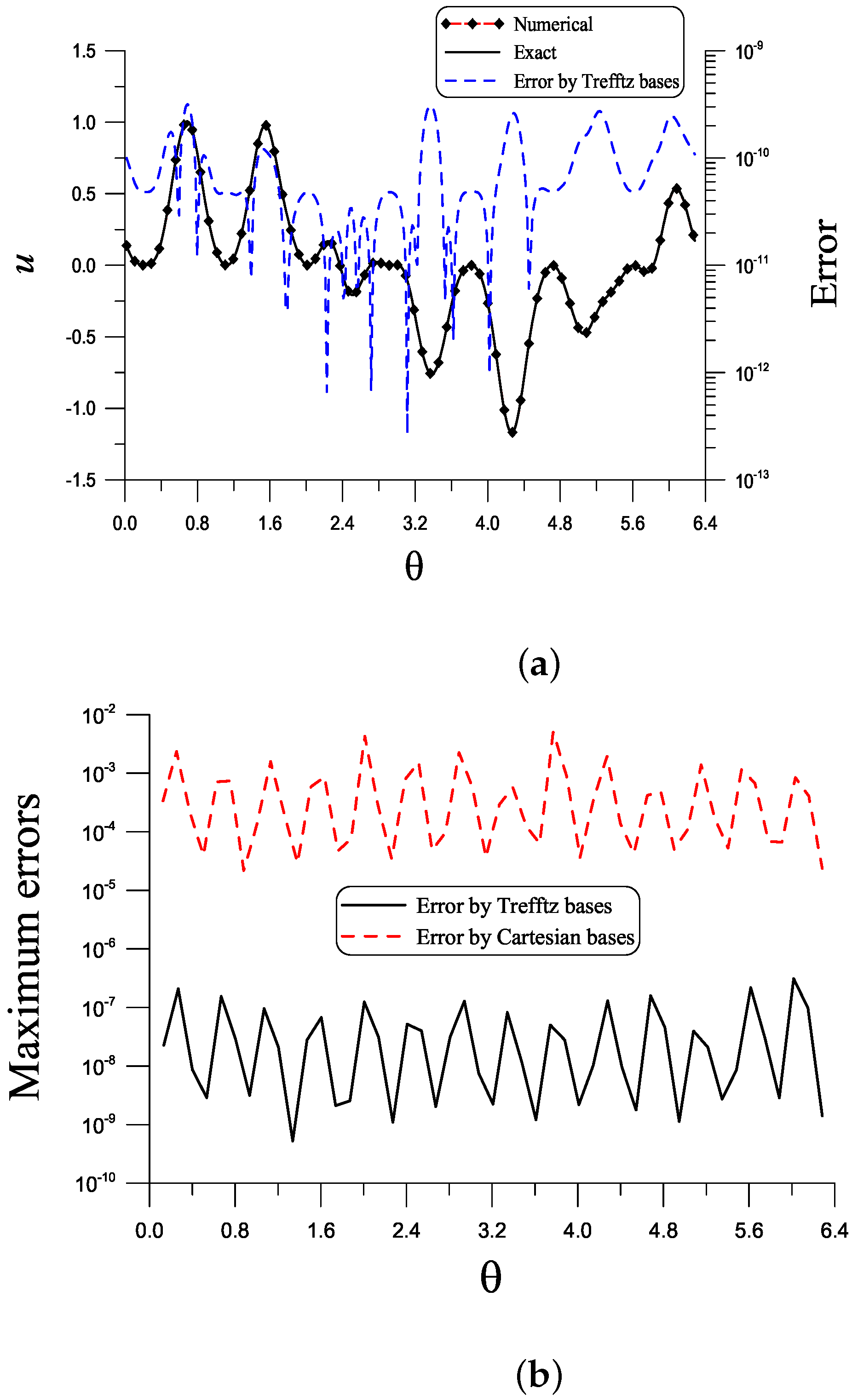
Example 2. We demonstrate a complex 3D Laplacian problem with We impose the Dirichlet boundary condition for this problem, where
collocated points are used to satisfy the boundary condition. Under Equation (
107) with
and
and
unknown coefficients, the Trefftz-type basis is convergent with 4070 steps. In
Figure 4a, the numerical and exact solutions on the curve of
are compared, which are almost coincident with the maximum error being
. In the entire domain, ME =
and RMSE =
are obtained as shown in
Figure 4b. Using Equation (
42), it does not converge within 10,000 steps and ME =
and RMSE =
are obtained as shown in
Figure 4b by a dashed line.
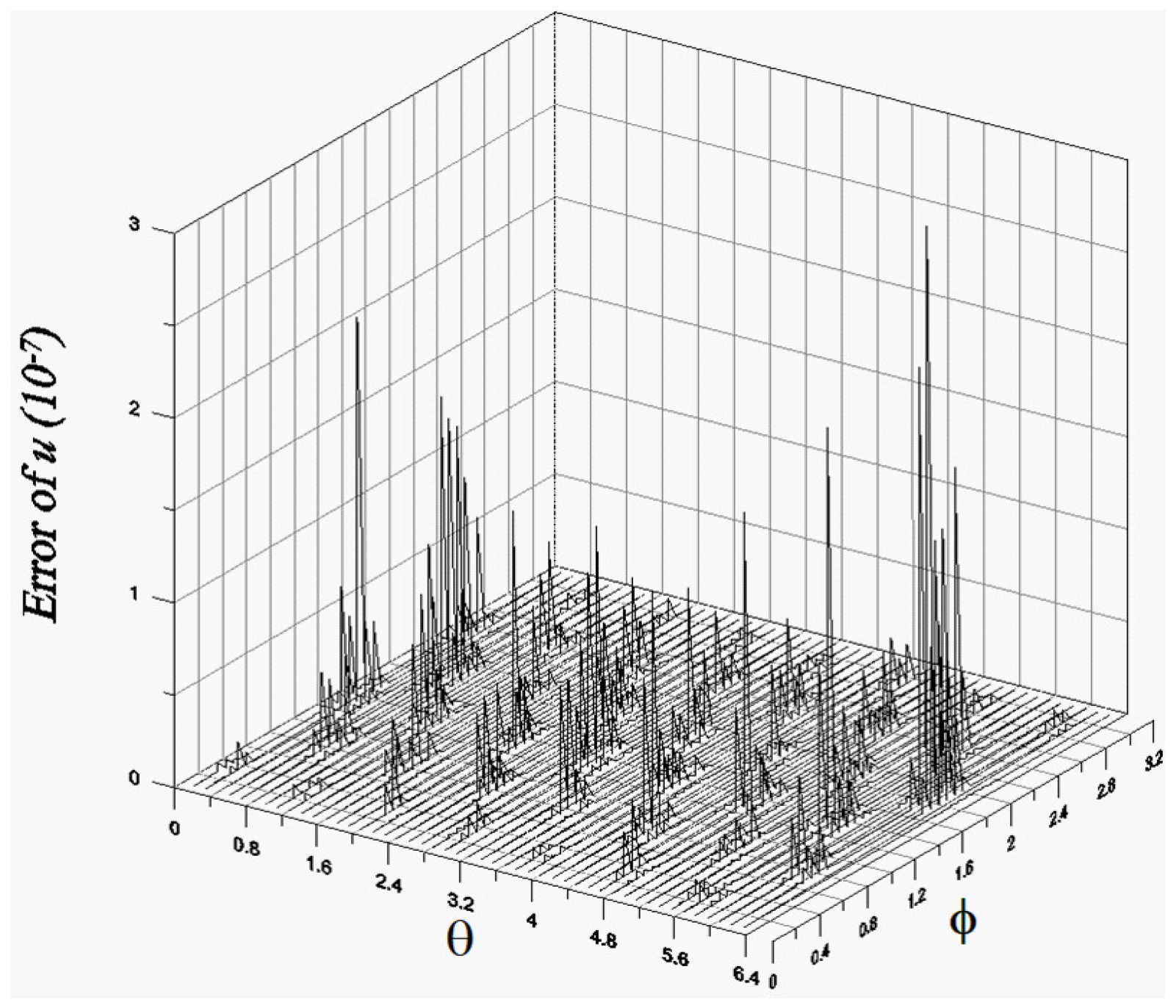
Figure 5 plots the error of numerical solution using the Trefftz bases over the plane
.
Example 3. We consider the following exact solution [18]: We impose the Dirichlet boundary condition for this problem, where
collocated points are used to satisfy the boundary condition. Under Equation (
112) with
and
,
unknown coefficients, and
, ME =
and RMSE =
are obtained, as shown in
Figure 6 by a solid line. Under Equation (
107) with
and
,
unknown coefficients, and
, ME =
and RMSE =
are obtained, as shown in
Figure 6 by a dashed line. Both the efficiency and accuracy of the Trefftz-type basis and the cylindrical Trefftz-type basis are better than that in [
18].
Figure 7 plots the error of numerical solution using the Trefftz bases over the plane
.
8. Conclusions
The topics treated in the paper were the new projective solutions of 2D, 3D, and n-dimensional Laplace equations. A new concept of projective variable w is introduced, such that we can transform the Laplace equations to the second-order ODEs with the leading term multiplied by the squared-norm of the characteristic vector, which must be a complex vector to satisfy a null equation. Different choices of the characteristic vector may offer many projective solutions as the bases. For the n-dimensional Laplace equation, we have established its analytic function theory, and the generalized Cauchy–Riemann equations were derived for the first time. The solutions of the 3D Laplace equation are easily expanded in terms of these analytic functions as the bases, and a powerful numerical technique was created to solve the 3D Laplace equation. Owing to its simple bases, the projective solutions method (PSM) outperforms the conventional methods. Numerical experiments of the 3D Laplace equation verified the accuracy and efficiency of the PSM by using the Trefftz-type bases for solving the 3D Laplace equation.
The projective variable w is essentially a single complex variable. So we can construct the analytic function based on the conventional complex analytic function theory; however, the resultant harmonic functions are defined in the multi-dimensional space, since w is a linear function of the coordinates of the multidimensional space. For the 3D Laplace equation, the presented theory used to construct the analytic function and harmonic function, and to derive the Cauchy–Riemann equations algebraically, outperforms the theory of the Moisil–Teodorescu system and the conventional multivariate complex analytic function theory, which is restricted to the even-dimensional space.