Irreversibility Analysis of Hydromagnetic Casson Fluid Flow Through an Inclined Channel with Isothermal Boundary Conditions
Abstract
1. Introduction
2. Problem Formulation
3. Method of Solution
4. Discussion of Results
5. Conclusions
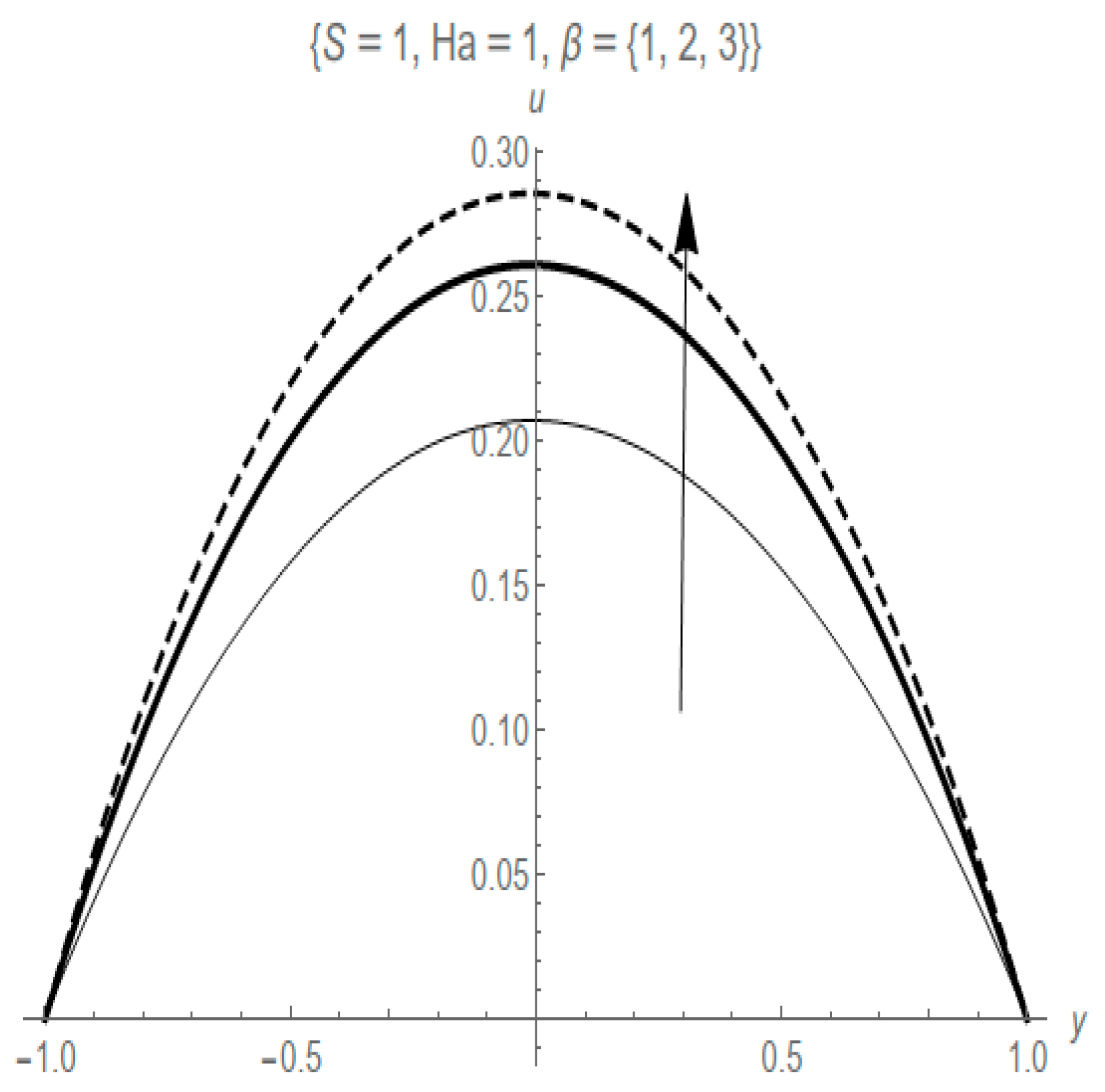
- The Casson fluid parameter increases fluid flow velocity and entropy generation rate while it decreases the fluid temperature profile.
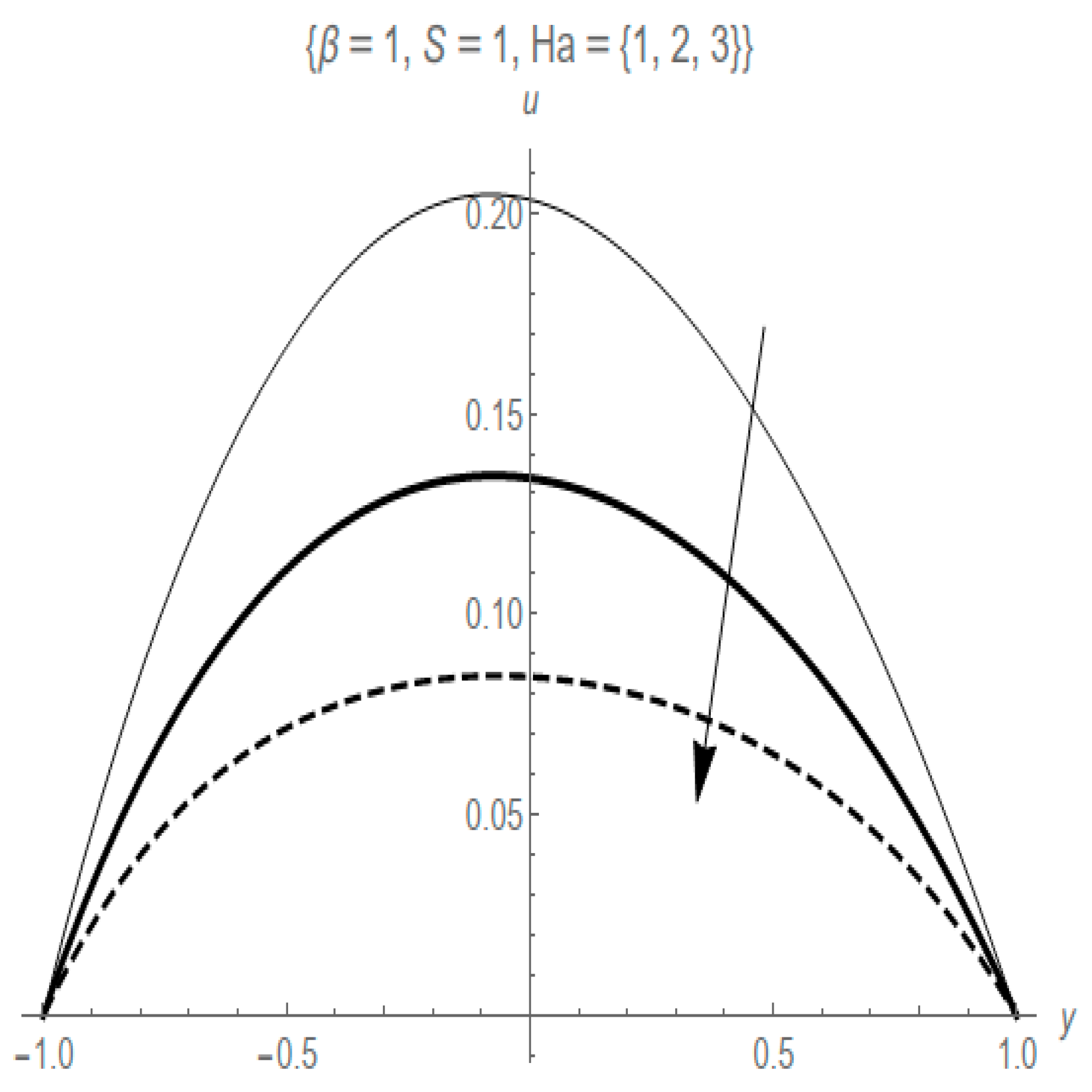
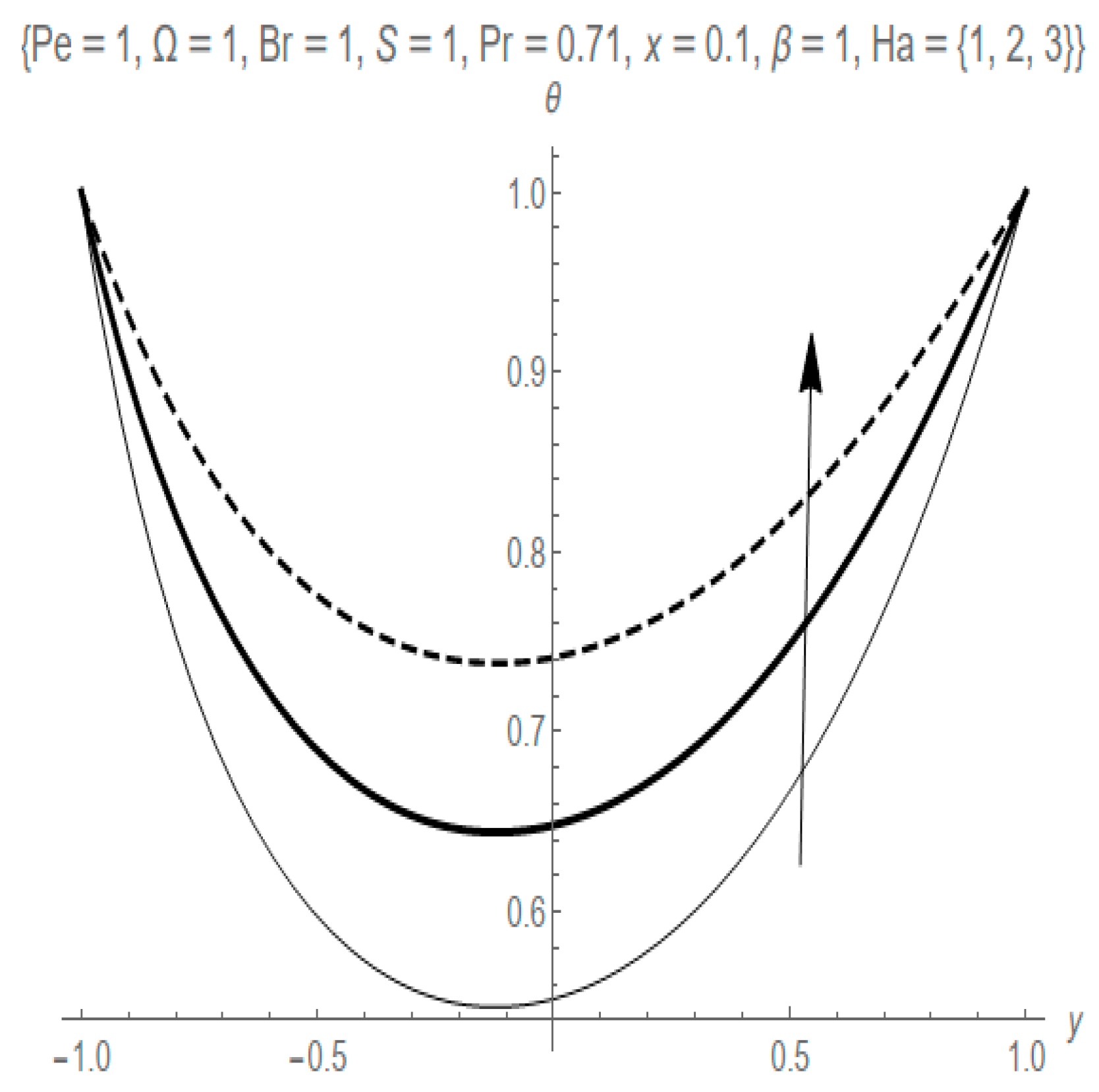
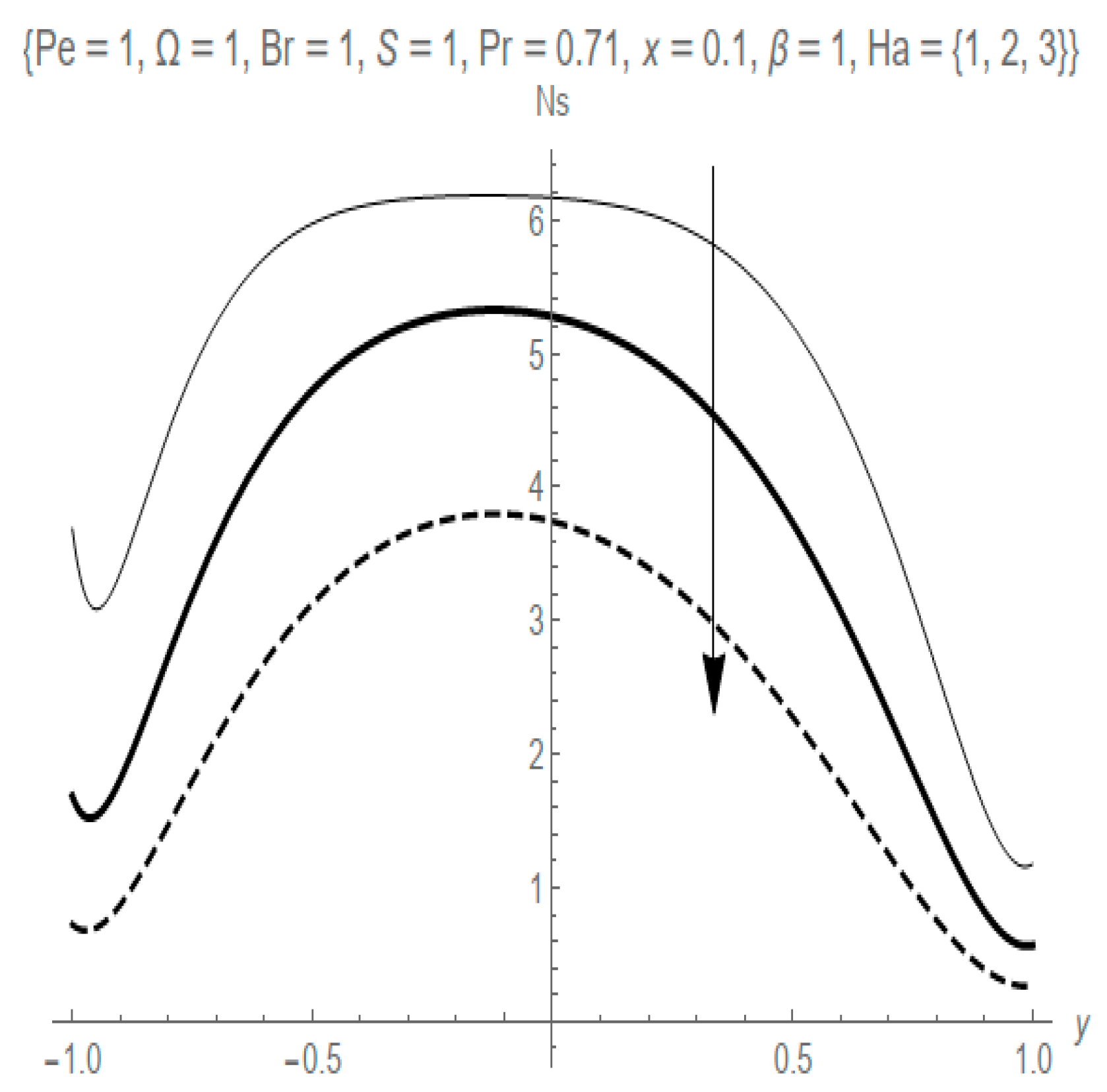
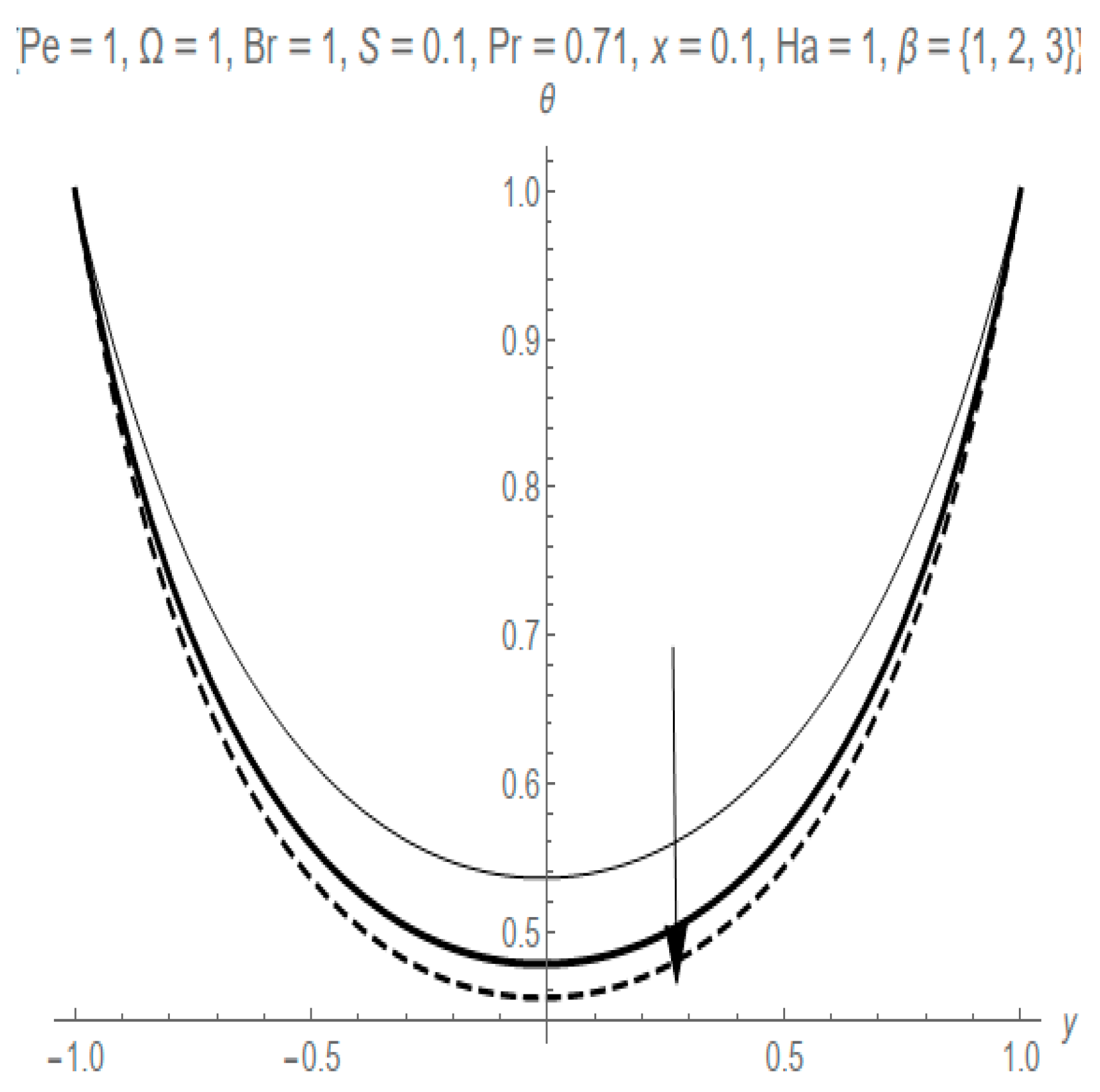
- The Hartmann number parameter decreases fluid flow velocity and entropy generation rate while it increases the fluid temperature profile.
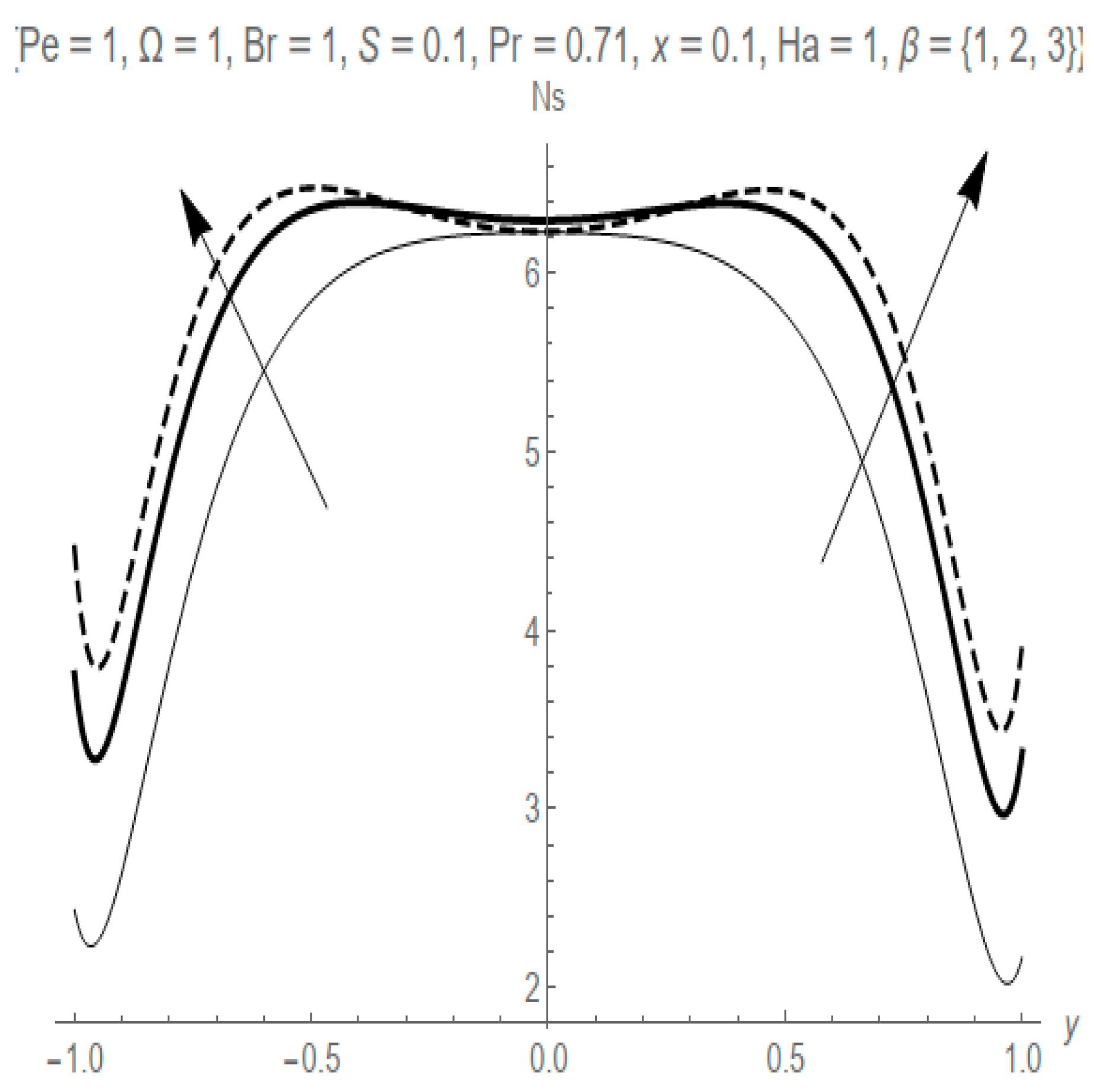
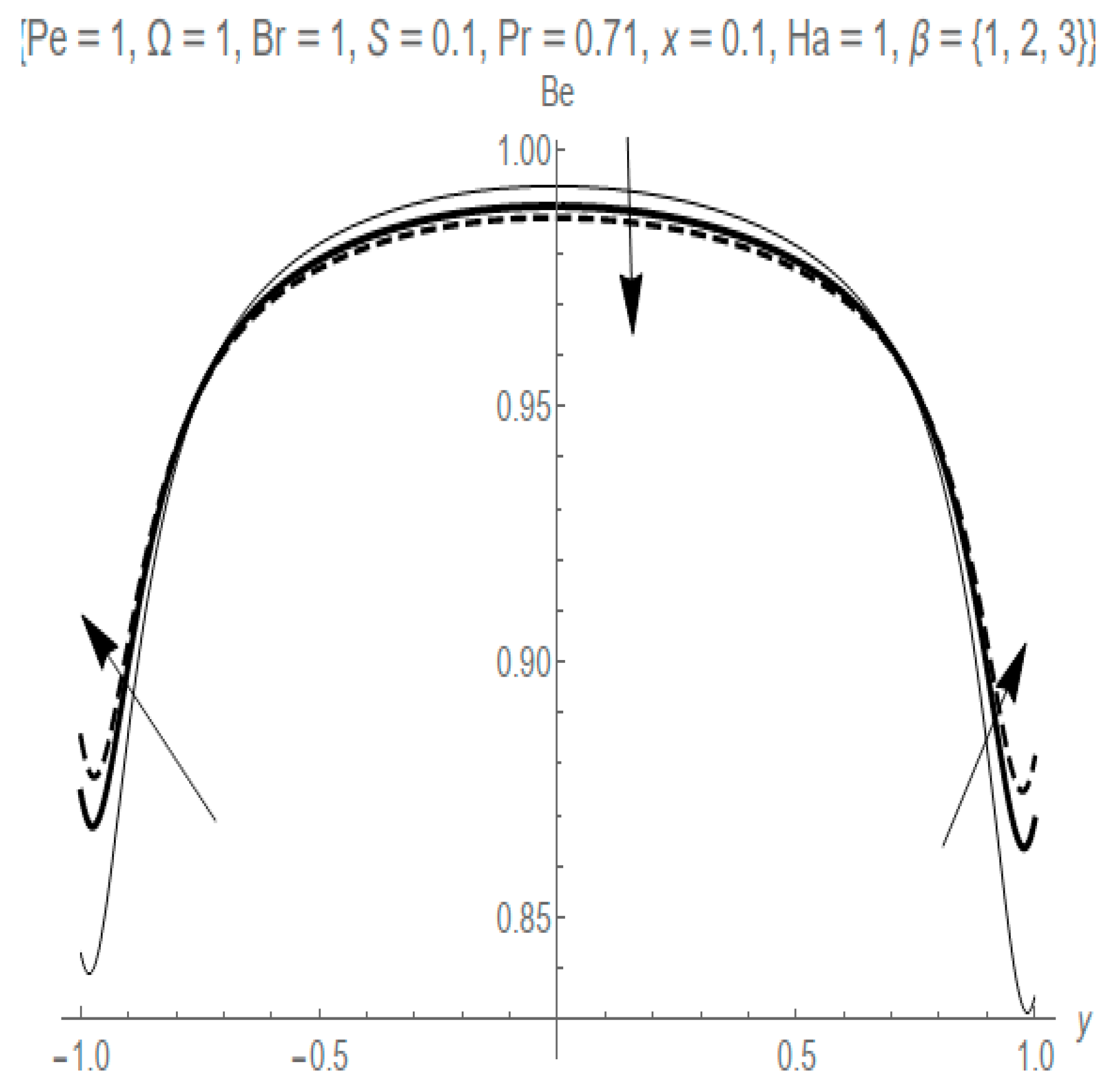
- The Casson fluid parameter causes the fluid friction irreversibility to dominate at the ends of the wall but weakens the dominance at the core area of the channel.
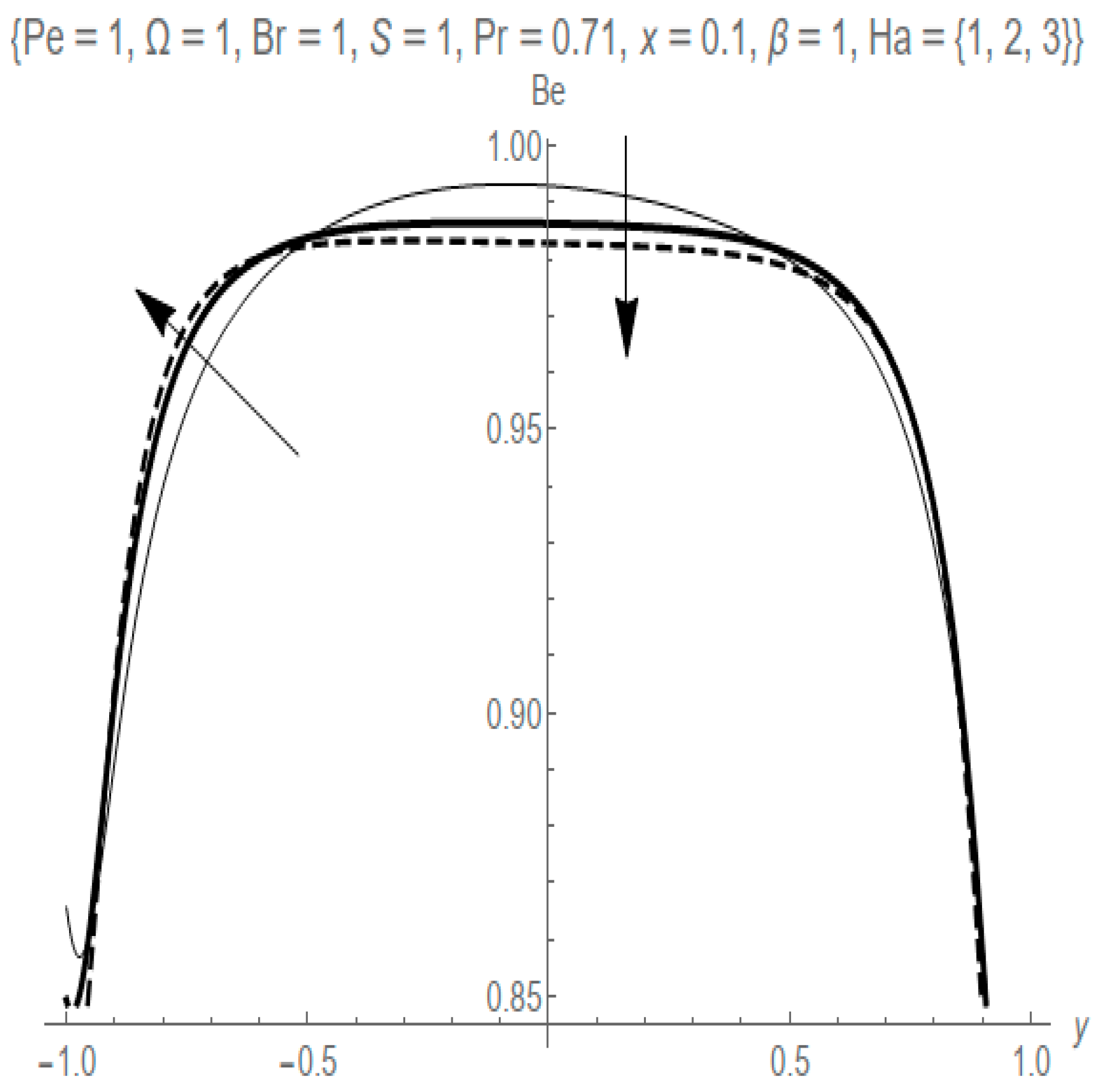
- The Hartmann number parameter influences the dominance of heat transfer irreversibility at the heated walls and decreases the dominance at the center of the channel.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| constant vertical velocity and fluid density, | |
| axial velocity and inclination angle, | |
| dynamic viscosity, Casson material | |
| electrical conductivity and constant magnetic induction. | |
| gravitational acceleration and thermal conductivity | |
| specific heat capacity, fluid temperature | |
| cartesian coordinate | |
| dimensionless cartesian coordinate | |
| fluid and heated wall temperatures. | |
| dimensionless velocity and temperature | |
| magnetic field and suction/injection | |
| Prandtl number and kinematic viscosity | |
| Peclet and Eckert numbers | |
| temperature difference and Brinkman number | |
| dimensionless entropy generation rate | |
| Be | Bejan Number (irreversibility) |
Appendix A
References
- Bejan, A. Entropy Generation Through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamental convective heat-transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar]
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar]
- Qayyum, S.; Khan, M.I.; Hayat, T.; Alsaedi, A.; Tamoor, M. Entropy generation in dissipative flow of Williamson fluid between two rotating disks. Int. J. Heat Mass. Transf. 2018, 127, 933–942. [Google Scholar]
- Khan, M.W.A.; Khan, M.I.; Hayat, T.; Alsaedi, A. Entropy generation minimization (EGM) of nanofluid flow by a thin moving needle with nonlinear thermal radiation. Phys. B Condens. Matter 2018, 534, 113–119. [Google Scholar]
- Yusuf, T.A.; Naveen Kumar, R.; Prasannakumara, B.C.; Adesanya, S.O. Irreversibility analysis in micropolar fluid film along an incline porous substrate with slip effects. Int. Commun. Heat Mass. Transf. 2021, 126, 105357. [Google Scholar]
- Rehman, A.U.; Mehmood, R.; Nadeem, S. Entropy analysis of radioactive rotating nanofluid with thermal slip. Appl. Therm. Eng. 2017, 112, 832–840. [Google Scholar] [CrossRef]
- Eegunjobi, A.S.; Makinde, O.D. Irreversibility analysis of hydromagnetic flow of couple stress fluid with radiative heat in a channel filled with a porous medium. Results Phys. 2017, 7, 459–469. [Google Scholar]
- Yusuf, T.; Mabood, F. Slip Effects and Entropy generation on inclined MHD flow of Williamson fluid through a permeable wall with chemical reaction via DTM. Math. Model. Eng. Probl. 2020, 7, 1–9. [Google Scholar] [CrossRef]
- Obalalu, A.M.; Memon, M.A.; Saleem, S.; Abbas, A.; Olayemi, O.A.; Ali, M.R.; Sadat, R.; Hendy, A.S. Thermal performance of Oldroy-B hybrid nanofluid in solar energy-based water pumping systems and entropy generation minimization. Case Stud. Therm. Eng. 2023, 51, 103476. [Google Scholar] [CrossRef]
- Saini, G.; Hanumagowda, B.N.; Mulki, H.; Raju, S.S.K.; Varma, S.V.K.; Barghout, K.; Murshid, N.; Al-Kouz, W. Entropy generation optimization in couple stress fluid flow with variable viscosity and aligned magnetic field. Sustainability 2023, 15, 2493. [Google Scholar] [CrossRef]
- Chen, L.; Xia, S.; Shi, S. Minimum entropy generation paths for generalized radiative heat transfer processes with heat leakage. Results Eng. 2024, 21, 101759. [Google Scholar] [CrossRef]
- Ng, C.-O. Combined pressure-driven and electroosmotic flow of Casson fluid through a slit microchannel. J. Non-Newton. Fluid Mech. 2013, 198, 1–9. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, S.I. Nonlinear radiation effects on squeezing flow of a Casson fluid between parallel disks. Aerosp. Sci. Technol. 2016, 48, 186–192. [Google Scholar] [CrossRef]
- Ramesh, K.; Devakar, M. Some analytical solutions for flows of Casson fluid with slip boundary conditions. Ain Shams Eng. J. 2015, 6, 967–975. [Google Scholar] [CrossRef]
- Atlas, M.; Hussain, S.; Sagheer, M. Entropy generation and unsteady Casson fluid flow squeezing between two parallel plates subject to Cattaneo-Christov heat and mass flux. Eur. Phys. J. Plus 2019, 134, 33. [Google Scholar] [CrossRef]
- Shadman Sakib, P.; Nasrin, R. Numerical appraisal of time-dependent peristaltic duct flow using Casson fluid. Int. J. Mech. Sci. 2022, 233, 107676. [Google Scholar] [CrossRef]
- Nadeem, S.; Ishtiaq, B.; Hamida, M.B.B.; Almutairi, S.; Ghazwani, H.A.; Eldin, S.M.; Al-Shafay, A.S. Reynolds nanofluid model for Casson fluid flow conveying exponential nanoparticles through a slandering sheet. Sci. Rep. 2023, 13, 1953. [Google Scholar] [CrossRef]
- Abbas, S.; Nisa, Z.U.; Nazar, M.; Amjad, M.; Ali, H.; Jan, A.Z. Application of heat and mass transfer to convective flow of Casson fluid in a microchannel with Caputo-Fabrizio derivative approach. Arab. J. Sci. Eng. 2024, 49, 1275–1286. [Google Scholar] [CrossRef]
- Komurgoz, G.; Arikoglu, A.; Turker, E.; Ozkol, I. Second-law analysis for an inclined channel containing porous-clear fluid layers by using the differential transform method. Numer. Heat Transf. Part. A 2010, 57, 603–623. [Google Scholar] [CrossRef]
- Hayat, T.; Shahida, B.; Rafiq, M.; Alsaedi, A.; Abbasi, F.M. Effect of an inclined magnetic field on peristaltic flow of Williamson fluid in an inclined channel with convective conditions. J. Magn. Magn. Mater. 2016. [Google Scholar] [CrossRef]
- Dar, A.A.; Elangovan, K. Influence of an inclined magnetic field and rotation on the peristaltic flow of a micropolar fluid in an inclined channel. New J. Sci. 2016, 5717542. [Google Scholar] [CrossRef]
- Abbas, Z.; Hasnaina, J.; Sajid, M. Hydromagnetic mixed convective two-phase flow of couple stress and viscous fluids in an inclined channel. Z. Naturforsch. 2014, 69a, 553–561. [Google Scholar] [CrossRef]
- Lerisson, G.; Ledda, P.G.; Balestra, G.; Gallaire, F. Instability of a thin viscous film flowing under an inclined substrate: Steady patterns. J. Fluid Mech. 2020, 898, A6. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanoliquid film flow due to a moving substrate and heat transfer. Eur. Phys. J. Plus 2020, 135, 1–13. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Egere, A.C.; Ukaegbu, J.C.; Lebelo, R.S. Influence of temperature-dependent properties on a gravity-driven thin film along inclined plate. Nonlinear Eng. 2020, 9, 118–123. [Google Scholar] [CrossRef]
- Vaddemani, R.R.; Kodi, R.; Mopuri, O. Characteristics of MHD Casson fluid past an inclined vertical porous plate. Mater. Today Proc. 2022, 49 Pt 5, 2136–2142. [Google Scholar] [CrossRef]
- Hafeez, N.M.; Abd-Alla, A.M.; Metwaly, T.M.N. Influences of rotation and mass and heat transfer on MHD peristaltic transport of Casson fluid through inclined plane. Alex. Eng. J. 2023, 68, 665–692. [Google Scholar] [CrossRef]
- Mopuri, O.; Sailakumari, A.; Ganjikunta, A.; Sudhakara, E.; VenkateswaraRajus, K.; Ramesh, P.; Ganteda, C.; Reddy, B.R.; Varma, S.V.K. Characteristics of MHD Jeffery fluid past an inclined vertical porous plate. CFD Lett. 2024, 16, 68–89. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Souayeh, B.; Rahimi-Gorji, M.; Khan, M.N.; Adeyemi, O.G. Heat irreversibility analysis for a couple stress fluid flow in an inclined channel with isothermal boundaries. J. Taiwan Inst. Chem. Eng. 2019, 101, 251–258. [Google Scholar] [CrossRef]
- Abbas, Z.; Rafiq, M.Y.; Alshomrani, A.S.; Ullah, M.Z. Analysis of entropy generation on peristaltic phenomena of MHD slip flow of viscous fluid in a diverging tube. Case Stud. Therm. Eng. 2021, 23, 100817. [Google Scholar] [CrossRef]
- Naz, R.; Noor, M.; Shah, Z.; Sohail, M.; Kumam, P.; Thounthong, P. Entropy generation optimization in MHD pseudoplastic fluid comprising motile microorganisms with stratification effect. Alex. Eng. J. 2020, 59, 485–496. [Google Scholar] [CrossRef]
- Jha, B.K.; Yusuf, T.S. Entropy generation in an inclined porous channel with suction/injection. Nonlinear Eng. 2020, 9, 94–101. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Khan, A.; Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng. Sci. Technol. Int. J. 2015, 18, 309–317. [Google Scholar] [CrossRef]
- Awais, M.; Raja, M.A.Z.; Awan, S.E.; Shoaib, M.; Ali, H.M. Heat and mass transfer phenomenon for the dynamics of Casson fluid through porous medium over shrinking wall subject to Lorentz force and heat source/sink. Alex. Eng. J. 2021, 60, 1355–1363. [Google Scholar] [CrossRef]
- Prameela, M.; Gangadhar, K.; Reddy, G.J. MHD free convective non-Newtonian Casson fluid flow over an oscillating vertical plate. Partial Differ. Equ. Appl. Math. 2022, 5, 100366. [Google Scholar] [CrossRef]
- Vishalakshi, A.B.; Mahabaleshwar, U.S.; Ahmad, M.H.; Sharifpur, M. An MHD Casson fluid flow past a porous stretching sheet with threshold Non-Fourier heat flux model. Alex. Eng. J. 2023, 69, 727–737. [Google Scholar] [CrossRef]
- Adel, M.; Khader, M.M.; Ahmad, H. MHD nanofluid flow and heat transfer caused by a stretching sheet that is heated convectively: An approximate solution using ADM. Case Stud. Therm. Eng. 2024, 60, 104683. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Njor, B.E.; Lebelo, R.S.; Adesanya, S.O. Irreversibility Analysis of Hydromagnetic Casson Fluid Flow Through an Inclined Channel with Isothermal Boundary Conditions. Mathematics 2025, 13, 1208. https://doi.org/10.3390/math13071208
Njor BE, Lebelo RS, Adesanya SO. Irreversibility Analysis of Hydromagnetic Casson Fluid Flow Through an Inclined Channel with Isothermal Boundary Conditions. Mathematics. 2025; 13(7):1208. https://doi.org/10.3390/math13071208
Chicago/Turabian StyleNjor, Bernard Ejugu, Ramoshweu Solomon Lebelo, and Samuel Olumide Adesanya. 2025. "Irreversibility Analysis of Hydromagnetic Casson Fluid Flow Through an Inclined Channel with Isothermal Boundary Conditions" Mathematics 13, no. 7: 1208. https://doi.org/10.3390/math13071208
APA StyleNjor, B. E., Lebelo, R. S., & Adesanya, S. O. (2025). Irreversibility Analysis of Hydromagnetic Casson Fluid Flow Through an Inclined Channel with Isothermal Boundary Conditions. Mathematics, 13(7), 1208. https://doi.org/10.3390/math13071208






