Energy Efficacy Enhancement in a Reactive Couple-Stress Fluid Induced by Electrokinetics and Pressure Gradient with Variable Fluid Properties
Abstract
1. Introduction
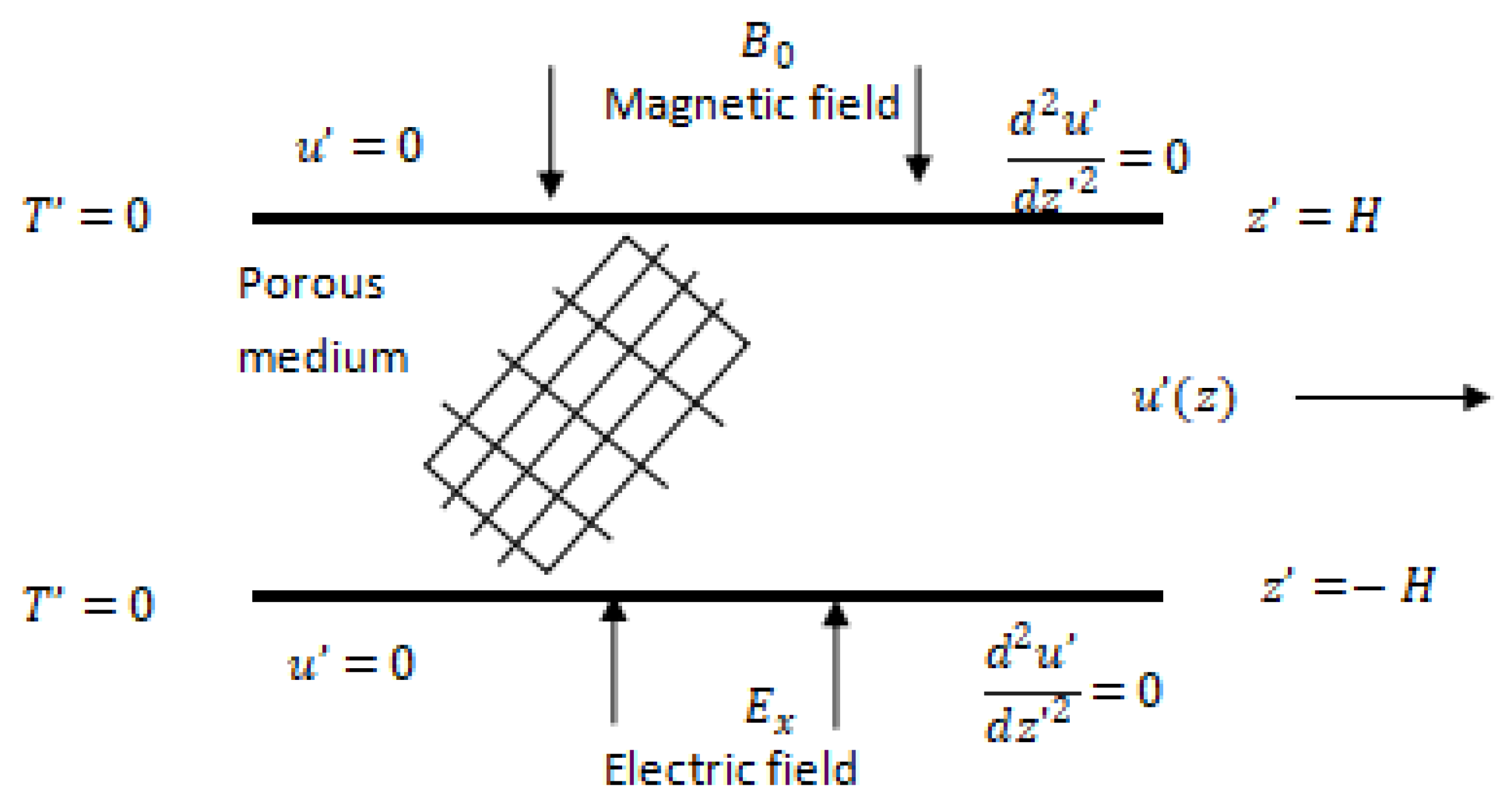
2. Model Derivation
2.1. Derivation of Potential Distribution
2.2. Conservation of Mass and Momentum
- The flow is steady, hydrodynamically and thermally fully developed,
- The flow is unidirectional, hence
- The electric field is applied along the and directions.
- The magnetic field is imposed along the direction.
2.3. Conservation of Energy
2.4. Entropy Generation Analysis
3. Method of Solution
4. Code Validation
5. Results and Discussion
6. Conclusions
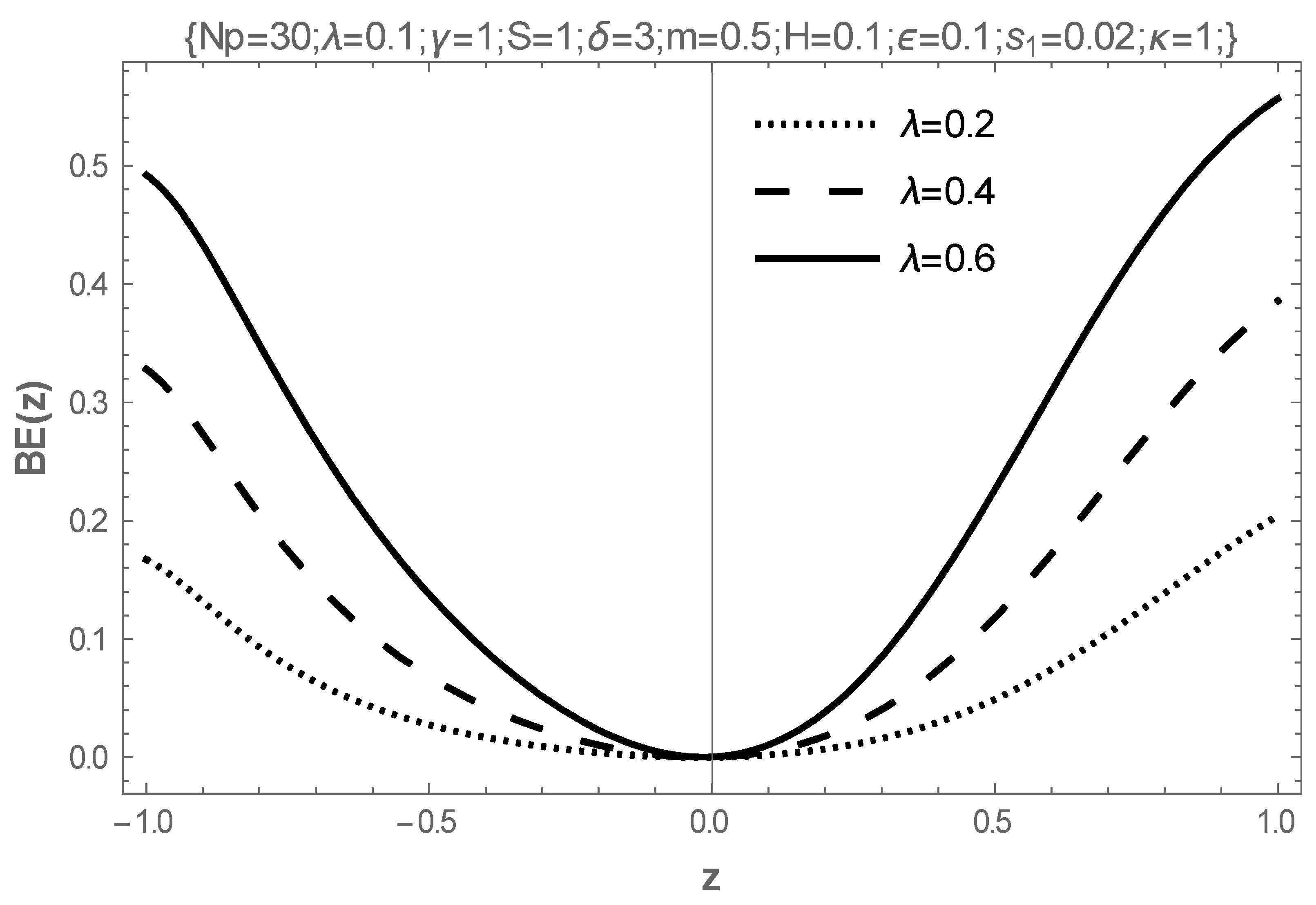
- The increasing values of the Hartmann number, electrokinetic width, electric field parameter, joule heat parameters, and the couple-stress parameter destabilize the flow, while the coefficient of viscosity and the activation energy parameter stabilize the flow.
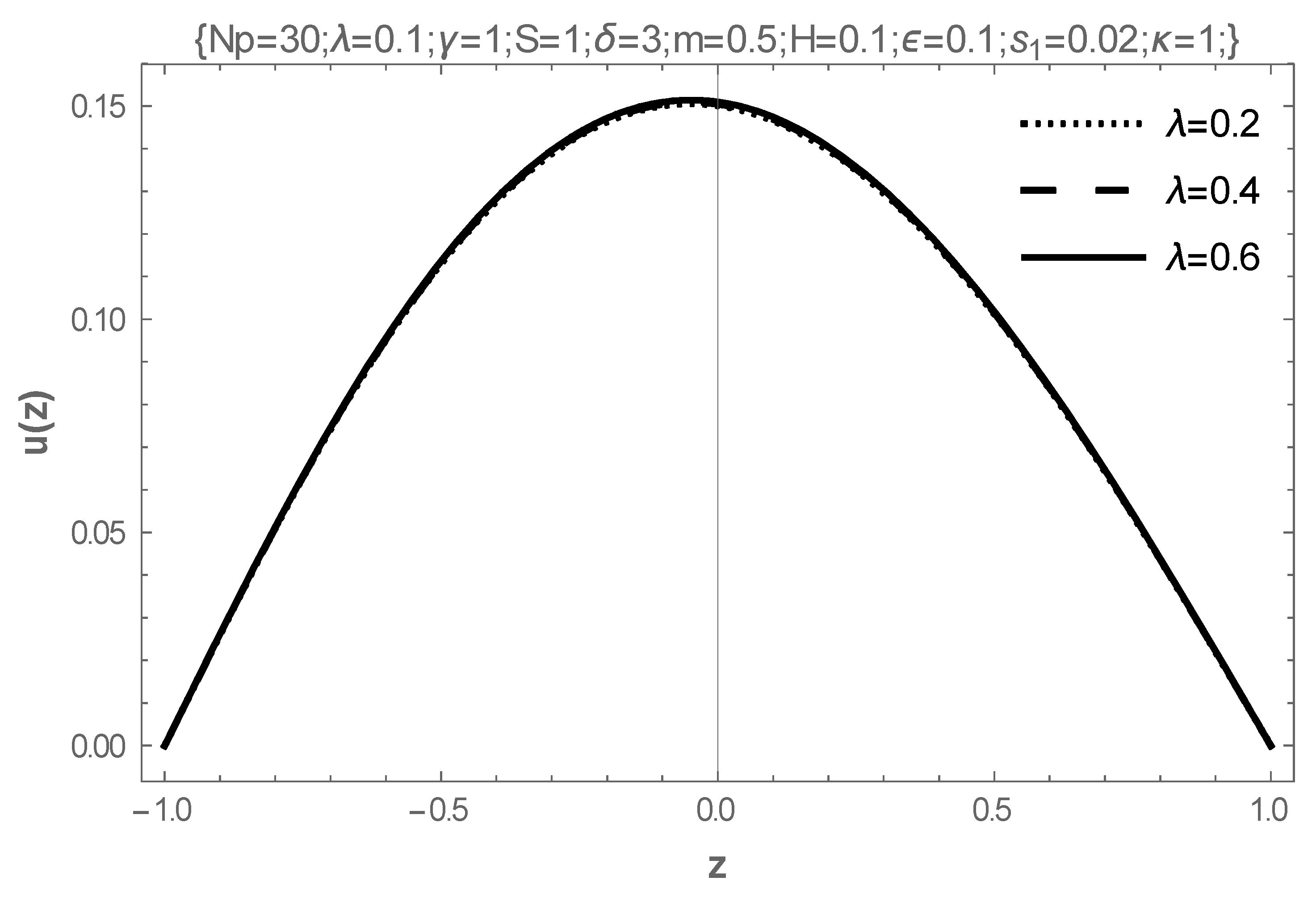
- The rising values of the Hartmann number, the coefficient of viscosity, and the electric field parameter enhance the flow of fluid, while the Frank-Kameneskii parameter does not have an effect on the flow velocity.
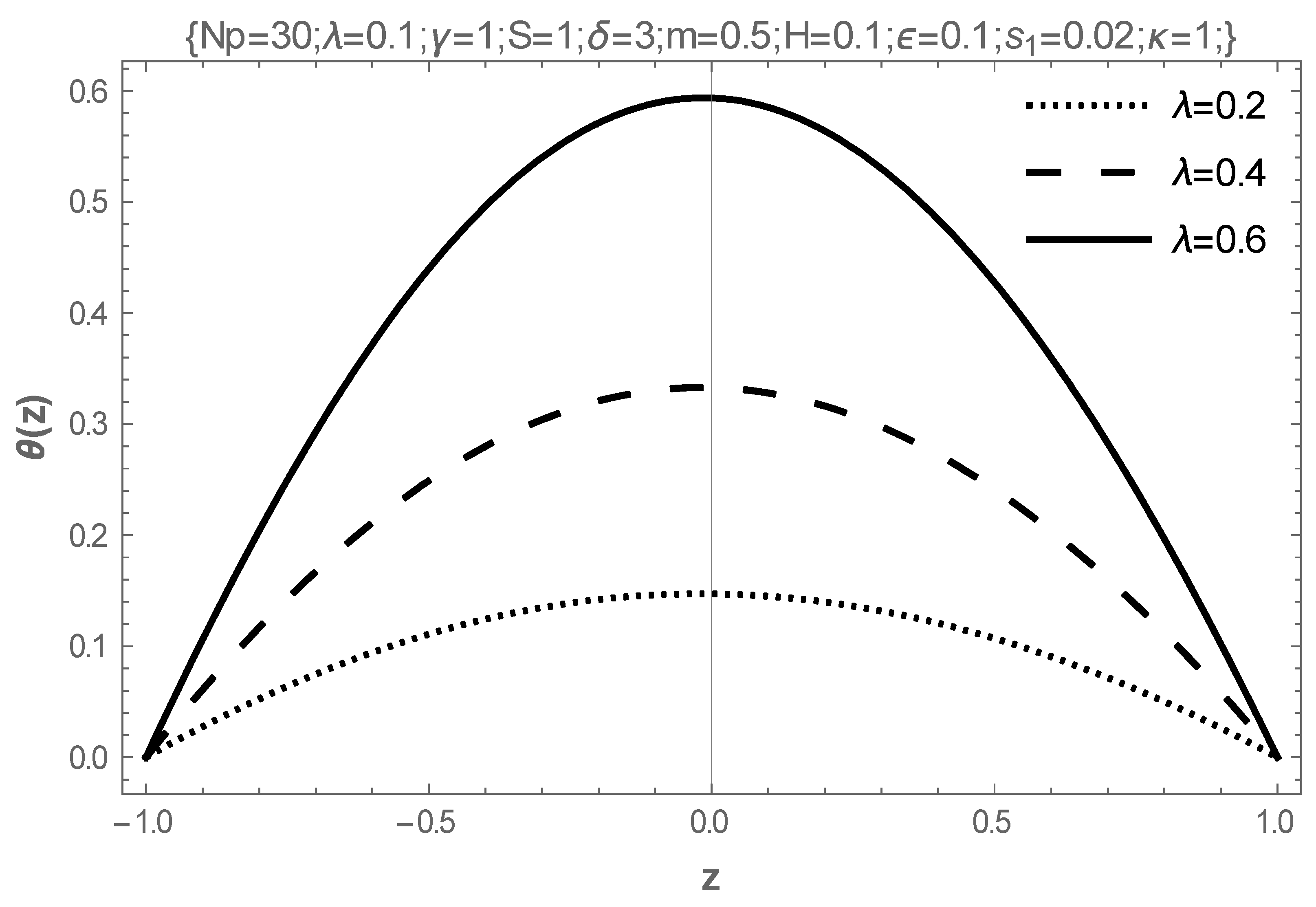
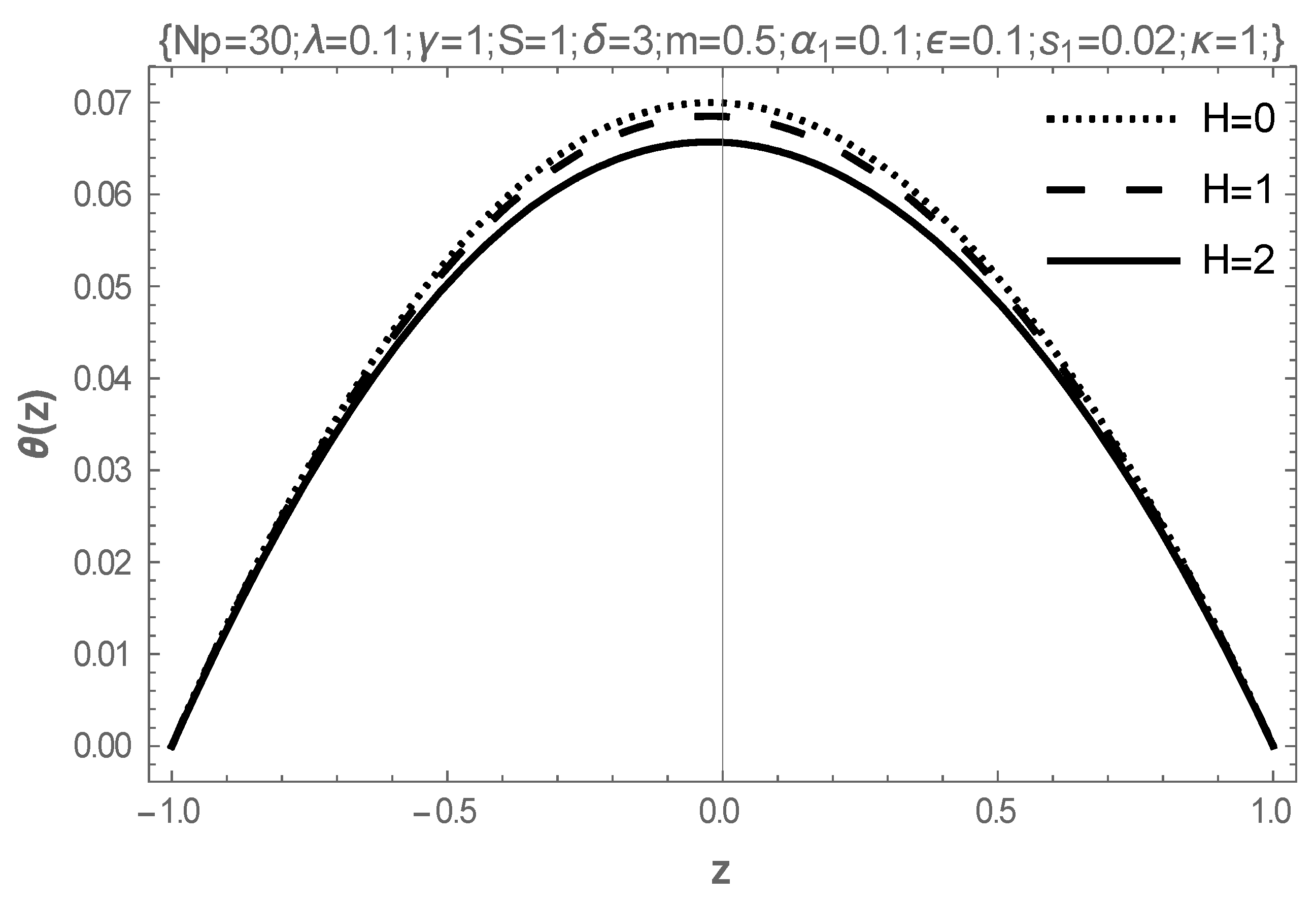
- In addition, intensifying the values of the Frank-Kameneskii parameter and the coefficient of viscosity elevates the temperature of the fluid, while the Hartmann number reduces the temperature.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| dimensionless velocity | dimensionless temperature | ||
| Horizontal coordinate | Hartmann number | ||
| activation energy parameter | m | Exponential Factor | |
| Joule heat parameters | Viscous Dissipation Parameter | ||
| dimensionless entropy generation | electric field parameter | ||
| electrokinetic width | Couple-stress parameter | ||
| pressure gradient | Frank-Kameneskii parameter | ||
| coefficient of viscosity |
References
- Elboughdiri, N.; Javid, K.; Shehzad, M.Q.; Benguerba, Y. Influence of chemical reaction on electro-osmotic flow of nanofluid through convergent multi-sinusoidal passages. Case Stud. Therm. Eng. 2024, 54, 103955. [Google Scholar] [CrossRef]
- Reddy, M.G.; Reddy, K.V.; Souayeh, B.; Fayaz, H. Numerical entropy analysis of MHD electro-osmotic flow of peristaltic movement in a nanofluid. Heliyon 2024, 10, e27185. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, D.; Bhushan, S.; Beg, O.A. Unsteady viscous flow driven by the combined effects of peristalsis and electro-osmosis. Alex. Eng. J. 2018, 57, 1349–1359. [Google Scholar] [CrossRef]
- Sakinder, S.; Salahuddin, T. A numerical study of electro-osmosis Williamson nanofluid flow in a permeable tapered channel. Alex. Eng. J. 2023, 81, 620–625. [Google Scholar] [CrossRef]
- Nazeer, M.; Hussain, F.; Ghafar, M.M.; Javed, M.A. Investigation of electro-osmotic flow of Hafnium particles mixed-up with Casson fluid in convergent geometry: Theoretical study of multiphase flow. Partial. Differ. Equ. Appl. Math. 2022, 6, 100448. [Google Scholar] [CrossRef]
- Abdul-Wahab, M.S.; Al-Saif, A.J. Studying the effects of electro-osmotic and several parameters on blood flow in stenotic arteries using CAGHPM. Partial. Differ. Equ. Appl. Math. 2024, 11, 100767. [Google Scholar] [CrossRef]
- Siva, T.; Jangili, S.; Kumbhakar, B. Analytical solution to optimise the energy generation in EHMD flow of non-Newtonian fluid through a microchannel. Pramana J. Phys. 2022, 96, 168. [Google Scholar] [CrossRef]
- Raju, U.; Rangabashyam, S.; Alhazmi, H.; Khan, I. Irreversible and reversible chemical reaction impacts on convective Maxwell fluid flow over a porous media with activation energy. Case Stud. Therm. Eng. 2024, 61, 104821. [Google Scholar] [CrossRef]
- Tanveer, A.; Jarral, S.; Saleem, S. Dynamic interactions in MHD Jeffrey fluid: Exploring peristalsis; electro osmosis and homogeneous/heterogeneous chemical reactions. Alex. Eng. J. 2024, 94, 354–365. [Google Scholar] [CrossRef]
- Prashanth, M.; Rao, V.S. The impact of soret, Dufour, and chemical reaction on MHD nanofluid over a stretching sheet. Partial. Differ. Equ. Appl. Math. 2024, 10, 100674. [Google Scholar] [CrossRef]
- Vijayalakshmi, K.; Chandulal, A.; Alhazmi, H.; Aljohani, A.F.; Khan, I. Effect of chemical reaction and activation energy on Riga plate embedded in a permeable medium over a Maxwell fluid flow. Case Stud. Therm. Eng. 2024, 59, 104457. [Google Scholar] [CrossRef]
- Iranian, D.; Karthik, S.; Seethalakshmy, A. Heat generation effects on Magnetohydrodynamic Powell-Eyring fluid flow along a vertical surface with a Chemical reaction. Forces Mech. 2023, 12, 100212. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Adeosun, A.T.; Lebelo, R.S.; Tisdell, C.C. Numerical investigation of reaction driven magneto-convective flow of Sisko fluid. Numer. Heat Transf. Part A Appl. 2024, 85, 1–14. [Google Scholar] [CrossRef]
- He, Z.; Arain, M.B.; Usman; Khan, W.A.; Alzahrani, A.R.; Muhammad, T.; Hendy, A.S.; Ali, M.R. Theoretical exploration of heat transport in a stagnant power-law fluid flow over a stretching spinning porous disk filled with homogeneous-heterogeneous chemical reactions. Case Stud. Therm. Eng. 2023, 50, 103406. [Google Scholar] [CrossRef]
- Prasad, K.V.; Vajravelu, K.; Datti, P.S. The effects of variable fluid properties on the hydro-magnetic flow and heat transfer over a non-linearly stretching sheet. Int. J. Therm. Sci. 2010, 49, 603–610. [Google Scholar] [CrossRef]
- Adeyemo, A.S.; Sibanda, P.; Goqo, S.P. Analysis of heat and mass transfer of a non-linear convective heat generating fluid flow in a porous medium with variable viscosity. Sci. Afr. 2024, 24, e02140. [Google Scholar] [CrossRef]
- Wu, Y.; Pruess, K. Integral solutions for transient fluid flow through a porous medium with pressure dependent permeability. Int. J. Rock Mech. Min. Sci. 2000, 37, 51–61. [Google Scholar] [CrossRef]
- Jalili, B.; Azar, A.A.; Jalili, P.; Ganji, D.D. Impact of variable viscosity on asymmetric fluid flow through the expanding/contracting porous channel: A thermal analysis. Case Stud. Therm. Eng. 2023, 52, 103672. [Google Scholar] [CrossRef]
- Obalalu, A.M.; Ajala, O.A.; Adeosun, A.T.; Akindele, A.O.; Oladapo, O.A.; Olajide, O.A.; Adegbite, P. Significance of variable electrical conductivity on non-Newtonian fluid flow between two vertical plates in the coexistence of Arrhenius energy and exothermic chemical reaction. Partial. Differ. Equ. Appl. Math. 2021, 4, 100184. [Google Scholar] [CrossRef]
- Ramakrishna, O.; Falodun, B.O.; Akinremi, O.J.; Omole, E.O.; Ismail, A.S.; Amoyedo, F.E. Thermodynamics of variable thermophysical properties of non-Newtonian fluids with the exploration of antiviral and antibacterial mechanisms using silver nanoparticles. Int. J. Thermofluids 2024, 22, 100648. [Google Scholar] [CrossRef]
- Sivaraj, R.; Kumar, B.R. Viscoelastic fluid flow over a moving vertical cone and flat plate with variable electric conductivity. Int. J. Heat Mass Transf. 2013, 61, 119–128. [Google Scholar] [CrossRef]
- Adeosun, A.T.; Ukaegbu, J.C. Effect of the variable electrical conductivity on the thermal stability of the MHD reactive squeezed fluid flow through a channel by a spectral collocation approach. Partial. Differ. Equ. Appl. Math. 2022, 5, 100256. [Google Scholar] [CrossRef]
- Salawu, S.O.; Obalalu, A.M.; Shamshuddin, M.D.; Fatunmbi, E.O.; Ajilore, O.J. Thermal stability of magneto-hybridized silicon and aluminum oxides nanoparticle in C3H8O2-Williamson exothermic reactive fluid with thin radiation for perovskite solar power. Kuwait J. Sci. 2024, 51, 100284. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Falade, J.A.; Ukaegbu, J.C.; Makinde, O.D. Adomian-Hermite-Padé approximation approach to thermal criticality for a reactive third grade fluid flow through porous medium. Theor. Appl. Mech. 2016, 43, 133–144. [Google Scholar] [CrossRef]
- Alireza, N.; Javad, A.S.; Amin, S.N.; Hamidreza, H.; Majid, V. Influence of monoethanolamine on thermal stability of starch in water based drilling fluid system. Petrol. Explor. Develop. 2018, 45, 167–171. [Google Scholar]
- Lebelo, R.S.; Mahlobo, R.K.; Adesanya, S.O. Reactant consumption and thermal decomposition analysis in a two-step combustible slab. Defect Diffus. Forum 2019, 393, 59–72. [Google Scholar] [CrossRef]
- Doninelli, M.; Marcoberardino, G.D.; Alessandri, I.; Invernizzi, C.M.; Iora, P. Fluorobenzene as new working fluid for high-temperature heat pumps and organic Rankine cycles: Energy analysis and thermal stability test. Energy Convers. Manag. 2024, 321, 119023. [Google Scholar] [CrossRef]
- Salawu, S.O.; Hassan, A.R.; Abolarinwa, A.; Oladejo, N.K. Thermal stability and entropy generation of unsteady reactive hydromagnetic Powell-Eyring fluid with variable electrical and thermal conductivities. Alex. Eng. J. 2019, 58, 519–529. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Banjo, P.O.; Lebelo, R.S. Exergy analysis for combustible third-grade fluid flow through a medium with variable electrical conductivity and porous permeability. Mathematics 2023, 11, 1882. [Google Scholar] [CrossRef]
- Hoetink, A.E.; Faes, T.J.C.; Visser, K.R.; Heethaar, R.M. On the flow dependency of the electrical conductivity of blood. IEEE Trans. Bio-Med. Eng. 2004, 51, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Farooq, M.; Nawaz, R.; Ayaz, M.; Ahmad, H.; Abu-Zinadah, H.; Chu, Y.M. Analysis of couple stress fluid flow with variable viscosity using two homotopy-based methods. Open Phys. 2021, 19, 134–145. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Prosviryakov, E.Y.; Ershkov, S.V. Mathematical analysis of steady non-isothermal flows of a micropolar fluid. Nonlinear Anal. Real World Appl. 2025, 84, 104294. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Ershkov, S.V.; Prosviryakov, E.Y.; Yudin, A.V. Exact solutions to the Oberbeck-Boussinesq equations for describing three-dimensional flows of micropolar liquids. Symmetry 2024, 16, 1669. [Google Scholar] [CrossRef]

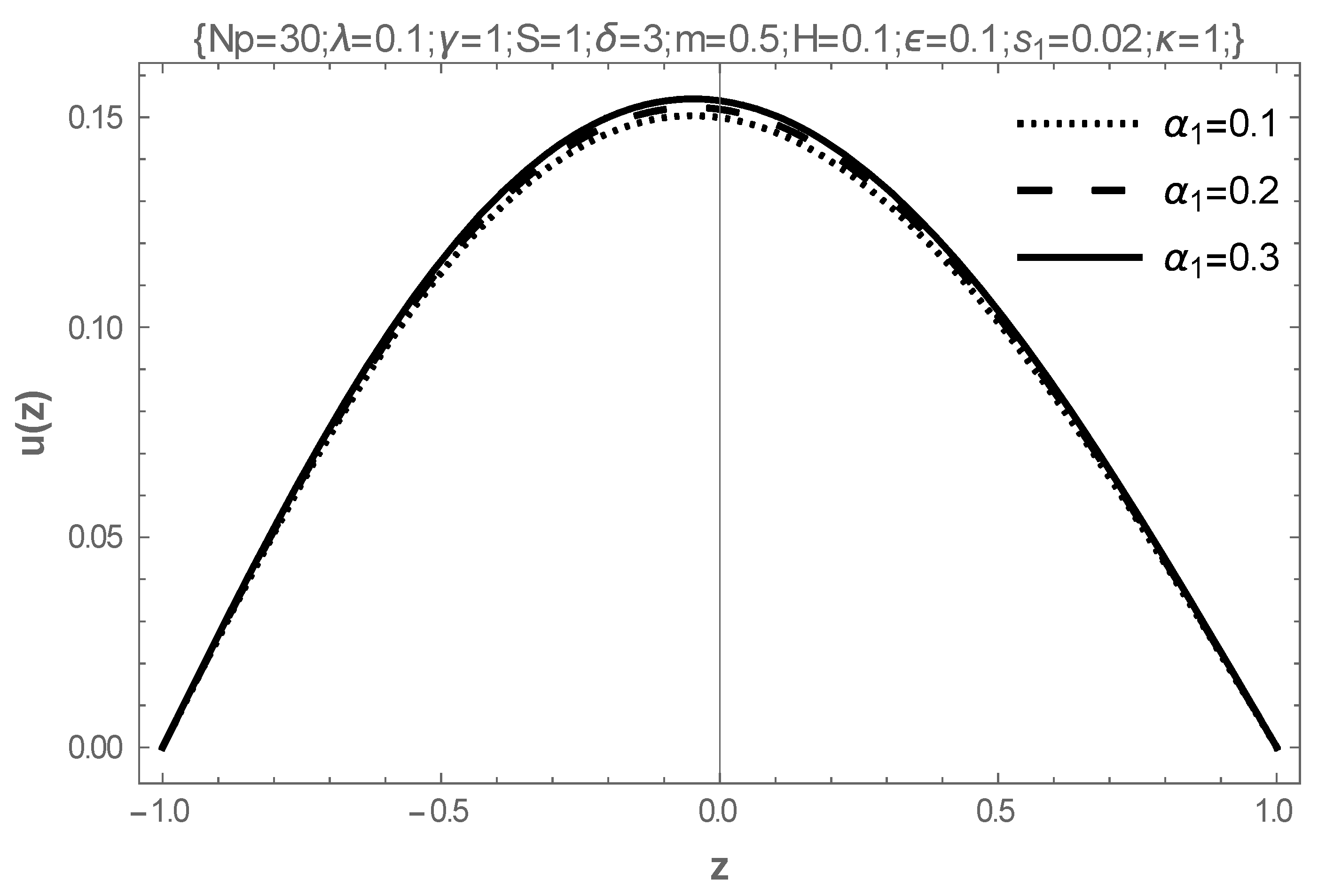
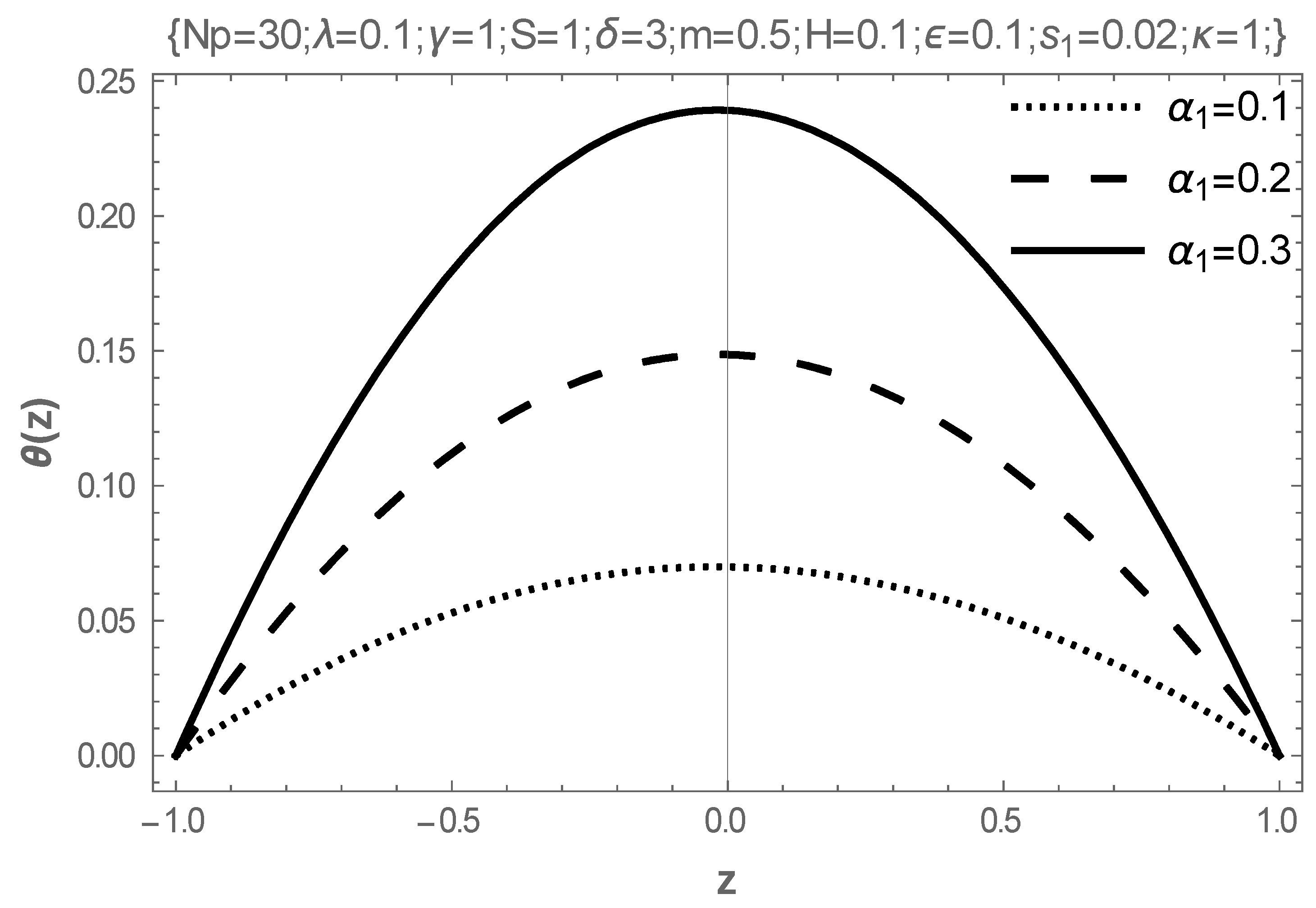

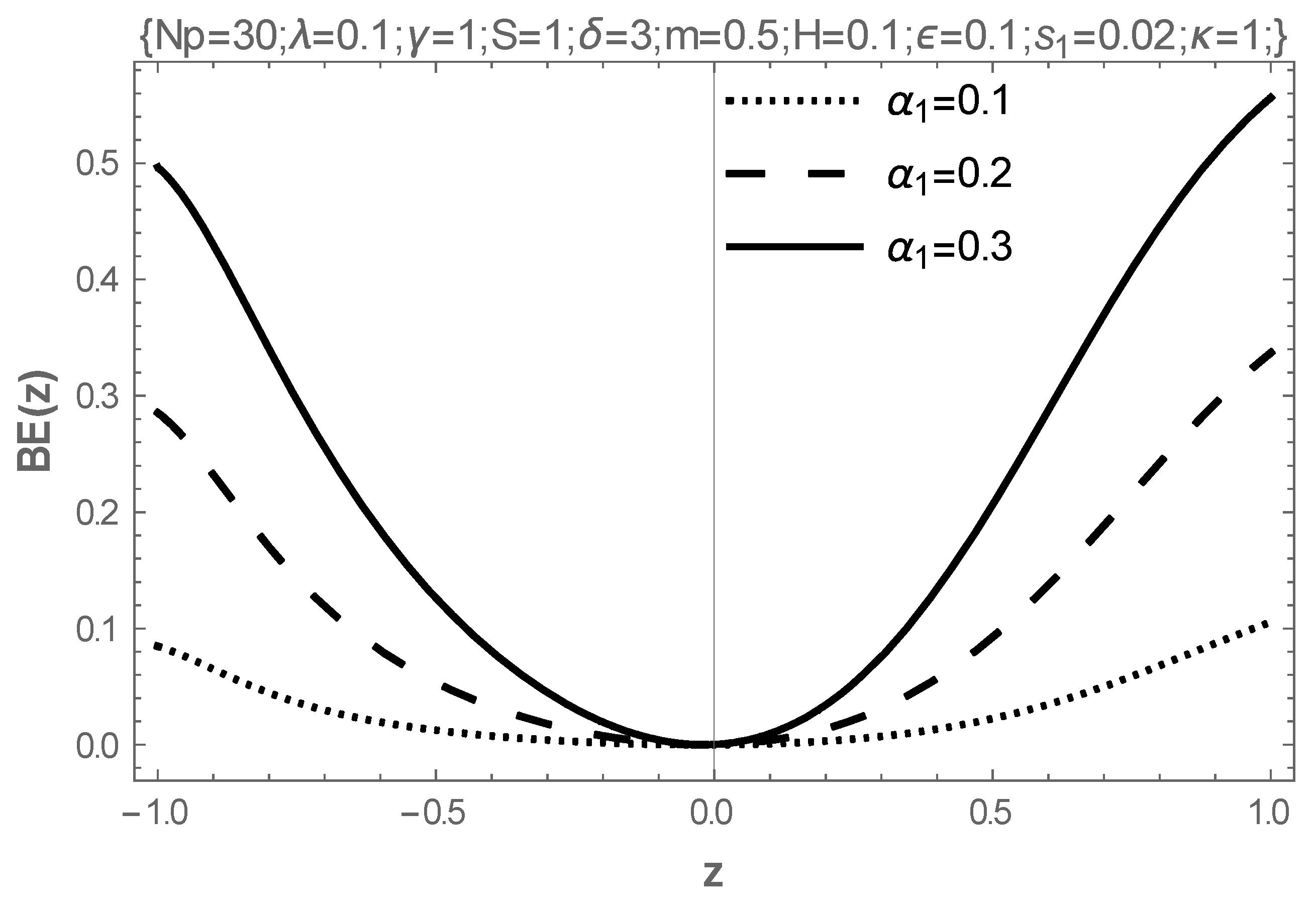
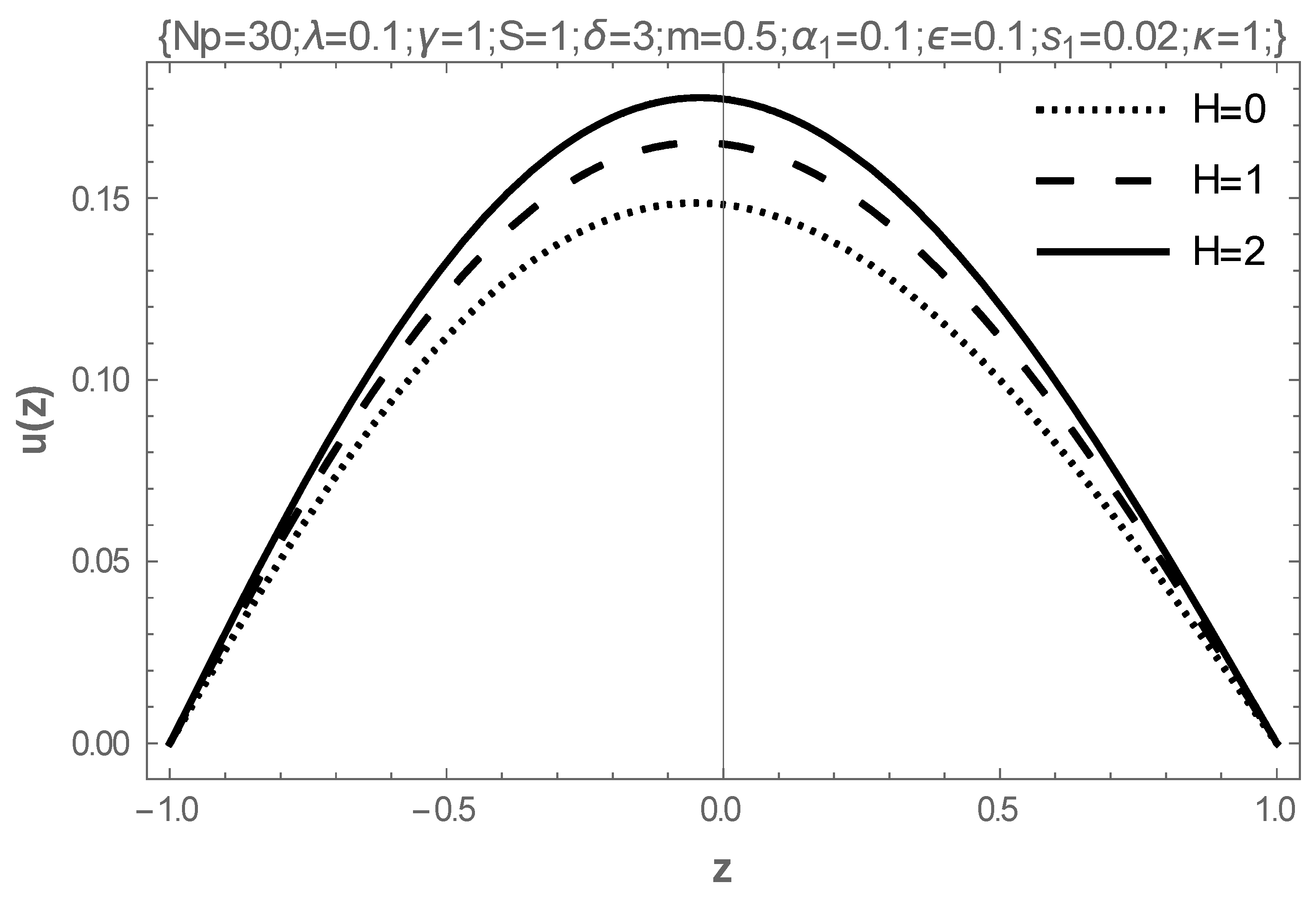


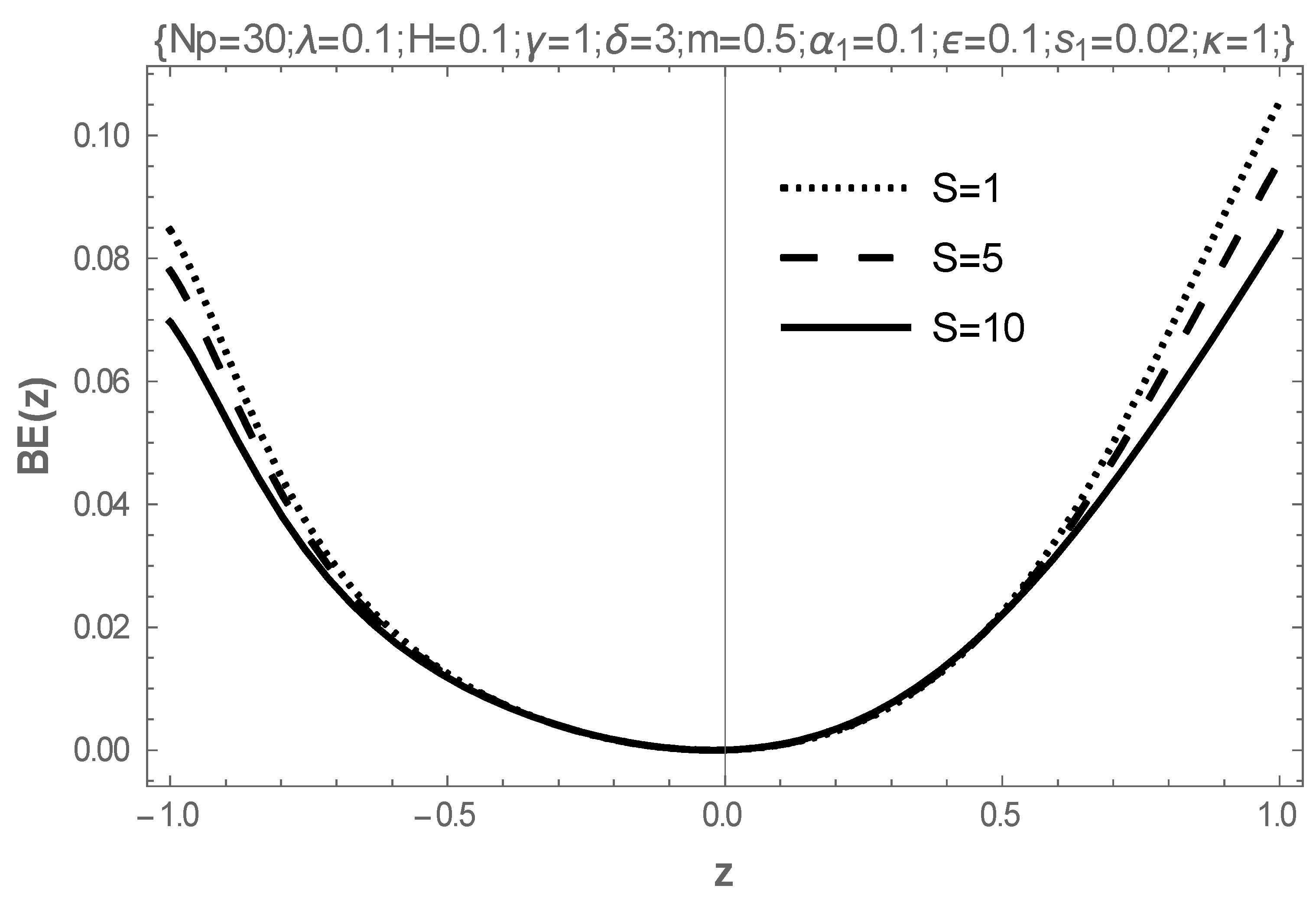

| (a) | |||
| (b) | |||
| 0.1 | 1 | 0.1 | 1 | ||||
| 0.1 | 1 | 0.1 | 1 | ||||
| 0.1 | 1 | 0.1 | 1 | ||||
| 0.1 | 1 | 0.1 | 1 | ||||
| 0.1 | 1 | 0.1 | 1 | ||||
| 0.1 | 1 | 0.1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banjo, P.O.; Lebelo, R.S.; Adesanya, S.O.; Unuabonah, E.I. Energy Efficacy Enhancement in a Reactive Couple-Stress Fluid Induced by Electrokinetics and Pressure Gradient with Variable Fluid Properties. Mathematics 2025, 13, 615. https://doi.org/10.3390/math13040615
Banjo PO, Lebelo RS, Adesanya SO, Unuabonah EI. Energy Efficacy Enhancement in a Reactive Couple-Stress Fluid Induced by Electrokinetics and Pressure Gradient with Variable Fluid Properties. Mathematics. 2025; 13(4):615. https://doi.org/10.3390/math13040615
Chicago/Turabian StyleBanjo, Peace O., Ramoshweu S. Lebelo, Samuel O. Adesanya, and Emmanuel I. Unuabonah. 2025. "Energy Efficacy Enhancement in a Reactive Couple-Stress Fluid Induced by Electrokinetics and Pressure Gradient with Variable Fluid Properties" Mathematics 13, no. 4: 615. https://doi.org/10.3390/math13040615
APA StyleBanjo, P. O., Lebelo, R. S., Adesanya, S. O., & Unuabonah, E. I. (2025). Energy Efficacy Enhancement in a Reactive Couple-Stress Fluid Induced by Electrokinetics and Pressure Gradient with Variable Fluid Properties. Mathematics, 13(4), 615. https://doi.org/10.3390/math13040615










