Joint Event Density and Curvature Within Spatio-Temporal Neighborhoods-Based Event Camera Noise Reduction and Pose Estimation Method for Underground Coal Mine
Abstract
1. Introduction
- A method for constructing a spherical spatio-temporal neighborhood is proposed by traversing events in the original set, discarding polarity, and using KD—trees for radius nearest neighbor search. The radius calculation is modified by adding a penalty coefficient before time, which addresses the challenge of non-uniform spatio-temporal data. This method enhances the tight correlation of spatio-temporal information in event data.
- The concept of event curvature is introduced, and its calculation process is mathematically derived. Based on the spherical spatio-temporal neighborhood, a method combining event density and event curvature for noise reduction is proposed. This method can preserve valid events as much as possible while considering the task of noise reduction, and obtaining clean and information-rich event flow data.
- A pose estimation method utilizing denoised events is presented. The event data are subjected to joint denoising. Two-dimensional event frames are generated from the filtered event data and used in conjunction with the OPNL method for initial pose estimation. Event line feature tracking and target pose optimization are carried out using the filtered event data and the initial pose estimation results.
2. Materials
2.1. Principle of Event Camera
2.2. Background Activity Noise Modelling
3. Methods
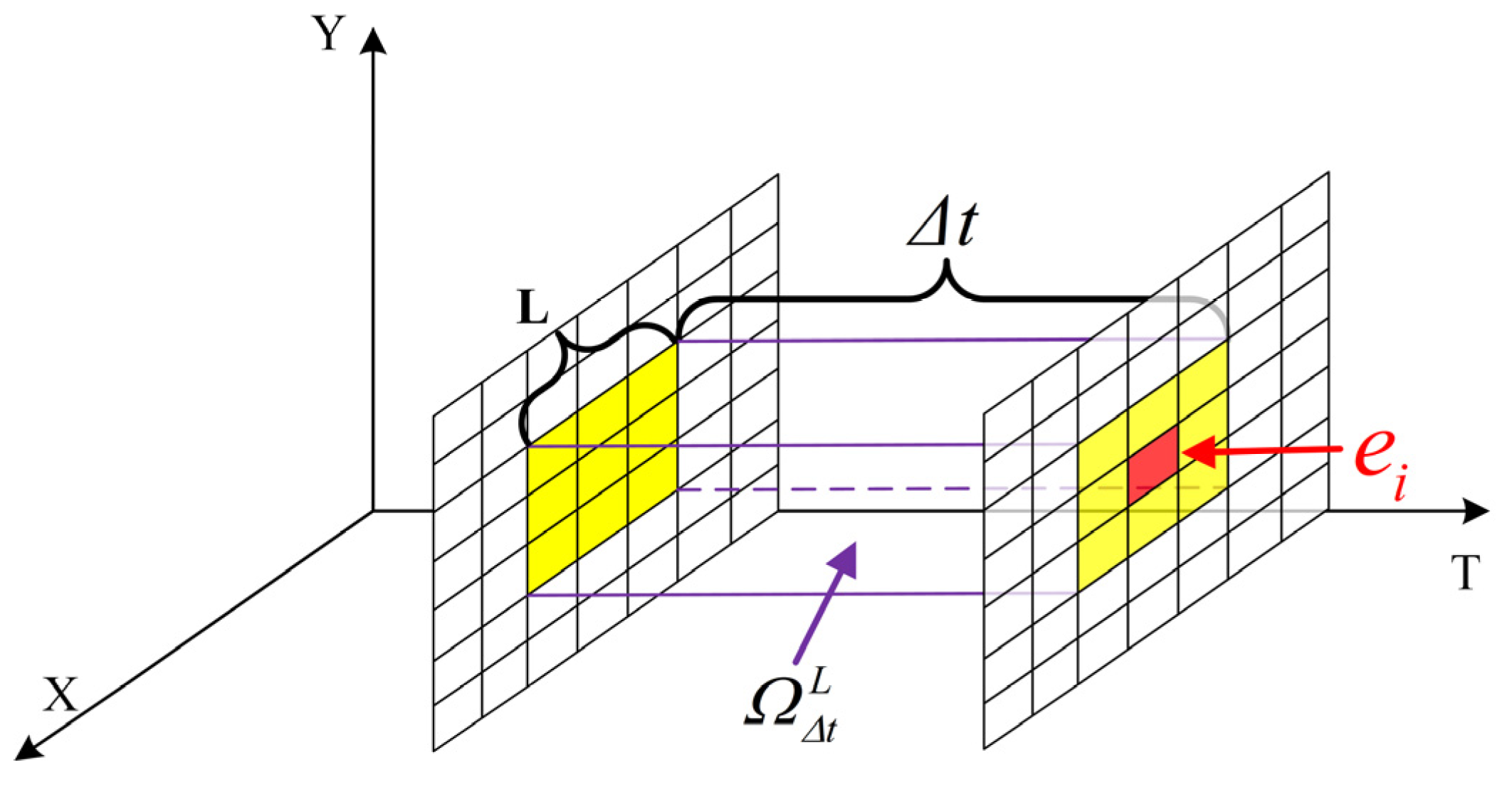
3.1. Spherical Spatio-Temporal Neighborhood
3.2. Event Density and Curvature Noise Reduction
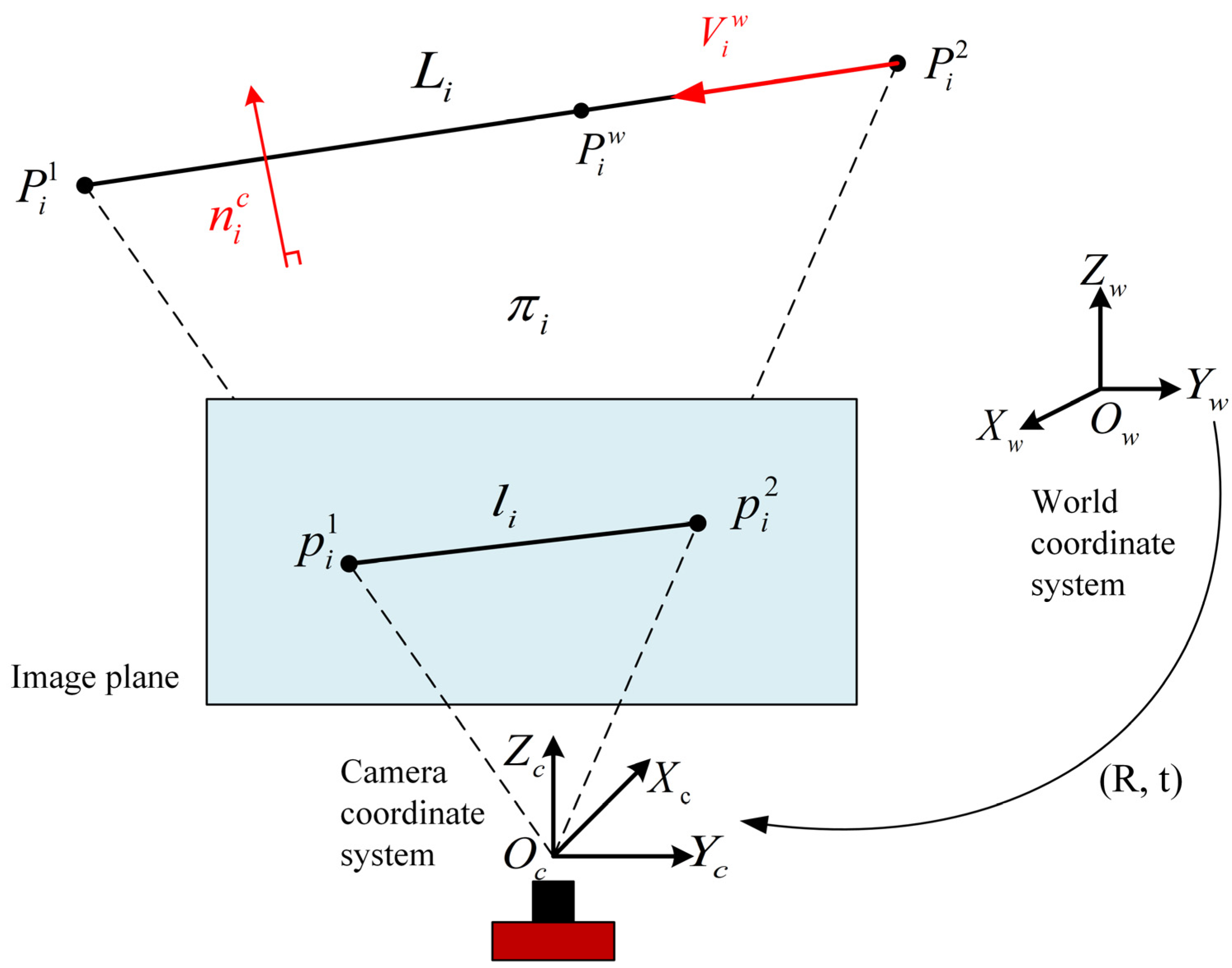
3.3. Noise-Reduced Event-Based Pose Estimation Framework
4. Results
4.1. Pure Noise Event Flow Noise Reduction
4.2. Event Data in Real-World Experimentation
4.2.1. DVSNoise20 Dataset Experimentation
4.2.2. Underground Coal Mine Laboratory Experimentation
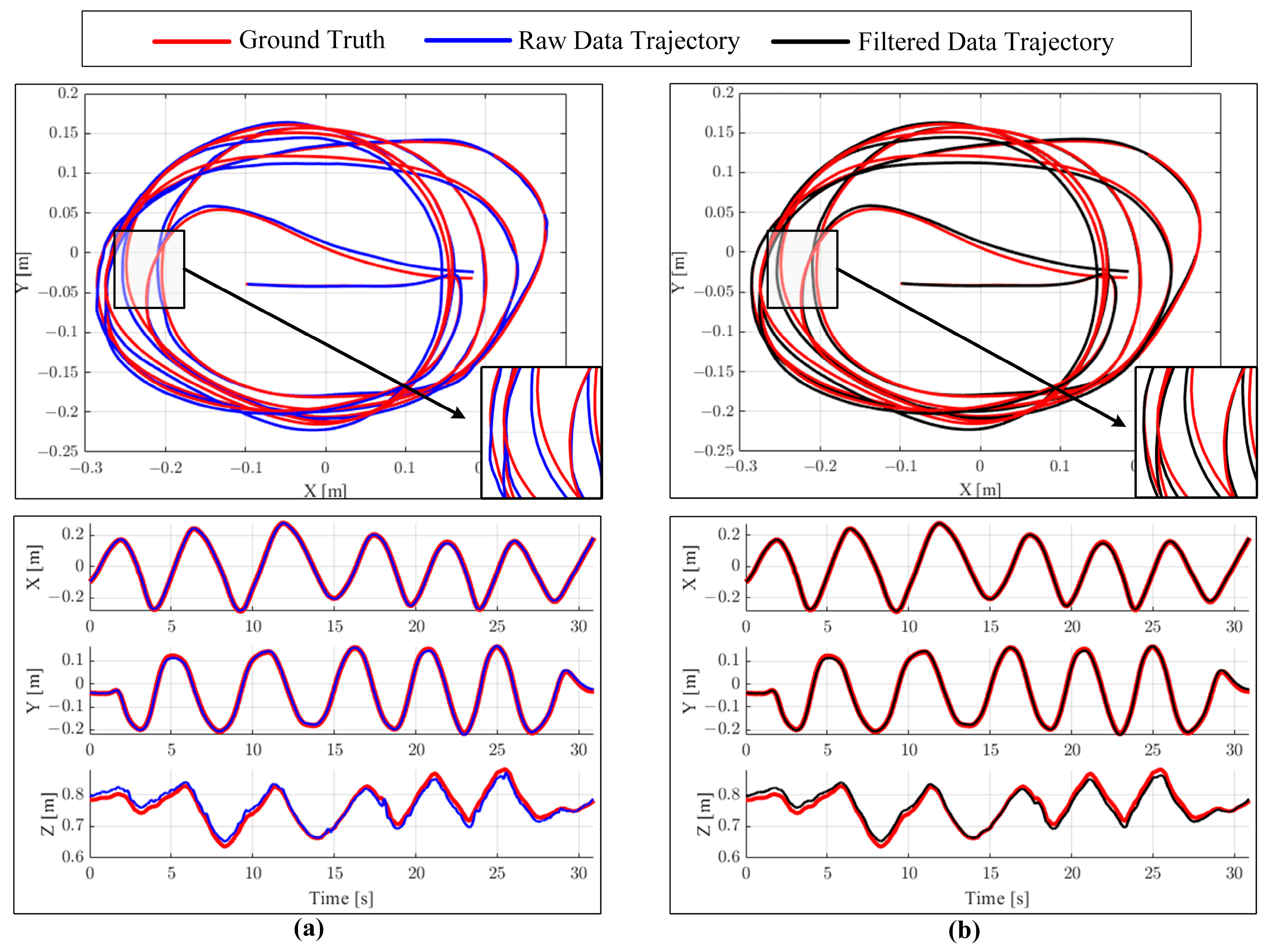
4.3. Pose Estimation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Wang, G.; Liu, Z.; Fu, J.; Wang, D.; Hao, Y.; Meng, L.; Zhang, J.; Zhou, Z.; Qin, J.; et al. Research of the present situation and development trend of intelligent coal mine construction market. Coal Sci. Technol. 2024, 52, 29–44. [Google Scholar]
- Taverni, G.; Moeys, D.P.; Li, C.; Cavaco, C.; Motsnyi, V.; Bello, D.S.S.; Delbruck, T. Front and Back Illuminated Dynamic and Active Pixel Vision Sensors Comparison. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 677–681. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, H.; Liang, L.; Zhang, J.; Song, B. Applications of Machine Vision in Coal Mine Fully Mechanized Tunneling Faces: A Review. IEEE Access 2023, 11, 102871–102898. [Google Scholar] [CrossRef]
- Delbrück, T.; Linares-Barranco, B.; Culurciello, E.; Posch, C. Activity-driven, event-based vision sensors. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010. [Google Scholar]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 × 128 120 dB 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef]
- Gallego, G.; Delbrück, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.J.; Conradt, J.; Scaramuzza, D.; et al. Event-based vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 154–180. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Liu, S.-C.; Delbruck, T. v2e: From video frames to realistic DVS events. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Delbruck, T. Frame-free dynamic digital vision. In Proceedings of the International Symposium on Secure-Life Electronics Advanced Electronics for Quality Life and Society, Tokyo, Japan, 6–7 March 2008; Volume 1. [Google Scholar]
- Czech, D.; Orchard, G. Evaluating noise filtering for event-based asynchronous change detection image sensors. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016. [Google Scholar]
- Liu, H.; Brandli, C.; Li, C.; Liu, S.C.; Delbruck, T. Design of a spatiotemporal correlation filter for event-based sensors. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015. [Google Scholar]
- Khodamoradi, A.; Kastner, R. O(N)-Space Spatiotemporal Filter for Reducing Noise in Neuromorphic Vision Sensors. IEEE Trans. Emerg. Top. Comput. 2018, 9, 15–23. [Google Scholar] [CrossRef]
- Feng, Y.; Lv, H.; Liu, H.; Zhang, Y.; Xiao, Y.; Han, C. Event Density Based Denoising Method for Dynamic Vision Sensor. Appl. Sci. 2020, 10, 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Du, B.; Shen, Y.; Wu, K.; Zhao, G.; Sun, J.; Wen, H. EV-gait: Event-based robust gait recognition using dynamic vision sensors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Duan, P.; Wang, Z.W.; Shi, B.; Cossairt, O.; Huang, T.; Katsaggelos, A.K. Guided event filtering: Synergy between intensity images and neuromorphic events for high performance imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8261–8275. [Google Scholar]
- Lagorce, X.; Orchard, G.; Galluppi, F.; Shi, B.E.; Benosman, R.B. HOTS: A Hierarchy of Event-Based Time-Surfaces for Pattern Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1346–1359. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, R.W.; Almatrafi, M.; Kaufman, J.R.; Asari, V.; Hirakawa, K. Inceptive event time-surfaces for object classification using neuromorphic cameras. In Proceedings of the Image Analysis and Recognition: 16th International Conference, ICIAR 2019, Waterloo, ON, Canada, 27–29 August 2019; Proceedings, Part II 16. Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Duan, P.; Wang, Z.W.; Zhou, X.; Ma, Y.; Shi, B. EventZoom: Learning to denoise and super resolve neuromorphic events. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Baldwin, R.W.; Almatrafi, M.; Asari, V.; Hirakawa, K. Event Probability Mask (EPM) and Event Denoising Convolutional Neural Network (EDnCNN) for Neuromorphic Cameras. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Fang, H.; Wu, J.; Li, L.; Hou, J.; Dong, W.; Shi, G. AEDNet: Asynchronous Event Denoising with Spatial-Temporal Correlation among Irregular Data. In Proceedings of the 30th ACM International Conference on Multimedia, Lisbon, Portugal, 10–14 October 2022. [Google Scholar]
- Hoffmann, R.; Weikersdorfer, D.; Conradt, J. Autonomous indoor exploration with an event-based visual SLAM system. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013. [Google Scholar]
- Kueng, B.; Mueggler, E.; Gallego, G.; Scaramuzza, D. Low-latency visual odometry using event-based feature tracks. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016. [Google Scholar]
- Censi, A.; Scaramuzza, D. Low-Latency Event-Based Visual Odometry. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 703–710. [Google Scholar]
- Kim, H.; Leutenegger, S.; Davison, A.J. Real-time 3D reconstruction and 6-DoF tracking with an event camera. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Rebecq, H.; Horstschaefer, T.; Gallego, G.; Scaramuzza, D. EVO: A Geometric Approach to Event-Based 6-DOF Parallel Tracking and Mapping in Real Time. IEEE Robot. Autom. Lett. 2016, 2, 593–600. [Google Scholar] [CrossRef]
- Vidal, A.R.; Rebecq, H.; Horstschaefer, T.; Scaramuzza, D. Ultimate SLAM? Combining Events, Images, and IMU for Robust Visual SLAM in HDR and High-Speed Scenarios. IEEE Robot. Autom. Lett. 2018, 3, 994–1001. [Google Scholar] [CrossRef]
- Gehrig, D.; Rebecq, H.; Gallego, G.; Scaramuzza, D. EKLT: Asynchronous photometric feature tracking using events and frames. Int. J. Comput. Vis. 2020, 128, 601–618. [Google Scholar] [CrossRef]
- Hidalgo-Carrió, J.; Gallego, G.; Scaramuzza, D. Event-aided direct sparse odometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Reverter Valeiras, D.; Orchard, G.; Ieng, S.H.; Benosman, R.B. Neuromorphic event-based 3d pose estimation. Front. Neurosci. 2016, 9, 522. [Google Scholar] [CrossRef] [PubMed]
- Reverter Valeiras, D.; Kime, S.; Ieng, S.H.; Benosman, R.B. An event-based solution to the perspective-n-point problem. Front. Neurosci. 2016, 10, 208. [Google Scholar]
- Jawaid, M.; Elms, E.; Latif, Y.; Chin, T.-J. Towards Bridging the Space Domain Gap for Satellite Pose Estimation using Event Sensing. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023. [Google Scholar]
- Liu, Q.; Xing, D.; Tang, H.; Ma, D.; Pan, G. Event-based Action Recognition Using Motion Information and Spiking Neural Networks. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence {IJCAI-21}, Montreal, QC, Canada, 19–27 August 2021. [Google Scholar]
- Yu, N.; Ma, T.; Zhang, J.; Zhang, Y.; Bao, Q.; Wei, X.; Yang, X. Adaptive Vision Transformer for Event-Based Human Pose Estimation. In Proceedings of the 32nd ACM International Conference on Multimedia, Melbourne, VIC, Australia, 28 October–1 November 2024. [Google Scholar]
- Liu, Z.; Guan, B.; Shang, Y.; Yu, Q.; Kneip, L. Line-Based 6-DoF Object Pose Estimation and Tracking with an Event Camera. IEEE Trans. Image Process. 2024, 33, 4765–4780. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Du, Z.; Guo, Z.; Ma, H. VRHCF: Cross-Source Point Cloud Registration via Voxel Representation and Hierarchical Correspondence Filtering. arXiv 2024, arXiv:2403.10085. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In Proceedings of the Computer Vision–ECCV 2010: 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; Proceedings, Part III 11. Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lei, H.; Akhtar, N.; Mian, A. Octree guided cnn with spherical kernels for 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wang, Z.; Hu, J.; Shi, Y.; Cai, J.; Pi, L. Target Fitting Method for Spherical Point Clouds Based on Projection Filtering and K-Means Clustered Voxelization. Sensors 2024, 24, 5762. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Xu, G.; Cheng, Y. An efficient and globally optimal method for camera pose estimation using line features. Mach. Vis. Appl. 2020, 31, 48. [Google Scholar] [CrossRef]









| Noise level | BAF | KNoise | YNoise | Ours | ||||
|---|---|---|---|---|---|---|---|---|
| Residual Noise | NRR | Residual Noise | NRR | Residual Noise | NRR | Residual Noise | NRR | |
| 500 | 34 | 93.20% | 0 | 100% | 0 | 100% | 0 | 100% |
| 3000 | 246 | 91.80% | 13 | 99.57% | 3 | 99.90% | 2 | 99.93% |
| 6000 | 581 | 90.32% | 42 | 99.30% | 16 | 99.73% | 6 | 99.90% |
| 9000 | 1077 | 88.03% | 106 | 98.82% | 89 | 99.01% | 67 | 99.26% |
| Bike | Stairs | LabFast | CheckerSlow | |
|---|---|---|---|---|
| Raw | 1.912 | 1.395 | 1.313 | 1.147 |
| BAF | 0.799 | 0.829 | 0. 961 | 1.068 |
| KNoise | 0.568 | 0.532 | 0.688 | 0.594 |
| YNoise | 0.796 | 0.790 | 0.917 | 1.128 |
| AEDNet | 0.809 | 0.830 | 1.130 | 1.197 |
| Ours | 1.898 | 1.392 | 1.286 | 1.289 |
| Seat | I-Beam Support | Cutting Head | Hydraulic Support | |
|---|---|---|---|---|
| Raw | 0.697 | 0.665 | 1.114 | 0.752 |
| BAF | 0.729 | 0.732 | 1.088 | 0.608 |
| KNoise | 0.520 | 0.589 | 0.887 | 0.586 |
| YNoise | 0.783 | 0.722 | 1.037 | 0.660 |
| AEDNet | 0.709 | 0.663 | 1.075 | 1.027 |
| Ours | 0.772 | 0.762 | 1.126 | 1.045 |
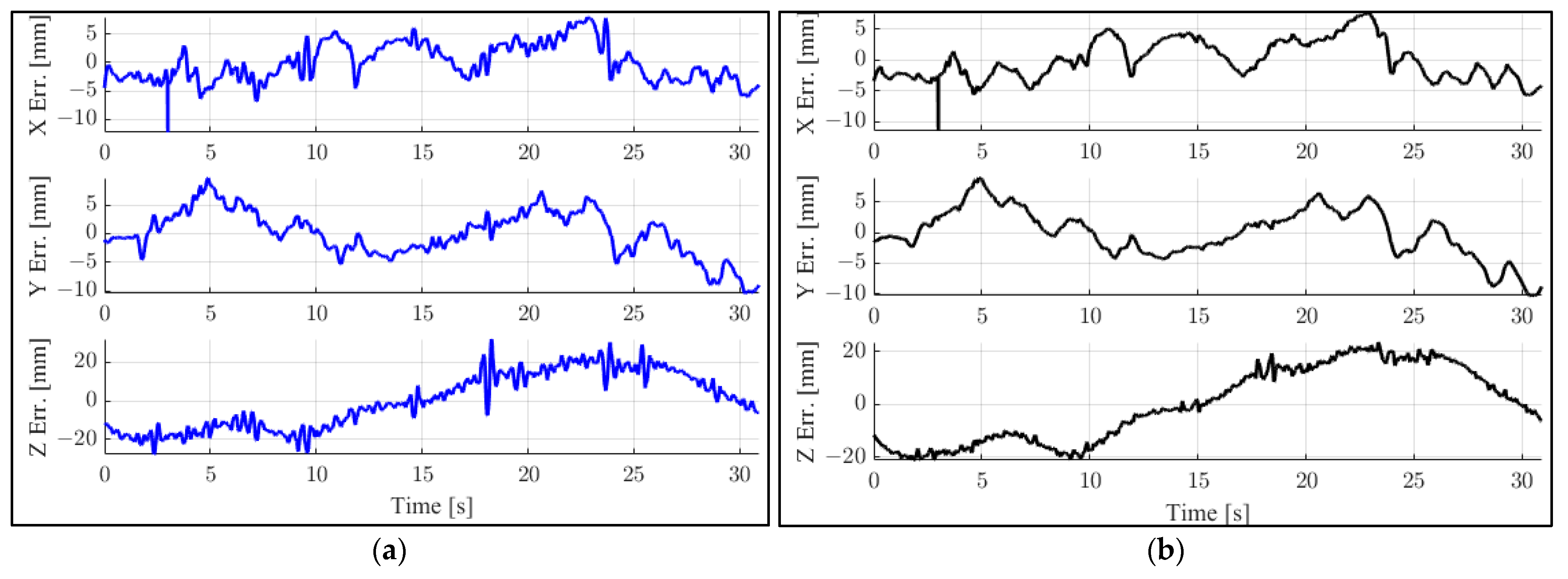
| Group | Ground Truth | Raw Data Pose | Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| x/mm | y/mm | z/mm | x/mm | y/mm | z/mm | x/mm | y/mm | z/mm | |
| 1 | −102.021 | −38.690 | 783.997 | −98.574 | −39.162 | 785.433 | −3.447 | 0.472 | −1.436 |
| 2 | 136.335 | −32.794 | 796.859 | 136.784 | −33.207 | 808.408 | −0.449 | 0.413 | −11.549 |
| 3 | −8.076 | −194.822 | 746.984 | −7.716 | −198.890 | 755.323 | −0.360 | 4.068 | −8.339 |
| 4 | −213.819 | 75.092 | 781.518 | −212.221 | 66.891 | 785.323 | −1.598 | 8.201 | −3.805 |
| 5 | 184.510 | 76.218 | 825.650 | 182.618 | 71.050 | 829.153 | 1.892 | 5.168 | −3.503 |
| 6 | 113.864 | −180.765 | 690.410 | 116.264 | −184.283 | 693.892 | −2.400 | 3.518 | −3.482 |
| 7 | −260.360 | −117.377 | 668.856 | −260.736 | −121.136 | 672.407 | 0.376 | 3.759 | −3.551 |
| 8 | −27.696 | 129.619 | 761.616 | −34.266 | 130.458 | 763.206 | 6.570 | −0.839 | −1.590 |
| 9 | 273.760 | 18.117 | 797.805 | 275.008 | 17.510 | 796.989 | −1.248 | 0.607 | 0.816 |
| 10 | 57.244 | −178.920 | 673.903 | 52.542 | −176.189 | 665.965 | 4.702 | −2.731 | 7.938 |
| 11 | −204.065 | −35.890 | 693.285 | −208.566 | −35.867 | 680.658 | 4.501 | −0.023 | 12.627 |
| 12 | 23.052 | 153.002 | 801.715 | 20.567 | 152.348 | 786.682 | 2.485 | 0.654 | 15.033 |
| 13 | 167.950 | −139.796 | 786.579 | 164.610 | −141.578 | 754.401 | 3.340 | 1.782 | 32.178 |
| 14 | −225.644 | −89.067 | 738.320 | −232.302 | −92.933 | 720.855 | 6.658 | 3.866 | 17.465 |
| 15 | −274.243 | −31.389 | 779.347 | −273.044 | −32.758 | 742.196 | −1.199 | 1.369 | 37.151 |
| Group | Ground Truth | Filtered Data Pose | Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| x/mm | x/mm | x/mm | x/mm | y/mm | z/mm | x/mm | y/mm | z/mm | |
| 1 | −102.021 | −100.586 | −100.586 | −100.586 | −39.162 | 785.433 | −1.435 | 0.119 | 0.174 |
| 2 | 136.335 | 136.065 | 136.065 | 136.065 | −33.207 | 808.408 | 0.270 | −0.197 | −9.834 |
| 3 | −8.076 | −7.196 | −7.196 | −7.196 | −198.890 | 755.323 | −0.880 | 3.807 | −7.915 |
| 4 | −213.819 | −212.234 | −212.234 | −212.234 | 66.891 | 785.323 | −1.585 | 8.475 | −4.121 |
| 5 | 184.510 | 182.887 | 182.887 | 182.887 | 71.050 | 829.153 | 1.623 | 4.888 | −2.542 |
| 6 | 113.864 | 116.133 | 116.133 | 116.133 | −184.283 | 693.892 | −2.269 | 3.376 | −3.214 |
| 7 | −260.360 | −261.775 | −261.775 | −261.775 | −121.136 | 672.407 | 1.415 | 3.911 | −6.857 |
| 8 | −27.696 | −34.020 | −34.020 | −34.020 | 130.458 | 763.206 | 6.324 | −0.504 | −1.726 |
| 9 | 273.760 | 273.980 | 273.980 | 273.980 | 17.510 | 796.989 | −0.220 | 0.429 | 2.924 |
| 10 | 57.244 | 52.472 | 52.472 | 52.472 | −176.189 | 665.965 | 4.772 | −2.456 | 7.421 |
| 11 | −204.065 | −208.350 | −208.350 | −208.350 | −35.867 | 680.658 | 4.285 | −0.392 | 14.149 |
| 12 | 23.052 | 20.952 | 20.952 | 20.952 | 152.348 | 786.682 | 2.100 | 0.071 | 16.264 |
| 13 | 167.950 | 166.029 | 166.029 | 166.029 | −141.578 | 754.401 | 1.921 | 3.031 | 19.000 |
| 14 | −225.644 | −231.394 | −231.394 | −231.394 | −92.933 | 720.855 | 5.750 | 4.358 | 23.491 |
| 15 | −274.243 | −274.063 | −274.063 | −274.063 | −32.758 | 742.196 | −0.180 | 0.017 | 32.700 |
| Data Type | Absolute Trajectory Error (mm) | |||
|---|---|---|---|---|
| Rmse | Mean | Median | Std | |
| Raw | 15.392 | 14.208 | 15.099 | 5.922 |
| Filtered | 15.043 | 14.052 | 15.218 | 5.374 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Jiang, J.; Zhang, X.; Ji, Y.; Zhu, L.; Xie, Y.; Ren, Z. Joint Event Density and Curvature Within Spatio-Temporal Neighborhoods-Based Event Camera Noise Reduction and Pose Estimation Method for Underground Coal Mine. Mathematics 2025, 13, 1198. https://doi.org/10.3390/math13071198
Yang W, Jiang J, Zhang X, Ji Y, Zhu L, Xie Y, Ren Z. Joint Event Density and Curvature Within Spatio-Temporal Neighborhoods-Based Event Camera Noise Reduction and Pose Estimation Method for Underground Coal Mine. Mathematics. 2025; 13(7):1198. https://doi.org/10.3390/math13071198
Chicago/Turabian StyleYang, Wenjuan, Jie Jiang, Xuhui Zhang, Yang Ji, Le Zhu, Yanbin Xie, and Zhiteng Ren. 2025. "Joint Event Density and Curvature Within Spatio-Temporal Neighborhoods-Based Event Camera Noise Reduction and Pose Estimation Method for Underground Coal Mine" Mathematics 13, no. 7: 1198. https://doi.org/10.3390/math13071198
APA StyleYang, W., Jiang, J., Zhang, X., Ji, Y., Zhu, L., Xie, Y., & Ren, Z. (2025). Joint Event Density and Curvature Within Spatio-Temporal Neighborhoods-Based Event Camera Noise Reduction and Pose Estimation Method for Underground Coal Mine. Mathematics, 13(7), 1198. https://doi.org/10.3390/math13071198







