Abstract
This paper introduces a novel kind of factorial hidden Markov model (FHMM), specifically the feedforward FHMM (FFHMM). In contrast to traditional FHMMs, the FFHMM is capable of directly utilizing supplementary information from observations through predefined states, which are derived using an automatic feature filter (AFF). We investigate two variations of FFHMM models that integrate predefined states with the FHMM: the direct FFHMM and the embedded FFHMM. In the direct FFHMM, alterations to one sub-hidden Markov model (HMM) do not affect the others, enabling individual improvements in HMM estimation. On the other hand, the sub-HMM chains within the embedded FFHMM are interconnected, suggesting that adjustments to one HMM chain may enhance the estimations of other HMM chains. Consequently, we propose two algorithms for these FFHMM models to estimate their respective hidden states. Ultimately, experiments conducted on two real-world datasets validate the efficacy of the proposed models and algorithms.
Keywords:
feedforward factorial hidden Markov model; automatic feature filter; Viterbi algorithm; additive factorial approximate MAP MSC:
65C20; 65C40
1. Introduction
The factorial hidden Markov model (FHMM) represents a variant of the Hidden Markov Model (HMM) that incorporates distributed state representations [1]. The latent state space encompasses multiple chains that evolve concurrently, collectively influencing the single observation at any given moment [2]. Due to its ability to model outcomes influenced by several independent, time-varying processes, the FHMM is suitable for a wide range of applications. For instance, the FHMM has been successfully utilized in various fields, including visual tracking [3], non-intrusive load monitoring (NILM) [4], consumers’ choice models [5], natural language processing [6], estimating tumor clonal composition [7], fault diagnosis [8], online skill rating [9], random telegraph noise [10], forecasting financial portfolios with value at risk [11], and pitch and formant tracking [12].
According to [13], an additive FHMM model is defined as
Model 1.
In this model, is the number of HMM chains; is the number of states in the i-th HMM; denotes the state of the i-th HMM at time t; is the initial state distribution for the i-th HMM, while is the initial state distribution for the i-th HMM at state j; is the transition matrix for the i-th HMM, and its element represents the probability of the i-th HMM being transferred from state to state ; is the aggregated observation; is the mean of the i-th HMM for state ; and is the covariance matrix. More specifically, Equation (3) can be explicitly written as
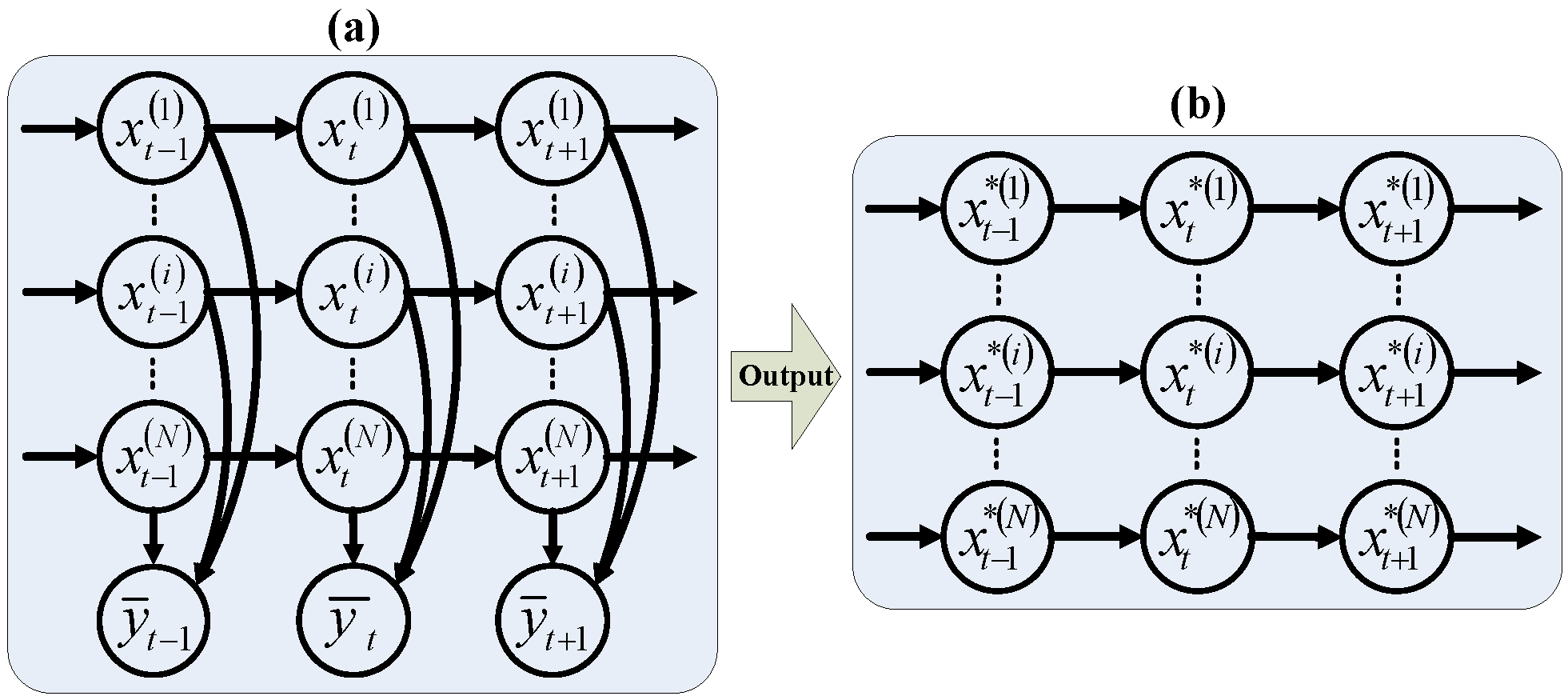
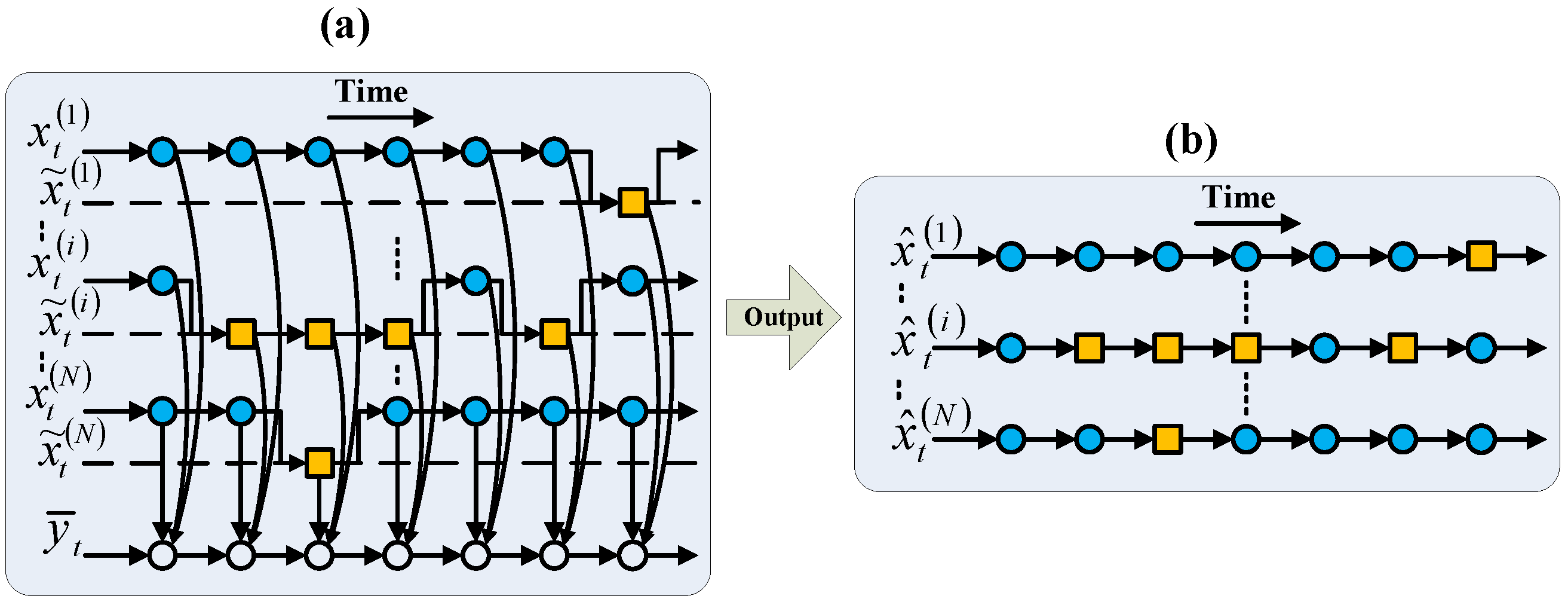
where and . A scheme of the FHMM model is depicted in Figure 1a. Then, the task of the FHMM is to estimate the states of all HMMs, which is illustrated in Figure 1b.
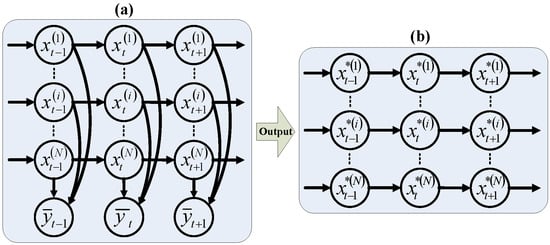
Figure 1.
Additive FHMM and its output of the optimal estimations for the individual HMMs. (a) Depicts the model of the FHMM [13]. (b) Depicts the optimal estimation for the individual HMMs.
To achieve optimal estimates, the Viterbi algorithm as described in [14] for Hidden Markov Models (HMMs) can be adapted for use with FHMMs, resulting in the EXACT algorithm. Nonetheless, the EXACT algorithm necessitates the enumeration of an exponential number of states, leading to significant computational demands and highlighting the need for approximate algorithms. Even particle approximations via particle filters [15] suffer from the curse of dimensionality in high-dimensional FHMMs. As the dimensionality increases, the state space becomes increasingly sparse, and the number of particles required to accurately represent the posterior distribution grows exponentially. A possible solution can be found in localised particle filters [16] and localised forward–backward algorithms [17], which trade-off accuracy to overcome the curse of dimensionality. As an alternative, Ref. [13] introduces an approximate approach termed the additive factorial approximate MAP (AFAMAP), designed to globally optimize state estimates within FHMMs. AFAMAP offers three advantages over other approximation techniques: (1) it accounts for the variations in observations between successive time points, (2) it employs robust component accounting to manage unmodeled observations effectively, and (3) it transforms the problem into a convex optimization task with a guaranteed global optimum.
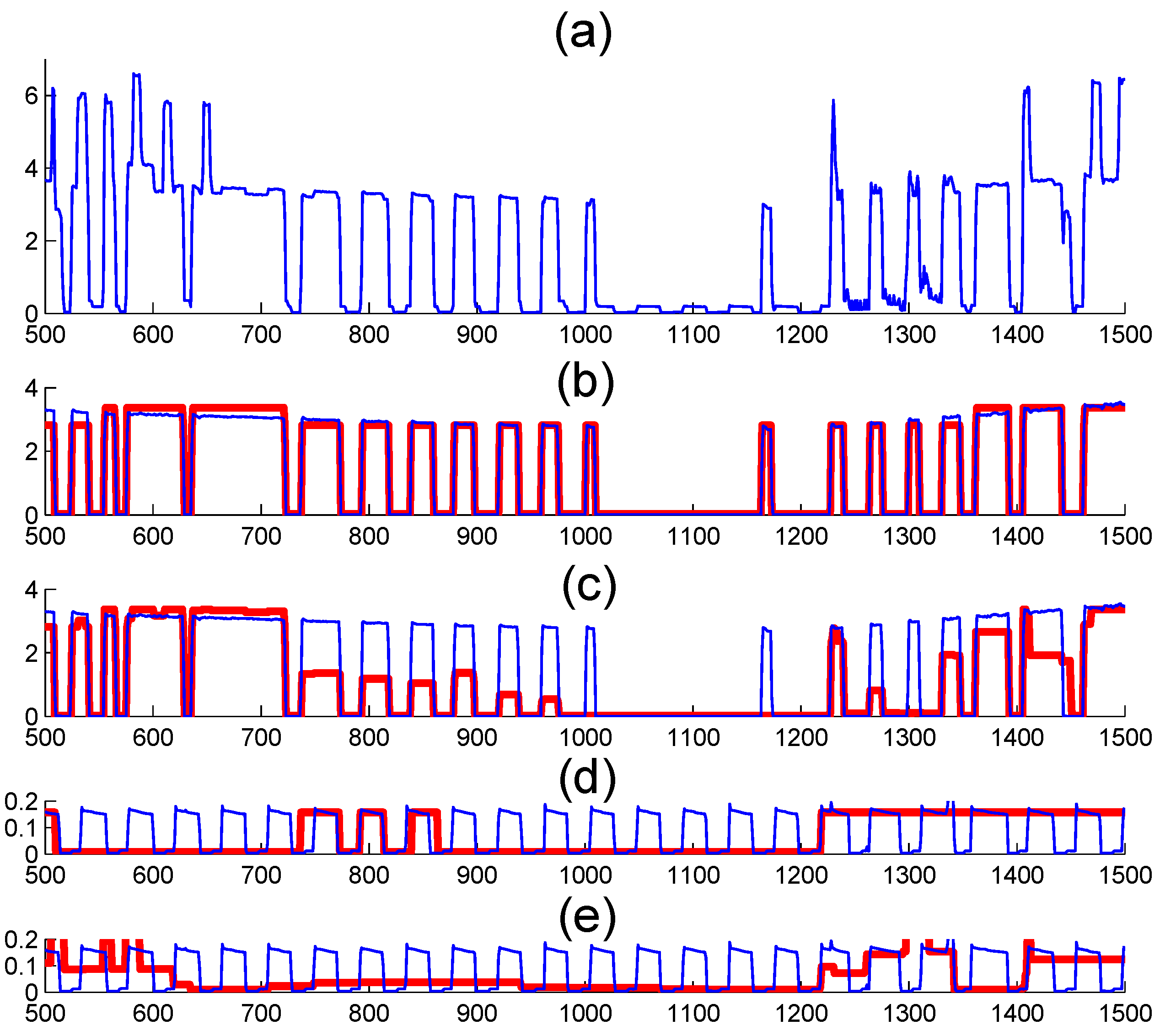
Nevertheless, in numerous instances, the FHMM struggles to detect hidden state variables that exhibit notable patterns but possess small magnitudes. In such scenarios, during specific time intervals, state variables with distinct patterns can be readily identified using alternative methods. In this paper, we define a pattern as significant if it is readily discernible from observations, such as the square-wave electricity consumption of a refrigerator, illustrated in Figure 2a between 1000 and 1200 min. To address these limitations of the FHMM, this paper proposes a feedforward FHMM (FFHMM) that employs predefined states via an automatic feature filter (AFF). The term “feedforward” is derived from feedforward control systems [18], referring to the predefined states in our context. In this study, we only utilize the AFF to extract information from testing data. Nonetheless, other forms of prior knowledge can also be employed to determine the predefined states. Consequently, our FFHMM framework can improve the performance of the FHMM by incorporating various additional pieces of information.
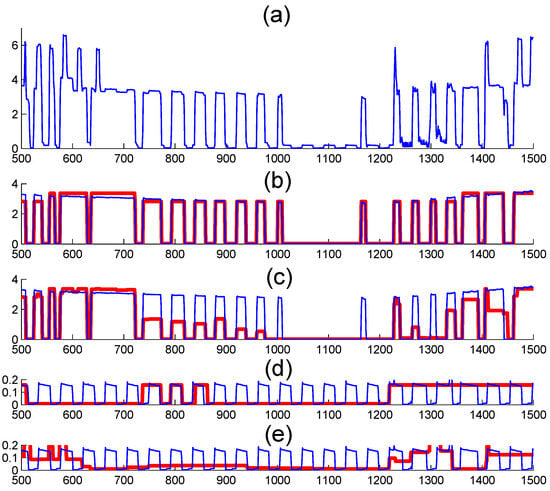
Figure 2.
An illustrative example reveals that both the exact Viterbi algorithm and the approximate AFAMAP algorithm, when applied to the FHMM, struggle to detect the electricity consumption of the refrigerator during the interval between 1000 and 1200 min. In this figure, the blue lines denote the actual consumption (ground truth), while the red lines represent the estimated consumption. The sub-figures are as follows: (a) displays the aggregated consumption (observation) for the entire household; (b) compares the actual consumption of air conditioner 1 with its estimation derived from the EXACT algorithm; (c) contrasts the actual consumption of air conditioner 1 with its approximation obtained through the AFAMAP algorithm; (d) shows the true consumption pattern of the refrigerator alongside its EXACT algorithm estimate; and (e) presents the actual consumption of the refrigerator with its approximation derived from the AFAMAP algorithm.
The remainder of this paper is structured as follows. In Section 2, we first introduce an AFF designed to identify significant patterns and treat them as predefined states. Subsequently, we present our key contributions: the direct FFHMM and embedded FFHMM. We also outline the exact and approximate algorithms associated with these models. The efficacy of the FFHMM models is evaluated in Section 3 through rigorous experimentation on two distinct datasets. Lastly, Section 4 summarizes the key points and findings of this paper.
2. Feedforward FHMM
In this section, we first introduce an automatic feature filter (AFF) aimed at extracting notable patterns from the aggregated observations—patterns that are discernible yet not accurately identified by the FHMM. The AFF subsequently facilitates the determination of certain predefined states. We then propose a novel model, the feedforward FHMM (FFHMM), which integrates the FHMM with these predefined states. Depending on the method of integration, we discuss two variations: the direct FFHMM and the embedded FFHMM.
2.1. Automatic Feature Filter
As previously discussed, the FHMM tends to overlook numerous significant patterns present in the observations, which could otherwise be utilized to refine its estimates for individual HMM chains. To address this issue, we have developed the following automatic feature filter:
- If for all such that , we have , then
- Otherwise,
where is the estimated status from the AFF for the i-th HMM chain at time t. is a selection function, whose output is the corresponding state of the i-th HMM chain if its j-th feature has been detected from the aggregated observation at time t. is the number of features we used for detecting the i-th HMM chain.
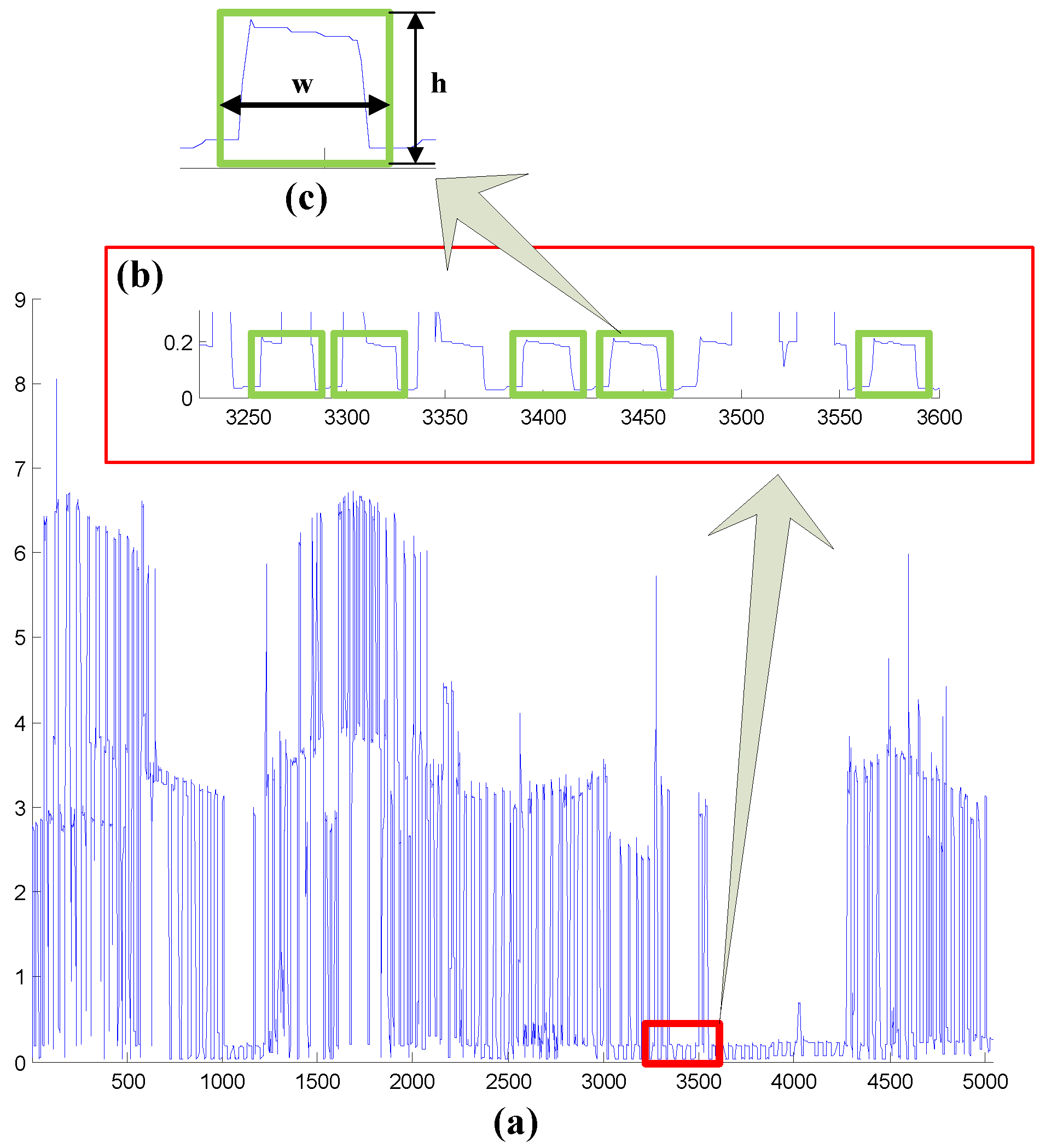
Figure 3 presents an illustration of the AFF method. Here, we employ green-colored operational windows with specified width w and height h as the features for detection purposes. The filter automatically retrieves the most similar pairs of w and h values. Following the clustering process, the selection function is responsible for determining the predefined state at time t.
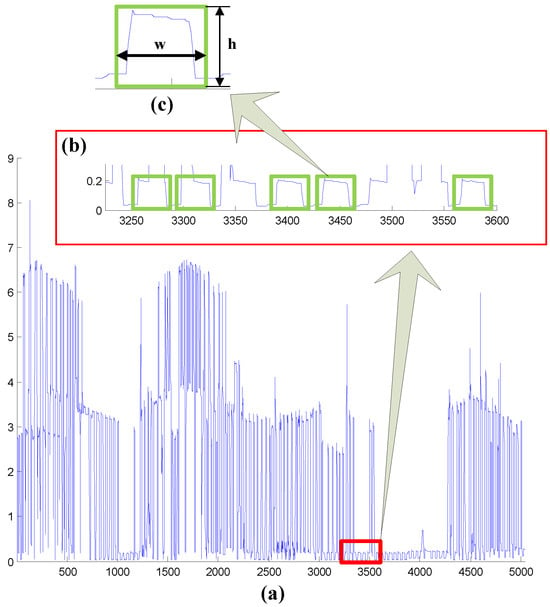
Figure 3.
Example of automatic feature filter (AFF). (a) Illustrates the aggregated observation, with a segment expanded to form sub-figure (b). Each green window in (b) encapsulates a similar pattern identified during the first step of the AFF process. In the second step of AFF, depicted in (c), the dimensions—width w and height h—of the windows are employed to classify the recognized patterns.
2.2. Direct FFHMM
Now, we examine two distinct approaches to integrating predefined states with the FHMM: first, a simple concatenation method, followed by a more intricate technique. Alongside these, we also introduce the EXACT algorithms and their derivatives, the AFAMAP algorithms.
Firstly, the straightforward method involves the direct fusion of estimates from the FHMM and AFF. Specifically, this entails substituting the non-zero estimates from the AFF into the corresponding positions within the FHMM. This approach gives rise to what we term the direct FFHMM model:
Model 2.
During , every individual HMM chain satisfies
where denotes the output estimation provided by the direct FFHMM for the i-th HMM at time t; represents the output from the AFF for the i-th HMM at time t, with indicating that no state has been retrieved by the AFF from the aggregated observation for the i-th HMM at time t; and finally, signifies the output of the FHMM as described in Model 1, which corresponds to the optimal estimation for the i-th HMM at time t.
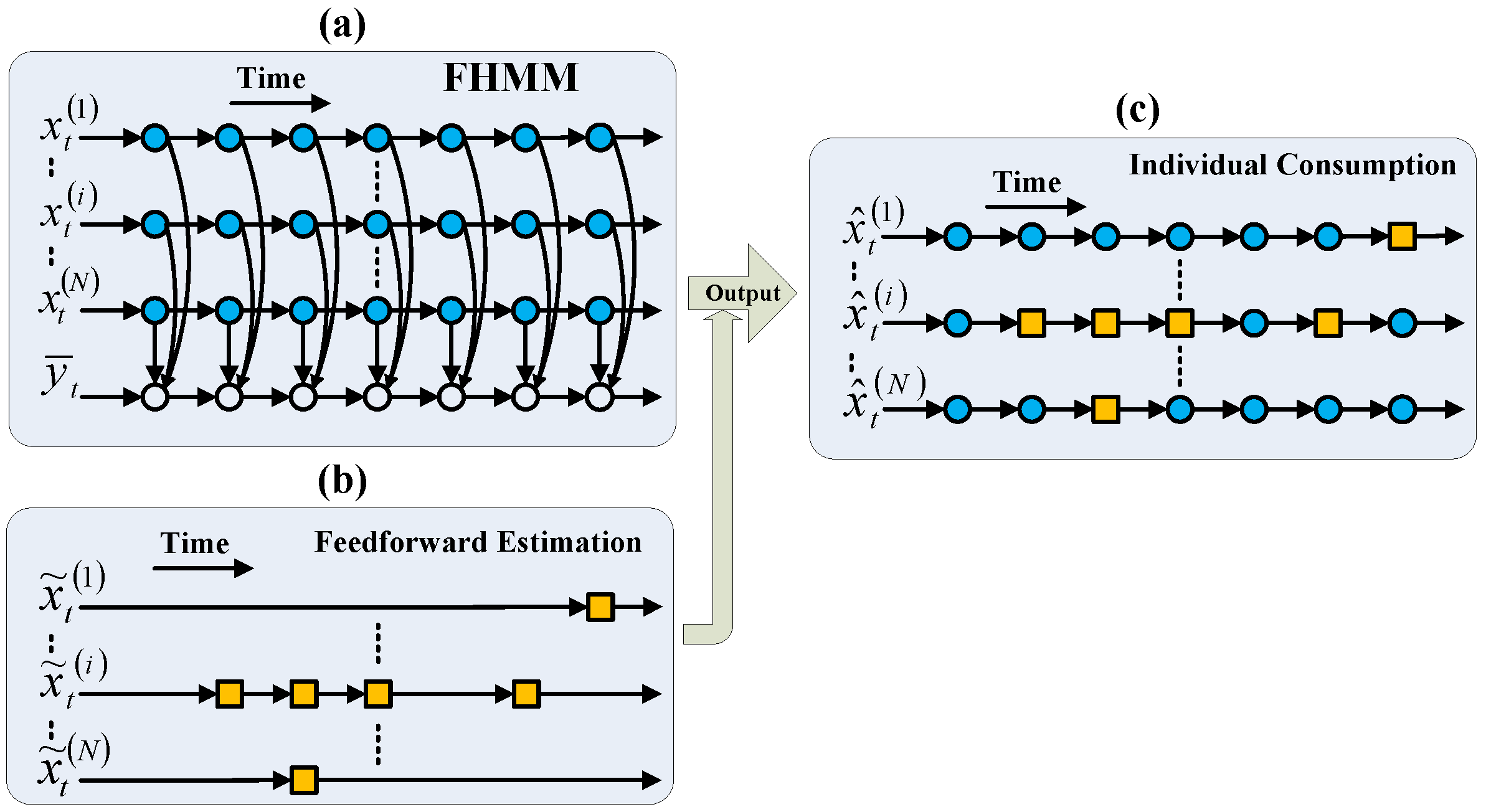
Figure 4 presents a schematic representation of the direct FFHMM approach. According to this figure, one can readily discern that the estimation for the individual HMM, denoted as , is chiefly reliant on the FHMM’s corresponding estimate . Nevertheless, there are instances at particular time points where the AFF yields non-zero estimations; in such cases, these AFF-derived estimates supersede those originating from the FHMM. Then, an EXACT algorithm for the direct FFHMM is proposed in Algorithm 1.
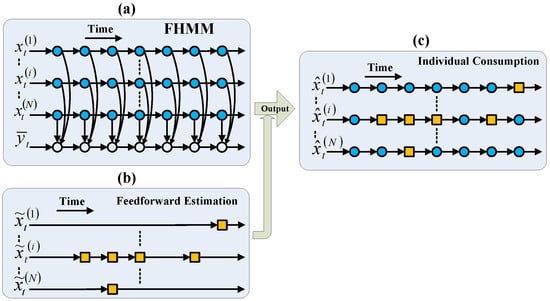
Figure 4.
Scheme of the direct FFHMM. (a) Incorporates the FHMM model. (b) Presents the estimation of the AFF, where each orange square denotes a state that has been identified by the AFF at a specific moment in time. In forming the output estimation of the FFHMM as shown in (c), the majority of state estimations are derived from the FHMM, with exceptions at certain time points where the AFF provides non-zero estimations.
| Algorithm 1: EXACT algorithm for direct FFHMM | |
| 1 | Initialization: . |
| 2 | Recursion: . |
| 3 | Termination: |
| 4 | Path backtracking: |
| 5 | Merging: |
In Algorithm 1, is the index of the estimation of the FFHMM for the i-th HMM at time t; is the index of the estimation of the AFF for the i-th HMM at time t, where means no state has been retrieved by the AFF from the aggregated observation for the i-th HMM at time t; and is the index of the optimal estimation for the i-th HMM at time t by the FHMM.
Evidently, Algorithm 1 employs the Viterbi algorithm within the proposed direct FFHMM. In this algorithm, all possible states are traced through the application of the dynamic programming algorithm approach. However, this method necessitates the enumeration of an exponentially large number of states, which in turn gives rise to substantial computational demands. In light of these computational challenges, we introduce an approximation, specifically Algorithm 2, with the aim of mitigating the heavy computational burden imposed by Algorithm 1.
| Algorithm 2: AFAMAP algorithm for direct FFHMM | |
| 1 | Input: , , , , , and . |
| 2 | Minimization: |
| 3 | Output: , predicted the output of individual HMM |
In Algorithm 2, is the aggregated observation; represents state means for N HMMs; and are the covariance matrices for the additive FHMM and difference FHMM, respectively; and and are regularization parameters. The cost function f in (17) is defined as
where and represents the changes in observations and states, given by
and
Meanwhile, the set of indicators is defined as
in which , , and ; ; . The minimization constraints are
In addition, the one-at-a-time condition leads to an extra constraint as
which means the off-diagonal elements of sum to at most one. The last term in the cost function is the robust component. It is used to handle unmodeled observations.
Clearly, the direct FFHMM possesses two notable advantages:
- Firstly, it simplifies the control over outcomes for a designated HMM chain. Specifically, as the AFF’s estimations directly supersede those of the FHMM during particular timeframes, the accuracy of the FFHMM for the target HMM chain is unlikely to decline, assuming the AFF’s accuracy is maintained with sufficient conservatism. Secondly, an aggressive AFF can be employed to enhance the performance of the target HMM chain, though this approach carries a risk of potentially exacerbating outcomes.
- Secondly, alterations in accuracy for the estimation of one HMM chain are independent of changes in others. This attribute facilitates the independent improvement in accuracy for each HMM chain. Additionally, customized AFFs can be applied to specific HMM chains, thereby achieving superior results.
2.3. Embedded FFHMM
In this subsection, we employ an alternative method to integrate predefined states with the FHMM, whereby the non-zero estimations from the AFF take the place of the hidden states within the embedded HMMs of the FHMM model. The structure of the embedded FFHMM can be described as follows:
Model 3.
- 1.
- The initial state:
- (a)
- If , then
- (b)
- Otherwise,
- 2.
- The state transition:
- (a)
- If , then
- (b)
- Otherwise,
- 3.
- The observation probability distribution:
The notations used in this model can be understood in reference to the preceding discussions. Figure 5 presents a diagram of the embedded FFHMM, where a hidden state from the FHMM is substituted by the non-zero estimation from the AFF for the i-th HMM at time t. The FFHMM’s output is the optimal estimation, determined by the observation probability distribution, as described in (29). Subsequently, we introduce the EXACT and AFAMAP algorithms designed for the embedded FFHMM, as outlined in Algorithms 3 and Algorithm 4, respectively.
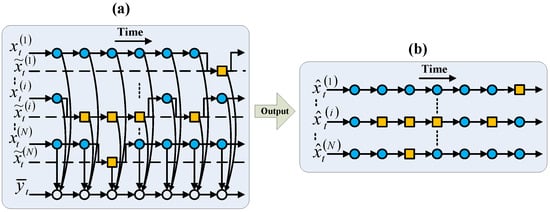
Figure 5.
Diagram of the embedded FFHMM. (a) Illustrates the amalgamation of the FHMM and the AFF estimations, with the orange square boxes representing the AFF replacing the hidden states of the FHMM. (b) Shows the estimation output of the FFHMM, where each orange square box signifies an estimation made by the AFF at the respective time.
| Algorithm 3: EXACT algorithm for embedded FFHMM | |
| 1 | Initialization: , ,
|
| 2 | Recursion: , , , ,
|
| 3 | Termination: |
| 4 | Path backtracking: |
In Algorithm 4, constraint is defined as
| Algorithm 4: AFAMAP algorithm for embedded FFHMM | |
| 1 | Input: , , , , , and . |
| 2 | Minimization: Output: , predicted individual HMM output |
As previously discussed in the earlier subsection, the estimations of the direct FFHMM for the target HMM chain are independent of other HMM chains. In contrast, the estimations of the embedded FFHMM for the target HMM chain are interconnected with other HMM chains via the observation probability distribution described in (29). Due to these interdependencies, enhancing the accuracy of the AFF for one HMM can indirectly influence the estimation accuracies of other HMMs. This represents a significant advantage of the embedded FFHMM approach. However, this also necessitates greater care in managing the embedded FFHMM, as these correlations can lead to unforeseen changes in the estimations of other HMM chains.
In summary, given their distinct characteristics, the following guidelines can be followed when selecting between the direct FFHMM and embedded FFHMM: Firstly, opt for the direct FFHMM if the goal is to independently improve the estimation of a single HMM chain. Secondly, choose the embedded FFHMM if the aim is to enhance not only the estimation of an individual HMM chain but also the estimations across multiple HMM chains simultaneously.
The computational complexity of the Viterbi algorithm applied to the FHMM is
where N is the number of HMMs, is the number of states in the i-th HMM, and T is the number of time steps. This exponential complexity makes the Viterbi algorithm intractable for large FHMMs. When contrasted with the exponential complexity, the cost associated with implementing the AFF is so minimal that it can be considered negligible. As a result, the computational complexities of the EXACT algorithms in Algorithms 1 and 3 are identical to those expressed in Equation (40), both of which exhibit an exponential-in-dimension computational cost.
Similarly, as per the findings in [13], the computational complexity of AFAMAP for the additive FHMM is approximately linear with respect to the number of HMMs. Consequently, the AFAMAP algorithms for the FFHMM presented in Algorithms 2 and 4 share the same computational complexity.
3. Results
In this section, we implement our models and algorithms to address the non-intrusive load monitoring (NILM) problem, showcasing their advantages over the traditional FHMM. The evaluations are conducted using the Pecan Street dataset [19] and the REDD [20] dataset.
The Pecan dataset comprises daily electricity consumption data from households located in the green-built Mueller community in Austin, Texas. This dataset encompasses both aggregated and appliance-level consumption data, collected at a sampling rate of Hz, meaning one sample is recorded per minute. Specifically, the Pecan dataset used in our experiment contains energy consumption data from 10 households over a one-week period, with one sample recorded every minute. The entire dataset consists of sampled points. The first half of these sampled points, i.e., 5040 points, are employed for training, while the remaining 5040 points are reserved for testing purposes.
Meanwhile, the power consumption data of house 1 from the REDD dataset are also utilized to validate our algorithms. The sampling rate of these data is Hz. We selected house 1 because it contains the most comprehensive information and features 18 devices [21].
3.1. Automatic Pattern Recognition Using AFF
In this subsection, we employ the AFF to identify similar patterns of refrigerator usage from aggregated observations. The effectiveness of the AFF is assessed using the metrics “Rate of Detection” and “precision”, which are defined as follows:
where , , and denote “true positive”, “false positive”, and “false negative”, respectively. These terms represent correct identifications, erroneous detections, and missed identifications. It is important to note that our definition of “Rate of Detection” differs from the conventional definition of “recall”, as outlined in [22]:
In the definition of “Rate of Detection”, we use “tp+fp+fn” to signify the total number of time points under evaluation, and “tp+fp” to denote the number of time points that have been identified by the AFF.
We then apply the AFF to the Pecan dataset, with the results presented in Table 1, evaluated based on the metrics of “Rate of Detection” and “precision”. These findings are derived from a moderate configuration of the AFF parameters. As discussed in the previous section, relaxing the variances of the filter window’s width w and height h can enhance the “Rate of Detection” but may lead to a decrease in “precision”. Conversely, tightening these variances can boost “precision” at the cost of a reduced “Rate of Detection”.

Table 1.
Performance of AFF on Pecan dataset.
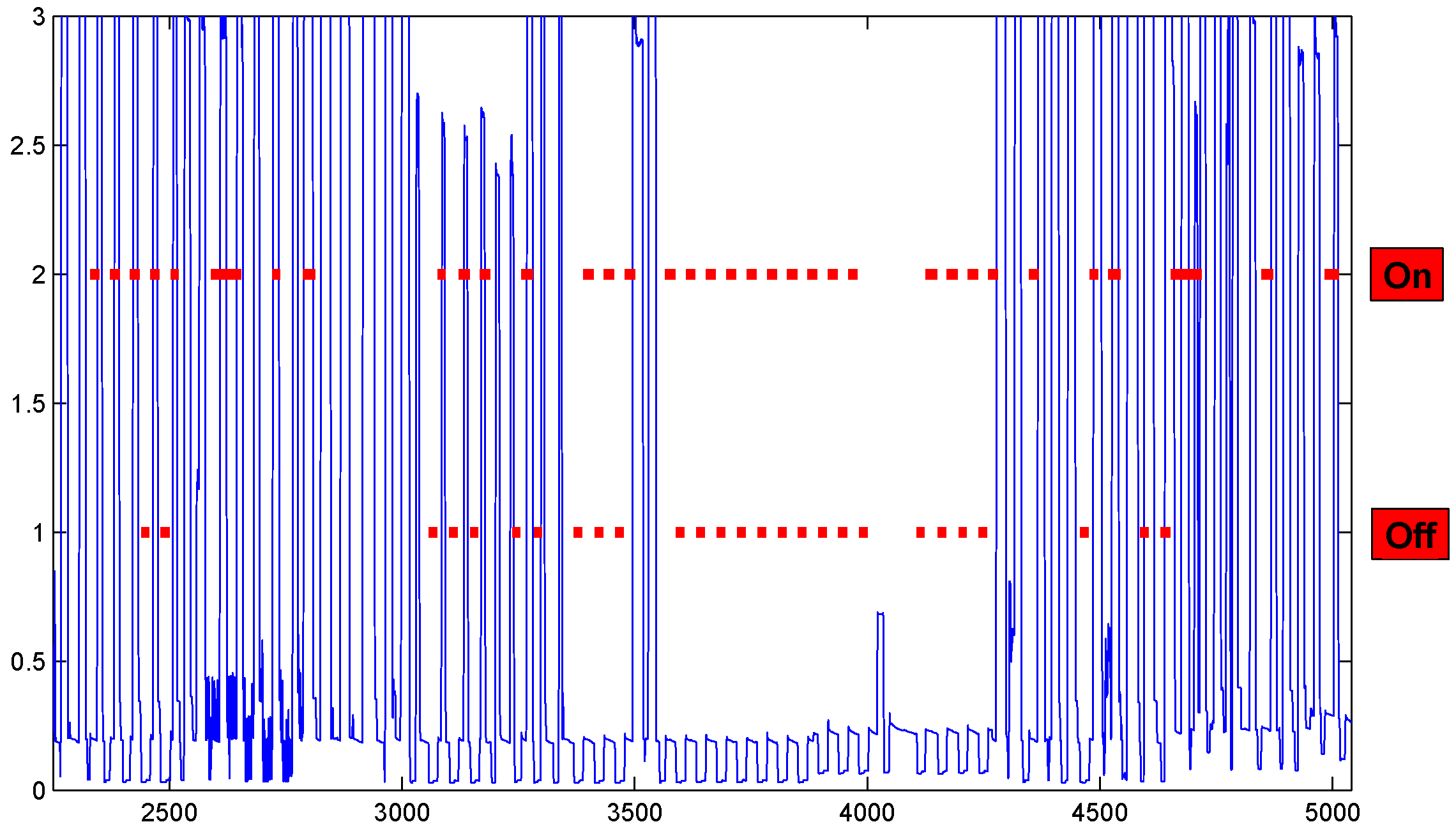
Assuming the refrigerator operates in two states, “turn on” (cooling) or “turn off” (standby), the AFF’s task is to identify the time periods during which these states can be classified as “on” or “off” by the AFF. To illustrate the detailed outcomes of our AFF, Figure 6 displays the estimated operational status of the refrigerator in the Pecan dataset. In this figure, higher red lines represent estimations of the “turn on” state, while lower red lines indicate the “turn off” state. When comparing these estimated states with the aggregated observations (depicted by the blue lines), we observe that the AFF has successfully captured most of the significant patterns of the refrigerator’s operation.
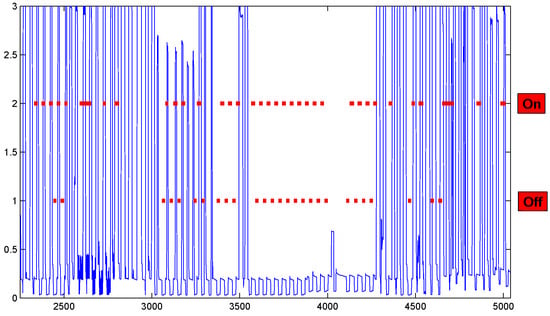
Figure 6.
The estimated status of the refrigerator in the Pecan dataset as determined by the AFF. The blue lines represent the aggregated energy consumption of the entire household, whereas the red lines depict the estimated status of the refrigerator by the AFF. When the red lines are at a height of 2, it indicates that the refrigerator is operating in the “On” state during the corresponding time intervals, as estimated by the AFF. Conversely, the lower red lines at a height of 1 signify the estimated “Off” state of the refrigerator.
In the subsequent subsection, the retrieved statuses will serve as the predefined states within the models of both the direct FFHMM and the embedded FFHMM.
3.2. Experiments Using Direct FFHMM and Embedded FFHMM
In order to assess the performance of various models and algorithms, we utilize the metric known as “total energy correctly assigned” [20], which is defined as follows:
where represents the observed total power consumption at time t, while denotes the actual power consumed by the i-th appliance at time t, with its corresponding estimate being . In our experimental setup, we apply both the EXACT and AFAMAP algorithms to both the direct FFHMM model and the embedded FFHMM model.
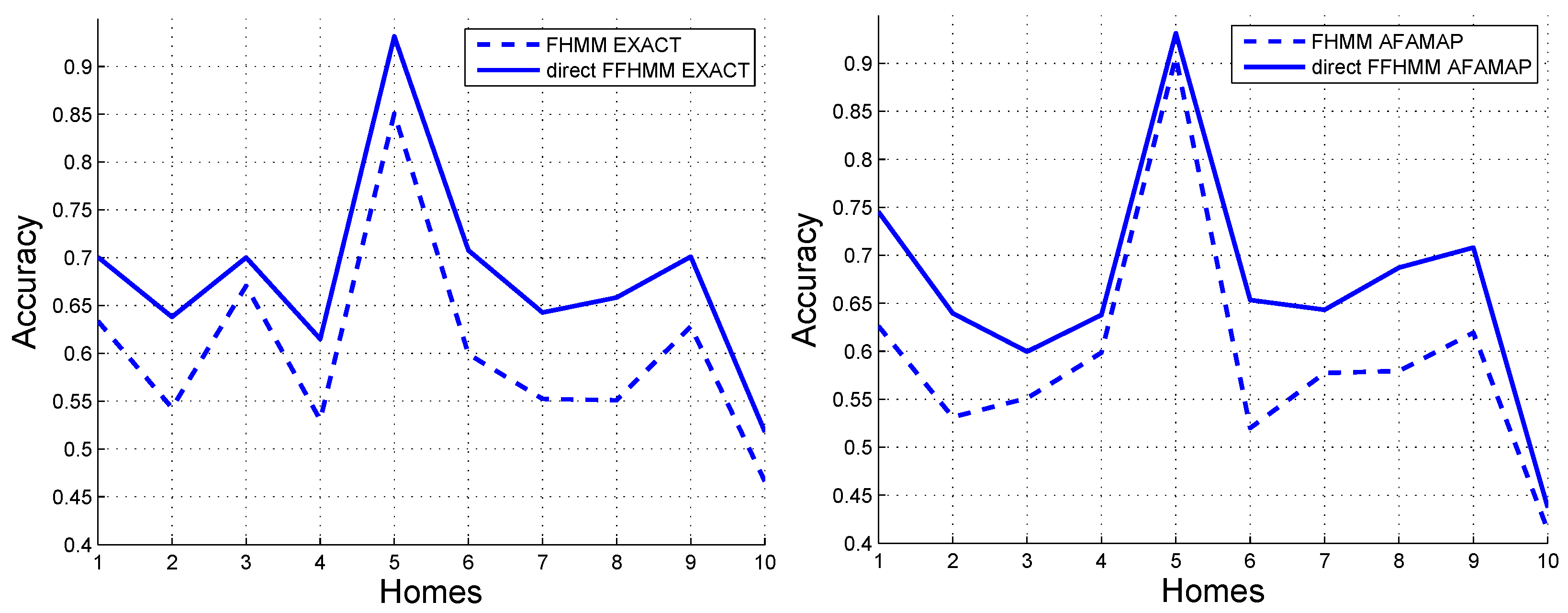
Based on the design presented in Figure 4, the direct FFHMM model can enhance—and is specifically designed to enhance—the performance of appliances with predefined states. In this experiment, the refrigerator serves as the target appliance. When compared to the FHMM, the direct FFHMM shows this enhancement. Therefore, we only need to compare the performances of the direct FFHMM and FHMM on the refrigerator, as illustrated in Figure 7. It is evident that, regardless of whether the EXACT algorithm or the AFAMAP algorithm is employed, the direct FFHMM invariably attains a higher level of accuracy compared to the FHMM. This is attributable to the fact that the AFF within the direct FFHMM model takes into account additional information that the FHMM overlooks.
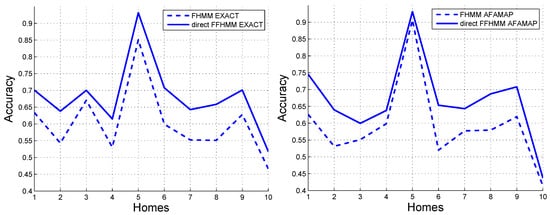
Figure 7.
Accuracy of energy disaggregation for refrigerator employing the FHMM and direct FFHMM models on the Pecan dataset. (Left) Results obtained with the EXACT algorithm. (Right) Results obtained with the AFAMAP algorihtm.
When using the EXACT algorithm, the mean of the difference in accuracy between the direct FFHMM and FHMM is , with a standard deviation of . The calculated T-statistic is . These statistical results clearly indicate that there is a highly significant difference in the performance of these two models. Additionally, the confidence interval for this difference is , further validating the advantage of the proposed direct FFHMM over the FHMM.
When the AFAMAP algorithm is utilized, the mean of the difference in accuracy between the direct FFHMM and the FHMM amounts to . The standard deviation associated with this difference is . A T-statistic of is computed. Such a T-statistic value strongly suggests that there exists a statistically significant difference in the performance of the two models. Moreover, the confidence interval for this performance difference is precisely determined to be in the range of , which further bolsters the conclusion that the performance of the direct FFHMM is better than that of the FHMM.
The estimation results by the EXACT and AFAMAP algorithms for the Pecan dataset using the embedded FFHMM model are presented in Table 2. The third column, labeled as “Ratio”, indicates the proportion of the cumulative consumption of each appliance relative to the total consumption of the entire household.

Table 2.
Accuracy of energy disaggregation on Pecan dataset employing the FHMM and embedded FFHMM models with the EXACT and the AFAMAP algorithms.
The bolded figures in Table 2 emphasize the best accuracies, which were all obtained by either the EXACT or AFAMAP algorithm. It is evident that the embedded FFHMM model has the potential to boost the performance of several additional appliances, albeit it may also lead to a decrease in performance for some.
These findings substantiate the assertions made in the preceding section, indicating that improvements for appliances are independent in the direct FFHMM model but become interdependent in the embedded model.
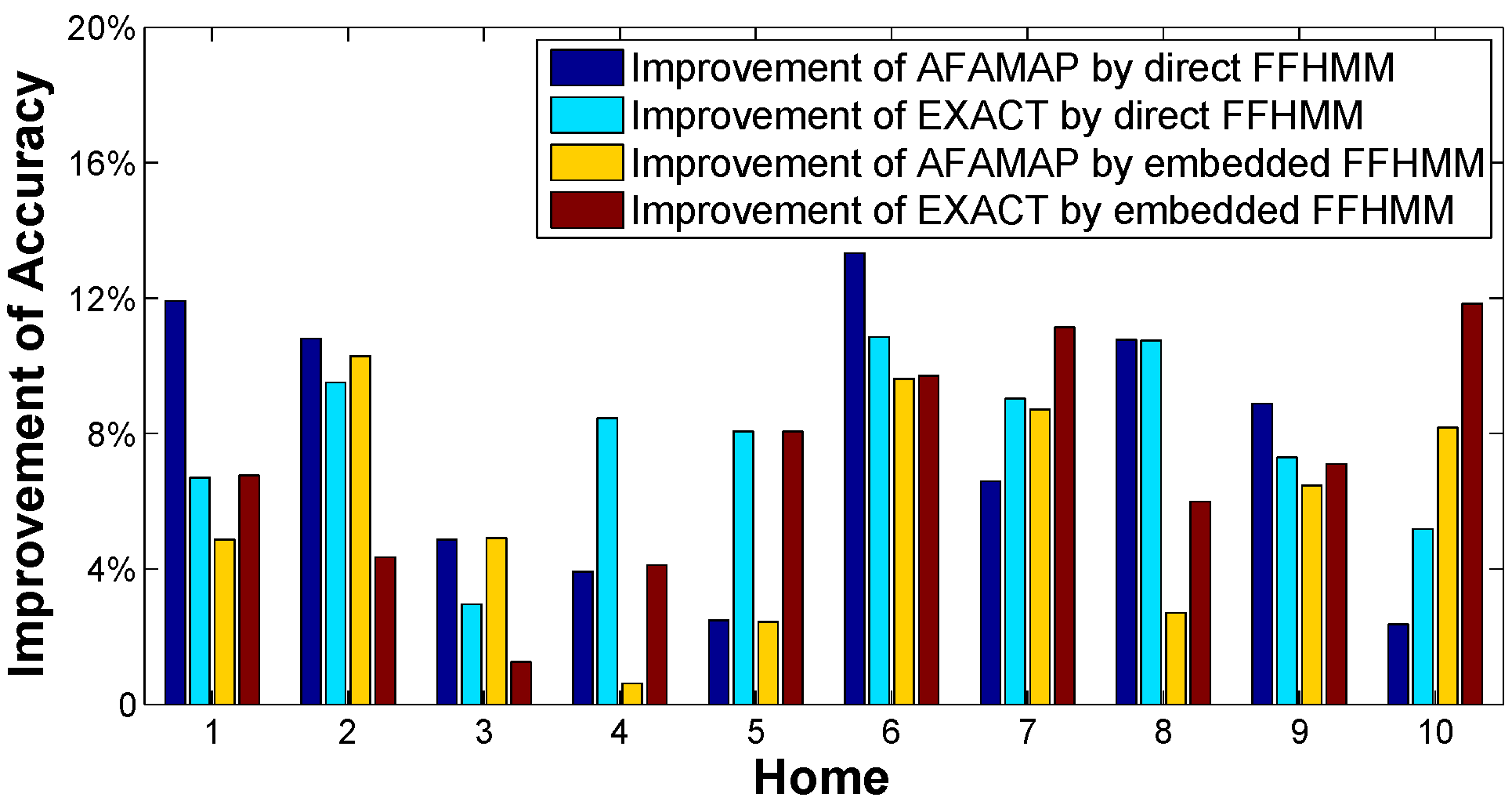
For ease of comparison, Figure 8 illustrates the enhancements in disaggregation accuracy for the refrigerator after substituting the FFHMM models for the FHMM model. Within the figure, the term “Improvement of AFAMAP by direct FFHMM” denotes the disparity between the accuracy achieved by the AFAMAP algorithm when applied to the direct FFHMM model and that of the FHMM model. A positive difference indicates that the accuracy derived from the FFHMM-based algorithm surpasses that of the FHMM-based algorithm, while a negative difference signifies the converse. The remaining three lines are derived in an analogous manner. Consequently, as all lines in the figure are above zero, it can be inferred that the FFHMM models yield superior disaggregation results across all households compared to the FHMM models.
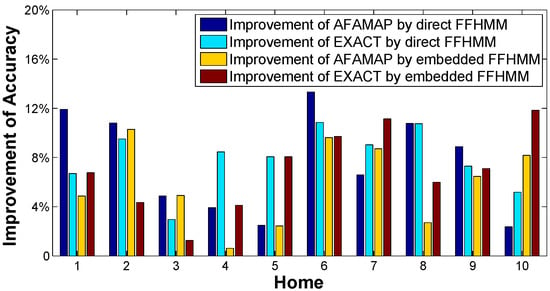
Figure 8.
The enhancement in accuracy observed for the refrigerator following the substitution of FFHMM models for the FHMM.
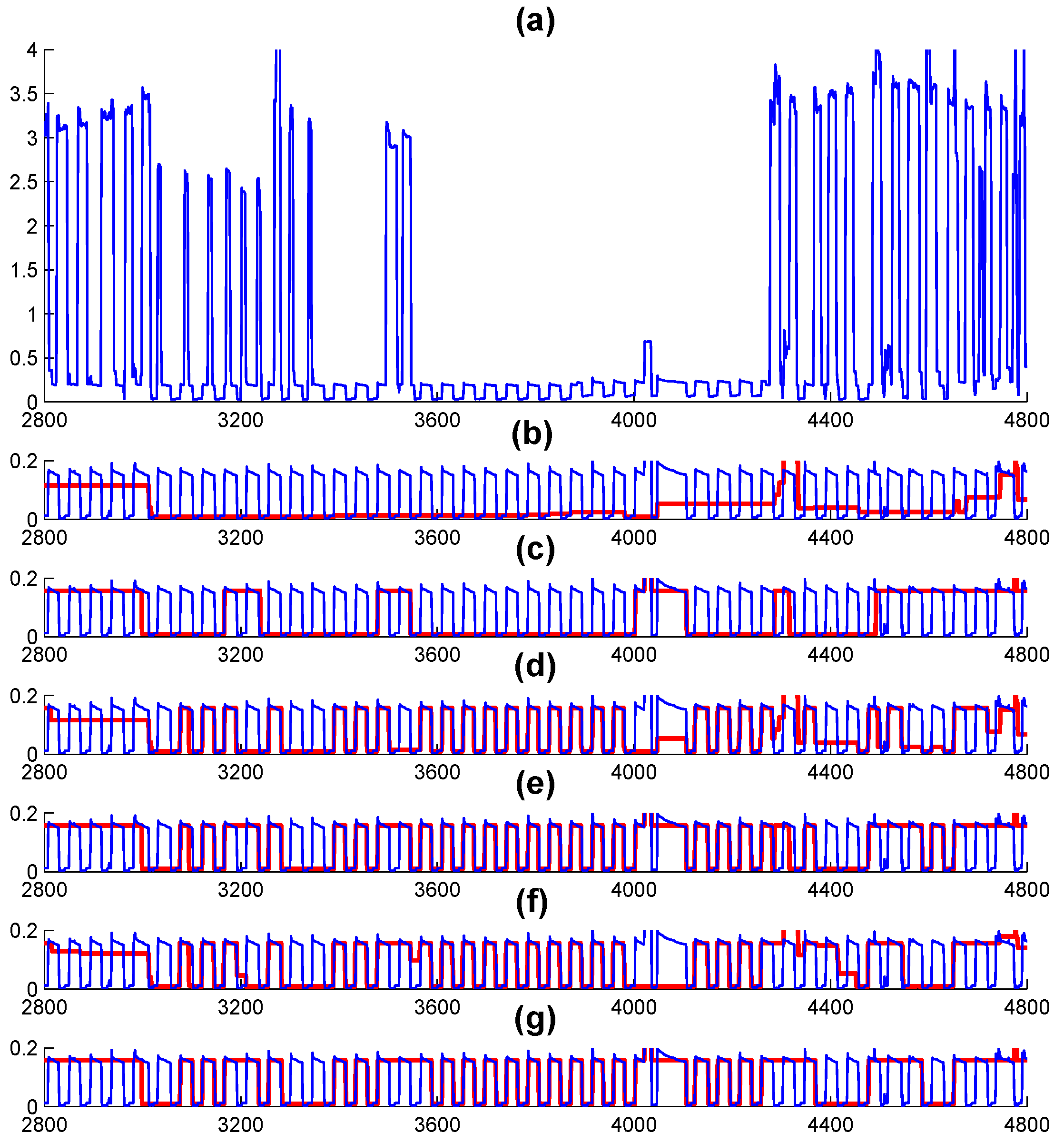
Figure 9 presents a detailed disaggregation analysis of the refrigerator. Upon examining the figure, it becomes evident that both the EXACT and AFAMAP algorithms significantly enhance the disaggregation results when applied to either the direct FFHMM or embedded FFHMM models. For instance, between 3600 and 4000 min, the operational status of the refrigerator is accurately estimated by the algorithms employing FFHMM models. In contrast, both the EXACT and AFAMAP algorithms based on the FHMM model fail to detect such significant patterns.
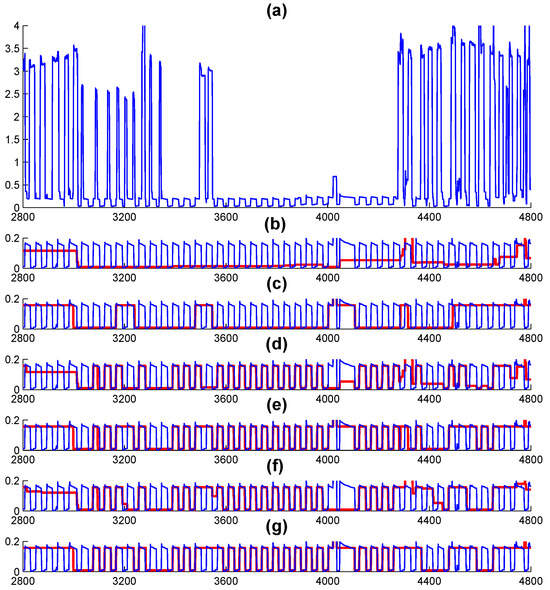
Figure 9.
Disaggregation results for the refrigerator within the Pecan dataset. The blue lines indicate the actual consumption, whereas the red lines display the disaggregation outcomes generated by the respective algorithms: (a) aggregated observation, (b) AFAMAP algorithm utilizing the FHMM, (c) EXACT algorithm with the FHMM, (d) AFAMAP algorithm utilizing the direct FFHMM, (e) EXACT algorithm employing the direct FFHMM, (f) AFAMAP algorithm utilizing the embedded FFHMM, and (g) EXACT algorithm with the embedded FFHMM.
Meanwhile, we apply FFHMM models to the REDD dataset. To demonstrate that the efficacy of our models is not confined to a single metric, we employ “precision”, “recall”, and “F-measure” to evaluate the performance of FFHMM models on the REDD dataset. The F-measure is defined as per [22]:
where the precision and recall are defined in (42) and (43), respectively.
On the REDD dataset, when the direct FFHMM model replaces the FHMM model, the enhancements in precision, recall, and F-measure of the AFAMAP algorithm for the refrigerator are , , and respectively. Meanwhile, the findings for the embedded FFHMM are presented in Table 3. Further detailed illustrations about the direct FFHMM and embedded FFHMM are provided in Figure 10. These outcomes bear resemblance to those obtained from experiments conducted on the Pecan dataset, thereby validating the effectiveness of the proposed FFHMM models.

Table 3.
REDD dataset using the FHMM and embedded FFHMM models with the AFAMAP algorithm.
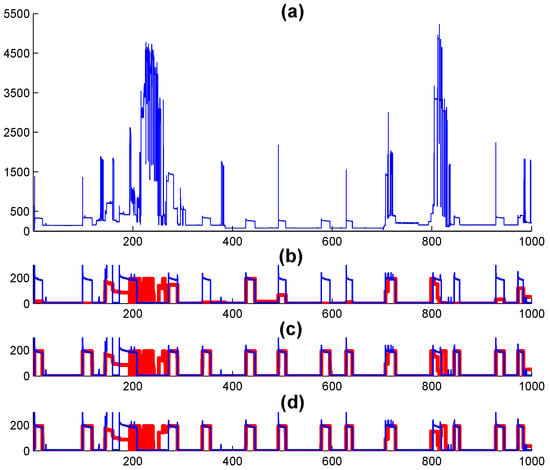
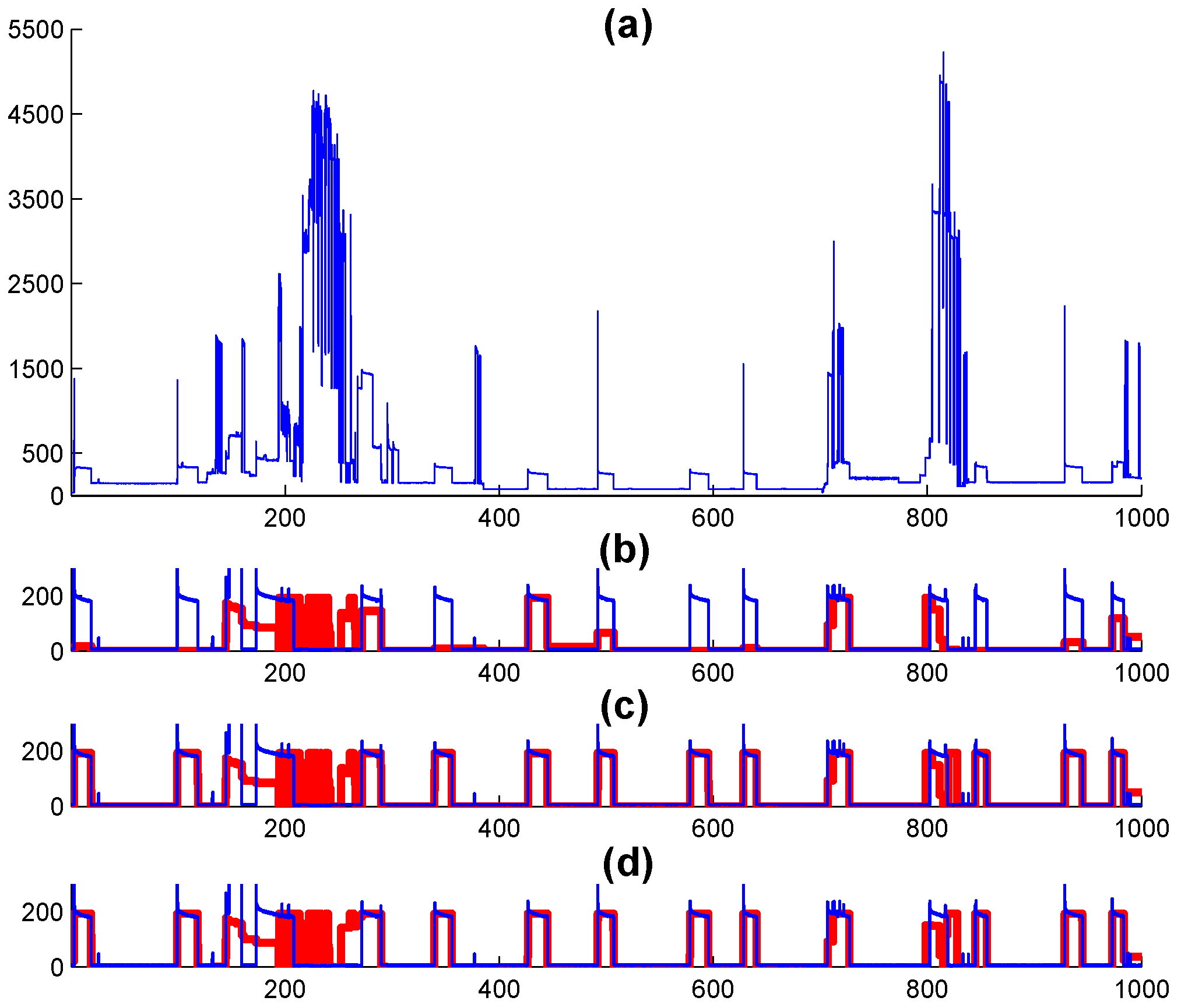
Figure 10.
Applying the AFAMAP algorithms for energy disaggregation of the refrigerator to the REDD dataset. (a) Presents the aggregated consumption. (b) Displays the estimation result based on the FHMM model (real consumption in blue and estimation result in red). (c) Illustrates the estimation result derived from the direct FFHMM model. (d) Shows the estimation result obtained through the embedded FFHMM model.
In this subsection, the proposed direct FFHMM and embedded FFHMM are demonstrated by their application to NILM. However, it is evident that these two models are not limited to NILM. As stated in the introduction, similar to the FHMM model, they can also be applied to a wide range of other domains. These include consumers’ choice models, estimating tumor clonal composition, fault diagnosis, online skill rating, and forecasting financial portfolios with value at risk.
4. Discussion
In order to leverage the information embedded within the aggregated observations, which is often significant yet overlooked by the FHMM, we employ an empirical automatic feature filter (AFF) to extract pertinent patterns designated as predefined states. The AFF utilized in this study is sufficient to showcase the efficacy of both the direct FFHMM and embedded FFHMM; however, more specialized approaches could be explored in future research to refine the identification of these predefined states with enhanced precision. Subsequently, we introduce the FFHMM model, which integrates the FHMM with these predefined states. The FFHMM can be classified into two distinct variants: the direct FFHMM and embedded FFHMM. In the former, the predefined states directly substitute the estimated outcomes of the FHMM, allowing for the independent enhancement of each individual HMM chain’s estimation. Conversely, in the embedded FFHMM, the hidden state variables of each HMM chain are replaced by the predefined states, which, in conjunction with the states of other HMM chains, determine the final outcome of the embedded FFHMM. As a result, within the embedded FFHMM framework, the estimation of multiple HMM chains can potentially be improved by merely defining some states for a single HMM chain. To validate the effectiveness of the FFHMM models, we conducted experiments on two real-world datasets, employing both the EXACT and AFAMAP algorithms.
Author Contributions
Conceptualization, Z.P.; methodology, Z.P.; software, Z.P.; validation, Z.P., W.H. and Y.Z.; formal analysis, Z.P.; investigation, Z.P.; resources, W.H. and Y.Z.; data curation, Z.P.; writing—original draft preparation, Z.P.; writing—review and editing, Z.P., W.H. and Y.Z.; visualization, Z.P.; supervision, W.H. and Y.Z.; project administration, W.H. and Y.Z.; funding acquisition, Z.P., W.H. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Discipline Construction and Promotion Project of Guangdong Province (No. 2022ZDJS065), Key Field Special Project of Scientific Research of Education Department of Guangdong Province (No. 2023ZDZX1014), Key Research Project of Guangdong Province Undergraduate Colleges and Universities Online Open Courses Guiding Committee (No. 2022ZXKC310), Scientific Research Project of Hanshan Normal University (No. XD202304 and No. XSZ202402), and Education and Teaching Reform Project of Hanshan Normal University (No. PX-161241546).
Data Availability Statement
The data presented in this study are available upon request from the corresponding authors.
Acknowledgments
The authors would like to thank the referees and the editors for their very useful suggestions, which significantly improved this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ghahramani, Z.; Jordan, M. Factorial hidden Markov models. Mach. Learn. 1997, 29, 245–273. [Google Scholar] [CrossRef]
- Schweiger, R.; Erlich, Y.; Carmi, S. FactorialHMM: Fast and exact inference in factorial hidden Markov models. Bioinformatics 2019, 35, 2162–2164. [Google Scholar] [CrossRef] [PubMed]
- Paeng, J.W.; Kwon, J. Visual tracking using interactive factorial hidden Markov models. IET Signal Process. 2021, 15, 365–374. [Google Scholar] [CrossRef]
- Kumar, P.; Abhyankar, A.R. A Time Efficient Factorial Hidden Markov Model-Based Approach for Non-Intrusive Load Monitoring. IEEE Trans. Smart Grid 2023, 14, 3627–3639. [Google Scholar] [CrossRef]
- Kani, A.; DeSarbo, W.S.; Fong, D.K. A factorial hidden Markov model for the analysis of temporal change in choice models. Cust. Needs Solut. 2018, 5, 162–177. [Google Scholar]
- Nepal, A.; Yates, A. Factorial Hidden Markov Models for Learning Representations of Natural Language. arXiv 2013, arXiv:1312.6168. [Google Scholar]
- Rahman, M.S.; Nicholson, A.E.; Haffari, G. HetFHMM: A Novel Approach to Infer Tumor Heterogeneity Using Factorial Hidden Markov Models. J. Comput. Biol. 2018, 25, 182–193. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, Y.; Wang, Z.; He, X.; Gao, M. Review on diagnosis techniques for intermittent faults in dynamic systems. IEEE Trans. Ind. Electron. 2019, 67, 2337–2347. [Google Scholar] [CrossRef]
- Duffield, S.; Power, S.; Rimella, L. A state-space perspective on modelling and inference for online skill rating. J. R. Stat. Soc. Ser. C Appl. Stat. 2024, 73, 1262–1282. [Google Scholar] [CrossRef]
- Puglisi, F.M.; Pavan, P. Factorial hidden Markov model analysis of random telegraph noise in resistive random access memories. ECTI Trans. Electr. Eng. Electron. Commun. 2014, 12, 24–29. [Google Scholar] [CrossRef]
- Saidane, M. Forecasting portfolio-Value-at-Risk with mixed factorial hidden Markov models. Croat. Oper. Res. Rev. 2019, 10, 241–255. [Google Scholar] [CrossRef]
- Durrieu, J.L.; Thiran, J.P. Source/filter factorial hidden markov model, with application to pitch and formant tracking. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 2541–2553. [Google Scholar]
- Kolter, J.; Jaakkola, T. Approximate inference in additive factorial hmms with application to energy disaggregation. In Proceedings of the International Conference on Artificial Intelligence and Statistics, La Palma, Spain, 21–23 April 2012. [Google Scholar]
- Rabiner, L. A tutorial on Hidden Markov Models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar]
- Chopin, N.; Papaspiliopoulos, O. An Introduction to Sequential Monte Carlo; Springer: Berlin/Heidelberg, Germany, 2020; Volume 4. [Google Scholar]
- Rebeschini, P.; Van Handel, R. Can local particle filters beat the curse of dimensionality? Ann. Appl. Probab. 2015, 25, 2809–2866. [Google Scholar] [CrossRef]
- Rimella, L.; Whiteley, N. Exploiting locality in high-dimensional Factorial hidden Markov models. J. Mach. Learn. Res. 2022, 23, 1–34. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Pearson: London, UK, 2018. [Google Scholar]
- Holcomb, C. Pecan Street Inc.: A test-bed for nilm. In Proceedings of the International Workshop on Non-Intrusive Load Monitoring, Pittsburgh, PA, USA, 7 May 2012. [Google Scholar]
- Kolter, J.; Johnson, M. REDD: A public data set for energy disaggregation research. In Proceedings of the Workshop on Data Mining Applications in Sustainability (SIGKDD), San Diego, CA, USA, 21 August 2011. [Google Scholar]
- Shao, H.; Marwah, M.; Ramakrishnan, N. A Temporal Motif Mining Approach to Unsupervised Energy Disaggregation: Applications to Residential and Commercial Buildings. In Proceedings of the Twenty-Seventh Conference on Artificial Intelligence (AAAI’13), Bellevue, WA, USA, 14–18 July 2013. [Google Scholar]
- Olson, D.; Delen, D. Advanced Data Mining Techniques, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).