Generalization of Ramsey Number for Cycle with Pendant Edges

Abstract

This paper explores various Ramsey numbers associated with cycles with pendant edges, including the classical Ramsey number, the star-critical Ramsey number, the Gallai–Ramsey number, and the star-critical Gallai–Ramsey number. These Ramsey numbers play a crucial role in combinatorial mathematics, determining the minimum number of vertices required to guarantee specific monochromatic substructures. We establish upper and lower bounds for each of these numbers, providing new insights into their behavior for cycles with pendant edges—graphs formed by attaching additional edges to one or more vertices of a cycle. The results presented contribute to the broader understanding of Ramsey theory and serve as a foundation for future research on generalized Ramsey numbers in complex graph structures.

1. Introduction

The strength of the related Ramsey numbers for a group of graphs is characterized by the idea of star-critical Ramsey numbers. Hook’s [1] classification, which was initially proposed in 2010, and later expanded in [2,3], is interested in the number of edges that must be added to a given complete graph in order to satisfy the Ramsey criteria between a vertex and a critical coloring. Star-critical Ramsey numbers have been extensively studied in various contexts. Budden and DeJonge [4] explored multicolor star-critical Ramsey numbers and their connection to Ramsey-good graphs. Haghi et al. [5] investigated the star-critical Ramsey number of $F_n$ versus $K_4$, providing insights into structural properties. Jayawardene [6] examined cycle-related star-critical Ramsey numbers against the complete graph $K_5$, while Jayawardene and Navaratna [7] focused on large cycles versus complete graphs. Further, Jayawardene et al. [8] analyzed cycle-based star-critical Ramsey numbers involving $K_4$, presenting new computational results. Li and Li [9] contributed additional findings on specific star-critical Ramsey numbers, and Wu et al. [10] explored the problem in the context of quadrilateral-related graphs, including wheel and star-critical cases. In their most recent paper, Liu and Su [11] investigated the idea of Gallai–Ramsey numbers. They proved some new results on the values of star-critical Gallai–Ramsey numbers and established some bounds on these values.

We first define terms and notations that will be used in this study before describing our results. This article focuses on finite, undirected, and simple graphs. The number of vertices in a graph G is denoted by $\left|G\right|$, which is also referred to as the order of G. The complete graph with n vertices is denoted by $K_n$, the path graph with n vertices is denoted by ${\mathcal{P}}_n$, and the star graph with $n+1$ vertices is denoted by $K_{1,n}$. If S is a subset of the vertices of G, then G[S] refers to the subgraph of G induced by S. E(A,B) denotes the set of edges in G that have one endpoint in A and the other in B, where A and B are two disjoint subsets of the vertices of G. If all the edges in E(A, B) are colored by a single color, then we use c(A, B) to denote this color. In the special case where A = {a}, we simply write c(a,{B}) and E(a,{B}).

We can obtain a new graph $G-H$ by removing all the edges of H from G, where H is a subgraph of G. The graph $K_{n-1}\cup K_{1,l}$ is formed by adding a new vertex v to the graph $K_{n-1}$ and connecting it to l vertices of $K_{n-1}$ by using l edges. We use the notation $\left[k\right]$ to represent the set of integers from 1 to k.

A graph with colored edges is said to be monochromatic if all of its edges have the same color, and rainbow if no two edges share the same color. To enlarge an edge-colored graph G by using another graph H, the following method is applied: First, each vertex of G is replaced with a copy of H. Then, for each edge e in G, a biclique$K_{\left|V\right(H\left)\right|,\left|V\right(H\left)\right|}$ is inserted between the corresponding copies of H, where all edges in this biclique are assigned the same color as e.

A biclique is a complete bipartite graph, denoted by $K_{m,n}$, where the vertex set is divided into two disjoint sets of sizes m and n. Every vertex in one set is adjacent to every vertex in the other set, while no edges exist within the same set. More formally, a graph $G=(V,E)$ is a biclique if there exists a partition $V=V_1\cup V_2$ such that every edge in E connects a vertex in $V_1$ to a vertex in $V_2$, and no edges exist within $V_1$ or $V_2$.

Ramsey theory is a branch of mathematics that deals with the behavior of the colorings of graphs. It provides the lower and upper bounds on the sizes of graphs needed to ensure the existence of subgraphs of a particular type. The Ramsey number, denoted by $R(G,H)$, is the smallest n such that any complete graph on n vertices is guaranteed to contain either a red subgraph isomorphic to G or a blue subgraph isomorphic to H. The concept of a critical graph, introduced by Hook [1], refers to a red–blue coloring of $K_{n-1}$ that does not contain a red subgraph isomorphic to G or a blue subgraph isomorphic to H. The most important goal is to determine the smallest integer l such that every red–blue-edge-colored complete graph $K_{n-1}$ combined with star $K_{1,l}$ contains either a red subgraph isomorphic to G or a blue subgraph isomorphic to H. As a result of the above problem, a new concept called the “star-critical Ramsey number” was introduced [3]. This number is represented by the symbol $r^{*}(G,H)$.

In [1], Hook introduced a classification of graphs based on their Ramsey numbers. The paper [2] further discusses critical graphs and how they relate to Ramsey numbers. The concept of star-critical Ramsey numbers was first introduced by Hook and Isaak in [3], where they looked for the lowest integer l such that any red–blue-edge-colored $K_{n-1}\cup K_{1,l}$ has a red or blue subgraph that is isomorphic to G. Recent studies have further expanded this topic. A comprehensive survey of star-critical Ramsey numbers is provided in [12], summarizing the progress since their introduction. The study [13] introduced the concept of a Ramsey-full graph, where a graph pair $(G,H)$ is said to be Ramsey-full if $r^{*}(G,H)=R(G,H)-1$. The paper [14] provides a dynamic survey on Ramsey theory, including an overview of Ramsey numbers. Additionally, the complete graph pair $\left(K_m\right)$ is Ramsey-full, as demonstrated by Hook and Isaak in [1]. More recent results from 2023 and 2024 discuss advancements in star-critical Ramsey numbers, including the investigation of large books in [15,16] and an overview of recent developments in [17]. These new findings contribute to a deeper understanding of the structural properties and sharpness of Ramsey numbers.

The Gallai–Ramsey number, denoted by $g{r}_l(K_3:G_1,G_2,\dots ,G_l)$, is the lowest number m such that a complete graph $K_m$ edge-colored with l colors will contain either a monochromatic $G_j$ in color j or a rainbow $K_3$, where j is an element of the set $\left[l\right]$. If all G’s are the same, we can represent $g{r}_l(K_3:G_1,G_2,\dots ,G_l)$ as $g{r}_l(K_3:G)$. It is worth noting that the relationship between the Gallai–Ramsey number and the Ramsey number is such that $g{r}_2(K_3:G_1,G_2)=R(G_1,G_2)$. To learn more about the Gallai–Ramsey number, please see [18,19].

The concept of the star-critical Gallai–Ramsey number was introduced in a recent paper by Su et al. [11], and some more results were found by M. Budden et al. in [20]. The definition of the star-critical Gallai–Ramsey number $g{r}_l^{*}(K_3:G_1,G_2,\dots G_l)$ is the minimum value of k such that in any l-edge-colored graph $K_{n-1}\cup K_{1,k}$ there exists either a rainbow $K_3$ or a monochromatic $G_i$ in color i for some $i\in \left[l\right]$.

Ramsey theory is a fundamental area in combinatorics that examines conditions ensuring the existence of monochromatic substructures in edge-colored graphs. While classical Ramsey numbers for cycles have been widely studied, the introduction of pendant edges adds new structural complexity, leading to intriguing mathematical challenges. This study extends the concept of Ramsey numbers to cycles with pendant edges, focusing on four key variations: the classical Ramsey number, the star-critical Ramsey number, the Gallai–Ramsey number, and the star-critical Gallai–Ramsey number. This work is motivated by the need to understand how the presence of pendant edges affects Ramsey properties and to establish rigorous upper and lower bounds for these numbers. The novelty of this research study lies in systematically analyzing these Ramsey numbers for cycles with pendant edges, offering new insights into their structural behavior. By addressing a gap in the literature, this study provides a solid foundation for future investigations into generalized Ramsey-type problems, contributing to the broader development of combinatorial mathematics.

The structure of the paper is as follows: The preliminary findings are presented in Section 2, which also gives a summary of key ideas and theorems from earlier research that form the basis of the investigation. The key findings are presented in Section 3, where we examine the Ramsey number, the Gallai–Ramsey number, the star-critical Gallai–Ramsey number, and the star-critical Ramsey number in relation to cycles with pendant edges. The work is finally concluded in Section 4, which summarizes the main conclusions and talks about possible future research topics.

2. Preliminaries

The uni-cyclic graph $F_{2,n}$, which is essential to our analysis, is introduced in this section. Adding $n-2$ pendant edges to a single vertex of cycle graph $C_4$ creates graph $F_{2,n}$ for $n\ge 3$. The center of the graph is the vertex in $F_{2,n}$ with degree n. Interestingly, $F_{2,n}$ has exactly the same number of vertices and edges as $n+2$. Figure 1 shows some demonstrations of $F_{2,n}$.

Indeed, graph $C_n^{+l}$ is precisely defined as the result of adding l distinct edges to cycle $C_n$ while connecting them to l distinct vertices of $C_n$. This definition leads to various configurations and structures depending on the values of n and l. Figure 2 visually presents several examples of $C_n^{+l}$ graphs, illustrating the concept and showcasing the diverse possibilities that arise from this construction.

Graph ${\mathcal{P}}_t$ is defined as the path of order t. For $t\ge 3$, we can depict ${\mathcal{P}}_t^{+}$ by introducing an additional edge connecting one end of the path to the vertex located at a distance of 2 from that end. This newly added edge forms a triangle within the graph. Notably, when $t=3$, ${\mathcal{P}}_3^{+}$ is equivalent to $K_3$, which represents a complete graph consisting of three vertices.

Now, we will present some important theorems that are very useful for proving the results in this article.

Definition 1.

A Gallai coloring of a complete graph is an edge coloring that avoids any triangle with all three edges having distinct colors (i.e., no rainbow triangles).

Theorem 1

(Gallai’s Theorem [21,22]). Let $K_n$ be a complete graph with a Gallai coloring (i.e., an edge coloring that avoids rainbow triangles). Then, the vertex set of $K_n$ can be partitioned into non-empty subsets $P_1,P_2,\cdots ,P_m$, where $m\ge 2$, such that the following apply:

• For any $1\le i<j\le m$, all edges between $P_i$ and $P_j$ are assigned the same color.
• Across all such pairs $(P_i,P_j)$, at most two distinct colors appear.

This theorem provides a key insight into the structure of Gallai colorings in complete graphs, allowing for the identification of distinct vertex partitions with specific edge color properties. By leveraging this theorem, it becomes possible to analyze and draw conclusions about the colorings of complete graphs while considering the relationships between different vertex sets and the colors of the connecting edges.

Theorem 2

([23]). For any integer $l\ge 3$,

$$r_2\left(F_{2,l}\right)=\left\{\begin{array}{cc}2l-1\hfill & ifliseven,\hfill \\ 2l\hfill & iflisodd.\hfill \end{array}\right.$$

Theorem 3

([23]). Let k and l be two positive integers:

• If $k\ge 1$ and $l\in \{3,4\}$, then $g{r}_k(K_3:F_{2,l})=r_2\left(F_{2,l}\right)+k-2$.
• If $k\ge 3$, then $g{r}_k(K_3:F_{2,5})=k+9$.
• If $k\ge 3$ and $l\ge 6$, then$k(l-1)+2\ge g{r}_k(K_3:F_{2,l})\ge \left\{\begin{array}{cc}5l/2+k-6\hfill & ifliseven,\hfill \\ (5l-1)/2+k-4\hfill & iflisodd.\hfill \end{array}\right.$

Theorem 4

([24]). For any $l\ge 3$ and $m\ge 3$,

$$g{r}_m(K_3:K_{1,l})=\left\{\begin{array}{cc}{\displaystyle \frac{5l-3}{2}}\hfill & iflisodd,\hfill \\ {\displaystyle \frac{5l}{2}}-3\hfill & ifliseven.\hfill \end{array}\right.$$

Theorem 5

([25]). For $t\ge 4$, the Ramsey number for graphs ${\mathcal{P}}_t^{+}$ and ${\mathcal{P}}_t^{+}$ is given by $R({\mathcal{P}}_t^{+},{\mathcal{P}}_t^{+})=2t-1$.

These theorems will serve as valuable tools in establishing the results discussed in this article.

3. Main Results

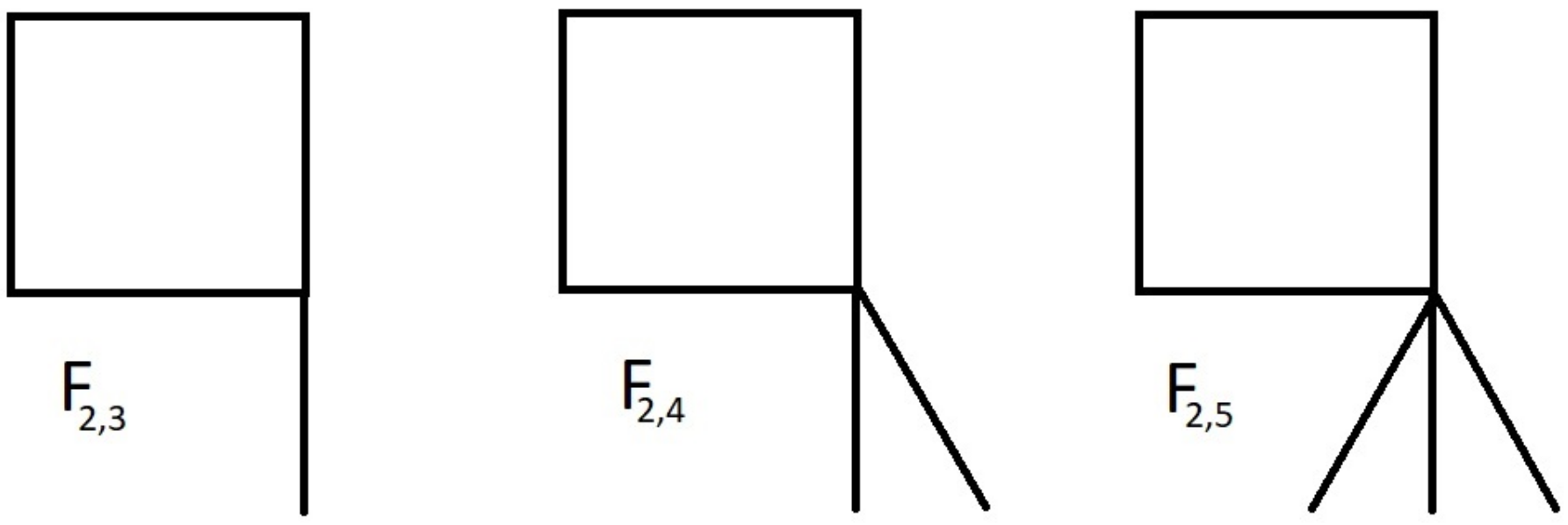
This section summarizes the study’s key findings, with an emphasis on the calculation and examination of different Ramsey numbers for cycles with pendant edges. In particular, we investigate the Gallai–Ramsey number, the star-critical Gallai–Ramsey number, the classical Ramsey number, and the star-critical Ramsey number. By giving precise upper and lower bounds for these values, we enhance Ramsey theory and shed light on the structural characteristics of these graphs.

3.1. Ramsey Number

Theorem 6.

$R(C_3^{+2},C_3^{+2})=9$.

Proof. 

In order to establish a lower bound, we initially sought to find a graph G of order 8 such that $C_3^{+2}$ is neither a subgraph of G nor a subgraph of the complement of G. Let us consider graph G defined as $G=2K_4$. It is well known that the complement of $2K_4$ is a bipartite graph $K_{4,4}$. Therefore, $C_3^{+2}$, which is a cycle of length 3 with two additional edges, is not a subgraph of either $2K_4$ or $K_{4,4}$. Hence, $R(C_3^{+2},C_3^{+2})\ge 9$.

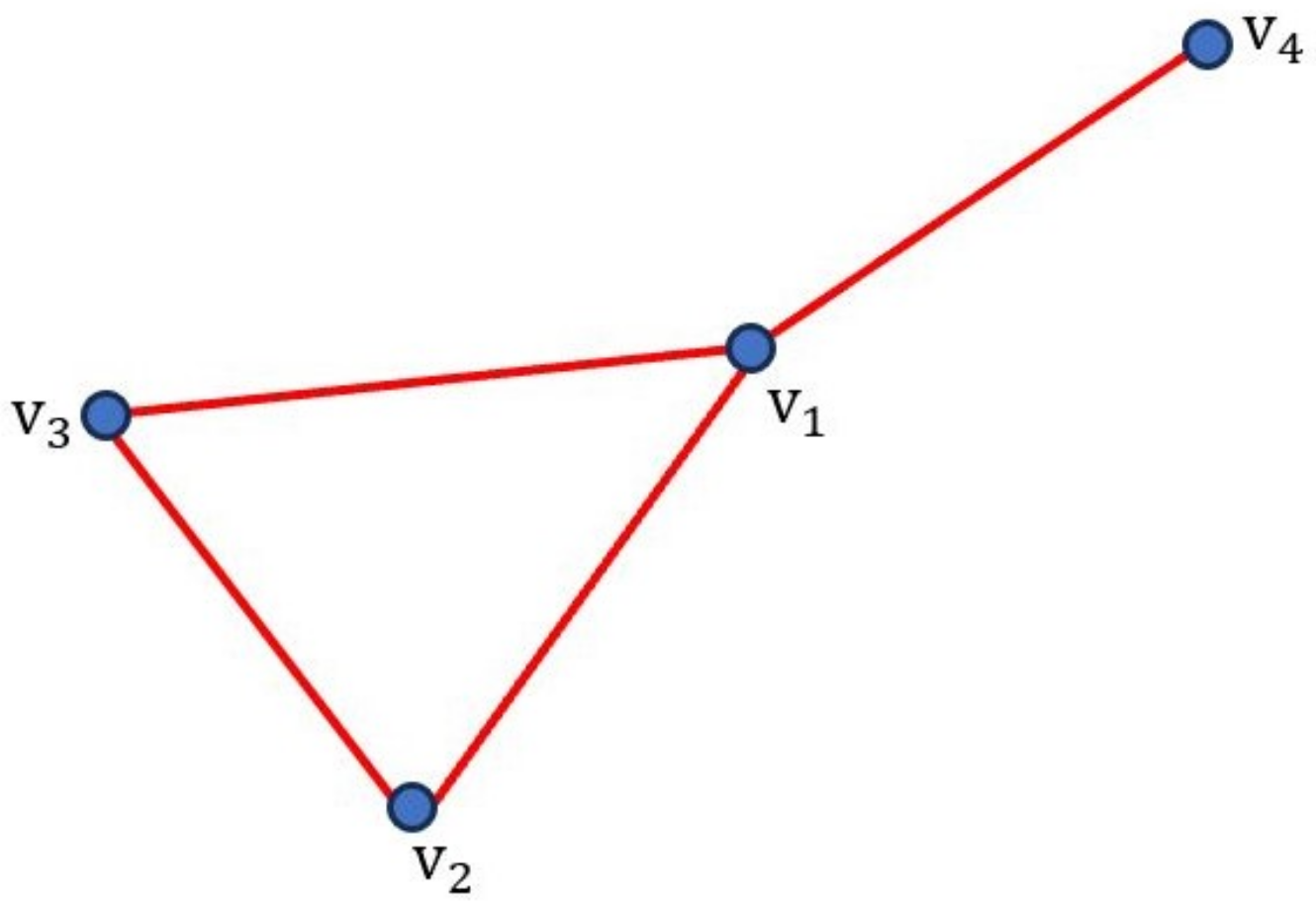
It is shown that any 2-coloring of $K_9$, using red and blue, must necessarily contain either a blue $C_3^{+2}$ or a red $C_3^{+2}$ to establish an upper bound. According to Theorem 5, every 2-coloring of $K_9$ contains a monochromatic $C_3^{+1}$. As illustrated in Figure 3, let us assume that the vertices of $K_9$ are $\{v_1,v_2,\dots ,v_8,v_9\}$ and that $v_1,v_2,v_3,v_4$ form a red $C_3^{+1}$.

Hence, all edges connecting $\{v_2,v_3\}$ to vertices $\{v_5,v_6,v_7,v_8,v_9\}$ must be blue; otherwise, a red $C_3^{+2}$ would be present.

Now, if there exists a single blue edge, say $\left(v_5{v}_6\right)$, in the subgraph induced by vertices $v_5,v_6,v_7,v_8,v_9$, then $K_9$ contains a blue $C_3^{+2}$ induced by $v_5,v_6,v_2,v_3$ and any of the other vertices, as shown in Figure 4.

As all edges in the induced subgraph formed by vertices $\{v_5,v_6,v_7,v_8,v_9\}$ are colored red, it follows that graph $K_9$ contains a red $K_5$. Therefore, there must exist a red $C_3^{+2}$.

Thus, we have shown that any 2-coloring of $K_9$ contains either a red $C_3^{+2}$ or a blue $C_3^{+2}$. This implies that $R(C_3^{+2},C_3^{+2})\le 9$, completing the proof of our main result. □

Theorem 7.

$R(C_3^{+3},C_3^{+3})=11$.

Proof. 

In order to establish a lower bound, we initially sought to find a graph G of order 10 such that $C_3^{+3}$ is neither a subgraph of G nor a subgraph of its complement. Let us consider graph G defined as $G=2K_5$. It is well known that the complement of $2K_5$ is a bipartite graph $K_{5,5}$. Therefore, $C_3^{+3}$, which is a cycle of length 3 with three additional edges, is not a subgraph of either $2K_5$ or $K_{5,5}$. Hence, $R(C_3^{+3},C_3^{+3})\ge 11$.

Our goal is to show that every 2-coloring of the complete graph on eleven vertices ($K_{11}$) must contain either a blue $C_3^{+3}$ or a red $C_3^{+3}$, thereby establishing an upper bound. According to Theorem 6, any 2-coloring of $K_{11}$ must include a monochromatic $C_3^{+2}$. Let us consider a graph F isomorphic to $K_{11}$. Without loss of generality, let the vertices of F be $\{v_1,v_2,\dots ,v_{10},v_{11}\}$. 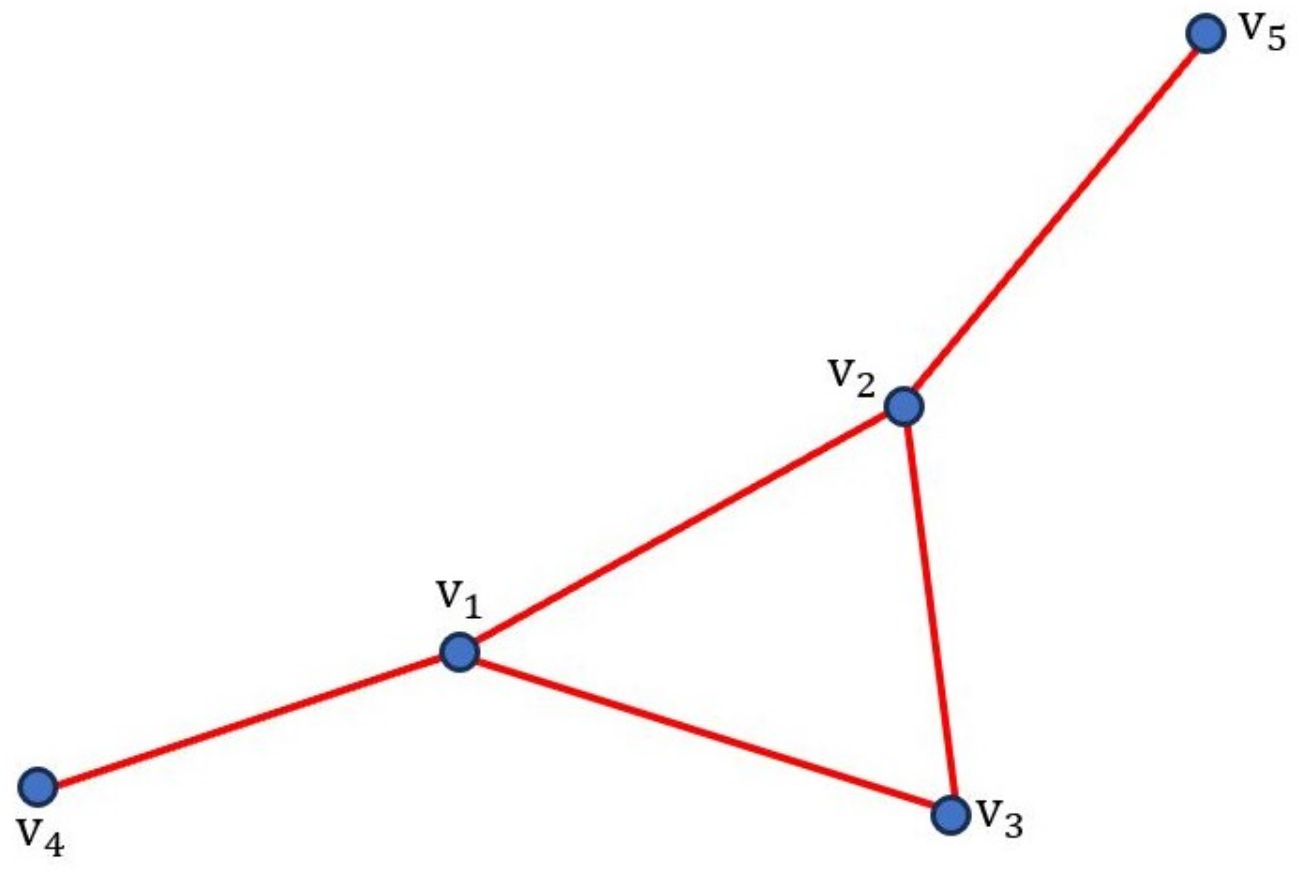As illustrated in Figure 5, vertices $v_1,v_2,v_3,v_4,$ and $v_5$ form a red $C_3^{+2}$.

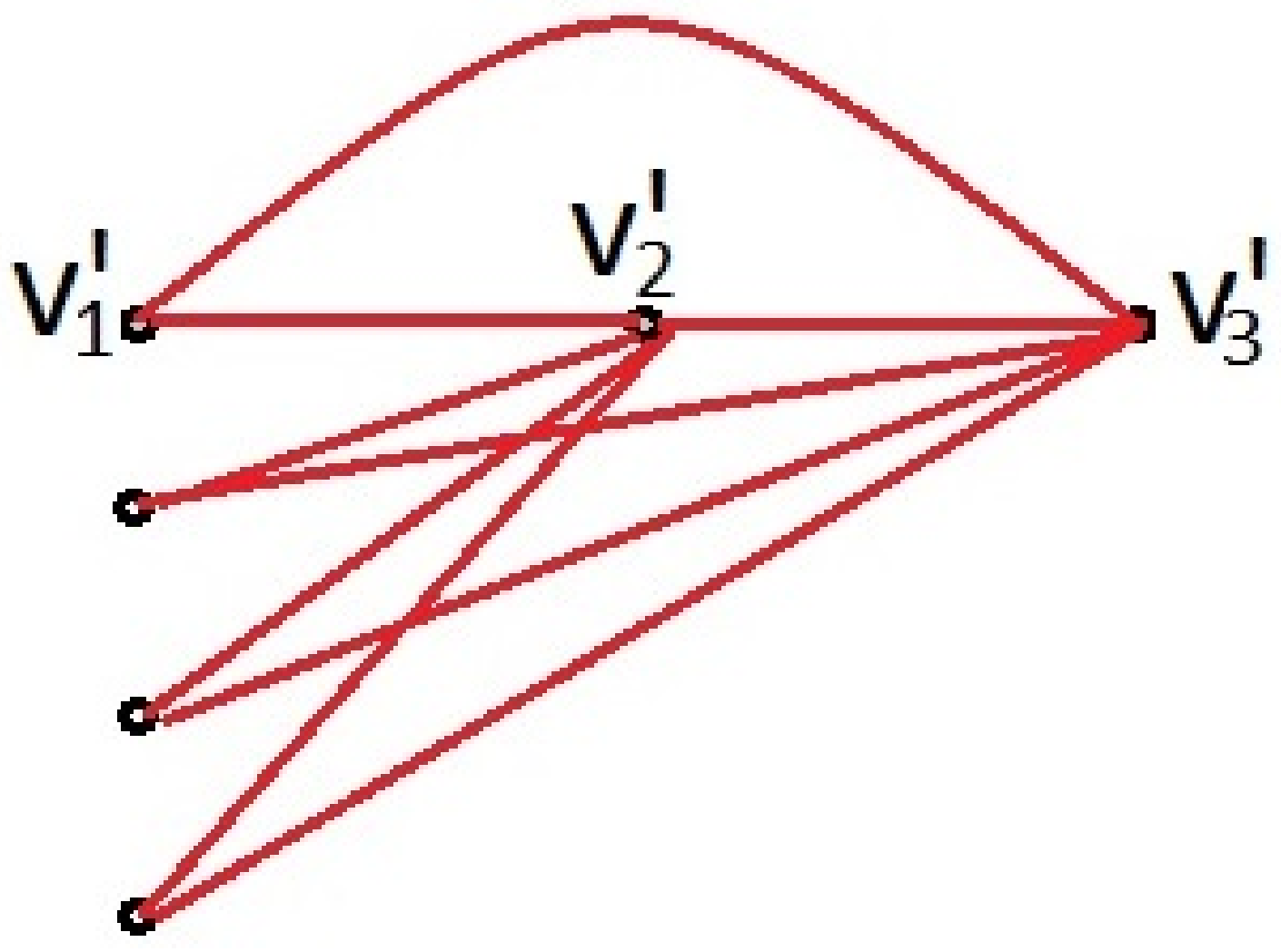
Hence, it can be concluded that in any 2-coloring of F, if $\{v_1,v_2,v_3,v_4,v_5\}$ are colored red to form a red $C_3^{+2}$, then all edges connecting vertex $v_3$ to vertices $\{v_6,v_7,\dots ,v_{11}\}$ must be colored blue. This is because if any of these edges were colored red, then a red $C_3^{+3}$ would be formed. □

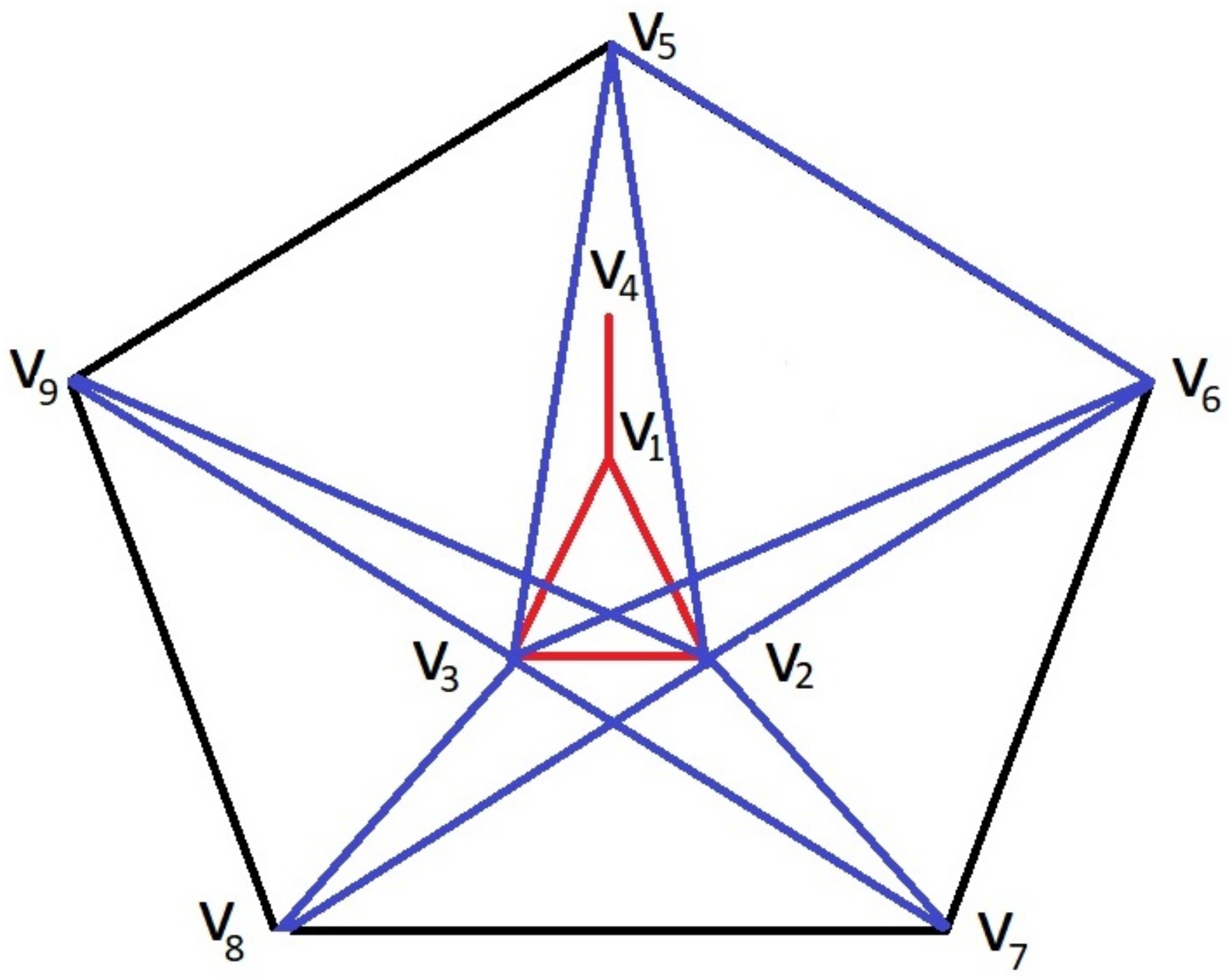
Claim 1.

If there exists a blue ${\mathcal{P}}_3$ in the induced subgraph of vertices $v_6,v_7,v_8,v_9,v_{10},v_{11}$, then graph F contains either a red or blue $C_3^{+3}$.

Proof. 

Let us assume that there exists a blue ${\mathcal{P}}_3$ in the induced subgraph of vertices $v_6,v_7,v_8,v_9,v_{10},v_{11}$, say $(v_6,v_7,v_8)$, as shown in Figure 6. If any edge connecting either $v_6$ or $v_8$ to vertices $\{v_1,v_2,v_4,v_5,v_9,v_{10},v_{11}\}$ is blue, then a blue $C_3^{+3}$ must exist. Therefore, we can conclude that all edges from $\{v_6,v_8\}$ to $\{v_1,v_2,v_4,v_5,v_9,v_{10},v_{11}\}$ must be red, and in this case, we obtain a red $C_3^{+3}$, as shown in Figure 6.

Therefore, we have shown that if there exists a blue ${\mathcal{P}}_3$ in the induced subgraph of vertices $v_6,v_7,v_8,v_9,v_{10},v_{11}$, then graph F contains either a red or blue $C_3^{+3}$. This completes the proof of the claim. □

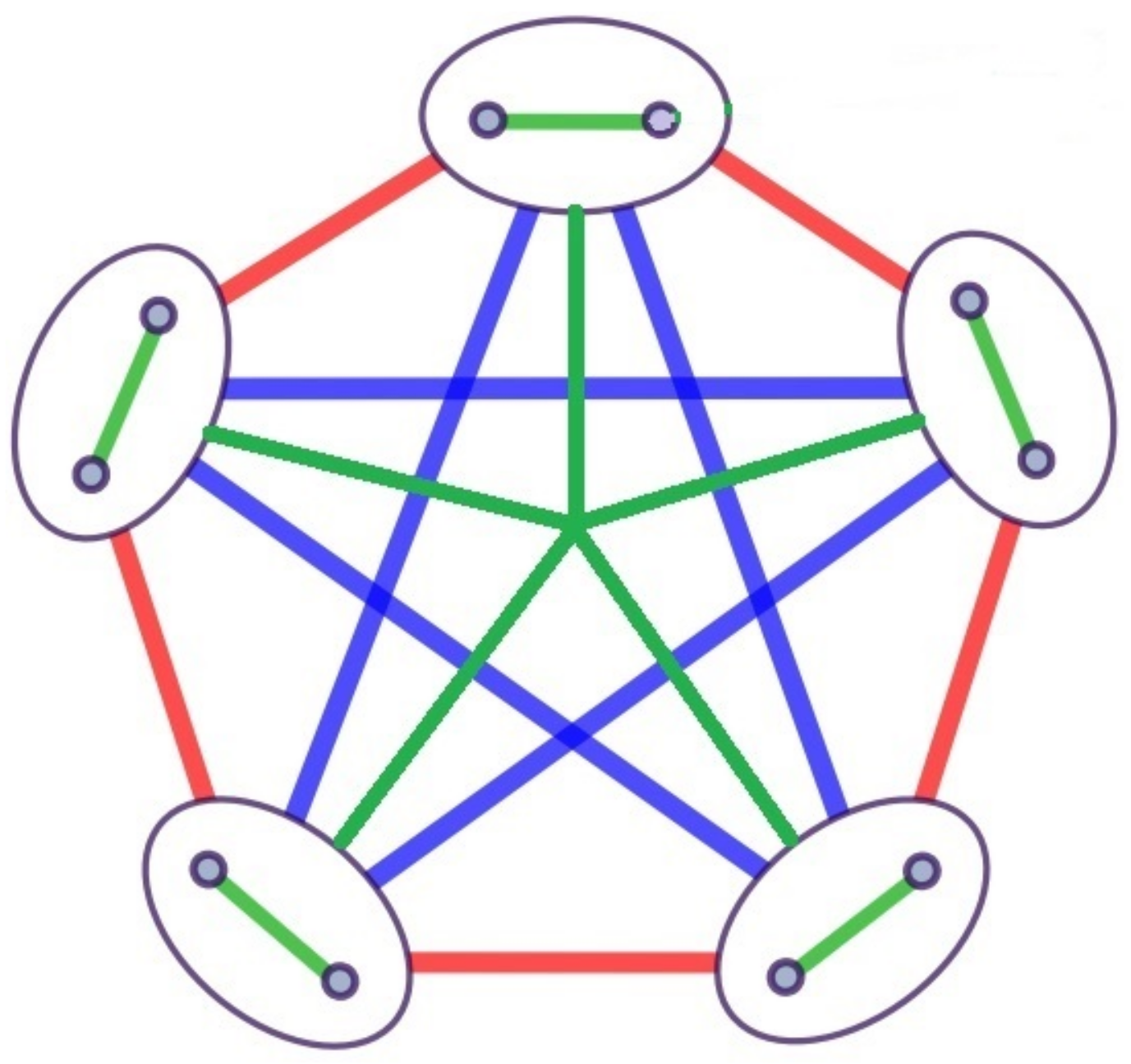
It is evident from the above Claim 1 that the induced subgraph $K_6$ formed by vertices $\{v_6,v_7,v_8,v_9,v_{10},v_{11}\}$ is free from a blue ${\mathcal{P}}_3$ (a path of order 3) in any 2-coloring of $K_6$, and this implies that $K_6$ contains a red $C_3^{+3}$.

As a consequence of all the above observation, any 2-coloring of F contains a monochromatic $C_3^{+3}$. Therefore, $R(C_3^{+3},C_3^{+3})\le 11$.

3.2. Star-Critical Ramsey Number

Theorem 8.

$r^{*}(C_3^{+3},C_3^{+3})=3.$

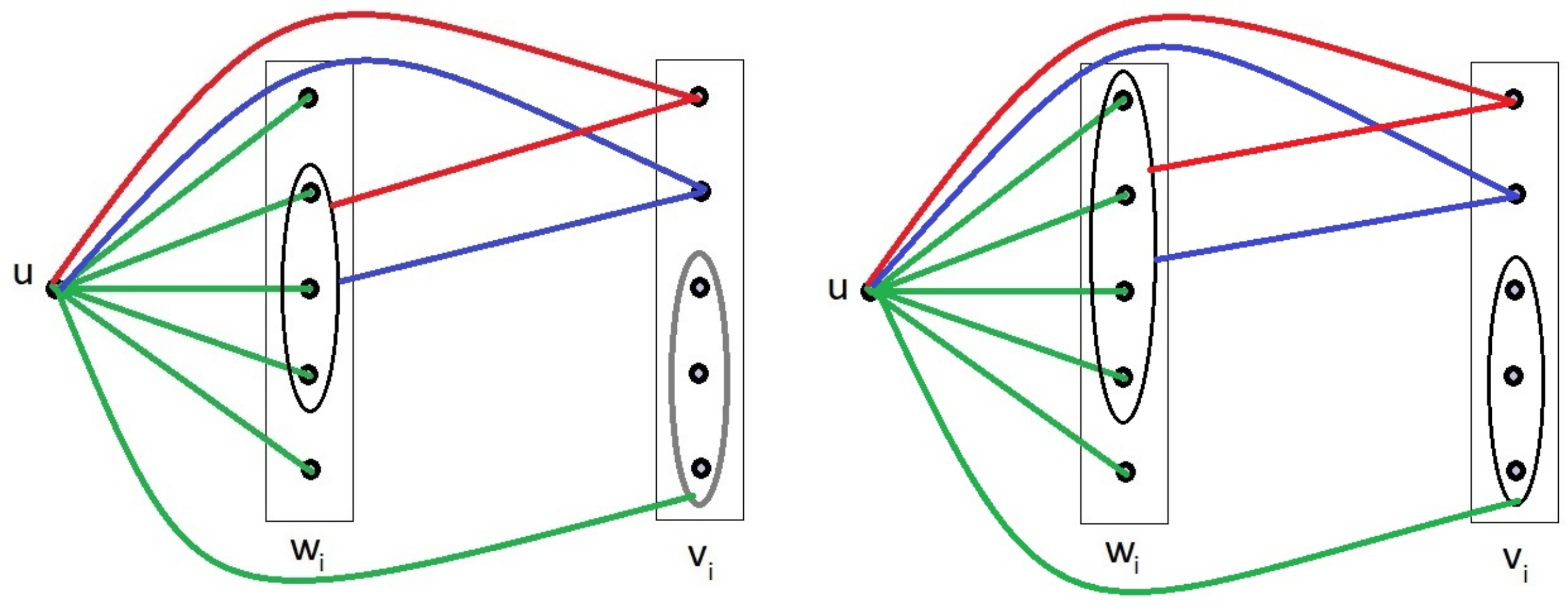
Proof. 

By utilizing Theorem 7, we can confidently assert that $R(C_3^{+3},C_3^{+3})=11$. However, proving this theorem requires us to first identify all critical colorings of $K_{10}$ for graph $C_3^{+3}$. This leads us to consider graph $K_{10}\cup K_{1,k}$, which is obtained by adding a new vertex to $K_{10}$ that is adjacent to k of the pre-existing vertices.

To establish the star-critical Ramsey number, denoted by $r^{*}(C_3^{+3},C_3^{+3})$, we aim to determine the minimum possible value of k such that every red–blue coloring of the edges of $K_{10}\cup K_{1,k}$, includes either a red or a blue copy of $C_3^{+3}$.

By utilizing Theorem 6, we can deduce that any 2-coloring of $K_{10}$ will inevitably include a monochromatic $C_3^{+2}$. To simplify the analysis, we assume that the vertices of $K_{10}$ are labeled $v_1,v_2,\dots ,v_{10}$ and vertices $v_1,v_2,v_3,v_4,v_5$ form a red $C_3^{+2}$.

As a consequence of this assumption, we can conclude that all edges connecting vertex $v_3$ to vertices $v_6,v_7,\dots ,v_{10}$ must be colored blue. This is due to the fact that if any of these edges were colored red, it would result in the formation of a red $C_3^{+3}$, as depicted in Figure 7. □

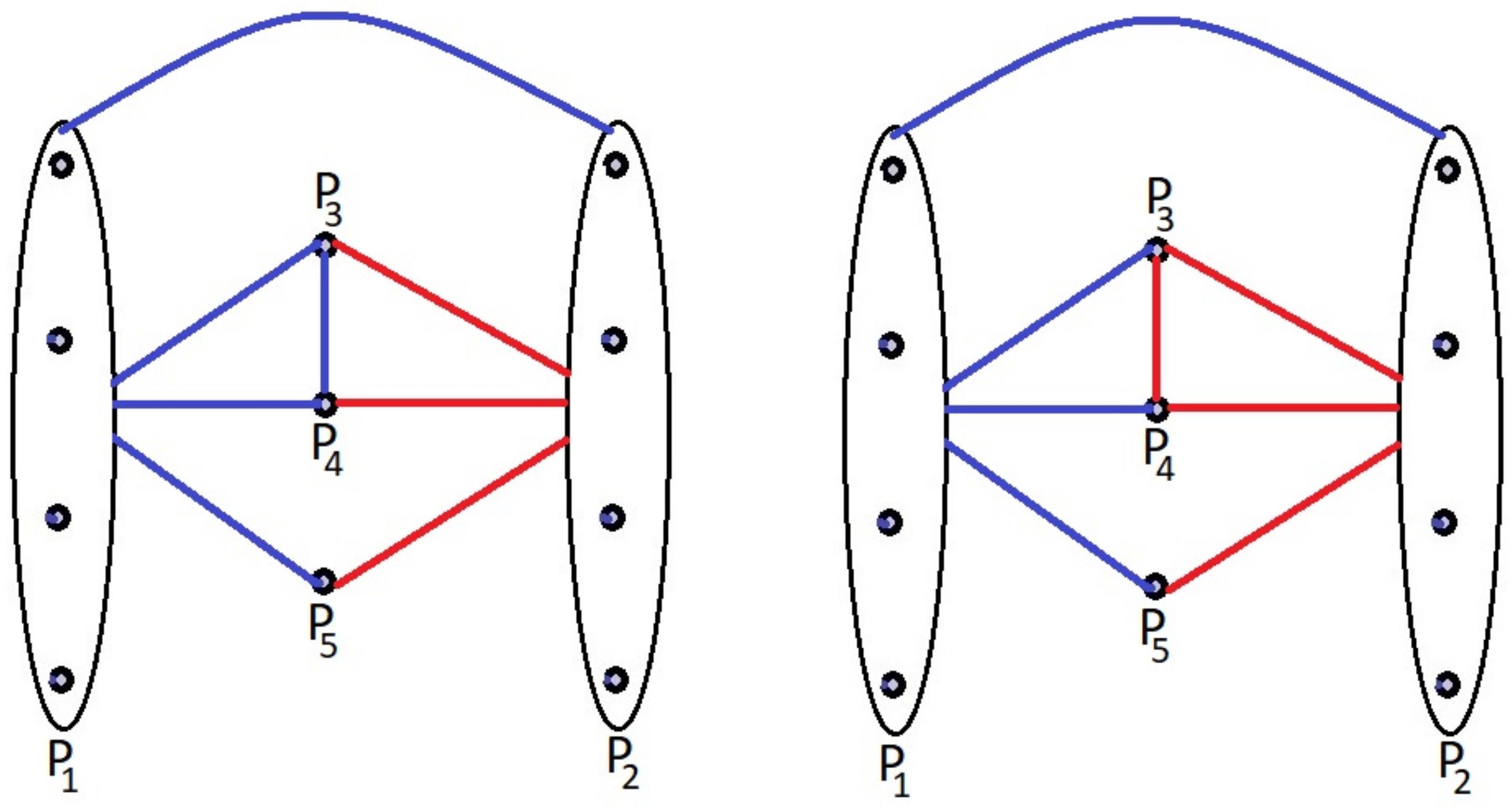
Claim 2.

If there exists a blue ${\mathcal{P}}_3$ (a path of order 3) in the induced subgraph of vertices $v_6,v_7,v_8,v_9,v_{10}$, then graph $K_{10}$ contains either a red or blue $C_3^{+3}$.

Proof. 

The proof is similar to Claim 1 □

Claim 3.

If there exists a blue $K_2$ in the induced subgraph of vertices $\{v_6,v_7,v_8,v_9,v_{10}\}$ or $\{v_1,v_2,v_3,v_4,v_5\}$, then graph $K_{10}$ contains monochromatic $C_3^{+3}$.

Proof. 

It is clear from the above Claim 2 that there can be at most two independent blue edges in the subgraph induced by vertices $v_6,v_7,v_8,v_9,v_{10}$. Hence, all other edges must be red. Therefore, all the edges between $\{v_6,v_7,v_8,v_9,v_{10}\}$ and $\{v_1,v_2,v_3,v_4,v_5\}$ are blue. Otherwise, there would exist a red $C_3^{+3}$. This implies that even a single blue edge in the subgraph induced by vertices $v_6,v_7,v_8,v_9,v_{10}$ would create a blue $C_3^{+3}$. The same argument can be applied to the other set of vertices. □

Consequently, based on the aforementioned Claims 2 and 3, we can establish that the sole admissible critical coloring of $K_{10}$ for the graph $C_3^{+3}$ consists of two red $K_5$ subgraphs, interconnected exclusively by blue edges. A visual representation of this coloring scheme can be observed in Figure 8.

Thus, it becomes evident that when considering a vertex v, a maximum of two additional (blue) edges can be introduced in the critical coloring of $K_{10}$ in such a way that the resulting graph does not contain either a red or a blue $C_3^{+3}$. As a consequence, every red–blue coloring of the edges of $K_{11}\cup K_{1,3}$ invariably comprises either a red copy of G or a blue copy of H.

Theorem 9.

$r^{*}(C_3^{+2},C_3^{+2})=2.$

Proof. 

The proof is similar to Theorem 8. □

3.3. Gallai–Ramsey Number

Lemma 1.

$g{r}_k(C_3:C_3^{+3})>\left\{\begin{array}{cc}10·5^{{\displaystyle \frac{k-2}{2}}},\hfill & ifkiseven\hfill \\ 5·5^{{\displaystyle \frac{k-1}{2}}},\hfill & ifkisodd\hfill \end{array}\right.$

Proof. 

In this study, we aim to demonstrate a theorem by employing an inductive methodology to construct a k-coloring scheme for the complete graph $K_n$. Our primary objective is to devise a coloring approach that possesses two crucial characteristics: the absence of rainbow triangles and the absence of monochromatic occurrences of $C_3^{+3}$. It is important to note that the value of n is contingent upon the parity of k and can be mathematically expressed as follows: $n=\left\{\begin{array}{cc}10·5^{{\displaystyle \frac{k-2}{2}}},\hfill & \mathrm{if}\mathrm{k}\mathrm{is}\mathrm{even}\hfill \\ 5·5^{{\displaystyle \frac{\mathrm{k}-1}{2}}},\hfill & \mathrm{if}\mathrm{k}\mathrm{is}\mathrm{odd}\hfill \end{array}\right.$

In the case where the parameter k is even, a 2-edge-colored complete graph denoted by $G_2$ is considered. This graph, represented by $K_{10}$, is constructed by using colors 1 and 2. The proven theorem (referred to as Theorem 7) guarantees the absence of monochromatic $C_3^{+3}$ in $G_2$.

Let us assume that $2i<k$ and that a $\left(2i\right)$-edge-colored complete graph $G_{2i}$ of $K_{n_{2i}}$ has already been constructed, satisfying the absence of rainbow $C_3$ and monochromatic $C_3^{+3}$, where

$$n_{2i}=10·5^{{\displaystyle \frac{2i-2}{2}}}.$$

Next, a 2-edge-colored complete graph denoted by $G_0$, represented by $K_5$, is considered. Colors $2i+1$ and $2i+2$ are used to color the edges of $G_0$. It can be proven that $G_0$ does not contain a monochromatic $K_3$, as the specified colors induce two monochromatic copies of $C_5$.

To proceed with the construction, $G_{2i+2}$ is defined as the blow-up of $G_0$ by a factor of 5, denoted by $G_0(5·G_{2i})$. A blow-up of a graph G, denoted by $G(F_1,F_2,\cdots ,F_n)$, is a transformation where each vertex $v_i$ of G is substituted with a distinct edge-colored complete subgraph $F_i$. The edges in this new graph are assigned colors based on the following rules:

If two vertices $x,y$ are both in the same subgraph $F_i$, their edge maintains the coloring from $F_i$, i.e.,

$$c_{G(F_1,F_2,\cdots ,F_n)}\left(xy\right)=c_{F_i}\left(xy\right).$$

If x and y belong to different subgraphs $F_i$ and $F_j$, the color of their connecting edge is determined by the color of edge $v_i{v}_j$ in the original graph G, i.e.,

$$c_{G(F_1,F_2,\cdots ,F_n)}\left(xy\right)=c_G\left(v_i{v}_j\right).$$

When all the subgraphs $F_i$ are identical, we simplify the notation to $G(n·F)$, meaning that each vertex in G is replaced by a copy of F.

By iteratively following this construction process, a k-edge coloring denoted by $G_k$ of $K_n$ is obtained, satisfying the absence of both rainbow $C_3$ and monochromatic $C_3^{+3}$. The value of n is determined as

$$n=10·5^{{\displaystyle \frac{k-2}{2}}}.$$

In the case of an odd value for k ($k\ge 3$), it is possible to construct a k-edge coloring of the complete graph $K_n$, denoted by $G_k$. The value of n is determined by

$$n=5·5^{{\displaystyle \frac{k-1}{2}}}.$$

The construction process ensures that $G_k$ does not contain a rainbow $C_3$ or a monochromatic $C_3^{+3}$. The proof of this claim relies on a step-by-step construction approach.

Let us consider the scenario where $2i-1<k$ and a $(2i-1)$-edge coloring of $K_{n_{2i-1}}$, denoted by $G_{2i-1}$, has been successfully constructed. Here,

$$n_{2i-1}=5·5^{{\displaystyle \frac{2i-2}{2}}}.$$

Let $G_{00}$ be a 2-edge-colored complete graph $K_5$, where colors $2i$ and $2i+1$ are used. It is important to note that $G_{00}$ is constructed in such a way that it does not contain a monochromatic $C_3$. By performing a blow-up operation on $G_{00}$ by using $G_{2i-1}$ with a factor of 5, denoted by $G_{00}(5·G_{2i-1})$, we obtain graph $G_{2i+1}$. □

Theorem 10.

$g{r}_k(C_3:C_3^{+3})=\left\{\begin{array}{cc}10·5^{{\displaystyle \frac{k-2}{2}}}+1,\hfill & ifkiseven\hfill \\ 5·5^{{\displaystyle \frac{k-1}{2}}}+1,\hfill & ifkisodd\hfill \end{array}\right.$

Proof. 

The lower bound can be obtained by applying Lemma 1. To establish the upper bound, an induction technique will be employed on the variable k. The base case of $k=1$ is self-evident, and the case of $k=2$ is equivalent to Theorem 7. Hence, assuming $k\ge 3$, let $K_n$ represent a complete graph with n vertices, and let G denote a Gallai coloring of $K_n$, where n is given by

• $10·5^{{\displaystyle \frac{k-2}{2}}}+1,\mathrm{if}\mathrm{k}\mathrm{is}\mathrm{even}$.
• $5·5^{{\displaystyle \frac{k-1}{2}}}+1,\mathrm{if}\mathrm{k}\mathrm{is}\mathrm{odd}$.

Considering the Gallai coloring of G as per Theorem 1, it can be concluded that a Gallai partition exists. Let us denote the two colors present in the Gallai partition as ‘red’ and ‘blue’. The partition is selected in such a way that the number of parts, denoted by m, is minimized. By applying Theorem 7 to the reduced graph, it follows that $m\le 10$. The parts of the partition are represented as $P_1,P_2,\dots ,P_m$. Assuming $|P_i|\ge |P_{i+1}|$ for all i with $1\le i\le m-1$, we define n as the number of parts in the Gallai partition with an order of at least 5. Thus, $|P_n|\ge 5$, and $|P_{n+1}|\le 4$.

Initially, we examine different cases based on the value of m. Later, we will examine different cases based on the value of n.

Let us assume that $2\le m\le 3$. When m = 3, there are at most two colors among parts $P_1,P_2,\mathit{and}{P}_3$. Without loss of generality, let us say that the color between $P_1$ and $P_2$ and between $P_1$ and $P_3$ is same. This implies that the vertices of $P_1$ and $V\left(G\right)\setminus P_1$ form a Gallai partition with exactly two parts, which contradicts the minimality of m; therefore, m = 2.

Case m = 2: Now, we assume that all edges between $P_1$ and $P_2$ are red. As $k\ge 3$, we have $\left|G\right|=|P_1|+|P_2|\ge 5·5+1$, which implies that there is at least one part of order at least 13. Therefore, we have $|P_1|\ge 13$.

Sub-case $|{\mathbf{P}}_{\mathbf{2}}|=\mathbf{1}$: The proof for the case when $|P_2|=1$ is similar to the proof given in Lemma 4 of [26] for the case where $|V_2|=1$.

Sub-case $|{\mathbf{P}}_{\mathbf{2}}|=\mathbf{2}$: To avoid the emergence of a red $C_3^{+3}$, it is essential that no red ${\mathcal{P}}_3$ (a path of order 3) exists within $P_1$; otherwise, this path, along with $P_2$ (the partition), would lead to the induction of a red $C_3^{+3}$. Thus, color 1 (red) generates a subgraph $H^{\prime }$ where each component in partition $P_1$ is a $K_2$.

To prevent the occurrence of both a rainbow $K_3$ and a monochromatic red ${\mathcal{P}}_3$ (a path of order 3), it is necessary for each pair of components to be connected by a single color only. Given that $C_3^{+3}$ is a subgraph of $K_{2,2,2}$ and $K_{1,3,3}$, the prevention of monochromatic $K_{2,2,2}$ necessitates that $H^{\prime }$ comprises no more than $2k$ components. Removing up to k vertices guarantees the absence of edges of color 1 (red) within partition $P_1$. Consequently, we derive the bound

$$\left|G\right|=|P_1|+|P_2|\le k+2[g{r}_{k-1}(C_3:C_3^{+3})-1]+2<n,$$

which results in a contradiction.

Sub-case $|{\mathbf{P}}_{\mathbf{2}}|\ge \mathbf{3}$: If $|P_i|\ge 3$ for i = 1, 2, then in order to avoid a red $C_3^{+3}$, there can be no red edges within $P_1$ and $P_2$. Since a color is missing within each $P_i$, we can apply induction on k within each $P_i$. This implies that $\left|G\right|=|P_1|+|P_2|\le 2|P_1|\le 2[g{r}_{k-1}(C_3:C_3^{+3})-1]<n,$ which is a contradiction. Therefore, we can assume that $m\ge 4$.

By assuming that $n\ge 4$ and $m\ge 6$, it can be shown that any selection of six parts, including $P_1,P_2,P_3,$ and $P_4$, will result in a reduced graph containing a monochromatic triangle. This triangle must include at least one part from the set $P_1,P_2,P_3,P_4$, indicating that the corresponding subgraph of G contains a monochromatic copy of $C_3^{+3}$, which contradicts our assumptions. Thus, it follows that either $4\le m\le 5$ or n is less than or equal to 3.

To proceed further, we will examine different cases based on the value of n. □

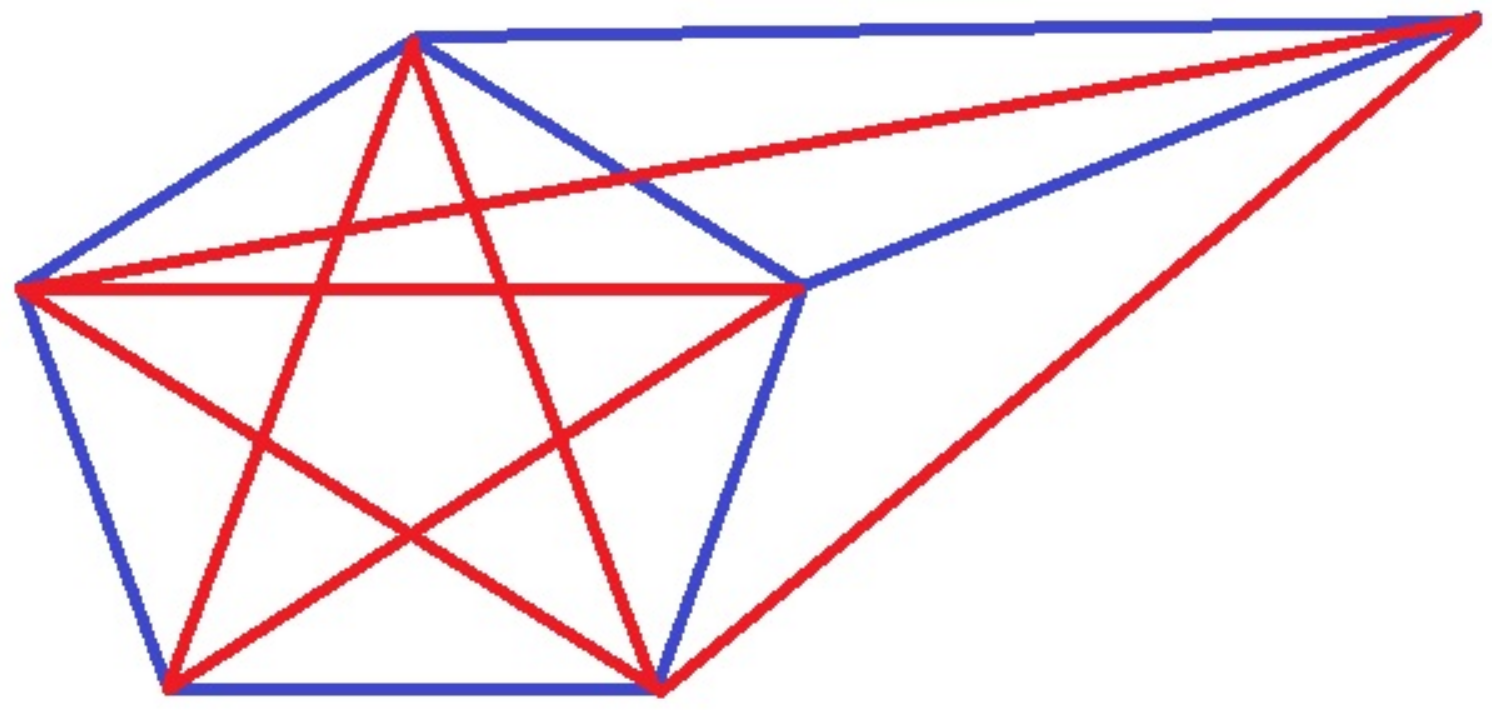
Claim 4.

Let us suppose that we have a Gallai partition with multiple parts, where the number of vertices in each part is less than 5 and all the edges between pairs of these parts are monochromatic. In this case, the total number of vertices in these parts cannot exceed 8.

Proof. 

Let us denote the parts by $P_1^{\prime },P_2^{\prime },\dots ,P_{m^{\prime }}^{\prime }$. When $m^{\prime }\le 2$, the conclusion is evident and requires no further explanation. However, in the case where $m^{\prime }\ge 3$, if we assume that all these parts are connected solely by red edges, it becomes evident that a red $C_3$ emerges by virtue of three distinct vertices ($v_1^{\prime },v_2^{\prime },v_3^{\prime }$) originating from different parts. Hence, we can have at most three more vertices to avoid red $C_3^{+3}$, as shown in Figure 9.

□

Claim 5.

Let $P_1$ and $P_2$ be two parts of a Gallai partition, each having an order of at least 4. Let us suppose that c represents the color of the edges between $P_1$ and $P_2$. In this case, it can be observed that there are no other parts in the Gallai partition that possess edges of color c connecting both $P_1$ and $P_2$.

Proof. 

Let us suppose that there exists a part $P_3$ in the Gallai partition that has color c edges connecting both $P_1$ and $P_2$. In this case, the union of $P_1$, $P_2$, and $P_3$ denoted by $P_1\cup P_2\cup P_3$ contains a monochromatic copy of $C_3^{+3}$. This leads to a contradiction. Therefore, the assumption of the existence of $P_3$ with color c edges connecting both $P_1$ and $P_2$ is false. □

Claim 6.

Let us consider $P_1$ and $P_2$, two parts of a Gallai partition, each with an order of at least 4. Let us assume that there are blue edges between $P_1$ and $P_2$. In this scenario, it can be observed that if there is one part $P_3$ in the Gallai partition that has blue edges connecting to $P_1$ and red edges connecting to $P_2$ and the order of $P_3$ is at least two, then it is unique. Otherwise, there can be at most two parts with an order equal to 1. Similarly, there can be at most one part with red edges connecting to $P_1$ and blue edges connecting to $P_2$ or two parts with an order equal to 1.

Proof. 

To arrive at a contradiction, let us assume the existence of two parts, $P_3$ and $P_4$, of order greater than or equal to 2 in the Gallai partition. These parts have red edges to $P_1$ and blue edges to $P_2$. Now, let us consider the edges between $P_3$ and $P_4$.

If the edges from $P_3$ to $P_4$ are red, then the union $P_1\cup P_3\cup P_4$ contains a red copy of $C_3^{+3}$. This contradicts the assumption. On the other hand, if the edges from $P_3$ to $P_4$ are blue, then the union $P_2\cup P_3\cup P_4$ contains a blue copy of $C_3^{+3}$. Once again, this contradicts our assumption.

If there exist three parts $P_3,P_4$, and $P_5$ of order 1, then a monochromatic $C_3^{+3}$ also exists, as shown in Figure 10.

Thus, in each case, a contradiction is reached.

The proof is indeed symmetric for two parts with red edges to $P_2$ and blue edges to $P_1$. □

Case n = 0: Let us consider the case where $n=0$, meaning that there are no parts in the Gallai partition with an order of at least 5. Our focus is on the colors of the edges from $P_1$ to $P_2\cup P_3\cup \dots \cup P_m$. Let $G_b$ represent the union of the parts with blue edges to $P_1$, and let $G_r$ denote the union of the parts with red edges to $P_1$.

Let us suppose, without loss of generality, that $|G_b|$ is at least 5. In this case, there can be no blue edges within $G_b$, as it would lead to the formation of a blue $C_3^{+3}$. Consequently, all edges between the parts in $G_b$ must be red. By applying Claim 4, we can deduce that $|G_b|\le 8$. Similarly, we have $|G_r|\le 8$. Thus, we have

$$\left|G\right|=|P_1|+|G_b|+|G_r|\le 4+8+8<n,$$

which results in a contradiction.

Case n = 1: In this case, let $|P_1|\ge 5$. Let us assume that $G_r$ represents the collection of parts that have red edges connected to $P_1$, while $G_b$ represents the collection of parts that have blue edges connected to $P_1$. Similar to the previous scenario, we can conclude that the size of $G_r$ is less than or equal to 8, and the size of $G_b$ is also less than or equal to 8. Given that m is the minimum value, it can be inferred that $G_b$ and $G_r$ cannot be empty. Consequently, there are no blue or red edges within $P_1$. We can conclude that the size of G is equal to the sum of the sizes of $P_1$, $G_b$, and $G_r$, i.e., $\left|G\right|=|P_1|+|G_b|+|G_r|$. This value is less than or equal to $[g{r}_{k-2}(C_3:C_3^{+3})-1]+16$. However, this value is less than n, indicating that the size of G is less than the given value of n.

Case n = 2: Let us consider the following scenario: The color red is designated for the edges connecting $P_1$ and $P_2$. Consequently, neither $P_1$ nor $P_2$ can contain any red edges. Furthermore, according to the assertion made in Claim 5, it is impossible for a component to possess red edges leading to both $P_1$ and $P_2$. In addition, Claim 6 postulates that there can be at most one component, denoted by $P_3$, which features red edges connecting to $P_1$ alongside blue edges leading to $P_2$. Similarly, there can exist at most one component, denoted by $P_4$, with blue edges linking to $P_1$ and red edges connecting to $P_2$. Let us define $G_r$ as the collective set of the remaining components that possess exclusively red edges connecting to $P_1\cup P_2$. Based on the findings of Claim 4, we can deduce that the cardinality of $G_r$ must satisfy the inequality $|G_r|\le 8$.

By virtue of the minimality of m, every part in question exhibits incident edges from other parts in both red and blue. This implies that neither $P_1$ nor $P_2$ possesses any red or blue edges. Consequently, we can infer that the cardinality of $P_i$ is limited by $g{r}_{k-2}(C_3:C_3^{+3})-1$, leading to $|P_i|\le g{r}_{k-2}(C_3:C_3^{+3})-1$. Hence, we can calculate the overall size of G by summing the sizes of $P_1$, $P_2$, $P_3$, $P_4$, and $G_r$, expressed as $\left|G\right|=|P_1|+|P_2|+|P_3|+|P_4|+|G_r|$. We can conclude that the size of G is less than or equal to $2[g{r}_{k-2}(C_3:C_3^{+3})-1]+16$, which is less than n, so it is a contradiction.

Case n ≥ 3: In order to prevent the occurrence of a monochromatic copy of $C_3^{+3}$, it is crucial to ensure that the triangle formed by the reduced graph, represented by the parts $\{P_1,P_2,P_3\}$, does not consist of edges of a single color. Let us assume, without loss of generality, that the edges connecting $P_2$ to $P_3$ are red, while all edges from $P_1$ to $P_2\cup P_3$ are blue. As a result, both $P_2$ and $P_3$ will not contain any red or blue edges, whereas $P_1$ will lack blue edges.

The first claim is that there cannot be a part with blue edges to $P_1$. If there were such a part, let us call it $P^{\prime }$ and assume that it has blue edges to $P_1$. To avoid a blue copy of $C_3^{+3}$, all edges from $P^{\prime }$ to $P_2\cup P_3$ must be red. However, this means that $P^{\prime }\cup P_2\cup P_3$ contains a red copy of $C_3^{+3}$, which is a contradiction. Thus, all edges from $P_1$ to $P_4\cup \dots \cup P_m$ must be red. As m is greater than or equal to 4, this means that $P_1$ does not contain any red edges either. Therefore, we have $|P_i|\le g{r}_{k-2}(C_3:C_3^{+3})-1$ for $1\le i\le 3.$

This paragraph describes the potential existence of certain parts in the graph. According to Claim 6, there is at most one part $P_4$ that has blue edges connecting it to $P_2$ and red edges connecting it to $P_3$. Similarly, there is at most one part $P_5$ that has red edges connecting it to $P_2$ and blue edges connecting it to $P_3$. Additionally, there is at most one part $P_6$ that has blue edges connecting it to both $P_2$ and $P_3$. It is important to note that the union of $P_4$, $P_5$, and $P_6$ is not empty, as the value of m was chosen to be minimal. Hence,

$$\begin{array}{l}\left|G\right|=|P_1|+|P_2|+|P_3|+|P_4|+|P_5|+|P_6|\le 3[g{r}_{k-2}(C_3:C_3^{+3})-1]+12.\\ \Rightarrow \left|G\right|<n\end{array}$$

Case n ≥ 4: When considering the case where n is greater than or equal to 4, it can be deduced that $4\le m\le 5$. Within the subgraph of the reduced graph, which is induced by the n parts having an order of at least 5, it has been previously established that the existence of a monochromatic triangle is not possible. If n is equal to 5, there exists only one coloring of $K_5$ that satisfies this condition. Conversely, if n is equal to 4, there are two possible colorings of $K_4$ that exhibit no monochromatic triangle. In both of these colorings, each vertex has at least one incident edge of each color, indicating that all corresponding parts with an order of at least 5 do not contain any red or blue edges.

Consequently, we can calculate the size of G by summing the sizes of all parts, expressed as $\left|G\right|={\sum }_{i=1}^m\left|P_i\right|$. This sum is less than or equal to $5[g{r}_{k-2}(C_3:C_3^{+3})-1]$. However, this value is less than n, which leads to a contradiction. Thus, this concludes the proof for this case, as well as the proof of the theorem.

3.4. Star-Critical Gallai–Ramsey Number

To prove that $g{r}_k^{*}(K_3:H)=l$, the following two steps need to be taken:

• Create a Gallai k-coloring of graph $K_{g{r}_k(K_3:H)-1}\cup K_{1,l-1}$ that does not have a monochromatic copy of H. This will show that $g{r}_k^{*}(K_3:H)\ge l$.
• Show that any Gallai k-coloring of graph $K_{g{r}_k(K_3:H)-1}\cup K_{1,l}$ contains a monochromatic copy of H. This will prove that $g{r}_k^{*}(K_3:H)\le l$.

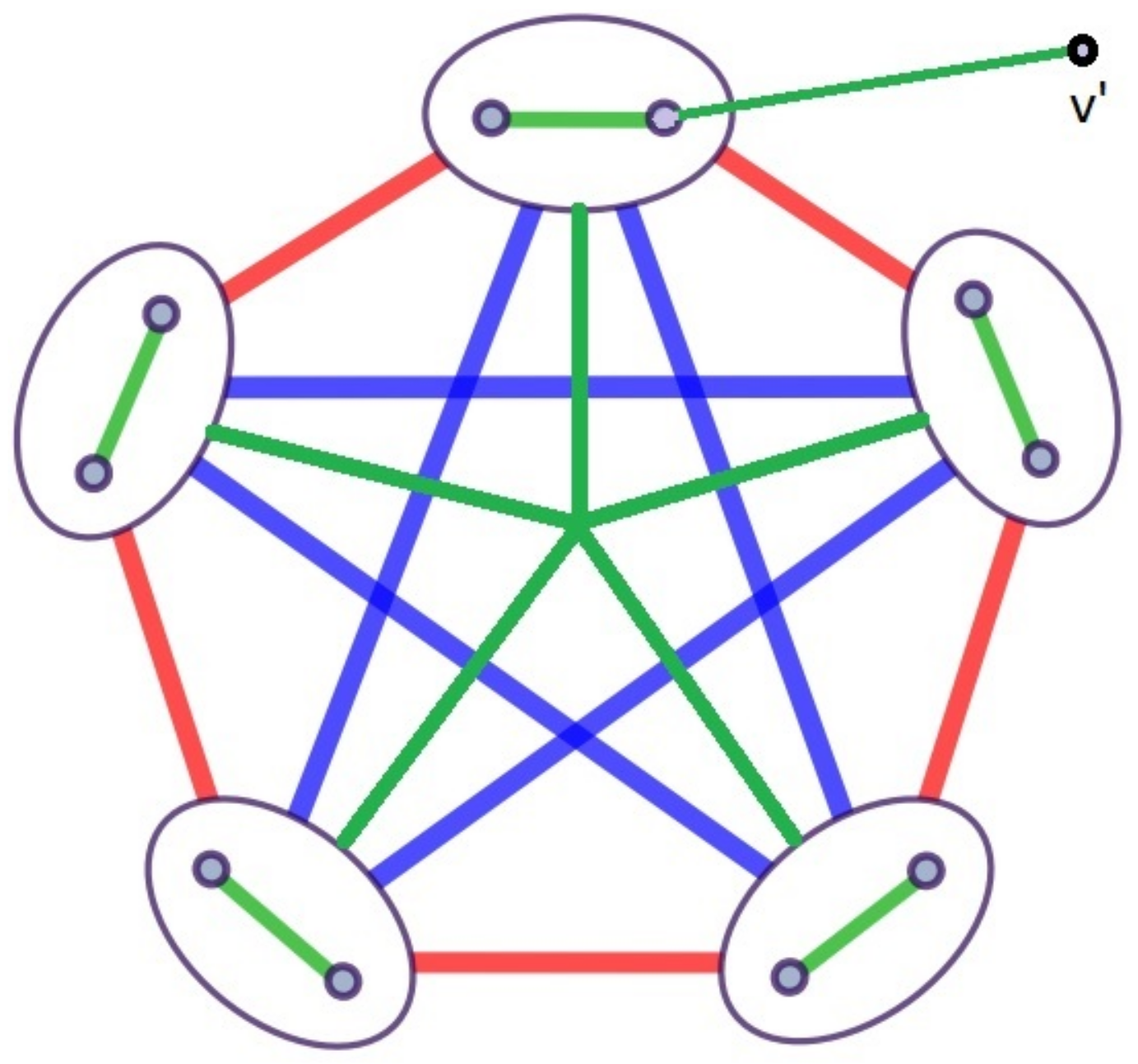
Theorem 11.

For any integer $l\ge 2$, $g{r}_l^{*}(K_3:F_{2,3})=l+3$.

Proof. 

By Theorem 3, $g{r}_l(K_3:F_{2,3})=l+4$. We know that $g{r}_l^{*}(K_3:F_{2,3})\le g{r}_l(K_3:F_{2,3})-1=l+3$. Therefore, we only need to prove that $g{r}_l^{*}(K_3:F_{2,3})\ge l+3$. Let $G=K_5\cup K_{1,4}$, with two colorings, red and blue, as shown in Figure 11. Clearly, G contains neither a rainbow $K_3$ nor a monochromatic $F_{2,3}$.

When l = 2. From the above observation, it is clear that if l = 2 then $g{r}_2^{*}(K_3:F_{2,3})>4$ implies that $g{r}_l^{*}(K_3:F_{2,3})=5=l+3.$

Case when $\mathbf{l}\ge \mathbf{3}$. We start by outlining the process used to determine the lower bound. Let us consider graph $G_2=G$, with edges colored 1 (red) and 2 (blue), as shown in Figure 11, ensuring that it does not contain a monochromatic $F_{2,3}$. To construct $G_3,G_4,\cdots ,G_l$, we begin with $G_2$ and iteratively add a new vertex for each i from 3 to l. Each new vertex is connected to all existing vertices in $G_{i-1}$, with the new edges colored i. This process continues until we obtain $G_l$, where each $G_i$ is formed by adding a vertex to $G_{i-1}$ and coloring the new edges with i. It is worth noting that $G_l$ can be viewed as a structure combining the complete graphs $K_{l+3}$ and $K_{1,l+2}$. Furthermore, $G_l$ does not contain any rainbow $K_3$ or monochromatic $F_{2,3}$. Hence, $g{r}_l^{*}(K_3:F_{2,3})\ge l+3$. □

Theorem 12.

For any integer $k\ge 2$, $g{r}_k^{*}(K_3:F_{2,4})=k+4$.

Proof. 

By Theorem 3, $g{r}_k(K_3:F_{2,4})=k+5$. We know that $g{r}_k^{*}(K_3:F_{2,4})\le g{r}_k(K_3:F_{2,4})-1=k+4$. Therefore, we only need to prove that $g{r}_k^{*}(K_3:F_{2,4})\ge k+4$. Let $G=K_6\cup K_{1,5}=K_7-e$, with two colorings, red and blue, as shown in Figure 12. Clearly, G contains neither a rainbow $K_3$ nor a monochromatic $F_{2,4}$.

Case when k = 2. From the above observation, it is clear that if k = 2 then $g{r}_2^{*}(K_3:F_{2,4})>5$ implies that $g{r}_k^{*}(K_3:F_{2,4})=6=k+4.$

Case when $\mathbf{k}\ge \mathbf{3}$. Let us start by explaining the construction that resulted in the lower bound. Let us consider graph $G_2=G$ with edges in color 1 (red) and 2 (blue), as shown in Figure 12, without monochromatic $F_{2,4}$. To construct $G_3$, $G_4$, …, $G_k$, we follow a similar procedure to the one used in Theorem 11. We start with an initial graph $G_2$, and then for each value of i from 3 to k, we add a new vertex to the graph and connect it to every vertex in $G_{i-1}$ by using edges of color i. This generates a new graph $G_i$ that has one more vertex than $G_{i-1}$, and all the edges added in this step are colored with the value i. We repeat this process for all values of i from 3 to k to obtain the sequence of graphs $G_3$, $G_4$, …, $G_k$. It is worth noting that the graph represented by $G_k$ is the result of combining the complete graphs $K_{k+4}$ and $K_{1,k+3}$. Furthermore, $G_k$ does not contain any rainbow $K_3$ or any monochromatic $F_{2,4}$. Hence, $g{r}_k^{*}(K_3:F_{2,4})\ge k+4$.

□

Lemma 2.

When k is equal to 3, the coloring of $K_{11}$ shown in Figure 13 is the only way such that it contains neither a rainbow $K_3$ nor a monochromatic $F_{2,5}$.

Proof. 

By Theorem 4, $K_{11}$ contains either a rainbow $K_3$ or a monochromatic $K_{1,5}$. Let us suppose that the complete graph $K_{11}$ contains a monochromatic $K_{1,5}$, denoted by H, with vertices $u,w_1,w_2,w_3,w_4,w_5$ and edge $E(u,w_i)$ colored green (color 3). Let $V\left(K_{11}\right)/V\left(H\right)$ denote the set of remaining vertices, which is $v_1,v_2,v_3,v_4,v_5$. To avoid having a monochromatic $F_{2,5}$ in the graph, there can be at most one edge colored green (color 3) between each vertex $v_i$ (where $1\le i\le 5$) and vertices $\{w_1,w_2,w_3,w_4,w_5\}$.

For the first case, let us suppose that $c(u,\left\{v_1\right\})=1$ (red). Then, edges $E(v_1,\{w_1,w_2,w_3,w_4,w_5\})$ cannot have color 2 (blue); otherwise, there exists a rainbow triangle $\{u,v_1,w_i,u\}$, as shown in Figure 14.

Now, for all other $v_i$, $c(u,\left\{v_i\right\})\ne 1$ (red); otherwise, we have a rainbow triangle or monochromatic $F_{2,5}$. Hence, there does not exist $c(u,\{v_i,v_j\})=1$ (red) or $c(u,\{v_i,v_j\})=2$ (blue).

For the second case, if there is a coloring as shown in Figure 15, i.e., $c(u,\left\{v_1\right\})=1$ (red), $c(u,\left\{v_2\right\})=2$ (blue), and $c(u,\{v_3,v_4,v_5\})=3$, then there are two sub-cases such that $c(v_1,\{w_2,w_3,w_4\})=1$ and $c(v_2,\{w_2,w_3,w_4\})=2$ or $c(v_1,\{w_1,w_2,w_3,w_4\})=1$ and $c(v_2,\{w_1,w_2,w_3,w_4\})=2$.

In the first sub-case, there always exists a rainbow triangle $(v_1,v_2,w_i)$. In the second sub-case, there are always at least two red or blue edges in the edge set $E(v_i,\{w_1,w_2,w_3,w_4\})$ for $v_3,v_4\mathit{and}{v}_5$. Hence, there exists either a red or a blue $F_{2,5}$. From the above observation it is clear that ‘u’ is connected to the green (color 3) edges at each vertex.

Now, we prove that every vertex of a graph $K_{11}$ - u is associated with exactly one green edge. Let us suppose that $v_1$ has no green edge; then, there exists an either red or blue $K_{1,5}$ with center $v_1$. By the same logic as ‘u’, $v_1$ is also connected to each vertex of $K_{11}$ by red–blue edges. But this is a contradiction, as $v_1$ has at least one green edge and $v_1$ is arbitrary, so each vertex has at least one green edge.

Now, if we say that $v_1$ has two green edges ($v_1{v}_2$) and ($v_1{w}_1$), then graph $K_{11}$ has a cycle of order 4 ($u{v}_2{v}_1{w}_{1}u$), so there exists a monochromatic $F_{2,5}$.

Therefore, based on all the above arguments, it is clear that only one critical coloring for $K_{11}$ is possible, as shown in Figure 13. □

Lemma 3.

For any integer $k\ge 3$, $g{r}_k^{*}(K_3:F_{2,5})\ge k-1$.

Proof. 

By Theorem 3, $g{r}_k(K_3:F_{2,5})=k+9$. Initially, we obtain the lower bound. Let us consider graph $G_3=K_{11}+e$, with edges in color 1 (red), 2 (blue), and 3 (green), as shown in Figure 16, without a monochromatic $F_{2,5}$.

To construct $G_4$, $G_5$, …, $G_k$ by using the approach described in Theorem 11, we begin with an initial graph $G_3$. We then construct a sequence of graphs by adding a new vertex to the previous graph and connecting it to every vertex. We then color the edges incident to the new vertex with a new color that has not been used before. This process is repeated for all values of i from 4 to k to obtain a sequence of graphs $G_4$, $G_5$, …, $G_k$. It should be noted that the graph denoted by $G_k$ is obtained by adding $k-2$ edges to the complete graph $K_{k+8}$. Additionally, $G_k$ does not have a rainbow $K_3$ or any monochromatic $F_{2,5}$. Hence, $g{r}_k^{*}(K_3:F_{2,4})\ge k-1$. □

Theorem 13.

For any integer $k\ge 3$, $g{r}_k^{*}(K_3:F_{2,5})=k-1$.

Proof. 

To establish the lower bound $g{r}_k^{*}(K_3:F_{2,5})\ge k-1$, we can utilize Lemma 3.

By applying Lemma 2, we can determine that for $k=3$, the inequality $g{r}_k^{*}(K_3:F_{2,5})\le k-1$ holds true.

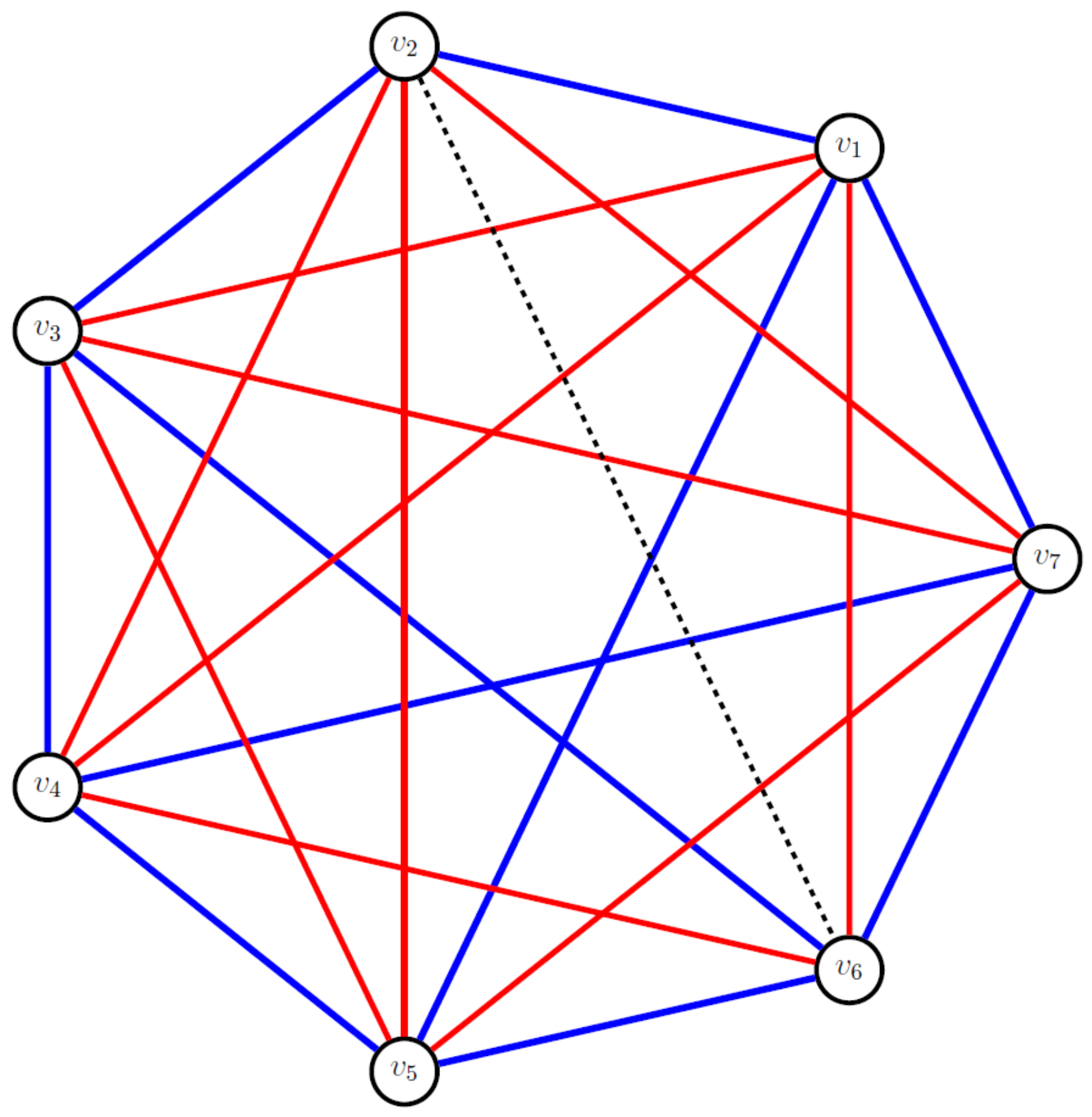
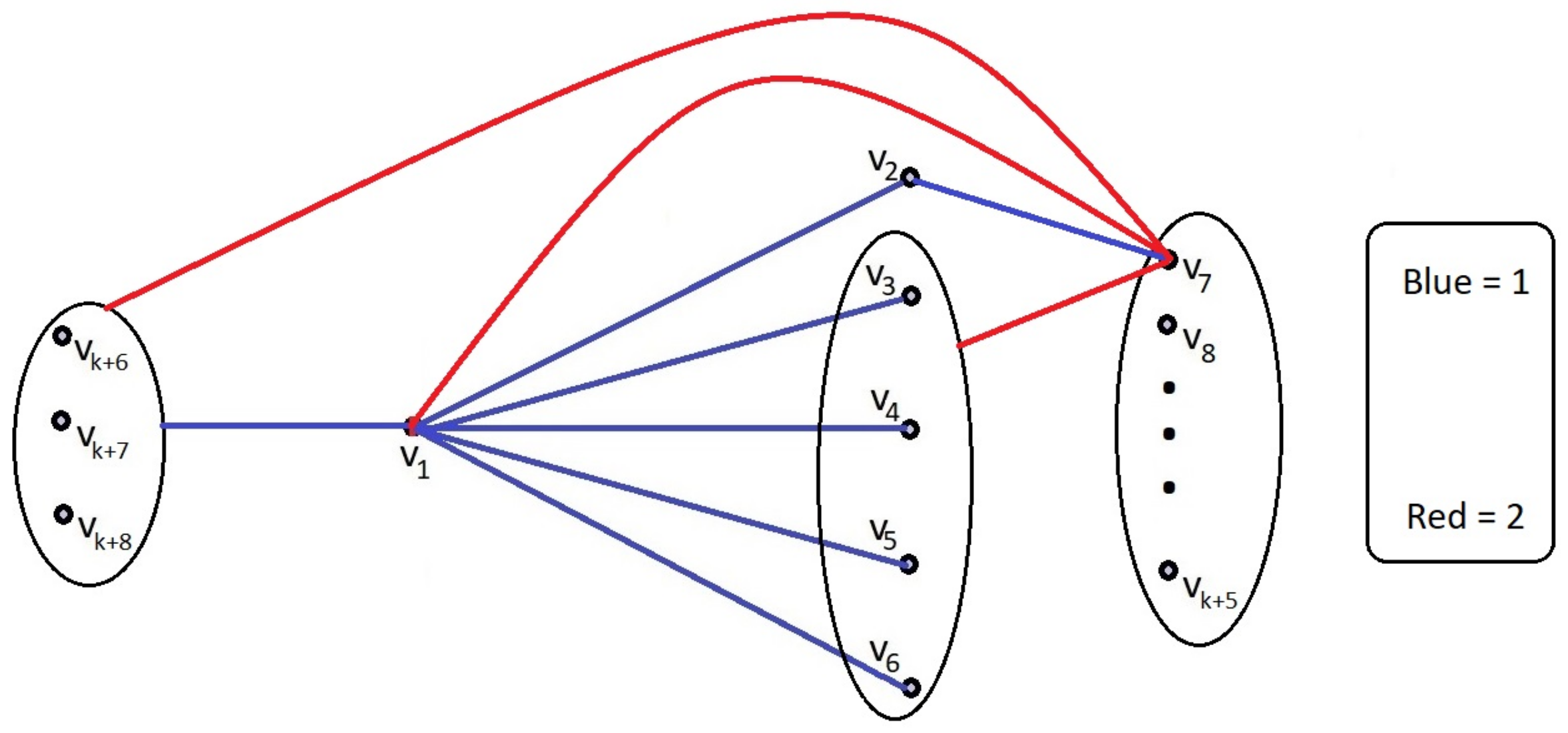
Case when $\mathbf{k}>\mathbf{3}$. By utilizing Theorem 3, we can confidently assert that $g{r}_k(K_3:F_{2,5})=k+9$. So, to prove this theorem, we find all critical colorings of $K_{k+8}$ such that it does not contain a monochromatic $F_{2,5}$ or a rainbow triangle. To establish the star-critical Gallai–Ramsey number, denoted by $g{r}_k^{*}(K_3:F_{2,5})$, we aim to determine the minimum possible value of l such that every k-coloring of the edges of $K_{k+9}\cup K_{1,l}$ includes a monochromatic copy of $F_{2,5}$ or a rainbow triangle.

Because $k>3$, we have $k+8\ge 12$. Therefore, by using Theorem 4, we can conclude that any k coloring of $K_{k+8}$ will contain a monochromatic $K_{1,5}$. For the sake of clarity, we shall label the k colors as the numbers 1, 2, 3, …, up to k, while the $k+8$ vertices shall be denoted by $v_1,v_2,...v_{k+8}$. Without loss of generality, let us assume that vertices $v_1,v_2,v_3,v_4,v_5,v_6$ form a monochromatic $K_{1,5}$ with $v_1$ as the center, in color 1 (blue). To prevent the formation of a monochromatic $F_{2,5}$ subgraph, we enforce the rule that for each $7\le i\le k+8$, there can be at most one edge utilizing color 1 in the set of edges $E\left(v_i,\{v_2,v_3,v_4,v_5,v_6\}\right)$. □

Claim 7.

In the scenario where any two edges originating from $v_1$ and connecting to vertices $\{v_7,v_8,...,v_{k+8}\}$ share a common color (excluding color 1), an intriguing outcome arises. It implies that graph $K_{k+8}$ will invariably encompass either a monochromatic $F_{2,5}$ subgraph or a captivating rainbow triangle.

Proof. 

We can prove this claim by employing a contradiction argument. Let us assume, without loss of generality, that $c(v_1,\{v_7,v_8\})=2$. In this case, we have a $C_4$ cycle in color 2, represented by $v_7{v}_i{v}_8{v}_j{v}_7$, where $i,j\in \{2,3,4,5,6\}$. This cycle, combined with vertices $\{v_1,v_2,v_3,v_4,v_5,v_6\}$, forms a monochromatic $F_{2,5}$ centered at either $v_7$ or $v_8$. This directly contradicts our assumption that the graph does not contain a monochromatic $F_{2,5}$. □

From the above claim, it is clear that graph $K_{k+8}$ contains a $K_{1,n}$ of color 1 (blue) where $n\ge 8$. This is illustrated in Figure 17.

Claim 8.

For each $7\le i\le k+5$, if $c(v_1,\left\{v_i\right\})=l$, where $2\le l\le k$, then there can only be color l in the set of edges $E\left(v_i,\{v_1,v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8}\}\right)$; otherwise, there exists a rainbow triangle or $F_{2,n}$.

Proof. 

Let us assume that $c(v_1,\left\{v_7\right\})=2$ and that there exists an edge, let us say $v_7{v}_2$, with a color $l^{\prime }$ different from 2 in the edge set

$$E(v_7,\{v_1,v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8}\}).$$

Case 1 (${\mathit{l}}^{\prime }\ne \mathbf{1}$): If $c\left(v_7{v}_2\right)=l^{\prime }$ and $l^{\prime }\ne 1$, then we can observe the presence of a rainbow triangle formed by vertices $v_1,v_7,v_2$.

Case 2 (${\mathit{l}}^{\prime }=\mathbf{1}$): If $c\left(v_7{v}_2\right)=l^{\prime }$ and $l^{\prime }=1$, then all the edges of color $l^{\prime }$ in the edge set

$$E(v_7,\{v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8}\})$$

must be present. This is because if a single edge of color other than 1 or 2 is present, a rainbow triangle is formed. On the other hand, if there is a single edge of color 1 in that set, a monochromatic $F_{2,n}$ with center $v_1$ would exist.

Based on the observations discussed above, we can determine the possible coloring of the graph, as shown in Figure 18 below.

By examining Figure 18, it becomes evident that any coloring of the edges connecting $v_2$ to $v_{k+6},v_{k+7},v_{k+8}$ would inevitably result in the formation of either a rainbow triangle or a monochromatic $F_{2,n}$. □

Claim 9.

If edge set $E(v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8})$ contains a ${\mathcal{P}}_3$ (path with three vertices) of color 1, then the graph will have a monochromatic $F_{2,n}$.

Proof. 

We can make the observation, from Figure 17, that the existence of a ${\mathcal{P}}_3$ (a path of order 3 ) of color 1 leads to the formation of a $C_4$ when combined with vertex $v_1$. Consequently, this results in a monochromatic $F_{2,5}$ centered at $v_1$. □

Claim 10.

The claim states that if edge set $E(v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8})$ contains a ${\mathcal{P}}_3$ (path with three vertices) of color l (excluding color 1), then $c(v_1,v_i)\ne l$ for $7\le i\le k+5$.

Proof. 

Let us assume that there exists a ${\mathcal{P}}_3$ (path with three vertices) of color l in the given edge set, where l is any color except 1. This $P_3$ can be denoted by $v_p{v}_q{v}_r$, where $v_p,v_q,v_r$ are distinct vertices in the set $v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8}$.

Let us suppose, for contradiction, that $c(v_1,v_i)=l$ for some i where $7\le i\le k+5$. This means that there exists an edge of color l between $v_1$ and $v_i$. Now, let us consider the subgraph formed by vertices $v_i,v_p,v_q,v_r$. This subgraph contains a monochromatic $C_4$. From Claim 8, we can deduce that all the edges from $v_i$ to $v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8}$ are of color l. This implies that there exists a monochromatic $F_{2,n}$ with cycle $v_i{v}_p{v}_q{v}_r$ and center $v_i$. This contradicts our assumption that the graph does not contain a monochromatic $F_{2,n}$.

Therefore, we conclude that $c(v_1,v_i)\ne l$ for $7\le i\le k+5$, as claimed. □

Claim 11.

If there exists an edge of color l (excluding color 1) in edge set $E(v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8})$, then for any $7\le i\le k+5$, we have $c(v_1,v_i)\ne l$.

Proof. 

Let us assume that there exists an edge $v_p{v}_q$ of color l in edge set $E(v_2,v_3,v_4,v_5,v_6,$$v_{k+6},v_{k+7},v_{k+8})$. We want to show that $c(v_1,v_i)\ne l$ for any $7\le i\le k+5$.

Since edge $v_p{v}_q$ has color l, without loss of generality, let us assume that $c(v_1,v_i)=l$. Now, let us consider vertex $v_i$. According to Claim 8, all the edges from $v_i$ to vertices $v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8}$ are of color l. Furthermore, we can observe that any coloring of the edges from $v_p$ and $v_q$ to $(v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8})-\{v_p,v_q\}$ would result in either a monochromatic $F_{2,5}$ or a rainbow triangle, both of which contradict our assumption.

However, this contradicts the assumption that the graph should not contain a monochromatic $F_{2,5}$. Therefore, we can conclude that $c(v_1,v_i)\ne l$ for any $7\le i\le k+5$.

Thus, the claim is proven. □

Claim 12.

If $c(v_1,v_i)=l$ and $c(v_1,v_j)=l^{\prime }$, where $i\ne j$ and $l\ne l^{\prime }$, then $c(v_i,v_j)=l$ or $c(v_i,v_j)=l^{\prime }$.

Proof. 

Let us assume that $c(v_1,v_i)=l$ and $c(v_1,v_j)=l^{\prime }$. Since $v_i\ne v_j$ and $l\ne l^{\prime }$, the only possible colors for edge $v_i{v}_j$ are l and $l^{\prime }$. This is because if edge $v_i{v}_j$ is colored with any other color, it would form a rainbow triangle with edges $v_1{v}_i$ and $v_1{v}_j$, which contradicts our assumption.

Therefore, we can conclude that $c(v_i,v_j)=l$ or $c(v_i,v_j)=l^{\prime }$. □

Claim 13.

The set of edges $E(v_1,v_7,v_8,v_3,\dots ,v_{k+4},v_{k+5})$ can have at most $k-2$ distinct colors, and any color other than 1 can be assigned to at most one edge.

Proof. 

The edge set $E(v_2,v_3,v_4,v_5,v_6,v_{k+6},v_{k+7},v_{k+8})$ must have at least two colors other than 1; otherwise, there would exist a monochromatic $F_{2,5}$ in the graph. Hence, by applying Claim 11, we can conclude that the given edge set can have at most $k-2$ distinct colors. □

By using all the above claims and Lemma 2, the critical k - coloring of $K_{k+8}$ is as follows:

• $c(v_1,v_i)=1,\mathit{if}i\in \{2,3,4,5,6,k+4,k+5,k+6,k+7,k+8\}.$
• $c(v_j,v_k)=l\mathit{and}c(v_j,v_i)=l,\mathit{if}c(v_1,v_j)=l,\mathit{where}j<k\mathit{and}j,k\in \{7,8,\dots k+2,k+3\},\mathit{and}l\in \{2,3,\dots k-3,k-2\}.$
• The coloring of the subgraph induced by vertices $v_1,v_2,v_3,v_4,v_5,v_6,v_{k+4},v_{k+5},v_{k+6},v_{k+7},v_{k+8}$ by using colors 1, k-1, and k can be performed in a similar manner as shown in Lemma 2.

Thus, it becomes evident that when considering a vertex v, a maximum of $k-2$ additional edges can be introduced in the critical k-coloring of $K_{k+8}$, such that $k-3$ edges satisfy $c(v,v_j)=c(v_j,v_1)$, where j belongs to $\{7,8,\dots ,k+2,k+3\}$, and one more edge can be attached from v to any vertex from the remaining vertices of $K_{k+8}$. This construction ensures that the resulting graph does not contain either a rainbow triangle or a monochromatic $F_{2,5}$.

As a consequence, it follows that every k-coloring of the edges of $K_{k+9}\cup K_{1,k-1}$ invariably comprises either a rainbow triangle or a monochromatic $F_{2,5}$, demonstrating the critical nature of the graph.

4. Conclusions

In conclusion, this research study helps us better understand Ramsey numbers for cycles with pendant edges. By studying different types of Ramsey numbers, including Gallai–Ramsey and star-critical Ramsey numbers, we have established upper and lower bounds that provide deeper insights into these graph properties. Our findings highlight important connections between cycle structures and Ramsey numbers, providing a solid foundation for future research. These results not only build on existing Ramsey theory but also encourage further studies on more complex graphs. Future research could extend these ideas to other graph families, such as sun graphs and comb graphs [27]. Additionally, exploring star-critical connected Ramsey numbers [28] for the graphs studied in this article may reveal more about structural limitations and general patterns in Ramsey theory.