How Can Viruses Affect the Growth of Zooplankton on Phytoplankton in a Chemostat?
Abstract
1. Introduction
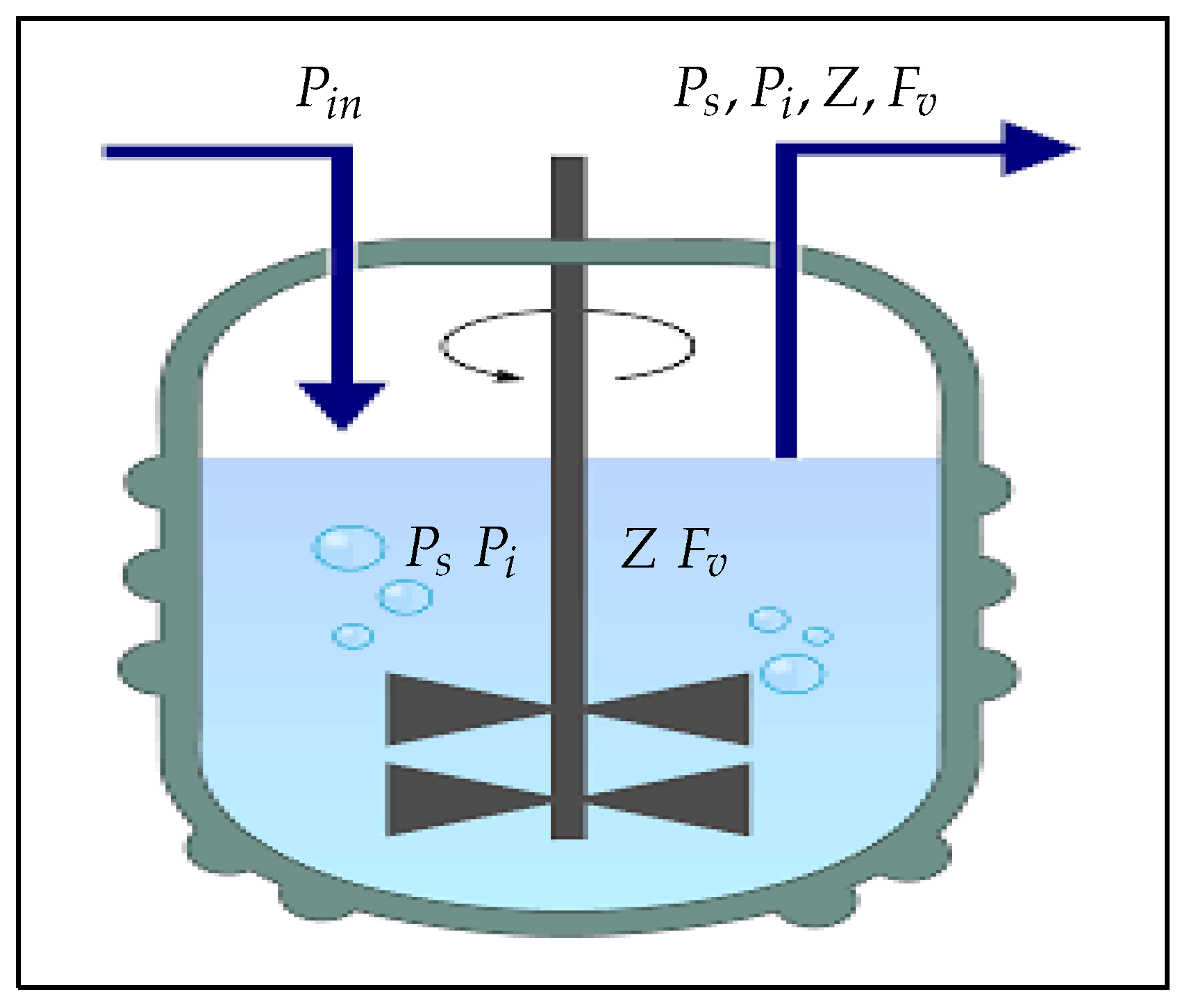
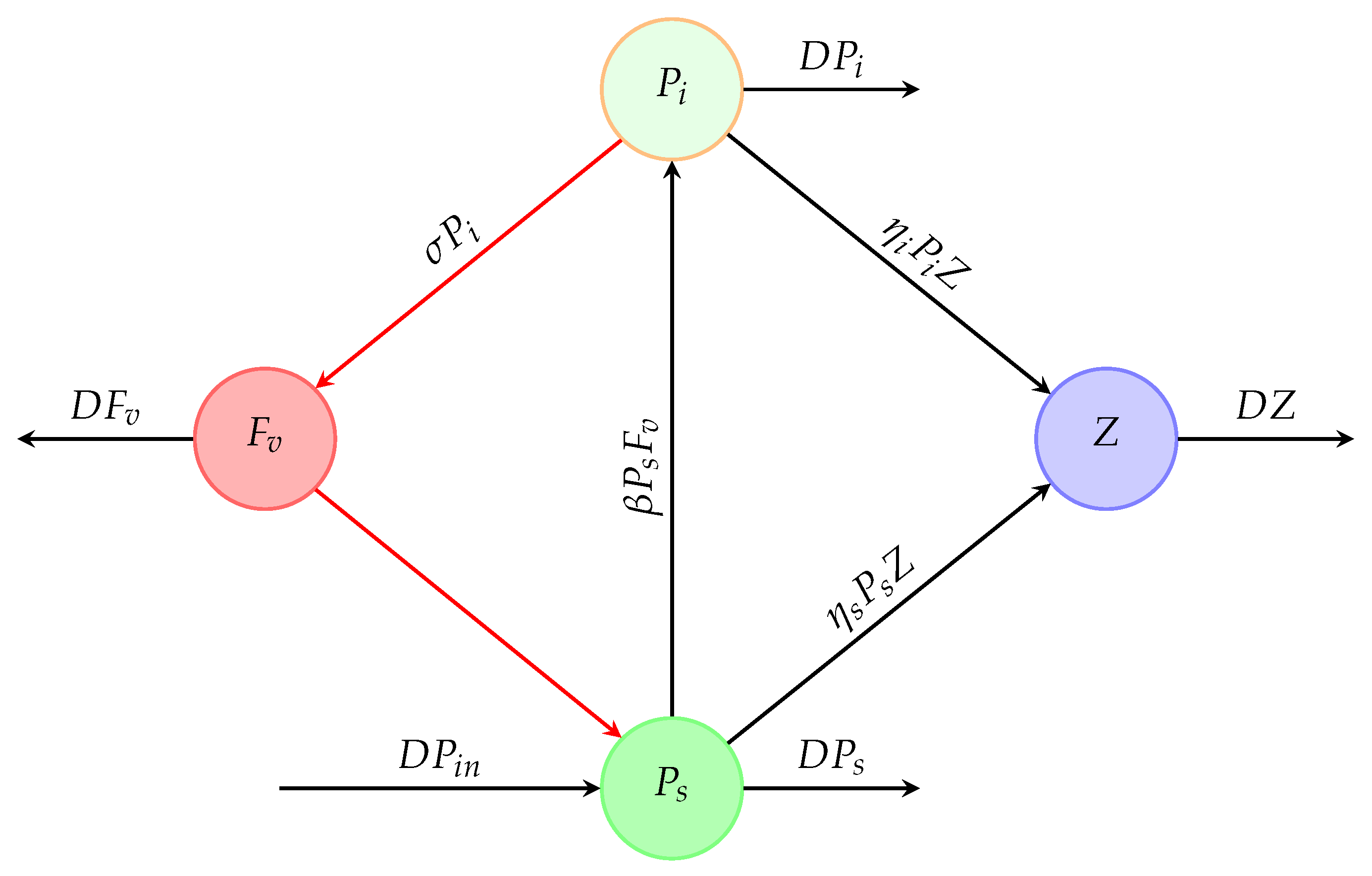
2. Mathematical Modeling
- The susceptible phytoplankton enter into the chemostat at a constant input concentration, .
- The susceptible phytoplankton become infected through direct contact with free viruses, , living in the system, with a transmission rate of .
- The zooplankton grow on susceptible and infected phytoplankton. The susceptible phytoplankton are consumed by the zooplankton Z at a rate of ; however, the infected phytoplankton are consumed by the zooplankton Z at a rate of .
- Let us denote by the virus replication factor in the infected phytoplankton , i.e., the lysis of infected phytoplankton, producing virus particles on average ().
- A1 .
- A2 .
3. Mathematical Results
3.1. The Ecosystem Without Free Viruses
- 1.
- There are no periodic orbits nor polycycles inside .
- 2.
- If (Assumptions A1–A2), then the equilibrium point exists and it is globally asymptotically stable, and is a saddle point.
- 3.
- If , then the equilibrium point is the unique equilibrium point of system (4), and it is globally asymptotically stable.
- Let be a solution of (4) inside . By using the change in variables and , we obtain the following equations:The divergence of system (4) is given by
- For (Assumptions A1–A2), exists and the Jacobian matrix at is given bySince trace and det , both eigenvalues have a negative real part, and the equilibrium point is therefore a locally asymptotically stable node. The Jacobian matrix evaluated at is therefore given byadmits two eigenvalues that are given byTherefore, the equilibrium is a saddle point with a stable manifold given by . Let and . By applying the Poincaré–Bendixon Theorem [40], the steady state is found to be globally asymptotically stable.
- If , then is the only steady state and is locally stable. Since any omega limit set is contained in the two-dimensional compact invariant set , and lies on the boundary of , is globally asymptotically stable according to the Poincaré-Bendixson Theorem.
3.2. The Complete System
- If , then we obtain a pure epidemic model with a steady state satisfyingThen, , and with . Therefore, we obtain two equilibrium points, and .The development of new infections and changes in the status of infected individuals are described by two equations in our example (Equations (2) and (4) in system (1)). We define the matrix F to represent the rate at which new infections develop in these two equations and V to represent the rate at which individuals are transferred into and out of these compartments by all other mechanisms in order to create the next generation matrix. Next, the non-singular matrix V and the nonnegative matrix F are provided by and . Therefore, . The spectral radius of the next generation matrix FV−1, which can be represented as follows, is the basic reproduction number of (1).Note that . Therefore, exists only if .The Jacobian matrix at is given bywhere its characteristic polynomial is given byadmits , , according to Assumptions A1 and A2, and . Therefore, is an unstable equilibrium point.The Jacobian matrix at is given byThe characteristic polynomial is given byNote thatTherefore, if , then exists, and its Jacobian, , admits three negative eigenvalues and one positive eigenvalue, and thus is an unstable equilibrium point.
- If , then we havewith . We obtain two cases: The first case corresponds to the free viruses satisfying , , , and thus . The disease-free equilibrium point is given by . The second case satisfies . Therefore, , , and . We obtain the endemic equilibrium point that is given by . We aim to define the basic reproduction number again. Both the non-singular matrix V and the nonnegative matrix F are provided by and . Therefore, . The spectral radius of (1) is the spectral radius of the next generation matrix FV−1, expressed as follows:Note that in a population where all phytoplankton are vulnerable to infection in the presence of zooplankton, the basic reproduction number, or , is the anticipated number of instances directly caused by one infected phytoplankton.Let be the Jacobian matrix at .The characteristic polynomial of is given byNote that . Therefore, if , then exists, and its Jacobian, , admits three negative eigenvalues (according to Assumptions A1–A2) and one positive eigenvalue, and thus is an unstable equilibrium point. is a stable equilibrium point only if .Let us discuss the existence and stability of the endemic equilibrium point . Note that means that . Furthermore, we have and . Therefore, if , then , and thus exists. Let be the Jacobian matrix at , which is given byThe characteristic polynomial of is given bywhere ,, , and . In order to use the Routh–Hurwitz criteria, one must see that and deduce that because . The calculation of the two other conditions was too large, so we used Maple 12 software to verify that and , and thus we obtained the local stability of the equilibrium point once it exists ().
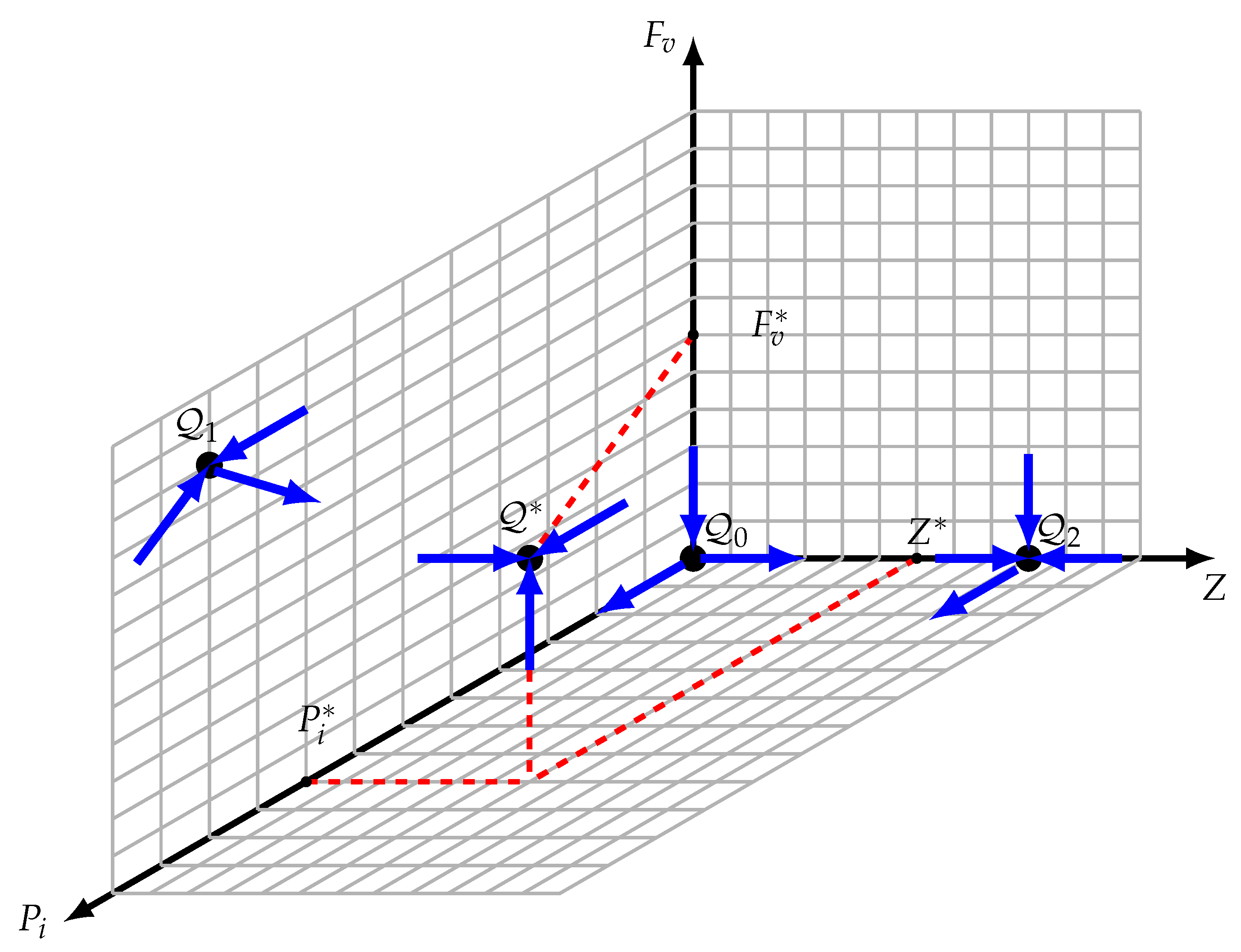
3.3. Reduction to 3D
3.4. The Periodic Orbits on the Faces
- It is easy to see that the axes and are invariant. By applying the following change in the notations and for , one obtains the following model:
- It is easy to see that the axes and are invariant. By applying the following change in the notations and for , one obtains the following model:
3.5. Persistence
- The omega limit set of , represented as , is assumed to include . It should be noted that is a saddle point with a dimension of one stable manifold, , that is limited to the -axis. In this case, is not the whole omega limit set . There is a point, , in , according to the Butler–McGehee lemma [40]. Note that the -axis is unbounded, but that is the -axis. The omega limit set of any orbit of the system (11) should be bounded since all of its orbits are bounded (within the limited set ). The existence of is contradicted by this. Consequently, should be confirmed.
- is assumed. Likewise, should not be the complete omega limit set ; hence, there is a point, , inside . Once is two-dimensional and completely contained in the face, this point should be inside the face. should contain the whole orbit via , just like in the cases of and . In Section 3.4, we demonstrated that there are no possible periodic orbits inside the face. The orbit becomes unbounded once , which runs counter to the assertion that is inside .
- is assumed. Given that is a saddle point, its stable manifold is limited to the plane and has two dimensions. Consequently, is not the whole omega limit set . Accordingly, a point, , exists inside according to the Butler–McGehee lemma [40]. Since lies entirely in the plane, and since the entire orbit through is in , this orbit is thus unbounded, which contradicts the fact that is inside .
3.6. Uniform Persistence of System (7)
- The dynamics are weakly persistent;
- The dynamics are dissipative;
- The restriction of to is isolated;
- The restriction of to is acyclic.
3.7. Uniform Persistence of System (1)
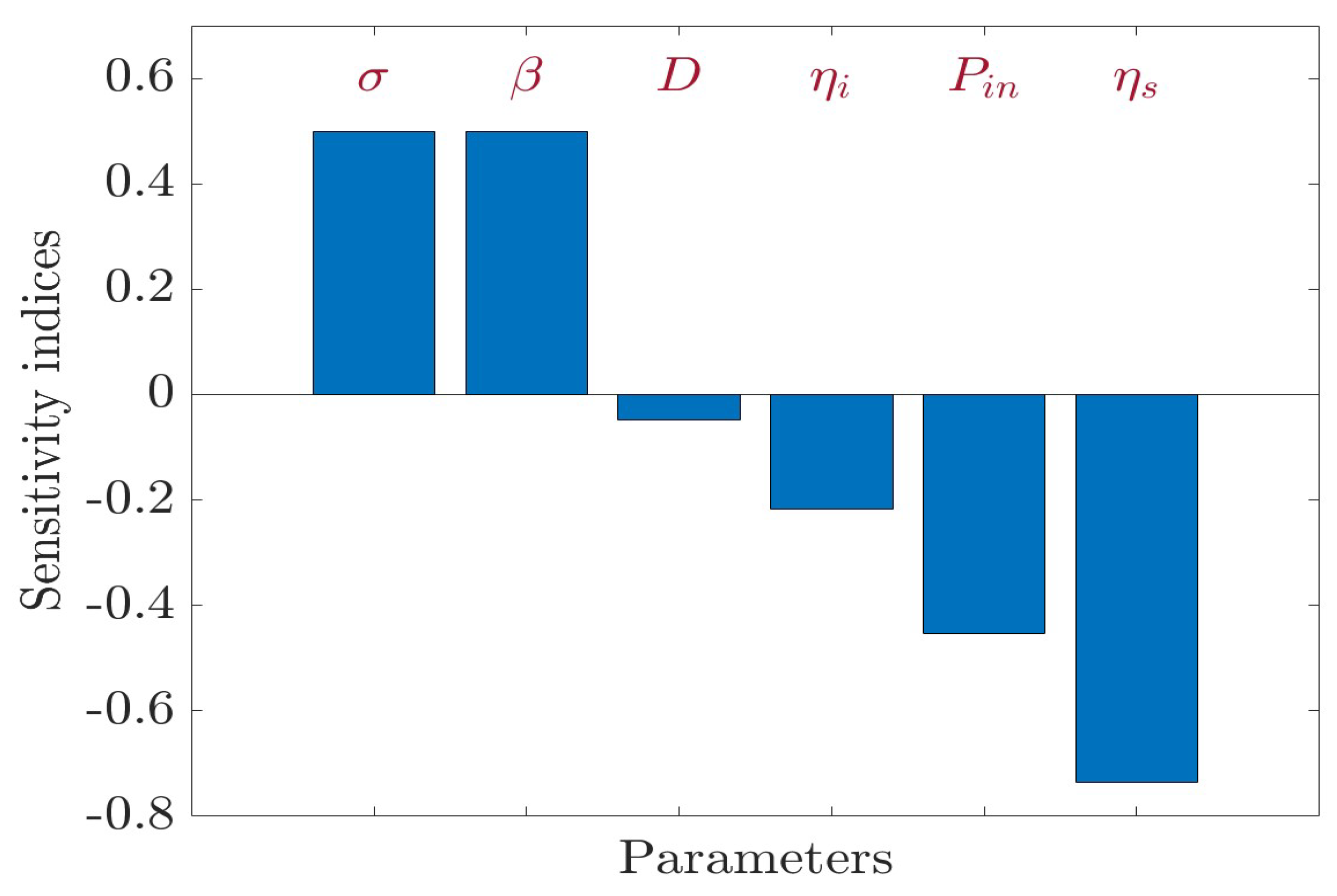
4. Sensitivity Analysis
5. Optimal Control Strategy
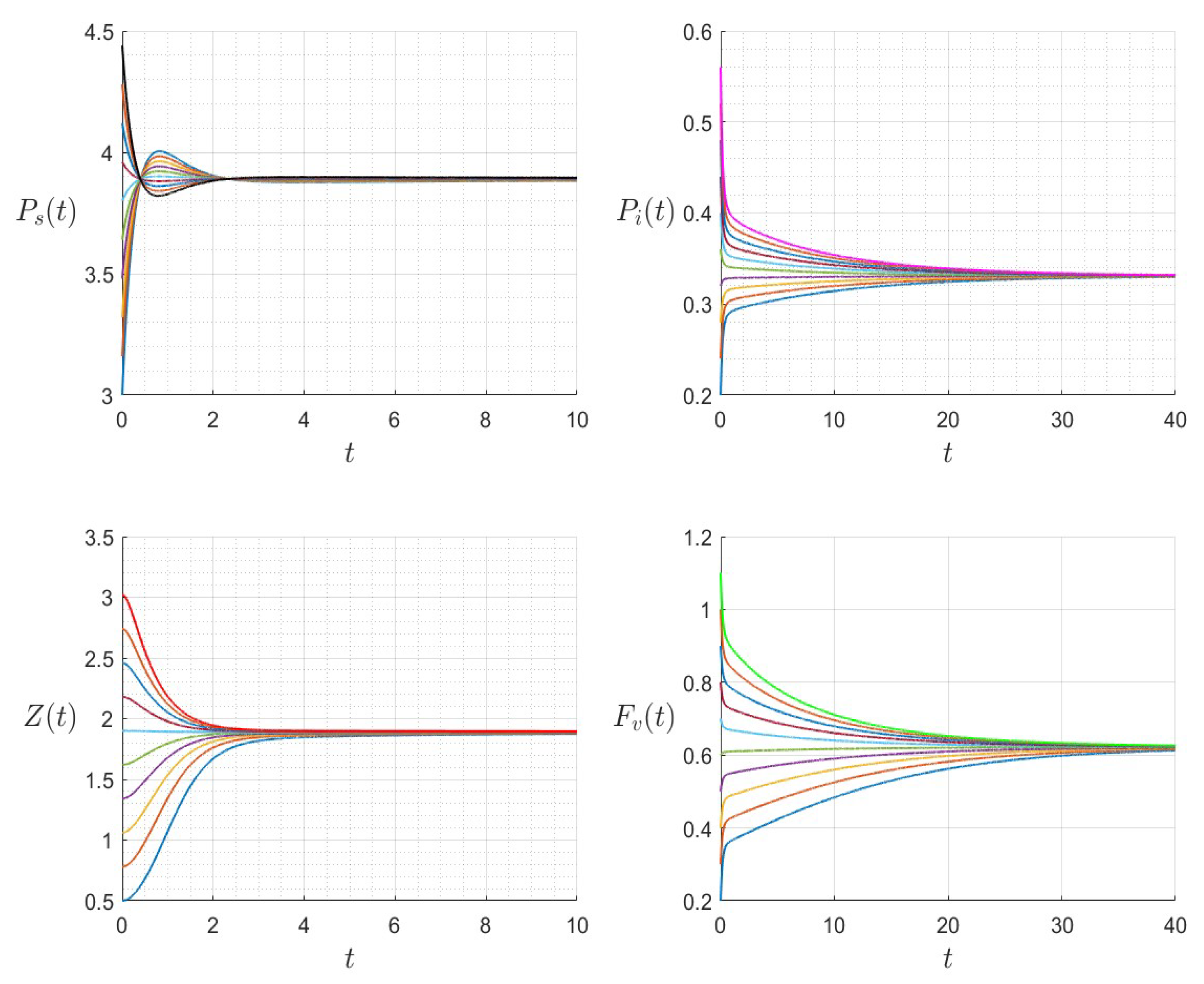
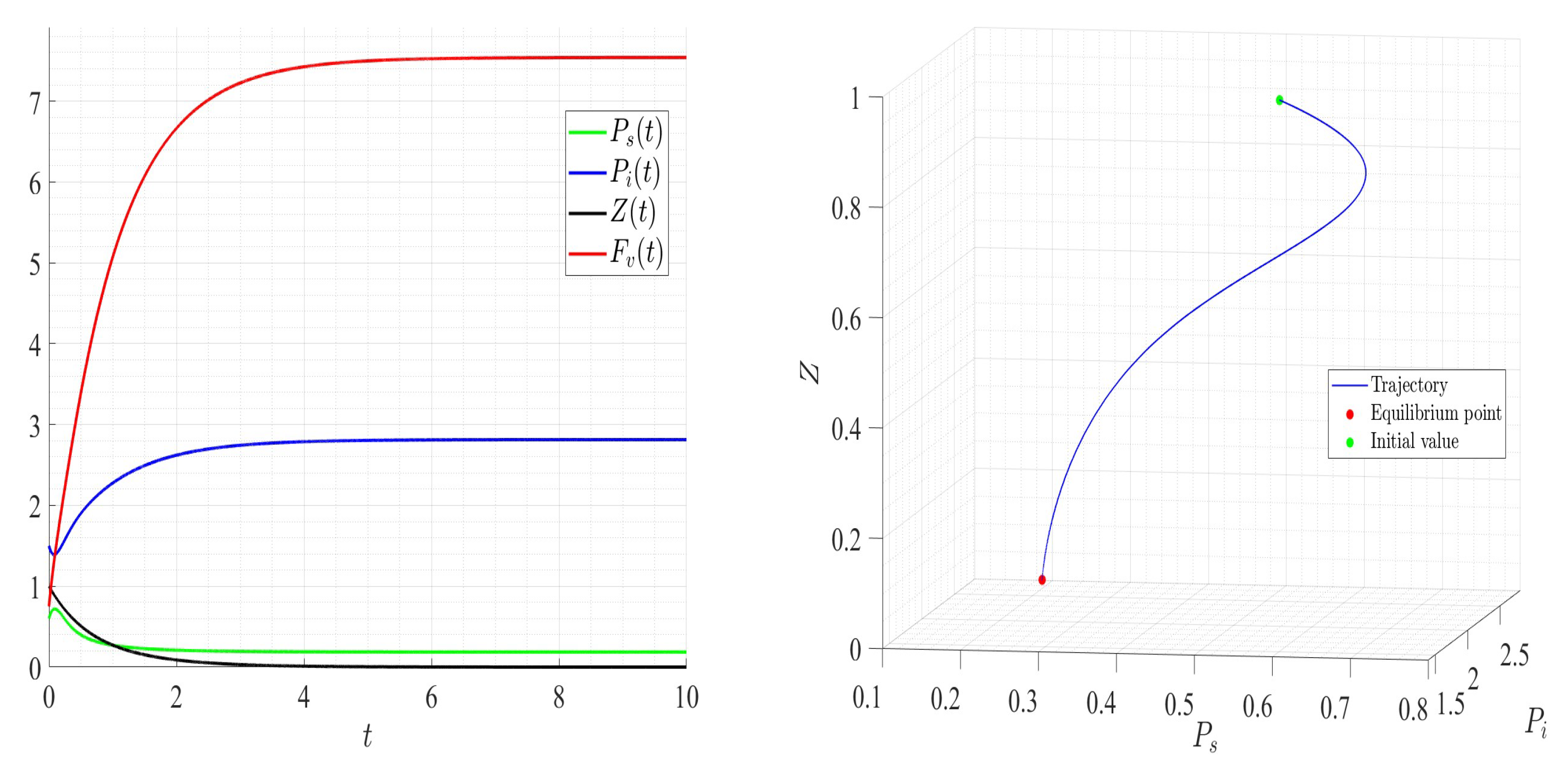
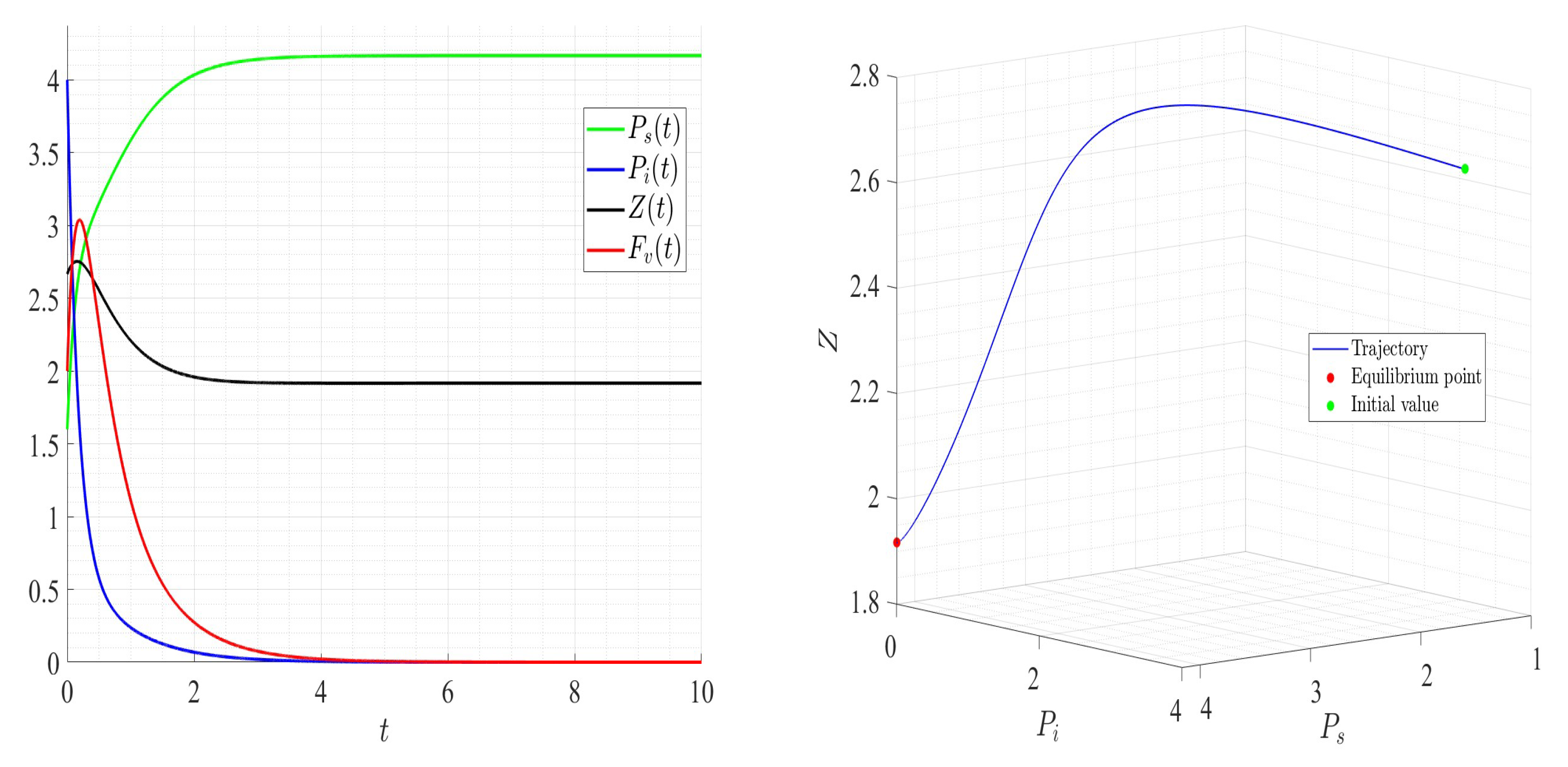
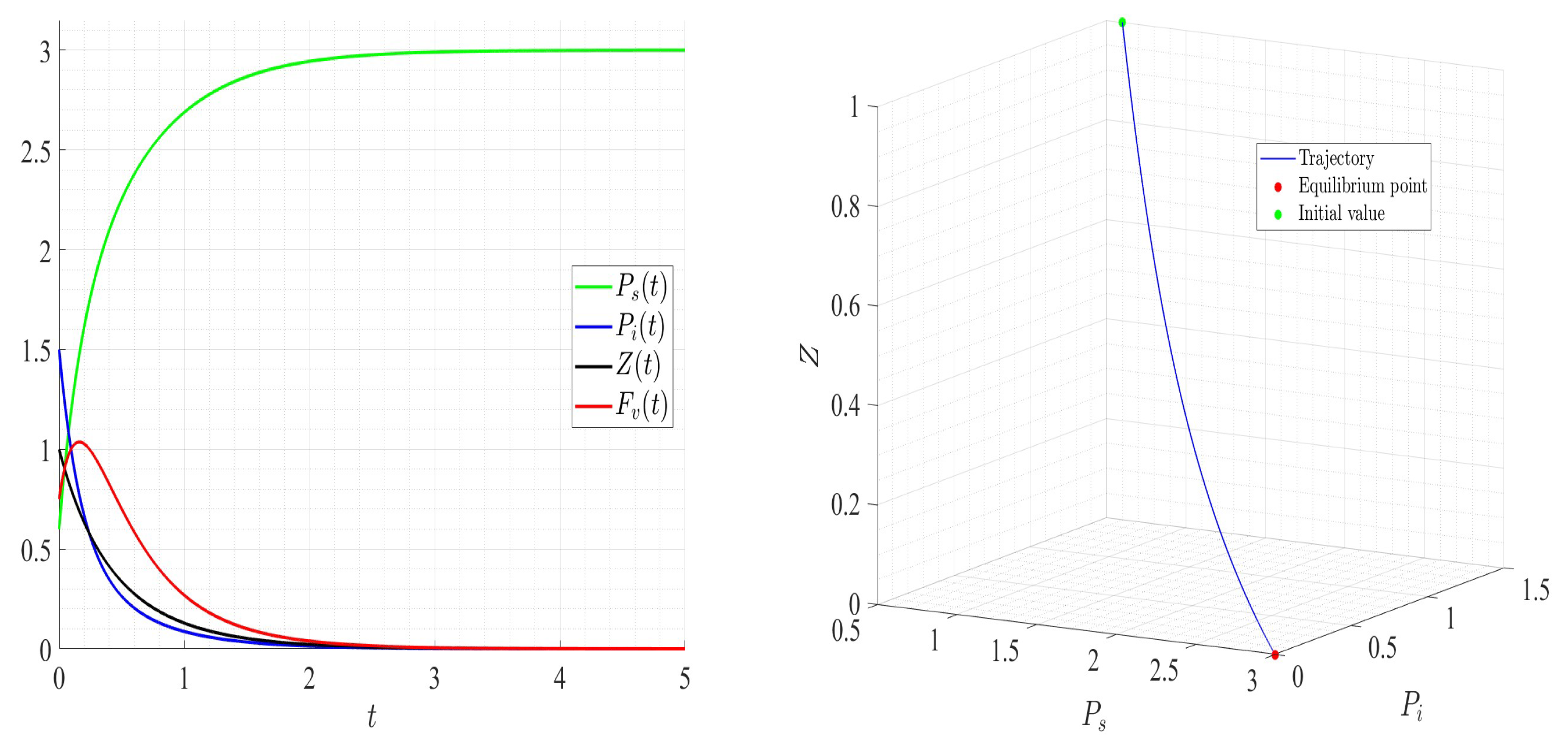
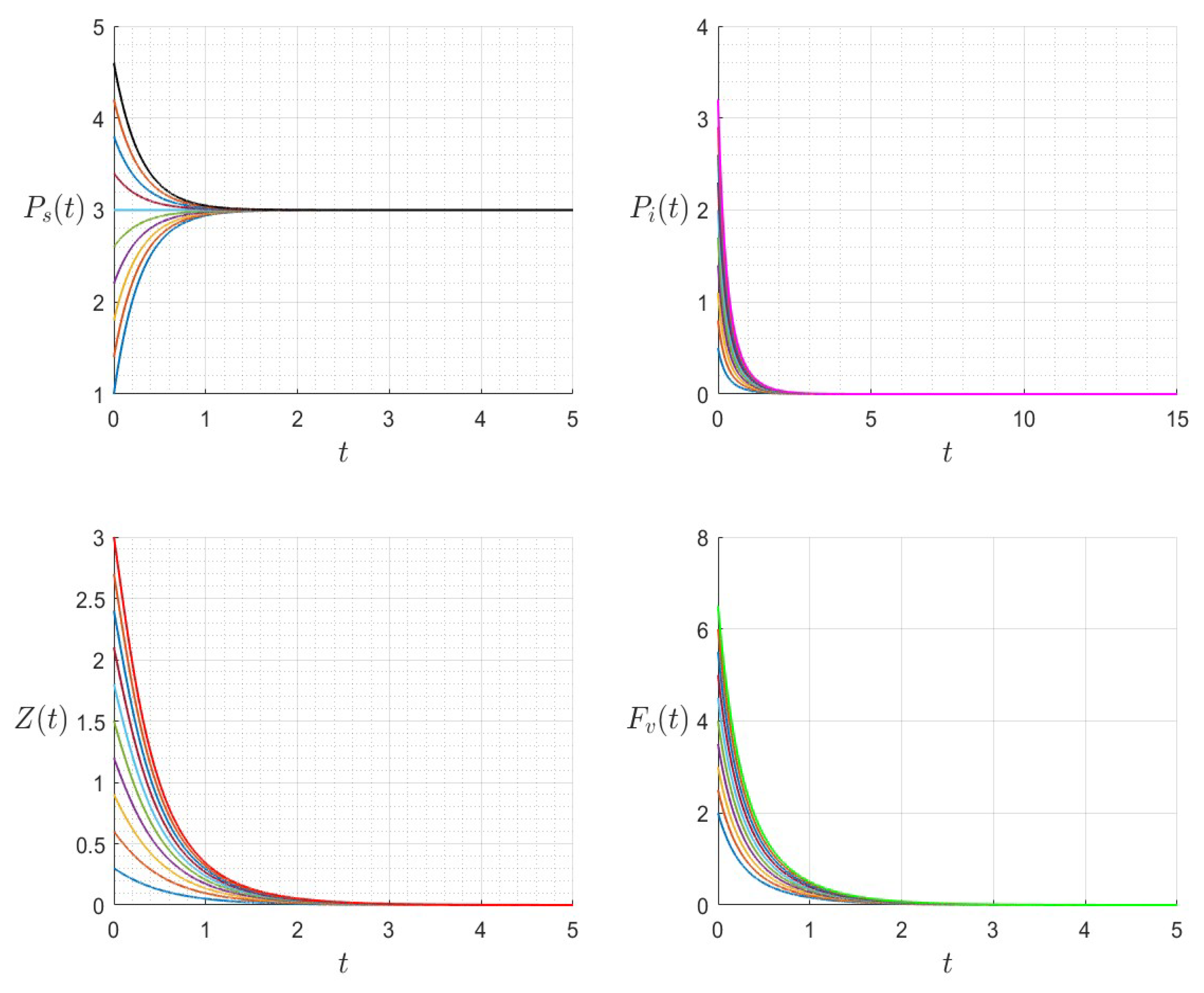
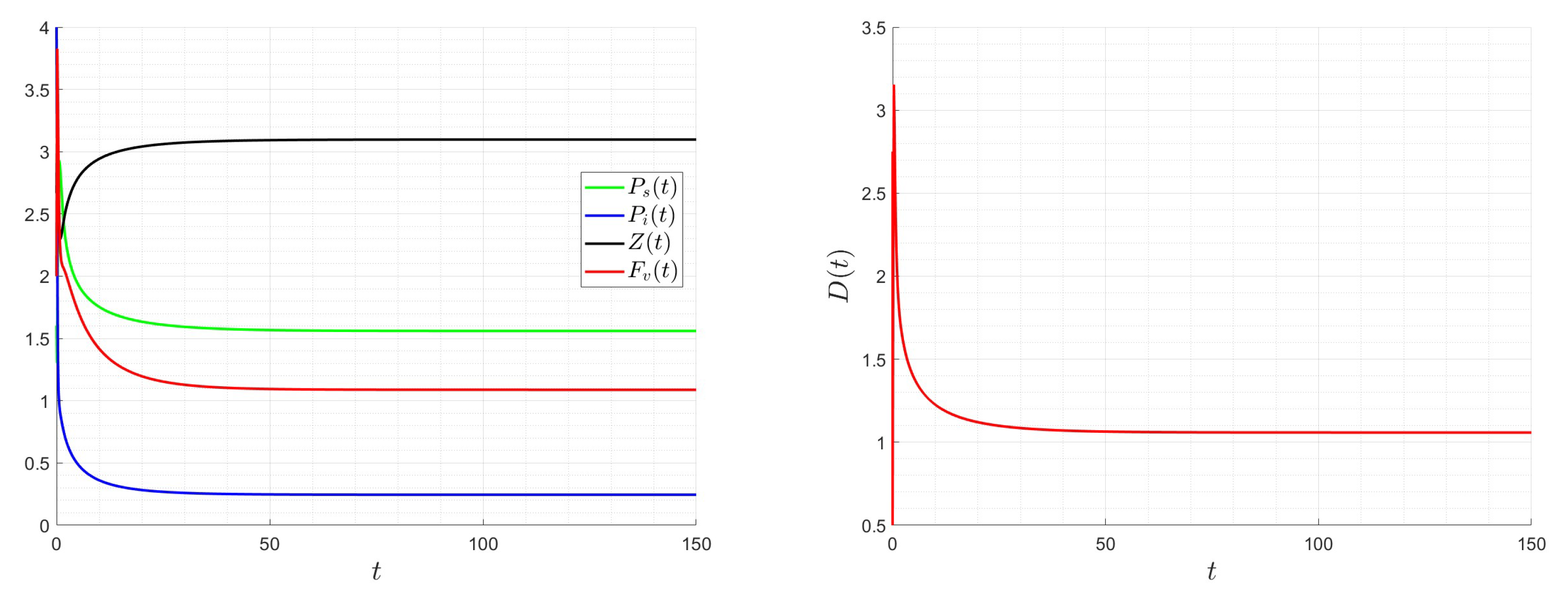
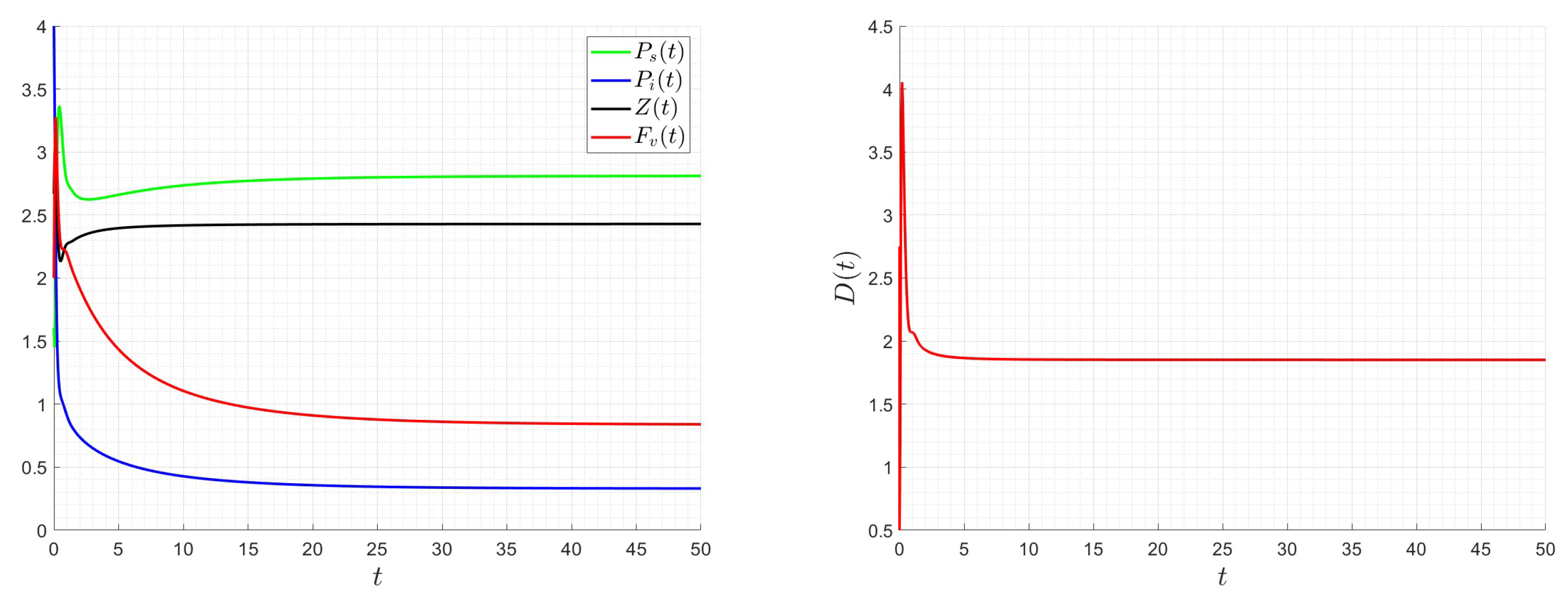
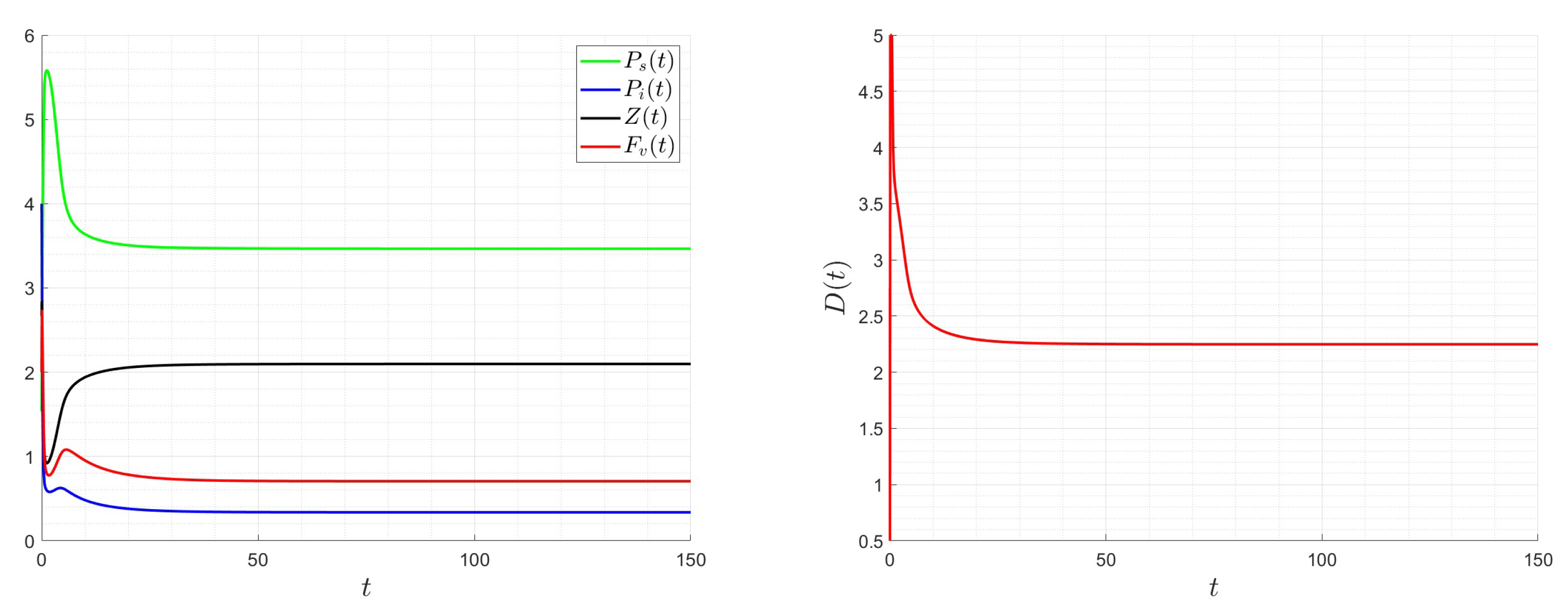
6. Numerical Investigations
6.1. Direct Problem
6.2. Optimal Control Problem
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. A Suitable Numerical Scheme for Resolving the Control Problem
References
- Lafferty, K.D.; Morris, A.K. Altered Behavior of Parasitized Killifish Increases Susceptibility to Predation by Bird Final Hosts. Ecology 1996, 77, 1390–1397. [Google Scholar] [CrossRef]
- Brooks, J.L.; Dodson, S.I. Predation, Body Size, and Composition of Plankton. Science 1965, 150, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Leibold, W. Biodiversity and nutrient enrichment in pond plankton communities. Evol. Ecol. Res. 1999, 1, 73–95. [Google Scholar]
- DeMott, W. Optimal foraging theory as a predictor of chemically mediated food selection by suspension-feeding copepods. Limnol. Oceanogr. 1989, 34, 140–154. [Google Scholar]
- Mitra, A.; Castellani, C.; Gentleman, W.C.; Jonasdottir, S.H.; Flynn, K.J.; Bode, A.; Halsband, C.; Kuhn, P.; Licandro, P.; Agersted, M.D.; et al. Bridging the gap between marine biogeochemical and fisheries sciences; configuring the zooplankton link. Prog. Oceanogr. 2014, 129, 176–199. [Google Scholar] [CrossRef]
- De Troch, M.; Grego, M.; Chepurnov, V.A.; Vincx, M. Food patch size, food concentration and grazing efficiency of the harpacticoid Paramphiascella fulvofasciata (Crustacea, Copepoda). J. Exp. Mar. Biol. Ecol. 2007, 343, 210–216. [Google Scholar] [CrossRef]
- DeMott, W.R. Discrimination between algae and artificial particles by freshwater and marine copepods. Limnol. Oceanogr. 1988, 33, 397–408. [Google Scholar] [CrossRef]
- Pal, J.; Bhattacharya, S.; Chattopadhyay, J. Does predator go for size selection or preferential toxic-nontoxic species under limited resource? OJBS 2010, 10, 11–16. [Google Scholar]
- Aberle, N.; Hillebrand, H.; Grey, J.; Wiltshire, K.H. Selectivity and competitive interactions between two benthic invertebrate grazers (Asellus aquaticus and Potamopyrgus antipodarum): An experimental study using 13C-and 15N-labelled diatoms. Freshwater Biol. 2005, 50, 369–379. [Google Scholar] [CrossRef]
- Danielsdottir, M.G.; Brett, M.T.; Arhonditsis, G.B. Phytoplankton food quality control of planktonic food web processes. Hydrobiologia 2007, 589, 29–41. [Google Scholar]
- Huntley, M.; Sykes, P.; Rohan, S.; Marin, V. Chemically-mediated rejection of dinoflagellate prey by the copepods Calanus pacificus and Paracalanus parvus: Mechanism, occurrence and significance. Mar. Ecol. Prog. Ser. 1986, 28, 105–120. [Google Scholar] [CrossRef]
- Fulton, R.S., III; Paerl, H. Effects of colonial morphology on zooplankton utilization of algal resources during blue-green algal (Microcystis aeruginosa) blooms. Limnol. Oceanogr. 1987, 32, 634–644. [Google Scholar] [CrossRef]
- Paffenhofer, G.A.; Sant, K.B.V. The feeding response of a marine planktonic copepod to quantity and quality of particles. Mar. Ecol. Prog. Ser. 1985, 27, 55–65. [Google Scholar] [CrossRef]
- Evans, C.; Pond, D.W.; Wilson, W.H. Changes in Emiliania huxleyi fatty acid profiles during infection with E. huxleyi virus 86: Physiological and ecological implications. Aquat. Microb. Ecol. 2009, 55, 219–228. [Google Scholar] [CrossRef]
- Bratbak, G.; Egge, J.K.; Heldal, M. Viral mortality of the marine alga Emiliania huxleyi (Haptophyceae) and termination of algal blooms. Mar. Ecol. Prog. Ser. 1993, 93, 39–48. [Google Scholar] [CrossRef]
- Evans, C.; Wilson, W. Preferential grazing of Oxyrrhis marina on virus infected Emiliania huxleyi. Limnol. Oceanogr. 2008, 53, 2035–2040. [Google Scholar] [CrossRef]
- Vermont, A.; Martnez, J.M.; Waller, J.D.; Gilg, I.C.; Leavitt, A.H.; Floge, S.A.; Archer, S.D.; Wilson, W.H.; Fields, D.M. Virus infection of Emiliania huxleyi deters grazing by the copepod Acartia tonsa. J. Plankton Res. 2016, 38, 1194–1205. [Google Scholar] [CrossRef]
- Townsend, D.W.; Keller, M.D.; Holligan, P.M.; Ackleson, S.G.; Balch, W.M. Blooms of the coccolithophore Emiliania huxleyi with respect to hydrography in the Gulf of Maine. Cont. Shelf Res. 1994, 14, 979–1000. [Google Scholar] [CrossRef]
- Wilson, W.H.; Tarran, G.A.; Schroeder, D.; Cox, M.; Oke, J.; Malin, G. Isolation of viruses responsible for the demise of an Emiliania huxleyi bloom in the English Channel. J. Mar. Biol. Assoc. U. K. 2002, 82, 369–377. [Google Scholar] [CrossRef]
- Evans, C.; Kadner, S.V.; Darroch, L.J.; Wilson, W.H.; Liss, P.S.; Malin, G. The relative significance of viral lysis and microzooplankton grazing as pathways of dimethylsulfoniopropionate (DMSP) cleavage: An Emiliania huxleyi culture study. Limnol. Oceanogr. 2007, 52, 1036–1045. [Google Scholar] [CrossRef]
- Strom, S.; Wolfe, G.; Holmes, J.; Stecher, H.; Shimeneck, C.; Sarah, L. Chemical defense in the microplankton I: Feeding and growth rates of heterophic protists on the DMS-producing phytoplankter Emiliania huxleyi. Limnol. Oceanogr. 2003, 48, 217–229. [Google Scholar] [CrossRef]
- Wolfe, G.V.; Steinke, M. Grazing-activated production of dimethyl sulfide (DMS) by two clones of Emiliania huxleyi. Limnol. Oceanogr. 1996, 41, 1151–1160. [Google Scholar] [CrossRef]
- Steinke, M.; Malin, G.; Liss, P.S. rophic interaction in the sea: An ecological role for climate relevant volatiles? J. Phycol. 2002, 38, 630. [Google Scholar] [CrossRef]
- Beretta, E.; Kuang, Y. Modeling and analysis of a marine bacteriophage infection. Math. Biosci. 1998, 149, 57–76. [Google Scholar] [CrossRef] [PubMed]
- Beltrami, E.; Carroll, T. Modeling the role of viral disease in recurrent phytoplankton blooms. J. Math. Biol. 1994, 32, 857–863. [Google Scholar] [CrossRef]
- Gakkhar, S.; Negi, K. A mathematical model for viral infection in toxin producing phytoplankton and zooplankton system. Appl. Math. Comp. 2006, 179, 301–313. [Google Scholar] [CrossRef]
- Chattopadhyay, J.; Pal, S. Viral infection on phytoplankton-zooplankton system: A mathematical model. Ecol. Model. 2002, 151, 15–28. [Google Scholar] [CrossRef]
- Samanta, S.; Dhar, R.; Pal, J.; Chattopadhyay, J. Effect of enrichment on plankton dynamics where phytoplankton can be infected from free viruses. Nonlinear Stud. 2013, 20, 223–236. [Google Scholar]
- Bairagi, N.; Roy, P.K.; Sarkar, R.R.; Chattopadhyay, J. Virus replication factor may be a controlling agent for obtaining disease-free system in a multi-species eco-epidemiological system. J. Biol. Syst. 2005, 13, 245–259. [Google Scholar] [CrossRef]
- Bairagi, N.; Adak, D. Complex dynamics of a predator-prey-parasite system: An interplay among infection rate, predator’s reproductive gain and preference. Ecol. Compl. 2015, 22, 1–12. [Google Scholar] [CrossRef]
- Bairagi, N.; Saha, S.; Chaudhuri, S.; Dana, S.K. Zooplankton selectivity and nutritional value of phytoplankton influences a rich variety of dynamics in a plankton population model. Phy. Rev. E 2019, 99, 012406. [Google Scholar]
- Antweiler, R.C.; Patton, C.J.; Taylor, H.E. Nutrients. In Chemical Data for Water Samples Collected During Four Upriver Cruises on the Mississippi River Between New Orleans, Louisiana, and Minneapolis, Minnesota, May 1990–April 1992; Moody, J.A., Ed.; U.S. Geological Survey Open-File Report 94-523; U.S. Geological Survey: Reston, VA, USA, 1995; pp. 89–125. [Google Scholar]
- Bester, K.; Hhnerfuss, H.; Brockmann, U.; Rick, H.J. Biological effects of triazine herbicide contamination on marine phytoplankton. Arch. Environ. Contam. Toxicol. 1995, 29, 277–283. [Google Scholar]
- Rueter, J.R.; Chisholm, S.W.; Morel, F. Effects of copper toxicity on silicon acid uptake and growth in Thalassiosira pseudonana. J. Phycol. 1981, 17, 270–278. [Google Scholar]
- Biswas, S.; Tiwari, P.K.; Kang, Y.; Pal, S. Effects of zooplankton selectivity on phytoplankton in an ecosystem affected by free-viruses and environmental toxins. Math. Biosci. Eng. 2020, 17, 1272–1317. [Google Scholar] [CrossRef] [PubMed]
- Alsolami, A.A.; El Hajji, M. Mathematical Analysis of a Bacterial Competition in a Continuous Reactor in the Presence of a Virus. Mathematics 2023, 11, 883. [Google Scholar] [CrossRef]
- Albargi, A.H.; El Hajji, M. Bacterial Competition in the Presence of a Virus in a Chemostat. Mathematics 2023, 11, 3530. [Google Scholar] [CrossRef]
- El Hajji, M. Influence of the presence of a pathogen and leachate recirculation on a bacterial competition. Int. J. Biomath. 2024. Online ready. [Google Scholar] [CrossRef]
- El Hajji, M.; Al-Subhi, A.Y.; Alharbi, M.H. Mathematical investigation for two-bacteria competition in presence of a pathogen with leachate recirculation. Int. J. Anal. Appl. 2024, 22, 45. [Google Scholar] [CrossRef]
- Smith, H.L.; Waltman, P. The Theory of the Chemostat. Dynamics of Microbial Competition; Cambridge Studies in Mathematical Biology; Cambridge University Press: Cambridge, UK, 1995; Volume 13. [Google Scholar] [CrossRef]
- Rana, S.; Samanta, S.; Bhattacharya, S.; Al-Khaled, K.; Goswami, A.; Chattopadhyay, J. The effect of nanoparticles on plankton dynamics: A mathematical model. BioSystems 2015, 127, 28–41. [Google Scholar] [CrossRef]
- Panja, P.; Mondal, S.K.; Jana, D.K. Effects of toxicants on phytoplankton-zooplankton-fish dynamics and harvesting. Chaos Solit. Fract. 2017, 104, 389–399. [Google Scholar]
- Yu, X.; Yuan, S.; Zhang, T. Survival and ergodicity of a stochastic phytoplankton-zooplankton model with toxin-producing phytoplankton in an impulsive polluted environment. Appl. Math. Comp. 2019, 347, 249–264. [Google Scholar]
- Thieme, H.R. Convergence results and a Poincaré-Bendixson trichotomy for asymptotically autonomous differential equations. J. Math. Biol. 1992, 30, 755–763. [Google Scholar] [CrossRef]
- Sobieszek, S.; Wade, M.J.; Wolkowicz, G.S.K. Rich dynamics of a three-tiered anaerobic food-web in a chemostat with multiple substrate inflow. Math. Biosci. Eng. 2020, 17, 7045–7073. [Google Scholar] [CrossRef] [PubMed]
- Butler, G.J.; Freedman, H.I.; Waltman, P. Uniformly persistent systems. Proc. Am. Math. Soc. 1986, 96, 425–429. [Google Scholar]
- Butler, G.; Wolkowicz, G. Predator-mediated coexistence in a chemostat: Coexistence and competition reversal. Math. Model. 1987, 8, 781–785. [Google Scholar] [CrossRef][Green Version]
- Chitnis, N.; Hyman, J.; Cushing, J. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar]
- Albargi, A.H.; El Hajji, M. Mathematical analysis of a two-tiered microbial food-web model for the anaerobic digestion process. Math. Biosci. Eng. 2023, 20, 6591–6611. [Google Scholar] [CrossRef]
- El Hajji, M. Mathematical modeling for anaerobic digestion under the influence of leachate recirculation. AIMS Math. 2023, 8, 30287–30312. [Google Scholar] [CrossRef]
- Fleming, W.; Rishel, R. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 1975. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman and Hall: Boca Raton, FL, USA, 2007. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F.; Trirogoff, K.N.; Neustadt, L.W. The Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar] [CrossRef]
- Labille, J.; Brant, J. Stability of nanoparticles in water. Nanomedicine 2010, 5, 985–998. [Google Scholar]
- Miao, A.J.; Schwehr, K.A.; Xu, C.; Zhang, S.J.; Luo, Z.; Quigg, A.; Santschi, P.H. The algal toxicity of silver engineered nanoparticles and detoxification by exopolymeric substances. Environ. Pollut. 2009, 157, 3034–3041. [Google Scholar] [CrossRef]
- Miller, R.J.; Bennett, S.; Keller, A.A.; Pease, S.; Lenihan, H. TiO2 nanoparticles are phototoxic to marine phytoplankton. PLoS ONE 2012, 7, e30321. [Google Scholar] [CrossRef] [PubMed]



| Variable | Description | Units |
|---|---|---|
| Concentration of susceptible phytoplankton | g phytoplankton/L | |
| Concentration of infected phytoplankton | g phytoplankton/L | |
| Concentration of zooplankton | g zooplankton/L | |
| Concentration of free viruses | g viruses/L | |
| Parameter | Description | Units |
| D | Dilution rate | h−1 |
| Consumption rate of susceptible phytoplankton | h−1 | |
| Consumption rate of infected phytoplankton | h−1 | |
| Susceptible phytoplankton input concentration | g phytoplankton/L | |
| Y | Phytoplankton-to-zooplankton yield coefficient | g zooplankton/g phytoplankton |
| Saturated incidence rate | new infections/h | |
| Virus replication factor | g infected phytoplankton/g virus |
| Parameter | Y | D | |||||
|---|---|---|---|---|---|---|---|
| Value | 8 |
| Parameter, p | Sensitivity Index, | Value |
|---|---|---|
| 0.5 | ||
| 0.5 | ||
| D | −0.0472 | |
| −0.217 | ||
| −0.4528 | ||
| −0.6712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuallem, N.A.; El Hajji, M. How Can Viruses Affect the Growth of Zooplankton on Phytoplankton in a Chemostat? Mathematics 2025, 13, 1192. https://doi.org/10.3390/math13071192
Almuallem NA, El Hajji M. How Can Viruses Affect the Growth of Zooplankton on Phytoplankton in a Chemostat? Mathematics. 2025; 13(7):1192. https://doi.org/10.3390/math13071192
Chicago/Turabian StyleAlmuallem, Nada A., and Miled El Hajji. 2025. "How Can Viruses Affect the Growth of Zooplankton on Phytoplankton in a Chemostat?" Mathematics 13, no. 7: 1192. https://doi.org/10.3390/math13071192
APA StyleAlmuallem, N. A., & El Hajji, M. (2025). How Can Viruses Affect the Growth of Zooplankton on Phytoplankton in a Chemostat? Mathematics, 13(7), 1192. https://doi.org/10.3390/math13071192






