Computational Construction of Sequential Efficient Designs for the Second-Order Model
Abstract
1. Introduction
2. Methodology
2.1. Derivation and Justification of Equation (2)
- k main effects ();
- two-factor interaction terms (, where );
- k quadratic terms (, for );
- A constant intercept term.
2.2. Initial Point Selection
- Ensuring good uniformity of distribution as the number of points (N) increases toward infinity.
- Achieving good distribution even for relatively small initial point sets.
- Providing a computationally efficient generation algorithm.
- Uniformly cover the design space, promoting a more representative exploration.
- Provide replicability, ensuring consistency in practical applications and enhancing the reproducibility of results.
2.3. Sequential Design Optimization
- Improved parameter estimation accuracy for both main effects and interaction terms.
- The retention of robust space coverage, critical for sequential design effectiveness.
2.4. Enhanced Robustness and Accuracy
2.5. Importance of the Quadratic Model
2.6. Summary of Contributions
- The incorporation of Sobol sequences for structured and robust initial design generation.
- The sequential addition of points based on trace minimization to balance statistical efficiency and space-filling properties.
- The comprehensive integration of the full quadratic regression model for capturing all relevant effects in high-dimensional settings.
- Enhanced robustness and accuracy through a focus on statistical efficiency and uniform design coverage.
2.7. Comparison with Adaptive Model-Based Frameworks
- Optimization Framework: Adaptive designs optimize the information matrix by incorporating uncertainty estimates (e.g., ), while the proposed method focuses on the deterministic optimization of the conditional trace.
- Space-Filling Properties: Traditional adaptive designs emphasize statistical efficiency but may neglect space-filling considerations, particularly in non-parametric settings. The proposed method explicitly integrates Sobol sequences to ensure adequate coverage of the design space
- Stopping Rules and Sample Size Determination: Adaptive designs often use stopping rules tied to parameter uncertainty, leading to variable sample sizes. The proposed method, however, employs a predetermined sample size, simplifying the design process while maintaining efficiency. The stopping criterion was chosen based on the following considerations:
- Balance Between Convergence and Computational Cost: A threshold of ensures that additional points contribute minimal improvement while avoiding excessive computational costs.
- Empirical Justification: Prior studies have demonstrated that values in this range provide an effective balance between early stopping and full convergence [36].
- Comparison with Adaptive Stopping Rules: Adaptive model-based designs often determine stopping dynamically based on parameter updates, which may introduce instability in early-stage experiments. In contrast, the proposed method ensures a stable sample size while maintaining a rigorous efficiency criterion.
2.8. Design Efficiency and Evaluation
2.8.1. D-Optimality Criterion
2.8.2. G-Optimality Criterion
2.8.3. A-Optimality Criterion
2.8.4. Prediction Variance Average
- Initial Selection Phase: A set of initial points is generated using Sobol sequences and optimized based on the design criterion.
- Sequential Phase: Additional points are iteratively added to improve the design’s efficiency while maintaining space-filling properties.
| Algorithm 1: Sequential design Algorithm |
|
3. Results
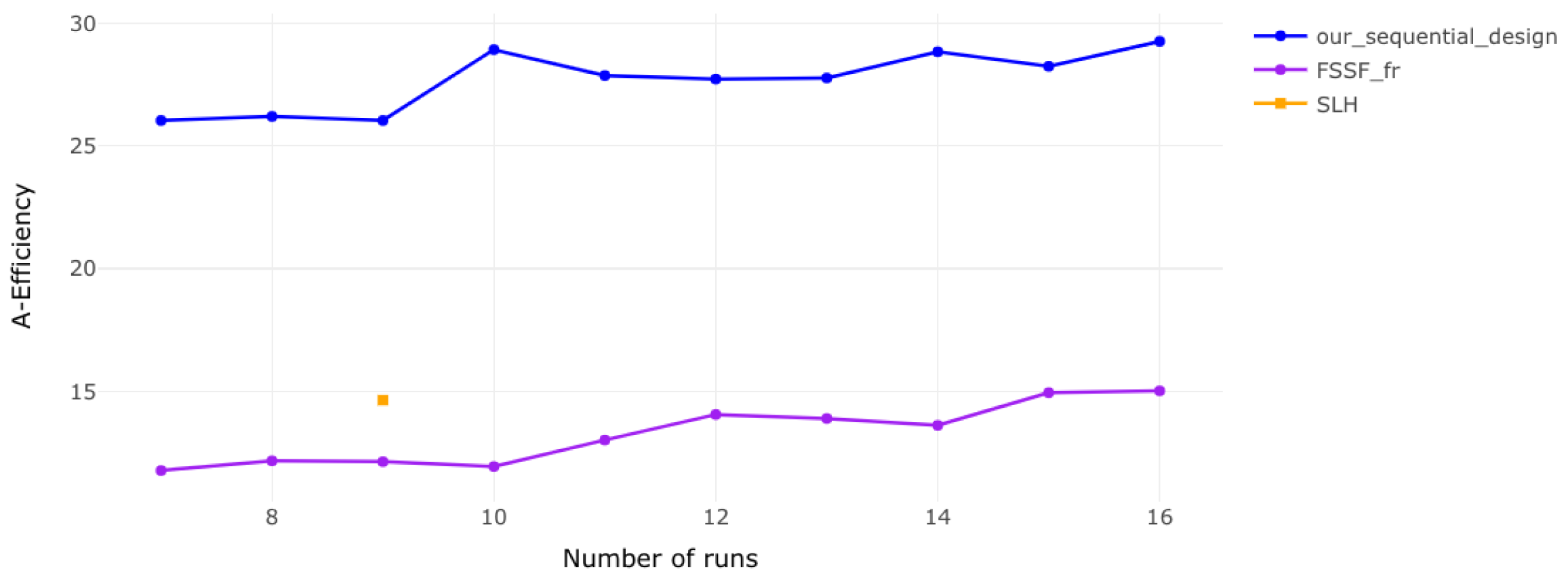
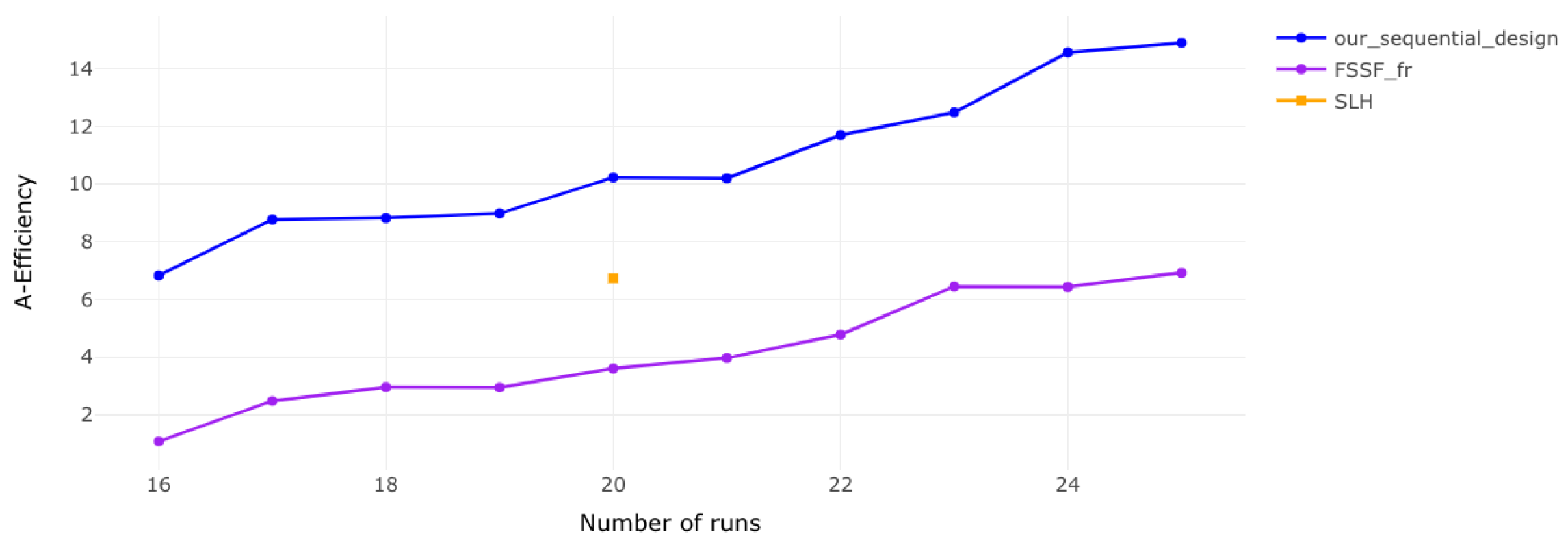
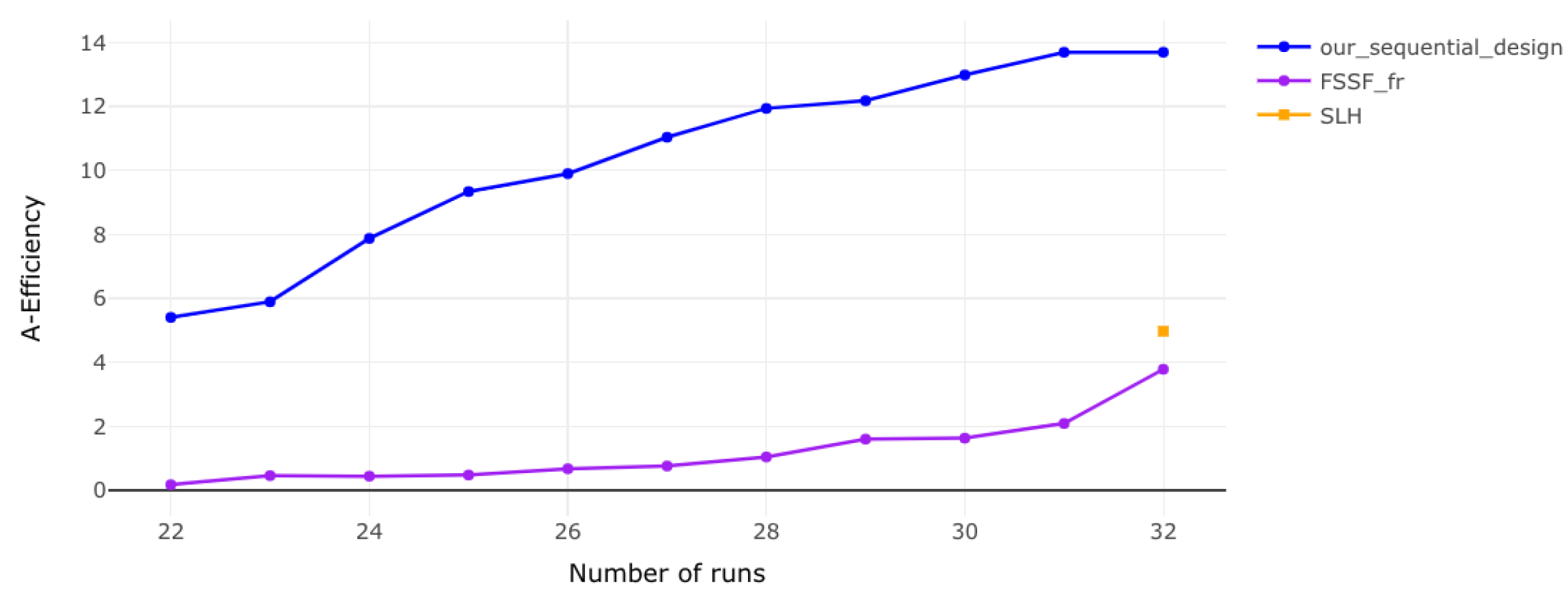
3.1. Sequential Design for the Second-Order Model Using Trace Criteria
3.2. Comparison of Our Sequential Design with Other Sequential Designs
3.3. Correlations: Comparison of Designs with Two or Three Factors and 9 or 16 Runs
Comparison Based on Minimum Distance
- For two factors and nine runs, our design achieves a minimum distance of 0.3296, which is significantly better than FSSF_fr’s 0.1768.
- For three factors and 16 runs, our design performs better as well, with a minimum distance of 0.3226 compared to FSSF_fr’s 0.1036.
| Factors | Number of Runs | Design | Minimum Distance |
|---|---|---|---|
| 2 | 9 | Our Design | 0.3296 |
| FSSF_fr | 0.1768 | ||
| 3 | 16 | Our Design | 0.3226 |
| FSSF_fr | 0.1036 | ||
| 4 | 20 | Our Design | 0.3227 |
| FSSF_fr | 0.1683 | ||
| 5 | 32 | Our Design | 0.3029 |
| FSSF_fr | 0.2306 |
3.4. Comparison of Design Methodologies and Performance Metrics
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ourD | Our sequential design for the second-order model |
| FSSF-Fr | Fully sequential space-filling (FSSF) design using the “forward-reflected” algorithm |
| SLH | Sequential Latin hypercube design with space-filling and projective properties |
| Tr | Trace |
| D | D-efficiency |
| G | G-efficiency |
| A | A-efficiency |
| Av | Prediction variance average |
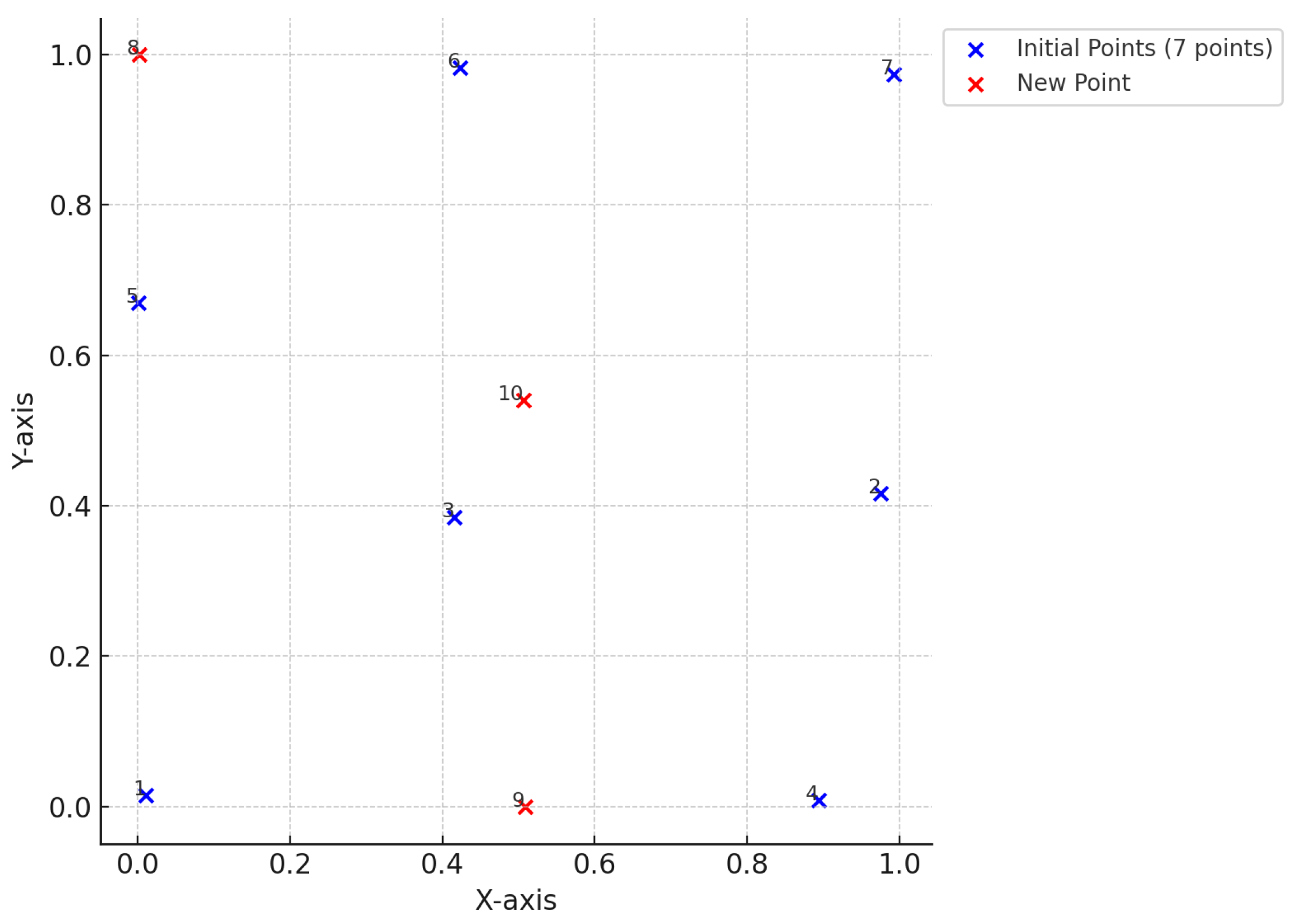
Appendix A. Examples of Sequential Designs
Appendix A.1. Sequential Design of k = 2 Factors (7 to 16 Runs)
| Column 1 | Column 2 |
|---|---|
| 0.0108 | 0.0152 |
| 0.9754 | 0.4164 |
| 0.4151 | 0.3848 |
| 0.8936 | 0.0090 |
| 0.0006 | 0.6701 |
| 0.4230 | 0.9825 |
| 0.9927 | 0.9738 |
| 0.0014 | 0.9997 |
| 0.5083 | 0.0002 |
| 0.5065 | 0.5409 |
| 0.0012 | 0.0003 |
| 0.0001 | 0.5036 |
| 0.4927 | 0.9999 |
| 0.4824 | 0.5103 |
| 0.4965 | 0.0000 |
| 0.9993 | 0.0002 |
Appendix A.2. Sequential Design of k = 3 Factors (11 to 20 Runs)
| Column 1 | Column 2 | Column 3 |
|---|---|---|
| 0.9489 | 0.9298 | 0.5936 |
| 0.0151 | 0.0001 | 0.0776 |
| 0.0892 | 0.9842 | 0.0651 |
| 0.8926 | 0.0686 | 0.1197 |
| 0.6779 | 0.4855 | 0.9602 |
| 0.0412 | 0.1950 | 0.9496 |
| 0.9244 | 0.2111 | 0.6416 |
| 0.1992 | 0.8467 | 0.8846 |
| 0.6439 | 0.3801 | 0.0191 |
| 0.5442 | 0.0311 | 0.7962 |
| 0.3187 | 0.5808 | 0.5546 |
| 0.0001 | 0.5328 | 0.0067 |
| 0.6945 | 0.9953 | 0.9991 |
| 0.9982 | 0.4900 | 0.9980 |
| 0.0001 | 0.6379 | 0.5325 |
| 0.9986 | 0.9564 | 0.0005 |
| 0.0050 | 0.9995 | 0.9994 |
| 0.0021 | 0.0005 | 0.5435 |
| 0.4515 | 0.0020 | 0.0003 |
| 0.4779 | 0.9998 | 0.4399 |
Appendix A.3. Sequential Design of k = 4 Factors (16 to 25 Runs)
| Column 1 | Column 2 | Column 3 | Column 4 |
|---|---|---|---|
| 0.8004 | 0.3871 | 0.3372 | 0.0349 |
| 0.1255 | 0.9333 | 0.9888 | 0.7225 |
| 0.9516 | 0.0196 | 0.1142 | 0.0115 |
| 0.5548 | 0.4490 | 0.9549 | 0.3405 |
| 0.6455 | 0.1757 | 0.6861 | 0.8420 |
| 0.1669 | 0.7563 | 0.0716 | 0.3428 |
| 0.1050 | 0.6564 | 0.3664 | 0.2843 |
| 0.8708 | 0.1134 | 0.8523 | 0.2076 |
| 0.0706 | 0.4149 | 0.4083 | 0.9451 |
| 0.2837 | 0.9606 | 0.5904 | 0.0116 |
| 0.2314 | 0.8367 | 0.7542 | 0.9133 |
| 0.8532 | 0.7932 | 0.8145 | 0.9897 |
| 0.2844 | 0.0576 | 0.0967 | 0.6681 |
| 0.7382 | 0.4451 | 0.2149 | 0.7985 |
| 0.8651 | 0.9732 | 0.3895 | 0.2021 |
| 0.2993 | 0.1959 | 0.9788 | 0.2796 |
| 0.5513 | 0.0551 | 0.5319 | 0.1995 |
| 0.0189 | 0.0092 | 0.6084 | 0.2688 |
| 0.4063 | 0.6484 | 0.0056 | 0.0053 |
| 0.4293 | 0.9766 | 0.4356 | 0.9578 |
| 0.0022 | 0.0638 | 0.1707 | 0.0103 |
| 0.9590 | 0.3177 | 0.0621 | 0.9871 |
| 0.9544 | 0.9599 | 0.9748 | 0.0930 |
| 0.0359 | 0.0232 | 0.9690 | 0.9665 |
| 0.9942 | 0.3493 | 0.4295 | 0.6215 |
Appendix A.4. Sequential Design of k = 5 Factors (22 to 32 Runs)
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 |
|---|---|---|---|---|
| 0.8748 | 0.5675 | 0.8638 | 0.1398 | 0.7457 |
| 0.7481 | 0.1674 | 0.6136 | 0.1525 | 0.0277 |
| 0.7440 | 0.9465 | 0.4857 | 0.0025 | 0.2365 |
| 0.3875 | 0.4907 | 0.3941 | 0.5573 | 0.6313 |
| 0.6944 | 0.7744 | 0.0610 | 0.8966 | 0.3124 |
| 0.3858 | 0.4305 | 0.8007 | 0.7548 | 0.8426 |
| 0.0526 | 0.2489 | 0.7832 | 0.0739 | 0.1329 |
| 0.6378 | 0.0178 | 0.7259 | 0.2564 | 0.2116 |
| 0.9698 | 0.9390 | 0.8631 | 0.7861 | 0.4452 |
| 0.9903 | 0.0137 | 0.9355 | 0.2168 | 0.0161 |
| 0.1084 | 0.9368 | 0.2316 | 0.3529 | 0.0021 |
| 0.3458 | 0.0266 | 0.2470 | 0.0988 | 0.9192 |
| 0.1278 | 0.8349 | 0.8604 | 0.3570 | 0.2671 |
| 0.2885 | 0.2786 | 0.0172 | 0.3057 | 0.4591 |
| 0.8074 | 0.9914 | 0.3319 | 0.2039 | 0.0049 |
| 0.0350 | 0.2948 | 0.6154 | 0.6402 | 0.2384 |
| 0.6112 | 0.9439 | 0.7649 | 0.2982 | 0.8385 |
| 0.1549 | 0.9050 | 0.1829 | 0.1756 | 0.5494 |
| 0.8250 | 0.7717 | 0.2551 | 0.8276 | 0.8249 |
| 0.3101 | 0.6220 | 0.9147 | 0.3522 | 0.0173 |
| 0.3818 | 0.1804 | 0.1956 | 0.8054 | 0.9347 |
| 0.0644 | 0.6569 | 0.1245 | 0.9066 | 0.7698 |
| 0.3975 | 0.0300 | 0.0085 | 0.0036 | 0.0198 |
| 0.9796 | 0.3742 | 0.3730 | 0.9933 | 0.0001 |
| 0.4223 | 0.6049 | 0.9818 | 0.9948 | 0.1036 |
| 0.9854 | 0.0117 | 0.0182 | 0.1064 | 0.4049 |
| 0.0669 | 0.0066 | 0.0429 | 0.6708 | 0.0246 |
| 0.9877 | 0.7664 | 0.0187 | 0.2724 | 0.0030 |
| 0.9812 | 0.2880 | 0.9867 | 0.9948 | 0.8081 |
| 0.9926 | 0.6139 | 0.4161 | 0.2625 | 0.9905 |
| 0.0465 | 0.0014 | 0.9897 | 0.7405 | 0.1975 |
| 0.2719 | 0.9703 | 0.7564 | 0.9937 | 0.9939 |
References
- do Amaral, J.V.S.; Montevechi, J.A.B.; de Carvalho Miranda, R.; dos Santos, C.H. Adaptive Metamodeling Simulation Optimization: Insights, Challenges, and Perspectives. Appl. Soft Comput. 2024, 165, 112067. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Pallmann, P.; Bedding, A.W.; Choodari-Oskooei, B.; Dimairo, M.; Flight, L.; Hampson, L.V.; Holmes, J.; Mander, A.P.; Odondi, L.; Sydes, M.R.; et al. Adaptive designs in clinical trials: Why use them, and how to run and report them. BMC Med. 2018, 16, 29. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems 25 (NIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the International Conference on Learning and Intelligent Optimization, Rome, Italy, 17–21 January 2011; pp. 507–523. [Google Scholar]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Gonzalez, J.; Dai, Z.; Hennig, P.; Lawrence, N. Batch Bayesian optimization via local penalization. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 9–12 May 2015; pp. 648–657. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar]
- Box, G.E.P.; Draper, N.R. Empirical Model-building and Response Surfaces; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Johnson, M.E.; Moore, L.M.; Ylvisaker, D. Minimax and maximin distance designs. J. Stat. Plan. Inference 1990, 26, 131–148. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, D.K.; Hu, X.; Ouyang, L. Sequential Latin hypercube design with both space-filling and projective properties. Qual. Reliab. Eng. Int. 2019, 35, 1941–1951. [Google Scholar] [CrossRef]
- Wu, C.F.J.; Hamada, M. Experiments Planning Analysis and Parameter Design Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Li, G.; Yang, J.; Wu, Z.; Zhang, W.; Okolo, P.; Zhang, D. A sequential optimal Latin hypercube design method using an efficient recursive permutation evolution algorithm. Eng. Optim. 2024, 56, 179–198. [Google Scholar] [CrossRef]
- Lu, L.; Anderson-Cook, C.M. Strategies for building surrogate models in multi-fidelity computer experiments. J. Stat. Plan. Inference 2021, 215, 163–175. [Google Scholar]
- Shang, B.; Apley, D.W. Fully-sequential space-filling design algorithms for computer experiments. J. Qual. Technol. 2021, 53, 173–196. [Google Scholar] [CrossRef]
- Lam, C.Q. Sequential Adaptive Designs in Computer Experiments for Response Surface Model Fit. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2008. [Google Scholar]
- Loeppky, J.L.; Moore, L.M.; Williams, B.J. Batch sequential designs for computer experiments. J. Stat. Plan. Inference 2010, 140, 1452–1464. [Google Scholar] [CrossRef]
- Ranjan, P.; Bingham, D.; Michailidis, G. Sequential experiment design for contour estimation from complex computer codes. Technometrics 2008, 50, 527–541. [Google Scholar] [CrossRef]
- Williams, B.J. Sequential Design of Computer Experiments to Minimize Integrated Response Functions. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2000. [Google Scholar]
- Barton, R.R. Simulation metamodels. In Proceedings of the IEEE 1998 Winter Simulation Conference, Washington, DC, USA, 13–16 December 1998; Volume 1, pp. 167–174. [Google Scholar] [CrossRef]
- Vieira, H.; Sanchez, S.; Kienitz, K.H.; Belderrain, M.C.N. Generating and improving orthogonal designs by using mixed integer programming. Eur. J. Oper. Res. 2011, 215, 629–638. [Google Scholar] [CrossRef]
- Siggelkow, N. Misperceiving interactions among complements and substitutes: Organizational consequences. Manag. Sci. 2002, 48, 900–916. [Google Scholar] [CrossRef]
- Steinberg, D.M.; Lin, D.K.J. A Construction Method for Orthogonal Latin Hypercube Designs. Biometrika 2006, 93, 279–288. [Google Scholar]
- Chan, L.Y.; Guan, Y.N.; Zhang, C.Q. A-optimal designs for an additive quadratic mixture model. Stat. Sin. 1998, 8, 979–990. [Google Scholar]
- Kiefer, J. General equivalence theory for optimum designs (approximate theory). Ann. Stat. 1974, 2, 849–879. [Google Scholar]
- Fedorov, V.V.; Leonov, S.L. Optimal Design for Nonlinear Response Models; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Paskov, S.; Traub, J.F. Faster Valuation of Financial Derivatives. J. Portf. Manag. 1996, 22, 113–123. [Google Scholar]
- Kreinin, A.; Merkoulovitch, L.; Rosen, D.; Zerbs, M. Measuring portfolio risk using quasi Monte Carlo methods. Algo Res. Q. 1998, 1, 17–26. [Google Scholar]
- Jäckel, P. Monte Carlo Methods in Finance; John Wiley & Sons: Hoboken, NJ, USA, 2002; Volume 5. [Google Scholar]
- L’Ecuyer, P.; Lemieux, C. Recent advances in randomized quasi-Monte Carlo methods. In Modeling Uncertainty: An Examination of Stochastic Theory, Methods, and Applications; Springer: New York, NY, USA, 2002; pp. 419–474. [Google Scholar]
- Glasserman, P. Monte Carlo Methods in Financial Engineering; Springer: New York, NY, USA, 2004. [Google Scholar]
- Sobol’, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’noi Mat. I Mat. Fiz. 1967, 7, 784–802. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]

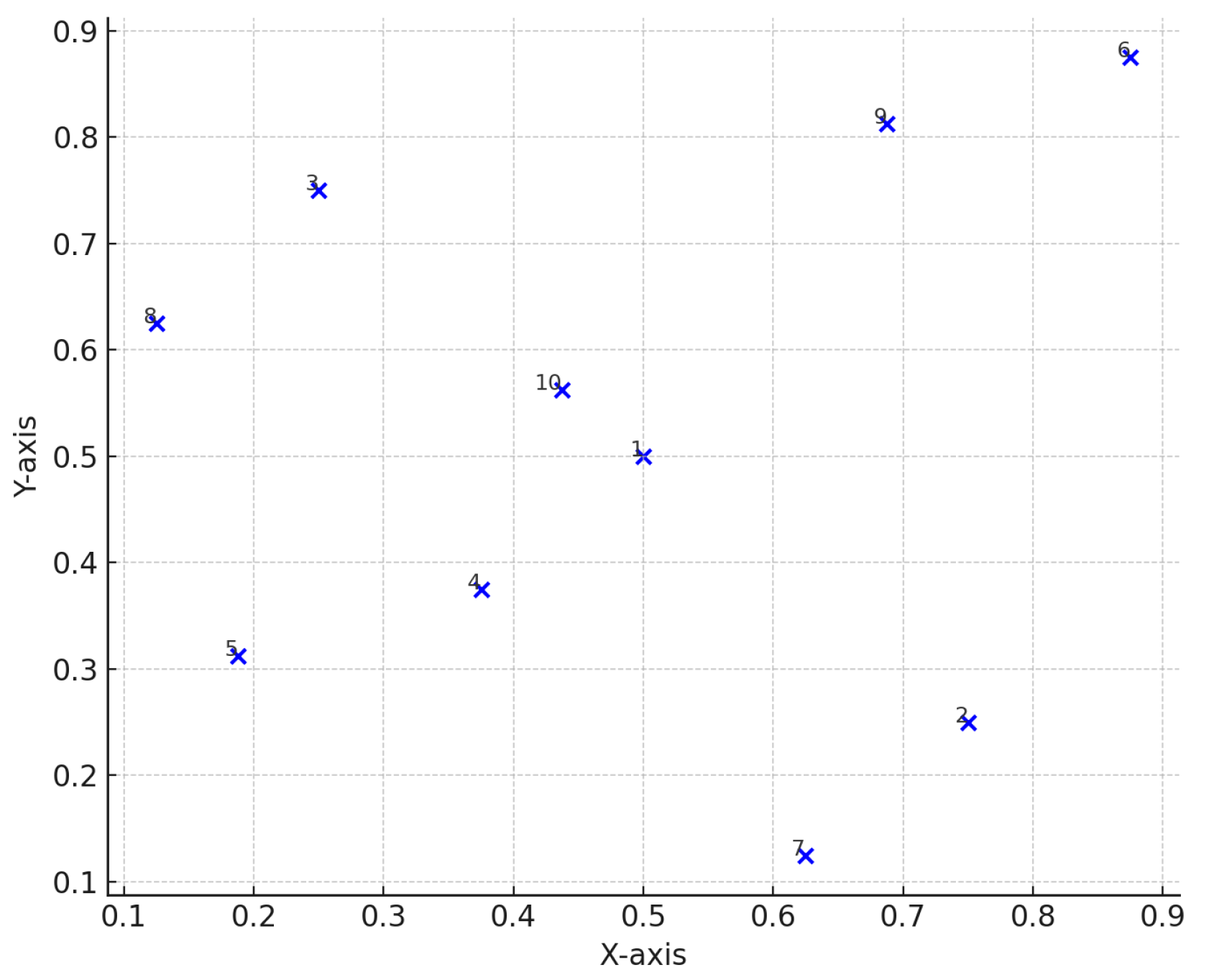
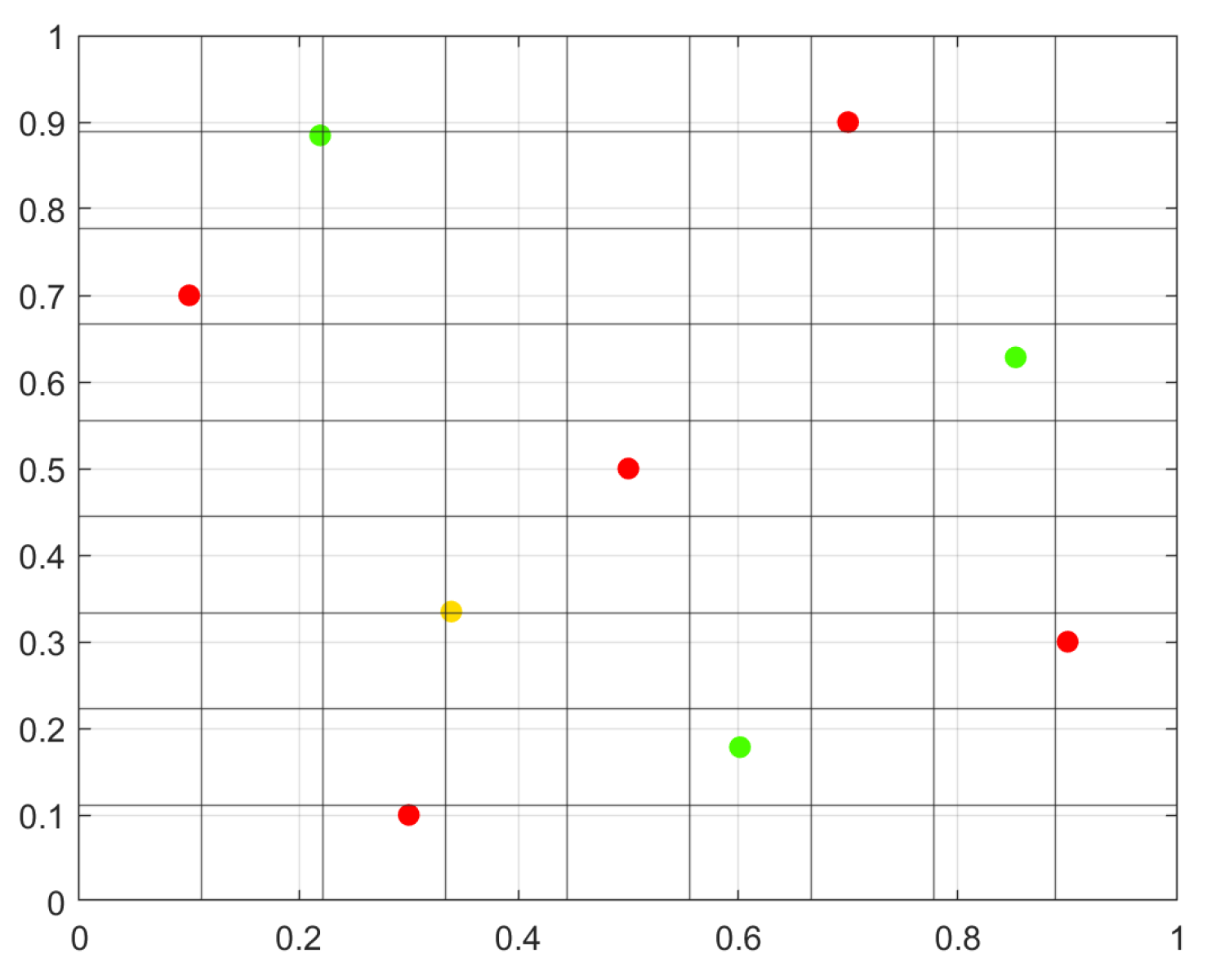
| Factors | Initial Points | Final Stage Points | Final Stage Trace |
|---|---|---|---|
| Low Dimensions | |||
| 2 | 7 | 107 | 3.2127 |
| 3 | 11 | 111 | 5.6875 |
| 4 | 16 | 116 | 8.6624 |
| 5 | 22 | 122 | 12.5512 |
| 6 | 29 | 129 | 17.0583 |
| 7 | 37 | 137 | 22.3663 |
| 8 | 46 | 146 | 28.6115 |
| 9 | 56 | 156 | 36.1949 |
| High Dimensions | |||
| 10 | 67 | 167 | 45.4068 |
| 15 | 137 | 237 | 161.8972 |
| 20 | 232 | 332 | 318.0626 |
| 25 | 352 | 452 | 532.7839 |
| 30 | 497 | 597 | 695.0685 |
| 50 | 1327 | 1427 | 2160.4203 |
| Stage | Added Points | Total Points |
|---|---|---|
| 0 | 5 | 5 |
| 1 | 1 | 6 |
| 2 | 3 | 9 |
| 3 | 9 | 18 |
| 4 | 9 | 27 |
| 5 | 27 | 54 |
| Factors | Runs | FSSF-Fr | SLH | OurD |
|---|---|---|---|---|
| 2 | 7 | D: 24.7669 G: 18.9696 A: 11.7767 Av: 1.0881 | — | D: 39.1484 G: 31.5732 A: 23.1105 Av: 0.6832 |
| 2 | 8 | D: 23.6650 G: 20.3167 A: 12.1736 Av: 0.9465 | — | D: 42.0133 G: 64.0922 A: 26.1995 Av: 0.5690 |
| 2 | 9 | D: 23.4023 G: 18.3680 A: 12.1379 Av: 0.8340 | D: 26.1130 G: 17.0283 A: 14.6439 Av: 0.6657 | D: 41.3294 G: 58.2041 A: 26.0332 Av: 0.5039 |
| 2 | 10 | D: 22.5185 G: 17.6445 A: 11.9384 Av: 0.7730 | — | D: 40.4839 G: 56.5988 A: 28.9187 Av: 0.3982 |
| 2 | 11 | D: 23.3769 G: 19.4645 A: 13.0183 Av: 0.6433 | — | D: 41.0431 G: 50.6808 A: 27.8620 Av: 0.3774 |
| 2 | 12 | D: 23.6797 G: 19.7362 A: 14.0594 Av: 0.5413 | — | D: 40.3945 G: 46.7551 A: 27.7220 Av: 0.3518 |
| 2 | 13 | D: 22.9500 G: 19.5947 A: 13.8959 Av: 0.5109 | — | D: 40.2663 G: 44.3747 A: 27.7662 Av: 0.3231 |
| 2 | 14 | D: 22.4351 G: 16.3744 A: 13.6185 Av: 0.4880 | — | D: 39.3278 G: 42.0330 A: 28.8340 Av: 0.2868 |
| 2 | 15 | D: 24.2301 G: 15.7860 A: 14.9466 Av: 0.4173 | — | D: 38.8010 G: 40.9047 A: 28.2392 Av: 0.2733 |
| 2 | 16 | D: 24.0166 G: 17.0450 A: 15.0236 Av: 0.3799 | — | D: 40.4946 G: 44.3569 A: 29.2564 Av: 0.2531 |
| Factors | Runs | FSSF-Fr | SLH | OurD |
|---|---|---|---|---|
| 3 | 11 | D: 18.8343 G: 11.3627 A: 10.1811 Av: 1.2357 | — | D: 27.6816 G: 19.6357 A: 15.3180 Av: 0.8749 |
| 3 | 12 | D: 18.4536 G: 10.5244 A: 10.2807 Av: 1.1169 | — | D: 27.6637 G: 18.1392 A: 15.8703 Av: 0.8005 |
| 3 | 13 | D: 17.8678 G: 9.7149 A: 9.7891 Av: 1.0713 | — | D: 27.8157 G: 16.3075 A: 16.2633 Av: 0.7218 |
| 3 | 14 | D: 18.4029 G: 9.0337 A: 9.5801 Av: 1.0136 | — | D: 27.6339 G: 13.7621 A: 16.5398 Av: 0.6518 |
| 3 | 15 | D: 19.6913 G: 9.9836 A: 10.3437 Av: 0.8435 | — | D: 27.8290 G: 14.0127 A: 17.3335 Av: 0.5867 |
| 3 | 16 | D: 20.2167 G: 9.6263 A: 10.5691 Av: 0.7752 | D: 15.4438 G: 4.1816 A: 7.5951 Av: 1.0409 | D: 30.7217 G: 30.7073 A: 18.9983 Av: 0.5003 |
| 3 | 17 | D: 19.5608 G: 9.0658 A: 9.6645 Av: 0.7709 | — | D: 32.6493 G: 38.2108 A: 21.1871 Av: 0.4416 |
| 3 | 18 | D: 20.9422 G: 15.6633 A: 11.0878 Av: 0.6253 | — | D: 32.8703 G: 29.3737 A: 20.9880 Av: 0.4219 |
| 3 | 19 | D: 20.3985 G: 16.4921 A: 11.2394 Av: 0.5892 | — | D: 33.0656 G: 26.2998 A: 20.8328 Av: 0.4032 |
| 3 | 20 | D: 20.2892 G: 14.5014 A: 12.1596 Av: 0.5303 | — | D: 33.1099 G: 25.4299 A: 21.6784 Av: 0.3640 |
| Factors | Runs | FSSF-Fr | SLH | OurD |
|---|---|---|---|---|
| 4 | 16 | D: 8.3689 G: 0.2494 A: 1.0808 Av: 12.9402 | — | D: 17.1096 G: 8.4618 A: 6.8236 Av: 1.6636 |
| 4 | 17 | D: 10.0333 G: 1.1614 A: 2.4820 Av: 4.3403 | — | D: 17.8390 G: 7.8289 A: 8.7681 Av: 1.2671 |
| 4 | 18 | D: 10.8964 G: 1.3795 A: 2.9577 Av: 3.4888 | — | D: 17.9452 G: 7.0877 A: 8.8190 Av: 1.1720 |
| 4 | 19 | D: 11.2482 G: 1.3308 A: 2.9476 Av: 3.2707 | — | D: 17.7695 G: 5.5715 A: 8.9794 Av: 1.1066 |
| 4 | 20 | D: 12.6619 G: 1.3019 A: 3.6069 Av: 2.5490 | D: 12.9971 G: 6.3643 A: 6.7221 Av: 1.4116 | D: 18.7674 G: 8.6146 A: 10.2229 Av: 0.9091 |
| 4 | 21 | D: 12.6367 G: 1.6628 A: 3.9717 Av: 2.2304 | — | D: 19.1734 G: 8.5066 A: 10.1981 Av: 0.8618 |
| 4 | 22 | D: 13.8387 G: 2.7889 A: 4.7780 Av: 1.7163 | — | D: 20.6896 G: 8.9131 A: 11.6897 Av: 0.7473 |
| 4 | 23 | D: 15.1767 G: 3.5594 A: 6.4504 Av: 1.1949 | — | D: 22.2090 G: 8.5906 A: 12.4763 Av: 0.6797 |
| 4 | 24 | D: 15.1078 G: 3.4581 A: 6.4304 Av: 1.1454 | — | D: 24.2912 G: 12.0503 A: 14.5507 Av: 0.5775 |
| 4 | 25 | D: 15.3069 G: 3.3706 A: 6.9210 Av: 1.0335 | — | D: 23.7704 G: 12.1565 A: 14.8842 Av: 0.5408 |
| Factors | Runs | FSSF-Fr | SLH | OurD |
|---|---|---|---|---|
| 5 | 22 | D: 7.1369 G: 0.0595 A: 0.1808 Av: 58.5489 | — | D: 13.5761 G: 2.1505 A: 5.4109 Av: 2.2441 |
| 5 | 23 | D: 7.4860 G: 0.1707 A: 0.4630 Av: 22.6007 | — | D: 14.5511 G: 2.2569 A: 5.8986 Av: 2.0280 |
| 5 | 24 | D: 7.7059 G: 0.1612 A: 0.4472 Av: 22.2431 | — | D: 15.3591 G: 3.4272 A: 6.8932 Av: 1.6620 |
| 5 | 25 | D: 8.2074 G: 0.1821 A: 0.4840 Av: 19.7216 | — | D: 16.0262 G: 4.1056 A: 7.8797 Av: 1.4018 |
| 5 | 26 | D: 8.9790 G: 0.2346 A: 0.6791 Av: 13.5747 | — | D: 17.4962 G: 6.2261 A: 9.3435 Av: 1.1184 |
| 5 | 27 | D: 9.4240 G: 0.2518 A: 0.7649 Av: 11.5442 | — | D: 18.3563 G: 6.0778 A: 9.9043 Av: 1.0214 |
| 5 | 28 | D: 9.7922 G: 0.3883 A: 1.0474 Av: 8.1414 | — | D: 19.1626 G: 7.8973 A: 11.0414 Av: 0.9090 |
| 5 | 29 | D: 9.9964 G: 0.5878 A: 1.6060 Av: 5.2469 | — | D: 20.2830 G: 7.6263 A: 11.9428 Av: 0.7973 |
| 5 | 30 | D: 9.8138 G: 0.6289 A: 1.6354 Av: 4.9971 | — | D: 20.1224 G: 8.9218 A: 12.1837 Av: 0.7532 |
| 5 | 31 | D: 10.0366 G: 0.8668 A: 2.0946 Av: 3.8307 | — | D: 20.8918 G: 9.5841 A: 12.9874 Av: 0.6954 |
| 5 | 32 | D: 10.6885 G: 1.2298 A: 3.7894 Av: 2.1426 | D: 11.5935 G: 1.3734 A: 4.9779 Av: 1.5681 | D: 21.7280 G: 9.7861 A: 13.6980 Av: 0.6297 |
| Factor Pairs | SLH Design | Our Design | FSSF_FR Design |
|---|---|---|---|
| X1 and X2 | 0.1403 | 0.0910 | 0.0992 |
| X1 and X12 | 0.1908 | 0.0708 | 0.1416 |
| X1 and X1X2 | 0.2465 | 0.1251 | 0.3768 |
| X1 and X22 | 0.2565 | 0.0438 | 0.6876 |
| X2 and X12 | 0.2345 | 0.2005 | 0.4179 |
| X2 and X1X2 | 0.2430 | 0.1017 | 0.4652 |
| X2 and X22 | 0.0381 | 0.0071 | 0.1416 |
| X12 and X1X2 | 0.1816 | 0.0759 | 0.3116 |
| fX12 and X22 | 0.1394 | 0.0582 | 0.1314 |
| X1X2 and X22 | 0.5908 | 0.0550 | 0.3116 |
| Factor Pairs | SLH Design | Our Design | FSSF_FR Design |
|---|---|---|---|
| X1 and X2 | 0.2847 | 0.0757 | 0.1172 |
| X1 and X3 | 0.0347 | 0.1494 | 0.0529 |
| X1 and X1*X1 | 0.0582 | 0.1178 | 0.1521 |
| X1 and X1*X2 | 0.2088 | 0.0945 | 0.1955 |
| X1 and X2*X2 | 0.0222 | 0.0829 | 0.1453 |
| X1 and X1*X3 | 0.0111 | 0.1598 | 0.1332 |
| X1 and X2*X3 | 0.0349 | 0.0131 | 0.2365 |
| X1 and X3*X3 | 0.2164 | 0.0323 | 0.0320 |
| X2 and X3 | 0.3149 | 0.0355 | 0.0957 |
| X2 and X1*X1 | 0.2811 | 0.0452 | 0.2342 |
| X2 and X1*X2 | 0.0986 | 0.0638 | 0.0233 |
| X2 and X2*X2 | 0.0418 | 0.1176 | 0.1137 |
| X2 and X1*X3 | 0.0495 | 0.0035 | 0.2091 |
| X2 and X2*X3 | 0.0467 | 0.1154 | 0.3233 |
| X2 and X3*X3 | 0.1224 | 0.0981 | 0.3757 |
| X3 and X1*X1 | 0.0759 | 0.3072 | 0.0236 |
| X3 and X1*X2 | 0.0694 | 0.0109 | 0.1994 |
| X3 and X2*X2 | 0.1066 | 0.1766 | 0.2596 |
| X3 and X1*X3 | 0.2868 | 0.0146 | 0.0892 |
| X3 and X2*X3 | 0.1709 | 0.1232 | 0.3152 |
| X3 and X3*X3 | 0.1185 | 0.1293 | 0.1504 |
| X1*X1 and X1*X2 | 0.5986 | 0.2444 | 0.3720 |
| X1*X1 and X2*X2 | 0.0236 | 0.0094 | 0.3210 |
| X1*X1 and X1*X3 | 0.0917 | 0.1339 | 0.4223 |
| X1*X1 and X2*X3 | 0.0956 | 0.1974 | 0.3508 |
| X1*X1 and X3*X3 | 0.1381 | 0.0481 | 0.3667 |
| X1*X2 and X2*X2 | 0.2686 | 0.2691 | 0.2117 |
| X1*X2 and X1*X3 | 0.4043 | 0.0995 | 0.3102 |
| X1*X2 and X2*X3 | 0.1333 | 0.0632 | 0.0496 |
| X1*X2 and X3*X3 | 0.1768 | 0.1972 | 0.0454 |
| X2*X2 and X1*X3 | 0.0362 | 0.0988 | 0.0306 |
| X2*X2 and X2*X3 | 0.0862 | 0.0708 | 0.295 |
| X2*X2 and X3*X3 | 0.4575 | 0.0700 | 0.1194 |
| X1*X3 and X2*X3 | 0.1700 | 0.1883 | 0.1409 |
| X1*X3 and X3*X3 | 0.0814 | 0.1067 | 0.2564 |
| X2*X3 and X3*X3 | 0.3151 | 0.0015 | 0.058 |
| Criteria | SLH Design | FSSF_FR Design | Our New Design |
|---|---|---|---|
| Initial Point Selection | Random | Random from Sobol Sequence | Random from Sobol Sequence |
| Minimum Number of Runs | Random Minimum | Start with no runs | Based on the number Factors |
| Sequential Refinement Strategy | Fill all empty intervals | Forward-Reflected Sobol Sequence | Sobol points that Minimize trace |
| Correlation Performance | Moderate | High (Low Correlation) | High (Low Correlation) |
| Full Quadratic Model efficiency | Moderate | High | Very High |
| Coverage of Design Space | Low | High | Very High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, N.; Georgiou, S.; Stylianou, S. Computational Construction of Sequential Efficient Designs for the Second-Order Model. Mathematics 2025, 13, 1190. https://doi.org/10.3390/math13071190
Alshammari N, Georgiou S, Stylianou S. Computational Construction of Sequential Efficient Designs for the Second-Order Model. Mathematics. 2025; 13(7):1190. https://doi.org/10.3390/math13071190
Chicago/Turabian StyleAlshammari, Norah, Stelios Georgiou, and Stella Stylianou. 2025. "Computational Construction of Sequential Efficient Designs for the Second-Order Model" Mathematics 13, no. 7: 1190. https://doi.org/10.3390/math13071190
APA StyleAlshammari, N., Georgiou, S., & Stylianou, S. (2025). Computational Construction of Sequential Efficient Designs for the Second-Order Model. Mathematics, 13(7), 1190. https://doi.org/10.3390/math13071190







