Benchmarking and Target Setting in Weight Restriction Context
Abstract
1. Introduction
2. Background: Benchmarking and Weight Restrictions
3. A Closest Target Model for Benchmarking with Weight Restrictions
3.1. A Closest Target Model for Benchmarking with Weight Restrictions
- Objective Function (6a): The goal is to minimize the total relative adjustment, which is expressed as the sum of the weighted input and output slacks associated with the AR (adjusted) projection. This objective function quantifies the distance between two benchmark targets: the initial Reference Target (obtained without weight restrictions) and the AR target (obtained with weight restrictions applied). By minimizing this distance, we ensure that the adjusted target remains as close as possible to the reference, thereby keeping the recommendations realistic.
- First Block of Constraints (6b), (6c), (6d), (6e), (6f), (6g), (6h), (6i) and (6j): These constraints guarantee that the projection of DMU0 onto the original efficient frontier (without weight restrictions) is performed correctly. Specifically, Constraints (6b) and (6c) model the balance between the observed inputs and outputs of DMU0 and the weighted combination of inputs and outputs from the set of efficient units E. Constraint (6d) ensures convexity by requiring that the weights sum to one. Constraints (6e), (6f), (6g), (6h) and (6i) impose the necessary conditions on the dual variables and incorporate the big-M method to handle binary variables in a mixed-integer programming setting. Finally, Constraint (6j) plays a crucial role in ensuring that the target derived from the first block of constraints corresponds to one of the possible closest targets obtained from the unrestricted model, Model (3). This is evident because the constraints in this block are structurally identical to those in Model (3), with Constraint (6j) serving as the objective function of Model (3), explicitly enforcing that its value remains equal to the optimal solution of the original problem. In other words, (6j) guarantees that the reference target is not arbitrarily chosen but is aligned with the minimal adjustment principle established in the unrestricted DEA framework.
- Second Block of Constraints (6k), (6l), (6m), (6n), (6o), (6p), (6q), (6r), (6s) and (6t): In this part, we introduce the conditions that ensure the projection associated with the weight-restricted (AR) technology lies on , the efficient frontier modified by the weight restrictions. Constraints (6k) and (6l) describe the adjusted balance between inputs and outputs by modifying the original targets through additional slacks. Constraint (6m) again guarantees convexity for the AR projection. Constraints (6n), (6o), (6p), (6q) and (6r) impose the analogous conditions on the dual variables within the AR context. Constraints (6s) and (6t) enforce the weight restrictions by bounding the ratios of the multipliers associated with the inputs and outputs, respectively.
3.2. Numerical Example
4. Empirical Example
4.1. Selection of Variables and Data
- PL: Number of hotel beds available.
- EN: Number of firms directly or indirectly involved in tourism. Includes, for example, hotels and similar establishments providing collective accommodation, restaurants, amusement parks, and other tourist attractions.
- EAP: Number of economically active people living in the locality. This variable includes people over 18 years of age who are employed or actively seeking employment.
- LP: Number of passengers arriving at each location. To reflect the impact on nearby localities (a decreasing proportion of passengers is assigned to locations within a radius of 15 km).
- AP: Number of passengers arriving on domestic and international flights corrected by the time of arrival at the location. Each airport influences a radius of 300 km.
4.2. DEA Analysis
4.3. Weight Restrictions
5. Conclusions
- We extend the closest target framework in Data Envelopment Analysis (DEA) by incorporating weight restrictions, ensuring that efficiency benchmarks align with expert-imposed constraints.
- Our model introduces a two-step target setting approach that minimizes deviations from the unrestricted closest target while ensuring compliance with weight-restricted efficiency conditions.
- We propose a novel methodological framework that enhances the interpretability of DEA results, particularly in constrained benchmarking scenarios, by preserving the original efficiency structure as much as possible.
- Our approach offers decision makers a more realistic and actionable benchmarking tool by integrating expert preferences, making it particularly valuable in sectors where managerial insights play a crucial role, such as tourism, healthcare, and banking.
- We demonstrate the applicability of our model through an empirical study of tourism localities in Córdoba, Argentina, providing a practical example of how weight-restricted DEA can inform resource allocation and policy decisions.
- By ensuring that improvement plans require minimal effort while adhering to imposed constraints, our model provides a structured methodology for strategic planning and performance enhancement across various industries.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| AR | Assurance Region |
| AR-I | Assurance Region Type I |
| DEA | Data Envelopment Analysis |
| DMU | Decision Making Unit |
| MILP | Mixed Integer Linear Programming |
| PPS | Production Possibility Set |
| SOS | Special Ordered Set |
| WR | Weight Restriction |
References
- Aparicio, J.; Lopez-Espin, J.J.; Martinez-Moreno, R.; Pastor, J.T. Benchmarking in Data Envelopment Analysis: An Approach Based on Genetic Algorithms and Parallel Programming. Adv. Oper. Res. 2014, 2014, 431749. [Google Scholar] [CrossRef]
- Ruiz, J.L.; Sirvent, I. Common benchmarking and ranking of units with DEA. Omega 2016, 65, 1–9. [Google Scholar] [CrossRef]
- Cook, W.D.; Ruiz, J.L.; Sirvent, I.; Zhu, J. Within-group common benchmarking using DEA. Eur. J. Oper. Res. 2017, 256, 901–910. [Google Scholar] [CrossRef]
- An, Q.; Tao, X.; Dai, B.; Xiong, B. Bounded-change target-setting approach: Selection of a realistic benchmarking path. J. Oper. Res. Soc. 2021, 72, 663–677. [Google Scholar] [CrossRef]
- Lozano, S.; Soltani, N. A modified discrete Raiffa approach for efficiency assessment and target setting. Ann. Oper. Res. 2020, 292, 71–95. [Google Scholar] [CrossRef]
- Ruiz, J.L.; Sirvent, I. Performance evaluation through DEA benchmarking adjusted to goals. Omega 2019, 87, 150–157. [Google Scholar] [CrossRef]
- Aparicio, J.; Monge, J.F.; Ramón, N. A new measure of technical efficiency in data envelopment analysis based on the maximization of hypervolumes: Benchmarking, properties and computational aspects. Eur. J. Oper. Res. 2021, 293, 263–275. [Google Scholar] [CrossRef]
- Borrás, F.; Ruiz, J.L.; Sirvent, I. Planning improvements through data envelopment analysis (DEA) benchmarking based on a selection of peers. Socio-Econ. Plan. Sci. 2024, 95, 102020. [Google Scholar] [CrossRef]
- Zofio, J.L.; Aparicio, J.; Barbero, J.; Zabala-Iturriagagoitia, J.M. Benchmarking performance through efficiency analysis trees: Improvement strategies for Colombian higher education institutions. Socio-Econ. Plan. Sci. 2024, 92, 101845. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Akbarian, O.; Banaitis, A.; Soltani, Z. Application of DEA in benchmarking: A systematic literature review from 2003–2020. Technol. Econ. Dev. Econ. 2021, 27, 175–222. [Google Scholar] [CrossRef]
- Piran, F.S.; Camanho, A.S.; Silva, M.C.; Lacerda, D.P. Internal Benchmarking for Efficiency Evaluations Using Data Envelopment Analysis: A Review of Applications and Directions for Future Research. In Advanced Mathematical Methods for Economic Efficiency Analysis: Theory and Empirical Applications; Macedo, P., Moutinho, V., Madaleno, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 143–162. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Thanassoulis, E.; Portela, M.; Despić, O. Data Envelopment Analysis: The Mathematical Programming Approach to Efficiency Analysis. In The Measurement of Productive Efficiency and Productivity Change; Oxford University Press: Oxford, UK, 2008; pp. 251–420. [Google Scholar] [CrossRef]
- Thompson, R.G.; Singleton, F.D.; Thrall, R.M.; Smith, B.A. Comparative Site Evaluations for Locating a High-Energy Physics Lab in Texas. Interfaces 1986, 16, 35–49. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Huang, Z.; Sun, D. Polyhedral Cone-Ratio DEA Models with an illustrative application to large commercial banks. J. Econom. 1990, 46, 73–91. [Google Scholar] [CrossRef]
- Thanassoulis, E.; Dyson, R. Estimating preferred target input-output levels using data envelopment analysis. Eur. J. Oper. Res. 1992, 56, 80–97. [Google Scholar] [CrossRef]
- Zhu, J. Data Envelopment Analysis with Preference Structure. J. Oper. Res. Soc. 1996, 47, 136–150. [Google Scholar] [CrossRef]
- Allen, R.; Athanassopoulos, A.; Dyson, R.G.; Thanassoulis, E. Weights restrictions and value judgements in Data Envelopment Analysis: Evolution, development and future directions. Ann. Oper. Res. 1997, 73, 13–34. [Google Scholar] [CrossRef]
- Cooper, W.W.; Ramón, N.; Ruiz, J.L.; Sirvent, I. Avoiding large differences in weights in cross-efficiency evaluations: Application to the ranking of basketball players. J. Cent. Cathedra Bus. Econ. Res. J. 2011, 4, 197–215. [Google Scholar] [CrossRef]
- Podinovski, V.V. Optimal weights in DEA models with weight restrictions. Eur. J. Oper. Res. 2016, 254, 916–924. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Models with Restricted Multipliers. In Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Springer: New York, NY, USA, 2007; pp. 177–213. [Google Scholar] [CrossRef]
- Podinovski, V. Side effects of absolute weight bounds in DEA models. Eur. J. Oper. Res. 1999, 115, 583–595. [Google Scholar] [CrossRef]
- Güner, S.; Antunes, J.J.M.; Seçkin Codal, K.; Wanke, P. Network centrality driven airport efficiency: A weight-restricted network DEA. J. Air Transp. Manag. 2024, 116, 102551. [Google Scholar] [CrossRef]
- Podinovski, V.V.; Athanassopoulos, A.D. Assessing the relative efficiency of decision making units using DEA models with weight restrictions. J. Oper. Res. Soc. 1998, 49, 500–508. [Google Scholar] [CrossRef]
- Davoodi, A.; Zhiani Rezai, H. Improving production possibility set with production trade-offs. Appl. Math. Model. 2015, 39, 1966–1974. [Google Scholar] [CrossRef]
- Podinovski, V.V. Production trade-offs and weight restrictions in data envelopment analysis. J. Oper. Res. Soc. 2004, 55, 1311–1322. [Google Scholar] [CrossRef]
- Aparicio, J.; Ruiz, J.L.; Sirvent, I. Closest targets and minimum distance to the Pareto-efficient frontier in DEA. J. Product. Anal. 2007, 28, 209–218. [Google Scholar] [CrossRef]
- Ruiz, J.L.; Sirvent, I. Benchmarking within a DEA framework: Setting the closest targets and identifying peer groups with the most similar performances. Int. Trans. Oper. Res. 2022, 29, 554–573. [Google Scholar] [CrossRef]
- Ramón, N.; Ruiz, J.L.; Sirvent, I. On the Use of DEA Models with Weight Restrictions for Benchmarking and Target Setting. In Advances in Efficiency and Productivity; Aparicio, J., Lovell, C.A.K., Pastor, J.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 149–180. [Google Scholar] [CrossRef]
- Ruiz, J.L.; Segura, J.V.; Sirvent, I. Benchmarking and target setting with expert preferences: An application to the evaluation of educational performance of Spanish universities. Eur. J. Oper. Res. 2015, 242, 594–605. [Google Scholar] [CrossRef]
- Razipour-GhalehJough, S.; Lotfi, F.H.; Jahanshahloo, G.; Rostamy-malkhalifeh, M.; Sharafi, H. Finding closest target for bank branches in the presence of weight restrictions using data envelopment analysis. Ann. Oper. Res. 2020, 288, 755–787. [Google Scholar] [CrossRef]
- Ramón, N.; Ruiz, J.L.; Sirvent, I. Cross-benchmarking for performance evaluation: Looking across best practices of different peer groups using DEA. Omega 2020, 92, 102169. [Google Scholar] [CrossRef]
- Guevel, H.P.; Ramón, N.; Aparicio, J. Benchmarking in data envelopment analysis: Balanced efforts to achieve realistic targets. Ann. Oper. Res. 2024, 1–24. [Google Scholar] [CrossRef]
- González-Rodríguez, M.; Díaz-Fernández, M.C.; Pulido-Pavón, N. Tourist destination competitiveness: An international approach through the travel and tourism competitiveness index. Tour. Manag. Perspect. 2023, 47, 101127. [Google Scholar] [CrossRef]
- Cheng, H.; Lu, Y.C.; Chung, J.T. Assurance region context-dependent DEA with an application to Taiwanese hotel industry. Int. J. Oper. Res. 2010, 8, 292–312. [Google Scholar] [CrossRef]
- Fernandes, V.A.; Pacheco, R.R.; Fernandes, E. A dynamic analysis of air transport and tourism in Brazil. J. Air Transp. Manag. 2022, 105, 102297. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Thrall, R.M. A structure for classifying and characterizing efficiency and inefficiency in data envelopment analysis. J. Product. Anal. 1991, 2, 197–237. [Google Scholar] [CrossRef]
- Ruiz, J.L.; Sirvent, I. Identifying suitable benchmarks in the way toward achieving targets using data envelopment analysis. Int. Trans. Oper. Res. 2022, 29, 1749–1768. [Google Scholar] [CrossRef]
- Podinovski, V. Computation of efficient targets in DEA models with production trade-offs and weight restrictions. Eur. J. Oper. Res. 2007, 181, 586–591. [Google Scholar] [CrossRef]
- Luna, L.I. Application of PCA with georeferenced data in the tourism industry: A case study in the province of Córdoba, Argentina. Tour. Econ. 2022, 28, 559–579. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S.; Poon, G.K.K. A data envelopment analysis method with assurance region for weight generation in the analytic hierarchy process. Decis. Support Syst. 2008, 45, 913–921. [Google Scholar] [CrossRef]
- Lai, P.; Potter, A.; Beynon, M.; Beresford, A. Evaluating the efficiency performance of airports using an integrated AHP/DEA-AR technique. Transp. Policy 2015, 42, 75–85. [Google Scholar] [CrossRef]
- Keskin, B.; Köksal, C.D. A hybrid AHP/DEA-AR model for measuring and comparing the efficiency of airports. Int. J. Product. Perform. Manag. 2019, 68, 524–541. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy process (AHP). J. Oper. Res. Soc. 1980, 41, 1073–1076. [Google Scholar]
- Thompson, R.G.; Langemeier, L.N.; Lee, C.T.; Lee, E.; Thrall, R.M. The role of multiplier bounds in efficiency analysis with application to Kansas farming. J. Econom. 1990, 46, 93–108. [Google Scholar] [CrossRef]
- Lee, H.; Park, Y.; Choi, H. Comparative evaluation of performance of national R&D programs with heterogeneous objectives: A DEA approach. Eur. J. Oper. Res. 2009, 196, 847–855. [Google Scholar] [CrossRef]
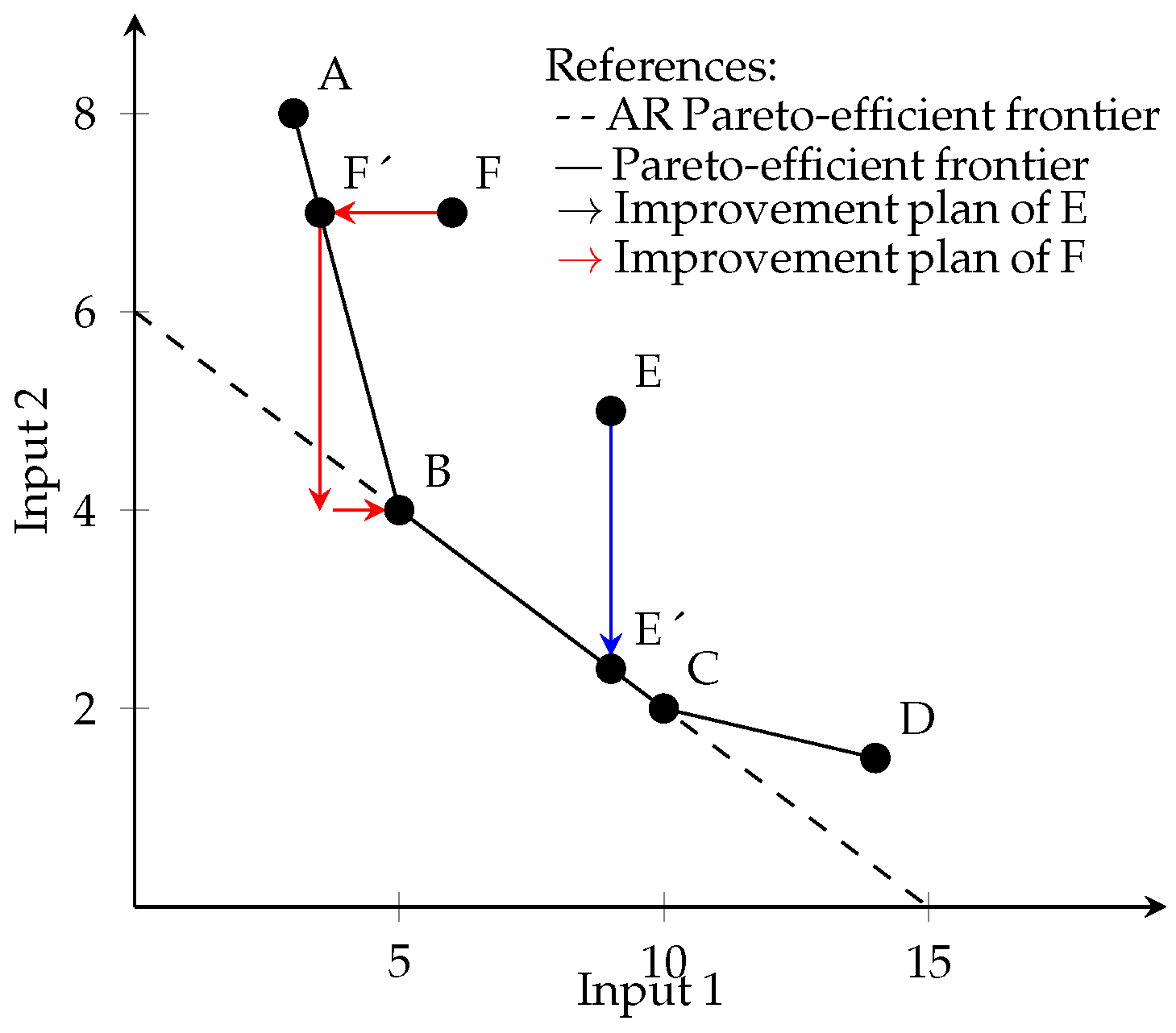
| DMU | X1 | X2 | Y1 | Condition | ||
|---|---|---|---|---|---|---|
| A | 3 | 8 | 10 | 0 | 6 | Pareto-Efficient |
| B | 5 | 4 | 10 | 0 | 0 | AR Pareto-Efficient |
| C | 10 | 2 | 10 | 0 | 0 | AR Pareto-Efficient |
| D | 14 | 1.5 | 10 | 0 | 4.5 | Pareto-Efficient |
| E | 9 | 5 | 10 | 2.6 | 0 | Non Pareto-Efficient |
| F | 6 | 7 | 10 | 2.5 | 4.5 | Non Pareto-Efficient |
| DMU | Targets | % of Changes | ||
|---|---|---|---|---|
| A | 5 | 4 | 66.66 | 50 |
| D | 10 | 2 | 28.57 | 0 |
| E | 9 | 2.4 | 0 | 52 |
| F | 6 | 3.6 | 16.66 | 42.58 |
| Code | Locality | Inputs | Outputs | |||
|---|---|---|---|---|---|---|
| PL | EN | EPA | LP | AT | ||
| AGO | Agua de Oro | 0.318 | 0.154 | 0.089 | 0.059 | 0.512 |
| AGR | Alta Gracia | 0.716 | 1.155 | 1.631 | 0.666 | 1.667 |
| ALM | Almafuerte | 0.184 | 0.319 | 0.345 | 0.525 | 0.433 |
| ALP | Arroyo Los Patos | 0.204 | 0.165 | 0.035 | 0.460 | 0.303 |
| ANI | Anisacate | 0.201 | 0.187 | 0.230 | 0.276 | 0.568 |
| ARY | Arroyito | 0.200 | 0.242 | 0.770 | 0.345 | 0.418 |
| BAL | Balnearia | 0.041 | 0.066 | 0.187 | 0.057 | 0.239 |
| BMA | Bialet Massé | 0.367 | 0.418 | 0.259 | 0.975 | 0.583 |
| CAB | Cabalango | 0.122 | 0.330 | 0.016 | 0.935 | 0.546 |
| CBA | Córdoba | 8.494 | 25.998 | 40.547 | 18.942 | 22.736 |
| CBL | Cuesta Blanca | 0.184 | 0.253 | 0.017 | 0.842 | 0.534 |
| CCA | Colonia Caroya | 0.215 | 0.418 | 0.692 | 0.192 | 1.043 |
| CCU | La Cumbrecita | 0.402 | 0.330 | 0.020 | 0.224 | 0.280 |
| CEJ | Cruz del Eje | 0.106 | 0.176 | 0.795 | 0.174 | 0.318 |
| CGR | Casa Grande | 0.172 | 0.154 | 0.037 | 0.429 | 0.523 |
| CMO | Capilla del Monte | 2.252 | 1.815 | 0.337 | 0.748 | 0.437 |
| CQN | Cosquín | 1.863 | 1.199 | 0.659 | 1.114 | 0.546 |
| CUA | Río Cuarto | 1.413 | 2.716 | 4.800 | 4.319 | 1.022 |
| EMB | Embalse | 0.365 | 0.594 | 0.260 | 0.494 | 0.407 |
| FRA | San Francisco | 0.569 | 0.561 | 1.898 | 1.086 | 0.845 |
| HGR | Huerta Grande | 2.238 | 0.583 | 0.207 | 0.695 | 0.516 |
| JES | Jesús María | 0.193 | 0.583 | 1.009 | 0.302 | 1.039 |
| LBO | Villa La Bolsa | 0.104 | 0.176 | 0.039 | 0.365 | 0.549 |
| LCA | Las Calles | 0.092 | 0.099 | 0.018 | 0.195 | 0.269 |
| LCO | Los Cocos | 0.508 | 0.253 | 0.037 | 0.467 | 0.448 |
| LCU | La Cumbre | 1.331 | 0.704 | 0.189 | 0.498 | 0.471 |
| LDR | Villa Dolores | 0.412 | 0.572 | 0.862 | 0.768 | 0.131 |
| LFA | La Falda | 4.688 | 1.595 | 0.439 | 1.512 | 0.538 |
| LGR | La Granja | 0.210 | 0.154 | 0.133 | 0.087 | 0.489 |
| LHO | Los Hornillos | 0.168 | 0.187 | 0.048 | 0.313 | 0.243 |
| LPO | La Población | 0.048 | 0.044 | 0.020 | 0.079 | 0.123 |
| LRA | Las Rabonas | 0.245 | 0.198 | 0.024 | 0.245 | 0.258 |
| LRE | Los Reartes | 0.550 | 0.561 | 0.082 | 0.261 | 0.411 |
| LSE | La Serranita | 0.230 | 0.165 | 0.016 | 0.162 | 0.531 |
| LVA | Las Varillas | 0.107 | 0.154 | 0.515 | 0.274 | 0.250 |
| MCL | Mina Clavero | 5.160 | 3.046 | 0.297 | 1.749 | 2.509 |
| MIR | Miramar | 0.843 | 0.792 | 0.076 | 0.562 | 0.202 |
| MSJ | Mayu Sumaj | 0.084 | 0.187 | 0.076 | 0.893 | 0.549 |
| NON | Nono | 1.346 | 1.023 | 0.054 | 0.675 | 0.291 |
| PAN | Panaholma | 0.032 | 0.066 | 0.006 | 0.223 | 0.228 |
| PGR | Potrero de Garay | 0.542 | 0.429 | 0.061 | 0.351 | 0.471 |
| RCE | Río Ceballos | 0.846 | 0.693 | 0.741 | 0.221 | 0.564 |
| RCR | Río Tercero | 0.230 | 0.429 | 1.398 | 0.908 | 0.949 |
| SAA | San Antonio de Arredondo | 0.362 | 0.363 | 0.159 | 0.848 | 0.546 |
| SAL | Salsipuedes | 0.253 | 0.286 | 0.440 | 0.068 | 0.557 |
| SJD | San José de la Dormida | 0.071 | 0.077 | 0.136 | 0.170 | 0.411 |
| SLO | San Lorenzo | 0.165 | 0.165 | 0.055 | 0.346 | 0.273 |
| SMS | San Marcos Sierra | 0.594 | 0.660 | 0.077 | 0.163 | 0.318 |
| SRC | Santa Rosa de Calamuchita | 3.560 | 3.057 | 0.511 | 1.547 | 2.015 |
| SRO | San Roque | 0.037 | 0.110 | 0.065 | 0.623 | 0.602 |
| TAN | Tanti | 1.003 | 0.748 | 0.289 | 0.693 | 0.542 |
| THU | Tala Huasi | 0.124 | 0.132 | 0.005 | 0.689 | 0.512 |
| UNQ | Unquillo | 0.075 | 0.396 | 0.700 | 0.201 | 0.557 |
| VAL | Villa Allende | 0.096 | 0.594 | 1.016 | 0.359 | 0.583 |
| VCA | Villa Ciudad de América | 0.279 | 0.176 | 0.031 | 0.275 | 0.497 |
| VCB | Villa Cura Brochero | 1.565 | 1.199 | 0.211 | 0.762 | 0.841 |
| VCP | Villa Carlos Paz | 13.407 | 5.620 | 1.870 | 7.189 | 7.198 |
| VDI | Villa del Dique | 0.619 | 0.528 | 0.137 | 0.500 | 0.273 |
| VGB | Villa General Belgrano | 3.176 | 2.013 | 0.313 | 1.508 | 2.382 |
| VGI | Villa Giardino | 1.688 | 0.693 | 0.194 | 1.179 | 0.504 |
| VHE | Valle Hermoso | 1.211 | 0.506 | 0.190 | 1.358 | 0.549 |
| VIC | Villa Río Icho Cruz | 0.397 | 0.275 | 0.075 | 0.988 | 0.546 |
| VLR | Villa Cdad Pque Los Reartes | 0.216 | 0.297 | 0.074 | 0.906 | 0.411 |
| VMA | Villa María | 0.993 | 0.638 | 2.652 | 2.048 | 1.451 |
| VPS | Villa Parque Siquimán | 0.190 | 0.231 | 0.093 | 0.905 | 0.594 |
| VRO | Villa de las Rosas | 0.081 | 0.165 | 0.154 | 0.327 | 0.202 |
| VRU | Villa Rumipal | 0.503 | 0.429 | 0.108 | 0.317 | 0.314 |
| VSC | Villa Santa Cruz del Lago | 0.261 | 0.154 | 0.096 | 0.859 | 0.564 |
| VTO | Villa del Totoral | 0.203 | 0.209 | 0.289 | 0.210 | 0.504 |
| VYA | Villa Yacanto | 0.275 | 0.341 | 0.090 | 0.296 | 0.265 |
| Code | Code | Code | Code | ||||
|---|---|---|---|---|---|---|---|
| AGO | 0.704 | CQN | 1.227 | LRE | 1.022 | UNQ | 1.068 |
| AGR | 0.146 | EMB | 0.794 | LSE | 0.600 | VAL | 1.224 |
| ALM | 0.414 | FRA | 0.606 | LVA | 0.647 | VCA | 0.574 |
| ALP | 0.210 | HGR | 1.753 | MIR | 1.146 | VCB | 0.828 |
| ANI | 0.512 | LBO | 0.358 | NON | 1.524 | VDI | 0.941 |
| ARY | 0.961 | LCA | 0.152 | PGR | 0.719 | VGI | 0.877 |
| BAL | 0.328 | LCO | 0.608 | RCE | 1.083 | VLR | 0.203 |
| BMA | 0.164 | LCU | 1.178 | SAA | 0.215 | VPS | 0.021 |
| CBL | 0.048 | LDR | 0.988 | SAL | 0.736 | VRO | 0.316 |
| CCU | 0.674 | LFA | 3.352 | SLO | 0.229 | VRU | 0.904 |
| CEJ | 0.866 | LGR | 0.512 | SMS | 1.163 | VTO | 0.634 |
| CGR | 0.312 | LHO | 0.279 | SRC | 1.156 | VYA | 0.566 |
| CMO | 1.967 | LRA | 0.341 | TAN | 0.781 |
| Exp1 | 0.6479 | 0.2299 | 0.1222 | 0.6667 | 0.3333 |
| Exp2 | 0.3338 | 0.5247 | 0.1416 | 0.3472 | 0.6528 |
| Exp3 | 0.3601 | 0.1279 | 0.5119 | 0.8333 | 0.1667 |
| Exp4 | 0.7028 | 0.1822 | 0.1149 | 0.3333 | 0.6667 |
| Exp5 | 0.4000 | 0.3667 | 0.2333 | 0.6667 | 0.3333 |
| Exp6 | 0.2000 | 0.6000 | 0.2000 | 0.8571 | 0.1429 |
| Exp7 | 0.3113 | 0.6227 | 0.0660 | 0.8333 | 0.1667 |
| Exp8 | 0.3591 | 0.5644 | 0.0765 | 0.8333 | 0.1667 |
| Exp9 | 0.6584 | 0.2618 | 0.0798 | 0.8571 | 0.1429 |
| Exp10 | 0.4577 | 0.4160 | 0.1263 | 0.8750 | 0.1250 |
| Exp11 | 0.4484 | 0.2884 | 0.2632 | 0.8333 | 0.1667 |
| Inefficient DMU | CAB | CBA | CUA | MSJ | LPO | PAN | SRO | THU | VCP | VMA |
|---|---|---|---|---|---|---|---|---|---|---|
| AGO | 0 | 0 | 0 | 0 | 0 | 0.469 | 0.531 | 0 | 0 | 0 |
| AGR | 0 | 0.031 | 0 | 0.89 | 0 | 0 | 0 | 0 | 0.024 | 0.055 |
| ALM | 0 | 0.007 | 0 | 0 | 0 | 0 | 0.993 | 0 | 0 | 0 |
| ALP | 0.174 | 0 | 0 | 0.108 | 0 | 0 | 0.339 | 0.379 | 0 | 0 |
| ANI | 0 | 0.002 | 0 | 0 | 0 | 0 | 0.972 | 0 | 0 | 0.026 |
| ARY | 0 | 0 | 0 | 0 | 0 | 0 | 0.925 | 0 | 0.008 | 0.067 |
| BAL | 0 | 0 | 0 | 0 | 0.032 | 0.968 | 0 | 0 | 0 | 0 |
| BMA | 0.333 | 0 | 0.037 | 0.614 | 0 | 0 | 0 | 0 | 0.016 | 0 |
| CBL | 0.605 | 0 | 0 | 0.036 | 0 | 0 | 0.038 | 0.321 | 0 | 0 |
| CCA | 0 | 0 | 0 | 0 | 0.209 | 0.791 | 0 | 0 | 0 | 0 |
| CCU | 0 | 0 | 0 | 0 | 0 | 0.86 | 0.14 | 0 | 0 | 0 |
| CEJ | 0 | 0 | 0 | 0 | 0.334 | 0.666 | 0 | 0 | 0 | 0 |
| CGR | 0.133 | 0 | 0 | 0.083 | 0 | 0 | 0.408 | 0.376 | 0 | 0 |
| CMO | 0.933 | 0 | 0.067 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CQN | 0.854 | 0 | 0.127 | 0 | 0 | 0 | 0 | 0 | 0.019 | 0 |
| EMB | 0 | 0 | 0 | 0 | 0 | 0 | 0.919 | 0 | 0.02 | 0.061 |
| FRA | 0 | 0.008 | 0 | 0 | 0 | 0 | 0.501 | 0 | 0 | 0.491 |
| HGR | 0.948 | 0 | 0.032 | 0 | 0 | 0 | 0 | 0 | 0.02 | 0 |
| JES | 0 | 0.018 | 0 | 0 | 0 | 0 | 0.98 | 0 | 0 | 0.002 |
| LBO | 0.28 | 0 | 0 | 0 | 0 | 0 | 0.52 | 0.2 | 0 | 0 |
| LCA | 0 | 0 | 0 | 0 | 0 | 0.89 | 0.11 | 0 | 0 | 0 |
| LCO | 0.573 | 0 | 0 | 0 | 0 | 0 | 0.427 | 0 | 0 | 0 |
| LCU | 0 | 0.002 | 0 | 0 | 0 | 0 | 0.982 | 0 | 0 | 0.016 |
| LDR | 0.899 | 0 | 0.101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| LFA | 0.912 | 0 | 0.088 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| LGR | 0 | 0 | 0 | 0 | 0 | 0.666 | 0.334 | 0 | 0 | 0 |
| LHO | 0 | 0 | 0 | 0 | 0 | 0.685 | 0.315 | 0 | 0 | 0 |
| LRA | 0 | 0 | 0 | 0 | 0 | 0.91 | 0.09 | 0 | 0 | 0 |
| LRE | 0 | 0 | 0 | 0 | 0 | 0.51 | 0.49 | 0 | 0 | 0 |
| LSE | 0.083 | 0 | 0 | 0 | 0 | 0 | 0.163 | 0.754 | 0 | 0 |
| LVA | 0 | 0 | 0 | 0 | 0 | 0.888 | 0.013 | 0.099 | 0 | 0 |
| MCL | 0.849 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.151 | 0 |
| MIR | 0 | 0 | 0 | 0 | 0 | 0.494 | 0.088 | 0.418 | 0 | 0 |
| NON | 0 | 0 | 0 | 0.517 | 0 | 0 | 0.213 | 0.27 | 0 | 0 |
| PGR | 0 | 0 | 0 | 0 | 0 | 0.35 | 0.65 | 0 | 0 | 0 |
| RCE | 0 | 0 | 0 | 0 | 0.009 | 0.991 | 0 | 0 | 0 | 0 |
| RCR | 0 | 0.01 | 0 | 0 | 0 | 0 | 0.877 | 0 | 0 | 0.113 |
| SAA | 0.274 | 0 | 0.014 | 0.693 | 0 | 0 | 0 | 0 | 0.019 | 0 |
| SAL | 0 | 0 | 0 | 0 | 0 | 0.614 | 0.386 | 0 | 0 | 0 |
| SJD | 0 | 0 | 0 | 0 | 0.367 | 0.633 | 0 | 0 | 0 | 0 |
| SLO | 0 | 0 | 0 | 0 | 0 | 0.583 | 0.417 | 0 | 0 | 0 |
| SMS | 0 | 0 | 0 | 0 | 0.181 | 0.819 | 0 | 0 | 0 | 0 |
| SRC | 0 | 0 | 0 | 0 | 0 | 0 | 0.759 | 0 | 0.229 | 0.012 |
| TAN | 0 | 0 | 0.021 | 0.916 | 0 | 0 | 0 | 0 | 0.063 | 0 |
| UNQ | 0 | 0.004 | 0 | 0 | 0 | 0 | 0.995 | 0 | 0 | 0.001 |
| VAL | 0 | 0.007 | 0 | 0 | 0 | 0 | 0.992 | 0 | 0 | 0.001 |
| VCA | 0.251 | 0 | 0 | 0.033 | 0 | 0 | 0.345 | 0.371 | 0 | 0 |
| VCB | 0 | 0 | 0 | 0 | 0 | 0 | 0.886 | 0 | 0.114 | 0 |
| VDI | 0.189 | 0 | 0 | 0.771 | 0 | 0 | 0 | 0 | 0.04 | 0 |
| VGB | 0.84 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.16 | 0 |
| VGI | 0.951 | 0 | 0.029 | 0 | 0 | 0 | 0 | 0 | 0.02 | 0 |
| VHE | 0.951 | 0 | 0.029 | 0 | 0 | 0 | 0 | 0 | 0.02 | 0 |
| VIC | 0.279 | 0 | 0 | 0.712 | 0 | 0 | 0 | 0 | 0.009 | 0 |
| VLR | 0.416 | 0 | 0.001 | 0.574 | 0 | 0 | 0 | 0 | 0.009 | 0 |
| VPS | 0 | 0 | 0 | 0.831 | 0 | 0 | 0.159 | 0 | 0.008 | 0.002 |
| VRO | 0 | 0 | 0 | 0 | 0 | 0.831 | 0.027 | 0.142 | 0 | 0 |
| VRU | 0 | 0 | 0 | 0 | 0 | 0.369 | 0.631 | 0 | 0 | 0 |
| VSC | 0 | 0 | 0 | 0.525 | 0 | 0 | 0.461 | 0 | 0.014 | 0 |
| VTO | 0 | 0.004 | 0 | 0 | 0 | 0 | 0.97 | 0 | 0 | 0.026 |
| VYA | 0 | 0 | 0 | 0 | 0 | 0.502 | 0.498 | 0 | 0 | 0 |
| Times as referents | 21 | 10 | 11 | 14 | 6 | 21 | 38 | 10 | 19 | 13 |
| Inefficient DMU | Inputs | Outputs | Inefficient DMU | Inputs | Outputs | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PL | EN | EPA | LT | AT | PL | EN | EPA | LT | AT | ||
| AGO | AGR | ||||||||||
| Data | 4571 | 14 | 2158 | 3713 | 4657 | Data | 10293 | 105 | 39542 | 41916 | 15161 |
| Targets | 489 | 8 | 897 | 27378 | 3874 | Targets | 10293 | 105 | 37215 | 105419 | 13242 |
| % Change | −89.2% | −42.0% | −58.1% | 638.9% | −16.7% | % Change | 0.0% | 0.0% | −5.9% | 151.4% | −12.7% |
| ALM | ALP | ||||||||||
| Data | 2645 | 29 | 8364 | 33042 | 3938 | Data | 2933 | 15 | 849 | 28951 | 2756 |
| Targets | 1409 | 27 | 8728 | 47643 | 6939 | Targets | 1294 | 15 | 849 | 46070 | 5020 |
| % Change | −46.5% | −6.4% | 4.2% | 44.2% | 76.0% | % Change | −56.0% | 0.0% | 0.0% | 59.0% | 82.4% |
| ANI | ARY | ||||||||||
| Data | 2889 | 17 | 5576 | 17371 | 5166 | Data | 2875 | 22 | 18668 | 21713 | 3802 |
| Targets | 1179 | 17 | 5576 | 44371 | 6166 | Targets | 2875 | 17 | 6134 | 48336 | 6439 |
| % Change | −59.3% | 0.0% | 0.0% | 155.7% | 19.3% | % Change | 0.0% | −23.0% | −67.2% | 122.8% | 69.1% |
| BAL | BMA | ||||||||||
| Data | 589 | 6 | 4534 | 3587 | 2174 | Data | 5276 | 38 | 6279 | 61364 | 5302 |
| Targets | 460 | 6 | 145 | 13720 | 2046 | Targets | 5276 | 38 | 6279 | 71622 | 6148 |
| % Change | −21.2% | 0% | −96.6% | 283.3% | −6.1% | % Change | 0.0% | 0.0% | 0.0% | 16.7% | 16.0% |
| CBL | CCA | ||||||||||
| Data | 2645 | 23 | 412 | 52993 | 4857 | Data | 3091 | 38 | 16777 | 12084 | 9486 |
| Targets | 1696 | 23 | 412 | 52993 | 4884 | Targets | 503 | 6 | 218 | 12084 | 1874 |
| % Change | −35.8% | 0.0% | 0.0% | 0.0% | 0.5% | % Change | −83.7% | −85.3% | −98.7% | 0.0% | −80.2% |
| CCU | CEJ | ||||||||||
| Data | 5779 | 30 | 485 | 14098 | 2547 | Data | 1524 | 16 | 19274 | 10951 | 2892 |
| Targets | 460 | 7 | 339 | 17559 | 2547 | Targets | 532 | 5 | 267 | 10951 | 1755 |
| % Change | −91.9% | −78.1% | −29.5% | 24.4% | 0.0% | % Change | −65.1% | −66.7% | −98.7% | 0.0% | −39.2% |
| CGR | CMO | ||||||||||
| Data | 2473 | 14 | 897 | 27000 | 4757 | Data | 32373 | 165 | 8170 | 47077 | 3975 |
| Targets | 1222 | 14 | 897 | 44811 | 5057 | Targets | 2990 | 45 | 8170 | 73070 | 5248 |
| % Change | −50.8% | 0.0% | 0.0% | 66.1% | 6.3% | % Change | −90.7% | −73.0% | 0.0% | 55.4% | 32.1% |
| CQN | EMB | ||||||||||
| Data | 26781 | 109 | 15977 | 70112 | 4966 | Data | 5247 | 54 | 6303 | 31091 | 3702 |
| Targets | 7619 | 67 | 15977 | 93147 | 6621 | Targets | 5247 | 23 | 6303 | 53056 | 7158 |
| % Change | −71.6% | −39.0% | 0.0% | 32.8% | 33.5% | % Change | 0.0% | −57.3% | 0.0% | 70.6% | 93.1% |
| FRA | HGR | ||||||||||
| Data | 8179 | 51 | 46015 | 68350 | 7685 | Data | 32171 | 53 | 5019 | 43741 | 4693 |
| Targets | 8179 | 51 | 39639 | 91825 | 10750 | Targets | 6224 | 47 | 5019 | 73636 | 6330 |
| % Change | 0.0% | 0.0% | −13.8% | 34.3% | 39.9% | % Change | −80.6% | −11.9% | 0.0% | 68.4% | 35.0% |
| JES | LBO | ||||||||||
| Data | 2774 | 53 | 24462 | 19007 | 9450 | Data | 1495 | 16 | 946 | 22972 | 4993 |
| Targets | 2774 | 53 | 19589 | 60420 | 9159 | Targets | 1121 | 16 | 946 | 45566 | 5166 |
| % Change | 0.0% | 0.0% | −19.9% | 217.8% | −3.1% | % Change | −24.7% | 0.0% | 0.0% | 98.2% | 3.4% |
| LCA | LCO | ||||||||||
| Data | 1323 | 9 | 436 | 12273 | 2447 | Data | 7303 | 23 | 897 | 29392 | 4075 |
| Targets | 460 | 6 | 291 | 16804 | 2447 | Targets | 1222 | 21 | 897 | 50475 | 5175 |
| % Change | −64.9% | −28.4% | −32.3% | 37.1% | 0.0% | % Change | −83.2% | −6.7% | 0.0% | 71.6% | 27.0% |
| LCU | LDR | ||||||||||
| Data | 19133 | 64 | 4582 | 31343 | 4284 | Data | 5923 | 52 | 20898 | 48336 | 1191 |
| Targets | 992 | 16 | 4582 | 43049 | 6003 | Targets | 3637 | 52 | 12146 | 80433 | 5402 |
| % Change | −94.8% | −75.7% | 0.0% | 37.2% | 40.2% | % Change | −38.6% | 0.0% | −41.9% | 66.4% | 354.3% |
| LFA | LGR | ||||||||||
| Data | 67390 | 145 | 10643 | 95161 | 4893 | Data | 3019 | 14 | 3224 | 5476 | 4447 |
| Targets | 3393 | 49 | 10643 | 77664 | 5348 | Targets | 474 | 7 | 630 | 22469 | 3211 |
| % Change | −95.0% | −66.1% | 0.0% | −18.4% | 9.2% | % Change | −84.1% | −47.6% | −80.8% | 311.1% | −27.9% |
| LHO | LRA | ||||||||||
| Data | 2415 | 17 | 1164 | 19699 | 2210 | Data | 3522 | 18 | 582 | 15420 | 2347 |
| Targets | 474 | 7 | 582 | 21965 | 3147 | Targets | 460 | 6 | 267 | 16238 | 2374 |
| % Change | −80.2% | −57.3% | −49.2% | 11.7% | 42.4% | % Change | −86.8% | −64.7% | −54.4% | 5.6% | 1.4% |
| LRE | LSE | ||||||||||
| Data | 7906 | 51 | 1988 | 16427 | 3738 | Data | 3306 | 15 | 388 | 10196 | 4829 |
| Targets | 489 | 8 | 849 | 26371 | 3738 | Targets | 1567 | 13 | 388 | 43993 | 4811 |
| % Change | −93.8% | −84.4% | −57.6% | 60.8% | 0.0% | % Change | −52.6% | −12.2% | 0.0% | 332.4% | −0.2% |
| LVA | MCL | ||||||||||
| Data | 1538 | 14 | 12486 | 17245 | 2274 | Data | 74175 | 277 | 7200 | 110077 | 22819 |
| Targets | 589 | 7 | 170 | 17245 | 2374 | Targets | 30676 | 103 | 7200 | 118447 | 14125 |
| % Change | −61.8% | −52.5% | −98.7% | 0.0% | 4.3% | % Change | −58.6% | −62.9% | 0.0% | 7.6% | −38.1% |
| MIR | NON | ||||||||||
| Data | 12118 | 72 | 1843 | 35371 | 1837 | Data | 19349 | 93 | 1309 | 42482 | 2647 |
| Targets | 1021 | 9 | 267 | 28510 | 3447 | Targets | 1222 | 14 | 1309 | 49154 | 5002 |
| % Change | −91.6% | −87.7% | −85.8% | −19.5% | 88.0% | % Change | −93.7% | −84.8% | 0.0% | 15.6% | 88.8% |
| PGR | RCE | ||||||||||
| Data | 7791 | 39 | 1479 | 22091 | 4284 | Data | 12161 | 63 | 17965 | 13909 | 5130 |
| Targets | 503 | 9 | 1067 | 30399 | 4284 | Targets | 460 | 6 | 145 | 13909 | 2065 |
| % Change | −93.5% | −78.0% | −27.2% | 37.7% | 0.0% | % Change | −96.2% | − 90.5% | −99.2% | 0.0% | −59.8% |
| RCR | SAA | ||||||||||
| Data | 3306 | 39 | 33893 | 57147 | 8631 | Data | 5204 | 33 | 3855 | 53371 | 4966 |
| Targets | 3306 | 39 | 18498 | 60923 | 8358 | Targets | 5204 | 33 | 3855 | 67343 | 6176 |
| % Change | 0.0% | 0.0% | −45.4% | 6.6% | −3.2% | % Change | 0.0% | 0.0% | 0.0% | 26.1% | 24.5% |
| SAL | SJD | ||||||||||
| Data | 3637 | 26 | 10667 | 4280 | 5066 | Data | 1021 | 7 | 3297 | 10699 | 3738 |
| Targets | 489 | 8 | 703 | 23727 | 3383 | Targets | 546 | 5 | 267 | 10699 | 1719 |
| % Change | −86.7% | −71.0% | −93.5% | 458.6% | −33.2% | % Change | −47.1% | −24.8% | −91.9% | 0.0% | −53.9% |
| SLO | SMS | ||||||||||
| Data | 2372 | 15 | 1333 | 21776 | 2483 | Data | 8539 | 60 | 1867 | 10259 | 2892 |
| Targets | 489 | 8 | 727 | 24545 | 3492 | Targets | 503 | 6 | 194 | 12399 | 1901 |
| % Change | −79.5% | −48.9% | −44.9% | 12.5% | 40.6% | % Change | −94.2% | −90.6% | −89.1% | 20.3% | −34.2% |
| SRC | TAN | ||||||||||
| Data | 51175 | 278 | 12389 | 97364 | 18326 | Data | 14418 | 68 | 7007 | 43615 | 4929 |
| Targets | 44649 | 125 | 12389 | 134874 | 19290 | Targets | 13599 | 53 | 7007 | 85657 | 8868 |
| % Change | −12.8% | −55.0% | 0.0% | 38.5% | 5.2% | % Change | −5.7% | −22.3% | 0.0% | 96.4% | 80.0% |
| UNQ | VAL | ||||||||||
| Data | 1078 | 36 | 16971 | 12650 | 5066 | Data | 1380 | 54 | 24632 | 22594 | 5302 |
| Targets | 1078 | 21 | 6013 | 44434 | 6376 | Targets | 1380 | 26 | 8413 | 47266 | 6867 |
| % Change | 0.0% | −42.8% | −64.6% | 251.7% | 26.0% | % Change | 0.0% | −51.2% | −65.9% | 109.1% | 29.6% |
| VCA | VCB | ||||||||||
| Data | 4011 | 16 | 752 | 17308 | 4520 | Data | 22497 | 109 | 5115 | 47958 | 7649 |
| Targets | 1323 | 16 | 752 | 46259 | 5030 | Targets | 22497 | 67 | 6570 | 86475 | 12333 |
| % Change | −67.0% | 0.0% | 0.0% | 167.3% | 11.2% | % Change | 0.0% | −38.3% | 28.3% | 80.2% | 61.2% |
| VDI | VGB | ||||||||||
| Data | 8898 | 48 | 3321 | 31469 | 2483 | Data | 45655 | 183 | 7588 | 94909 | 21664 |
| Targets | 8898 | 39 | 3321 | 72440 | 7385 | Targets | 32344 | 107 | 7588 | 121909 | 14652 |
| % Change | 0.0% | −18.6% | 0.0% | 130.3% | 197.7% | % Change | −29.2% | −41.5% | 0.0% | 28.4% | −32.4% |
| VGI | VHE | ||||||||||
| Data | 24265 | 63 | 4703 | 74203 | 4584 | Data | 17408 | 46 | 4606 | 85468 | 4993 |
| Targets | 6181 | 46 | 4703 | 73070 | 6321 | Targets | 6181 | 46 | 4606 | 72944 | 6321 |
| % Change | −74.5% | −26.7% | 0.0% | −1.5% | 37.8% | % Change | −64.5% | 0.0% | 0.0% | −14.7% | 26.5% |
| VIC | VLR | ||||||||||
| Data | 5707 | 25 | 1818 | 62182 | 4966 | Data | 3105 | 27 | 1794 | 57021 | 3738 |
| Targets | 3062 | 25 | 1818 | 60420 | 5521 | Targets | 3105 | 27 | 1794 | 61049 | 5502 |
| % Change | −46.5% | 0.0% | 0.0% | −2.8% | 11.3% | % Change | 0.0% | 0.0% | 0.0% | 7.1% | 47.3% |
| VPS | VRO | ||||||||||
| Data | 2731 | 21 | 2255 | 56958 | 5402 | Data | 1164 | 15 | 3734 | 20580 | 1837 |
| Targets | 2731 | 20 | 2255 | 56958 | 5593 | Targets | 647 | 7 | 170 | 18881 | 2528 |
| % Change | 0.0% | −4.2% | 0.0% | 0.0% | 3.5% | % Change | −44.6% | −53.6% | −95.2% | −8.3% | 37.9% |
| VRU | VSC | ||||||||||
| Data | 7231 | 39 | 2618 | 19951 | 2856 | Data | 3752 | 14 | 2327 | 54063 | 5130 |
| Targets | 503 | 9 | 1042 | 29958 | 4220 | Targets | 3637 | 21 | 2327 | 54063 | 6075 |
| % Change | −93.1% | −78.1% | −60.2% | 50.2% | 47.8% | % Change | −3.3% | 48.8% | 0.0% | 0.0% | 18.5% |
| VTO | VYA | ||||||||||
| Data | 2918 | 19 | 7007 | 13217 | 4584 | Data | 3953 | 31 | 2182 | 18629 | 2410 |
| Targets | 1294 | 19 | 6449 | 45378 | 6339 | Targets | 489 | 8 | 849 | 26559 | 3765 |
| % Change | −55.7% | 0.0% | −7.7% | 244.1% | 38.1% | % Change | −87.5% | −74.2% | −60.8% | 42.4% | 56.0% |
| Inefficient DMU | CAB | CBA | CUA | MSJ | LPO | PAN | SRO | THU | VCP | VMA |
|---|---|---|---|---|---|---|---|---|---|---|
| BMA | 0.333 | 0 | 0.037 | 0.614 | 0 | 0 | 0 | 0 | 0.017 | 0 |
| CCA | 0 | 0 | 0 | 0 | 0.209 | 0.791 | 0 | 0 | 0 | 0 |
| CCU | 0 | 0 | 0 | 0 | 0 | 0.86 | 0.14 | 0 | 0 | 0 |
| CEJ | 0 | 0 | 0 | 0 | 0.334 | 0.666 | 0 | 0 | 0 | 0 |
| EMB | 0.941 | 0 | 0.046 | 0 | 0 | 0 | 0 | 0 | 0.014 | 0 |
| JES | 0 | 0.018 | 0 | 0 | 0 | 0 | 0.98 | 0 | 0 | 0.002 |
| LRA | 0 | 0 | 0 | 0 | 0 | 0.92 | 0.08 | 0 | 0 | 0 |
| LRE | 0 | 0 | 0 | 0 | 0 | 0.51 | 0.49 | 0 | 0 | 0 |
| MCL | 0.849 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.151 | 0 |
| RCE | 0 | 0 | 0 | 0 | 0.009 | 0.991 | 0 | 0 | 0 | 0 |
| RCR | 0 | 0.01 | 0 | 0 | 0 | 0 | 0.877 | 0 | 0 | 0.113 |
| SAA | 0.274 | 0 | 0.014 | 0.693 | 0 | 0 | 0 | 0 | 0.019 | 0 |
| VAL | 0 | 0.007 | 0 | 0 | 0 | 0 | 0.993 | 0 | 0 | 0 |
| VGB | 0.84 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.16 | 0 |
| VGI | 0.948 | 0 | 0.028 | 0 | 0 | 0 | 0 | 0 | 0.024 | 0 |
| VHE | 0.951 | 0 | 0.029 | 0 | 0 | 0 | 0 | 0 | 0.02 | 0 |
| VIC | 0.279 | 0 | 0 | 0.712 | 0 | 0 | 0 | 0 | 0.009 | 0 |
| VLR | 0.416 | 0 | 0.002 | 0.574 | 0 | 0 | 0 | 0 | 0.009 | 0 |
| VSC | 0 | 0 | 0 | 0.525 | 0 | 0 | 0.461 | 0 | 0.014 | 0 |
| VYA | 0 | 0 | 0 | 0 | 0 | 0.842 | 0 | 0.158 | 0 | 0 |
| Times as referents | 15 | 5 | 12 | 12 | 14 | 27 | 24 | 12 | 15 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guevel, H.P.; Ramón, N.; Aparicio, J. Benchmarking and Target Setting in Weight Restriction Context. Mathematics 2025, 13, 1175. https://doi.org/10.3390/math13071175
Guevel HP, Ramón N, Aparicio J. Benchmarking and Target Setting in Weight Restriction Context. Mathematics. 2025; 13(7):1175. https://doi.org/10.3390/math13071175
Chicago/Turabian StyleGuevel, Hernán P., Nuria Ramón, and Juan Aparicio. 2025. "Benchmarking and Target Setting in Weight Restriction Context" Mathematics 13, no. 7: 1175. https://doi.org/10.3390/math13071175
APA StyleGuevel, H. P., Ramón, N., & Aparicio, J. (2025). Benchmarking and Target Setting in Weight Restriction Context. Mathematics, 13(7), 1175. https://doi.org/10.3390/math13071175







