On New Generalized Mitrinović-Adamović-Type Inequalities

Abstract

In this paper, we establish new generalized Mitrinović-Adamović-type inequalities in a wider range $(0,\pi )$ by using the monotonicity of certain functions. These inequalities contain sharp and tractable bounds for the function ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3.$ All the main results are also true in $(-\pi ,0)$ due to the symmetry of the curves involved.

1. Introduction

An obvious relation $\cos x<{\displaystyle \frac{\sin x}{x}},x\in (0,\pi /2)$ was refined in [1,2] as

$$\begin{array}{c}\hfill \cos x<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right).\end{array}$$

(1)

The inequality (1) is known in the literature as Mitrinović–Adamović inequality. In recent years, some mathematicians tried to refine and extend the inequality (1). For instance, the inequality

$$\begin{array}{c}\hfill {\cos }^4{\displaystyle \frac{x}{2}}<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

appeared in the references [3,4,5]. Mortici [6] and Chouikha [7] independently obtained, respectively, the following double inequalities:

$$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{x^4}{15}}-{\displaystyle \frac{23x^6}{1890}}<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{x^4}{15}},x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

and

$$\begin{array}{c}\hfill \cos x+x^3\left(1-{\displaystyle \frac{x^2}{63}}\right){\displaystyle \frac{\sin x}{15}}<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{x^3\sin x}{15}},x\in \left(0,{\displaystyle \frac{\pi }{2}}\right).\end{array}$$

We observe that it is not difficult to show the validity of (1) in an interval $\left(0,\pi \right).$ In this direction, Zhu [8] achieved the inequalities

$$\begin{array}{c}\hfill \cos x<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<{\displaystyle \frac{8}{{\pi }^3}}+\left(1-{\displaystyle \frac{8}{{\pi }^3}}\right)\cos x,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right),\end{array}$$

$$\begin{array}{c}\hfill {\displaystyle \frac{8}{{\pi }^3}}+\left(1-{\displaystyle \frac{8}{{\pi }^3}}\right)\cos x<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<{\displaystyle \frac{1+\cos x}{2}},x\in \left({\displaystyle \frac{\pi }{2}},\pi \right)\end{array}$$

and

$$\begin{array}{c}\hfill \left(1-{\displaystyle \frac{32}{{\pi }^5}}{x}^2\right)\cos x+{\displaystyle \frac{32}{{\pi }^5}}{x}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\left(1-{\displaystyle \frac{2}{15}}{x}^2\right)\cos x+{\displaystyle \frac{2}{15}}{x}^2,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right),\end{array}$$

$$\begin{array}{c}\hfill \left(1-{\displaystyle \frac{1}{2{\pi }^2}}{x}^2\right)\cos x+{\displaystyle \frac{1}{2{\pi }^2}}{x}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\left(1-{\displaystyle \frac{32}{{\pi }^5}}{x}^2\right)\cos x+{\displaystyle \frac{32}{{\pi }^5}}{x}^2,x\in \left({\displaystyle \frac{\pi }{2}},\pi \right).\end{array}$$

On the other hand, W.-D. Jiang [9] very recently maintained the uniformity and sharpness of the bounds for ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ in a wider range $(0,\pi )$ and established a better double inequality

$$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{21}{5}}{\displaystyle \frac{x^3\sin x}{63+x^2}}<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{{\pi }^2}{15}}{\displaystyle \frac{x^3\sin x}{{\pi }^2-x^2}},x\in (0,\pi )\end{array}$$

(2)

along with

$$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{x^3\sin x}{15+\frac{5}{21}{x}^2}}<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{x^3\sin x}{15+\frac{{\pi }^6-960}{16{\pi }^2}{x}^2}},x\in (0,\pi /2).\end{array}$$

(3)

We also refer the reader to [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] and the references therein for more information on this topic.

In this work, by using the monotonicity of certain functions, we establish new generalized Mitrinović–Adamović-type inequalities in a wider range $(0,\pi )$. We obtain sharp bounds for ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ in a wider range $(0,\pi )$ and refine double inequalities (2)–(3).

2. Lemmas for Bernoulli Numbers

Recall that the Bernoulli numbers $B_n$ can be generated by

$${\displaystyle \frac{z}{e^z-1}}={\displaystyle \sum _{n=0}^{\infty }}{B}_n{\displaystyle \frac{z^n}{n!}}=1-{\displaystyle \frac{z}{2}}+{\displaystyle \sum _{k=1}^{\infty }}{B}_{2k}{\displaystyle \frac{z^{2k}}{\left(2k\right)!}},\left|z\right|<2\pi ,$$

and all of the Bernoulli numbers $B_{2k+1}$ for $k\in \mathbb{N}$ equal 0. For more details, we refer the interested readers to the research monograph [25].

To prove our main results, we need the following important lemmas.

Lemma 1

(see [8,9,25]). Let $B_{2k}(k\in \mathbb{N})$ be the even indexed Bernoulli numbers. Then, for $\left|x\right|<\pi$, the following identities hold:

$${\displaystyle \frac{x}{\sin x}}=1+\sum _{k=1}^{\infty }{\displaystyle \frac{2(2^{2k-1}-1)\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k},$$

$$\cot x={\displaystyle \frac{1}{x}}-\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k}\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k-1},$$

$${\displaystyle \frac{1}{{\sin }^{2}x}}={\displaystyle \frac{1}{x^2}}+\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k-2},$$

$${\displaystyle \frac{\cos x}{{\sin }^{2}x}}={\displaystyle \frac{1}{x^2}}-\sum _{k=1}^{\infty }{\displaystyle \frac{2(2k-1)(2^{2k-1}-1)\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k-2},$$

$${\displaystyle \frac{\cos x}{{\sin }^{3}x}}={\displaystyle \frac{1}{x^3}}-\sum _{k=2}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)(k-1)\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k-3},$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\sin }^{3}x}}& ={\displaystyle \frac{1}{x^3}}+{\displaystyle \frac{1}{2}}\sum _{k=2}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k-3}+{\displaystyle \frac{1}{2x}}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k}-2)\left|B_{2k}\right|}{\left(2k\right)!}}{x}^{2k-1},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\cos x}{{\sin }^{4}x}}& =-{\displaystyle \frac{1}{3x^3}}-{\displaystyle \frac{1}{6x}}-\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)}{6·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}\hfill \\ \hfill & -\sum _{k=2}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)(2k-3)}{6·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-4},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\sin }^{4}x}}& ={\displaystyle \frac{1}{x^4}}+\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)(2k-2)(2k-3)}{6·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-4}+{\displaystyle \frac{2}{3x^2}}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k+1}(2k-1)}{3·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}.\hfill \end{array}$$

Lemma 2

(see [26]). For $k\in \mathbb{N},$ we have

$$\begin{array}{c}\hfill \left|B_{2k}\right|>{\displaystyle \frac{2\left(2k\right)!}{{\pi }^{2k}(2^{2k}-1)}},\end{array}$$

(4)

where $B_{2k}$ are the even indexed Bernoulli numbers.

The following well-known Qi’s inequality for Bernoulli numbers is crucial in this paper.

Lemma 3

(see [27]). For $k\in \mathbb{N},$ the even indexed Bernoulli numbers satisfy

$$\begin{array}{c}\hfill {\displaystyle \frac{|B_{2k+2}|}{|B_{2k}|}}>{\displaystyle \frac{2^{2k-1}-1}{2^{2k+1}-1}}{\displaystyle \frac{(2k+1)(2k+2)}{{\pi }^2}}.\end{array}$$

(5)

We now establish some new auxiliary results for even indexed Bernoulli numbers.

Lemma 4.

For $k=4,5,6,\cdots ,$ we have

$$\begin{array}{c}\hfill \left|B_{2k}\right|>{\displaystyle \frac{2k}{3(2^{2k}-1)}}.\end{array}$$

(6)

Proof. 

It is obvious that

$$3\left(2k\right)!>{\pi }^{2k}·k,\mathrm{for}k=4,5,6,\cdots .$$

From this, we write

$${\displaystyle \frac{2\left(2k\right)!}{{\pi }^{2k}(2^{2k}-1)}}>{\displaystyle \frac{2k}{3(2^{2k}-1)}},\mathrm{for}k=4,5,6,\cdots .$$

Combining this with the inequality (4), we obtain the inequality (6). □

Lemma 5.

For $k=4,5,6,\cdots ,$ it is true that

$$\begin{array}{c}\hfill {\displaystyle \frac{|B_{2k+2}|}{|B_{2k}|}}>{\displaystyle \frac{2(2k-1)(2k+1)(2k+2)}{3(2^{2k+2}-1)}}.\end{array}$$

(7)

Proof. 

Since,

$$2^{2k+2}-1>2^{2k+1}-1$$

and

$$3(2^{2k-1}-1)>2{\pi }^2(2k-1),$$

for $k=4,5,6,\cdots ,$ we obtain

$$3(2^{2k-1}-1)(2^{2k+2}-1)>2{\pi }^2(2k-1)(2^{2k+1}-1),$$

for $k=4,5,6,\cdots .$ Equivalently, we write

$${\displaystyle \frac{(2^{2k-1}-1)(2k+1)(2k+2)}{{\pi }^2(2^{2k+1}-1)}}>{\displaystyle \frac{2(2k-1)(2k+1)(2k+2)}{3(2^{2k+2}-1)}},k=4,5,6,\cdots .$$

Combining this with (5), we obtain the desired inequality (7). □

Lemma 6.

Let $k=3,4,5,\cdots .$ Then, it holds that

$${\displaystyle \frac{|B_{2k+2}|}{|B_{2k}|}}>{\displaystyle \frac{(2k+1)(2k+2)P\left(k\right)}{3\left[16k(2^{2k+2}-2)(2k+1)-14k(2k+1)·2^{2k+2}-15·2^{2k+2}\right]}},$$

where $P\left(k\right)=\left[16(2k-1)(2^{2k-1}-1)+48(2^{2k-1}-1)-24(2^{2k}-2)-7·2^{2k}(2k-1)\right].$

Proof. 

In view of Lemma 3, it suffices to prove

$${\displaystyle \frac{(2^{2k-1}-1)}{{\pi }^2(2^{2k+1}-1)}}>{\displaystyle \frac{16(2k-1)(2^{2k-1}-1)+48(2^{2k-1}-1)-24(2^{2k}-2)-7·2^{2k}(2k-1)}{3\left[16k(2k+1)(2^{2k+2}-2)-14k(2k+1)·2^{2k+2}-15·2^{2k+2}\right]}}$$

for $k=3,4,5,\cdots .$ Equivalently,

$$\begin{array}{c}{\pi }^2(2^{2k+1}-1)\left[16(2k-1)(2^{2k-1}-1)+48(2^{2k-1}-1)-24(2^{2k}-2)-7·2^{2k}(2k-1)\right]\hfill \\ \hfill <3(2^{2k-1}-1)\left[16k(2k+1)(2^{2k+2}-2)-14k(2k+1)·2^{2k+2}-15·2^{2k+2}\right].\end{array}$$

A direct computation gives

$$\begin{array}{cc}\hfill & (4{\pi }^2·2^{2k}-2{\pi }^2)(2k·2^{2k}-2^{2k}-32k+16)\hfill \\ \hfill & <(3·2^{2k}-6)(16k^2·2^{2k}-64k^2+8k·2^{2k}-60·2^{2k}-32k),\hfill \end{array}$$

which can be put as

$$\begin{array}{cc}\hfill & \left[(48k^2+24k+4{\pi }^2)·2^{2k}+(32{\pi }^{2}k+360)\right]·2^{2k}+(384k^2+192k+32{\pi }^2)\hfill \\ \hfill & >\left[(8{\pi }^{2}k+180)·2^{2k}+288k^2+(66{\pi }^2+144k)\right]·2^{2k}+64{\pi }^{2}k.\hfill \end{array}$$

Since

$$384k^2+192k+32{\pi }^2>64{\pi }^{2}k,$$

for $k=3,4,5,\cdots ,$ we only need to prove that

$$Q\left(k\right)>0,\mathrm{for}k=3,4,5,\cdots ,$$

where

$$Q\left(k\right)=(48k^2+24k+4{\pi }^2-8{\pi }^{2}k-180)·2^{2k}+(32{\pi }^{2}k+360-288k^2-66{\pi }^2-144k).$$

Now, $k\ge 3$ implies

$$\begin{array}{cc}\hfill Q\left(k\right)& \ge (48k^2+24k+4{\pi }^2-8{\pi }^{2}k-180)·64+(32{\pi }^{2}k+360-288k^2-66{\pi }^2-144k)\hfill \\ \hfill & =2784k^2+1392k+190{\pi }^2-480{\pi }^{2}k-11160\hfill \\ \hfill & \ge 2784·3k+1392k+190{\pi }^2-480{\pi }^{2}k-11160\hfill \\ \hfill & =(9744-480{\pi }^2)k+(190{\pi }^2-11160)\hfill \\ \hfill & \ge (9744-480{\pi }^2)·3+(190{\pi }^2-11160)=(29232+190{\pi }^2)-12600>0.\hfill \end{array}$$

□

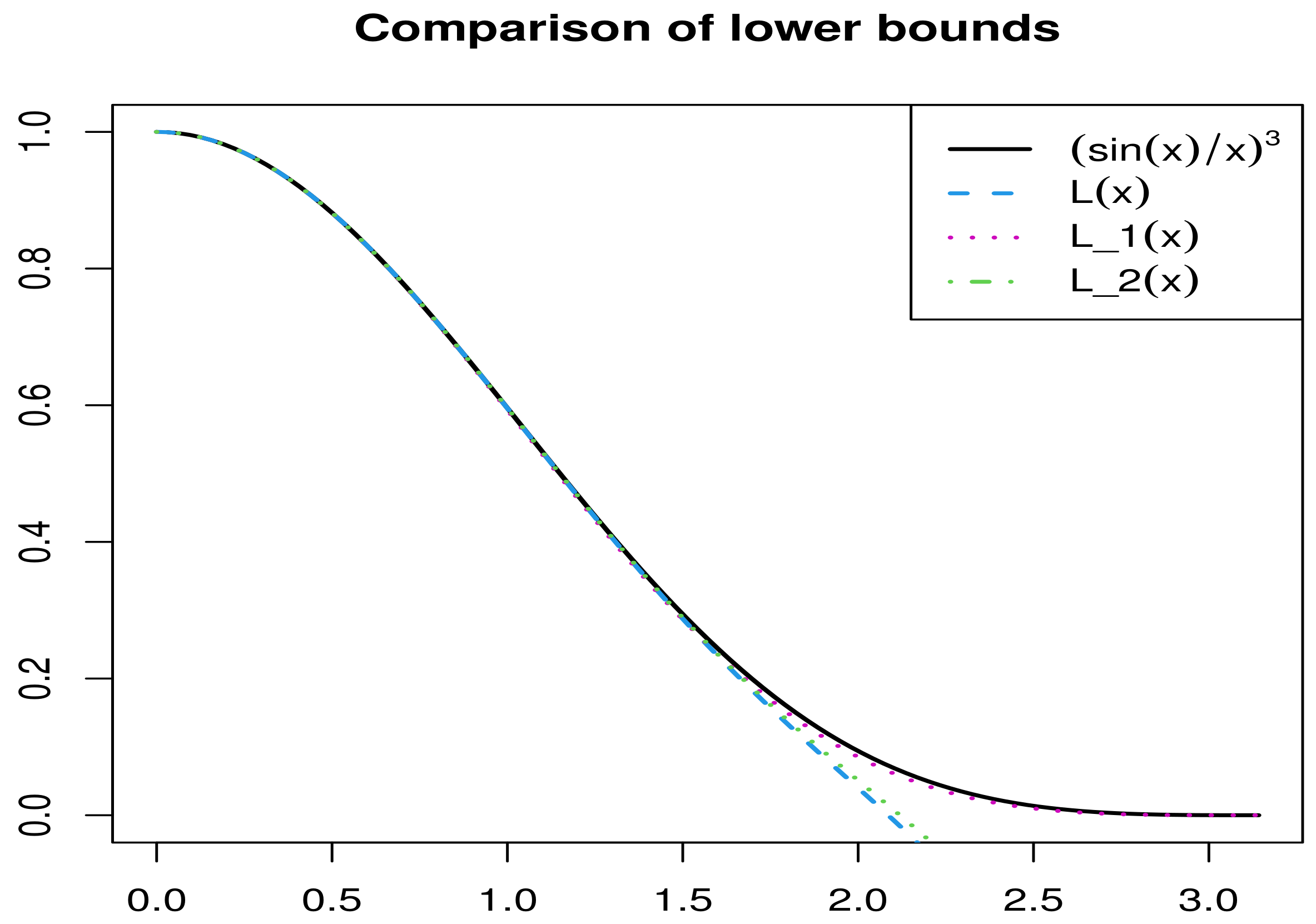
3. Some New Generalized Mitrinović–Adamović-Type Inequalities

We are now in a position to state and prove our main results.

Theorem 1.

The function

$$f\left(x\right)={\displaystyle \frac{{\left(\frac{\sin x}{x}\right)}^3-\cos x}{{(1-\cos x)}^2}}$$

is strictly decreasing on $(0,\pi ).$

Proof. 

The differentiation of $f\left(x\right)$ gives

$$\begin{array}{c}{(1-\cos x)}^4{f}^{\prime }\left(x\right)\hfill \\ \hfill \hspace{1em}=(1-\cos x)\left[(1-\cos x)\left({\displaystyle \frac{3{\sin }^{2}x(x\cos x-\sin x)}{x^4}}+\sin x\right)-2\sin x\left({\displaystyle \frac{{\sin }^{3}x-x^3\cos x}{x^3}}\right)\right],\end{array}$$

and then deduces

$$\begin{array}{cc}\hfill x^4& {(1-\cos x)}^3{f}^{\prime }\left(x\right)\hfill \\ \hfill & =(1-\cos x)(3x{\sin }^{2}x\cos x-3{\sin }^{3}x+x^4\sin x)-2\sin x(x{\sin }^{3}x-x^4\cos x)\hfill \\ \hfill & =3x{\sin }^{2}x\cos x-3{\sin }^{3}x+x^4\sin x-3x{\sin }^{2}x+x{\sin }^{4}x+3{\sin }^{3}x\cos x+x^4\sin x\cos x\hfill \\ \hfill & ={\sin }^{3}x·\varphi \left(x\right),\hfill \end{array}$$

where

$$\varphi \left(x\right)=3x\cot x-3+x^4{\displaystyle \frac{1}{{\sin }^{2}x}}-3{\displaystyle \frac{x}{\sin x}}+x\sin x+3\cos x+x^4{\displaystyle \frac{\cos x}{{\sin }^{2}x}}.$$

Using power series expansions in Lemma 1, and known series expansions of $\sin x$ and $\cos x,$ we have

$$\begin{array}{cc}\hfill \varphi \left(x\right)& =2x^2-\sum _{k=1}^{\infty }{\displaystyle \frac{3·2^{2k}}{\left(2k\right)!}}|B_{2k}|x^{2k}+\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)}{\left(2k\right)!}}|B_{2k}|x^{2k+2}-\sum _{k=1}^{\infty }{\displaystyle \frac{6(2^{2k-1}-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k}\hfill \\ \hfill & +\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{x}^{2k+2}+\sum _{k=1}^{\infty }{\displaystyle \frac{3{(-1)}^k}{\left(2k\right)!}}{x}^{2k}-\sum _{k=1}^{\infty }{\displaystyle \frac{2(2^{2k-1}-1)(2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & =-\sum _{k=1}^{\infty }{\displaystyle \frac{3·2^{2k+2}}{(2k+2)!}}|B_{2k+2}|x^{2k+2}+\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & -\sum _{k=1}^{\infty }{\displaystyle \frac{6(2^{2k+1}-1)}{(2k+2)!}}\left|B_{2k+2}\right|x^{2k+2}+\sum _{k=1}^{\infty }{\displaystyle \frac{{(-1)}^k}{(2k+1)!}}{x}^{2k+2}+\sum _{k=1}^{\infty }{\displaystyle \frac{3{(-1)}^{k+1}}{(2k+2)!}}{x}^{2k+2}\hfill \\ \hfill & -\sum _{k=1}^{\infty }{\displaystyle \frac{2(2^{2k-1}-1)(2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & :=\sum _{k=1}^{\infty }{\displaystyle \frac{a_k}{(2k+2)!}}{x}^{2k+2},\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill a_k& =2^{2k}(2k+1)(2k+2)(2k-1)|B_{2k}|-2(2k+1)(2k+2)(2^{2k-1}-1)(2k-1)\left|B_{2k}\right|\hfill \\ \hfill & -3·2^{2k+2}|B_{2k+2}|-6(2^{2k+1}-1)\left|B_{2k+2}\right|+{(-1)}^k(2k+2)+3{(-1)}^{k+1}\hfill \\ \hfill & =2(2k-1)(2k+1)(2k+2)|B_{2k}|-6(2^{2k+2}-1)\left|B_{2k+2}\right|+(2k+2){(-1)}^k+3{(-1)}^{k+1}.\hfill \end{array}$$

We calculate $a_1=a_2=0$ and $a_3=-{\displaystyle \frac{128}{3}}.$

Next, we claim that $a_k<0$ for $k=4,5,6,7,8,\cdots .$ First, we need to prove $a_k<0$ for $k=4,6,8,\cdots ,$ that is,

$$\begin{array}{c}\hfill (2k+2)+2(2k-1)(2k+1)(2k+2)|B_{2k}|<3+6(2^{2k+2}-1)\left|B_{2k+2}\right|\end{array}$$

(8)

for $k=4,6,8,\cdots ,$ and then $a_k<0$ for $k=5,7,9,\cdots ,$ that is,

$$\begin{array}{c}\hfill (1-2k)+2(2k-1)(2k+1)(2k+2)|B_{2k}|<6(2^{2k+2}-1)\left|B_{2k+2}\right|\end{array}$$

(9)

for $k=5,7,9,\cdots .$ Now, by Lemma 4 and Lemma 5, we, respectively, have

$$\begin{array}{c}\hfill (2k+2)<3(2^{2k+2}-1)\left|B_{2k+2}\right|,k=3,4,5,\cdots \end{array}$$

(10)

and

$$\begin{array}{c}\hfill 2(2k-1)(2k+1)(2k+2)|B_{2k}|<3(2^{2k+2}-1)\left|B_{2k+2}\right|,k=4,5,6,\cdots .\end{array}$$

(11)

Combining (10) with (11), we obtain

$$(2k+2)+2(2k-1)(2k+1)(2k+2)|B_{2k}|<6(2^{2k+2}-1)\left|B_{2k+2}\right|,k=4,5,6,\cdots ,$$

which implies (8). Also, the inequality (11) implies (9). Thus, $a_k\le 0$ for $k=1,2,3,4,5,\cdots .$ Therefore, we conclude that $\varphi \left(x\right)<0,x\in (0,\pi )$ and consequently $f^{\prime }\left(x\right)<0,x\in (0,\pi ).$ This shows that $f\left(x\right)$ is strictly decreasing on $(0,\pi ).$ The proof is completed. □

The following new generalized Mitrinović–Adamović-type inequality can be established by applying Theorem 1.

Theorem 2.

The following double inequalities are valid:

(i)

The double inequality

$$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{8}{{\pi }^3}}{(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

(12)

holds with the best possible constants ${\displaystyle \frac{8}{{\pi }^3}}$ and ${\displaystyle \frac{4}{15}}$.

(ii)

The double inequality

$$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{1}{4}}{(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2,x\in \left(0,\pi \right)\end{array}$$

(13)

holds with the best possible constants ${\displaystyle \frac{1}{4}}$ and ${\displaystyle \frac{4}{15}}$.

Proof. 

Applying Theorem 1, we have

$$f\left(0^{+}\right)>f\left(x\right)>f(\pi /2^{-}),$$

and

$$f\left(0^{+}\right)>f\left(x\right)>f\left({\pi }^{-}\right).$$

From the limits

$$\underset{x\to 0^{+}}{\lim }f\left(x\right)={\displaystyle \frac{4}{15}},\underset{x\to \pi /2^{-}}{\lim }f\left(x\right)={\displaystyle \frac{8}{{\pi }^3}},\underset{x\to {\pi }^{-}}{\lim }f\left(x\right)={\displaystyle \frac{1}{4}},$$

we can show the desired inequalities (12) and (13). □

Remark 1.

The left inequality of (13) can be written as

$${\left({\displaystyle \frac{1+\cos x}{2}}\right)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3,x\in (0,\pi ).$$

This inequality was first proved by Neuman and Sándor [4] and reappeared in [15]. However, it was shown to be true on $\left(0,{\displaystyle \frac{\pi }{2}}\right)$ only.

Remark 2.

It can be observed that the right inequality of (13) is in fact true for $x>0.$ This fact can be verified graphically at https://www.desmos.com/calculator (accessed on 1 March 2025). Let us write

$$\begin{array}{cc}\hfill L\left(x\right)& =\cos x+{\displaystyle \frac{21}{5}}{\displaystyle \frac{x^3\sin x}{63+x^2}},U\left(x\right)=\cos x+{\displaystyle \frac{{\pi }^2}{15}}{\displaystyle \frac{x^3\sin x}{{\pi }^2-x^2}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill L_1\left(x\right)& =\cos x+{\displaystyle \frac{1}{4}}{(1-\cos x)}^2,U_1\left(x\right)=\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2\hfill \end{array}$$

for $x\in (0,\pi ).$ Then, we compare graphically the bounds in (13) with those in (2).

The numerical calculations and graphs in Figure 1 show that the lower bound $L_1\left(x\right)$ of ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ in (13) is sharper than the corresponding lower bound $L\left(x\right)$ in (2) for $x>\lambda \approx 1.5301,$ whereas the upper bound $U_1\left(x\right)$ of ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ in (13) is uniformly sharper than the corresponding upper bound $U\left(x\right)$ in (2).

In what follows, we further refine the bounds of ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3.$

Theorem 3.

The function

$$g\left(x\right)={\displaystyle \frac{1}{x^6}}\left[{\left({\displaystyle \frac{\sin x}{x}}\right)}^3-\cos x-{\displaystyle \frac{4}{15}}{(1-\cos x)}^2\right]$$

is strictly increasing on $(0,\pi ).$

Proof. 

Differentiating $g\left(x\right)$ with respect to x yields

$$\begin{array}{cc}\hfill x^{10}{g}^{\prime }\left(x\right)& =x\left[3{\sin }^{2}x\cos x+x^3\sin x-3x^2\cos x-{\displaystyle \frac{8}{15}}{x}^3(1-\cos x)\sin x-{\displaystyle \frac{12}{15}}{x}^2{(1-\cos x)}^2\right]\hfill \\ \hfill & -9\left[{\sin }^{3}x-x^3\cos x-{\displaystyle \frac{4}{15}}{x}^3{(1-\cos x)}^2\right]\hfill \\ \hfill & =3x{\sin }^{2}x\cos x+{\displaystyle \frac{7}{15}}{x}^4\sin x-{\displaystyle \frac{7}{5}}{x}^3\cos x+{\displaystyle \frac{8}{15}}{x}^4\sin x\cos x-{\displaystyle \frac{12}{15}}{x}^2\hfill \\ \hfill & -{\displaystyle \frac{12}{15}}{x}^2{\cos }^{2}x-9{\sin }^{3}x+9x^3\cos x+{\displaystyle \frac{12}{5}}{x}^3-{\displaystyle \frac{24}{5}}{x}^3\cos x+{\displaystyle \frac{12}{5}}{x}^3{\cos }^{2}x\hfill \\ \hfill & =3x{\sin }^{2}x\cos x+{\displaystyle \frac{7}{15}}{x}^4\sin x+{\displaystyle \frac{14}{5}}{x}^3\cos x+{\displaystyle \frac{8}{15}}{x}^4\sin x\cos x+{\displaystyle \frac{16}{5}}{x}^3\hfill \\ \hfill & -{\displaystyle \frac{8}{5}}{x}^3{\sin }^{2}x-9{\sin }^{3}x.\hfill \end{array}$$

This can be written as ${\displaystyle \frac{x^{10}}{{\sin }^{3}x}}=\psi \left(x\right),$ where

$$\psi \left(x\right)=3x\cot x+{\displaystyle \frac{7}{15}}{x}^4{\displaystyle \frac{1}{{\sin }^{2}x}}+{\displaystyle \frac{14}{5}}{x}^3{\displaystyle \frac{\cos x}{{\sin }^{3}x}}+{\displaystyle \frac{8}{15}}{x}^4{\displaystyle \frac{\cos x}{{\sin }^{2}x}}+{\displaystyle \frac{16}{5}}{x}^3{\displaystyle \frac{1}{{\sin }^{3}x}}-{\displaystyle \frac{8}{5}}{x}^3{\displaystyle \frac{1}{\sin x}}-9.$$

Utilizing Lemma 1, we obtain

$$\begin{array}{cc}\hfill \psi \left(x\right)& =3-\sum _{k=1}^{\infty }{\displaystyle \frac{3·2^{2k}}{\left(2k\right)!}}|B_{2k}|x^{2k}+{\displaystyle \frac{7}{15}}{x}^2+\sum _{k=1}^{\infty }{\displaystyle \frac{7}{15}}{\displaystyle \frac{2^{(}2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}+{\displaystyle \frac{14}{5}}\hfill \\ \hfill & -\sum _{k=2}^{\infty }{\displaystyle \frac{14}{5}}{\displaystyle \frac{2^{2k}(2k-1)(k-1)}{\left(2k\right)!}}|B_{2k}|x^{2k}+{\displaystyle \frac{8}{15}}{x}^2-\sum _{k=1}^{\infty }{\displaystyle \frac{8}{15}}{\displaystyle \frac{2(2k-1)(2^{2k-1}-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & +{\displaystyle \frac{16}{5}}+\sum _{k=2}^{\infty }{\displaystyle \frac{8}{5}}{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)}{\left(2k\right)!}}|B_{2k}|x^{2k}+{\displaystyle \frac{8}{5}}{x}^2+\sum _{k=1}^{\infty }{\displaystyle \frac{8}{5}}{\displaystyle \frac{(2^{2k}-2)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & -{\displaystyle \frac{8}{5}}{x}^2-\sum _{k=1}^{\infty }{\displaystyle \frac{16}{5}}{\displaystyle \frac{(2^{2k-1}-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k+2}-9\hfill \\ \hfill & =x^2+\sum _{k=1}^{\infty }\left[{\displaystyle \frac{8}{5}}{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)}{\left(2k\right)!}}-{\displaystyle \frac{14}{5}}{\displaystyle \frac{2^{2k}(2k-1)(k-1)}{\left(2k\right)!}}-{\displaystyle \frac{3·2^{2k}}{\left(2k\right)!}}\right]\left|B_{2k}\right|x^{2k}\hfill \\ \hfill & +\sum _{k=1}^{\infty }\left[{\displaystyle \frac{7}{15}}{\displaystyle \frac{2^{2k}(2k-1)}{\left(2k\right)!}}+{\displaystyle \frac{8}{5}}{\displaystyle \frac{(2^{2k}-2)}{\left(2k\right)!}}-{\displaystyle \frac{16}{5}}{\displaystyle \frac{(2^{2k-1}-1)}{\left(2k\right)!}}-{\displaystyle \frac{16}{15}}{\displaystyle \frac{(2k-1)(2^{2k-1}-1)}{\left(2k\right)!}}\right]\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & =x^2+\sum _{k=1}^{\infty }\left[{\displaystyle \frac{8(2^{2k}-2)(2k-1)(2k-2)-14·2^{2k}(2k-1)(k-1)-15·2^{2k}}{5·\left(2k\right)!}}\right]\left|B_{2k}\right|x^{2k}\hfill \\ \hfill & +\sum _{k=1}^{\infty }\left[{\displaystyle \frac{7·2^{2k}(2k-1)+24(2^{2k}-2)-48(2^{2k-1}-1)-16(2k-1)(2^{2k-1}-1)}{15·\left(2k\right)!}}\right]\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & =x^2+\sum _{k=0}^{\infty }\left[{\displaystyle \frac{16k(2k+1)(2^{2k+2}-2)-14k(2k+1)·2^{2k+2}-15·2^{2k+2}}{5·(2k+2)!}}\right]\left|B_{2k+2}\right|x^{2k+2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }\left[{\displaystyle \frac{7·2^{2k}(2k-1)+24(2^{2k}-2)-48(2^{2k-1}-1)-16(2k-1)(2^{2k-1}-1)}{15·\left(2k\right)!}}\right]\left|B_{2k}\right|x^{2k+2}\hfill \\ \hfill & =\sum _{k=3}^{\infty }{\displaystyle \frac{1}{5·\left(2k\right)!}}{b}_k{x}^{2k+2}\hfill \end{array}$$

where

$$\begin{array}{c}{b}_k={\displaystyle \frac{\left(16k(2^{2k+2}-2)(2k+1)-14k(2k+1)·2^{2k+2}-15·2^{2k+2}\right)}{(2k+1)(2k+2)}}\left|B_{2k+2}\right|\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{\left(16(2k-1)(2^{2k-1}-1)+48(2^{2k-1}-1)-24(2^{2k}-2)-7·2^{2k}(2k-1)\right)}{3}}\left|B_{2k}\right|.\end{array}$$

By Lemma 6, $b_k>0.$ This proves that $\psi \left(x\right)$ and hence $g^{\prime }\left(x\right)$ is positive, implying that $g\left(x\right)$ is strictly increasing on $(0,\pi ).$ The proof is completed. □

Theorem 4.

The following double inequalities are valid:

(i)

The double inequality

$$\begin{array}{c}\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{945}}{x}^6<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{256}{{\pi }^6}}\left({\displaystyle \frac{1}{15}}-{\displaystyle \frac{2}{{\pi }^3}}\right)x^6,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

(14)

holds with the best possible constants $-{\displaystyle \frac{1}{945}}$ and $-{\displaystyle \frac{256}{{\pi }^6}}\left({\displaystyle \frac{1}{15}}-{\displaystyle \frac{2}{{\pi }^3}}\right).$

(ii)

The double inequality

$$\begin{array}{c}\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{945}}{x}^6<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{15{\pi }^6}}{x}^6,x\in (0,\pi )\end{array}$$

(15)

holds with the best possible constants $-{\displaystyle \frac{1}{945}}$ and $-{\displaystyle \frac{1}{15{\pi }^6}}.$

Proof. 

Applying Theorem 3, we obtain

$$g\left(0^{+}\right)<g\left(x\right)<g(\pi /2^{-}),$$

and

$$g\left(0^{+}\right)<g\left(x\right)<g\left({\pi }^{-}\right).$$

The double inequalities (14) and (15) follow due to the limits

$$\underset{x\to 0}{\lim }g\left(x\right)=-{\displaystyle \frac{1}{945}},\underset{x\to \pi /2^{-}}{\lim }g\left(x\right)=-{\displaystyle \frac{64}{{\pi }^6}}\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{8}{{\pi }^3}}\right),\mathrm{and}\underset{x\to \pi }{\lim }g\left(x\right)=-{\displaystyle \frac{1}{15{\pi }^6}}.$$

□

Remark 3.

If we suppose

$$L_2\left(x\right)=\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{945}}{x}^6$$

and

$$U_2\left(x\right)=\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{15{\pi }^6}}{x}^6,$$

then it is obvious that $U_2\left(x\right)<U_1\left(x\right)$ for all $x\in (0,\pi ).$ Based on Figure 2 and some numerical calculations, it is found that $L_1\left(x\right)<L_2\left(x\right)$ for $x\in (0,{\lambda }^{*})$ where ${\lambda }^{*}\approx 1.5969.$

The curves $E_1\left(x\right)=L_2\left(x\right)-L\left(x\right),$ and $E_2\left(x\right)=U\left(x\right)-U_2\left(x\right)$ depicted in the following Figure 3 show that the double inequality (2) is completely refined to (15).

Lemma 7.

Let

$$\begin{array}{cc}\hfill T\left(k\right)& =(2^{2k-1}-1)·[16k^3(2^{2k+2}-1)-(2176k+1980)·2^{2k}+544k+720]\hfill \\ \hfill & -(2^{2k+1}-1)(2k-1){\pi }^2·(2^{2k}+90k-136).\hfill \end{array}$$

Then, $T\left(k\right)>0$ for $k=7,8,9,\cdots .$

Proof. 

We rewrite $T\left(k\right)$ as

$$\begin{array}{cc}\hfill T\left(k\right)& =(2^{2k+1}-4)·[4k^3(2^{2k+2}-1)-(544k+495)·2^{2k}+136+180]\hfill \\ \hfill & -(2^{2k+1}-1)(2k-1){\pi }^2·(2^{2k}+90k-136).\hfill \end{array}$$

Clearly,

$$2^{2k}+2^{2k}>2^{2k}+(90k-132),\mathrm{for}k=7,8,9,\cdots .$$

Therefore

$$\begin{array}{c}\hfill (2^{2k+1}-4)>(2^{2k}+90k-136),k=7,8,9,\cdots .\end{array}$$

(16)

Similarly,

$$16k^3+2{\pi }^2>(544+4{\pi }^2)k+495,\mathrm{for}k=7,8,9,\cdots$$

implies

$$(16k^3+2{\pi }^2)·2^{2k}+(136+2{\pi }^2)k+(180-{\pi }^2)>[(544+4{\pi }^2)k+495]·2^{2k}.$$

Then, we have

$$\begin{array}{c}\hfill 4k^3(2^{2k+2}-1)-(544k+495)·2^{2k}+136k+180>(2^{2k+1}-1)(2k-1){\pi }^2\end{array}$$

(17)

for $k=7,8,9,\cdots .$ From (16) and (17), we obtain $T\left(k\right)>0$ for $k=7,8,9,\cdots .$ □

It is still possible to refine the inequalities of Theorem 3. We present the following more refined results.

Theorem 5.

The function

$$h\left(x\right)={\displaystyle \frac{\left[{\left(\frac{\sin x}{x}\right)}^3-\cos x-\frac{4}{15}{(1-\cos x)}^2\right]}{x^2{(1-\cos x)}^2}}$$

is strictly increasing on $(0,\pi ).$

Proof. 

By the differentiation of $h\left(x\right),$ we have

$$\begin{array}{cc}\hfill {\left[x(1-\cos x)\right]}^4·h^{\prime }\left(x\right)& =x(1-\cos x)\left({\displaystyle \frac{3{\sin }^{2}x\cos x}{x^3}}-{\displaystyle \frac{3{\sin }^{3}x}{x^4}}+{\displaystyle \frac{7}{15}}\sin x+{\displaystyle \frac{8}{15}}\sin x\cos x\right)\hfill \\ \hfill & -(2-2\cos x+2x\sin x)\left({\displaystyle \frac{{\sin }^{3}x}{x^3}}-{\displaystyle \frac{7}{15}}\cos x-{\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{15}}{\cos }^{2}x\right)\hfill \\ \hfill & ={\displaystyle \frac{3{\sin }^{2}x\cos x}{x^2}}-5{\displaystyle \frac{{\sin }^{3}x}{x^3}}+x\sin x+x\sin x\cos x-3{\displaystyle \frac{{\sin }^{2}x}{x^2}}+{\displaystyle \frac{{\sin }^{4}x}{x^2}}\hfill \\ \hfill & +5{\displaystyle \frac{{\sin }^{3}x\cos x}{x^3}}-{\displaystyle \frac{2}{15}}\cos x+{\displaystyle \frac{2}{15}}+{\displaystyle \frac{6}{15}}{\sin }^{2}x+{\displaystyle \frac{8}{15}}{\sin }^{2}x\cos x\hfill \\ \hfill & :={\sin }^{4}x·\lambda \left(x\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \lambda \left(x\right)& ={\displaystyle \frac{3}{x^2}}{\displaystyle \frac{\cos x}{{\sin }^{2}x}}-{\displaystyle \frac{5}{x^3}}{\displaystyle \frac{1}{\sin x}}+x{\displaystyle \frac{1}{{\sin }^{3}x}}+x{\displaystyle \frac{\cos x}{{\sin }^{3}x}}-{\displaystyle \frac{3}{x^2}}{\displaystyle \frac{1}{{\sin }^{2}x}}+{\displaystyle \frac{1}{x^2}}\hfill \\ \hfill & +{\displaystyle \frac{5}{x^3}}\cot x-{\displaystyle \frac{2}{15}}{\displaystyle \frac{\cos x}{{\sin }^{4}x}}+{\displaystyle \frac{2}{15}}{\displaystyle \frac{1}{{\sin }^{4}x}}+{\displaystyle \frac{6}{15}}{\displaystyle \frac{1}{{\sin }^{2}x}}+{\displaystyle \frac{8}{15}}{\displaystyle \frac{\cos x}{{\sin }^{2}x}}.\hfill \end{array}$$

We plan to use the series expansions given in Lemma 1 to obtain

$$\begin{array}{cc}\hfill \lambda \left(x\right)& ={\displaystyle \frac{3}{x^4}}-\sum _{k=1}^{\infty }{\displaystyle \frac{3(2^{2k}-2)(2k-1)}{\left(2k\right)!}}|B_{2k}|x^{2k-4}-{\displaystyle \frac{5}{x^4}}-\sum _{k=1}^{\infty }{\displaystyle \frac{5(2^{2k}-2)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-4}+{\displaystyle \frac{1}{x^2}}\hfill \\ \hfill & +\sum _{k=2}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)}{2·\left(2k\right)!}}|B_{2k}|x^{2k-2}+{\displaystyle \frac{1}{2}}+\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k}-2)}{2·\left(2k\right)!}}\left|B_{2k}\right|x^{2k}+{\displaystyle \frac{1}{x^2}}\hfill \\ \hfill & -\sum _{k=2}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)(k-1)}{\left(2k\right)!}}|B_{2k}|x^{2k-2}-{\displaystyle \frac{3}{x^2}}-\sum _{k=1}^{\infty }{\displaystyle \frac{3·2^{2k}(2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-4}+{\displaystyle \frac{1}{x^2}}+{\displaystyle \frac{5}{x^4}}\hfill \\ \hfill & -\sum _{k=1}^{\infty }{\displaystyle \frac{5·2^{2k}}{\left(2k\right)!}}|B_{2k}|x^{2k-4}+{\displaystyle \frac{2}{45x^3}}+{\displaystyle \frac{1}{45x}}+\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)}{45·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=2}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)(2k-3)}{45·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-4}+{\displaystyle \frac{2}{15x^4}}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{2^{2k}(2k-1)(2k-2)(2k-3)}{45·\left(2k\right)!}}|B_{2k}|x^{2k-4}+{\displaystyle \frac{4}{45x^2}}+\sum _{k=1}^{\infty }{\displaystyle \frac{4}{45}}{\displaystyle \frac{2^{2k}(2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}\hfill \\ \hfill & +{\displaystyle \frac{6}{15x^2}}+\sum _{k=1}^{\infty }{\displaystyle \frac{6}{15}}{\displaystyle \frac{2^{2k}(2k-1)}{\left(2k\right)!}}|B_{2k}|x^{2k-2}+{\displaystyle \frac{8}{15x^2}}-\sum _{k=1}^{\infty }{\displaystyle \frac{8}{15}}{\displaystyle \frac{(2^{2k}-2)(2k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}.\hfill \end{array}$$

After simplifying, $\lambda \left(x\right)$ can be written as

$$\begin{array}{cc}\hfill & \lambda \left(x\right)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{45x}}+{\displaystyle \frac{181}{45x^2}}+{\displaystyle \frac{2}{45x^3}}+{\displaystyle \frac{2}{15x^4}}+\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k}-2)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{[4·2^{2k}+2^{2k}-2](2k-1)}{45·\left(2k\right)!}}|B_{2k}|x^{2k-2}+\sum _{k=2}^{\infty }{\displaystyle \frac{[2^{2k}-2-2^{2k}](2k-1)(k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{\left[\frac{(2k-2)(2k-3)}{45}-3\right]·2^{2k}(2k-1)}{\left(2k\right)!}}|B_{2k}|x^{2k-4}-\sum _{k=1}^{\infty }{\displaystyle \frac{[3(2k-1)+5](2^{2k}-2)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-4}\hfill \\ \hfill & +\sum _{k=2}^{\infty }{\displaystyle \frac{(2^{2k}-2)(2k-1)(2k-2)(2k-3)}{45·\left(2k\right)!}}|B_{2k}|x^{2k-4}+\sum _{k=1}^{\infty }[3·2^{2k}-4(2^{2k}-2)]{\displaystyle \frac{2(2k-1)}{15·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill \lambda \left(x\right)& =\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{45x}}+{\displaystyle \frac{181}{45x^2}}+{\displaystyle \frac{2}{45x^3}}+{\displaystyle \frac{2}{15x^4}}\right)+\sum _{k=2}^{\infty }{\displaystyle \frac{(2^{2k-2}-2)}{(2k-2)!}}\left|B_{2k-2}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{(5·2^{2k}-2)(2k-1)}{45·\left(2k\right)!}}|B_{2k}|x^{2k-2}-\sum _{k=2}^{\infty }{\displaystyle \frac{2(2k-1)(k-1)}{\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=0}^{\infty }{\displaystyle \frac{\left[\frac{2k(2k-1)}{45}-3\right]·2^{2k+2}(2k+1)}{(2k+2)!}}|B_{2k+2}|x^{2k-2}-\sum _{k=0}^{\infty }{\displaystyle \frac{(6k+8)(2^{2k+2}-2)}{(2k+2)!}}\left|B_{2k+2}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k+2}-2)(2k+1)\left(2k\right)(2k-1)}{45·(2k+2)!}}|B_{2k+2}|x^{2k-2}-\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k}-8)·2(2k-1)}{15·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2},\hfill \end{array}$$

which is equivalent to

$$\begin{array}{cc}\hfill \lambda \left(x\right)& =\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{45x}}+{\displaystyle \frac{181}{45x^2}}+{\displaystyle \frac{2}{45x^3}}+{\displaystyle \frac{2}{15x^4}}\right)+\left(1-{\displaystyle \frac{1}{x^2}}-{\displaystyle \frac{7}{3x^2}}\right)+\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k-2}-2)}{(2k-2)!}}\left|B_{2k-2}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{\left[\frac{(5·2^{2k}-2)}{45}-2(k-1)\right]}{\left(2k\right)!}}(2k-1)\left|B_{2k}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{\left[\frac{2k(2k-1)}{45}-3\right]·2^{2k+2}(2k+1)}{(2k+2)!}}|B_{2k+2}|x^{2k-2}-\sum _{k=1}^{\infty }{\displaystyle \frac{(6k+8)(2^{2k+2}-2)}{(2k+2)!}}\left|B_{2k+2}\right|x^{2k-2}\hfill \\ \hfill & +\sum _{k=1}^{\infty }{\displaystyle \frac{(2^{2k+2}-2)(2k+1)\left(2k\right)(2k-1)}{45·(2k+2)!}}|B_{2k+2}|x^{2k-2}-\sum _{k=1}^{\infty }{\displaystyle \frac{2(2^{2k}-8)(2k-1)}{15·\left(2k\right)!}}\left|B_{2k}\right|x^{2k-2},\hfill \end{array}$$

that is,

$$\lambda \left(x\right)=\left({\displaystyle \frac{3}{2}}+{\displaystyle \frac{1}{45x}}+{\displaystyle \frac{31}{45x^2}}+{\displaystyle \frac{2}{45x^3}}+{\displaystyle \frac{2}{15x^4}}\right)+\sum _{k=1}^{\infty }{\displaystyle \frac{c_k}{(2k-2)!}}{x}^{2k-2}.$$

Here,

$$\begin{array}{cc}\hfill c_k& =(2^{2k-2}-2)|B_{2k-2}|+{\displaystyle \frac{[5·2^{2k}-2-90(k-1)]}{90k}}|B_{2k}|+{\displaystyle \frac{[2k(2k-1)-135]·2^{2k+2}}{45(2k+2)\left(2k\right)(2k-1)}}\left|B_{2k+2}\right|\hfill \\ \hfill & -{\displaystyle \frac{(6k+8)(2^{2k+2}-2)}{(2k+2)(2k+1)\left(2k\right)(2k-1)}}|B_{2k+2}|+{\displaystyle \frac{(2^{2k+2}-2)}{45(2k+2)}}|B_{2k+2}|-{\displaystyle \frac{(2^{2k}-8)}{15k}}\left|B_{2k}\right|.\hfill \end{array}$$

We write $c_k$ conveniently as

$$\begin{array}{cc}\hfill c_k& =(2^{2k-2}-2)|B_{2k-2}|+{\displaystyle \frac{(5·2^{2k}-90k+88)}{90k}}|B_{2k}|+{\displaystyle \frac{(4k^2-2k-135)·2^{2k}}{45k(k+1)(2k-1)}}\left|B_{2k+2}\right|\hfill \\ \hfill & +{\displaystyle \frac{(2^{2k+2}-2)(8k^3-272k-360)}{45(2k+2)(2k+1)\left(2k\right)(2k-1)}}|B_{2k+2}|-{\displaystyle \frac{(2^{2k}-8)}{15k}}\left|B_{2k}\right|\hfill \\ \hfill & =(2^{2k-2}-2)|B_{2k-2}|+{\displaystyle \frac{[16k^3(2^{2k+2}-1)-(2176k+1980)·2^{2k}+544k+720]}{45(2k+2)(2k+1)\left(2k\right)(2k-1)}}\left|B_{2k+2}\right|\hfill \\ \hfill & -{\displaystyle \frac{(2^{2k}+90k-136)}{90k}}\left|B_{2k}\right|.\hfill \end{array}$$

From this, we obtain $c_1=-{\displaystyle \frac{85}{54}}.$ So,

$$\lambda \left(x\right)=\left(-{\displaystyle \frac{2}{27}}+{\displaystyle \frac{1}{45x}}+{\displaystyle \frac{31}{45x^2}}+{\displaystyle \frac{2}{45x^3}}+{\displaystyle \frac{2}{15x^4}}\right)+\sum _{k=2}^{\infty }{\displaystyle \frac{c_k}{(2k-2)!}}{x}^{2k-2}$$

where the function in the parentheses is strictly decreasing on $(0,\pi ).$ Hence,

$$\begin{array}{cc}\hfill \lambda \left(x\right)& >\left(-{\displaystyle \frac{2}{27}}+{\displaystyle \frac{1}{45\pi }}+{\displaystyle \frac{31}{45{\pi }^2}}+{\displaystyle \frac{2}{45{\pi }^3}}+{\displaystyle \frac{2}{15{\pi }^4}}\right)+\sum _{k=2}^{\infty }{\displaystyle \frac{c_k}{(2k-2)!}}{x}^{2k-2}\hfill \\ \hfill & =\left[{\displaystyle \frac{({\pi }^3+31{\pi }^2+2\pi +6)}{45{\pi }^4}}-{\displaystyle \frac{2}{27}}\right]+{\displaystyle \frac{37703}{38178\times (2!)}}{x}^2+{\displaystyle \frac{449}{1890\times (4!)}}{x}^4+{\displaystyle \frac{79073}{135135\times (6!)}}{x}^6\hfill \\ \hfill & +{\displaystyle \frac{56513281}{8918910\times (8!)}}{x}^8+{\displaystyle \frac{13078211909763}{186943326570\times (10!)}}{x}^{10}+\sum _{k=7}^{\infty }{\displaystyle \frac{c_k}{(2k-2)!}}{x}^{2k-2}.\hfill \end{array}$$

The values of $c_k$’s in the above expression for $k=2,3,\cdots ,6$ are calculated using the Bernoulli numbers ([25], Chapter 23). For proving $\lambda \left(x\right)>0$ on $(0,\pi ),$ it suffices to prove $c_k>0$ for $k=7,8,9,\cdots .$ Now, we rewrite $c_k$ as follows:

$$\begin{array}{c}{c}_k=(2^{2k-2}-2)|B_{2k-2}|+|B_{2k}|\times \hfill \\ \left\{{\displaystyle \frac{[16k^3(2^{2k+2}-1)-(2176k+1980)·2^{2k}+544k+720]}{45(2k+2)(2k+1)\left(2k\right)(2k-1)}}{\displaystyle \frac{|B_{2k+2}|}{|B_{2k}|}}-{\displaystyle \frac{(2^{2k}+90k-136)}{90k}}\right\}.\end{array}$$

Since

$$16k^3(2^{2k+2}-1)-(2176k+1980)·2^{2k}+544k+720>0\mathrm{for}k=7,8,9,\cdots ,$$

by using Qi’s inequality (5) and applying Lemma 7. we have

$$\begin{array}{cc}\hfill c_k& >(2^{2k-2}-2)|B_{2k-2}|+|B_{2k}|\times \hfill \\ \hfill & \left\{{\displaystyle \frac{[16k^3(2^{2k+2}-1)-(2176k+1980)·2^{2k}+544k+720](2^{2k-1}-1)}{45\left(2k\right)(2k-1)(2^{2k+1}-1){\pi }^2}}-{\displaystyle \frac{(2^{2k}+90k-136)}{90k}}\right\}\hfill \\ \hfill & =(2^{2k-2}-2)\left|B_{2k-2}\right|+{\displaystyle \frac{|B_{2k}|·T\left(k\right)}{90k(2k-1)(2^{2k+1}-1){\pi }^2}}>0.\hfill \end{array}$$

Thus, $\lambda \left(x\right)>0$, implying that $h^{\prime }\left(x\right)>0,x\in (0,\pi ).$ Therefore, $h\left(x\right)$ is strictly increasing on $(0,\pi ).$ The proof is completed. □

Theorem 6.

The following double inequalities are valid:

(i)

The double inequality

$$\begin{array}{c}\cos x+\left[{\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{945}}{x}^2\right]{(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+\left[{\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{{\pi }^2}}\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{8}{{\pi }^3}}\right)x^2\right]{(1-\cos x)}^2,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

(18)

holds with the best possible constants $-{\displaystyle \frac{4}{945}}$ and $-{\displaystyle \frac{4}{{\pi }^2}}\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{8}{{\pi }^3}}\right).$

(ii)

The double inequality

$$\begin{array}{c}\cos x+\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{945}}{x}^2\right){(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{1}{60{\pi }^2}}{x}^2\right){(1-\cos x)}^2,x\in (0,\pi )\end{array}$$

(19)

holds with the best possible constants $-{\displaystyle \frac{4}{945}}$ and $-{\displaystyle \frac{1}{60{\pi }^2}}.$

Proof. 

Applying Theorem 5, we obtain

$$h\left(0^{+}\right)<h\left(x\right)<h(\pi /2^{-}),$$

and

$$h\left(0^{+}\right)<h\left(x\right)<h\left({\pi }^{-}\right).$$

Then, using the limits

$$\underset{x\to 0^{+}}{\lim }h\left(x\right)=-{\displaystyle \frac{4}{945}},\underset{x\to \pi /2^{-}}{\lim }h\left(x\right)=-{\displaystyle \frac{4}{{\pi }^2}}\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{8}{{\pi }^3}}\right),\mathrm{and}\underset{x\to {\pi }^{-}}{\lim }h\left(x\right)=-{\displaystyle \frac{1}{60{\pi }^2}},$$

we can prove our conclusion. □

Remark 4.

It is worth noting that the double inequality (21) is a refinement of (15). Because

$${\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{945}}{x}^6<\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{945}}{x}^2\right){(1-\cos x)}^2⟺1-{\displaystyle \frac{x^2}{2}}<\cos x$$

and

$$\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{1}{60{\pi }^2}}{x}^2\right){(1-\cos x)}^2<{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{15{\pi }^6}}{x}^6⟺\cos x<1-{\displaystyle \frac{2x^2}{{\pi }^2}}$$

where the right-side inequalities are true due to the double inequality $1-{\displaystyle \frac{x^2}{2}}<\cos x<1-{\displaystyle \frac{4x^2}{{\pi }^2}}$ as proved in [28].

Remark 5.

In our new generalized Mitrinović–Adamović-type inequalities, we have compared our bounds of ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ in a larger interval $(0,\pi )$ with the old ones, i.e., with the corresponding bounds of (2). A similar numerical and/or graphical comparison can be made to show that the double inequalities (14) and (20) are superior to (3). In conclusion, we obtained stronger and superior bounds for the function ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ than those in (2)–(3). Moreover, all the main results of the paper hold in $(-\pi ,0)$ because of the the symmetry of curves involved. Thus, our bounds provide the better alternatives.

Remark 6.

Our results can be used to bound the so-called sinc function, i.e., ${\displaystyle \frac{\sin x}{x}},$ which is extensively used in mathematics, physics and engineering. For instance, the double inequality (13) can be written as

$${\left[\cos x+{\displaystyle \frac{1}{4}}{(1-\cos x)}^2\right]}^{1/3}<{\displaystyle \frac{\sin x}{x}}<{\left[\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2\right]}^{1/3},x\in \left(0,\pi \right).$$

Remark 7.

An interesting application of our new generalized Mitrinović–Adamović-type inequalities is to find the value ${\displaystyle \frac{3\pi }{8}}$ of the integral ${\int }_0^{\infty }{\left({\displaystyle \frac{\sin x}{x}}\right)}^{3}dx.$ It is known that there are some complex standard methods; however, it is difficult to evaluate ${\int }_0^p{\left({\displaystyle \frac{\sin x}{x}}\right)}^{3}dx,$ for any $p>0.$ In such a case, we need to rely on an approximate value of the integral. Here, we can better approximate the integral ${\int }_0^p{\left({\displaystyle \frac{\sin x}{x}}\right)}^{3}dx,0<p\le \pi$ by using one of our main results. In particular, we approximate ${\int }_0^{\pi }{\left({\displaystyle \frac{\sin x}{x}}\right)}^{3}dx$ by selecting the inequality (21) as the best candidate whose bounds are tractable. Thus, integrating (21) from 0 to π, we have

$$I_1<{\int }_0^{\pi }{\left({\displaystyle \frac{\sin x}{x}}\right)}^{3}dx<I_2,$$

where

$$I_1={\int }_0^{\pi }\cos dx+{\int }_0^{\pi }\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{945}}{x}^2\right){(1-\cos x)}^{2}dx,$$

and

$$I_2={\int }_0^{\pi }\cos dx+{\int }_0^{\pi }\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{1}{60{\pi }^2}}{x}^2\right){(1-\cos x)}^{2}dx.$$

After expanding ${(1-\cos x)}^2,$ using simple formulae of integration and integrating by parts, we obtain

$$I_1={\displaystyle \frac{(361-2{\pi }^2)\pi }{945}}\mathit{and}{I}_2={\displaystyle \frac{47\pi }{120}}-{\displaystyle \frac{17}{240\pi }}.$$

Then,

$${\int }_0^{\pi }{\left({\displaystyle \frac{\sin x}{x}}\right)}^{3}dx\approx {\displaystyle \frac{I_1+I_2}{2}}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{(361-2{\pi }^2)\pi }{945}}+{\displaystyle \frac{47\pi }{120}}-{\displaystyle \frac{17}{240\pi }}\right]\approx 1.1712$$

which is very close to the exact value $\approx 1.1896.$

4. Conclusions

In this paper, we established various new generalized Mitrinović–Adamović-type inequalities as follows:

• (See Theorem 2):

  (i)

  The double inequality

  $$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{8}{{\pi }^3}}{(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

  holds with the best possible constants ${\displaystyle \frac{8}{{\pi }^3}}$ and ${\displaystyle \frac{4}{15}}$.

  (ii)

  The double inequality

  $$\begin{array}{c}\hfill \cos x+{\displaystyle \frac{1}{4}}{(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2,x\in \left(0,\pi \right)\end{array}$$

  holds with the best possible constants ${\displaystyle \frac{1}{4}}$ and ${\displaystyle \frac{4}{15}}$.

• (See Theorem 4):

  (i)

  The double inequality

  $$\begin{array}{c}\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{945}}{x}^6<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{256}{{\pi }^6}}\left({\displaystyle \frac{1}{15}}-{\displaystyle \frac{2}{{\pi }^3}}\right)x^6,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

  holds with the best possible constants $-{\displaystyle \frac{1}{945}}$ and $-{\displaystyle \frac{256}{{\pi }^6}}\left({\displaystyle \frac{1}{15}}-{\displaystyle \frac{2}{{\pi }^3}}\right).$

  (ii)

  The double inequality

  $$\begin{array}{c}\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{945}}{x}^6<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+{\displaystyle \frac{4}{15}}{(1-\cos x)}^2-{\displaystyle \frac{1}{15{\pi }^6}}{x}^6,x\in (0,\pi )\end{array}$$

  holds with the best possible constants $-{\displaystyle \frac{1}{945}}$ and $-{\displaystyle \frac{1}{15{\pi }^6}}.$

• (See Theorem 6):

  (i)

  The double inequality

  $$\begin{array}{c}\cos x+\left[{\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{945}}{x}^2\right]{(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+\left[{\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{{\pi }^2}}\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{8}{{\pi }^3}}\right)x^2\right]{(1-\cos x)}^2,x\in \left(0,{\displaystyle \frac{\pi }{2}}\right)\end{array}$$

  (20)

  holds with the best possible constants $-{\displaystyle \frac{4}{945}}$ and $-{\displaystyle \frac{4}{{\pi }^2}}\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{8}{{\pi }^3}}\right).$

  (ii)

  The double inequality

  $$\begin{array}{c}\cos x+\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{945}}{x}^2\right){(1-\cos x)}^2<{\left({\displaystyle \frac{\sin x}{x}}\right)}^3\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}<\cos x+\left({\displaystyle \frac{4}{15}}-{\displaystyle \frac{1}{60{\pi }^2}}{x}^2\right){(1-\cos x)}^2,x\in (0,\pi )\end{array}$$

  (21)

  holds with the best possible constants $-{\displaystyle \frac{4}{945}}$ and $-{\displaystyle \frac{1}{60{\pi }^2}}.$

In these new generalized Mitrinović–Adamović-type inequalities, we have compared our bounds of ${\left({\displaystyle \frac{\sin x}{x}}\right)}^3$ in a larger interval $(0,\pi )$ with the old ones. We believe that our results will assist us in obtaining novel expression results related to other generalized Mitrinović–Adamović-type inequalities in future studies.