Study of Impact of Moment Information in Demand Forecasting on Distributionally Robust Fulfillment Rate Improvement Algorithm
Abstract
1. Introduction
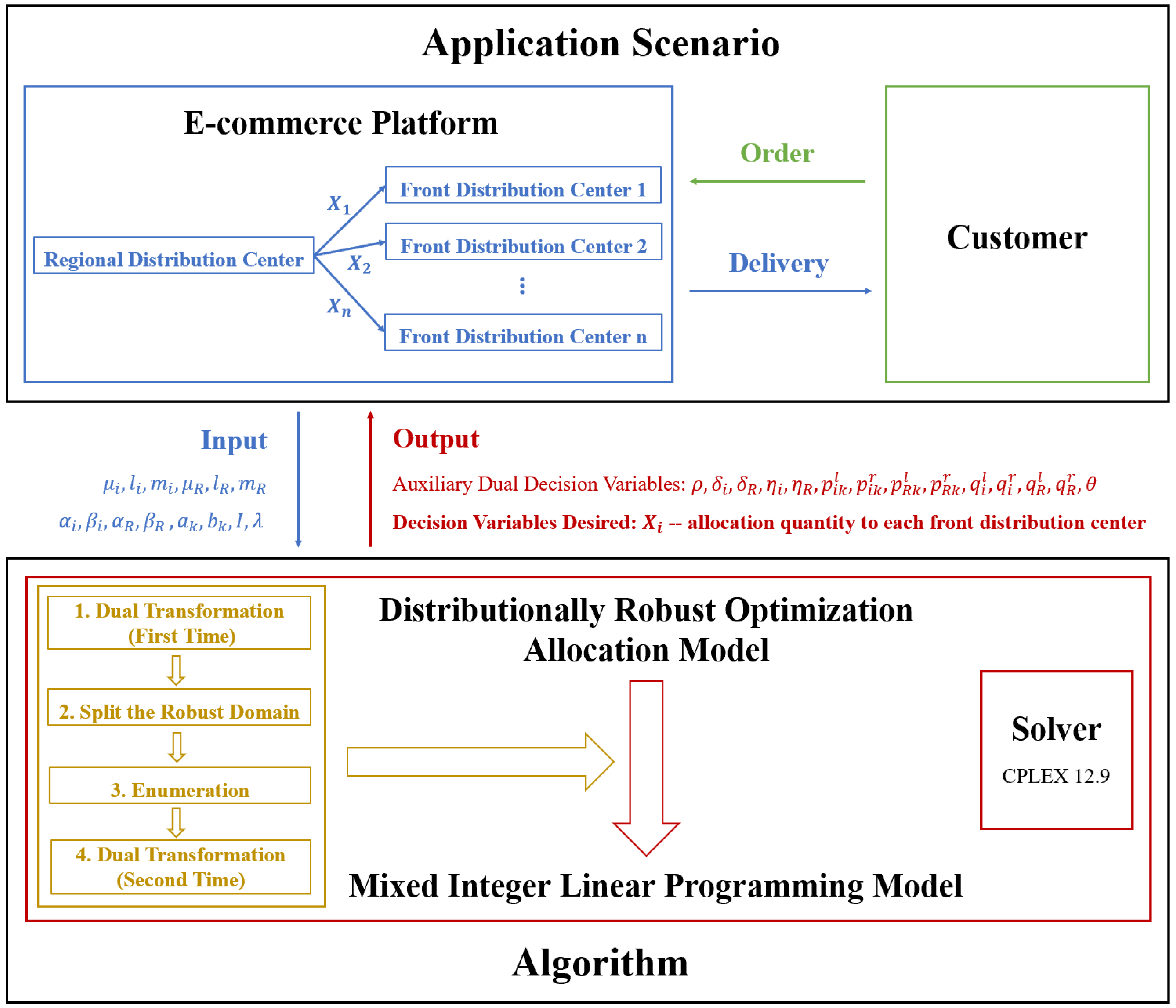
2. Model and Algorithm
2.1. Basic Model
2.1.1. Notation and Parameter Settings
- A.
- Notation
- Set of merchandises: , where represents the wth merchandise;
- Set of regions: , where represents the jth region;
- Set of front distribution centers: , where represents the ith front distribution center;
- R represents the regional distribution center.
- B.
- Parameter Settings
- Demand vector of merchandise w in region j: , where represents the demand of merchandise w in the zone covered by the ith front distribution center in region j and represents the demand of merchandise w in the zone directly served by the regional distribution center in region j;
- Total initial inventory available of merchandise w in region j: , which is the sum of inventory of merchandise w held at the regional distribution center and the front distribution centers in region j.
2.1.2. Decision Variable
- Allocation quantity vector of merchandise w in region j: ), where represents the amount of merchandise w allocated to the ith front distribution center in region j.
2.1.3. Objective Function
- Order fulfillment function: , where the decision variable is and the parameters are and .
- A.
- Order Fulfillment Calculation
- Orders fulfilled by front distribution center i: ;
- Orders fulfilled by all front distribution centers: ;
- Orders fulfilled by the regional distribution center:, where the first part represents the inventory left in the regional distribution center after allocation and the second part represents the orders needed to be fulfilled by the regional distribution center;
- Orders fulfilled altogether:.
- B.
- Lost Sales Calculation
- Orders could be fulfilled if there is no allocation: ;
- Orders actually fulfilled: , which has been derived in the previous part;
- Lost sales caused by allocation: , which is the gap between the quantity of orders could be fulfilled if there is no allocation and the quantity of orders actually fulfilled.
- C.
- Balance Coefficient Setting
- Balance coefficient: , which can be adjusted according to the specific requirements of the platform.
2.1.4. Constraints
- Total inventory constraint: ;
- Integer constraint: .
2.2. Distributionally Robust Optimization
2.2.1. Objective Function
2.2.2. Ambiguity Set
2.2.3. Distributionally Robust Optimization Model
2.3. Transformation and Approximation
- Set as the dual variables of the constraints ;
- Set as the dual variables of the constraints ;
- Set as the dual variables of the constraints ;
- Set as the dual variables of the constraints ;
- Set as the dual variables of the constraints ;
- Set as the dual variables of the constraints ;
- Set as the dual variable of the constraint ;
- Set as the dual variable of the constraint ;
- Set as the dual variable of the constraint .
2.4. Algorithm
3. Numerical Experiment
3.1. Experiments on Synthetic Data
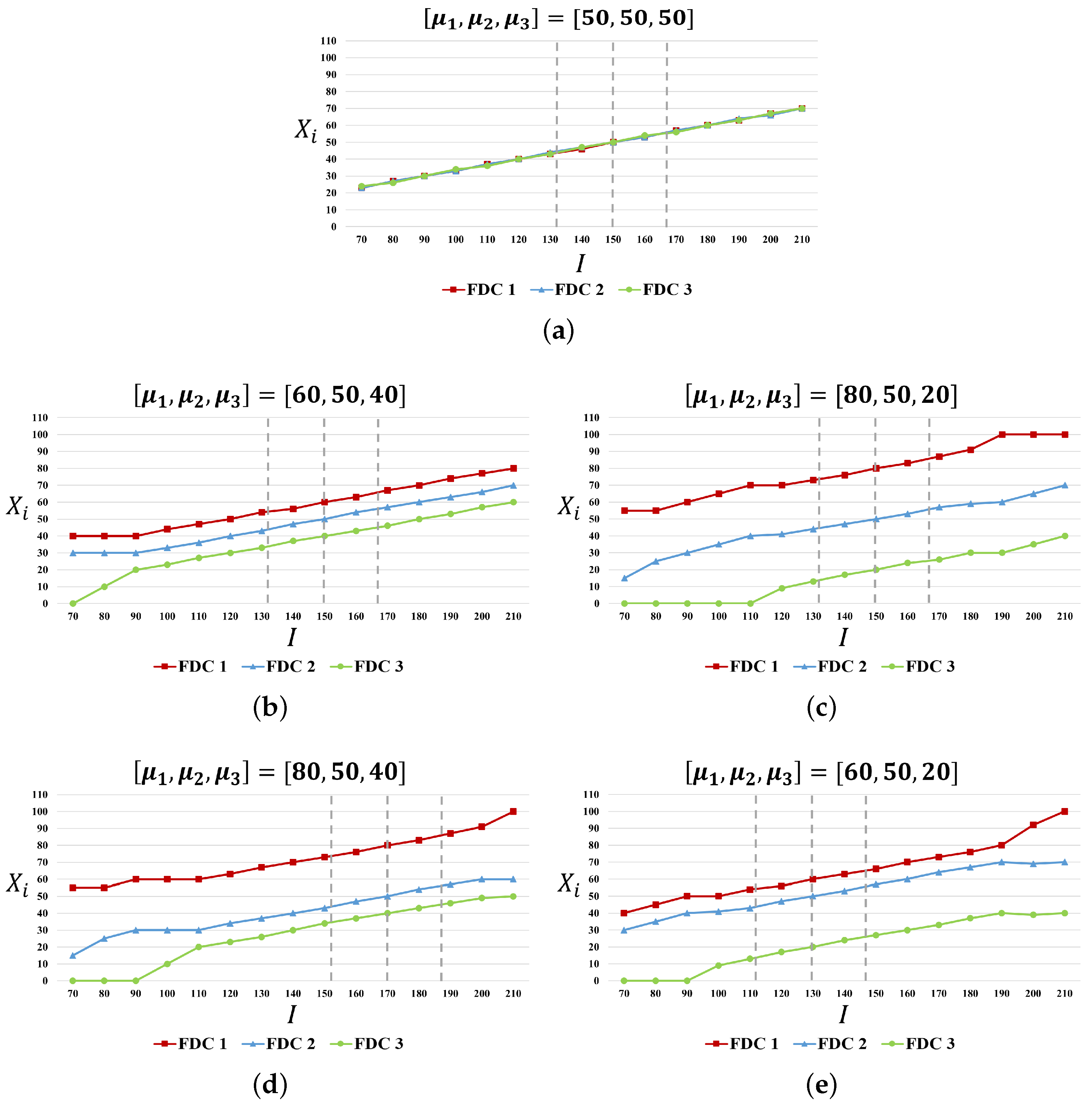
3.1.1. Experiment 1: Impact of Forecasted Mean on the Allocation Rule
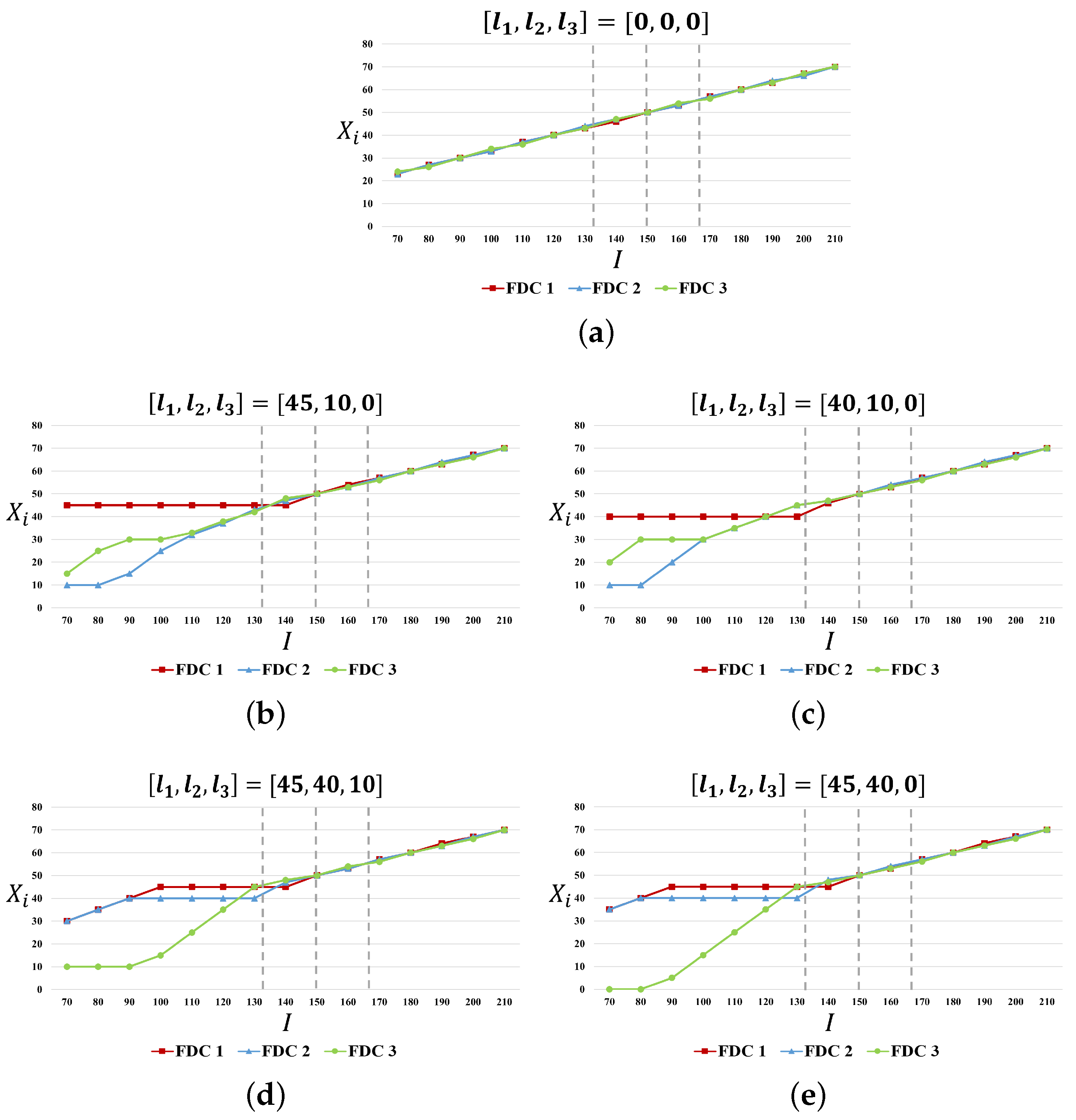
3.1.2. Experiment 2: Impact of Forecasted Variance on the Allocation Rule
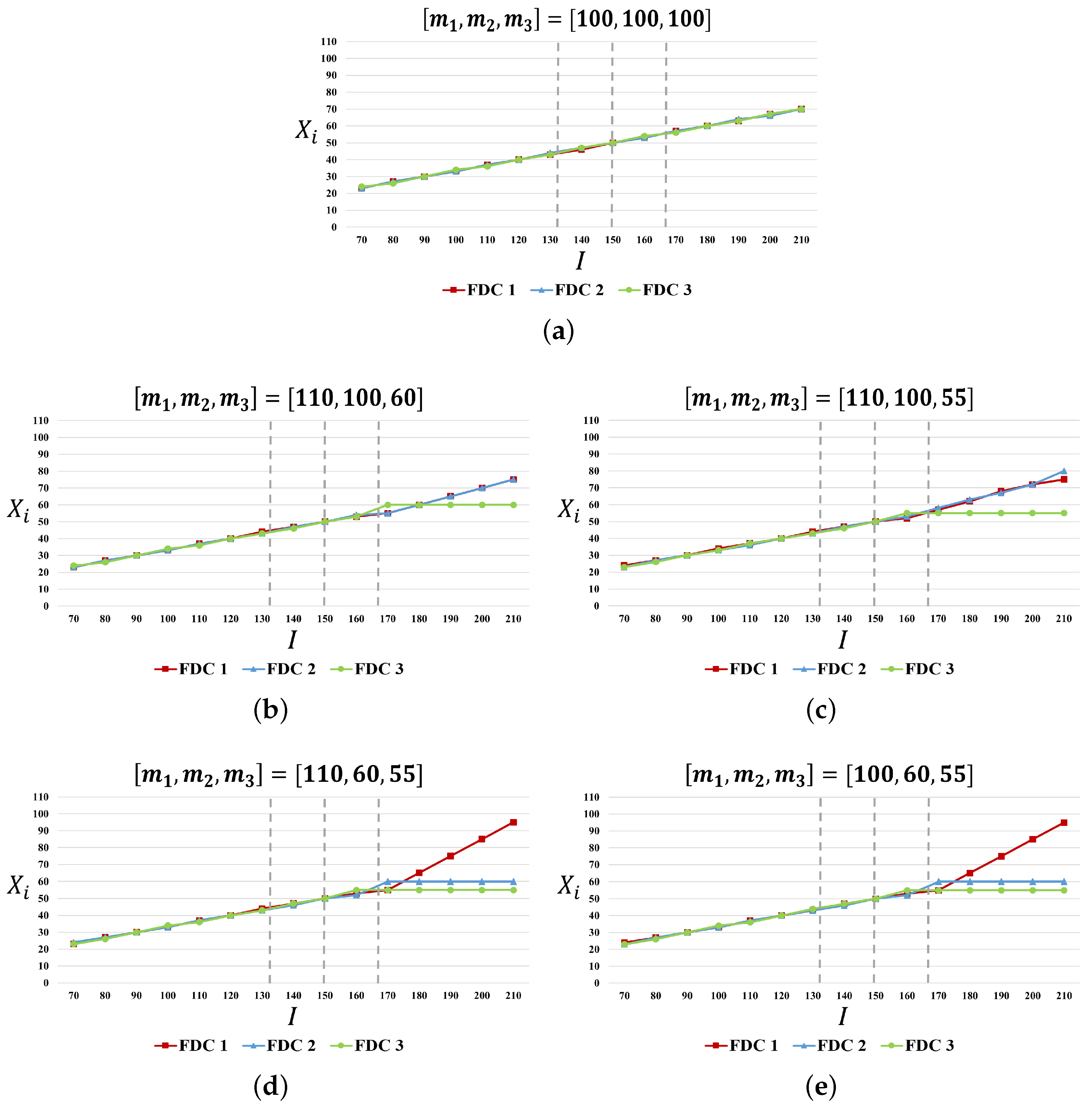
3.1.3. Experiment 3: Impact of Forecasted Bound on the Allocation Rule
3.1.4. Experiment 4: Impact of Forecasted Variance on the Fulfillment Rates at a Fixed Inventory Level
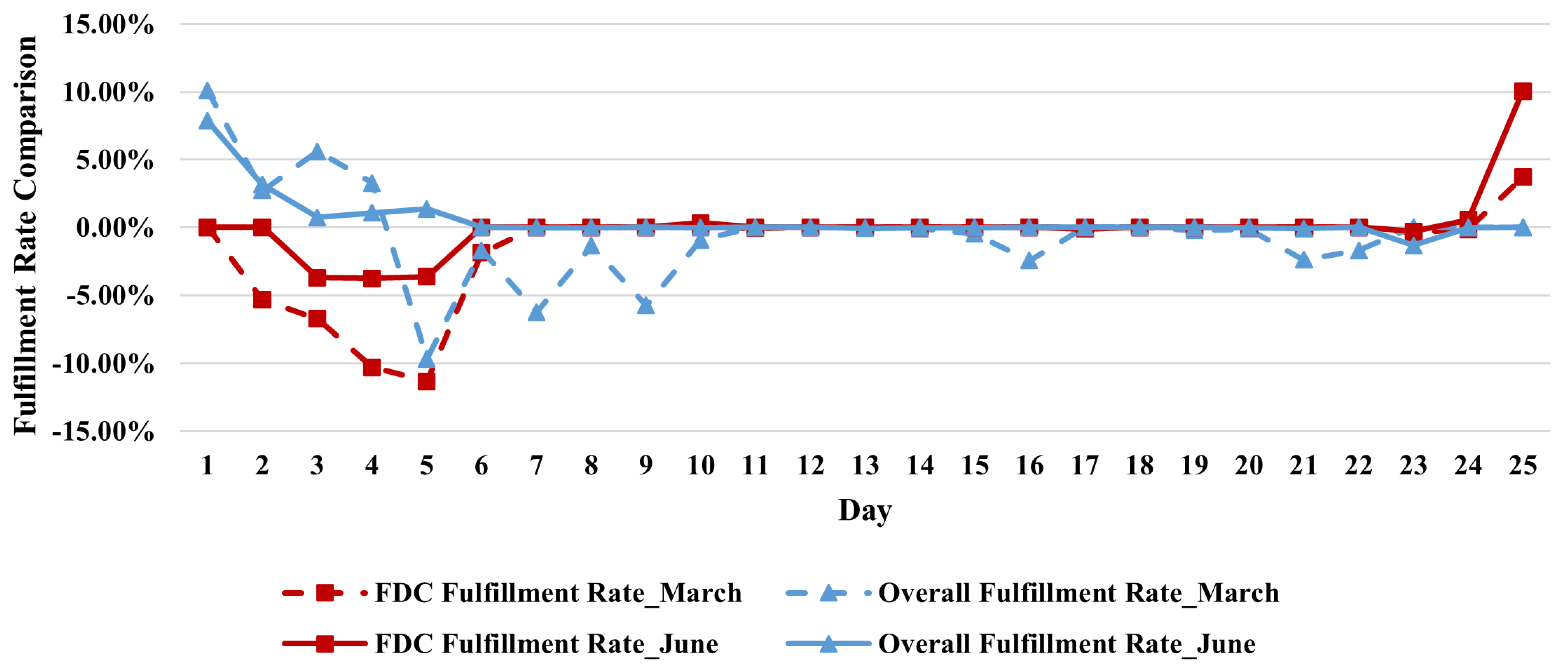
3.2. Experiment on Real Industry Data
4. Discussion
4.1. Results
4.1.1. Impact of Forecasted Mean on the Allocation Rule
4.1.2. Impact of Forecasted Variance on the Allocation Rule
4.1.3. Impact of Forecasted Bound on the Allocation Rule
4.1.4. Impact of Forecasted Variance on the Fulfillment Rates at a Fixed Inventory Level
4.1.5. Impact of Forecasted Variance on the Fulfillment Rates at Different Inventory Levels
4.2. Limitation
4.3. Extension
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lai, G.; Liu, H.; Xiao, W.; Zhao, X. “Fulfilled by amazon”: A strategic perspective of competition at the e-commerce platform. Manuf. Serv. Oper. Manag. 2022, 24, 1406–1420. [Google Scholar] [CrossRef]
- Lei, Y.; Jasin, S.; Sinha, A. Joint dynamic pricing and order fulfillment for e-commerce retailers. Manuf. Serv. Oper. Manag. 2018, 20, 269–284. [Google Scholar] [CrossRef]
- Das, S.; Ravi, R.; Sridhar, S. Order fulfillment under pick failure in omnichannel ship-from-store programs. Manuf. Serv. Oper. Manag. 2023, 25, 508–523. [Google Scholar] [CrossRef]
- Miao, S.; Jasin, S.; Chao, X. Asymptotically optimal Lagrangian policies for multi-warehouse, multi-store systems with lost sales. Oper. Res. 2022, 70, 141–159. [Google Scholar] [CrossRef]
- Dai, B.; Chen, H.; Li, Y.; Zhang, Y.; Wang, X.; Deng, Y. Inventory replenishment planning of a distribution system with storage capacity constraints and multi-channel order fulfilment. Omega 2021, 102, 102356. [Google Scholar] [CrossRef]
- DeValve, L.; Wei, Y.; Wu, D.; Yuan, R. Understanding the value of fulfillment flexibility in an online retailing environment. Manuf. Serv. Oper. Manag. 2023, 25, 391–408. [Google Scholar] [CrossRef]
- Bebitoğlu, B. Multi-Location Assortment Optimization Under Capacity Constraints. Ph.D. Thesis, Bilkent Universitesi, Ankara, Turkey, 2016. [Google Scholar]
- Li, X.; Lin, H.; Liu, F. Shall We Only Store Popular Products? Warehouse Assortment Selection for E-Companies. Available online: https://ssrn.com/abstract=4212027 (accessed on 7 September 2022).
- Lin, F.; Fang, X.; Gao, Z. Distributionally robust optimization: A review on theory and applications. Numer. Algebr. Control. Optim. 2022, 12, 159–212. [Google Scholar] [CrossRef]
- Liu, Y.; Pichler, A.; Xu, H. Discrete approximation and quantification in distributionally robust optimization. Math. Oper. Res. 2019, 44, 19–37. [Google Scholar] [CrossRef]
- Cheramin, M.; Cheng, J.; Jiang, R.; Pan, K. Computationally efficient approximations for distributionally robust optimization under moment and Wasserstein ambiguity. INFORMS J. Comput. 2022, 34, 1768–1794. [Google Scholar] [CrossRef]
- Delage, E.; Ye, Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 2010, 58, 595–612. [Google Scholar] [CrossRef]
- Hanasusanto, G.A.; Kuhn, D. Conic programming reformulations of two-stage distributionally robust linear programs over Wasserstein balls. Oper. Res. 2018, 66, 849–869. [Google Scholar] [CrossRef]
- Liu, Y.; Meskarian, R.; Xu, H. Distributionally robust reward-risk ratio optimization with moment constraints. SIAM J. Optim. 2017, 27, 957–985. [Google Scholar]
- Ardestani-Jaafari, A.; Delage, E. Robust optimization of sums of piecewise linear functions with application to inventory problems. Oper. Res. 2016, 64, 474–494. [Google Scholar]
- Feng, H.; Feng, M.; Wang, Q.; Jin, Q.; Zhang, Y.; Cao, L.; Hao, X. Improving Front Distribution Center Fulfillment Rates: A Distributionally Robust Approach. Available online: https://ssrn.com/abstract=5054555 (accessed on 26 June 2024).
- Liu, H.; Yu, Y.; Benjaafar, S.; Wang, H. Price-directed cost sharing and demand allocation among service providers with multiple demand sources and multiple facilities. Manuf. Serv. Oper. Manag. 2022, 24, 647–663. [Google Scholar]
- Chen, Y.; Marković, N.; Ryzhov, I.O.; Schonfeld, P. Data-driven robust resource allocation with monotonic cost functions. Oper. Res. 2022, 70, 73–94. [Google Scholar]
- Jasin, S.; Sinha, A. An LP-based correlated rounding scheme for multi-item e-commerce order fulfillment. Oper. Res. 2015, 63, 1336–1351. [Google Scholar]
- Hwang, D.; Jaillet, P.; Manshadi, V. Online resource allocation under partially predictable demand. Oper. Res. 2021, 69, 895–915. [Google Scholar]
- Angelus, A. A multiechelon inventory problem with secondary market sales. Manag. Sci. 2011, 57, 2145–2162. [Google Scholar] [CrossRef]
- Klosterhalfen, S.T.; Minner, S.; Willems, S.P. Strategic safety stock placement in supply networks with static dual supply. Manuf. Serv. Oper. Manag. 2014, 16, 204–219. [Google Scholar]
- Shang, K.H.; Tao, Z.; Zhou, S.X. Optimizing reorder intervals for two-echelon distribution systems with stochastic demand. Oper. Res. 2015, 63, 458–475. [Google Scholar]
- Zhu, H.; Chen, Y.; Hu, M.; Yang, Y. Technical Note–A Simple Heuristic Policy for Stochastic Distribution Inventory Systems with Fixed Shipment Costs. Oper. Res. 2021, 69, 1651–1659. [Google Scholar] [CrossRef]
- Ding, S.; Kaminsky, P.M. Centralized and decentralized warehouse logistics collaboration. Manuf. Serv. Oper. Manag. 2020, 22, 812–831. [Google Scholar] [CrossRef]
- Drent, M.; Arts, J. Expediting in two-echelon spare parts inventory systems. Manuf. Serv. Oper. Manag. 2021, 23, 1431–1448. [Google Scholar] [CrossRef]
- Shen, X.; Yu, Y.; Song, J.-S. Optimal policies for a multi-echelon inventory problem with service time target and expediting. Manuf. Serv. Oper. Manag. 2022, 24, 2310–2327. [Google Scholar] [CrossRef]
- Zhen, L.; Wang, W.; Zhuge, D. Optimizing locations and scales of distribution centers under uncertainty. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 2908–2919. [Google Scholar] [CrossRef]
- Huang, J.; Shi, X. Solving the location problem of front distribution center for omni-channel retailing. Complex Intell. Syst. 2023, 9, 2237–2248. [Google Scholar] [CrossRef]
- Shi, Y. Solving Inventory Assortment Problem by Utilizing Product Embedding. 2018. Available online: https://medium.com/jd-technology-blog/solving-inventory-assortment-problem-by-utilizing-product-embedding-807f992cb35a (accessed on 3 December 2018).
- Axsäter, S. A new decision rule for lateral transshipments in inventory systems. Manag. Sci. 2003, 49, 1168–1179. [Google Scholar] [CrossRef]
- Xu, P.J.; Allgor, R.; Graves, S.C. Benefits of reevaluating real-time order fulfillment decisions. Manuf. Serv. Oper. Manag. 2009, 11, 340–355. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 152, 9–28. [Google Scholar] [CrossRef]
- Nagy, G.; Wassan, N.A.; Speranza, M.G.; Archetti, C. The vehicle routing problem with divisible deliveries and pickups. Transp. Sci. 2015, 49, 271–294. [Google Scholar] [CrossRef]
- Franceschetti, A.; Honhon, D.; Laporte, G.; Van Woensel, T. A shortest-path algorithm for the departure time and speed optimization problem. Transp. Sci. 2018, 52, 756–768. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Parameters estimate of autoregressive moving average and autoregressive integrated moving average models and compare their ability for inflow forecasting. J. Math. Stat. 2012, 8, 330–338. [Google Scholar]
- Natarajan, K.; Sim, M.; Uichanco, J. Tractable robust expected utility and risk models for portfolio optimization. Math. Financ. 2010, 20, 695–731. [Google Scholar]
- Nickel, S.; Steinhardt, C.; Schlenker, H.; Burkart, W. Decision Optimization with IBM ILOG CPLEX Optimization Studio; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Kim, S.; Pasupathy, R.; Henderson, S.G. A guide to sample average approximation. In Handbook of Simulation Optimization; Springer: Berlin/Heidelberg, Germany, 2015; pp. 207–243. [Google Scholar]


| Front Distribution Center | Inventory Allocation Balance | Fulfillment Rate Improvement | Allocation Direction † Permitted | |
|---|---|---|---|---|
| Jasin and Sinha (2015) [19] | ✓ | ✓ | 2 | |
| Bebitoğlu (2016) [7] | ✓ | ✓ | 2 | |
| Lei et al. (2018) [2] | ✓ | ✓ | 2 | |
| Ding and Kaminsky (2020) [25] | ✓ | ✓ | 1, 2, 3 | |
| Dai et al. (2021) [5] | ✓ | ✓ | ✓ | 1, 2, 3 |
| Drent and Arts (2021) [26] | ✓ | ✓ | 1, 2, 3 | |
| Hwang et al. (2021) [20] | ✓ | |||
| Chen et al. (2022) [18] | ✓ | |||
| Liu et al. (2022) [17] | ✓ | |||
| Miao et al. (2022) [4] | ✓ | ✓ | 1, 2 | |
| Shen et al. (2022) [27] | ✓ | ✓ | 1, 2 | |
| Das et al. (2023) [3] | ✓ | 1 | ||
| DeValve et al. (2023) [6] | ✓ | ✓ | ✓ | 1, 2 |
| Li et al. (2023) [8] | ✓ | |||
| This Research | ✓ | ✓ | ✓ | 1 |
| FDC 1 † | ||||||||||||||
| FDC 2 | 25 | 0 | 100 | |||||||||||
| FDC 3 | ||||||||||||||
| FDC 1 | 50 | 60 | 80 | 80 | 60 | |||||||||
| FDC 2 | 50 | 50 | 50 | 50 | 50 | |||||||||
| FDC 3 | 50 | 40 | 20 | 40 | 20 | |||||||||
| I | ||||||||||||||
| 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 |
| FDC 1 † | ||||||||||||||
| FDC 2 | 50 | 0 | 100 | |||||||||||
| FDC 3 | ||||||||||||||
| FDC 1 | 25 | 100 | 400 | 400 | 400 | |||||||||
| FDC 2 | 25 | 25 | 25 | 100 | 100 | |||||||||
| FDC 3 | 25 | 1 | 1 | 1 | 25 | |||||||||
| I | ||||||||||||||
| 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 |
| FDC 1 † | ||||||||||||||
| FDC 2 | 50 | 25 | 100 | |||||||||||
| FDC 3 | ||||||||||||||
| FDC 1 | 0 | 45 | 40 | 45 | 45 | |||||||||
| FDC 2 | 0 | 10 | 10 | 40 | 40 | |||||||||
| FDC 3 | 0 | 0 | 0 | 10 | 0 | |||||||||
| I | ||||||||||||||
| 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 |
| FDC 1 † | ||||||||||||||
| FDC 2 | 50 | 25 | 0 | |||||||||||
| FDC 3 | ||||||||||||||
| FDC 1 | 100 | 110 | 110 | 110 | 100 | |||||||||
| FDC 2 | 100 | 100 | 100 | 60 | 60 | |||||||||
| FDC 3 | 100 | 60 | 55 | 55 | 55 | |||||||||
| I | ||||||||||||||
| 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 |
| Parameters | |||||
| Algorithm 1 | |||||
| FDCs † | |||||
| RDC | |||||
| Algorithm 2 | |||||
| FDCs | |||||
| RDC | |||||
| Total Inventory | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, H. Study of Impact of Moment Information in Demand Forecasting on Distributionally Robust Fulfillment Rate Improvement Algorithm. Mathematics 2025, 13, 1172. https://doi.org/10.3390/math13071172
Feng H. Study of Impact of Moment Information in Demand Forecasting on Distributionally Robust Fulfillment Rate Improvement Algorithm. Mathematics. 2025; 13(7):1172. https://doi.org/10.3390/math13071172
Chicago/Turabian StyleFeng, Haodong. 2025. "Study of Impact of Moment Information in Demand Forecasting on Distributionally Robust Fulfillment Rate Improvement Algorithm" Mathematics 13, no. 7: 1172. https://doi.org/10.3390/math13071172
APA StyleFeng, H. (2025). Study of Impact of Moment Information in Demand Forecasting on Distributionally Robust Fulfillment Rate Improvement Algorithm. Mathematics, 13(7), 1172. https://doi.org/10.3390/math13071172





