Operator-Based Approach for the Construction of Solutions to (CD(1/n))k-Type Fractional-Order Differential Equations
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Power Series
2.2. Algebras of Fractional Power Series
2.3. Isomorphism Between and Taylor Series
2.4. Subalgebras of
2.5. Caputo Differentiation of Fractional Power Series
2.6. Perfect FDEs
2.6.1. Reduction of Perfect FDEs to ODEs
2.6.2. Cauchy Problem for Perfect FDEs
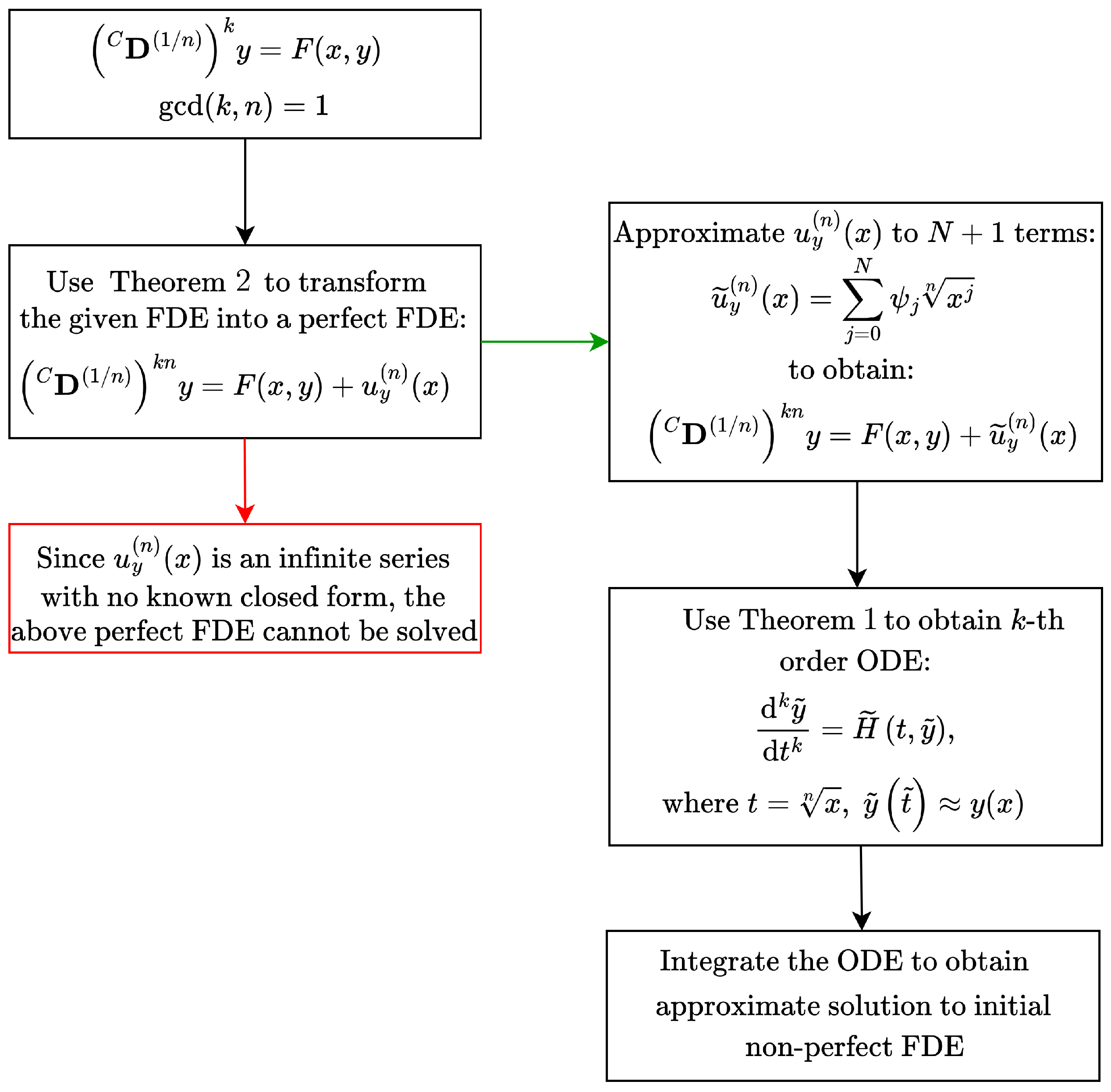
3. Main Results
3.1. Higher-Order Perfect FDEs
3.2. Transformation of Riccati-Type FDE into Perfect FDE
- Non-perfect Cauchy problem
- Perfect Cauchy problem
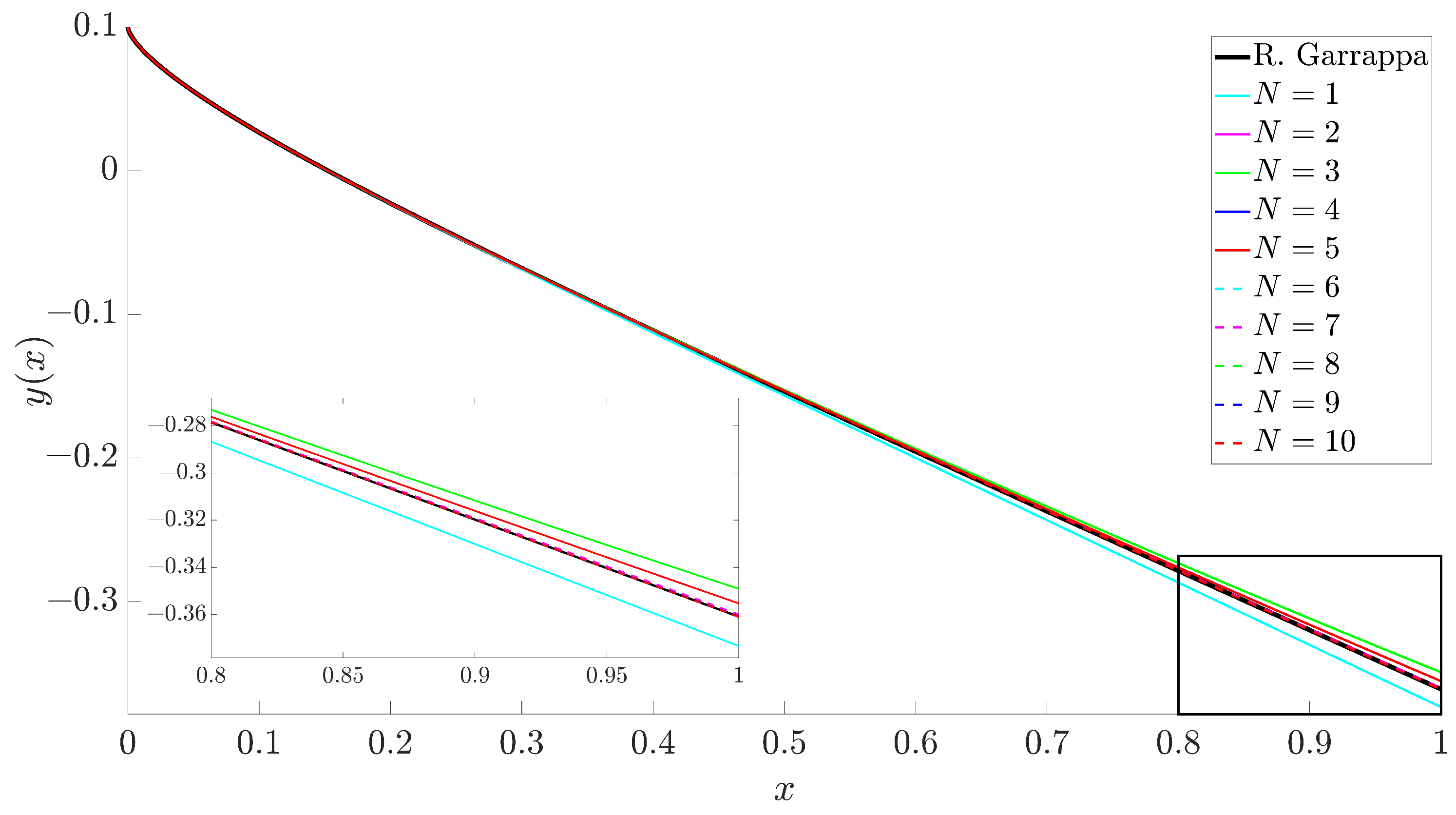
4. Numerical Application of the Proposed Approach
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.P.; Alrihieli, H.F.; Algehyne, E.A.; Khan, M.A.; Alshahrani, M.Y.; Alraey, Y.; Riaz, M.B. Application of piecewise fractional differential equation to COVID-19 infection dynamics. Results Phys. 2022, 39, 105685. [Google Scholar] [CrossRef]
- Farman, M.; Xu, C.; Shehzad, A.; Akgul, A. Modeling and dynamics of measles via fractional differential operator of singular and non-singular kernels. Math. Comput. Simul. 2024, 221, 461–488. [Google Scholar]
- Edward, S. A fractional order model for the transmission dynamics of shigellosis. Heliyon 2024, 10, e31242. [Google Scholar] [CrossRef] [PubMed]
- Mahdy, A.M.; Almalki, N.; Higazy, M. A general fractional breast cancer model: Model graph energy, Caputo-Fabrizio derivative existence and uniqueness plus numerical simulation. Partial Differ. Eq. Appl. Math. 2024, 10, 100723. [Google Scholar] [CrossRef]
- Agarwal, R.; Airan, P.; Agarwal, R.P. Exploring the Landscape of Fractional-Order Models in Epidemiology: A Comparative Simulation Study. Axioms 2024, 13, 545. [Google Scholar] [CrossRef]
- Chauhan, R.; Singh, R.; Kumar, A.; Thakur, N.K. Role of prey refuge and fear level in fractional prey–predator model with anti-predator. J. Comput. Sci. 2024, 81, 102385. [Google Scholar] [CrossRef]
- Singh, J.; Agrawal, R.; Baleanu, D. Dynamical analysis of fractional order biological population model with carrying capacity under Caputo-Katugampola memory. Alex. Eng. J. 2024, 91, 394–402. [Google Scholar] [CrossRef]
- Matouk, A. Applications of the generalized gamma function to a fractional-order biological system. Heliyon 2023, 9, e18645. [Google Scholar] [CrossRef]
- Seralan, V.; Vadivel, R.; Gunasekaran, N.; Radwan, T. Dynamics of Fractional-Order Three-Species Food Chain Model with Vigilance Effect. Fractal Fract. 2025, 9, 45. [Google Scholar] [CrossRef]
- Li, H.; ur Rahman, G.; Naz, H.; Gómez-Aguilar, J. Modeling of implicit multi term fractional delay differential equation: Application in pollutant dispersion problem. Alex. Eng. J. 2024, 94, 1–22. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, X.; Duan, L.; Gong, Q.; Wang, Y.; Ao, X. A novel method for state of health estimation of lithium-ion batteries based on fractional-order differential voltage-capacity curve. Appl. Energy 2025, 377, 124404. [Google Scholar]
- Jornet, M.; Nieto, J.J. On a nonlinear stochastic fractional differential equation of fluid dynamics. Phys. D Nonlinear Phenom. 2024, 470, 134400. [Google Scholar]
- Huseynov, I.T.; Mahmudov, N.I. A class of Langevin time-delay differential equations with general fractional orders and their applications to vibration theory. J. King Saud Univ.-Sci. 2021, 33, 101596. [Google Scholar] [CrossRef]
- Abdou, M.A. An analytical method for space–time fractional nonlinear differential equations arising in plasma physics. J. Ocean Eng. Sci. 2017, 2, 288–292. [Google Scholar]
- Srivastava, H.M.; Adel, W.; Izadi, M.; El-Sayed, A.A. Solving some physics problems involving fractional-order differential equations with the Morgan-Voyce polynomials. Fractal Fract. 2023, 7, 301. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore; River Edge, NJ, USA, 2000. [Google Scholar]
- Graef, J.R.; Kong, L.; Ledoan, A.; Wang, M. Stability analysis of a fractional online social network model. Math. Comput. Simul. 2020, 178, 625–645. [Google Scholar]
- Jin, T.; Yang, X. Monotonicity theorem for the uncertain fractional differential equation and application to uncertain financial market. Math. Comput. Simul. 2021, 190, 203–221. [Google Scholar]
- Kumar, Y.; Singh, V.K. Computational approach based on wavelets for financial mathematical model governed by distributed order fractional differential equation. Math. Comput. Simul. 2021, 190, 531–569. [Google Scholar]
- Sene, N. Analytical investigations of the fractional free convection flow of Brinkman type fluid described by the Caputo fractional derivative. Results Phys. 2022, 37, 105555. [Google Scholar]
- Sawangtong, W.; Sawangtong, P. An analytical solution for the Caputo type generalized fractional evolution equation. Alex. Eng. J. 2022, 61, 5475–5483. [Google Scholar]
- Hassan, A.; Arafa, A.; Rida, S.; Dagher, M.; El Sherbiny, H. Adapting semi-analytical treatments to the time-fractional derivative Gardner and Cahn-Hilliard equations. Alex. Eng. J. 2024, 87, 389–397. [Google Scholar]
- Fan, Z.Y.; Ali, K.K.; Maneea, M.; Inc, M.; Yao, S.W. Solution of time fractional Fitzhugh–Nagumo equation using semi analytical techniques. Results Phys. 2023, 51, 106679. [Google Scholar]
- Kheybari, S.; Darvishi, M.T.; Hashemi, M.S. A semi-analytical approach to Caputo type time-fractional modified anomalous sub-diffusion equations. Appl. Numer. Math. 2020, 158, 103–122. [Google Scholar]
- Li, C.; N’Gbo, N.; Su, F. Finite difference methods for nonlinear fractional differential equation with ψ-Caputo derivative. Phys. D Nonlinear Phenom. 2024, 460, 134103. [Google Scholar]
- Sivalingam, S.; Kumar, P.; Trinh, H.; Govindaraj, V. A novel L1-Predictor-Corrector method for the numerical solution of the generalized-Caputo type fractional differential equations. Math. Comput. Simul. 2024, 220, 462–480. [Google Scholar]
- Saeed, U.; ur Rehman, M. A new scheme for the solution of the nonlinear Caputo–Hadamard fractional differential equations. Alex. Eng. J. 2024, 105, 56–69. [Google Scholar]
- Raghavendran, P.; Gunasekar, T.; Gochhait, S. Application of artificial neural networks for existence and controllability in impulsive fractional Volterra-Fredholm integro-differential equations. Appl. Math. Sci. Eng. 2024, 32, 2436440. [Google Scholar]
- Navickas, Z.; Telksnys, T.; Marcinkevicius, R.; Ragulskis, M. Operator-based approach for the construction of analytical soliton solutions to nonlinear fractional-order differential equations. Chaos Solitons Fractals 2017, 104, 625–634. [Google Scholar]
- Marcinkevicius, R.; Telksniene, I.; Telksnys, T.; Navickas, Z.; Ragulskis, M. The construction of solutions to CD(1/n) type FDEs via reduction to (CD(1/n))n type FDEs. AIMS Math. 2022, 7, 16536–16554. [Google Scholar] [CrossRef]
- Timofejeva, I.; Navickas, Z.; Telksnys, T.; Marcinkevicius, R.; Ragulskis, M. An Operator-Based Scheme for the Numerical Integration of FDEs. Mathematics 2021, 9, 1372. [Google Scholar] [CrossRef]
- Navickas, Z.; Telksnys, T.; Timofejeva, I.; Marcinkevicius, R.; Ragulskis, M. The Fractal Structure of Analytical Solutions to Fractional Riccati Equation. Fractals 2023, 32, 2340130. [Google Scholar] [CrossRef]
- Formichella, S.; Straub, A. Gaussian binomial coefficients with negative arguments. Ann. Comb. 2019, 23, 725–748. [Google Scholar]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Telksniene, I.; Navickas, Z.; Marcinkevičius, R.; Telksnys, T.; Čiegis, R.; Ragulskis, M. Operator-Based Approach for the Construction of Solutions to (CD(1/n))k-Type Fractional-Order Differential Equations. Mathematics 2025, 13, 1169. https://doi.org/10.3390/math13071169
Telksniene I, Navickas Z, Marcinkevičius R, Telksnys T, Čiegis R, Ragulskis M. Operator-Based Approach for the Construction of Solutions to (CD(1/n))k-Type Fractional-Order Differential Equations. Mathematics. 2025; 13(7):1169. https://doi.org/10.3390/math13071169
Chicago/Turabian StyleTelksniene, Inga, Zenonas Navickas, Romas Marcinkevičius, Tadas Telksnys, Raimondas Čiegis, and Minvydas Ragulskis. 2025. "Operator-Based Approach for the Construction of Solutions to (CD(1/n))k-Type Fractional-Order Differential Equations" Mathematics 13, no. 7: 1169. https://doi.org/10.3390/math13071169
APA StyleTelksniene, I., Navickas, Z., Marcinkevičius, R., Telksnys, T., Čiegis, R., & Ragulskis, M. (2025). Operator-Based Approach for the Construction of Solutions to (CD(1/n))k-Type Fractional-Order Differential Equations. Mathematics, 13(7), 1169. https://doi.org/10.3390/math13071169







