Nonlocal Harmonically Varying Heat in a Magneto-Thermoelastic Thick Plate Using Simple and Refined Lord and Shulman Theories
Abstract
1. Introduction
2. Modified Nonlocal Thermoelasticity
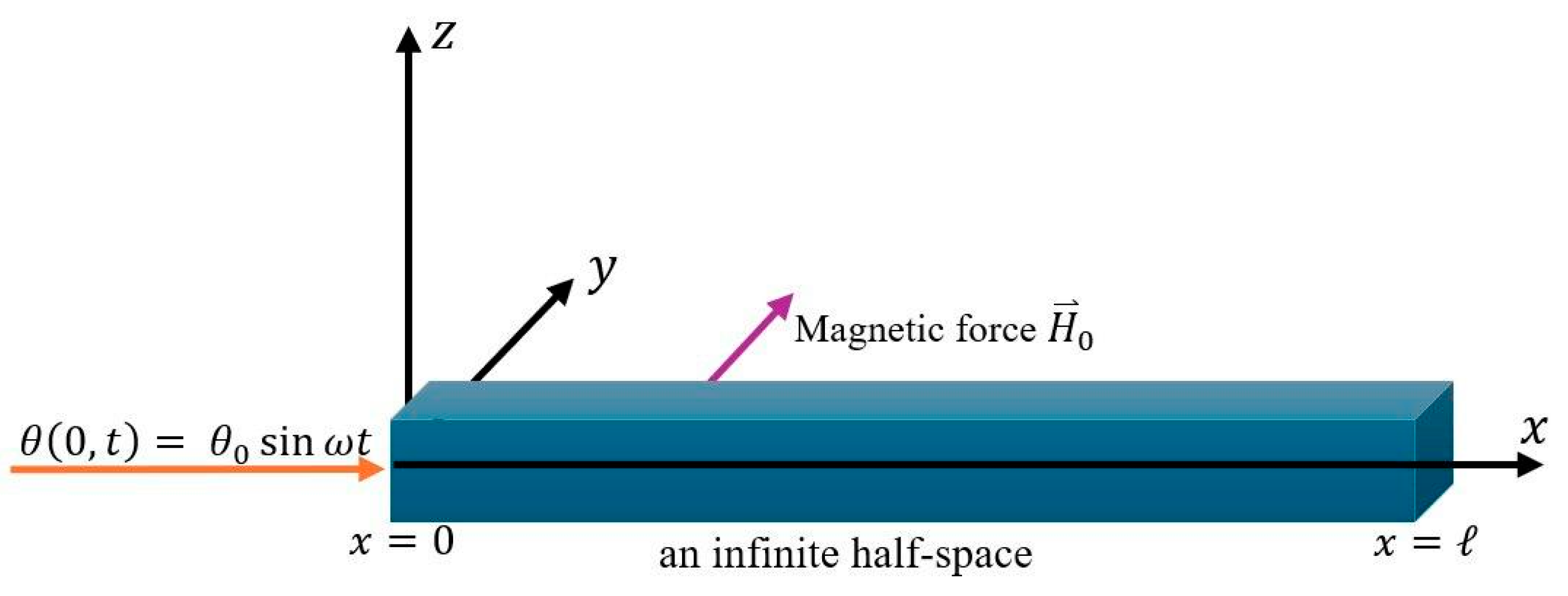
3. Plan of the Problem
4. Solution of the Problem in Laplace Transform Domain
5. Numerical Inversion of Laplace Transform
6. Numerical Results
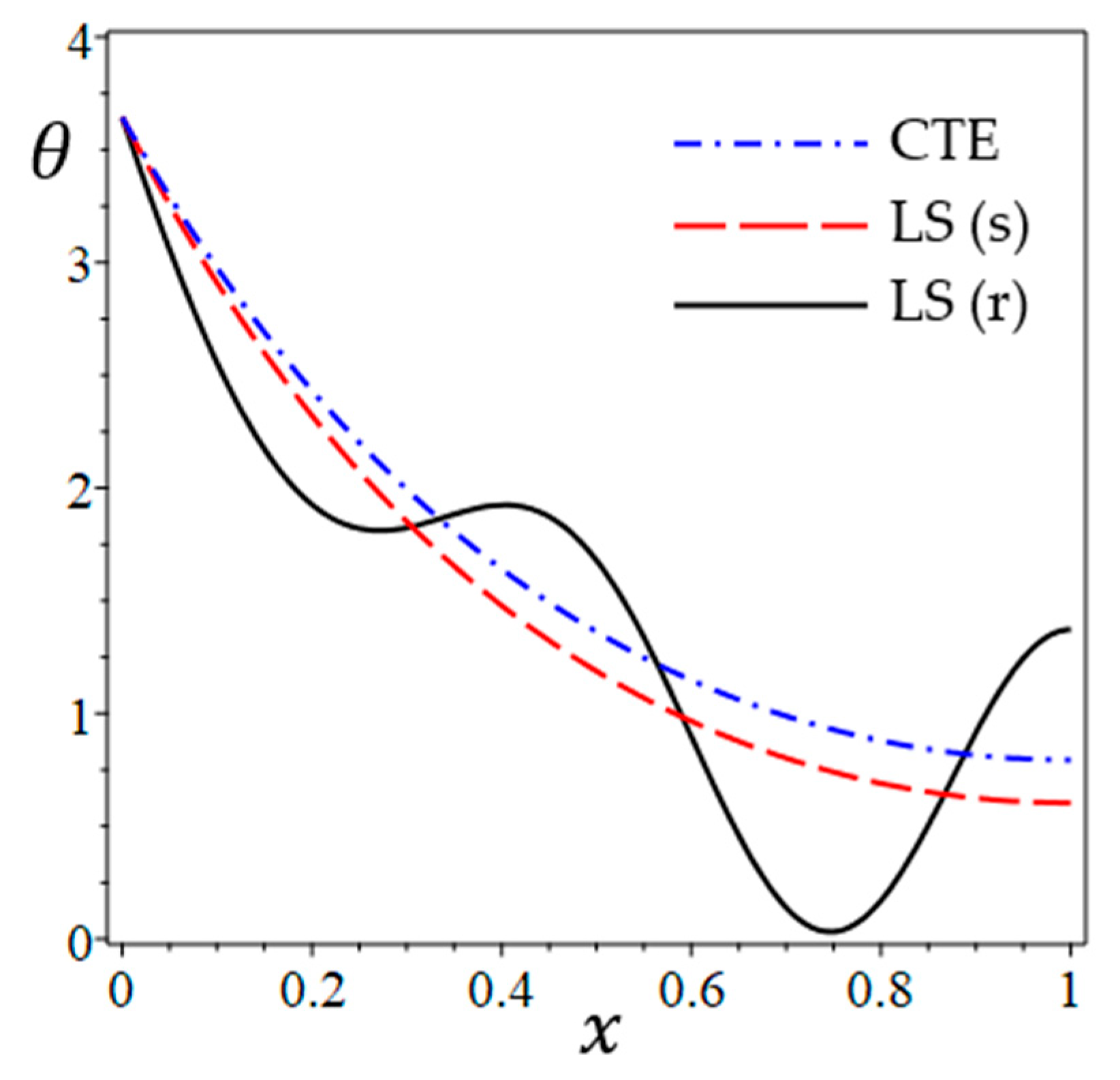
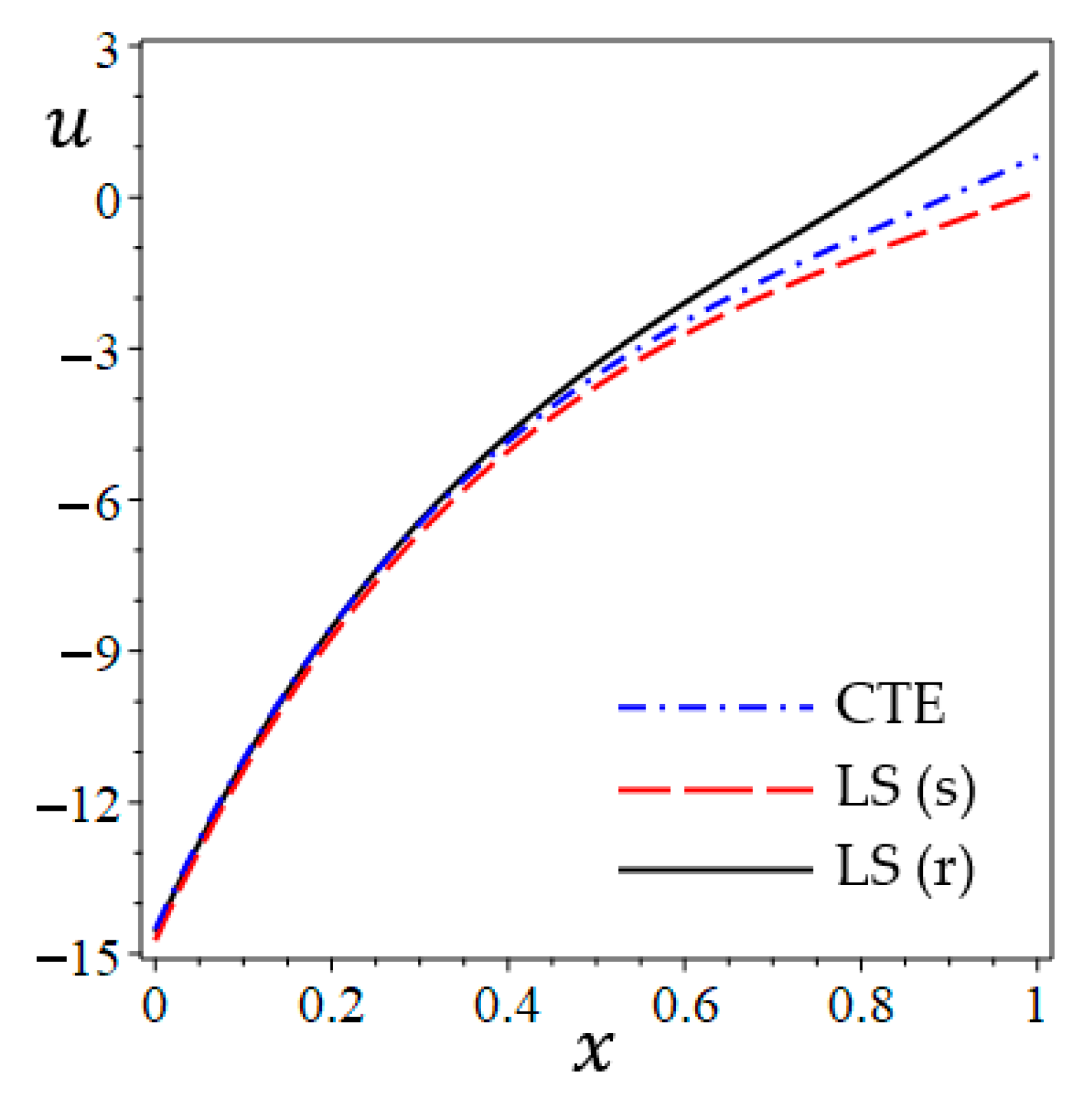
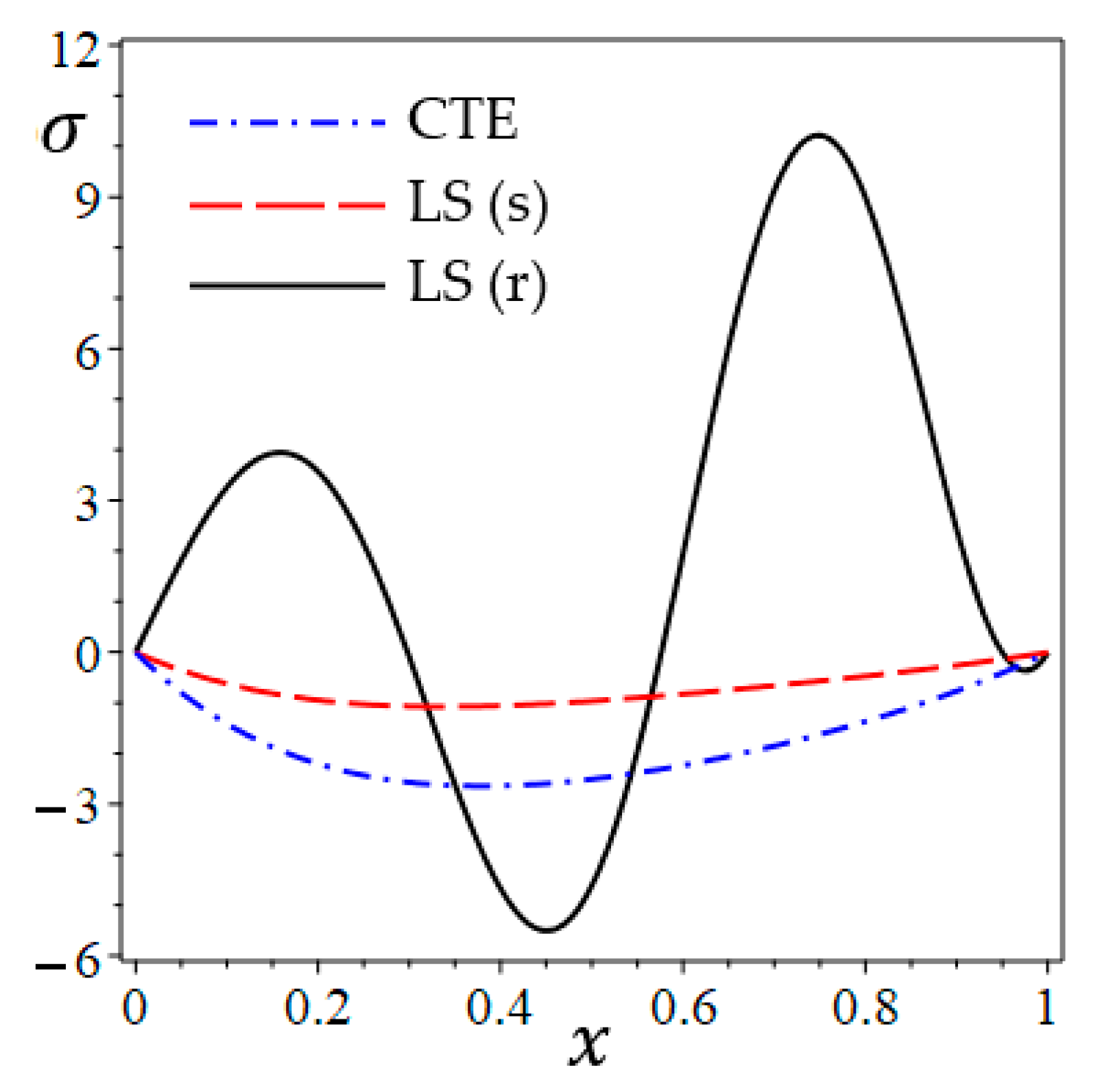
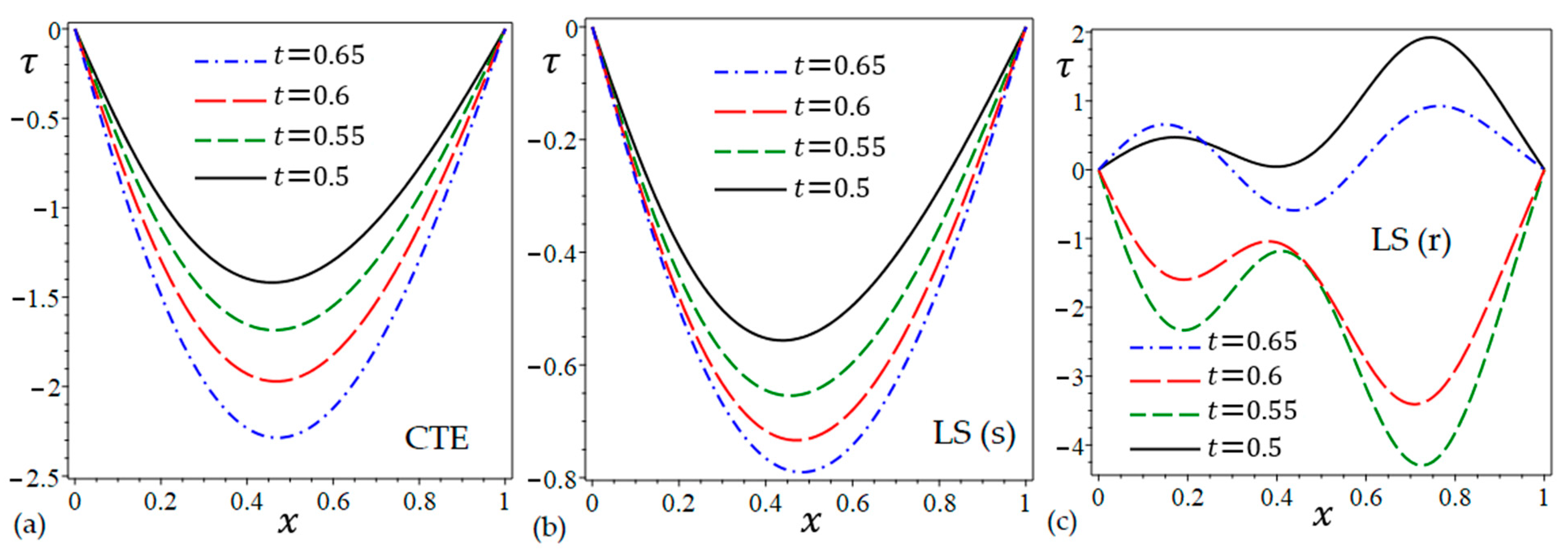
6.1. The Study of CTE, Simple, and Refined LS Models
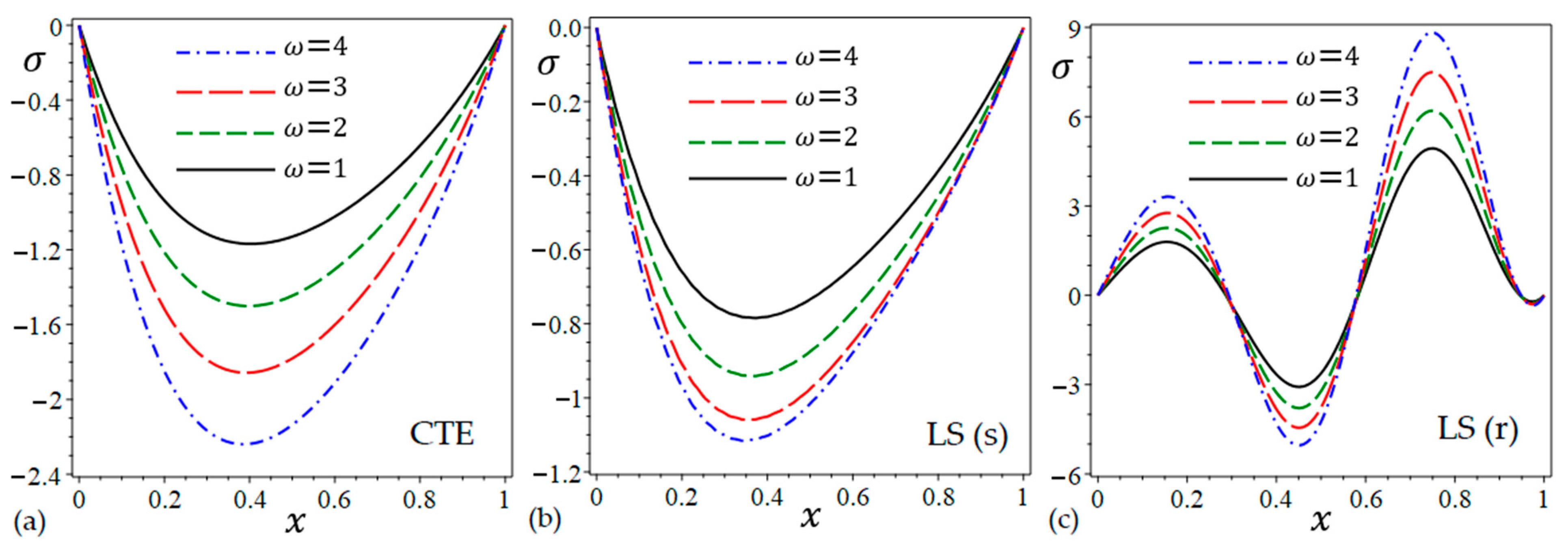
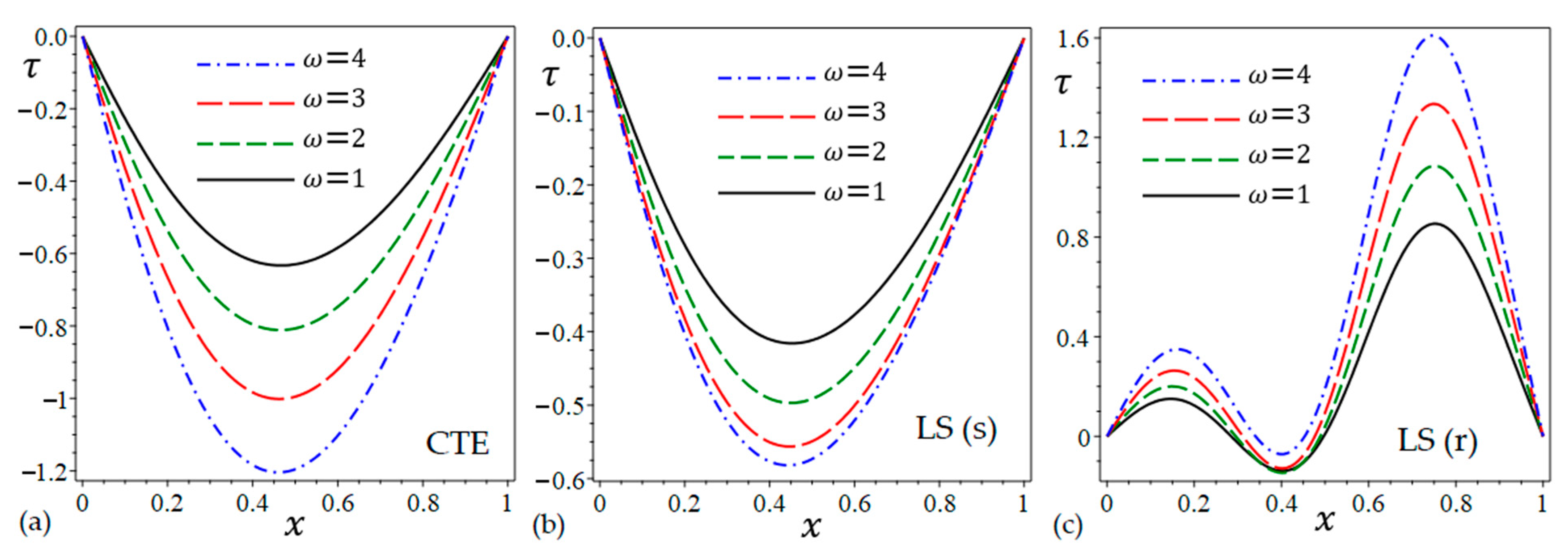
6.2. The Effect of the Angular Frequency of Thermal Vibration
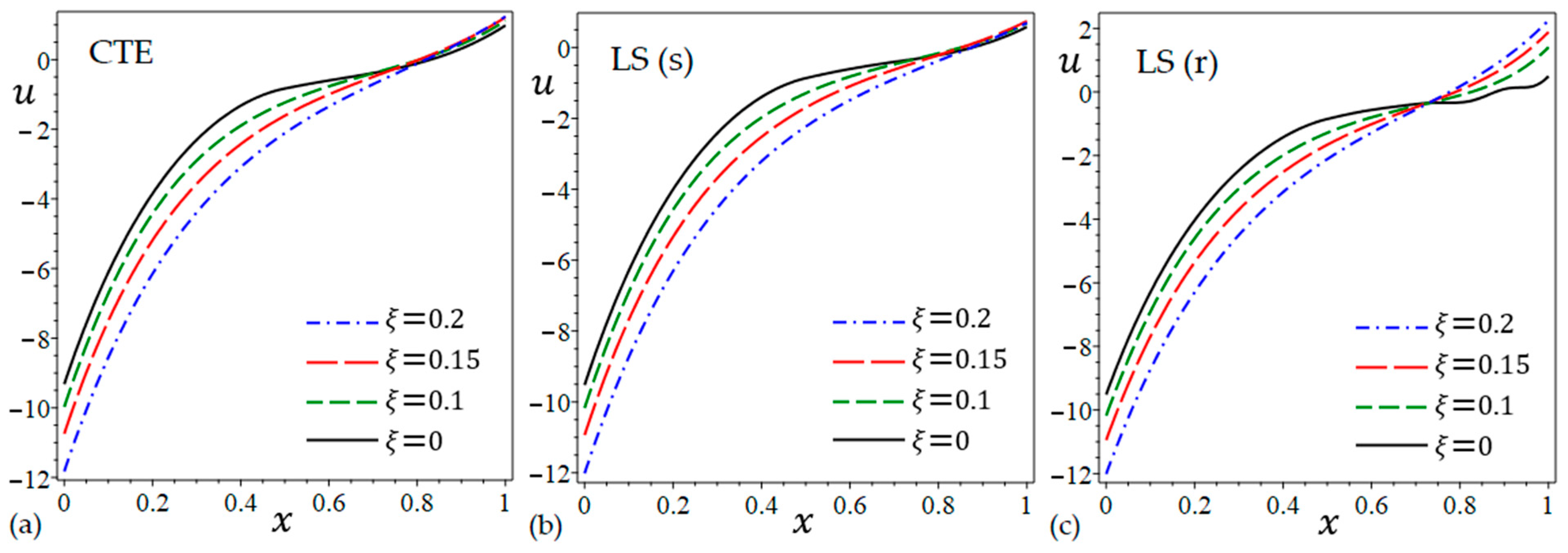
6.3. The Effect of Nonlocal Parameter
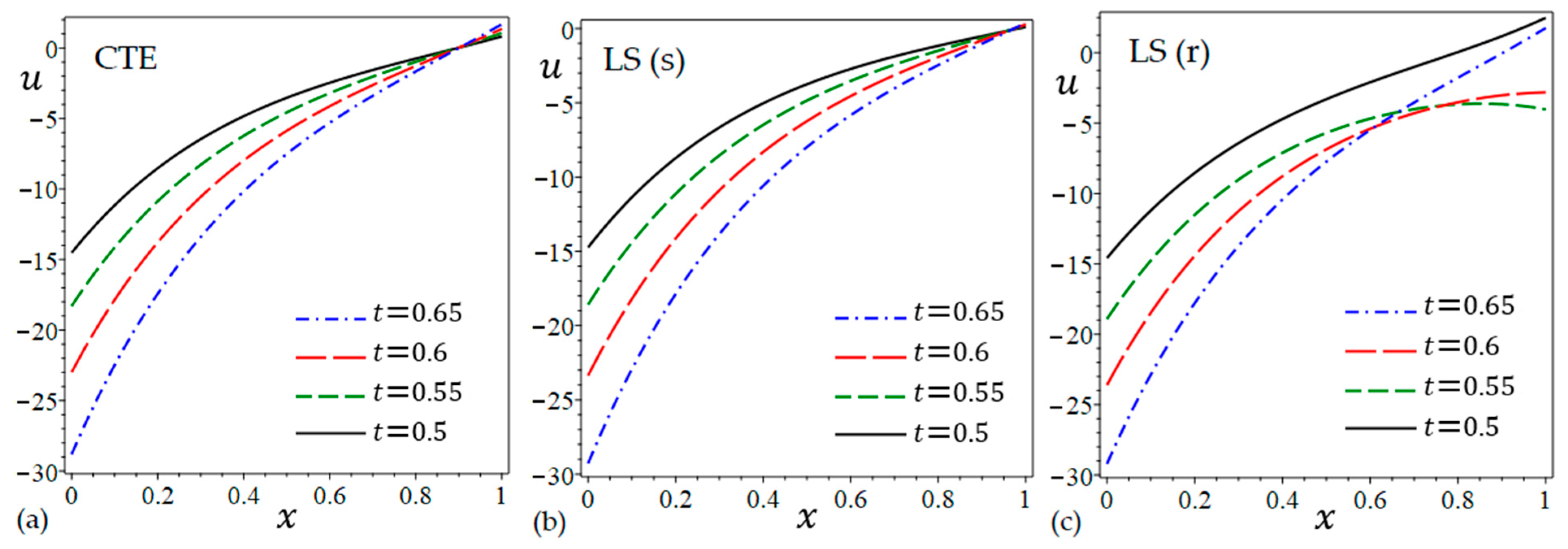
6.4. The Effect of Time Parameter
7. Conclusions
- Thermal vibration angular frequency has a substantial impact on all fields studied.
- Increasing the nonlocal parameter value escalates the temperature and nonlocal stress , while reducing the displacement.
- The LS (r) theory can cause a variation in the results across the plate due to the theory’s additional terms. This may cause significant fluctuations in the responses of some physical fields.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Inan, E.; Eringen, A. Nonlocal theory of wave propagation in thermoelastic plates. Int. J. Eng. Sci. 1991, 29, 831–843. [Google Scholar] [CrossRef]
- Bachher, M.; Sarkar, N. Nonlocal theory of thermoelastic materials with voids and fractional derivative heat transfer. Waves Random Complex Media 2019, 29, 595–613. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.-D.; Guo, Y.-Q.; Dong, Y.; Huang, X. A generalized magneto-thermoviscoelastic problem of a single-layer plate for vibration control considering memory-dependent heat transfer and nonlocal effect. J. Heat Transf. 2019, 141, 082002. [Google Scholar] [CrossRef]
- Mondal, S. Memory response for thermal distributions moving over a magneto-thermoelastic rod under Eringen’s nonlocal theory. J. Therm. Stress. 2020, 43, 72–89. [Google Scholar] [CrossRef]
- Zenkour, A.; Abouelregal, A. Magnetothermoelastic interaction in a rod of finite length subjected to moving heat sources via Eringen’s nonlocal model. J. Eng. Phys. Thermophys. 2022, 95, 651–661. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Karimi Zeverdejani, P.; Kiani, Y. Nonlinear generalized thermoelasticity of FGM finite domain based on Lord–Shulman theory. Waves Random Complex Media 2022, 32, 575–596. [Google Scholar] [CrossRef]
- Xue, Z.; Cao, G.; Yu, Y.; Liu, J. Coupled thermoelastic fracture analysis of a cracked fiber reinforced composite hollow cylinder by fractional Cattaneo-Vernotte models. Theor. Appl. Fract. Mech. 2022, 121, 103538. [Google Scholar] [CrossRef]
- Mirzaei, M. Lord–Shulman nonlinear generalized thermoviscoelasticity of a strip. Int. J. Struct. Stab. Dyn. 2020, 20, 2050017. [Google Scholar]
- Alshaikh, F. Effects of thermal relaxation times and porosity in a Lord-Shulman and refined multi-phase lags model of generalized thermoelasticity. Mech. Based Des. Struct. Mach. 2023, 51, 438–449. [Google Scholar] [CrossRef]
- Oskouie, M.F.; Ansari, R.; Rouhi, H. Studying nonlinear thermomechanical wave propagation in a viscoelastic layer based upon the Lord-Shulman theory. Mech. Adv. Mater. Struct. 2020, 27, 800–806. [Google Scholar]
- Guha, S.; Singh, A.K.; Singh, S. Thermoelastic damping and frequency shift of different micro-scale piezoelectro-magneto-thermoelastic beams. Phys. Scr. 2023, 99, 015203. [Google Scholar]
- Karimipour Dehkordi, M.; Kiani, Y. Lord–Shulman and Green–Lindsay-based magneto-thermoelasticity of hollow cylinder. Acta Mech. 2024, 235, 51–72. [Google Scholar]
- Aljadani, M.H.; Zenkour, A.M. Effect of magnetic field on a thermoviscoelastic body via a refined two-temperature Lord–Shulman model. Case Stud. Therm. Eng. 2023, 49, 103197. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Refined Lord–Shulman theory for 1D response of skin tissue under ramp-type heat. Materials 2022, 15, 6292. [Google Scholar] [CrossRef]
- Aljadani, M.H.; Zenkour, A.M. Effect of hydrostatic initial stress on a rotating half-space in the context of a two-relaxation power-law model. Mathematics 2022, 10, 4727. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Saeed, T.; Al-Raezah, A.A. A 1D thermoelastic response of skin tissue due to ramp-type heating via a fractional-order Lord–Shulman model. J. Comput. Appl. Mech. 2023, 54, 365–377. [Google Scholar]
- Amin, M.; Nasr, A.M.A.A.; El-Bary, A.; Abo-Dahab, S. Propagation of surface waves in generalized thermoelastic media under influence of magnetic field and rotation and its applications in engineering and geophysics. Mech. Based Des. Struct. Mach. 2022, 50, 3417–3440. [Google Scholar]
- Ezzat, M.A. Fundamental solution in generalized magneto-thermoelasticity with two relaxation times for perfect conductor cylindrical region. Int. J. Eng. Sci. 2004, 42, 1503–1519. [Google Scholar]
- Yadav, A.K. Reflection of plane waves in a fraction-order generalized magneto-thermoelasticity in a rotating triclinic solid half-space. Mech. Adv. Mater. Struct. 2022, 29, 4273–4290. [Google Scholar]
- Tiwari, R. Analysis of phase lag effect in generalized magneto thermoelasticity with moving heat source. Waves Random Complex Media 2024, 34, 1133–1150. [Google Scholar]
- Abo-Dahab, S.; Hussein, N.S.; Abd-Alla, A.; Alshehri, H. Thermal stresses for a generalized magneto-thermoelasticity on non-homogeneous orthotropic continuum solid with a spherical cavity. Mech. Based Des. Struct. Mach. 2022, 50, 915–934. [Google Scholar]
- Lotfy, K.; El-Bary, A.; Sarkar, N. Memory-dependent derivatives (MDD) of magneto-thermal-elastic waves excited by laser pulses for two-temperature theory. Waves Random Complex Media 2022, 32, 2177–2196. [Google Scholar]
- Zenkour, A.M. Magneto-thermal shock for a fiber-reinforced anisotropic half-space studied with a refined multi-dual-phase-lag model. J. Phys. Chem. Solids 2020, 137, 109213. [Google Scholar]
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Faghidian, S.A.; Shirazi, A.H. Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Univ. Ser. Mech. Eng. 2021, 19, 633–656. [Google Scholar]
- Kaur, I.; Singh, K. Forced Flexural Vibrations due to Time-Harmonic Source in a Thin Nonlocal Rectangular Plate with Memory-Dependent Derivative. Mech. Solids 2023, 58, 1257–1270. [Google Scholar]
- Sharma, D.K.; Sharma, A.; Mondal, S.; Bachher, M. Transient thermo-diffusive responses in a nonlocal elastic sphere due to harmonically varying heat sources. GEM-Int. J. Geomath. 2023, 14, 6. [Google Scholar]
- Babaei, M.; Chen, Z. Transient thermopiezoelectric response of a one-dimensional functionally graded piezoelectric medium to a moving heat source. Arch. Appl. Mech. 2010, 80, 803–813. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Zenkour, A.M. Nonlocal thermoelastic model for temperature-dependent thermal conductivity nanobeams due to dynamic varying loads. Microsyst. Technol. 2018, 24, 1189–1199. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar]
- Wang, H.; Dong, K.; Men, F.; Yan, Y.; Wang, X. Influences of longitudinal magnetic field on wave propagation in carbon nanotubes embedded in elastic matrix. Appl. Math. Model. 2010, 34, 878–889. [Google Scholar]
- Abouelregal, A.E.; Zenkour, A.M. Magnetothermoelastic vibrations on a viscoelastic microbeam subjected to a laser heat source. Arch. Mech. 2021, 73, 3–26. [Google Scholar]
- Allehaibi, A.M.; Zenkour, A.M. Magneto-thermoelastic response in an infinite medium with a spherical hole in the context of high order time-derivatives and triple-phase-lag model. Materials 2022, 15, 6256. [Google Scholar] [CrossRef]
- Das, N.; Lahiri, A.; Sarkar, S. Eigenvalue approach to three dimensional coupled thermoelasticity in a rotating transversely isotropic medium. Tamsui Oxf. J. Math. Sci. 2009, 25, 237–257. [Google Scholar]
- Bachher, M.; Sarkar, N.; Lahiri, A. Generalized thermoelastic infinite medium with voids subjected to a instantaneous heat sources with fractional derivative heat transfer. Int. J. Mech. Sci. 2014, 89, 84–91. [Google Scholar] [CrossRef]
- Santra, S.; Lahiri, A.; Das, N. Eigenvalue approach on thermoelastic interactions in an infinite elastic solid with voids. J. Therm. Stress. 2014, 37, 440–454. [Google Scholar] [CrossRef]
- Churchill, R.V. Operational Mathematics; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Honig, G.; Hirdes, U. A method for the numerical inversion of Laplace transforms. J. Comput. Appl. Math. 1984, 10, 113–132. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zenkour, A.M.; Aljadani, M.H. Nonlocal Harmonically Varying Heat in a Magneto-Thermoelastic Thick Plate Using Simple and Refined Lord and Shulman Theories. Mathematics 2025, 13, 1160. https://doi.org/10.3390/math13071160
Zenkour AM, Aljadani MH. Nonlocal Harmonically Varying Heat in a Magneto-Thermoelastic Thick Plate Using Simple and Refined Lord and Shulman Theories. Mathematics. 2025; 13(7):1160. https://doi.org/10.3390/math13071160
Chicago/Turabian StyleZenkour, Ashraf M., and Maryam H. Aljadani. 2025. "Nonlocal Harmonically Varying Heat in a Magneto-Thermoelastic Thick Plate Using Simple and Refined Lord and Shulman Theories" Mathematics 13, no. 7: 1160. https://doi.org/10.3390/math13071160
APA StyleZenkour, A. M., & Aljadani, M. H. (2025). Nonlocal Harmonically Varying Heat in a Magneto-Thermoelastic Thick Plate Using Simple and Refined Lord and Shulman Theories. Mathematics, 13(7), 1160. https://doi.org/10.3390/math13071160






