GSA-KAN: A Hybrid Model for Short-Term Traffic Forecasting

Abstract

Short-term traffic flow forecasting is an essential part of intelligent transportation systems. However, it is challenging to model traffic flow accurately due to its rapid changes over time. The Kolmogorov–Arnold Network (KAN) has shown parameter efficiency with lower memory and computational overhead via spline-parametrized functions to handle high-dimensional temporal data. In this paper, we propose to unlock the potential of the Kolmogorov–Arnold network for traffic flow forecasting by optimizing its parameters with a heuristic algorithm. The gravitational search algorithm learns to understand optimized KANs for different traffic scenarios. We conduct extensive experiments on four real-world benchmark datasets from Amsterdam, the Netherlands. The RMSE of GSA-KAN is reduced by $3.95\%$, $6.96\%$, $2.71\%$, and $2.29\%$, and the MAPE of GSA-KAN is reduced by $6.66\%$, $5.88\%$, $6.41\%$, and $4.87\%$ on the A1, A2, A4, and A8 datasets, respectively. The experimental results demonstrate that GSA-KAN performs advanced parametric and nonparametric models.

1. Introduction

The accessibility and diversity of transportation infrastructure are fundamental to urban development and economic growth. Accurate short-term traffic flow forecasting plays a pivotal role in intelligent transportation systems (ITSs), enabling optimal route recommendations for drivers and supporting urban management in mitigating traffic congestion [1]. By analyzing historical traffic data, this technology aims to predict future traffic patterns and anomalies, offering actionable insights for dynamic traffic control [2]. Despite technological advancements, short-term traffic flow prediction remains challenging due to its inherent nonlinearity, susceptibility to external disturbances (e.g., accidents or weather events), and noise-induced seasonal variations [3].

Short-term traffic flow forecasting typically operates within a 15-min prediction horizon. Existing approaches fall into two categories, i.e., parametric and non-parametric models [4]. Classical parametric methods, including moving average [5], linear discriminant analysis [6,7], conditional random fields [8], Gaussian mixture models [9], and Kalman filtering [10], often struggle with underfitting and fail to capture complex nonlinear relationships in traffic dynamics. Non-parametric alternatives, such as gray models [11], support vector regression [12], artificial neural networks [13], extreme learning machines [14,15], and long short-term memory networks [16], demonstrate enhanced flexibility but face limitations in computational efficiency and robustness.

The evolution of deep learning has significantly advanced traffic flow prediction through contributions from multiple research teams. For example, Yang et al. [17] use convolutional neural networks (CNNs) to model spatio-temporal dependencies in traffic dynamics. Wei et al. [18] improve temporal feature extraction by integrating LSTM with autoencoders. Zheng et al. [19] developed a CNN-LSTM hybrid architecture to capture multiscale correlations, and Abduljabbar et al. [20] introduce bidirectional LSTM models to improve the robustness of prediction. In addition, Zhang et al. [21] proposed a physics-informed deep learning framework that integrates traffic flow models with computational graph methods, enhancing the physical interpretability of predictions. Similarly, Zhang et al. [22] introduced EF-former for short-term passenger flow prediction during large-scale events, demonstrating the effectiveness of attention mechanisms in handling irregular traffic patterns. Despite these advancements, challenges persist in scenarios requiring multi-source data fusion or adaptive resolution switching. Recent studies [23,24] have further explored multi-frequency spatial–temporal graph networks and hybrid pre-training strategies [25], yet their reliance on extensive labeled data and high computational overhead limits real-time applicability. Despite these advances, critical challenges hinder their practical implementation. Deep learning models require substantial computational resources, particularly when processing large-scale datasets, limiting their scalability in real-time applications [26].

A notable advancement is the Kolmogorov–Arnold Network (KAN) [27], a novel neural architecture grounded in the Kolmogorov–Arnold representation theorem. Unlike conventional multilayer perceptrons (MLPs) with fixed nodal activation functions [28,29], KAN replaces linear weights with spline-parameterized univariate functions along the edges, allowing adaptive resolution switching without retraining. This design confers superior interpretability and precision in the approximation of nonlinear systems. Researchers have extended KAN’s utility to diverse domains: Vaca-Rubio et al. [30] demonstrate its efficacy in time series forecasting, Bresson et al. [31] integrate KAN with graph learning for spatial data modeling, and Li et al. [32] apply it to medical image segmentation. Additionally, KAN can be paired with radial basis function networks [33], a classical learning technique. Moreover, KAN training, based on sparsification and regularization, risks overfitting and slow convergence. Furthermore, the performance is highly sensitive to data quality. Noise or missing data may lead to significant accuracy degradation. One possible reason is suboptimal generalization without robust hyperparameters for dynamic traffic conditions.

To address these issues, we rethink the model training for traffic flow forecasting as $\widehat{\mathcal{Y}}=\mathcal{F}\left(\mathcal{X}\right)$. We aim to find an optimal $\mathcal{F}$ using the historical traffic flow and ground truth. In this way, we can learn a model to learn $\mathcal{F}$ using heuristic algorithms as ${\mathcal{F}}^{\ast }=\mathcal{G}(\mathcal{X},\mathcal{Y},\mathcal{F})$. According to this idea, we propose a hybrid Kolmogorov–Arnold network (KAN) optimized with a gravitational search algorithm (GSA), termed GSA-KAN. We overcome the rigidity of traditional models in handling non-linear traffic flow dynamics through spline-parameterized univariate functions to reduce the computational overhead. The GSA’s global search capabilities automatically determine the optimal ${\mathcal{F}}^{\ast }$ to enhance adaptability to complex traffic patterns. An empirical study on Amsterdam highway datasets demonstrates the superiority of the model. The GSA-KAN not only outperforms both parametric and non-parametric baselines but also exhibits exceptional robustness in determining an optimal KAN.

The contributions of this paper are summarized as follows.

• We rethink the model optimization for traffic flow forecasting from a data-driven perspective and exemplify a gravitational search algorithm-improved Kolmogorov–Arnold network.
• We propose a hybrid learning model to automatically find an optimal model for accurate traffic flow forecasting.
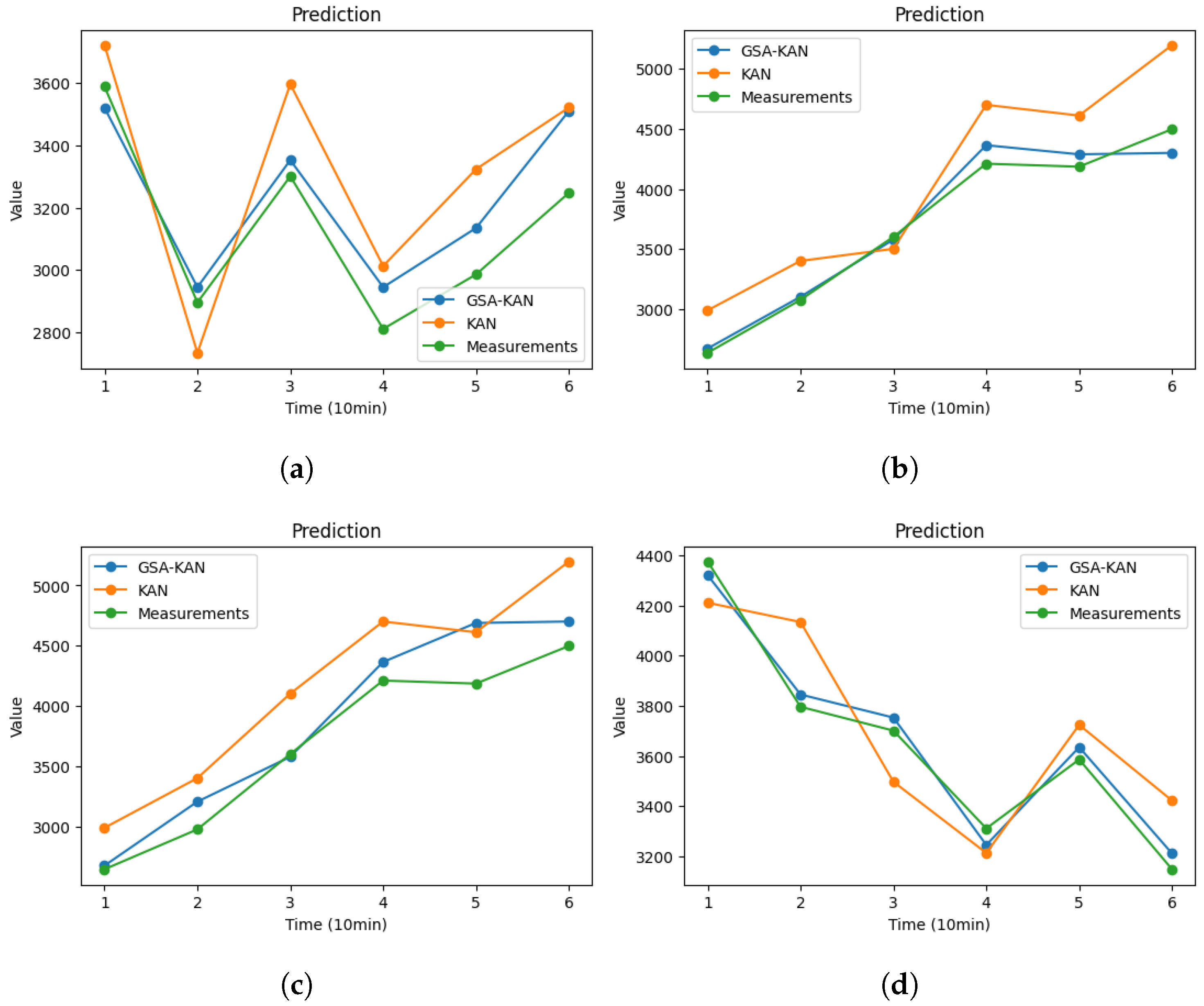
• We conduct extensive experiments on four real-world benchmark datasets to evaluate the effectiveness of our proposed model. The experimental results demonstrate that our GSA-KAN model outperforms existing parametric and nonparametric models for both the root mean square error (RMSE) and the mean absolute percentage error (MAPE), highlighting its potential for practical applications in traffic management.

The remainder of the paper is as follows. The methodology is presented in the second section. The experimental evaluation of real-world data from Amsterdam, the Netherlands, is discussed in the third section, and the conclusion is presented in the final section.

2. Methodology

In this section, we introduce the Kolmogorov–Arnold network (KAN) and the gravitational search algorithm (GSA). Subsequently, we demonstrate the integration of these two algorithmic models, as illustrated in Figure 1. Following this, we provide a detailed explanation of the collaboration between GSA and KAN. Lastly, we present the performance of the hybrid model, GSA-KAN, in short-term traffic flow forecasting.

2.1. Problem Definition

Traffic flow forecasting is a supervised learning task that utilizes historical traffic data to predict future traffic conditions. To conduct such predictions, we initially construct historical traffic flow $X_{t_0-c:t_0-1}$ from $t_0-c$ to $t_0-1$ as a sequence, $X_{t_0-c:t_0-1}=[x_{t_0-c},\dots ,x_{t_0-2},x_{t_0-1}]\in {\mathbb{R}}^c$, that spans c time steps (e.g., $c=6$ for 60 min of aggregated data at 10-min intervals). This vector is crucial for forecasting future traffic flow, $y_t$. The objective is to predict the future traffic flow sequence $Y_{t_0:T}=[y_{t_0},y_{t_0+1},\dots ,y_{t_0+T}]\in {\mathbb{R}}^T$ for T future time steps (e.g., $T=3$ for a 30-min prediction horizon). Here, $t_0$ marks the start of the prediction period, c defines the length of the historical time window, and T specifies the prediction horizon. For example, in the Amsterdam highway dataset, the input dimension is 6 (representing 60 min of historical traffic flow), and the output dimension is 3 (representing 30 min of predicted traffic flow). The model architecture aligns with these dimensions: the input layer processes historical values, c, while the output layer generates predicted values, T. This formulation ensures the precise mapping of historical patterns to future trends, enabling robust support for traffic management systems to mitigate congestion and optimize efficiency.

2.2. Gravitational Search Algorithm

The gravitational search algorithm (GSA) is an optimization searching technique based on Newton’s equation of gravity proposed by Rashedi et al. [34,35]. The location of the i-th particle in d-dimensional space with k particles is written as $X_i$ = ($x_i^1$, $x_i^2$,... $x_i^d$) for $i=1,2,\dots ,k$. The velocity of the i-th particle is $V_i=(v_i^1,v_i^2,\dots ,v_i^d)$. Particle inertial mass can be adjusted with

$$\begin{array}{cc}\hfill fi{t}_i\left(t\right)& =f{v}_i\left(t\right)-f{v}_i(t-1),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill m_i\left(t\right)& ={\displaystyle \frac{\left|fi{t}_i\left(t\right)\right|-max\left|fi{t}_i\left(t\right)\right|}{min\left|fi{t}_i\left(t\right)\right|-max\left|fi{t}_i\left(t\right)\right|}}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill M_i\left(t\right)& ={\displaystyle \frac{m_i\left(t\right)}{{\sum }_{j=1}^k{m}_j\left(t\right)}},\hfill \end{array}$$

(3)

where the fitness of the i-th particle at iteration t is represented by $f{v}_i\left(t\right)$. The starting point is zero. At the t-th iteration, the force of gravity applied through the j-th particle to the i-th particle is

$$F_{ij}\left(t\right)=G\left(t\right){\displaystyle \frac{M_j\left(t\right)\times M_i\left(t\right)}{R_{ij}\left(t\right)+r}}\left(x_j\left(t\right)-x_i\left(t\right)\right),$$

(4)

where $M_j\left(t\right)$ represents the mass of the j-th particle, and $M_i\left(t\right)$ is the mass of the i-th particle. $x_i\left(t\right)$ is the position information of the i-th particle at generation t, i.e., the parameter of the current solution, and $x_j\left(t\right)$ is the position information of the j-th particle at generation t. The following is a summary of the position information of the j-th particle’s location information. The Euclidian distance between the i-th and j-th particles is indicated as $R_{ij}\left(t\right)$. A constant r keeps the denominator from decreasing to zero. $G\left(t\right)$ is the gravitational constant that decays with time, indicated as

$$G\left(t\right)=G_0{e}^{-v_T^t},$$

(5)

where $G_0$ is the starting value of the gravity constant, while v is a manually modified constant. T is the utmost iteration. The total acceleration of the i-th particle $a_i\left(t\right)$ consists of the acceleration due to gravitational pull of all particles on it:

$$a_i\left(t\right)={\displaystyle \frac{1}{M_i\left(t\right)}}\sum _{j\in \mathrm{Kbest},j\ne i}{F}_{ij}\left(t\right),$$

(6)

where $Kbest$ is the top best-adapted particle in the generation of K particles (sorted by mass) that achieve the best performance on i-th particle, which exerts a gravitational force. The gravitational force that the j-th particle applies to the i-th particle is denoted as $F_{ij}\left(t\right)$. The particle’s location and velocity will be updated with the help of this acceleration. The particle modifies its speed with each repetition, which is expressed as

$$v_i(t+1)=\beta ·v_i\left(t\right)+a_i\left(t\right),$$

(7)

where $v_i(t+1)$ is the velocity of the i-th particle at generation $t+1$. $a_i\left(t\right)$ is the acceleration of the i-th particle at generation t. $\beta$ is the velocity decay factor, which is set from 0 to 1 to control the momentum of the particle. The particle’s location is updated based on its velocity, which is given by

$$x_i(t+1)=x_i\left(t\right)+v_i(t+1).$$

(8)

where $x_i(t+1)$ is the position information of the i-th particle at generation $t+1$, i.e., the parameter set of the KAN model. In this way, the location of every particle updates to find the optimal KAN settings.

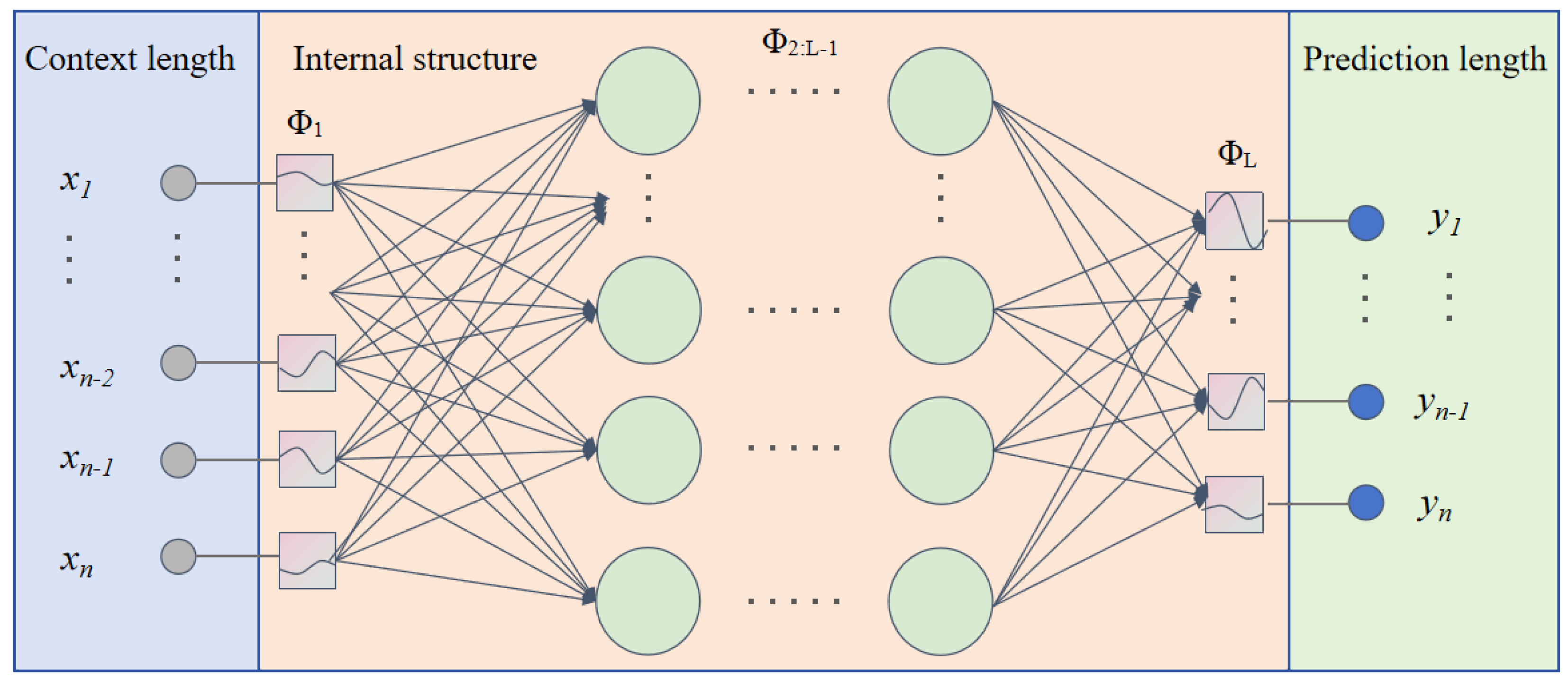
2.3. Kolmogorov–Arnold Networks

The Kolmogorov–Arnold network (KAN) is a neural network architecture based on the Kolmogorov–Arnold transcendence theorem [36]. According to the Kolmogorov–Arnold transcendence theorem, any constant function can be approximated by a weighted sum of a finite set of univariate functions [37,38]. This principle lends theoretical support to developing generalized approximate models using neural networks [39]. The KAN architecture can approximate arbitrary multidimensional functions [40]. KAN is also an optimized multilayer perceptron (MLP) for various applications. In a conventional MLP, a weight matrix connects the input layer to the hidden layer, and then an activation function is applied before linking to the output layer through another weight matrix. However, the hidden layer’s output is connected to the output layer through a spline function in KAN, and the input layer directly connects to the hidden layer. The main difference between KAN and MLP is that, in KAN, instead of providing a linear form for the nonlinear activation function, a spline approximation of the primary scalar function in each neuron is used. Adjustable parameters are fed to the scalar function values of each elementary neuron at grid points, and then a cubic spline is constructed between these grid points. Figure 2 illustrates the structural differences between the MLP and KAN network architectures.

KAN can achieve efficient multi-dimensional function approximation while maintaining low computational complexity with a well-designed network structure and careful parameter tuning. KAN exhibits strong generalization performance, making it versatile across various tasks. The training process of KAN is optimized by minimizing the error-producing function, primarily through the gradient descent and backpropagation techniques. The core idea of the KAN architecture is to replace the fixed activation function in the conventional MLP with a spline-based learnable univariate function. Specifically, for an input vector, $x\in {\mathbb{R}}^n$, and any continuous function, $f:{\mathbb{R}}^n\to \mathbb{R}$, the KAN objective is to find a set of functions $\Phi$ and $\varphi$ through

$$f\left(x\right)=\sum _{q=1}^{2n+1}{\Phi }_q\left(\sum _{p=1}^n{\varphi }_{q,p}\left(x_p\right)\right),$$

(9)

where ${\Phi }_q$ denotes the outer-layer functions, which act on the output of the inner-layer functions, and the q index denotes the different functions of the outer layer. ${\varphi }_{q,p}\left(x_p\right)$ denotes the inner-layer functions, which are learnable univariate functions and which capture local features of the input data, and the p index denotes the p-th element of the input vector x. Furthermore, the inner layer function ${\varphi }_{q,p}$ is summed from 1 to n, where n denotes the dimension of the input vector, and the final sum is used as input to the outer-layer function, i.e., the output of the inner layer function is integrated. In the summation representation of the outer-layer functions, ${\Phi }_q$, from 1 to $2n+1$, $2n+1$, is the number of outer-layer functions according to the Kolmogorov–Arnold representation theorem. The outputs of all the outer functions are summed up to obtain the final output, $f\left(x\right)$ [41]. However, in the traditional MLP, the function $f\left(x\right)$ is approximated:

$$f\left(x\right)\approx \sum _{i=1}^N{a}_i\sigma (w·x+b),$$

(10)

where $\sigma$ is a fixed activation function, w and b are weight and bias parameters, and $a_i$ is the weight of the output layer. In contrast, each weight, w, is replaced with a learnable univariate function, $\varphi$, and each activation function, $\sigma$, is replaced with $\Phi$ in KANs. This design allows KANs to be more flexible in capturing complex patterns in the data. According to the Kolmogorov–Arnold representation theorem, any multivariate continuous function, f, can be represented as a finite combination of univariate functions. For KANs, we generalize this to arbitrary width and depth. Let the structure of a KAN be represented by the integer array $[n_0,n_1,\dots ,n_L]$, where $n_i$ is the number of nodes in the first number of nodes in the ith layer. For the activation function ${\varphi }_{l,j,i}$ from layer l to layer $l+1$, the pre-activation value is $x_{l,i}$, and the post-activation value can be expressed as

$${\tilde{x}}_{l,j}={\varphi }_{l,j,i}\left(x_{l,i}\right),$$

(11)

where the node x of the $l+1$ layer is the sum of all incoming post-activation values and can be expressed in the form of the following equation:

$$x_{l+1,j}=\sum _{i=1}^{n_l}{\varphi }_{l,j,i}\left(x_{l,i}\right),$$

(12)

Expressed in the form of a matrix, it has the following form:

$$x_{l+1}={\Phi }_l{x}_l$$

(13)

where ${\Phi }_l$ is the function matrix of the l-th layer. For the whole KAN network, if the input vector $x_0\in {\mathbb{R}}^{n_0}$ is given, the output y is as follows:

$$y=KAN\left(x\right)={\Phi }_L\circ {\Phi }_{L-1}\circ \dots \circ {\Phi }_1\circ {\Phi }_0{x}_0$$

(14)

Equation (14) is the network’s final output. The KAN model aims to minimize the discrepancy between the network’s predictions and the actual target values through training on sample data. To achieve this, gradient descent [42,43] is employed to minimize the loss function. The back-propagation (BP) technique [44] is used to efficiently adjust the network parameters.

2.4. KAN Traffic Flow Forecasting

We formulate traffic flow forecasting as a supervised learning problem. It consists of a training dataset with inputs and outputs $[X_{t_0-c:t_0-1},Y_{t_0:T}]$ at history and prediction lengths. For ease of presentation, we define both the input sequence X and the output sequence Y as [1, n], but with different actual lengths. Meanwhile, we describe our framework as a two-layer KAN, where the input layer itself is not accounted for as a layer. The two-layer KAN design is rooted in the Kolmogorov–Arnold representation theorem, which asserts that any continuous multivariate function can be represented as a superposition of univariate functions through two layers [40]. This theoretical guarantee ensures that a two-layer structure is sufficient to approximate complex traffic flow dynamics without over-parameterization. This theoretical guarantee ensures that a two-layer structure is sufficient to approximate complex traffic flow dynamics without over-parameterization.

To further verify the validity of our choice, we compared the performance of one-, two-, and three-layer KAN architectures on the A1 dataset, as presented in the table below.

As shown in

Table 1. The $RMSEs$ (vehs/h) and training times per iteration (or iterations) of the various layers of KAN in the A1 dataset.

Layers	RMSE	Per-Iteration Training Time
One	301.23	13.5
Two	289.67	15.2
Three	293.45	23.4

, the two-layer architecture has the lowest RMSE (289.67 veh/h) and a training time of 15.2 s per iteration. The one- and three-layer models have much higher RMSE than the two-layer model. Moreover, the per-iteration training times of the one- and two-layer models are similar. This demonstrates the validity of our choice.

The output and input layers will consist of $N_o$ and $N_i$ nodes corresponding to the total number of time steps in the predicted and historical data values. The internal functions form a KAN layer, $N_{in}=N_i$, $N_{out}=n$; the external functions form another KAN layer, $N_{in}=n$, $N_{out}=N_o$. Thus, the KAN of this structure can be expressed as follows:

$$y=\mathrm{KAN}\left(x\right)=({\Phi }_2\circ {\Phi }_1)x$$

(15)

where ${\Phi }_1$ and ${\Phi }_2$ are two univariate functions inside the KAN layer. The basic framework of the KAN architecture with L layers in dealing with the traffic flow forecasting problem is shown in Figure 3:

The learnable activations are indicated in boxes. The output function ${\Phi }_2$ produces the $N_o$ output value corresponding to the predicted value by transforming the previous layers.

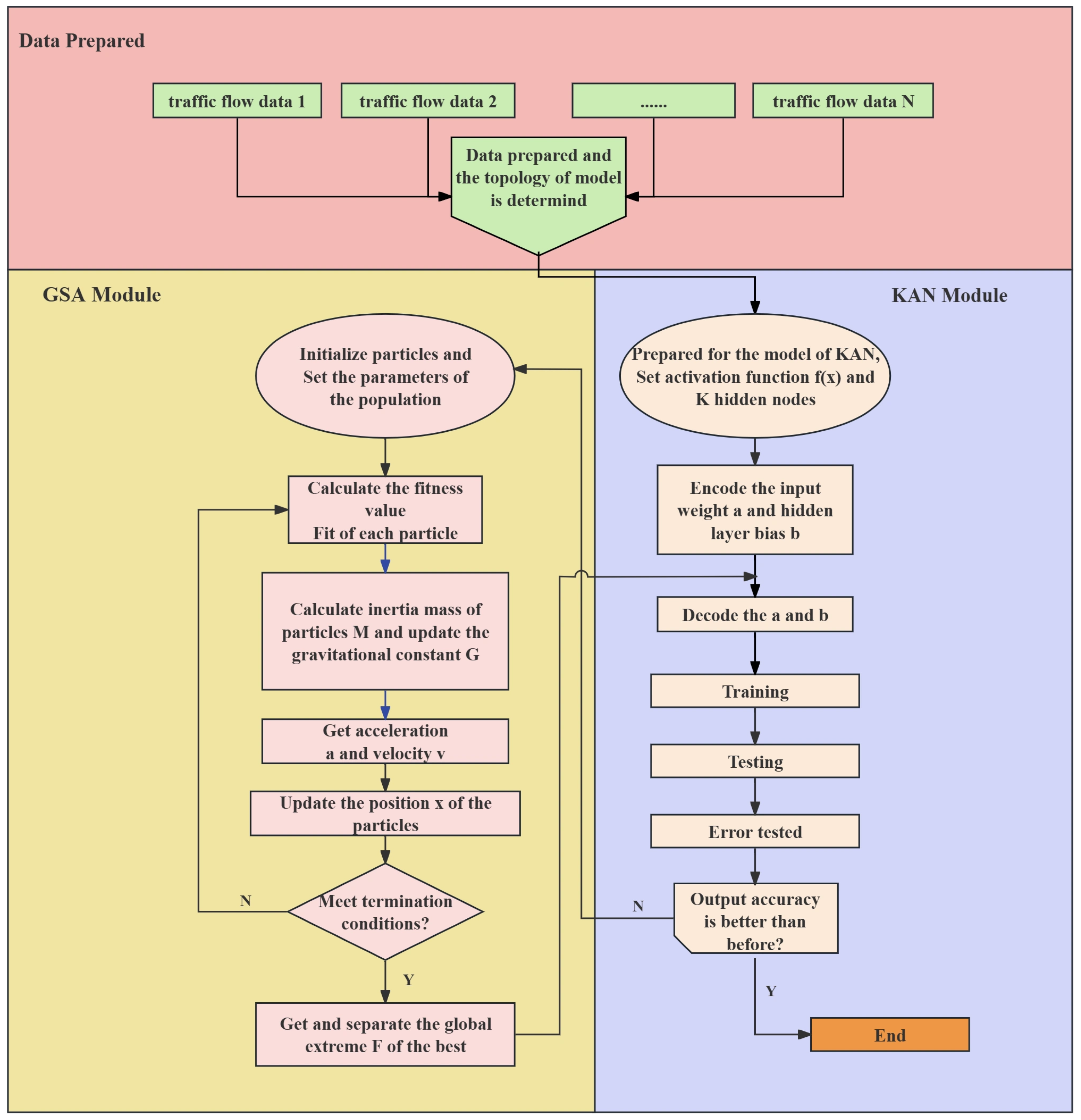
2.5. Hybrid GSA-KAN Algorithm

In modern machine learning algorithms [45], the performance of neural networks heavily depends on the parameter optimization process of the model [46]. The training of KAN is primarily restricted to BP algorithms [47], which are sensitive to initial parameters and prone to falling into local optimal solutions. To address this issue, GSA, a global optimization technique based on gravity theory, can enhance KAN’s global search capabilities, thereby optimizing KAN’s parameters. Therefore, we introduce a hybrid model, GSA-KAN, which leverages GSA’s global search capabilities to refine KAN’s parameters. This enables the model to better approximate complex functions and improve its generalization ability. In this hybrid model, GSA optimizes the biases and weights of the KAN network to minimize the model’s error function. Through GSA’s gravitational search process, the model transcends local optimal solutions, achieving superior performance. The framework of the GSA-KAN algorithm we designed mainly consists of the following steps.

• Step 1. The parameters such as the dimension, d, of the search space, the number of particles, k, the gravitational constant, G, the gravitational constant decay rate, v, and the maximum number of iterations, T, are first set.
• Step 2. The position, x, and velocities, v, of k groups of particles are randomly generated via

  $$x_i=x_{\min }+(x_{\max }-x_{\min })·\delta ,$$

  (16)

  $$v_i=v_{\max }·(\delta -0.5),$$

  (17)

  where $x_{min}$ and $x_{max}$ define the boundaries of the parametric search space, $v_{max}$ is the maximum value of the velocity, and $\delta$ is a random number from 0 to 1. Each group of particles represents a set of parameters with weights and biases in the KAN model.
• Step 3. Calculate the fitness value for each particle using the KAN model, which is generally the opposite of the prediction error value.
• Step 4. Calculate the repulsive and gravitational forces between particles by means of the relevant equations defined in the GSA model.
• Step 5. The velocity and position of the particles are updated based on the gravitational force and the current velocity.
• Step 6. Repeat steps 3–5 until the maximum number of iterations is reached or other stopping conditions are met.
• Step 7. Output the optimized KAN model parameters and use them for traffic flow forecasting.

The algorithm is detailed in Algorithm 1.

Algorithm 1: Framework of GSA-KAN

The main innovations of our proposed GSA-KAN model are outlined as follows:

• Hybrid architecture of gravitational search algorithm (GSA) and Kolmogorov–Arnold network (KAN): To the best of our knowledge, this is the first work to integrate the GSA with KAN. This hybrid framework automates the optimization of hyperparameters (e.g., B-spline grid points and regularization factors) while preserving the parameter efficiency of KAN, thereby addressing the limitations of manual tuning in traditional models.
• Dynamic resolution adaptation: We propose a novel adaptive grid adjustment strategy for the B-spline functions in KAN. Unlike fixed-resolution approaches, this strategy dynamically adjusts grid density based on traffic flow volatility, such as variations between peak hours and off-peak hours, enabling higher prediction accuracy during abrupt traffic changes.
• Robustness-driven optimization: While conventional GSA focuses solely on minimizing prediction error, our enhanced GSA incorporates a dual-objective function that balances RMSE and model sparsity. This design prevents overfitting and enhances interpretability, as validated in our experiments.

3. Experiments

We evaluate the performance of the KAN and GSA-KAN models on four real-world benchmark datasets from the Amsterdam highway. The proposed model is designed for traffic flow prediction within a well-defined operational context to ensure practical relevance and methodological rigor. Traffic flow data is collected from fixed-loop detectors, such as the MONICA system deployed across Amsterdam’s highway network, which provides reliable and spatially consistent measurements. These detectors are strategically installed on closed highway systems, where uninterrupted traffic flow is observed without interference from intersections or traffic signals, thus simplifying the modeling of pure longitudinal dynamics. To align with real-world traffic management protocols, the raw data are aggregated into 10-min intervals, a temporal granularity widely adopted in both academic research and operational practices. This configuration not only captures essential traffic patterns but also balances computational efficiency with predictive accuracy, ensuring the applicability of the model to dynamic highway environments.

3.1. Dataset Description

Wang et al. [48] created the Amsterdam highway dataset from data collected for four freeways in Amsterdam, the Netherlands, i.e., the A1, the A2, the A4, and the A8. The geographical coverage of the dataset is illustrated in Figure 4. The MONICA ring detectors collected the data comprising the datasets for these freeways between 20 May and 24 June 2010, resulting in five weeks of data. Summaries of the traffic flow are provided every minute. The traffic flow statistics of 1 min are combined in the same way to create a 10-min aggregation. The four datasets represent different highway types, including international highways and short interconnecting lines, etc.

Among the freeways, the A1 has the maximum carrying capacity and significant changes in traffic flow rate over time. The A2, one of the most congested freeways in the Netherlands, experiences particular congestion during morning and evening rush hours. The A4 freeway is situated at the border between Amsterdam and Belgium. The A8 freeway is the shortest, with a distance of less than 10 km. As a result, forecasting traffic flows on these four highways presents a significant challenge. For the erroneous and missing values in the dataset, we use the average of simultaneous measurements from other weeks to fill in [49]. Specifically, if data were missing for minute t, we used the traffic average from the same time slot (e.g., 8:00–8:10 AM Monday) in previous weeks. This approach maintains the periodicity of traffic flow while ensuring computational efficiency. As Zhang et al. [21] noted, short-term forecasting relies heavily on time-relatedness in traffic data. Weekly averaging using historical data patterns effectively reduces periodic noise. In comparison, methods like KNN [50] can capture local features but require more computational resources and may cause overfitting.

3.2. Evaluation Criteria

We use two common criteria to evaluate the GSA-KAN model. To evaluate the model effectiveness, we primarily utilize the mean absolute percentage error (MAPE) and the root mean square error (RMSE). The RMSE measures the difference between the prediction and the ground truth. Smaller RMSEs indicate more accurate predictions. MAPE evaluates the accuracy of a model by calculating the percentage discrepancy between the prediction and the ground truth. The advantage of MAPE is that it expresses the result as a relative error, which is easier to interpret. The expressions for these metrics are as follows.

$$\begin{array}{ccc}RMSE& =\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{k=1}^N{({\widehat{y}}_i-y_i)}^2},MAPE\hfill & ={\displaystyle \frac{1}{N}}\sum _{k=1}^N\left|{\displaystyle \frac{{\widehat{y}}_i-y_i}{y_i}}\right|\times 100\%,\end{array}$$

(18)

where N represents the sample size, i.e., the general anticipated number of data points. $y_i$ is the ground truth, and ${\widehat{y}}_i$ indicates the prediction at time k.

3.3. Experimental Settings

Real-time fluctuations in traffic flow occur, particularly during peak hours in the morning and evening, when congestion is most common, while nighttime traffic flow significantly decreases [51]. The objective of this study is to forecast changes in traffic flow over a specific period, rather than minute-to-minute fluctuations. We aggregate the minute-by-minute data into 10-min intervals.

The dataset for this study comprised five weeks of measurements, with each highway’s data split into two parts. One part was used to train the model, and the rest was used for testing, as in previous studies [52,53]. After selecting the training data from the initial four weeks, we predicted traffic flow for the fifth week. The training data consisted of ten sets, with nine used for training and the tenth serving as a validation set to verify the model’s accuracy. In this study, the hyperparameter settings of the depth, L, determined the number of layers of the model, which we initialized to 3. The model uses B-splines of order $k=3$. The number of grid points G was set to 5. We set the learning rate to $0.001$ and optimized it using Adam’s optimizer, with the maximum number of iterations set to 1000. The regularization factor was set to $[{10}^{-3},{10}^{-1}]$. Additionally, the GSA model parameters used to optimize the KAN model are presented in

Table 2. Configuring the parameters of GSA.

Parameters	Value
Population size	300
Maximum number of iterations	100
$G_0$	100
v	20

below.

As indicated by our previous research [54,55], the GSA optimization algorithm’s RMSEs gradually stabilized after about 80 iterations, indicating convergence. Thus, for the main model, GSA-KAN, we optimized its performance and prevented overfitting by setting the maximum number of iterations to 100 and the average number of iterations to 50.

To conduct a comprehensive and unbiased evaluation of the GSA-KAN framework’s performance, we trained and predicted the aforementioned dataset using several popular machine learning models. We then compared their RMSEs and MAPEs. The following models were selected for comparison in this study.

Support vector machine regression (SVR): Zhou et al. [56] provide a detailed explanation of SVR. To minimize the overall deviation from the hyperplane, the SVR incorporates a tolerance margin between the actual and estimated values. The width parameter and regression horizon were set to 8 and $3\times {10}^{-6}$, respectively. For short-term traffic flow forecasts, we assigned the cost parameter to the maximum difference.

Gray model (GM): Guo et al. [57] proposed and optimized this model. GM facilitates improved modeling when dealing with incomplete data. We used the GM(1,1) model in this study, and the hyperparameters were mainly the coefficients a and b in the model. These parameters were automatically optimized via the least squares method, and after this optimization, we set a to −0.4 and b to −8.8.

Decision tree (DT): DT, which relies on regression and classification trees, makes no assumptions and is robust against missing data [58]. We chose Gini as the division criterion in this study and set the maximum depth to 70.

Artificial neural network (ANN): An ANN, generated via a vast number of interconnected neurons, possesses strong self-learning capabilities, effectively handles high-dimensional and complex data, and demonstrates efficient parallel computing [59]. In this traffic flow-forecasting task weight, the number of hidden layers was set to 1, the mean square error objective was set to 0.001, the diffusion of radial basis function was set to 2000, and the maximum number of neurons in the hidden layer and the number of neurons added according to the default values was set to 40 and 25, respectively.

Long short-term memory (LSTM) [60]: In summary, LSTM, an innovative type of recurrent neural network, effectively retains long-term memory and forgets irrelevant information when necessary. In this experiment, the batch size, hyperparameter units, validation split, and epochs were set to 32, 256, 0.05, and 50, respectively.

Extreme learning machine (ELM) [61]: An ELM is a single-hidden layer feedforward neural network that can be readily applied to learning tasks such as regression, classification, clustering, and more. We set the number of nodes in the input layer to 9, the number of nodes in the hidden layer to 11, and the number of nodes in the output layer to 1. The number of weight thresholds to be optimized for the ELM network was set to 110, and the maximum number of iterations was 1000.

3.4. Experimental Results and Discussion

The GSA optimization results vary for each run due to the random and erratic dispersal of the particles. Therefore, for the KAN and GSA-KAN models, we report the average of 50 runs as the findings for each dataset. The Amsterdam motorway dataset was used as an experimental scenario to validate the effectiveness of the proposed models in handling the nonlinearity and unpredictability of traffic flow. The $RMSEs$ and $MAPEs$ are presented in

Table 3. The $RMSEs$ (vehs/h) of the various prediction models were calculated using the Amsterdam Highway dataset.

Models	A1	A2	A4	A8
SVR	329.09	259.74	253.66	190.33
GM	347.94	261.36	275.35	189.57
DT	316.57	224.79	243.19	238.35
ANN	299.64	212.95	225.86	166.50
LSTM	294.52	211.31	224.68	168.91
ELM	294.10	201.67	222.07	169.15
KAN	289.67	208.74	221.74	163.86
GSA-KAN	287.80	198.12	219.73	162.69

and

Table 4. The $MAPEs$(%) of the various forecasting models were calculated using the Amsterdam Highway dataset.

Models	A1	A2	A4	A8
SVR	14.34	12.22	12.23	12.48
GM	12.49	10.90	13.22	12.89
DT	12.08	10.86	12.34	13.62
ANN	12.61	10.89	12.49	12.53
LSTM	12.82	11.06	13.51	12.56
ELM	11.82	10.34	12.05	12.42
KAN	11.84	10.34	11.86	12.16
GSA-KAN	11.77	10.25	11.69	11.92

, respectively.

Table 3 presents a comparison between several models across four datasets.

Our GSA-KAN outperforms both standard parametric and nonparametric approaches in terms of the root mean square error for the A1, A2, A4, and A8 datasets, with respective values of 287.80, 198.12, 219.73, and 162.69. For example, the RMSE of the GSA-KAN in these datasets is reduced by $3.95\%$, $6.96\%$, $2.71\%$, and $2.29\%$, respectively, compared to an ANN. Compared to ELM, the RMSE of our GSA-KAN is reduced by $2.14\%$, $1.76\%$, $1.05\%$, and $3.82\%$, respectively. For the traditional KAN model, the optimized GSA-KAN model achieves improvements in RMSE of $0.65\%$, $5.09\%$, $0.91\%$, and $0.71\%$ on the A1, A2, A4, and A8 datasets, respectively. Although the computational time increases by approximately $12\%$, the significant improvement in prediction precision, particularly in the A2 data set, demonstrates the superiority of GSA-KAN in handling complex variations in traffic flow. This improvement, which balances computational cost and predictive performance, highlights the potential of GSA-KAN for practical applications.

Although our GSA-KAN has a low error in terms of RMSE, MAPE is also a crucial metric. $MAPE$ is particularly suitable for comparing model performance on complex datasets and long-time series [62]. Table 4 shows that our GSA-KAN consistently outperforms other approaches in terms of MAPE on the Amsterdam dataset, with scores of 11.77, 10.25, 11.69, and 11.92, respectively. Specifically, the MAPE of the GSA-KAN is reduced by $6.66\%$, $5.88\%$, $6.41\%$, and $4.87\%$ on the A1, A2, A4, and A8 datasets, respectively, compared to ANN. Moreover, when compared to ELM, our GSA-KAN’s MAPE on the four datasets decreases by $0.42\%$, $0.87\%$, $2.99\%$, and $4.03\%$, respectively.

The visualization outcomes for the short-term traffic flow forecasts of the GSA-KAN and KAN models are presented in Figure 5. The blue line represents the true situation, depicting the raw data from the Amsterdam dataset. The green dashed line indicates the predicted values from the KAN model, while the red dashed line represents the values predicted via our GSA-KAN model. Our GSA-KAN demonstrates excellent fitting and prediction abilities. The difference between the expected and actual measured values is smaller both late at night and early in the morning, when there is less traffic, but the correlation error is larger.

To demonstrate our model’s superior performance, we present a visual comparison of the MAPEs between our model and the best-performing existing model, ELM, in Figure 6 below.

To further enhance the model’s functionality, we optimized the GSA-KAN model by adjusting the iteration numbers for the GSA algorithm while keeping the other parameters constant to control for variables [63].In this study, the GSA method was set to a maximum of 100 iterations. Figure 7 below demonstrates how the RMSE and MAPE values of the GSA-KAN model change with varying numbers of GSA algorithm iterations.

As is evident from the above chart, the RMSE and MAPE values of the model decrease approximately with an increase in the number of iterations of the GSA algorithm, with the optimal fit achieved at around 30 iterations. To further showcase the improved functionality of our model and minimize the randomness of prediction performance, we conduct subsequent experiments focusing on moments with significant traffic flow variations to assess the model’s prediction stability. In Figure 8 below, we present a visualization comparing our model’s predicted data with the actual data during instances of drastic traffic flow changes.

In Figure 8, ‘measurements’ represent the ground truth. Based on our study of fluctuating traffic flow, we observe that the GSA-KAN model, optimized by the GSA model, exhibits robust performance. However, there remains considerable room for further development and refinement.

In conclusion, our approach surpasses other state-of-the-art models. The studies presented above illustrate the impact of learning capacity and training data quality on the effectiveness of learning-based prediction models. To improve the model’s output, we consistently train and iterate the KAN and GSA-KAN models, focusing on their temporal learning capabilities. Our model is trained using a dataset of highway inbound flow, which exhibits strong regularity and is largely independent of traffic flows from road networks. This will contribute valuable insights to traffic flow research.

3.5. Hyperparameter Sensitivity Study

We experimented with two important hyperparameters in the KAN model: the B-spline order, k, and the number of grid points, G. Because the order of the B-spline affects the smoothness and fitting ability of the spline function, a higher order can provide a smoother function but may lead to overfitting, especially in the case of noisy data. The number of grid points, G, on the other hand, determines the fineness of the spline function. More grid points provide a finer representation of the function but also increase the complexity and computational cost of the model. It directly affects the representation ability of the spline function and the model’s ability to capture dynamic changes in traffic data. We explored the parameter sensitivity by testing the $MAPEs$ values of different parameters on the A1 and A2 datasets.

The selection of hyperparameters was grounded in both theoretical principles and empirical observations. For instance, the B-spline order k = 3 was chosen based on the trade-off between approximation accuracy and computational efficiency, as cubic splines (k = 3) are widely recognized for balancing smoothness and flexibility in function approximation. Similarly, the grid point number G = 5 was determined through preliminary sensitivity analysis, which indicated that finer grids (G > 5) yield marginal performance gains at significantly higher computational costs.

Figure 9a illustrates the results of varying the B-spline order k from 1 to 5 on the A1 and A2 datasets. We can find that the prediction performance on both datasets is greatly improved when k is increased from 1 to 3. However, when k increases from 3 to 5, the prediction performance gradually decreases on both datasets, probably due to overfitting caused by too large a k.

Figure 9b shows the results of the change in the number of grid points from 1 to 9 on both datasets. We can find that G reaches the best performance when increasing from 1 to 5. However, the performance keeps decreasing when increasing from 5 to 9.

3.6. Limitations and Future Work

In this study, we only used four traditional traffic flow forecasting datasets, in which the traffic flow sampling interval was fixed and the prediction task was regular. The dataset was obtained from a highway where the traffic flow is seldom affected by the surrounding environment. The model lacks wide application in the current extremely complex transportation system, and there is potential for prediction experiments on more complex datasets. In future research, we will conduct a comprehensive ablation study to rigorously evaluate each component of GSA-KAN, including the dual-objective optimization and hybrid architecture, across diverse traffic scenarios (e.g., urban networks with intersections). This will further validate the generalizability and robustness of our framework. Additionally, we plan to improve our model to estimate traffic flow on metropolitan thoroughfares, considering the significant correlation between these roads’ junctions. Moreover, we plan to optimize the KAN using other heuristic algorithms and further investigate traffic flow under multiple attributes, such as weather conditions, special events, road construction, and pedestrian activity. By integrating these multi-source data, we aim to enhance the model’s robustness and adaptability in real-world scenarios, providing more accurate and reliable traffic flow predictions.

4. Conclusions

Accurate traffic flow forecasting is a milestone in transportation intelligence. In this paper, we have proposed a hybrid learning model to simultaneously train a traffic flow forecasting model and optimize the hyperparameters of the model. We first proposed to forecast the future traffic flow with the Kolmogorov–Arnold network due to its parameter efficiency with lower memory and computational overhead. Then, we optimized the hyperparameters of the Kolmogorov–Arnold network using a gravitational search algorithm in a data-driven fashion. We evaluated our model on four real-world benchmark datasets from Amsterdam, the Netherlands. We achieved decreasing RMSEs of $3.95\%$, $6.96\%$, $2.71\%$, and $2.29\%$ and decreasing MAPEs of $6.66\%$, $5.88\%$, $6.41\%$, and $4.87\%$ on the A1, A2, A4, and A8 datasets, respectively. The results demonstrate that GSA-KAN is promising for traffic flow forecasting.