Linear Sixth-Order Conservation Difference Scheme for KdV Equation
Abstract
1. Introduction
2. Finite Difference Scheme and Conservation Laws
3. Existence and Uniqueness of the Difference Solution
4. Convergence and Stability
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korteveg, D.J.; de Vries, G. On the change of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Morikawa, G.K.; Swenson, E.V. Korteweg-de Vries equation for nonlinear hydromagnetic waves in a warm collision-free plasma. Phys. Fluids 1969, 12, 2090–2093. [Google Scholar]
- Miura, R.M.; Gardner, C.S.; Kruskal, M.D. Korteweg-de Vries equation and generalizations.II. Existence of conservation laws and constants of motion. J. Math. Phys. 1968, 9, 1204–1209. [Google Scholar] [CrossRef]
- Su, C.S.; Gardner, C.S. Korteweg-de Vries equation and generalizations. III. Derivation of the Korteweg-de Vries equation and Burgers equation. J. Math. Phys. 1969, 10, 536–539. [Google Scholar] [CrossRef]
- Osborne, A.R. Nonlinear Fourier analysis for the infinite-interval Korteweg-de Vries equation I: An algorithm for the direct scattering transform. J. Comput. Phys. 1991, 94, 284–313. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Hereman, W.; Korpel, A.; Banerjee, P.P. A general physical approach to solitary wave construction from linear solutions. Wave Motion 1985, 7, 283–289. [Google Scholar] [CrossRef]
- Sanz-Serna, J.M.; Christie, I. Petrov-Galerkin methods for nonlinear dispersive waves. J. Comput. Phys. 1981, 39, 94–102. [Google Scholar] [CrossRef]
- Amein, N.K.; Ramadan, M.A. A small time solutions for the KdV equation using Bubnov-Galerkin finite element method. J. Egypt Math. Soc. 2011, 19, 118–125. [Google Scholar] [CrossRef]
- Karczewska, A.; Rozmej, P.; Szczeciński, M.; Boguniewicz, B. Finite element method for extended KdV equations. Int. J. Appl. Math. Comput. Sci. 2016, 26, 555–567. [Google Scholar] [CrossRef]
- Benkhaldoun, F.; Seaid, M. New finite-volume relaxation methods for the third-order differential equations. Commun. Comput. Phys. 2008, 4, 820–837. [Google Scholar]
- Shen, Q. A meshless method of lines for the numerical solution of KdV equation using radial basis functions. Eng. Anal. Bound. Elem. 2009, 33, 1171–1180. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Martin, D.K. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef]
- Wang, H.P.; Wang, Y.S.; Hu, Y.Y. An explicit scheme for the KdV equation. Chin. Phys. Lett. 2008, 25, 2335–2338. [Google Scholar]
- Vliegenthart, A.C. On finite-difference methods for the Korteweg-de Vries equation. J. Eng. Math. 1971, 5, 137–155. [Google Scholar] [CrossRef]
- Greig, I.S.; Morris, J.L. A hopscotch method for the Korteweg-de Vries equation. J. Comput. Phys. 1976, 20, 64–80. [Google Scholar] [CrossRef]
- Shen, J.L.; Wang, X.Q.; Sun, Z.Z. The conservation and convergence of two finite difference schemes for KdV equations with initial and boundary value conditions. Numer. Math. Theor. Meth. Appl. 2020, 13, 253–280. [Google Scholar]
- Wang, X.P.; Sun, Z.Z. A second order convergent difference scheme for the initial-boundary value problem of Korteweg-de Vires equation. Numer. Methods Partial. Differ. Equ. 2021, 37, 2873–2894. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, P. A reduced high-order compact finite difference scheme based on proper orthogonal decomposition technique for KdV equation. Appl. Math. Comput. 2018, 339, 535–545. [Google Scholar] [CrossRef]
- Guo, Z.; Wu, M.M.; Hu, J. A conservative difference scheme with sixth-order spatial accuracy for the KdV equation. J. Sichuan Univ. Nat. Sci. Ed. 2023, 60, 031006. (In Chinese) [Google Scholar]
- Wang, T.; Guo, B.; Zhang, L. New conservative difference schemes for a coupled nonlinear Schrödinger system. Appl. Math. Comput. 2010, 217, 1604–1619. [Google Scholar]
- Zhou, Y.L. Application of Discrete Functional Analysis to the Finite Difference Method; International Academic Publishers: Beijing, China, 1990. [Google Scholar]
- Wang, T. Maximum norm error bound of a linearized difference scheme for a coupled nonlinear Schrödinger equations. J. Comput. Appl. Math. 2011, 235, 4237–4250. [Google Scholar]
- Temimi, H.; Ben-Romdhane, M.; Baccouch, M.; Musa, M.O. A two-branched numerical solution of the two-dimensional Bratu’s problem. Appl. Numer. Math. 2020, 153, 202–216. [Google Scholar]
- Kasenov, S.E.; Tleulesova, A.M.; Sarsenbayeva, A.E.; Temirbekov, A.N. Numerical solution of the Cauchy problem for the Helmholtz equation using Nesterov’s accelerated method. Mathematics 2024, 12, 2618. [Google Scholar] [CrossRef]
- Khalil, M.M.; Rehman, S.U.; Ali, A.H.; Nawaz, R.; Belal, B. New modifications of natural transform iterative method and q-homotopy analysis method applied to fractional order KDV-Burger and Sawada–Kotera equations. Partial. Differ. Equ. Appl. Math. 2024, 12, 100950. [Google Scholar]
- Abdul-Hassan, N.Y.; Kadum, Z.J.; Ali, A.H. An efficient third-order scheme based on Runge–Kutta and Taylor series expansion for solving initial value problems. Algorithms 2024, 17, 123. [Google Scholar] [CrossRef]

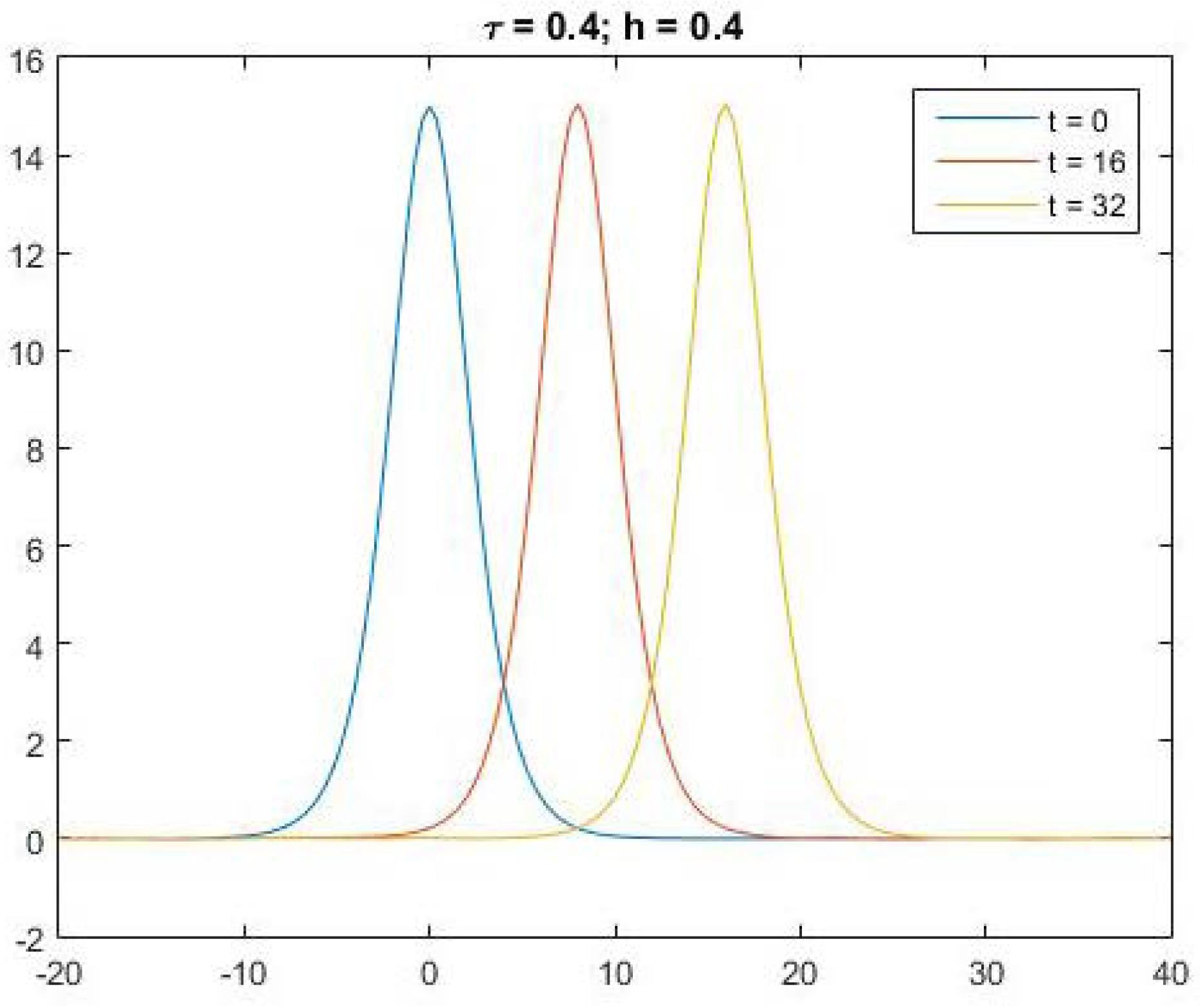
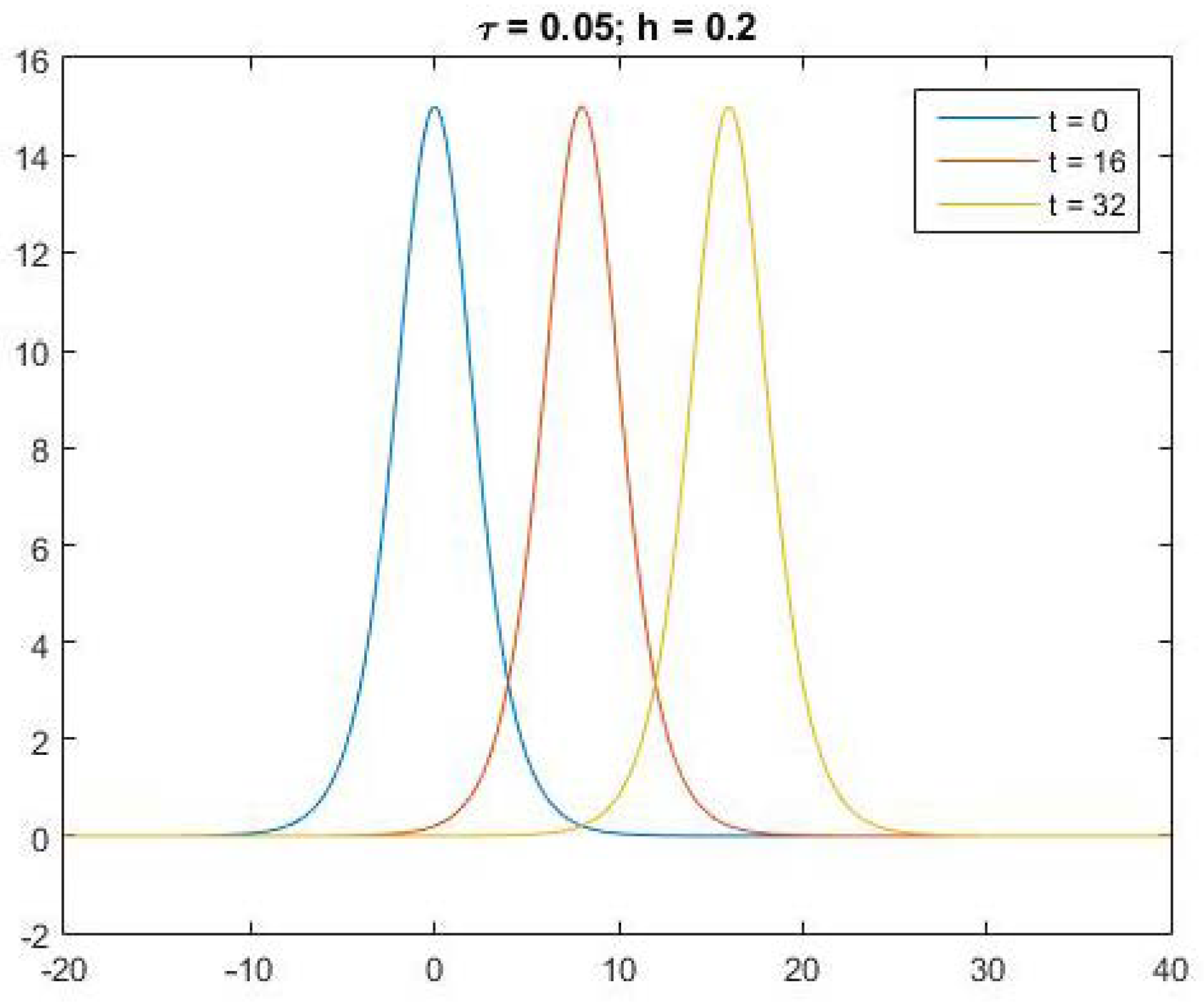
| t = 3.2 | – | – | 1.3157 × | 5.5531 × | 2.1406 × | 8.8211 × |
| t = 6.4 | 1.1135 × | 4.5588 × | 1.6453 × | 7.4362 × | 2.6198 × | 1.1337 × |
| t = 9.6 | 1.5820 × | 6.9156 × | 1.9591 × | 9.8618 × | 3.0740 × | 1.4817 × |
| t = 12.8 | 2.0214 × | 8.0950 × | 2.3343 × | 1.2369 × | 3.6743 × | 1.9569 × |
| t = 16.0 | 2.4357 × | 1.0679 × | 2.7560 × | 1.4574 × | 4.3512 × | 2.2924 × |
| t = 19.2 | 2.8437 × | 1.2064 × | 3.2298 × | 1.7029 × | 4.9380 × | 2.4631 × |
| t = 22.4 | 3.2398 × | 1.3248 × | 3.7477 × | 2.0014 × | 5.9378 × | 3.2336 × |
| t = 25.6 | 3.6183 × | 1.5395 × | 4.1745 × | 2.1108 × | 6.5077 × | 3.3226 × |
| t = 28.8 | 3.9812 × | 1.6528 × | 4.7112 × | 2.3874 × | 7.4561 × | 3.9540 × |
| t = 32.0 | 4.3176 × | 1.7444 × | 5.3390 × | 2.7774 × | 8.2891 × | 4.3216 × |
| t = 3.2 | – | – | 5.942 | – | – | 5.976 |
| t = 6.4 | – | 6.081 | 5.973 | – | 5.938 | 6.035 |
| t = 9.6 | – | 6.335 | 5.994 | – | 6.132 | 6.056 |
| t = 12.8 | – | 6.436 | 5.989 | – | 6.032 | 5.982 |
| t = 16.0 | – | 6.466 | 5.985 | – | 6.195 | 5.990 |
| t = 19.2 | – | 6.460 | 6.031 | – | 6.147 | 6.111 |
| t = 22.4 | – | 6.434 | 5.980 | – | 6.049 | 5.952 |
| t = 25.6 | – | 6.438 | 6.003 | – | 6.189 | 5.989 |
| t = 28.8 | – | 6.401 | 5.982 | – | 6.113 | 5.916 |
| t = 32.0 | – | 6.338 | 6.009 | – | 5.973 | 6.006 |
| t = 0 | 1.4142123912 | 0.2357022604 | 1.4142124684 | 0.2357022604 |
| t = 3.2 | 1.4160938190 | 0.2357022604 | 1.4142431545 | 0.2357022604 |
| t = 6.4 | 1.4160300272 | 0.2357022604 | 1.4142408716 | 0.2357022604 |
| t = 9.6 | 1.4160715005 | 0.2357022604 | 1.4142452148 | 0.2357022604 |
| t = 12.8 | 1.4163743439 | 0.2357022604 | 1.4142508295 | 0.2357022604 |
| t = 16.0 | 1.4164056443 | 0.2357022604 | 1.4142476000 | 0.2357022604 |
| t = 19.2 | 1.4161496430 | 0.2357022604 | 1.4142420138 | 0.2357022604 |
| t = 22.4 | 1.4158790080 | 0.2357022604 | 1.4142390517 | 0.2357022604 |
| t = 25.6 | 1.4156623709 | 0.2357022604 | 1.4142358229 | 0.2357022604 |
| t = 28.8 | 1.4155983199 | 0.2357022604 | 1.4142326146 | 0.2357022604 |
| t = 32.0 | 1.4155092729 | 0.2357022604 | 1.4142314379 | 0.2357022604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Hu, J.; Chen, Z. Linear Sixth-Order Conservation Difference Scheme for KdV Equation. Mathematics 2025, 13, 1132. https://doi.org/10.3390/math13071132
He J, Hu J, Chen Z. Linear Sixth-Order Conservation Difference Scheme for KdV Equation. Mathematics. 2025; 13(7):1132. https://doi.org/10.3390/math13071132
Chicago/Turabian StyleHe, Jie, Jinsong Hu, and Zhong Chen. 2025. "Linear Sixth-Order Conservation Difference Scheme for KdV Equation" Mathematics 13, no. 7: 1132. https://doi.org/10.3390/math13071132
APA StyleHe, J., Hu, J., & Chen, Z. (2025). Linear Sixth-Order Conservation Difference Scheme for KdV Equation. Mathematics, 13(7), 1132. https://doi.org/10.3390/math13071132






