Dynamics of a Class of Chemical Oscillators with Asymmetry Potential: Simulations and Control over Oscillations †
Abstract
1. Introduction
2. The New Model
Considerations in the Light of Melnikov’s Approach
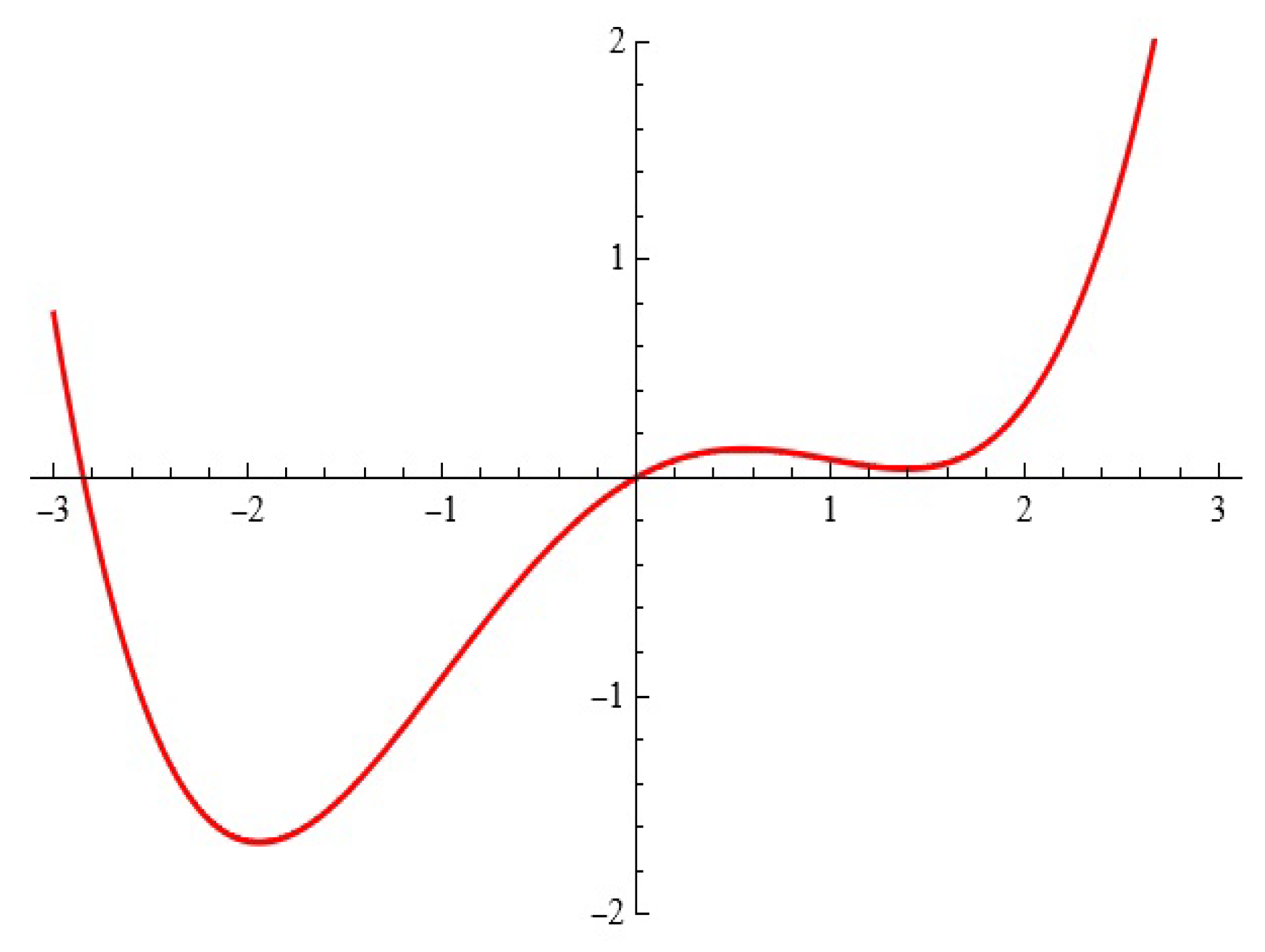
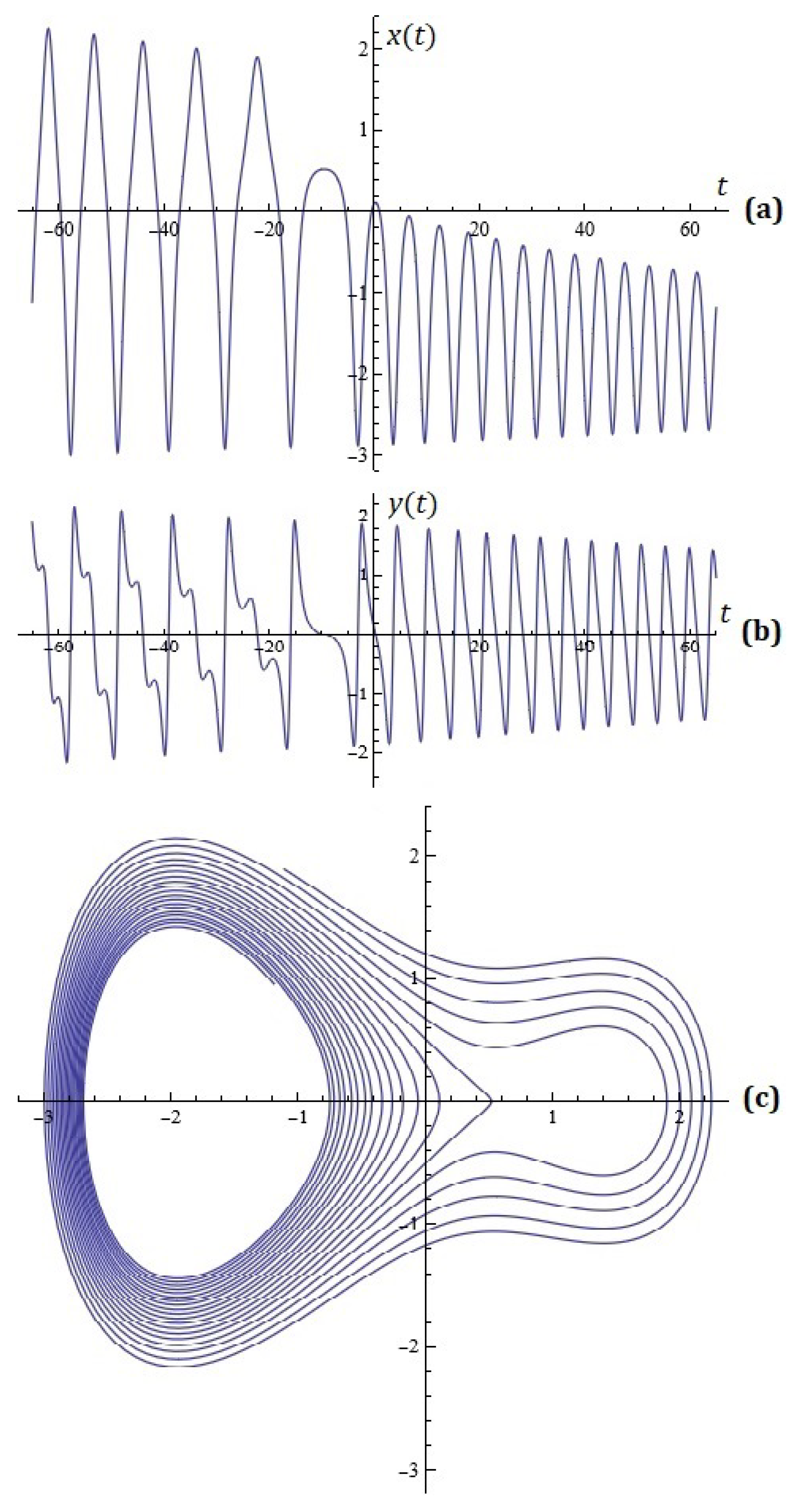
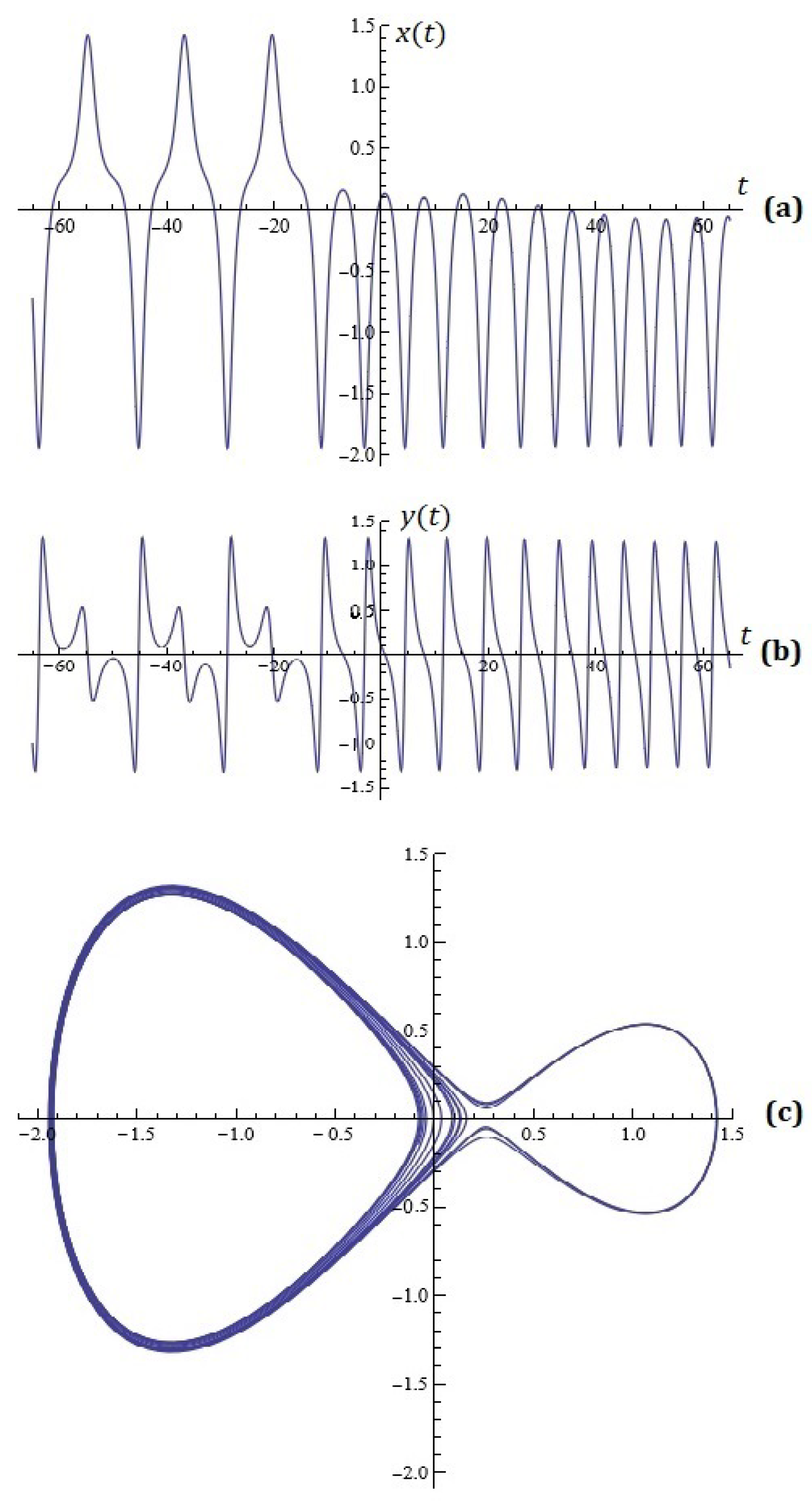
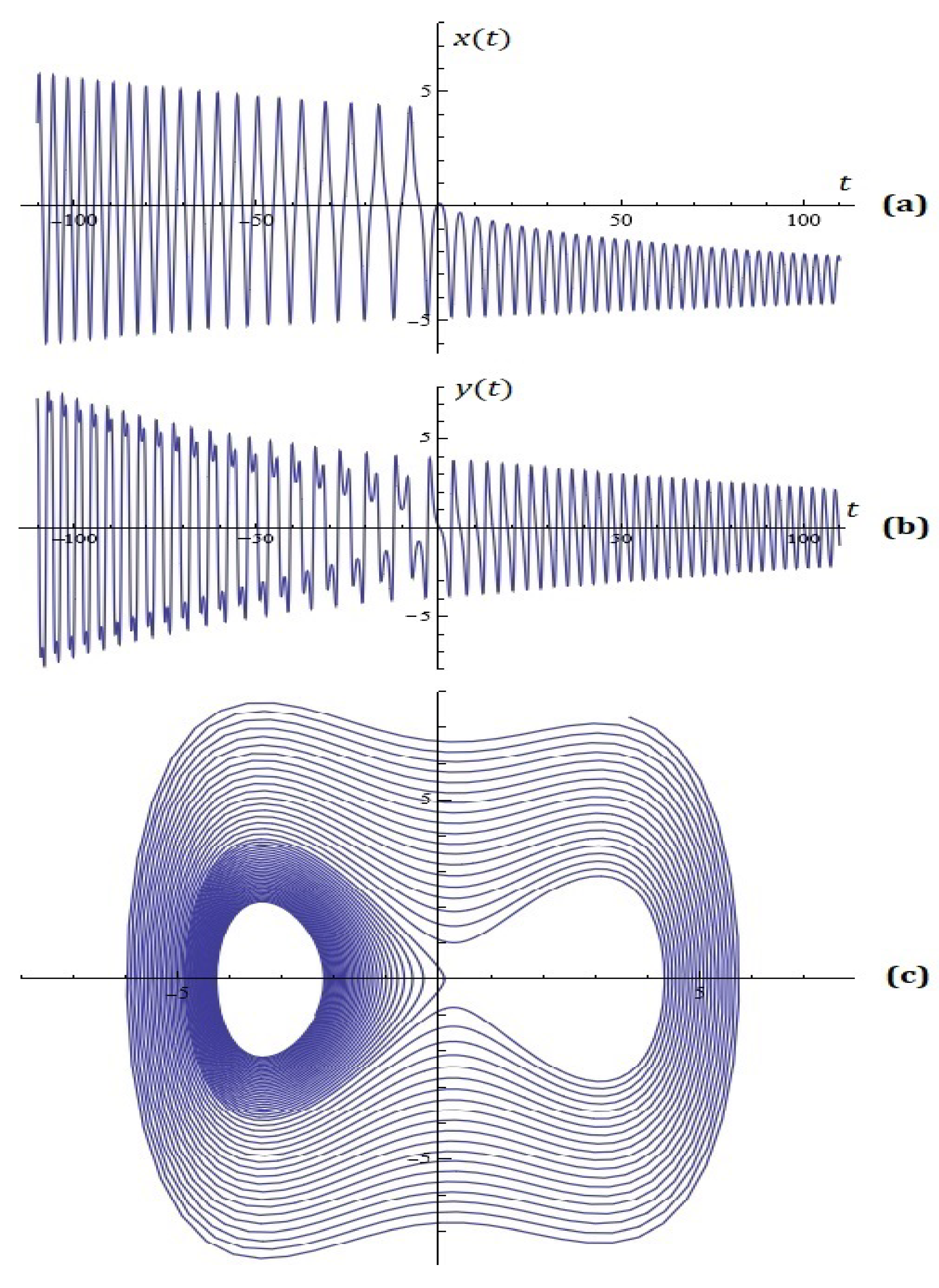
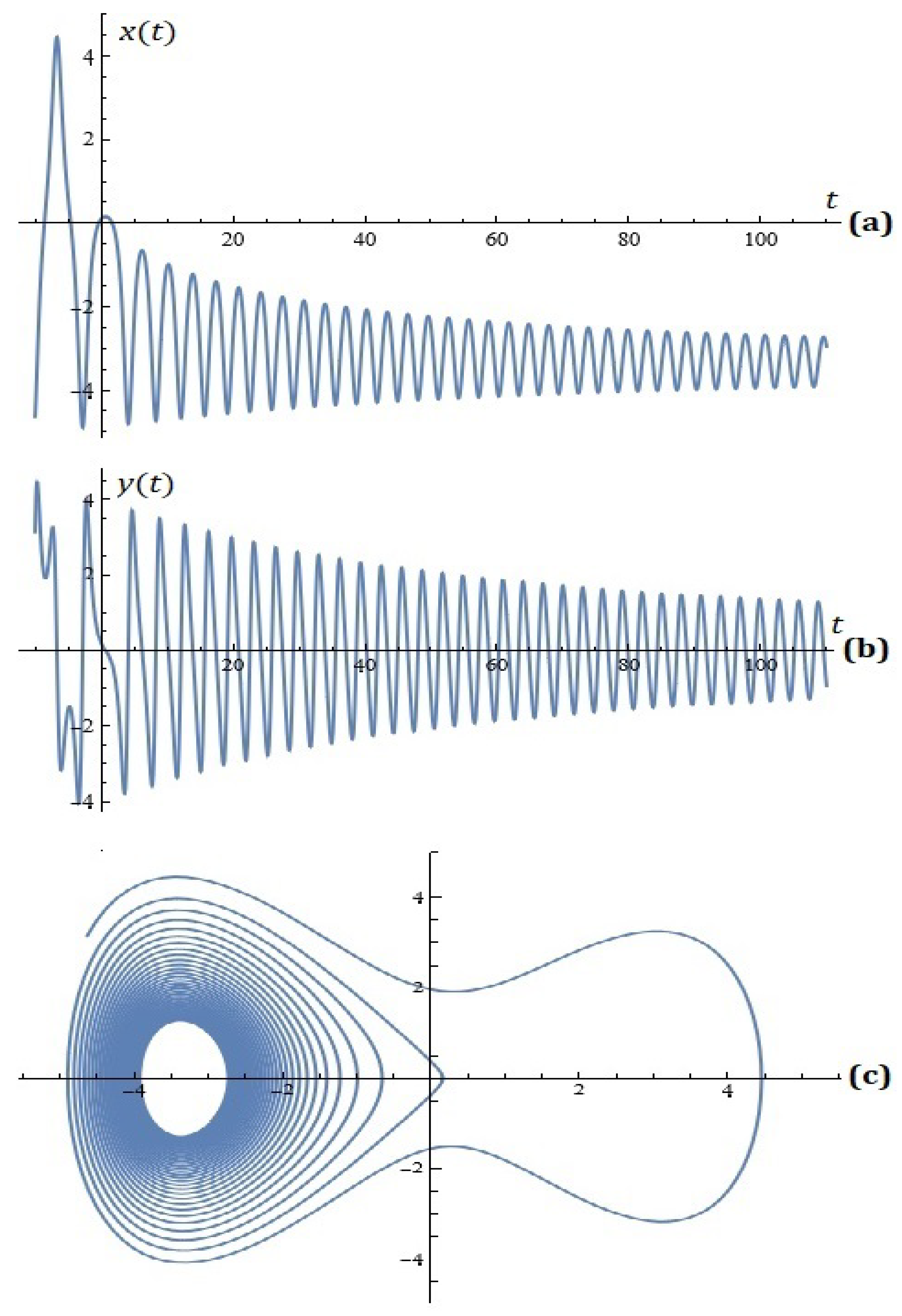
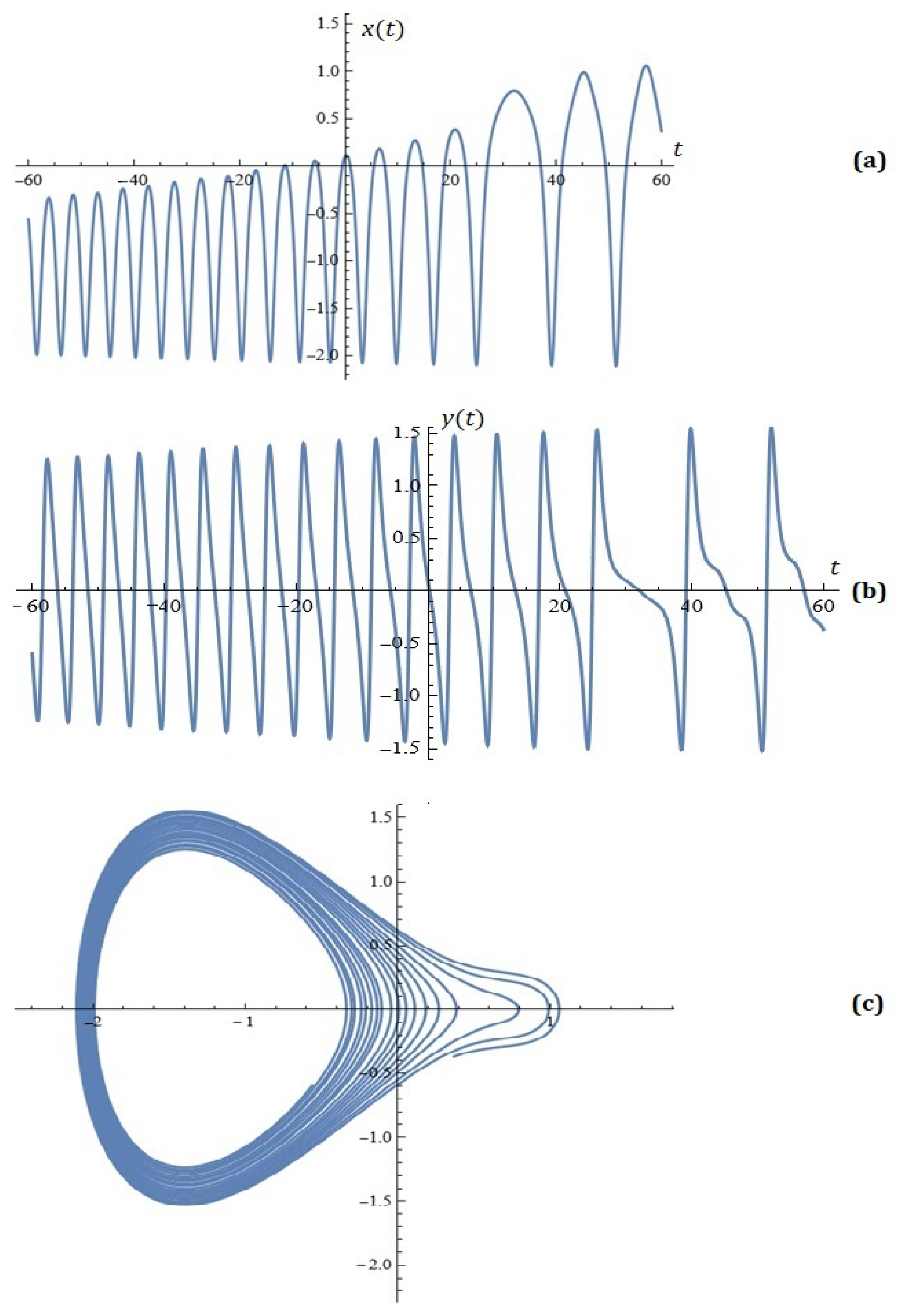
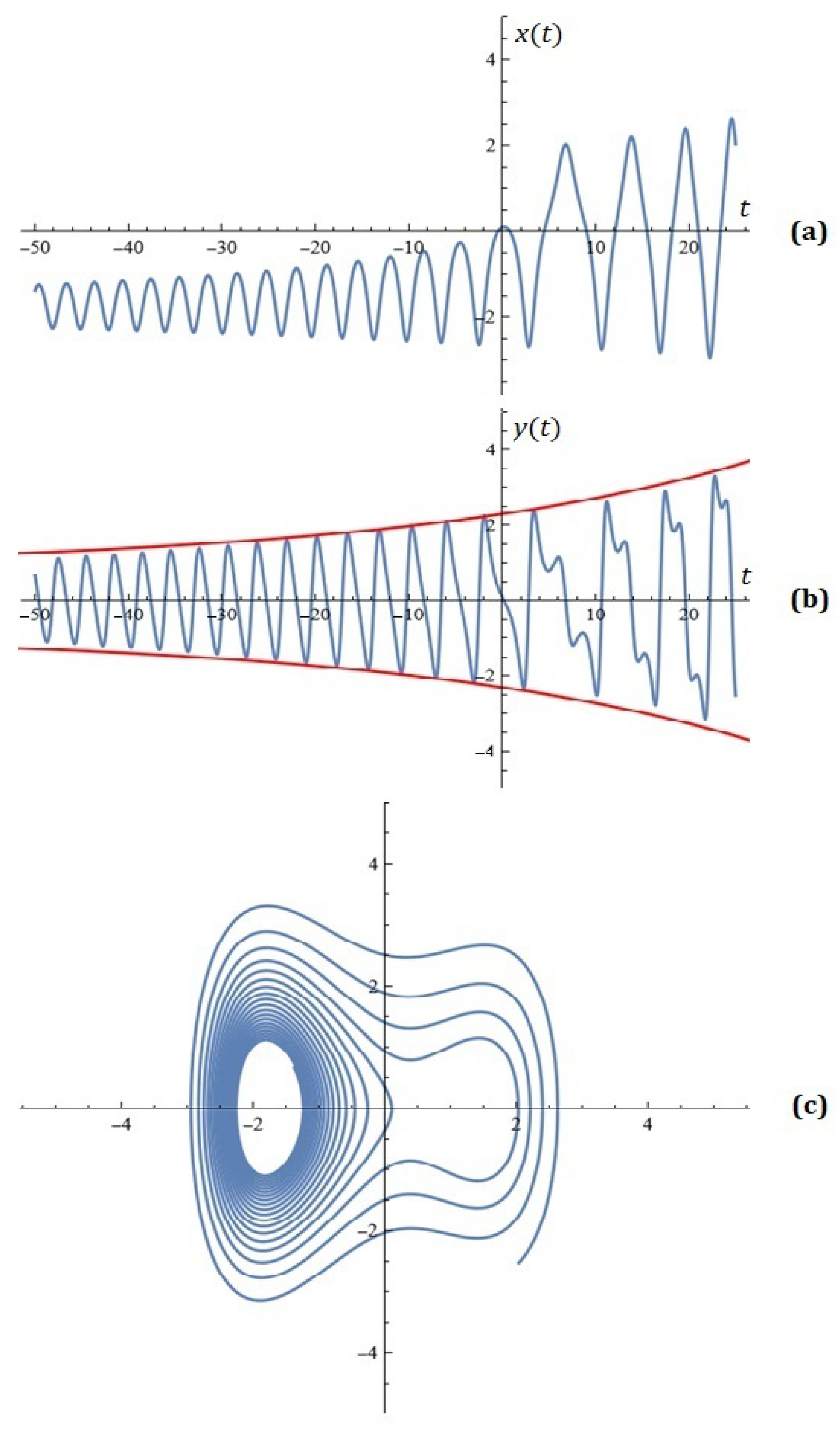
3. Some Simulations
4. The New Modified Model
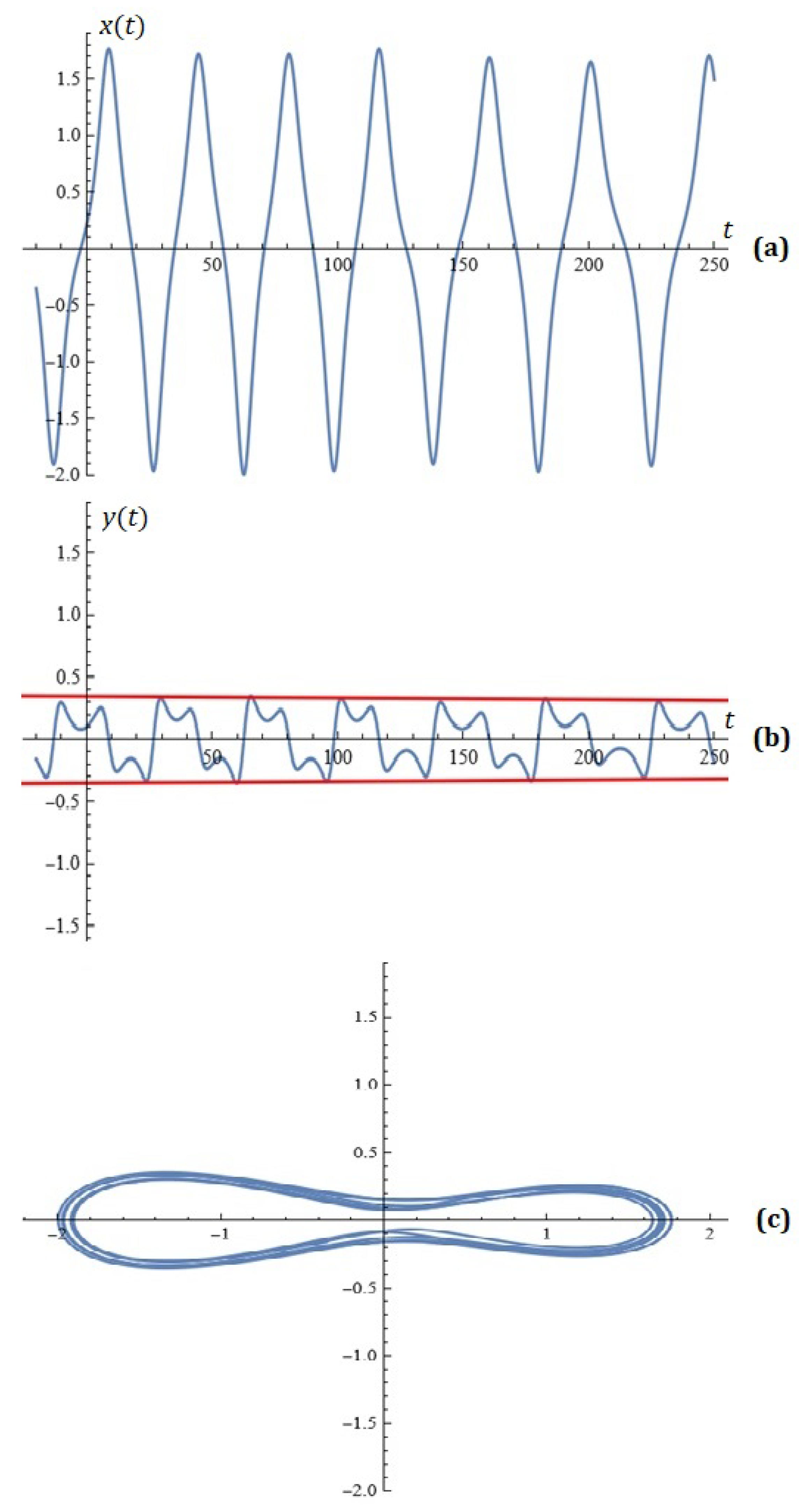
4.1. Potential Oscillation Control: Approximation with Limitations
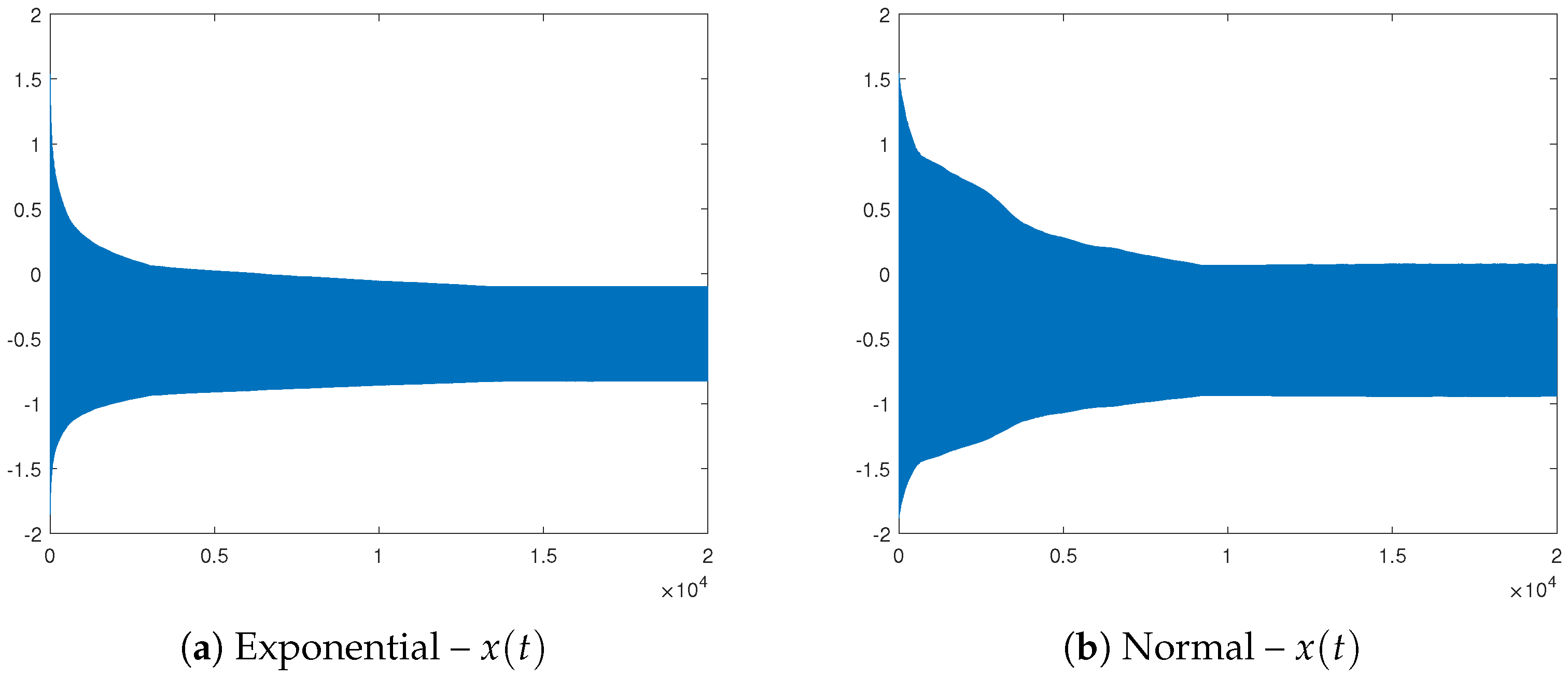
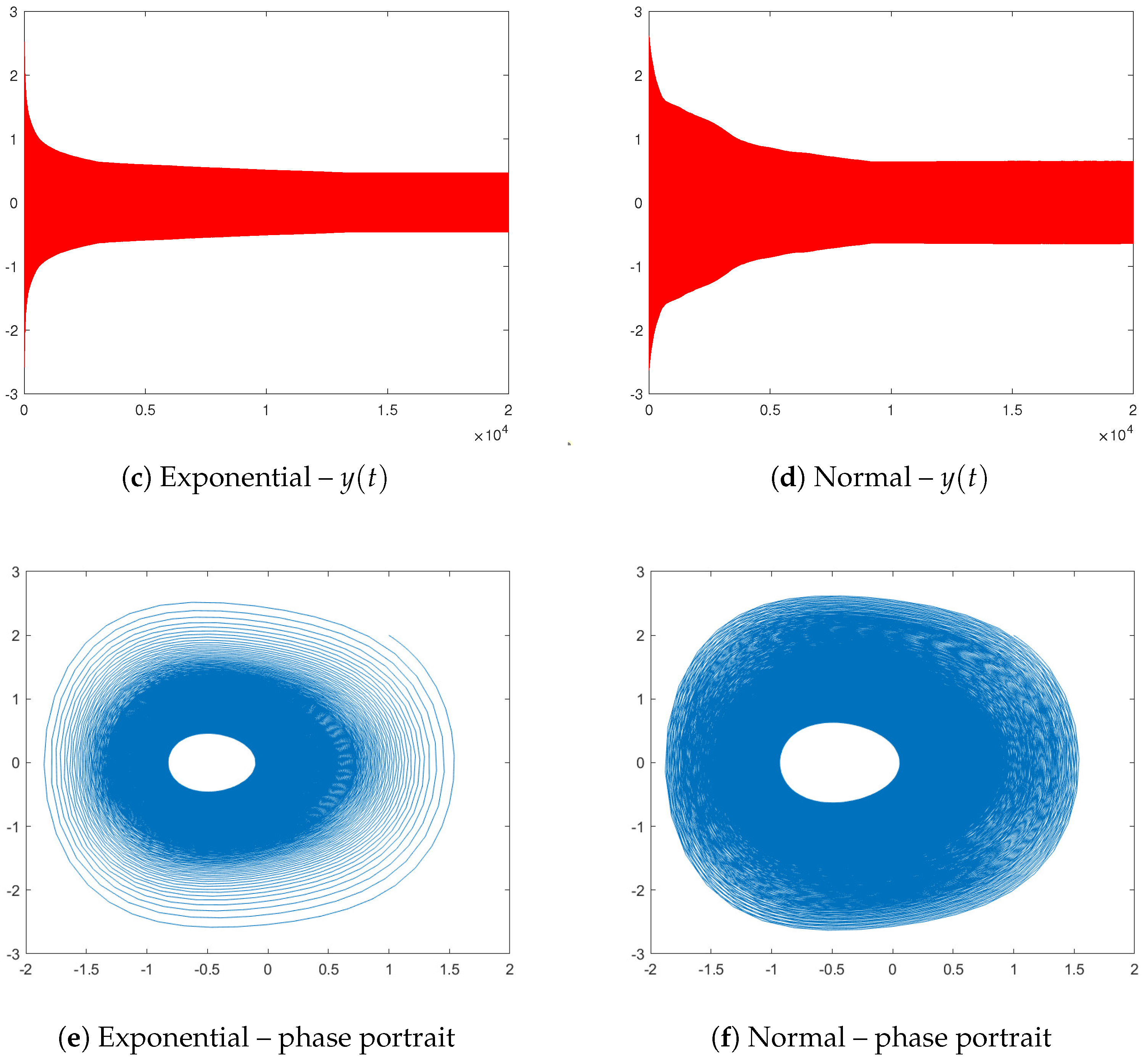
4.2. Probabilistic Construction to Possible Control over the Oscillations
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boissonade, J.; De Kepper, P. Transitions from bistability to limit cycle oscillations. Theoretical analysis and experimental evidence in an open chemical system. J. Phys. Chem. 1980, 84, 501–506. [Google Scholar] [CrossRef]
- Zhabotinskii, A.M. Biological and Biochemical Oscillators; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Epstein, I.R.; Showalter, K. Nonlinear chemical dynamics: Oscillations, patterns, and chaos. J. Phys. Chem. 1996, 100, 13132–13147. [Google Scholar] [CrossRef]
- Belousov, B.P. Oscillations and Travelling Waves in Chemical Systems; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Zhabotinsky, A.M.; Buchholtz, F.; Kiyatkin, A.B.; Epstein, I.R. Oscillations and waves in metal-ion-catalyzed bromate oscillating reactions in highly oxidized states. J. Phys. Chem. 1993, 97, 7578–7584. [Google Scholar] [CrossRef]
- Zhang, D.; Gyorgyi, L.; Peltier, W.R. Deterministic chaos in the Belousov-Zhabotinsky reaction: Experiments and simulations. Chaos 1993, 3, 723–745. [Google Scholar] [CrossRef]
- Ali, F.; Menzinger, M. Stirring effects and phase-dependent inhomogeneity in chemical oscillations: The Belousov-Zhabotinsky reaction in a CSTR. J. Phys. Chem. A 1997, 101, 2304–2309. [Google Scholar] [CrossRef]
- Bartuccelli, M.; Gentile, G.; Wright, J.A. Stable dynamics in forced systems with sufficiently high/low forcing frequency. Chaos 2016, 26, 083108. [Google Scholar] [CrossRef] [PubMed]
- Miwadinou, C.H.; Monwanoua, A.V.; Yovoganc, J.; Hinvia, L.A.; Nwagoum Tuwae, P.R.; Chabi Orou, J.B. Modeling nonlinear dissipative chemical dynamics by a forced modified Van der Pol-Duffing oscillator with asymmetric potential: Chaotic behaviors predictions. Chin. J. Phys. 2018, 56, 1089–1104. [Google Scholar] [CrossRef]
- Olabode, D.L.; Miwadinou, C.H.; Monwanou, A.V.; Chabi Orou, J.B. Horseshoes chaos and its passive control in dissipative nonlinear chemical dynamics. Phys. Scr. 2018, 93, 085203. [Google Scholar] [CrossRef]
- Olabode, D.L.; Miwadinou, C.H.; Monwanou, V.A.; Chabi Orou, J.B. Effects of passive hydrodynamics force on harmonic and chaotic oscillations in nonlinear chemical dynamics. Physica D 2019, 386, 49–59. [Google Scholar] [CrossRef]
- Miwadinou, C.H.; Monwanou, A.V.; Hinvi, A.L.; Koukpemedji, A.A.; Ainamon, C.; Orou, J.B.C. Melnikov chaos in a modified Rayleigh-Duffing oscillator with ϕ6 potential. Int. J. Bifurc. Chaos 2016, 26, 1650085. [Google Scholar] [CrossRef]
- Ainamon, C.; Miwadinou, C.H.; Monwanou, A.V.; Orou, J.B.C. Analysis of multiresonance and chaotic behavior of the polarization in materials modeled by a duffing equation with multifrequency excitations. Appl. Phys. Res. 2014, 6, 74–86. [Google Scholar] [CrossRef]
- Miwadinou, C.H.; Monwanou, A.V.; Chabi Orou, J.B. Active control of the parametric resonance in the modified Rayleigh-Duffing oscillator. Afr. Rev. Phys. 2014, 9, 227–235. [Google Scholar]
- Miwadinou, C.H.; Monwanou, A.V.; Chabi Orou, J.B. Effect of nonlinear dissipation on the basin boundaries of a driven two-well modified rayleigh-duffing oscillator. Int. J. Bifurc. Chaos 2015, 25, 1550024. [Google Scholar] [CrossRef]
- Miwadinou, C.H.; Hinvi, A.L.; Monwanou, A.V.; Chabi Orou, J.B. Nonlinear dynamics of a ϕ6 modified duffing oscillator: Resonant oscillations and transition to chaos. Nonlinear Dyn. 2017, 88, 97–113. [Google Scholar] [CrossRef]
- Adechinanm, A.; Kpomahou, Y.; Hinvi, L.; Miwadinou, C. Chaos, coexisting attractors and chaos control in a nonlinear dissipative chemical oscillator. Chin. J. Phys. 2022, 77, 2694–2697. [Google Scholar]
- Adechinan, J.A.; Kpomahou, Y.J.F.; Miwadinou, C.H.; Hinvi, L.A. Dynamics and active control of chemical oscillations modeled as a forced generalized Rayleigh oscillator with asymmetric potential. Int. J. Basic Appl. Sci. 2021, 10, 20–31. [Google Scholar]
- Melnikov, V.K. On the stability of a center for time–periodic perturbation. Trans. Mosc. Math. Soc. 1963, 12, 3–52. [Google Scholar]
- Golev, A.; Terzieva, T.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Simulation on a Generalized Oscillator Model: Web-Based Application. C. R. L’Acad. Bulg. Sci. 2024, 77, 230–237. [Google Scholar] [CrossRef]
- Lente, G. Deterministic kinetics in chemistry and systems biology. In Briefs in Molecular Science; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Murray, J.D. Mathematical Biology: I. An Introduction, 3rd ed.; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Garfinkel, A.; Shevtsov, J.; Guo, Y. Modeling Life. The Mathematics of Biological Systems; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Goriely, A. The Mathematics and Mechanics of Biological Growth; Springer: New York, NY, USA, 2017. [Google Scholar]
- Feinberg, M. Foundations of Chemical Reaction Network Theory; Springer: London, UK, 2019. [Google Scholar]
- Kyurkchiev, N.; Markov, S. On the numerical solution of the general kinetic “K-angle” reaction system. J. Math. Chem. 2016, 54, 792–805. [Google Scholar] [CrossRef]
- Borisov, M.; Markov, S. The two-step exponential decay reaction network: Analysis of the solutions and relation to epidemiological SIR models with logistic and Gompertz type infection contact patterns. J. Math. Chem. 2021, 59, 1283–1315. [Google Scholar]
- Mincheva, M. Oscillations in non-mass action kinetics models of biochemical reaction networks arising from pairs of subnetworks. J. Math. Chem. 2012, 50, 1111–1125. [Google Scholar]
- Pogliani, L.; Berberan-Santos, M.N.; Martinho, J.M.G. Matrix and convolution methods in chemical kinetics. J. Math. Chem. 1996, 20, 193–210. [Google Scholar]
- Hernandez, B.; Mendoza, E.; de los Reyes V, A.A. Fundamental decompositions and multistationarity of power–law kinetic systems. MATCH Commun. Math. Comput. Chem. 2020, 83, 403–434. [Google Scholar]
- Villareal, K.A.M.; Hernandez, B.S.; Lubenia, P.V.N. Derivation of steady state parametrizations of chemical reaction networks with n independent and identical subnetworks. MATCH Commun. Math. Comput. Chem 2024, 91, 337–365. [Google Scholar] [CrossRef]
- Radulescu, O.; Gorban, A.; Zinovyev, A.; Lilienbaum, A. Robust simplifications of multiscale biochemical networks. BMC Syst. Biol. 2008, 2, 86. [Google Scholar] [CrossRef]
- Rao, S.; van der Schaft, A.; van Eunen, K.; Bakker, B.; Jayawardhana, B. A model reduction method for biochemical reaction networks. BMC Syst. Biol. 2014, 8, 52. [Google Scholar]
- Markov, S. Building reaction kinetic models for amiloid fibril growth. Biomath 2016, 5, 1607311. [Google Scholar]
- Markov, S. Reaction networks reveal new links between Gompertz and Verhulst growth functions. Biomath 2019, 8, 1904167. [Google Scholar] [CrossRef]
- Anguelov, R.; Borisov, M.; Iliev, A.; Kyurkchiev, N.; Markov, S. On the chemical meaning of some growth models possessing Gompertzian–type property. Math. Methods Appl. Sci. 2018, 41, 8365–8376. [Google Scholar]
- Craciun, G.; Feinberg, M. Multiple equilibria in complex chemical reaction networks: II. The species-reaction graph. SIAM J. Appl. Math. 2006, 66, 1321–1338. [Google Scholar]
- Markov, S.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. A note on the n-stage growth model. Overview. Biomath Commun. 2018, 5, 79–100. [Google Scholar]
- Alabugin, I.V.; Manoharan, M.; Zeidan, T.A. Homoanomeric effects in six-membered heterocycles. J. Am. Chem. Soc. 2003, 125, 14014–14031. [Google Scholar] [PubMed]
- Zhang, Y.; Zhang, J. Existence of a Global Attractor for the Reaction–Diffusion Equation with Memory and Lower Regularity Terms. Mathematics 2024, 12, 3374. [Google Scholar] [CrossRef]
- Gradstein, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Piskunov, N. Calcul Diffrentiel et Integral, 9th ed.; Tome II; MIR: Moscow, Russia, 1980. [Google Scholar]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Investigations of Modified Classical Dynamical Models: Melnikov’s Approach, Simulations and Applications, and Probabilistic Control of Perturbations. Mathematics 2025, 13, 231. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. One More Thing on the Subject: Generating Chaos via x|x|a−1, Melnikov’s Approach Using Simulations. Mathematics 2025, 13, 232. [Google Scholar] [CrossRef]
- Ullah, M.; Behl, R.; Argyros, I. Some High-Order Iterative Methods for Nonlinear Models Originating from Real Life Problems. Mathematics 2020, 8, 1249. [Google Scholar] [CrossRef]
- Argyros, I.K.; Sharma, D.; Argyros, C.I.; Parhi, S.K.; Sunanda, S.K. A Family of Fifth and Sixth Convergence Order Methods for Nonlinear Models. Symmetry 2021, 13, 715. [Google Scholar] [CrossRef]
- Kumar, S.; Bhagwan, J.; Jäntschi, L. Optimal Derivative-Free One-Point Algorithms for Computing Multiple Zeros of Nonlinear Equations. Symmetry 2022, 14, 1881. [Google Scholar] [CrossRef]
- Shams, M.; Kausar, N.; Araci, S.; Oros, G.I. Artificial hybrid neural network-based simultaneous scheme for solving nonlinear equations: Applications in engineering. Alex. Eng. J. 2024, 108, 292–305. [Google Scholar]
- Thangkhenpau, G.; Panday, S.; Bolunduet, L.C.; Jantschi, L. Efficient Families of Multi-Point Iterative Methods and Their Self-Acceleration with Memory for Solving Nonlinear Equations. Symmetry 2023, 15, 1546. [Google Scholar] [CrossRef]
- Akram, S.; Khalid, M.; Junjua, M.-U.-D.; Altaf, S.; Kumar, S. Extension of King’s Iterative Scheme by Means of Memory for Nonlinear Equations. Symmetry 2023, 15, 1116. [Google Scholar] [CrossRef]
- Cordero, A.; Janjua, M.; Torregrosa, J.R.; Yasmin, N.; Zafar, F. Efficient four parametric with and without-memory iterative methods possessing high efficiency indices. Math. Probl. Eng. 2018, 2018, 8093673. [Google Scholar] [CrossRef]
- Hu, S.; Zhou, L. Chaotic dynamics of an extended Duffing-van der Pol system with a non-smooth perturbation and parametric excitation. Z. Naturforschung Teil A 2023, 78, 1015–1030. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Dynamics of a Class of Chemical Oscillators with Asymmetry Potential: Simulations and Control over Oscillations. Mathematics 2025, 13, 1129. https://doi.org/10.3390/math13071129
Kyurkchiev N, Zaevski T, Iliev A, Kyurkchiev V, Rahnev A. Dynamics of a Class of Chemical Oscillators with Asymmetry Potential: Simulations and Control over Oscillations. Mathematics. 2025; 13(7):1129. https://doi.org/10.3390/math13071129
Chicago/Turabian StyleKyurkchiev, Nikolay, Tsvetelin Zaevski, Anton Iliev, Vesselin Kyurkchiev, and Asen Rahnev. 2025. "Dynamics of a Class of Chemical Oscillators with Asymmetry Potential: Simulations and Control over Oscillations" Mathematics 13, no. 7: 1129. https://doi.org/10.3390/math13071129
APA StyleKyurkchiev, N., Zaevski, T., Iliev, A., Kyurkchiev, V., & Rahnev, A. (2025). Dynamics of a Class of Chemical Oscillators with Asymmetry Potential: Simulations and Control over Oscillations. Mathematics, 13(7), 1129. https://doi.org/10.3390/math13071129







