Abstract
The symmetry group of a (discrete) Painlevé equation provides crucial information on the properties of the equation. In this paper, we argue against the commonly held belief that the symmetry group of a given equation is solely determined by its surface type as given in the famous Sakai classification. We will dispel this misconception by using a specific example of a d-PII equation, which corresponds to a half-translation on the root lattice dual to its surface-type root lattice but becomes a genuine translation on a sub-lattice thereof that corresponds to its real symmetry group. The latter fact is shown in two different ways, first by a brute force calculation, and then through the use of normalizer theory, which we believe to be an extremely useful tool for this purpose. We finish the paper with the analysis of a sub-case of our main example, which arises in the study of gap probabilities for Freud unitary ensembles, and the symmetry group of which is even further restricted due to the appearance of a nodal curve on the surface on which the equation is regularized.
MSC:
33D45; 34M55; 34M56; 14E07; 39A13
1. Introduction
The theory of discrete Painlevé equations is roughly a quarter of a century old, and during this time, we have achieved a very good understanding of these equations. However, a lot of terminology reflects the historic development of the theory, which can lead to various misconceptions. One of the goals of the present paper is to address some of these misconceptions, particularly the relationship between the surface-type and the symmetry-type classification schemes, as well as the relationship between an equation and its symmetry group. But let us begin with the following definition:
Definition 1.
An (abstract) discrete Painlevé equation is a triple , where and are two root sub-systems (described by affine Dynkin diagrams) of the affine root system . The root system describes the geometry of the configuration space of the dynamics, the (fully) extended affine Weyl group (see Definition 2) of type describes the symmetry group of this configuration space, and the equation itself is described by an element of infinite order (a translation or quasi-translation), where is its equivalence class w.r.t. conjugations in .
This definition may seem rather unconventional. In particular, there is no actual equation in the definition. We think that this may, in fact, be the benefit of the suggested approach. To see this, as well as to understand the connection to a more traditional definition of a discrete Painlevé equation, we need to revisit some history.
The name discrete Painlevé equation is, of course, due to connections with differential Painlevé equations. Recall that Painlevé equations appeared at the beginning of the twentieth century in an attempt to define nonlinear special functions as solutions of nonlinear ordinary differential equations (ODEs), similar to the classical special functions such as Airy, Bessel, and many others, which solve linear differential equations. For solutions of nonlinear ODE, one encounters the phenomenon of movable singular points (i.e., depending on the initial conditions), and if such a singularity is, for example, a branch point, we cannot talk about the Riemann surface for the general solution of the equation. P. Painlevé suggested to study ODEs, whose general solution has no movable critical points other than poles. We now say that an ODE has the Painlevé property if the general solution of the equation is free of movable critical points where it loses local single-valuedness. Painlevé, together with his student, B. Gambier, found that an equation in the form that has the Painlevé property can be put into one of fifty canonical forms, of which six cannot be reduced to linear equations or solved in terms of classical special functions. These equations are now known as Painlevé equations, and their solutions are called Painlevé transcendents. Differential Painlevé equations play an increasingly important role in modern mathematical physics, and we recommend [1,2,3] and the references therein to the interested reader.
The term discrete Painlevé equation probably appeared in the literature for the first time in the paper [4], following earlier works [5,6] on two-dimensional quantum gravity. This result quickly attracted the attention of researchers working with discrete integrable systems [7,8]. A large number of examples of discrete Painlevé equations have been obtained in the work of B. Grammaticos and A. Ramani who applied the singularity confinement criterion to deautonomizations of discrete integrable autonomous mappings, such as QRT maps (see the survey [9] and references therein). In this approach, the term discrete Painlevé equation denoted a certain second-order non-autonomous recurrence relation that has one of the differential Painlevé equations as a continuous limit. It is worth noting that the first example of such a non-autonomous recurrence goes back at least 50 years earlier to the 1939 paper by J. Shohat on orthogonal polynomials [10], but Shohat did not take a continuous limit, and so the relationship to differential Painlevé equations was missed.
This approach resulted in names such as d-PII, or q-PVI, or alt. d-PI being given to certain recurrences based on the existence of a continuous limit. However, it quickly became clear that this naming scheme is quite confusing, and also that there are a lot more discrete Painlevé equations than differential ones. An important breakthrough is due to H. Sakai [11] who, following the earlier works of K. Okamoto [12] for the differential Painlevé equations, approached discrete Painlevé equations from the point of view of algebraic geometry. Sakai’s work clarified the algebraic nature of discrete Painlevé equations and also resulted in a clear classification scheme. However, a certain care is necessary when using this classification scheme, and this is precisely the point that we want to address.
Let us first sketch some of the key points of Sakai’s approach, referring the reader to the survey [13], as well as Sakai’s original paper [11], for careful statements and details. Sakai’s point of view is that discrete Painlevé equations are discrete dynamical systems on certain families of rational algebraic surfaces, called generalized Halphen surfaces. These families can be obtained by blowing up a configuration of eight points on (or, alternatively, a configuration of nine points on ). In the generic case, these points lie on a unique elliptic curve D that can be thought of as a divisor of a section of the anti-canonical bundle, i.e., the polar divisor of some rational 2-form , . After blowing up those points, we obtain a surface X with a unique effective anti-canonical divisor . The Picard lattice of X is generated by the coordinate classes and the classes of the exceptional divisors of the blowups,
Varying the locations of the blowup points, but still keeping them in a general position, creates a family of such surfaces; the type of this family is denoted by the symbol . The group of symmetries of this family, in the sense of Cremona isometries, on the level of the Picard lattice and their realization as the Cremona action by automorphisms of the family, is the affine Weyl group . This group has translation elements that, when acting on the surface family, define elliptic discrete Painlevé equations. The location of points in the configuration evolves with each step, so the dynamics is non-autonomous. The embedding of the curve can be given in terms of elliptic functions, and the point evolution becomes additive in the argument of these elliptic functions. When written in coordinates, say, in the affine chart of , the coordinates of the blowup points become coefficients in the evolution equations, and this is what is meant by an elliptic difference equation.
The next step is to consider various degenerations, e.g., the elliptic curve on which our configuration of points lies can degenerate into a rational curve with a cusp or a node, and then under further degenerations become reducible, where each component is a rational curve. We can then write this decomposition of the anti-canonical divisor into irreducible components as , where are the multiplicities. The intersection configuration (w.r.t. to the usual intersection product on given on the generators as and zero otherwise) is given by the negative of a generalized Cartan matrix of affine type, and so the degenerations can be described using the language of affine Dynkin diagrams. The resulting classification scheme is given in Figure 1. Note that differential Painlevé equations also appear on this diagram via the types of surfaces which provide their spaces of initial conditions as constructed by Okamoto [12].
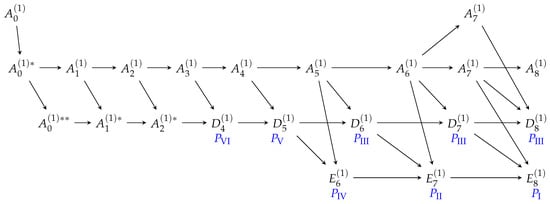
Figure 1.
Surface-type classification scheme for Painlevé equations.
This diagram gives a complete classification of the possible configuration spaces on which discrete Painlevé dynamics can occur. In [11], Sakai also computed the groups of Cremona isometries and their Cremona action for each of these families as extensions of affine Weyl groups of the types shown in Figure 2. Very often in the literature, especially in applications of discrete Painlevé equations, it is that second classification scheme that is being used. However, it has been known for a long time that there are examples of discrete Painlevé dynamics that stay on some proper sub-families of the general configuration space, and if we restrict our attention to such sub-families, the symmetry group of that sub-family is different from the full symmetry group [14,15,16,17]. In this way, we can obtain symmetry groups that do not appear explicitly in the classification scheme in Figure 2. Two particularly important examples of such sub-families are related to the existence of so-called nodal curves, which form obstructions to Cremona isometries, as explained in [11], and the notion of projective reduction introduced by K. Kajiwara, N. Nakazono, and T. Tsuda [18]. For the projective reduction scenario, the element of the extended affine Weyl group corresponding to the dynamics is only a quasi-translation (i.e., it is an element of infinite order that becomes a translation after being raised to some power). However, it is possible to choose a sub-family in the generic family by imposing some parameter constraints, so that the dynamics becomes a translation, both in terms of the evolution of the coefficients in the equation and in terms of the symmetry group of the sub-family. The existence of nodal curves also corresponds to parameter constraints, and we note that combinations of constraints from both projective reduction and nodal curves are possible. Here we adopt the point of view that the symmetry group of a discrete Painlevé equation is that of the surface (sub-)family forming its configuration space, and whose translation elements generate the resulting dynamics.
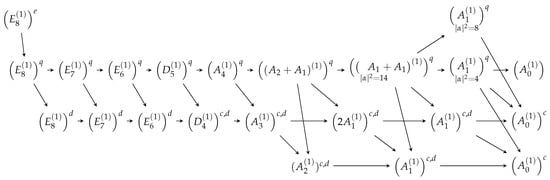
Figure 2.
Symmetry-type classification scheme for Painlevé equations, with e, q, d, c indicating types associated with elliptic, q-difference, additive difference, and differential Painlevé equations, respectively.
We illustrate this situation by considering one of the most well-known and well-studied examples of discrete Painlevé equations, a discrete d-PII equation:
where , , and are some complex parameters. According to [9], the case of Equation (1) was first identified as a discrete analogue of PII in [7], after having appeared around the same time in [19], and its continuous limit to a special case of PII taken.
We show that d-PII given by Equation (1) is a discrete dynamical system on a sub-family of the Sakai -family, with the actual symmetry group , and that the dynamics is indeed described by a translation element in this group.
The paper is organized as follows: In the next section, we give a brief summary of the algebro-geometric data for the standard realization of the -family, following [13]. In Section 3, we explain how Equation (1) fits into this framework, give the parameter constraint that defines the sub-family, and describe its symmetry group. We would like to stress again here that by the symmetry group of a discrete Painlevé equation we mean an extended affine Weyl group whose birational representation on a surface sub-family generates the equation, rather than the discrete symmetries of the equation itself. In Section 4, we consider an example of a recurrence that appeared in a recent paper by Chao Ming and Liwei Wang [20]. That example is Equation (1) with an additional constraint on the parameters, which results in the appearance of a so-called nodal curve, thus further restricting the symmetry group of the equation. This example is particularly interesting as it combines two different types of parameter constraints. In the final section, we give a brief summary and formulate our conclusions.
2. The Algebro-Geometric Data and Discrete Painlevé Equations on the Sakai Surface Family
2.1. Geometric Realization
To make the paper self-contained, in this section we reproduce some standard facts about the -Sakai surface family, following [13], and review some standard examples of discrete Painlevé equations on that surface. This was also considered in detail in ([21] [Appendix]) so we only collect some essential information here. Surfaces in this family are characterized by the condition that the configuration of the irreducible components (equivalently, their classes called the surface roots) of the unique effective anti-canonical divisor is described by an affine Dynkin diagram of type shown on Figure 3.
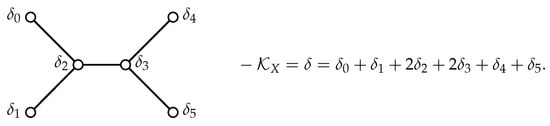
Figure 3.
Affine Dynkin diagram .
There are different geometric realizations of this family, corresponding to different choices of the surface roots. For example, in [13] the surface root basis is
and in [11] it is taken as
The resulting surface families are equivalent via an explicit birational change of variables, as carefully explained in ([21] [Appendix]) We choose the surface root basis as in Equation (2). The standard basis of the symmetry roots , , for this configuration is shown in Figure 4.
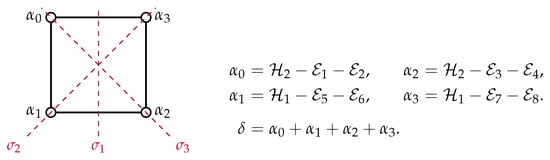
Figure 4.
The symmetry root basis for the standard symmetry sub-lattice.
After making some normalization choices, we can then take the corresponding point configuration on with affine coordinates , as shown in Figure 5 (this will be explained in detail in Section 3.1, and we refer the reader unfamiliar with such schematic representations of point configurations and surfaces in the context of the geometry of Painlevé equations to, e.g., [13,15,22]). Using the Period Map defined through the standard symplectic form , we can introduce, for each symmetry root , a canonical parameter , known as the root variable. These root variables satisfy the usual normalization condition and parameterize the blowup points in Figure 5 as follows:
where t is an additional parameter, the notation for which reflects connections to differential Painlevé equations. This is the same parameterization of the point configuration as in section 8.2.18 of [13]. Now, allowing the root variables and parameter t to vary, one obtains a family of surfaces , parameterized by the root variables and the extra parameter—. The geometric realization of the surface family also carries data of the enumeration of the blowups in terms of the parameters, and this gives a natural identification of all into a single lattice, which we denote as .
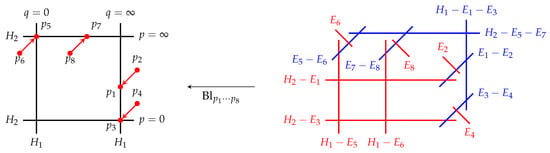
Figure 5.
A standard realization of the surface. Here we use the actual divisors rather than their divisor classes. For example, is the proper transform of the line under the blowup procedure, and it is the unique effective divisor in the class , and so on.
2.2. Affine Weyl Symmetry Group
We call elements defined in Figure 4 roots because they give a set of simple roots for the standard affine root system in the space equipped with the symmetric bilinear form defined on the basis elements in terms of the intersection product on , . In particular, we obtain the standard affine Cartan matrix
The abstract affine Weyl group , defined in terms of generators and relations that are encoded by the affine Dynkin diagram ,
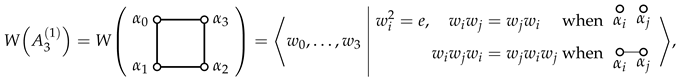 can now be realized via reflections in the roots , , which can be defined on the whole of ,
can now be realized via reflections in the roots , , which can be defined on the whole of ,
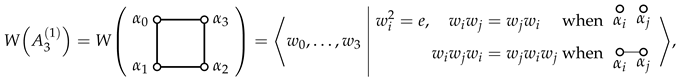 can now be realized via reflections in the roots , , which can be defined on the whole of ,
can now be realized via reflections in the roots , , which can be defined on the whole of ,Then is the simple system of the root system, reflections are called simple reflections, and the affine root system is , where . We denote by the simple roots of the underlying root system , where .
The anti-canonical divisor class is in and, in fact, is the null root of the root system,
where is the highest root of the underlying root system.
Let . Recall that in the case, the fundamental weights are given explicitly in terms of the simple roots by
Then in V we have two important lattices: the root lattice and the weight lattice of the finite system.
For any element , we can define the associated translation by
These translations satisfy and, for any automorphism w of preserving the intersection form and , . When , this gives the usual translations on the root lattice Q, and the standard fact is that
and the semi-direct product structure is realized explicitly via , where the reflection corresponding to the highest root , written in terms of generators, is .
However, if we take translations associated to , the same construction results in a larger group known as the extended affine Weyl group. In the case of a finite crystallographic root system, it is known that the quotient is a finite Abelian group which corresponds to some but not necessarily all automorphisms of the affine Dynkin diagram, (see [23] [VI] for descriptions of these finite groups for the Dynkin diagrams of finite type root systems).
In our case, , the dihedral group of order 8, which can be generated by reflections and , as shown in Figure 4, but it is convenient to include one more automorphism (see Figure 4). These act on the symmetry and the surface root bases as permutations (here we use the standard cycle notation):
They can also be represented as compositions of reflections (that are no longer in roots in the system but rather in the larger system containing it) when acting on the Picard lattice,
where is a reflection (5) in (note also that a transposition is induced by a reflection in the root ).
The automorphisms corresponding to are only the rotations . Then, we obtain the extended affine Weyl group
In the case at hand, the equality in Equation (7) is realized by
with the translations by fundamental weights acting by
This also gives us the expressions in terms of generators
At the same time, for the geometric Painlevé theory, we need to include all of the diagram automorphisms. To keep track of this distinction, we introduce the following terminology.
Definition 2.
The fully extended affine Weyl group (of type ) is .
The semi-direct product structure of is given by the action of on via .
The group describes the symmetries of the surface family constructed in Section 2. This is via an action of on point configurations by elementary birational maps on and root variables (which lift to isomorphisms , which can also be thought of as automorphisms of the family of surfaces, which induce the linear actions of w on by pullback or pushforward depending on the convention). This is known as a birational representation of , and the action of by automorphisms of is called the Cremona action [11]. We describe this birational representation in the following Lemma ([21] [Section A.3]).
Lemma 1.
The birational representation of , written in the affine -chart and the root variables , is as follows: Reflections on are induced by the elementary birational mappings, also denoted by ,
Note that the parameter t can also change when we consider the Dynkin diagram automorphisms, so it is convenient to include it among the root variables. The actions of the generators of , as well as , are given by the following birational mappings:
2.3. Examples of Discrete Painlevé Equations
There are two standard examples of discrete Painlevé equations on this surface family. The first one is ([13] (8.23)) and it corresponds to the translation , i.e., its action on the symmetry roots by pushforward is given by
This equation can be written as , where
which gives an isomorphism , where the root variable evolution and normalization are given by
When comparing Equations (8) and (10), it should be noted that there is a correspondence between actions on root variables and simple roots, but the action by pushforward of the map on simple roots is inverse to the evolution of root variables, which is explained in terms of the definition of the period map in, for example, [15]. As is often the case, Equation (9) naturally defines two half-maps, and (the additional negative sign here is related to the Möbius group gauge action) and the full mapping decomposes as , where is above with root variables evolved according to Equation (10).
In terms of the action of the generators of on and root variables, as in Lemma 1, these mappings can be decomposed as
The second example, called a d-PIV equation in [11], is the mapping that corresponds via pushforward to the translation . It is written in the multiplicative-additive form
where (without loss of generality it can be normalized to ), the root variable evolution is given by and , the action on the symmetry roots is
and the decomposition of the mapping in terms of the generators is .
Using Equations (4) and (6), one sees that , while , and therefore, the associated translations and are not conjugate in (since for any and , and w preserves the intersection form). Hence, and are not related under conjugation by any element of . So, the corresponding equations are not equivalent under a change of variables corresponding to conjugation by any of the birational mappings in Lemma 1. Furthermore, Equation (11) corresponds to a different geometric realization, as can be seen by the choice of the surface roots in Equation (3). Since our example is related to Equation (8), we do not go into details here (see [21] [Appendix]).
3. d-PII Equation
Let us now consider the d-PII Equation (1). First, we need to show that the dynamics is indeed regularized on a family of surfaces. This is a standard computation that we only outline here; for a detailed description, see, e.g., [22].
3.1. The Surface Family for the d-PII Dynamics
We first rewrite Equation (1) as a system,
and then as a mapping (the parameter should not be confused with a symmetry root, but the notation is traditional and the context makes it clear). Using the standard notation , and the same for y, the forward mapping is given by
and the backward mapping is
Note that these mappings indeed define an additive non-autonomous discrete dynamics, since the coefficients in the mapping are (affine) functions of the time step n.
Next, extend the dynamics from to by introducing, in addition to the affine chart , three more charts , , and , where and . We then see the appearance of base points where both the numerator and the denominator of the rational mapping vanish simultaneously. For example, the forward mapping, given by Equation (13), when written in the -chart in the domain, becomes
and we immediately see the base points in that chart.
These indeterminacies of the mapping are resolved using the blowup procedure which, on the coordinate level, is just a change of variables. For example, blowing up a point introduces two charts and near this point via
where the coordinates and are the slope coordinates on the -“line of slopes” or the exceptional divisor E that we “bubble” at the point of the blowup. We then extend this algebraic mapping to the new chart, see if there are more base points that we need to blow up and continue this process until the mapping becomes an isomorphism after a finite number of blowups, which is always the case for the discrete Painlevé dynamics. In our example, the full set of the base points consists of the following four cascades of infinitely near points:
We see that, up to linear change of variables and parameter matching,
the point configuration is exactly the one shown in Figure 5. This also gives us the root variables in terms of the parameters , , , and n:
Note that in this case, there are some relations among the root variables .
3.2. Dynamics on the Picard Lattice
Let us now understand how the d-PII dynamics relates to the examples of standard discrete Painlevé equations considered in Section 2.3. With the change of variables given in Equation (14) and identification of parameters given in Equation (15), we can consider the d-PII dynamics on (possibly, a proper sub-family of) the configuration space from the geometric realization above. Direct computation shows that the mapping induces the linear map given by
Hence, we obtain the following action on the symmetry roots and the root variables (which is induced by the pullback and is therefore inverse)
This action is therefore not a translation element of . It is, however, a quasi-translation. Indeed, it is a half of the standard translation described in Equation (8): . This can be seen either directly via the action on the symmetry roots, or by decomposing in terms of the generators of the symmetry group,
and computing using the relations between generators of ,
Definition 3.
Thus, the mapping does not correspond to a non-autonomous additive difference equation, in the sense that the coefficients in the mapping cannot be written as affine functions of n. Indeed, the resulting equation, written for generic parameters constrained by becomes
If we regard the evolution of root variables under in Equation (19) as a system of difference equations for , its general solution is given by
where are constants, subject to if we assume the normalization . The dynamics defined by in Equation (19) can then be written as the equation
with given by Equation (20), and we see that the coefficients of the equation are no longer affine functions of n. The fact that, using a quasi-translation on the full surface family, the root variables allow one to still write down an equation with coefficients being explicit functions of n, was the point of the paper [24].
However, looking at the expressions of the root variables given by Equation (15) from the actual d-PII equation, we observe that, independent of the parameter values, the root variables satisfy the constraint
Restricting to the sub-locus of the surfaces in the whole family whose parameters satisfy this condition recovers the translational nature of the dynamics. Indeed,
and so , . Thus, is a linear and is a constant function of n, exactly as in Equation (1).
Since the evolution of the root variables in Equation (19) decouples into and pairs, we can visualize what happens by looking at them individually. In Figure 6 we show the evolution of for a generic pair of parameters (left) and for a pair satisfying the constraint (right) (see [18]).
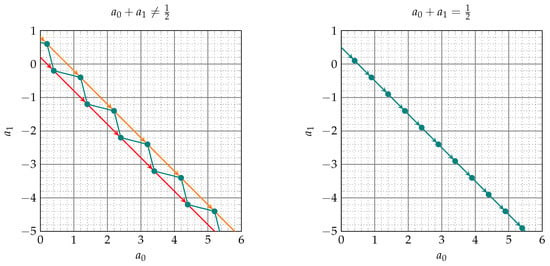
Figure 6.
Parameter dynamics in the plane.
Thus, we are interested in the following question:
We consider this question in the next sub-section.
3.3. The Symmetry Group of the Constrained Family
In this section, we determine the subgroup of such that its action on the root variables fixes the constraint (21). That is,
There are two possibilities:
Since , this parameter condition, on the level of the symmetry roots, becomes
We have the following main result describing the symmetry group of the d-PII equation.
Theorem 1.
The subgroup of compatible with the constraint on root variables coming from d-PII is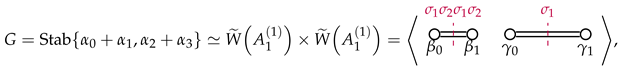 where
where
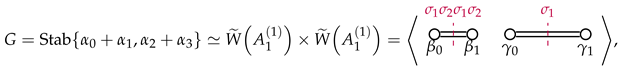 where
whereWe will give two proofs of this below—the first by direct calculation using elementary facts about affine Weyl groups and the second making use of the theory of normalizers of parabolic subgroups in Coxeter groups due to Brink and Howlett [25,26] (see [27] for an introduction to applications of this theory in the context of discrete Painlevé equations).
Before this, let us make some remarks about the description of G as an affine Weyl group and also its realization at the level of . Note that are roots of the root system in since , and the corresponding reflections as automorphisms of are defined in the usual way,
However, and the reflection is only defined on . Nevertheless, this formula does define the action on the -roots, since
Thus, we can decompose this action in terms of the generators,
and so we interpret as on the whole of . Similarly, .
Note that the induced action of the dynamics in Equation (12) on the new roots becomes a translation on the -sub-lattice
and so, formally, . Indeed, with the interpretation of Equation (22), this is exactly what we have,
The fact that the element , which is a quasi-translation in , is a translation element with respect to the structure of G, as an extended affine Weyl group, can be understood in terms of normalizer theory. This will be explained in Remark 1 at the end of this section.
Proof of Theorem 1
(direct computation). Recall from Section 2.2 that we have
and isomorphisms in Equation (23) are realized by
We have , so is a normal subgroup of , and we can choose as a representative of the non-trivial coset. Then, we can write any element of as
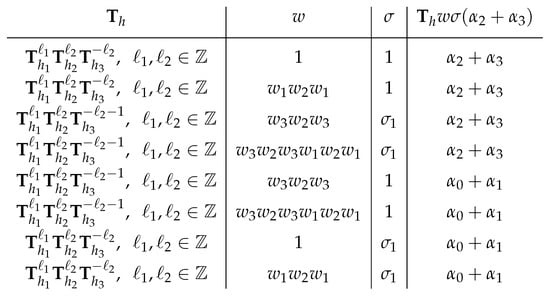
The idea then is for each of the finite number of choices of and w to represent the cosets , with , and , we can compute , and similarly . Since is of order 24, we have 48 choices for . We list the infinite families of elements in the form that exhausts all elements of the stabilizer in Figure 7.

Figure 7.
Elements in G and their action on .
This allows us to see that the stabilizer is generated as follows:
Computing some relations among these, we can identify this by inspection as isomorphic to
This is via the following expressions for the generators of in terms of those of the stabilizer as in Equation (24).
We can also rewrite these in terms of the original generators of as follows:
Verifying that the subgroups and coincide is achieved by direct calculation. □
Before we give the proof of Theorem 1 using normalizer theory, note that this approach is motivated by the following earlier observations: The element that gives rise to the d-PII Equation (13) is a quasi-translation of order two by squared length one, as defined in [16]. That is, , where is a translation associated to a weight of squared length one. Moreover, it was found in Section 3.3 that the problem of finding the symmetries of the d-PIIequation is reduced to finding the setwise stabilizer of in . The stabilizer of an subsystem in an affine Weyl group (or an extension thereof) can be computed largely by methods developed to compute the normalizer of a standard parabolic subgroup of a Coxeter group. We can make use of general results of [25] to compute a set of generators, establish its structure as an extended affine Weyl group with an underlying root system, and then construct an element of quasi-translation of order two by squared length one from considering a translation in the weight lattice of this underlying root system. Finally, we show that this quasi-translation is related to the element by conjugation. That is, the symmetry group of is this extended affine Weyl group under the same conjugation.
Proof of Theorem 1
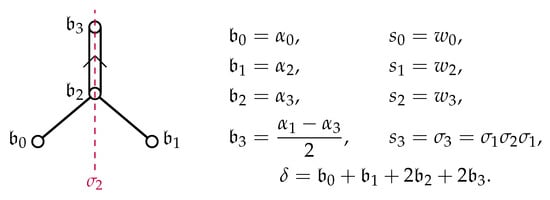
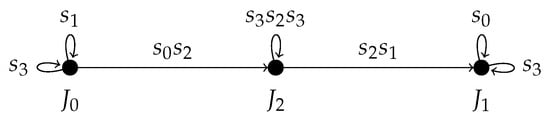

(normalizer theory). When W is an affine Weyl group with a simple system and a root system , a subset defines a standard parabolic subgroup . If can be written as a product of standard parabolic subgroups with , then we call the irreducible components of J. The standard parabolic subgroup is itself a Coxeter group, and we can consider the associated root system . When is finite, the subset J is called spherical, and in this case, the irreducible components of will be finite Weyl groups. The results of [25] that we will use state that the normalizer of in W is given by , where is the setwise stabilizer of J, and, further, provide a way to obtain a presentation of in terms of generators and relations.
To outline the Brink–Howlett construction of the presentation of , we introduce some notations. For a spherical subset , we let denote the unique longest element in with respect to the usual Bruhat ordering on W. This is the ordering of elements by length , defined as the minimal length of an expression for w in terms of simple reflections. When , we regard as the identity element. In the Brink–Howlett framework, disjoint subsets determine a unique element , which, in the cases relevant to us, has the following simple description. Let with be such that is finite. Let and denote by the union of the irreducible components of L, which have a non-empty intersection with I. Then, is spherical and
When consists of only a single simple root, we write , and note that when corresponds to a node of the Dynkin diagram not joined to any of those corresponding to elements of J, we have , since and .
For an affine Weyl group W and , the group presentation of is obtained in the Brink–Howlett framework using a groupoid constructed as follows: Let be the set of W-associates of J. Then, consider the set
This has the structure of a groupoid with (partial) operation . This can be represented as a graph whose vertices correspond to elements of , with vertices connected by an edge when there exists such that . The graph may also have loops, i.e., edges from a vertex to itself, when there exists such that .
Then, paths in the graph correspond to elements of , and elements of correspond to paths beginning and ending at the vertex J:
Further, itself has the structure of a Coxeter group (see [25] for details), which often turns out to be an affine Weyl group or an extension thereof. The above results do not immediately solve our problem of computing and describing G, but they take care of most of it. Some extra work is required, which firstly comes from the fact that is not purely an affine Weyl group and secondly from the fact that we want to compute the setwise stabilizer not of some , but rather of , where J is spherical and is the highest root of . With the first fact in mind, we begin by noting that we can view as the extended affine Weyl group . To do this, take the simple system of the root system in as above and introduce
In particular, from Equations (25) and (4), we see that , and . Then, forms a simple system for a root system of type , with the Cartan matrix given by
Here, is the same bilinear form on as was used for the root system, but note that for B-type root systems, the generalized Cartan matrix is not symmetric. The affine Weyl group
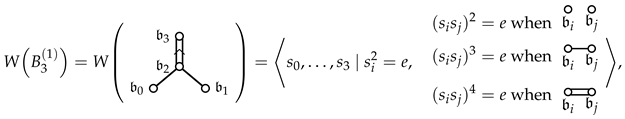 is realized as linear transformations of by the actions of simple reflections The root system here is then , and includes reflections , , which act on by
Note that is a root of the -system, so , but that not all roots of the -system are roots of the -system, and, in particular, that the simple reflection acts on as the automorphism of the Dynkin diagram of the -system. This is why we use notation to distinguish the reflections associated to elements of from the reflections . The single non-trivial automorphism of the Dynkin diagram is given by , and we have , with generators satisfying the defining relations given in Equation (26), as summarized in Figure 8:
The generator of is not accounted for in this extension, and we have . The reason for introducing this description is that it makes it easier to apply the normalizer theory to compute the relevant stabilizer—we can now work with an extension of an affine Weyl group by a smaller Dynkin diagram automorphism group. In addition, the different root lengths of the two root systems in Theorem 1 can be clearly seen in terms of roots of different lengths in the system.
is realized as linear transformations of by the actions of simple reflections The root system here is then , and includes reflections , , which act on by
Note that is a root of the -system, so , but that not all roots of the -system are roots of the -system, and, in particular, that the simple reflection acts on as the automorphism of the Dynkin diagram of the -system. This is why we use notation to distinguish the reflections associated to elements of from the reflections . The single non-trivial automorphism of the Dynkin diagram is given by , and we have , with generators satisfying the defining relations given in Equation (26), as summarized in Figure 8:
The generator of is not accounted for in this extension, and we have . The reason for introducing this description is that it makes it easier to apply the normalizer theory to compute the relevant stabilizer—we can now work with an extension of an affine Weyl group by a smaller Dynkin diagram automorphism group. In addition, the different root lengths of the two root systems in Theorem 1 can be clearly seen in terms of roots of different lengths in the system.
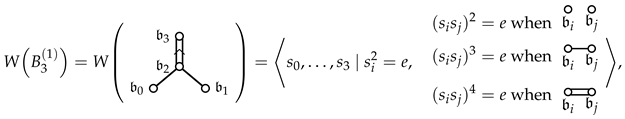 is realized as linear transformations of by the actions of simple reflections The root system here is then , and includes reflections , , which act on by
is realized as linear transformations of by the actions of simple reflections The root system here is then , and includes reflections , , which act on by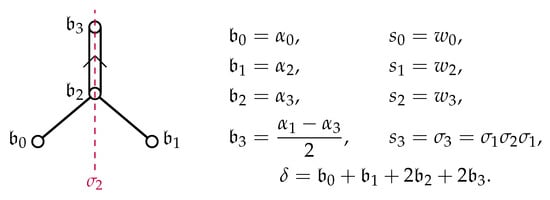
Figure 8.
Extension of to .
Note that we can use an element of , e.g., , to send the set to , so the group G we wish to compute is conjugate to
To compute , we first compute for in the affine Weyl group using the Brink–Howlett method and then find the elements which exchange and . Once this has been achieved, finally, we consider the extra elements coming from the extension of to .
We begin by constructing the graph associated with the groupoid for and . The vertices correspond to W-associates of J, the set of which is
where we note that is not included because is a short root. To determine where the edges are, one proceeds to calculate, for each vertex , the element for each . If , then one draws an edge from to , labeled by the element . The graph for the case at hand is given in Figure 9.

Figure 9.
Graph for the groupoid for and .
It will be convenient to denote paths in the graph according to the vertices through which they pass read from right to left, e.g., for the path from to . To account for loops, we use the symbol for the element itself, e.g., , to indicate the loop from to itself via . For a path p in this notation, we denote by the composition of the elements corresponding to the edges and loops in the path, e.g., for a path that starts at , traverses a loop via , and then goes to via .
From Figure 9, we see that the elements corresponding to paths starting and ending at can be obtained as compositions of the following elements and their inverses:
where we have identified these as reflections associated to some roots .
Invoking the Brink–Howlett result that consists of elements corresponding to paths starting and ending at J, we have a set of generators. Since , we have
Each of the subgroups , are individually isomorphic to copies of defined using simple systems and as groups of linear transformations of the subspaces of spanned by these. We want to describe the quasi-translation elements of , such as that corresponding to the d-PII dynamics, as translation elements with respect to the affine Weyl group structure of . In the case of the non-simply laced type of the ambient group, as we have here with , this requires some care.
We introduce elements and of to play the roles of simple systems for the two copies and of in . Since is a long root of , we take , but for the short root , we instead introduce , and . Even though is not an element of , by use of the notation, we still write for the reflection . This scaling is necessary for the description of quasi-translation elements of in terms of weights from the affine Weyl group structure of to be compatible with that of translation elements in terms of the weights of the finite system, which we will say more about in Remark 1 below. It also demonstrates the origin of the different root lengths of the -type systems in Theorem 1. We summarize the - and -systems, as well as the relations to the - and -systems in Figure 10.

Figure 10.
Root system of type .
We next consider the setwise stabilizer in of not just but also of . This is straightforward and we need only to add a single generator since , where g is any element such that . To see this, note that any element of leaves invariant, so if are such that , then . We can find such an element immediately as , which acts on the as
Adding this element as a generator to the description of in Equation (28), we see it causes the addition of a Dynkin diagram automorphism , as indicated in Figure 10, since . We then have
Lastly, we have to consider the elements of which have not been accounted for as part of . First, we consider the extension of to by adding the generator , corresponding to the automorphism of the Dynkin diagram that permutes the simple roots according to . We see that does not add any new elements to the stabilizer beyond already found, since . Finally, considering the extra Dynkin diagram automorphism which is not accounted for in , we see that this does indeed add a new generator to the stabilizer. We have , and , so because is an involution, we have . To determine whether this extension adds any elements to the setwise stabilizer of , we just have to determine whether there exist such that . In this case, we would obtain a new element such that . This does indeed happen. For example, with , and we obtain an element corresponding to the remaining automorphism of the diagram . Note that adding as a generator to accounts for all of the set . This is because if , , with , are such that , then , and also already includes all elements of that interchange and .
We then arrive at the desired description of the setwise stabilizer
where expressions for the generators in terms of those of and are collected below:
Finally, we conjugate the generators of by to obtain the description of G in Theorem 1 via
and we are done. □
Remark 1.
For the ω-system given in Figure 10 (the underlying root system for found earlier), we choose instead of using , which also gives a set of simple roots for a root system of type, for reasons given as follows. For the root system with simple roots (where ) which gives , the fundamental weight of the underlying root system is defined by
where is the simple coroot of the underlying finite root system. A “translation" by in is given by , which is not a translation in since not only permutes the set , but it also permutes the set by construction. That is, is a quasi-translation. Earlier, we mentioned that we want to construct a quasi-translation of order two by squared length of one. This gives us the condition,
Choosing , we have the simple coroot , and . That is, we have . In fact
in terms of the fundamental weights of the root system. One can check that , moreover we have . That is, is a quasi-translation of order two by squared length of one. Moreover, it is related to under conjugation by :
4. Relation with the Discrete Painlevé XXXIV Equation and Recurrence Coefficients for Freud Unitary Ensembles
It is possible to further constrain the parameters in the d-PII dynamics. In this section, we describe one such example that recently appeared in studying gap probabilities of Freud unitary ensembles [20]
Remark 2.
In the next few paragraphs, we use the notation of that paper to make it easier to follow. Unfortunately, it clashes with some of our prior notations. The meaning is clear from the context and we change notation once we arrive at the discrete Painlevé equation in question.
To study the gap probability that the interval is free of eigenvalues of the Freud unitary ensemble, the authors consider the weight function of the form , where , , and is the usual characteristic function of the interval I. Then, the gap probability can be expressed in terms of Hankel determinants as
where
and is the usual square -norm of monic orthogonal polynomials,
These monic orthogonal polynomials obey a recurrence relation
where the recurrence coefficient satisfies
The recurrence coefficients are the main objects of study in [20], where it is shown that for they satisfy the equations in the so-called discrete Painlevé XXXIV hierarchy defined in [28]. We are interested in the case when the weight is the usual Gaussian weight. Then, the recurrence coefficients satisfy the equation
see ([20], Theorem 2.1). This difference equation becomes the d-PXXXIV equation
of ([28], (4.2)), where and the parameters are
It turns out that Equation (29) is just a different geometric realization of the same abstract d-PII Equation (18), but the parameter values in Equation (30) result in an appearance of a so-called nodal curve, which further restricts the size of the symmetry group.
To see this, we first rewrite Equation (29) as a mapping by putting , , etc., to get
The base points of this mapping, together with its inverse, are
and the resulting point configuration and its resolution are shown in Figure 11, where we use to denote the exceptional divisor of the blowup at .
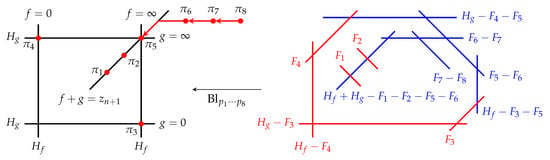
Figure 11.
The Sakai surface for the d-PXXXIV equation.
Looking at the configuration of -curves in Figure 11 we immediately see that this is indeed a -surface. In fact, the change of basis on the Picard lattices given by
results in the following matching of the surface roots,
and the symmetry roots,
The symplectic form for this point configuration is
and the root variables are
and we see again that the constraint in Equation (21) holds, .
The mapping given by Equation (31) induces the mapping on the Picard lattice given by
Hence, we obtain exactly the same action on the symmetry roots and the root variables as in Equations (16) and (17),
In fact, d-PII discrete Painlevé Equation (1) and d-PXXXIV Equation (29) are related by the following birational change of variables and parameter identification:
However, for the Freud weight, parameters take very special values given in Equation (30) and the corresponding root variables become
Note that we now have , which is the nodal curve condition for the symmetry root . Indeed, with these values of parameters, the base points and coalesce along the line into the point . A more careful computation, in fact, shows that we obtain a cascade of two infinitely close points (that we still denote by ):
The resulting Sakai surface is shown in Figure 12, and the nodal curve is a -curve disjoint from the anti-canonical divisor .
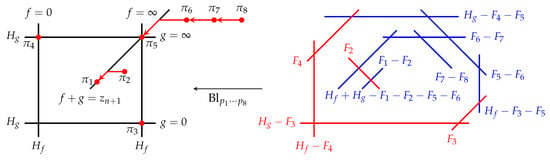
Figure 12.
The Sakai surface for the constrained d-PXXXIV equation.
Thus, in addition to fixing the constraint Equation (21), we now also need to fix the nodal curve condition , which further restricts the symmetry group of the equation.
Theorem 2.
The subgroup of compatible with the constraint
on root variables is
Proof.
We already have from Theorem 1 that the subgroup of is compatible with the constraint is . To find the additional condition on the actions of symmetries on necessary to respect the additional constraint , we require geometric considerations. The need for these considerations arises from the fact that the additional constraint corresponds to the value of the period map on a root of the system being 0, and thus implies the existence of the nodal curve (see [11] Prop. 22) whereas the constraint does not correspond to any nodal curves in this way.
While on the level of root variables the actions of some elements may respect the constraint algebraically, on the level of they might not respect the effectiveness of the divisor classes, and hence do not give automorphisms of the sub-family of surfaces defined by the existence of this nodal curve. For example, the action of the reflection on root variables is such that , so it preserves the subset , but on the level of , it does not preserve the effectiveness of the divisor classes on the surfaces with nodal curves, so its Cremona action does not restrict to the sub-family. A generic surface in the sub-family defined by the constraints in Equation (32) has only a single nodal curve corresponding to the class . Symmetries compatible with these constraints must preserve the subset of corresponding to the set of nodal curves, so we arrive at the description of the symmetry subgroup H of the sub-family of surfaces defined by the constraints in Equation (32) as the elements of G that fix .
From the description of , we see that the only element of the first factor that fixes is the identity. To see this, note that , where is the quasi-translation in corresponding to a translation in , which generates the subgroup of translations associated to the weight lattice of the underlying root system. On the other hand, every element of fixes , so we have the result. □
5. Discussion
In this paper, we advocate the point of view that what should be called the symmetry group of a discrete Painlevé equation is the group of symmetries of the surface (sub-)family forming its configuration space, and the translation elements of which generate the resulting dynamics. In particular, it is an extended affine Weyl group whose birational representation on the surface sub-family generates the equation. For many discrete Painlevé equations that appear in the literature, this symmetry group will not be the full, generic symmetry group attached to the surface type of their configuration space as given in Sakai’s classification, but rather a subgroup of that generic symmetry group.
We explain this crucial difference using a specific example of a well-known d-PII equation that does not correspond to a genuine translation element of the generic symmetry group. We identify the surface sub-family that is left invariant under the dynamics defined by the equation and then calculate its symmetry group in two different ways: first by a brute force calculation and then by using elements from the normalizer theory of parabolic subgroups of Coxeter groups. It is important to emphasize here that the first approach—the brute force calculation—will become unwieldy and ultimately unfeasible for equations with higher dimensional (symmetry) root lattices. The normalizer theory-based proof, on the contrary, is almost entirely algorithmic and further provides insight into the nature of quasi-translations in the generic symmetry group as translations in the relevant symmetry subgroup.
With respect to the comparison of the two methods, we make the following additional remarks. The methods based on direct calculation and normalizer theory will yield the same result when applied to compute the setwise stabilizer in an extended affine Weyl group of a sub-root system of the whole root system on which the group acts. Once the question of computing the symmetry group for a given discrete Painlevé equation is rephrased as that of computing such a setwise stabilizer, the problem is solved by the normalizer theory, with minor extra work required when the sub-root system is of affine type and when the larger group is a fully extended affine Weyl group, and thus not immediately a Coxeter group, as we have explained in the Proof of Theorem 1 (normalizer theory) above. If the subset of roots that needs to be stabilized is not directly a root system, then further considerations outside of the normalizer theory would be required.
We end the paper with a similar analysis for a sub-case of our main example, which arises in the study of gap probabilities for Freud unitary ensembles, and the symmetry group of which is even further restricted due to the appearance of a nodal curve on the surface on which the equation is regularized.
The approach that we have presented is, of course, not restricted to the d-PII equation. At present, we are studying some other examples that have parameter constraints and special symmetry groups, with the aim of creating a refined classification scheme for discrete Painlevé equations that takes these subcases into account. We also plan to study the effects of reducing the full symmetry group on the structure and behavior of solutions, especially the special rational, algebraic, and hypergeometric-type special function solutions, as well as the structure of the tau functions.
Author Contributions
All four authors contributed equally to the conceptualization, methodology, formal analysis, investigation, original draft preparation, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
A.S research was funded by the Japan Society for the Promotion of Science (JSPS) KAKENHI grant 24K22843. R.W. research was funded by the JSPS KAKENHI grants 22H01130 and 23K22401. The APC was waived.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
A.S. and R.W. would like to thank the Japan Society for the Promotion of Science (JSPS) for financial support through the KAKENHI grants. A.D. would like to acknowledge support from the BIMSA start-up fund. Y.S. would like to thank R. B. Howlett and N. Nakazono for the enlightening discussions.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Conte, R.; Musette, M. The Painlevé Handbook, 2nd ed.; Mathematical Physics Studies; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Conte, R. (Ed.) The Painlevé Property; CRM Series in Mathematical Physics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Fokas, A.S.; Its, A.R.; Kapaev, A.A.; Novokshenov, V.Y. Painlevé Transcendents; Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2006; Volume 128. [Google Scholar]
- Its, A.R.; Kitaev, A.V.; Fokas, A.S. Matrix models of two-dimensional quantum gravity, and isomonodromic solutions of Painlevé “discrete equations”. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 1991, 187, 3–30, 171, 174. [Google Scholar]
- Brézin, É.; Kazakov, V.A. Exactly solvable field theories of closed strings. Phys. Lett. B 1990, 236, 144–150. [Google Scholar] [CrossRef]
- Gross, D.J.; Migdal, A.A. A nonperturbative treatment of two-dimensional quantum gravity. Nuclear Phys. B 1990, 340, 333–365. [Google Scholar]
- Nijhoff, F.W.; Papageorgiou, V.G. Similarity reductions of integrable lattices and discrete analogues of the Painlevé II equation. Phys. Lett. A 1991, 153, 337–344. [Google Scholar]
- Papageorgiou, V.G.; Nijhoff, F.W.; Grammaticos, B.; Ramani, A. Isomonodromic deformation problems for discrete analogues of Painlevé equations. Phys. Lett. A 1992, 164, 57–64. [Google Scholar]
- Grammaticos, B.; Ramani, A. Discrete Painlevé Equations: A Review; Discrete Integrable Systems; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 644, pp. 245–321. [Google Scholar]
- Shohat, J. A differential equation for orthogonal polynomials. Duke Math. J. 1939, 5, 401–417. [Google Scholar] [CrossRef]
- Sakai, H. Rational surfaces associated with affine root systems and geometry of the Painlevé equations. Comm. Math. Phys. 2001, 220, 165–229. [Google Scholar] [CrossRef]
- Okamoto, K. Sur les feuilletages associés aux équations du second ordre à points critiques fixes de P. Painlevé. Jpn. J. Math. (N.S.) 1979, 5, 1–79. [Google Scholar]
- Kajiwara, K.; Noumi, M.; Yamada, Y. Geometric aspects of Painlevé equations. J. Phys. A 2017, 50, 073001. [Google Scholar]
- Atkinson, J.; Howes, P.; Joshi, N.; Nakazono, N. Geometry of an elliptic difference equation related to Q4. J. Lond. Math. Soc. 2016, 93, 763–784. [Google Scholar]
- Carstea, A.S.; Dzhamay, A.; Takenawa, T. Fiber-dependent deautonomization of integrable 2D mappings and discrete Painlevé equations. J. Phys. A 2017, 50, 405202. [Google Scholar] [CrossRef]
- Shi, Y. Two variations on (A3 × A1 × A1)(1) type discrete Painlevé equations. Proc. A. 2019, 475, 20190299. [Google Scholar]
- Takenawa, T. Weyl group symmetry of type D5(1) in the q-Painlevé V equation. Funkcial. Ekvac. 2003, 46, 173–186. [Google Scholar] [CrossRef]
- Kajiwara, K.; Nakazono, N.; Tsuda, T. Projective reduction of the discrete Painlevé system of type (A2 + A1)(1). Int. Math. Res. Not. IMRN 2011, 4, 930–966. [Google Scholar] [CrossRef]
- Periwal, V.; Shevitz, D. Unitary-matrix models as exactly solvable string theories. Phys. Rev. Lett. 1990, 64, 1326–1329. [Google Scholar] [CrossRef]
- Min, C.; Wang, L. The discrete Painlevé XXXIV hierarchy arising from the gap probability distributions of Freud random matrix ensembles. arXiv 2025, arXiv:2412.18782. [Google Scholar]
- Chen, Y.; Dzhamay, A.; Hu, J. Gap Probabilities in the Laguerre Unitary Ensemble and discrete Painlevé equations. J. Phys. A 2020, 53, 354003. [Google Scholar]
- Dzhamay, A.; Filipuk, G.; Stokes, A. Recurrence coefficients for discrete orthogonal polynomials with hypergeometric weight and discrete Painlevé equations. J. Phys. A 2020, 53, 495201. [Google Scholar] [CrossRef]
- Bourbaki, N.; Lie Groups and Lie Algebras. Elements of Mathematics; Springer: Berlin/Heidelberg, Germany, 2002; Chapters 4–6. [Google Scholar]
- Stokes, A. Full-parameter discrete Painlevé systems from non-translational Cremona isometries. J. Phys. A 2018, 51, 495206. [Google Scholar] [CrossRef]
- Brink, B.; Howlett, R.B. Normalizers of parabolic subgroups in Coxeter groups. Invent. Math. 1999, 136, 323–351. [Google Scholar] [CrossRef]
- Howlett, R.B. Normalizers of parabolic subgroups of reflection groups. J. Lond. Math. Soc. 1980, 21, 62–80. [Google Scholar]
- Shi, Y. Translations in affine Weyl groups and their applications in discrete integrable systems. arXiv 2022, arXiv:2210.13736. [Google Scholar]
- Cresswell, C.; Joshi, N. The discrete first, second and thirty-fourth Painlevé hierarchies. J. Phys. A 1999, 32, 655–669. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).