Zappa–Szép Groupoids of Inverse Semigroups and an Alternative Proof of Billhardt’s λ-Semidirect Products

Abstract

The aim of this paper is to introduce and study Zappa-Szép groupoids of inverse semigroups. Some properties of such kinds of groupoids are explored. As an application, an alternative proof of Billhardt’s $\lambda$-semidirect products is given. We finish with several examples that highlight the versatility and applicability of Zappa-Szép groupoids in various types of inverse semigroups.

1. Introduction

Direct, semidirect, and Zappa–Szép products offer methods for decomposing algebraic structures, each serving as a natural extension of the one before it. The Zappa–Szép products for semigroups involve mutual actions between two semigroups, which are closely linked to the operations of Mealy machines, or automata that produce output [1]. The Zappa–Szép products of semigroups were thoroughly developed by Kunze [2], who provided applications of these products to translational hulls, Bruck–Reilly extensions, and Rees matrix semigroups. Recent advancements in Zappa–Szép products [3,4], show that inverse semigroups are now a vibrant area of research. As they provide a unified framework for addressing various algebraic questions, they are set to remain a crucial subject in the field. Neumann [5] was the first to adopt the term semidirect product to formulate wreath products of semigroups. An entire depiction of semidirect products of monoids that are inverse monoids was given by Nico [6]. A semidirect product obtained by two inverse semigroups is not necessarily inverse. In ref. [7], Billhardt bypasses this predicament by adjusting the definition of semidirect products in the inverse case to attain the $\lambda$-semidirect products. The $\lambda$-semidirect product of inverse semigroups is now an inverse semigroup. In ref. [8], Billhardt also applied this outcome to the left ample case in which a component is a semilattice. In addition, the same approach was applied to the $\lambda$-semidirect product of semilattices as well as a left restriction semigroup [9]. In ref. [10], for given two restriction semigroups S and T, the author demonstrated that $\lambda$-semidirect product is also liable to modify the defined actions by specific conditions.

The Zappa–Szép product of groups was developed by G. Zappa in [11] as a generalization of the semidirect product of groups. Brin [12] extended the applicability of the Zappa–Szép products to multiplicative structures more general than groups with emphasis on categories and monoids. The texts [1,13,14] mainly investigated the Zappa–Szép products of groups of several classes of semigroups.

In this paper, we investigate the Zappa–Szép products of inverse semigroups by the “groupoid approach”. We pick out a subset of a Zappa–Szép products of two inverse semigroups and show that with restriction of the binary operation, the given subset is a groupoid. By using this groupoid and Ehresmann–Schein–Nambooripad Theorem of inverse semigroups given in [15], an alternative proof of Billhardt’s $\lambda$-semidirect products explored in [7] is obtained. Terminologies and notations not given in the paper can be found in [15,16].

There exists a close relationship between inverse semigroups and inductive groupoids. Schein made this relationship clear when he established that to any inverse semigroup, there correlates a corresponding inductive groupoid and the contra is true [10]. Theorem 3.4. After, Nambooripad made further contributions and assumed Schein’s results to the regular case and put them in the framework of an isomorphism among categories. Lawson later collectively joined these results in one theorem in [15] and termed it Ehresmann–Schein–Nambooripad theorem to represent the diversified origin of all its components. We shall further explain this correspondence.

1.1. From Inverse Semigroups to Inductive Groupoids

In order to obtain a groupoid from an inverse semigroup, we need to identify the following: The vertex set, the set of arrows, the start and finish of an arrow, the identity arrow, the composition of arrows, and the inverse of an arrow. This is achieved as follows: Let S be an inverse semigroup with the partial order relation, with meet semilattices. of idempotents $E\left(S\right)$. We associate to S a directed graph whose vertices are labeled by the idempotents of S and whose arrows are labeled by the elements of S such that for each arrow s the idempotent $s{s}^{-1}=$ dom s (i.e., where the arrow begins) and the idempotent $s^{-1}s=$ cod s (i.e., where the arrow finishes). An idempotent $e\in E\left(S\right)$ determines the identity arrow at $e.$ The arrow representing $s^{-1}$ is simply the opposite of the one representing s since dom $s^{-1}=$ cod s and cod $s^{-1}=$ dom $s.$ If $s,t\in S$ are any two elements of S such that cod $s=s^{-1}s=t{t}^{-1}=$ dom t i.e., the arrow t starts at the ends of the arrow $s,$ then the composite arrow $s\circ t:$ dom $s⟼$ cod t is defined such that $s\circ t=st\in S$ (i.e., $s\circ t=st$ only when the corresponding arrows match head-to-tail) such that $st$ starts at $\left(st\right){\left(st\right)}^{-1}=st{t}^{-1}{s}^{-1}=s{s}^{-1}s{s}^{-1}=s{s}^{-1}=$ dom $s,$ and finishes at ${\left(st\right)}^{-1}\left(st\right)=t^{-1}{s}^{-1}st=t^{-1}t{t}^{-1}t=t^{-1}t=$ cod $t,$ and then associativity follows from associativity in S. Thus, we have a groupoid denoted by $G\left(S\right)$. The natural order on S endows the groupoid $G\left(S\right)$ with the structure of an ordered groupoid. To see this we verify the axioms $\left(OG1\right),\left(OG2\right)$ and $\left(OG3\right)$. If $s\le t$ this implies that $s=ft$ for some idempotent f. Then $s^{-1}=t^{-1}f.$ Then $s^{-1}\le t^{-1}.$ Hence $\left(OG1\right)$ holds. Let $x\le y,u\le v$. Let the composition $xu$ and $yv$ are defined, then there are idempotents e and f such that $x=ye$ and $u=vf$. Thus, $xu=yevf$. Since $ev=vi$ for some idempotent i, we have $xu=yv\left(if\right)$, and so $xu\le yv.$ Thus, $\left(OG2\right)$ holds. Let $s\in S$ and e be an idempotent such that $e\le s{s}^{-1}.$ Then $\left(e\mid s\right)=es$ such that $es\le s$ from the definition of the partial order. Also, $\left(es\right){\left(es\right)}^{-1}=es{s}^{-1}e=e.$ Now let $b\le s$ be such that $b{b}^{-1}=e,$ so we have $b=b{b}^{-1}s=es.$ Then $\left(e\mid s\right)=es$ is unique. Hence $\left(OG3\right)$ hold. Similar proof for ${\left(OG3\right)}^{*}$. Since the set of idempotents $E\left(S\right)$ form a meet semilattices., then $G\left(S\right)$ is an inductive groupoid.

1.2. From Inductive Groupoids to Inverse Semigroups

Given an inductive groupoid $\left(G,\le \right)$ the partial composition of arrows on G may be extended to an everywhere defined composition that gives G the structure of an inverse semigroup $S\left(G\right).$ This can be achieved as follows. We construct the inverse semigroup from the inductive groupoid. The elements of the inverse semigroup $S\left(G\right)$ are the arrows in the inductive groupoid G and since in the groupoid G for every arrow s there is an inverse arrow $s^{-1}$ such that $\left(s{s}^{-1}\right)s=s$ and $s^{-1}\left(s{s}^{-1}\right)=s^{-1},$ then $s^{-1}$ will be the inverse of s. If the arrows of the groupoid G match up, then we know how to compose them, but if they do not match up, we do the following. Let $x,y\in G$ and let $e=x^{-1}x\wedge y{y}^{-1}$ (the greatest lower bound). Put $x⊛y=\left(x\mid e\right)\left(e\mid y\right).$ The pseudoproduct of x and y (where $\left(x\mid e\right)$ is the corestriction of x to e and $\left(e\mid y\right)$ is the restriction of y to e) and thus x and y do match up in $G.$ As in Figure 1.

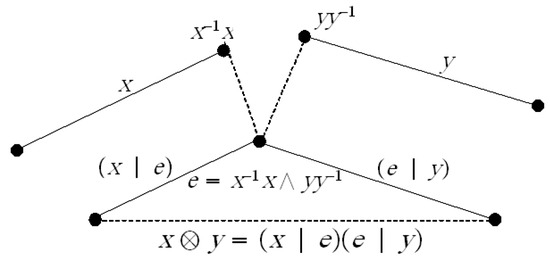
Figure 1. The pseudoproduct of x and $y$.

The next result provides a neat, order-theoretic way of viewing the pseudoproduct.

Proposition 1

([15]). Let S be an ordered groupoid. For each pair $x,y\in S$ put

$$⟨x,y⟩=\left\{\left(x^{\prime },y^{\prime }\right)\in S\times S:x^{\prime }{x}^{\prime -1}=y^{{\prime }^{-1}}{y}^{\prime } \mathrm{and} x^{\prime }\le x \mathrm{and} y^{\prime }\le y\right\}$$

regarded as a subset of the ordered set $S\times S$. Then $x⊛y$ exists if and only if there is a maximum element $(x^{\prime },y^{\prime })$ of $⟨x,y⟩.$ In which case, $x⊛y=x^{\prime }{y}^{\prime }.$

It shown in [15] that $\left(G,⊛\right)$ is an inverse semigroup that is

• The pseudoproduct $x⊛y$ of x and y is associative.
• $\left(G,⊛\right)$ is a regular semigroup, since if $x,y\in S$ and $xy$ exists in the groupoid $G$ then $xy=x⊛y.$ However, for each element $x\in S$ we have $x=x{x}^{-1}x$ and $x^{-1}=x^{-1}x{x}^{-1}.$
• The idempotents of $\left(G,⊛\right)$ are precisely the identities of $\left(G,.\right).$ Now let e and f be two idempotents of $\left(G,⊛\right).$ If $e\le f$ then $\left(e\mid f\right)=$$\left(f\mid e\right)=e,$ since $\left(e\mid f\right)$ is the unique restriction of f to e. As restriction is unique, this means only one element of G can be less than f with domain e. Now $\left(e\mid f\right)\le f$ and dom $\left(e\mid f\right)=e$ but $e\le f$ and dom $e=e$ so $e=\left(e\mid f\right).$ Similarly for $\left(f\mid e\right)$ with codomain not domain. Thus, the idempotents of $\left(G,⊛\right)$ commute.

2. Zappa–Szép Groupoids

In this section, we shall construct Zappa–Szép groupoids from the Zappa–Szép products of inverse semigroups. The purpose of this section is to provide an overview and a deeper understanding of the construction and basic properties of Zappa–Szép groupoids derived from Zappa–Szép products of inverse semigroups. In this analysis, we summarize the Zappa–Szép product concept, emphasizing its significance and its characteristics. Our next step will be to systematically construct groupoids based on these products, highlighting the mathematical implications and methods involved. These groupoids are described structurally and functionally, demonstrating their theoretical importance and laying the foundation for further applications in semigroup theory. Through detailed discussions and rigorous proofs, we aim to provide a comprehensive understanding of how these groupoids can be characterized and utilized within broader mathematical contexts. We first recall the notion of the Zappa–Szép product of two inverse semigroups and give some necessary properties of Zappa–Szép products of inverse semigroups.

Suppose that we have semigroups A and B and assume we have maps

$$A\times B\to A,(a,b)\mapsto b·a \mathsf{a}\mathsf{n}\mathsf{d} A\times B\to B,(a,b)\mapsto b^a$$

satisfying the following conditions: For all $a,a^{\prime }\in A$ and $b,b^{\prime }\in B$,

• (ZS1) $b{b}^{\prime }·a=b·(b^{\prime }·a),$
• (ZS2) $b·(a{a}^{\prime a}·a^{\prime }),$
• (ZS3)${\left(b^a\right)}^{a^{\prime }}=b^{a{a}^{\prime }},$
• (ZS4) $(b{b}^{\prime a}=b^{b^{\prime }·a}{b}^{\prime a}.$

Define a binary operation on $A\times B$ by

$$(a,b)(a^{\prime },b^{\prime })=(a(b·a^{\prime a^{\prime }}{b}^{\prime }).$$

Then, $A\times B$ forms a semigroup. We call this semigroup the Zappa–Szép product of A and B and denote it by $A\bowtie B$.

Lemma 1.

Suppose that S and T are two inverse semigroups and $a,b,c\in S$, $t,u,v\in T$. Then in $S\bowtie T$, we have the following results:

(i) 

If $t^{b{b}^{-1}}=t$, then ${(t·b)}^{-1}=t^b·b^{-1}$.

(ii) 

If $t^{-1}t·b=b$, then ${\left(t^b\right)}^{-1}={\left(t^{-1}\right)}^{t·b}$.

(iii) 

If $a^{-1}a$ acts trivially on both $t^{-1}$ and $t{t}^{-1}$ and $t{t}^{-1}·a^{-1}a=a^{-1}a$, then $t^{(t^{-1}·a^{-1}a)}=t$.

(iv) 

If $u{u}^{-1}$ acts trivially on $b^{-1}$ and on $b^{-1}b,$ and $b^{-1}b$ acts trivially on $u{u}^{-1}$, then $b={\left(u{u}^{-1}\right)}^{b^{-1}}·b.$

Proof. 

For (i), by (ZS2), we compute

$$(t·b)(t^b·b^{-1})(t·b)=(t·b{b}^{-1})(t·b)=(t·b{b}^{-1})(t^{b{b}^{-1}}·b)=t·b,$$

and

$$(t^b·b^{-1})(t·b)(t^b·b^{-1})=(t^b·b^{-1})(t·b{b}^{-1})=(t^b·b^{-1})(t^{b{b}^{-1}}·b{b}^{-1})=t^b·b^{-1}.$$

Thus, ${(t·b)}^{-1}=t^b·b^{-1}.$

For (ii), we have

$$t^b{\left(t^{-1}\right)}^{(t·b)}{t}^b=t^b{\left(t^{-1}t\right)}^b=t^{(t^{-1}t·b)}{\left(t^{-1}t\right)}^b={\left(t{t}^{-1}t\right)}^b=t^b,$$

and

$${\left(t^{-1}\right)}^{(t·b)}{t}^b{\left(t^{-1}\right)}^{(t·b)}={\left(t^{-1}t\right)}^b{\left(t^{-1}\right)}^{(t·b)}={\left(t^{-1}t{t}^{-1}\right)}^{(t·b)}={\left(t^{-1}\right)}^{(t·b)}.$$

Therefore ${\left(t^b\right)}^{-1}={\left(t^{-1}\right)}^{t·b}.$

For (iii), we have

$$t^{-1}=t^{-1}t{t}^{-1}=t^{-1}{\left(t{t}^{-1}\right)}^{a^{-1}a}=t^{-1}{t}^{(t^{-1}·a^{-1}a)}{t}^{-1},$$

and

$$\begin{array}{cc}\hfill \left(t^{(t^{-1}·a^{-1}a)}\right)t^{-1}\left(t^{(t^{-1}·a^{-1}a)}\right)& =\left(t^{(t^{-1}·a^{-1}a)}\right){\left(t^{-1}\right)}^{a^{-1}a}\left(t^{(t^{-1}·a^{-1}a)}\right)\hfill \\ \hfill & =\left({\left(t{t}^{-1}\right)}^{a^{-1}a}\right)\left(t^{(t^{-1}·a^{-1}a)}\right)\hfill \\ \hfill & =\left({\left(t{t}^{-1}\right)}^{(t{t}^{-1}·a^{-1}a)}\right)\left(t^{(t^{-1}·a^{-1}a)}\right)\hfill \\ \hfill & =t^{(t^{-1}·a^{-1}a)}.\hfill \end{array}$$

Hence $t^{(t^{-1}·a^{-1}a)}=t.$

For (iv), we have

$$b^{-1}=b^{-1}b{b}^{-1}=(u{u}^{-1}·b^{-1}b)b^{-1}=b^{-1}({\left(u{u}^{-1}\right)}^{b^{-1}}·b)b^{-1},$$

and

$$\begin{array}{cc}\hfill ({\left(u{u}^{-1}\right)}^{b^{-1}}·b)b^{-1}({\left(u{u}^{-1}\right)}^{b^{-1}}·b)& =({\left(u{u}^{-1}\right)}^{b^{-1}}·b)(u{u}^{-1}·b^{-1})({\left(u{u}^{-1}\right)}^{b^{-1}}·b)\hfill \\ \hfill & =({\left(u{u}^{-1}\right)}^{b^{-1}}·b)(u{u}^{-1}·b^{-1}b)\hfill \\ \hfill & =({\left(u{u}^{-1}\right)}^{b^{-1}}·b)({\left(u{u}^{-1}\right)}^{b^{-1}b}·b^{-1}b)\hfill \\ \hfill & ={\left(u{u}^{-1}\right)}^{b^{-1}}·b.\hfill \end{array}$$

Hence $b={\left(u{u}^{-1}\right)}^{b^{-1}}·b.$ □

Now we consider the following subset

$$B_{\bowtie }\left(P\right)=\left\{\begin{array}{c}(a,t)\in S\times T:t{t}^{-1}·a^{-1}=a^{-1},t{t}^{-1}·\left(a^{-1}a\right)=a^{-1}a,\\ {\left(t^{-1}\right)}^{a^{-1}a}=t^{-1},{\left(t{t}^{-1}\right)}^{a^{-1}a}=t{t}^{-1}\end{array}\right\}$$

of the Zappa–Szép product $P=S\bowtie T$ of two inverse semigroups S and T.

Proposition 2.

If $(a,t),(b,u)\in B_{\bowtie }\left(P\right)$ such that

$$t^{-1}·a^{-1}a=b{b}^{-1} and t^{-1}t={\left(u{u}^{-1}\right)}^{b^{-1}}.$$

(1) 

$a(t·b){(t·b)}^{-1}{a}^{-1}=a{a}^{-1}$.

(2) 

${\left[t^{b}u{u}^{-1}{\left(t^b\right)}^{-1}\right]}^{{(t·b)}^{-1}{a}^{-1}}={\left(t{t}^{-1}\right)}^{a^{-1}}$.

(3) 

$u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u=u^{-1}u$.

(4) 

$u^{-1}{\left(t^b\right)}^{-1}·[{(t·b)}^{-1}{a}^{-1}a (t·b)]=u^{-1}·b{b}^{-1}$.

Proof. 

By Lemma 1-(iii), we have $t^{b{b}^{-1}}=t^{(t^{-1}·a^{-1}a)}=t$ and so by Lemma 1-(i), we have

$$a(t·b){(t·b)}^{-1}{a}^{-1}=a(t·b)(t^b·b^{-1})a^{-1}=a(t·b{b}^{-1})a^{-1}=a{a}^{-1},$$

So $\left(1\right)$ holds. We also have

$$t^{b}u{u}^{-1}{\left(t^b\right)}^{-1}=t^b{\left(t^{-1}t\right)}^b{\left(t^b\right)}^{-1}=t^b{\left(t^{-1}\right)}^{t·b}{t}^b{\left(t^b\right)}^{-1}$$

$$=t^b{\left(t^{-1}\right)}^{t·b}{t}^b{\left(t^{-1}\right)}^{t·b}=t^b{\left(t^{-1}\right)}^{t·b}=t^{\left(t^{-1}t\right)·b}{\left(t^{-1}\right)}^{t·b}={\left(t{t}^{-1}\right)}^{t·b}.$$

Then

$${\left(t{t}^{-1}\right)}^{(t·b){(t·b)}^{-1}}={\left(t{t}^{-1}\right)}^{(t·b)(t^b·b^{-1})}={\left(t{t}^{-1}\right)}^{t·b{b}^{-1}}={\left(t{t}^{-1}\right)}^{a^{-1}a}=t{t}^{-1},$$

and so $\left(2\right)$ holds.

Now by Lemma 1-(ii), $t^{-1}t·b=b$ and so by Lemma 1-(iv) we have

$$u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u=u^{-1}{\left(t^{-1}t\right)}^{b}u=u^{-1}\left(u{u}^{-1}\right)u=u^{-1}u,$$

and $\left(3\right)$ holds.

For $\left(4\right),$ using the fact that $t^{b{b}^{-1}}=t,$ we have

$$\begin{array}{cc}\hfill {(t·b)}^{-1}{a}^{-1}a(t·b)& ={(t·b)}^{-1}(t·b{b}^{-1})(t·b)={(t·b)}^{-1}(t·b)(t^b·b^{-1})(t·b)\hfill \\ \hfill & ={(t·b)}^{-1}(t·b)=(t^b·b^{-1})(t·b)=t^b·b^{-1}b,\hfill \end{array}$$

and so $\left(4\right)$ becomes

$$u^{-1}{\left(t^b\right)}^{-1}·[{(t·b)}^{-1}{a}^{-1}a (t·b)]=u^{-1}{\left(t^b\right)}^{-1}\left(t^b\right)·\left(b^{-1}b\right).$$

Now from $\left(3\right)$ we have $u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u=u^{-1}u$ and so

$$u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u{u}^{-1}=u^{-1}u{u}^{-1}=u^{-1}.$$

Thus, $\left(u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u{u}^{-1}\right)·b^{-1}b=u^{-1}·b^{-1}b$ which implies

$$u^{-1}{\left(t^b\right)}^{-1}\left(t^b\right)·(u{u}^{-1}·b^{-1}b)=u^{-1}·b^{-1}b$$

since $u{u}^{-1}·b^{-1}b=b^{-1}b.$ Thus, $\left(4\right)$ holds. □

Proposition 3.

Let $(a,t),(b,u)\in B_{\bowtie }\left(P\right)$ such that

$$t^{-1}·a^{-1}a=b{b}^{-1} and t^{-1}t={\left(u{u}^{-1}\right)}^{b^{-1}},$$

and denote $(c,v)=(a(t·b),t^{b}u)$.

(5) 

$c^{-1}c={(t·b)}^{-1}(t·b)$ and acts trivially on $v^{-1}$ and $v{v}^{-1};$

(6) 

$v{v}^{-1}={\left(t{t}^{-1}\right)}^{t·b}$ and acts trivially on $c^{-1}$ and $c^{-1}c.$

Proof. 

From the proof of Proposition 2-$\left(4\right)$, we have

$$c^{-1}c={(t·b)}^{-1}{a}^{-1}a(t·b)={(t·b)}^{-1}(t·b)=t^b·b^{-1}b.$$

Then

$$\begin{array}{cc}\hfill {\left(u^{-1}{\left(t^b\right)}^{-1}\right)}^{t^b·\left(b^{-1}b\right)}& ={\left(u^{-1}\right)}^{[{\left(t^b\right)}^{-1}{t}^b·\left(b^{-1}b\right)]}{\left({\left(t^b\right)}^{-1}\right)}^{(t^b·b^{-1}b)}\hfill \\ \hfill & ={\left(u^{-1}\right)}^{[{\left(t^{-1}\right)}^{t·b}{t}^b·\left(b^{-1}b\right)]}{\left[{\left(t^{-1}\right)}^{t·b}\right]}^{t^b·\left(b^{-1}b\right)}\hfill \\ \hfill & ={\left(u^{-1}\right)}^{[{\left(t^{-1}t\right)}^b·\left(b^{-1}b\right)]}{\left(t^{-1}\right)}^{t·\left(b{b}^{-1}b\right)}=u^{-1}{\left(t^b\right)}^{-1}.\hfill \end{array}$$

From the proof of Proposition 2-$\left(2\right)$, we have

$${\left(t^{b}u{u}^{-1}{\left(t^b\right)}^{-1}\right)}^{(t^b·b^{-1}b)}={\left(t{t}^{-1}\right)}^{(t·b)(t^b·\left(b^{-1}b\right))}={\left(t{t}^{-1}\right)}^{t·\left(b{b}^{-1}b\right)}={\left(t{t}^{-1}\right)}^{t·b}.$$

This proves $\left(5\right).$ For $\left(6\right)$, we have from the proof of Proposition 2-$\left(2\right)$, $v{v}^{-1}=t^{b}u{u}^{-1}{\left(t^b\right)}^{-1}={\left(t{t}^{-1}\right)}^{t·b},$ and

$${\left(t{t}^{-1}\right)}^{t·b}·{(t·b)}^{-1}{a}^{-1}=({\left(t{t}^{-1}\right)}^{t·b}·{(t·b)}^{-1})({\left(t{t}^{-1}\right)}^{(t·b){(t·b)}^{-1}}·a^{-1})$$

From the proof of Proposition 2-$\left(2\right)$, we have

$$\begin{array}{cc}\hfill {\left(t{t}^{-1}\right)}^{t·b}·{(t·b)}^{-1}{a}^{-1}& =({\left(t{t}^{-1}\right)}^{t·b}·(t^b·b^{-1}))(t{t}^{-1}·a^{-1})\hfill \\ \hfill & =({\left(t{t}^{-1}t\right)}^b·b^{-1})(t{t}^{-1}·a^{-1})\hfill \\ \hfill & =(t^b·b^{-1})a^{-1}={(t·b)}^{-1}{a}^{-1}.\hfill \end{array}$$

Now

$${vv}^{-1}·c^{-1}c=(v{v}^{-1}·c^{-1})({\left(v{v}^{-1}\right)}^{c^{-1}}·c)=c^{-1}({\left(v{v}^{-1}\right)}^{c^{-1}}·c)$$

and so, to conclude the proof of $\left(6\right)$ we need to show that ${\left(v{v}^{-1}\right)}^{c^{-1}}·c=c$. However, by Lemma 1-(i) and Lemma 1-(iv),

$$\begin{array}{cc}\hfill {\left(v{v}^{-1}\right)}^{c^{-1}}·c& ={\left(t{t}^{-1}\right)}^{(t·b){(t·b)}^{-1}{a}^{-1}}·\left[a(t·b)\right]={\left(t{t}^{-1}\right)}^{a^{-1}}·a(t·b)\hfill \\ \hfill & =({\left(t{t}^{-1}\right)}^{a^{-1}}·a)({\left(t{t}^{-1}\right)}^{a^{-1}a}·(t·b)).\hfill \end{array}$$

We have

$$a{a}^{-1}({\left(v{v}^{-1}\right)}^{c^{-1}}·c)=a{a}^{-1}({\left(t{t}^{-1}\right)}^{a^{-1}}·a)(t·b)$$

and

$$a^{-1}a=t{t}^{-1}·a^{-1}a=(t{t}^{-1}·a^{-1})({\left(t{t}^{-1}\right)}^{a^{-1}}·a)$$

so that $a^{-1}a=a^{-1}({\left(t{t}^{-1}\right)}^{a^{-1}}·a).$ Then

$${\left(v{v}^{-1}\right)}^{c^{-1}}·c^{-1}c=c^{-1}({\left(v{v}^{-1}\right)}^{c^{-1}}·c)=c^{-1}a{a}^{-1}({\left(v{v}^{-1}\right)}^{c^{-1}}·c)$$

$$=c^{-1}a{a}^{-1}({\left(t{t}^{-1}\right)}^{a^{-1}}·a)(t·b)=c^{-1}a(t·b)=c^{-1}c.$$

Thus, $\left(5\right)$ and $\left(6\right)$ hold. □

Recall that a groupoid is a small category in which every arrow has an inverse. The following theorem gives our desired Zappa–Szép groupoids.

Theorem 1.

The set $B_{\bowtie }\left(P\right)$ is a groupoid under the restriction of the binary operation in the Zappa–Szép product $P=S\bowtie T$ of two inverse semigroups S and T. Moreover, the following statements are true:

• vertex set is $E\left(B_{\bowtie }\left(P\right)\right)=\{(e,p)\in E\left(S\right)\times E\left(T\right):p·e=e,p^e=p\};$
• arrow set $B_{\bowtie }\left(P\right);$
• the inverse arrow for $(a,t)\in B_{\bowtie }\left(P\right)$ is $(t^{-1}·a^{-1},{\left(t^{-1}\right)}^{a^{-1}});$
• identity arrow at $(e,p)$ is $(e,p);$
• an arrow $(a,t)$ starts at $(a{a}^{-1},{\left(t{t}^{-1}\right)}^{a^{-1}}),$ finishes at $(t^{-1}·\left(a^{-1}a\right),t^{-1}t);$
• two arrows $(a,t)$,$(b,u)\in$$B_{\bowtie }\left(P\right)$ are composable if and only if

  $$(t^{-1}·\left(a^{-1}a\right),t^{-1}t)=(b{b}^{-1},{\left(u{u}^{-1}\right)}^{b^{-1}}),$$
  and the product is given by $(a,t)(b,u)=(a(t·b),t^{b}u).$

Proof. 

We need to prove for every $(a,t)$$\in B_{\bowtie }\left(P\right)$ such that $(a,t)$ is an arrow from $(a,t){(a,t)}^{-1}=(a{a}^{-1},{\left(t{t}^{-1}\right)}^{a^{-1}})$ to ${(a,t)}^{-1}(a,t)=(t^{-1}·\left(a^{-1}a\right),t^{-1}t).$ And $(b,u)\in B_{\bowtie }\left(P\right)$ such that $(b,u)$ is an arrow from $(b,u){(b,u)}^{-1}=(b{b}^{-1},{\left(u{u}^{-1}\right)}^{b^{-1}})$ to ${(b,u)}^{-1}(b,u)=(u^{-1}·\left(b^{-1}b\right),u^{-1}u)$ such that

$$(t^{-1}·\left(a^{-1}a\right),t^{-1}t)=(b{b}^{-1},{\left(u{u}^{-1}\right)}^{b^{-1}})$$

(1)

(that is $(a,t)$ ends where $(b,u)$ begins) then the composite of arrows defined by $(a,t)(b,u)=(a(t·b),t^{b}u)$ makes $B_{\bowtie }\left(P\right)$ a groupoid, i.e., we need to check the followings.

• If $(a,t)$$\in B_{\bowtie }\left(P\right)$, then ${(a,t)}^{-1}=(t^{-1}·a^{-1},{\left(t^{-1}\right)}^{a^{-1}})\in B_{\bowtie }\left(P\right)$. That is, we need to prove that if

  $$t{t}^{-1}·a^{-1}=a^{-1},t{t}^{-1}·\left(a^{-1}a\right)=a^{-1}a,{\left(t^{-1}\right)}^{a^{-1}a}=t^{-1},{\left(t{t}^{-1}\right)}^{a^{-1}a}=t{t}^{-1},$$

  then

  $$\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}·{(t^{-1}·a^{-1})}^{-1}={(t^{-1}·a^{-1})}^{-1},$$

  $$\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}·\left[{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})\right]={(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1}),$$

  $${\left[{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}\right]}^{{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})}={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1},$$

  $${\left[\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}\right]}^{{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})}=\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}.$$

In fact, by Lemma 1-(i) and (ii) we have ${\left({\left(t^{-1}\right)}^{a^{-1}}\right)}^{-1}={\left(t\right)}^{t^{-1}·a^{-1}}$ and ${(t^{-1}·a^{-1})}^{-1}={\left(t^{-1}\right)}^{a^{-1}}·a.$ Moreover,

$$\begin{array}{cc}\hfill \left({\left(t^{-1}\right)}^{a^{-1}}\right){\left({\left(t^{-1}\right)}^{a^{-1}}\right)}^{-1}·{(t^{-1}·a^{-1})}^{-1}& =\left({\left(t^{-1}\right)}^{a^{-1}}\right)\left({\left(t\right)}^{t^{-1}·a^{-1}}\right)·({\left(t^{-1}\right)}^{a^{-1}}·a)\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}{\left(t^{-1}\right)}^{a^{-1}}·a\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}}{\left(t{t}^{-1}\right)}^{a^{-1}}·a\hfill \\ \hfill & ={\left(t^{-1}\right)}^{t{t}^{-1}·a^{-1}}{\left(t{t}^{-1}\right)}^{a^{-1}}·a\hfill \\ \hfill & ={\left(t^{-1}t{t}^{-1}\right)}^{a^{-1}}·a={\left(t^{-1}\right)}^{a^{-1}}·a.\hfill \end{array}$$

This implies that

$$\left({\left(t^{-1}\right)}^{a^{-1}}\right){\left({\left(t^{-1}\right)}^{a^{-1}}\right)}^{-1}·{(t^{-1}·a^{-1})}^{-1}={\left(t^{-1}\right)}^{a^{-1}}·a.$$

(2)

We calculate

$$\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}·\left[{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})\right]$$

$$=\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]·[({\left(t^{-1}\right)}^{a^{-1}}·a)\left((t^{-1}·a^{-1})\right].$$

Now

$$\begin{array}{cc}\hfill \left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]·({\left(t^{-1}\right)}^{a^{-1}}·a)& ={\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}{\left(t^{-1}\right)}^{a^{-1}}·a\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}}{\left(t{t}^{-1}\right)}^{a^{-1}}·a\hfill \\ \hfill & ={\left(t^{-1}\right)}^{t{t}^{-1}·a^{-1}}{\left(t{t}^{-1}\right)}^{a^{-1}}·a\hfill \\ \hfill & ={\left(t^{-1}t{t}^{-1}\right)}^{a^{-1}}·a={\left(t^{-1}\right)}^{a^{-1}}·a,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{({\left(t^{-1}\right)}^{a^{-1}}·a)}·(t^{-1}·a^{-1})\hfill \\ \hfill & =\left\{{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t\right)}^{t^{-1}·a^{-1}}·({\left(t^{-1}\right)}^{a^{-1}}·a)}{\left[{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{{\left(t^{-1}\right)}^{a^{-1}}·a}\right\}·(t^{-1}·a^{-1})\hfill \\ \hfill & =\left\{{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t{t}^{-1}\right)}^{a^{-1}}·a}{\left(t\right)}^{(t^{-1}·a^{-1})({\left(t^{-1}\right)}^{a^{-1}}·a)}\right\}·(t^{-1}·a^{-1})\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t{t}^{-1}\right)}^{a^{-1}}·a}{\left(t\right)}^{t^{-1}·a^{-1}a}{\left(t^{-1}\right)}^{a^{-1}a}·a^{-1}\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t{t}^{-1}\right)}^{a^{-1}}·a}{\left(t{t}^{-1}\right)}^{a^{-1}a}·a^{-1}\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t{t}^{-1}\right)}^{a^{-1}}·a}{\left({\left(t{t}^{-1}\right)}^{a^{-1}}\right)}^a·a^{-1}\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t{t}^{-1}\right)}^{a^{-1}}\right]}^a·a^{-1}={\left[{\left(t^{-1}\right)}^{t{t}^{-1}·a^{-1}}{\left(t{t}^{-1}\right)}^{a^{-1}}\right]}^a·a^{-1}\hfill \\ \hfill & ={\left(t^{-1}t{t}^{-1}\right)}^{a^{-1}a}·a^{-1}={\left(t^{-1}\right)}^{a^{-1}a}·a^{-1}=t^{-1}·a^{-1}.\hfill \end{array}$$

Then

$$\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}·\left[{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})\right]={(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1}).$$

(3)

We calculate

$$\begin{array}{cc}\hfill {\left[{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}\right]}^{{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})}& ={\left[{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{({\left(t^{-1}\right)}^{a^{-1}}·a)(t^{-1}·a^{-1})}\hfill \\ \hfill & ={\left[{\left(t\right)}^{(t^{-1}·a^{-1})({\left(t^{-1}\right)}^{a^{-1}}·a)}\right]}^{(t^{-1}·a^{-1})}\hfill \\ \hfill & ={\left(t\right)}^{(t^{-1}·a^{-1}a)({\left(t^{-1}\right)}^{a^{-1}a}·a^{-1})}={\left(t\right)}^{t^{-1}·a^{-1}a{a}^{-1}}={\left(t\right)}^{t^{-1}·a^{-1}}.\hfill \end{array}$$

Thus

$${\left[{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}\right]}^{{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})}={\left(t\right)}^{t^{-1}·a^{-1}}.$$

(4)

We calculate

$$\begin{array}{cc}\hfill {\left[\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}\right]}^{{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})}& ={\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{({\left(t^{-1}\right)}^{a^{-1}}·a)(t^{-1}·a^{-1})}\hfill \\ \hfill & ={\left({\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{({\left(t^{-1}\right)}^{a^{-1}}·a)}\right)}^{(t^{-1}·a^{-1}).}\hfill \end{array}$$

Now

$$\begin{array}{cc}\hfill {\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{{\left(t^{-1}\right)}^{a^{-1}}·a}& ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{\left({\left(t\right)}^{t^{-1}·a^{-1}}\right)·({\left(t^{-1}\right)}^{a^{-1}}·a)}{\left[{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{{\left(t^{-1}\right)}^{a^{-1}}·a}\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t\right)}^{t^{-1}·a^{-1}}{\left(t^{-1}\right)}^{a^{-1}}·a}{\left(t\right)}^{(t^{-1}·a^{-1})({\left(t^{-1}\right)}^{a^{-1}}·a)}\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t{t}^{-1}\right)}^{a^{-1}}·a}{\left(t\right)}^{t^{-1}·a^{-1}a}.\hfill \end{array}$$

By Lemma 1 part (iv) we have ${\left(t{t}^{-1}\right)}^{a^{-1}}·a=a.$ Thus

$$\begin{array}{cc}\hfill & {\left({\left[{\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\right]}^{({\left(t^{-1}\right)}^{a^{-1}}·a)}\right)}^{(t^{-1}·a^{-1})}\hfill \\ \hfill & ={\left[{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{{\left(t{t}^{-1}\right)}^{a^{-1}}·a}{\left(t\right)}^{t^{-1}·a^{-1}a}\right]}^{(t^{-1}·a^{-1})}\hfill \\ \hfill & ={\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{({\left(t{t}^{-1}\right)}^{a^{-1}}·a)({\left(t\right)}^{t^{-1}·a^{-1}a}·(t^{-1}·a^{-1}))}{\left(t\right)}^{(t^{-1}·a^{-1}a)(t^{-1}·a^{-1})}\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}({\left(t{t}^{-1}\right)}^{a^{-1}}·a)({\left(t\right)}^{t^{-1}·a^{-1}a}{\left(t^{-1}\right)}^{a^{-1}a}·a^{-1})}{\left(t\right)}^{(t^{-1}·a^{-1}a)({\left(t^{-1}\right)}^{a^{-1}a}·a^{-1})}\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}({\left(t{t}^{-1}\right)}^{a^{-1}}·a)({\left(t{t}^{-1}\right)}^{a^{-1}a}·a^{-1})}{\left(t\right)}^{t^{-1}·a^{-1}a{a}^{-1}}\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}({\left(t{t}^{-1}\right)}^{a^{-1}}·a)(t{t}^{-1}·a^{-1})}{\left(t\right)}^{t^{-1}·a^{-1}}\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}a{a}^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}\hfill \\ \hfill & ={\left(t^{-1}\right)}^{a^{-1}}{\left(t\right)}^{t^{-1}·a^{-1}}.\hfill \end{array}$$

Hence

$${\left[\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}\right]}^{{(t^{-1}·a^{-1})}^{-1}(t^{-1}·a^{-1})}=\left[{\left(t^{-1}\right)}^{a^{-1}}\right]{\left[{\left(t^{-1}\right)}^{a^{-1}}\right]}^{-1}.$$

(5)

Thus, by (2)–(5), we have ${(a,tt)}^{-1}\in$ $B_{\bowtie }\left(P\right)$.

• $(a(t·b),t^{b}u)$ starts at $(a{a}^{-1},{\left(t{t}^{-1}\right)}^{a^{-1}}).$ In fact, $(a(t·b),t^{b}u)$ starts at

  $$\begin{array}{c}\hfill (a(t·b){\left[a(t·b)\right]}^{-1},{\left[\left(t^{b}u\right){\left(t^{b}u\right)}^{-1}\right]}^{{\left(a(t·b)\right)}^{-1}})=(a(t·b){(t·b)}^{-1}{a}^{-1},{\left[t^{b}u{u}^{-1}{\left(t^b\right)}^{-1}\right]}^{{(t·b)}^{-1}{a}^{-1}}).\end{array}$$

By Proposition 2-$\left(1\right),\left(2\right)$ and the matching condition (1), we have

$$a(t·b){(t·b)}^{-1}{a}^{-1}=a{a}^{-1} \mathrm{and} {\left(t^{b}u{u}^{-1}{\left(t^b\right)}^{-1}\right)}^{{(t·b)}^{-1}{a}^{-1}}={\left(t{t}^{-1}\right)}^{a^{-1}}$$

which means that $(a(t·b),t^{b}u)$ starts at $(a{a}^{-1},{\left(t{t}^{-1}\right)}^{a^{-1}})$.

• $(a(t·b),t^{b}u)$ ends at $(u^{-1}·\left(b^{-1}b\right),u^{-1}u).$ In fact, $(a(t·b),t^{b}u)$ ends at

  $$\begin{array}{c}\hfill ({\left(t^{b}u\right)}^{-1}·\left[{\left(a(t·b)\right)}^{-1}a(t·b)\right],{\left(t^{b}u\right)}^{-1}{t}^{b}u)=(u^{-1}{\left(t^b\right)}^{-1}·\left[{(t·b)}^{-1}{a}^{-1}a(t·b)\right],u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u).\end{array}$$

By Proposition 2-$\left(3\right),$$\left(4\right)$ and the matching condition (1),

$$u^{-1}{\left(t^b\right)}^{-1}·[{(t·b)}^{-1}{a}^{-1}a (t·b)]=u^{-1}·b{b}^{-1}$$

and $u^{-1}{\left(t^b\right)}^{-1}{t}^{b}u=u^{-1}u.$ Thus, $\left(a\left(t·b\right),t^{b}u\right)$ ends at $\left(u^{-1}·\left(b^{-1}b\right),u^{-1}u\right)$.

• $(a(t·b),t^{b}u)\in B_{\bowtie }\left(P\right).$ We have to prove

  $$\begin{array}{cc}\hfill \left(t^{b}u{\left(t^{b}u\right)}^{-1}\right)·({\left(a(t·b)\right)}^{-1}\left(a(t·b)\right)& ={\left(a(t·b)\right)}^{-1}\left(a(t·b)\right)\hfill \\ \hfill \left(t^{b}u{\left(t^{b}u\right)}^{-1}\right)·{\left(a(t·b)\right)}^{-1}& ={\left(a(t·b)\right)}^{-1}\hfill \\ \hfill {\left(t^{b}u{\left(t^{b}u\right)}^{-1}\right)}^{({\left(a(t·b)\right)}^{-1}\left(a(t·b)\right)}& =\left(t^{b}u{\left(t^{b}u\right)}^{-1}\right)\hfill \\ \hfill \left[\right(t^{b}u{{)}^{-1}]}^{({\left(a(t·b)\right)}^{-1}\left(a(t·b)\right)}& ={\left(t^{b}u\right)}^{-1}.\hfill \end{array}$$

From Proposition 3 with $(c,v)=(a(t·bt),t^{b}u)$, the results follows. □

3. An Alternative Proof of Billhardt’s $\lambda$-Semidirect Product

In this section, we shall give an alternative proof of Billhardt’s $\lambda$-semidirect product using the result in the previous section and the ESN Theorem. We first recall some notions and results.

Let S be a groupoid and let ≤ be a partial order on S. Then $(S,\le )$ is an ordered groupoid if the following axioms hold.

(OG1)

$x\le y\Rightarrow x^{-1}\le y^{-1}$ for all $x,y\in S.$

(OG2)

If $x\le y,u\le v,$ and the compositions $xu$ and $yv$ are defined, then $xu\le yv$ for all $x,y,u,v\in S.$

(OG3)

Let $x\in S$ and let be e an identity such that $e\le x{x}^{-1}.$ Then there exists a unique element $(e\mid x),$ called the restriction of x to e, such that $(e\mid x)\le x$ and $(e\mid x){(e\mid x)}^{-1}=e.$

An ordered groupoid is said to be inductive if the partially ordered set of its identities forms a meet semilattices.

Lemma 2

([15]). Let S be an inductive groupoid. Denote $(x\mid e)={(e\mid x^{-1})}^{-1}$ for all $x\in S$ with $e\le x^{-1}x$. Then S forms an inverse semigroup with respect to the following multiplication

$$x\otimes y=(x\mid (x^{-1}x\wedge y{y}^{-1}))((x^{-1}x\wedge y{y}^{-1})\mid y)forallx,y\in S.$$

Now, we consider the Zappa–Szép groupoids of inverse semigroups S and T such that the action of S on T is trivial. In this case, it is easy to see that

$$B_{\bowtie }\left(P\right)=\left\{\begin{array}{c}(a,t)\in S\times T:t{t}^{-1}·a=a\end{array}\right\}.$$

We shall denote $B_{\bowtie }\left(P\right)$ by $B\left(P\right)$ in this case, where $P=S\bowtie T$. By Theorem 1, we have the following result.

Proposition 4.

Suppose the set $B\left(P\right)$ with composition given by

$(a,t)(b,u)=\left(a\right(t·b),tu)$ is defined if and only if $(t^{-1}·\left(a^{-1}a\right),t^{-1}t)=(b{b}^{-1},u{u}^{-1})$.

Then $B\left(P\right)$ is a groupoid with the set of identities

$$E\left(B\right(P\left)\right)=\left\{\right(e,p)\in E(S)\times E(T):p·e=e\}.$$

Now we introduce a partial order on $B\left(P\right)$.

Proposition 5.

Suppose $B\left(P\right)=\{(a,t)\in P:t{t}^{-1}·a=a\}$ with ordering given by

$(a,t)\le (b,u)⟺a\le t{t}^{-1}·b$ and $t\le u$.

Then $B\left(P\right)$ is a partially ordered set such that $E\left(B\right(P\left)\right)$ is a meet lattice.

Proof. 

To prove that ≤ defined on $B\left(P\right)$ is a partial order, we need to check ≤ is reflexive, transitive and antisymmetric.

It is reflexive since $(a,t)\in B\left(P\right)$ and so $t{t}^{-1}·a=a.$ Therefore $a\le t{t}^{-1}·a$ and (trivially), $t\le t.$ This implies that $(a,t)\le (a,t).$

It is transitive for assume that $(a,t)\le (b,u)\le (c,v)$. Then $a\le t{t}^{-1}·b,t\le u$ and $b\le u{u}^{-1}·c,u\le v.$ Since $t\le u\le v$ this implies that $t\le v.$ Also $a\le t{t}^{-1}·b\le t{t}^{-1}·(u{u}^{-1}·c)= t{t}^{-1}u{u}^{-1}·c$. However, $t\le u$ and this implies that $t{t}^{-1}u{u}^{-1}=t{t}^{-1}.$ Hence $a\le t{t}^{-1}·c.$

It is antisymmetric for assume that $(a,t)\le (b,u)\le (a,t).$ Then $a\le t{t}^{-1}·b,t\le u$ and $b\le u{u}^{-1}·a,u\le t.$ Now, $t\le u\le t$ implies that $t=u,$ and then $a\le t{t}^{-1}·b=u{u}^{-1}·b=b$ which implies $a\le b,$ by symmetry $b\le a,$ then $a=b.$

To show the partially ordered set $\left(E\right(B\left(P\right)),\le )$ is a meet semilattices, we need to prove that each pair of elements $(e,p)$ and $(f,q)\in E\left(B\right(P\left)\right)$ has a greatest lower bound. We shall prove $(e,p)\wedge (f,q)=\left(\right(q·e\left)\right(p·f),pq).$ First we show that $\left(\right(q·e\left)\right(p·f),pq)\in E\left(B\right(P\left)\right)$. Observe that $\left(\right(q·e\left)\right(p·f),pq)$ is an idempotent if and only if

${\left[(q·e)(p·f)\right]}^2=(q·e)(p·f)$, ${\left(pq\right)}^2=pq$ and $pq·\left(\right(q·e\left)\right(p·f\left)\right)=(q·e)(p·f).$

Since the idempotents of S and T are commute, we have ${\left[(q·e)(p·f)\right]}^2=(q·e)(p·f)$ and ${\left(pq\right)}^2=pq.$ Moreover,

$$pq·\left(\right(q·e\left)\right(p·f\left)\right)=(pq·(q·e\left)\right)(pq·(p·f\left)\right)=(pq·e)(pq·f)=(q·(p·e\left)\right)(p·(q·f\left)\right)=(q·e)(p·f).$$

Second we show that $\left(\right(q·e\left)\right(p·f),pq)\le (e,p),(f,q).$ Observe that

$$\left(\right(q·e\left)\right(p·f),pq)\le (e,p) ⟺(q·e)(p·f)\le pq·e,pq\le p.$$

Obviously, $pq\le p$. Moreover, we have $pq·e=qp·e=q·e$ and $(q·e)(p·f)\le q·e$ since $p·f$ is an idempotent. This implies that $(q·e)(p·f)\le pq·e$. Similarly, $\left(\right(q·e\left)\right(p·f),pq)\le (f,q).$ Now suppose that $(x,y)\in E\left(B\right(P\left)\right)$ is such that $(x,y)\le (e,p),(f,q)$. Then $x\le y·e,y\le p$ and $x\le y·f,y\le q.$ It follows that $y\le pq,$ and so

$$(x,y)\le \left(\right(q·e\left)\right(p·f),pq)\iff x\le y·\left[\right(q·e\left)\right(p·f\left)\right].$$

But

$$y·\left[\right(q·e\left)\right(p·f\left)\right]=(yq·e)(yp·f)=(y·e)(y·f)\ge x.$$

Thus, $(e,p)\wedge (f,q)=\left(\right(q·e\left)\right(p·f),pq).$ □

Proposition 6.

The partially ordered set $\left(B\right(P),\le )$ is an inductive groupoid.

Proof. 

We must prove $\left(OG1\right),\left(OG2\right)$ and $\left(OG3\right)$. To verify $\left(OG1\right)$, suppose that $(a,t),(b,u)\in B\left(P\right)$ are such that $(a,t)\le (b,u)$ so that $a\le t{t}^{-1}·b$ and $t\le u.$ Then by $\left(OG1\right)$ in the inverse semigroup T, we deduce that $t^{-1}\le u^{-1}$. It follows that $t^{-1}=t^{-1}t{u}^{-1}.$ Then,

$$a\le t{t}^{-1}·b\Rightarrow a^{-1}\le t{t}^{-1}·b^{-1}\Rightarrow t^{-1}·a^{-1}\le t^{-1}t{t}^{-1}·b^{-1}=t^{-1}t{u}^{-1}·b^{-1}$$

and hence $(t^{-1}·a^{-1},t^{-1})\le (u^{-1}·b^{-1},u^{-1})$, as required.

To verify $\left(OG2\right)$, suppose that $(a,t),(b,u),(c,v),(d,w)\in B\left(P\right)$ such that $(a,t)\le (b,u)$ and $(c,v)\le (d,w).$ Suppose that $(a,t)(c,v)$ and $(b,u)(d,w)$ are defined. Then

$$(a,t)(c,v)\le (b,u)(d,w)\iff \left(a\right(t·c),tv)\le \left(b\right(u·d),uw),$$

that is

$$a(t·c)\le \left(tv\right){\left(tv\right)}^{-1}·\left[b(u·d)\right] \mathrm{and} tv\le uw.$$

Now

$$\begin{array}{cc}\hfill \left(tv\right){\left(tv\right)}^{-1}·\left[b(u·d)\right]& =tv{v}^{-1}{t}^{-1}·\left[b(u·d)\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& =t{t}^{-1}t{t}^{-1}·\left[b(u·d)\right] \sin \mathrm{ce} t^{-1}t=v{v}^{-1}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \hspace{1em}& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =t{t}^{-1}·\left[b(u·d)\right] \mathrm{by} \left(SM1\right)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& =(t{t}^{-1}·b)(t{t}^{-1}·(u·d))\hfill \end{array}$$

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& =(t{t}^{-1}·b)(t{t}^{-1}u·d) \sin \mathrm{ce} t\le u\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}& =(t{t}^{-1}·b)(t·d).\hfill \end{array}$$

Since $(a,t)\le (b,u)$ if and only if

$$a\le t{t}^{-1}·b,t\le u$$

(9)

and $(c,v)\le (d,w)$ if and only if

$$c\le v{v}^{-1}·d,v\le w.$$

(10)

From (9) and (10), we deduce that $t\le u,v\le w$ which implies that

$$tv\le uw$$

(11)

and $c\le v{v}^{-1}·d$ implies that $t·c\le t·(v{v}^{-1}·d).$ Thus

$$t·c\le t·d.$$

(12)

From (9), (11) and (12), we have $a(t·c)\le \left(tv\right){\left(tv\right)}^{-1}·\left[b(u·d)\right]$ and $tv\le uw.$ Thus, $\left(OG2\right)$ holds.

To verify $\left(OG3\right)$, suppose that $(a,t)\in B\left(P\right)$ and $(e,p)\le (a,t){(a,t)}^{-1}.$ Then we need to find a unique element $(x,y)\in B\left(P\right)$ such that (•) $(x,y){(x,y)}^{-1}=(e,p)$ and ($••$) $(x,y)\le (a,t).$ We define this element of $B\left(P\right)$ by $(x,y)=\left(\right(e,p)\mid (a,t\left)\right)=\left(e\right(p·a),pt).$ Since $e\le p·a{a}^{-1}$ and $p\le t{t}^{-1}.$ Then

$$\begin{array}{cc}\hfill (x,y){(x,y)}^{-1}& =(e(p·a){(p·a)}^{-1}e,pt{t}^{-1}p)\hfill \\ \hfill & =(e(p·a){(p·a)}^{-1},pt{t}^{-1})\hfill \\ \hfill & =(e(p·a{a}^{-1}),pt{t}^{-1})\hfill \\ \hfill & =(e,p).\hfill \end{array}$$

This proves (•). Now $\left(e\right(p·a),pt)\le (a,t)$ if and only if $e(p·a)\le \left(pt{t}^{-1}p\right)·a$ and $pt\le t.$ However, $\left(pt{t}^{-1}p\right)·a=\left(pt{t}^{-1}\right)·a=p·a.$ Then $e(p·a)\le p·a$, since $e\in E\left(S\right)$ and $pt\le t$ since $p\in E\left(T\right).$ Thus, ($••$) holds.

Now suppose that $(x^{\prime },y^{\prime })$ also satisfy (•) and ($••$). So, we have $x^{\prime }{x}^{{\prime }^{-1}}=e,y^{\prime }{y}^{{\prime }^{-1}}=p,x^{\prime }\le y^{\prime }{y}^{{\prime }^{-1}}·a,y^{\prime }\le t,$ so $y^{\prime }\in T,y^{\prime }\le t,y^{\prime }{y}^{{\prime }^{-1}}=p$ by uniqueness of restriction in T. We deduce $y^{\prime }=pt.$ Also $x^{\prime }{x}^{{\prime }^{-1}}=e,x^{\prime }\le y^{\prime }{y}^{{\prime }^{-1}}·a=\left(pt{t}^{-1}p\right)·a=p·a$ by uniqueness of restriction in S. We deduce $x^{\prime }=e(p·a).$ Thus, $\left(OG3\right)$ holds. □

Theorem 2

([7]). Let S and T be inverse semigroups such that T acts on S by endomorphisms. Then $\{(a,t)\in S\times T:a=t{t}^{-1}·a\}$ forms an inverse semigroup with respect to the operation

$$(a,t)(b,u)=((\left(tu\right){\left(tu\right)}^{-1}·a)(t·b),tu).$$

Proof. 

Suppose that $(a,t),(b,u)\in B\left(P\right)$. Since ${(a,t)}^{-1}(a,t)=(t^{-1}·a^{-1}a,t^{-1}t)$ and $(b,u){(b,u)}^{-1}=(b{b}^{-1},u{u}^{-1})$, we form the pseudoproduct $(a,t)\otimes (b,u)$ using the greatest lower bound

$$\begin{array}{cc}\hfill \ell & ={(a,t)}^{-1}(a,t)\wedge (b,u){(b,u)}^{-1}=(t^{-1}·a^{-1}a,t^{-1}t)\wedge (b{b}^{-1},u{u}^{-1})\hfill \\ \hfill & =((u{u}^{-1}{t}^{-1}·a^{-1}a)(t^{-1}t·b{b}^{-1}),t^{-1}tu{u}^{-1}).\hfill \end{array}$$

Put $(u{u}^{-1}{t}^{-1}·a^{-1}a)(t^{-1}t·b{b}^{-1})=\gamma$. We now compute $((a,t)\mid \ell )=((a,t)\mid (\gamma ,t^{-1}tu{u}^{-1}))$. Now

$$\begin{array}{cc}\hfill \left(\right(a,t)\mid \ell )& ={((\gamma ,t^{-1}tu{u}^{-1})\mid (t^{-1}·a^{-1},t^{-1}))}^{-1}={(\gamma (t^{-1}tu{u}^{-1}·t^{-1}·a^{-1}),t^{-1}tu{u}^{-1}{t}^{-1})}^{-1}\hfill \\ \hfill & ={(\gamma (t^{-1}tu{u}^{-1}{t}^{-1}·a^{-1}),t^{-1}tu{u}^{-1}{t}^{-1})}^{-1}={(\gamma (u{u}^{-1}{t}^{-1}·a^{-1}),u{u}^{-1}{t}^{-1})}^{-1}\hfill \\ \hfill & =({\left(u{u}^{-1}{t}^{-1}\right)}^{-1}·{\left(\gamma (u{u}^{-1}{t}^{-1}·a^{-1})\right)}^{-1},{\left(u{u}^{-1}{t}^{-1}\right)}^{-1})\hfill \\ \hfill & =(tu{u}^{-1}·(u{u}^{-1}{t}^{-1}·a){\gamma }^{-1},tu{u}^{-1})\hfill \\ \hfill & =(tu{u}^{-1}·(u{u}^{-1}{t}^{-1}·a)(t^{-1}t·b{b}^{-1})(u{u}^{-1}{t}^{-1}·a^{-1}a),tu{u}^{-1})\hfill \\ \hfill & =(tu{u}^{-1}·(u{u}^{-1}{t}^{-1}·a)(u{u}^{-1}{t}^{-1}·a^{-1}a)(t^{-1}t·b{b}^{-1}),tu{u}^{-1})\hfill \\ \hfill & =(tu{u}^{-1}·(u{u}^{-1}{t}^{-1}·a{a}^{-1}a)(t^{-1}t·b{b}^{-1}),tu{u}^{-1})\hfill \\ \hfill & =((tu{u}^{-1}u{u}^{-1}{t}^{-1}·a)(tu{u}^{-1}{t}^{-1}t·b{b}^{-1}),tu{u}^{-1})\hfill \\ \hfill & =((tu{u}^{-1}{t}^{-1}·a)(tu{u}^{-1}·b{b}^{-1}),tu{u}^{-1})\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill (\ell \mid (b,u\left)\right)& =(((u{u}^{-1}{t}^{-1}·a^{-1}a)(t^{-1}t·b{b}^{-1}),t^{-1}tu{u}^{-1})\mid (b,ut))\hfill \\ \hfill & =((u{u}^{-1}{t}^{-1}·a^{-1}a)(t^{-1}t·b{b}^{-1})(t^{-1}tu{u}^{-1}·b),t^{-1}tu{u}^{-1}u)\hfill \\ \hfill & =((u{u}^{-1}{t}^{-1}·a^{-1}a)(t^{-1}t·b{b}^{-1})(t^{-1}tu{u}^{-1}·b),t^{-1}tu).\hfill \end{array}$$

Write $\left(\right(a,t)\mid \ell )=x$ and $(\ell \mid (b,u\left)\right)=y.$ Then the pseudoproduct $(a,t)\otimes (b,u)$ is equal to $\left(\right(a,t)\mid \ell )(\ell \mid (b,u\left)\right)$

$$\begin{array}{cc}\hfill xy& =((tu{u}^{-1}{t}^{-1}·a)(tu{u}^{-1}·b{b}^{-1})(tu{u}^{-1}{t}^{-1}·a^{-1}a)(tu{u}^{-1}·b{b}^{-1})(tu{u}^{-1}·b),tu)\hfill \\ \hfill & =((tu{u}^{-1}{t}^{-1}·a)(tu{u}^{-1}·b{b}^{-1})(tu{u}^{-1}{t}^{-1}·a^{-1}a)(tu{u}^{-1}·b{b}^{-1})(tu{u}^{-1}·b),tu)\hfill \\ \hfill & =((tu{u}^{-1}{t}^{-1}·a{a}^{-1}a)(tu{u}^{-1}·b{b}^{-1}b{b}^{-1}b),tu)\hfill \\ \hfill & =((tu{u}^{-1}{t}^{-1}·a)(tu{u}^{-1}·b),tu)\hfill \\ \hfill & =((tu{u}^{-1}{t}^{-1}·a)(t·(u{u}^{-1}·b)),tu)\hfill \\ \hfill & =((tu{u}^{-1}{t}^{-1}·a)(t·b),tu).\hfill \end{array}$$

Thus, $(a,t)\otimes (b,u)=((a,t)\mid \ell )(\ell \mid (b,u))=((tu{u}^{-1}{t}^{-1}·a)(t·b),tu),$ and this is exactly the binary operation defined by Billhardt (cf. [7]). The fact that this binary operation makes $B\left(P\right)$ an inverse semigroup follows from its construction as the pseudoproduct on an inductive groupoid. □

4. Examples

In this section, we explore various practical examples to illustrate the theoretical constructs discussed earlier in the paper. These examples are purposefully chosen to demonstrate the versatility and applicability of the Zappa–Szép groupoids across different types of inverse semigroups. By examining specific cases, we aim to provide the reader with a clearer understanding of how abstract concepts manifest in more concrete scenarios. Each example is designed to highlight the unique characteristics and potential real-world applications of the Zappa–Szép construction, filling the gap between theoretical insight and practical application. The section will sequentially address different configurations of semigroups and groupoids, showcasing the breadth and depth of the Zappa–Szép groupoids’ impact in the field.

For any inverse semigroups S and T such that $P=S\bowtie T$ is the Zappa–Szép product of S and T, $B_{\bowtie }\left(P\right)$ is a groupoid with $E\left(B_{\bowtie }\left(P\right)\right)$ an ordered set of idempotents. Sometimes this is true in other cases as in examples $\left(1\right)$ where we have trivial actions $,\left(2\right)$ where S and T are groups only idempotents are $1_S,1_T$ and for groups we would assume these act trivially $,\left(3\right)$ where $S=A$ is a Clifford semigroup and $T=\mathbb{Z}$ here we find $B_{\bowtie }\left(P\right)$ is a group and $\left(4\right)$ where $P=A\bowtie A$ where A is a semilattice with regular actions, here we find that $B_{\bowtie }\left(P\right)\cong A.$ But sometimes we have $B_{\bowtie }\left(P\right)$ is not inductive as in example $\left(5\right)$ where the partially ordered set of identities do not form a meet semilattice. So, we can say in general the construction does not proceed any further in general. Then in [1], we choose $S=E,T=G$. Therefore, $E\left(B_{\bowtie }\left(P\right)\right)=E$ is a semilattice, and we can extend the ordering on E to an ordering on $B_{\bowtie }\left(P\right)$ to get an inductive groupoid and so an inverse semigroup.

1.

If the action of S on T is trivial, so $P=S\bowtie T=S⋊T$ the familiar semidirect product, then $B_{\bowtie }\left(P\right)=B\left(P\right)$ as in Section 4.

2.

If S and T are groups, then $B_{\bowtie }\left(P\right)=P=S\bowtie T$ is again a group. Here we would expect $B_{\bowtie }\left(P\right)$ to be a groupoid with set of vertices

$$\left\{\left(e,p\right)\in E\left(S\right)\times E\left(T\right):p·e=e,p^e=p\right\} ,$$

However, then $e=1_S,p=1_T$ so there is only one vertex $\left(1_S, 1_T\right)$ and a groupoid with one vertex is a group.

3.

If $A=\left\{e,t,f,b\right\}$ a Clifford semigroup and $B=\left(\mathbb{Z},+\right).$ Suppose that the action of $\mathbb{Z}$ on A for each $m\in \mathbb{Z}$ is as follows: $m·e=f, m·t=b, m·f=f, m·b=b.$ Observe that $m·a=fa$ for all $a\in A.$ The action of A on $\mathbb{Z}$ as follows: $m^e=m, m^f=m, m^t=-m, m^b=-m.$ Thus, $M=A\bowtie \mathbb{Z}=\left\{\left(a,m\right):a\in A,m\in B\right\}$ the Zappa–Szép product of A and $B.$ We have $B_{\bowtie }\left(P\right)=\left\{\left(f,0\right),\left(b,0\right)\right\}$ is a groupoid with one vertex. So $B_{\bowtie }\left(P\right)$ is just the cyclic group of order $2.$

4.

If $P=A\bowtie A$ the Zappa–Szép product of a band A with left and right regular actions of A on itself, we take here A a semilattice (which is of course inverse) with the same actions, so we have then $P=A\bowtie A$ the Zappa–Szép product of a semilattice A with itself. The multiplication is given by: $\left(a,b\right)\left(c,d\right)=\left(abc,bcd\right).$ where $a,b,c,d\in A.$ Thus, $B_{\bowtie }\left(P\right)=\left\{\left(a,a\right):a\in A\right\}.$ Hence $B_{\bowtie }\left(P\right)\cong A$ via the function $\theta :B_{\bowtie }\left(P\right)\to A$ given by $\theta \left(a,a\right)=a$ which is clear injective, surjective and homomorphism function and hence $B_{\bowtie }\left(P\right)$ is an inductive groupoid and so an inverse semigroup. The ordering on $B_{\bowtie }\left(P\right)$ is given by the ordering on A that is

$$\left(a,a\right)\le \left(b,b\right) \mathrm{in} B_{\bowtie }\left(P\right)⟺a\le b \mathrm{in} A.$$

5.

If $A=\left\{1,e,f\right\}$ and $B=\left\{1,b\right\}$. Thus

$$P=A\bowtie B=\left\{\left(1,1\right),\left(1,b\right),\left(e,1\right),\left(e,b\right),\left(f,1\right),\left(f,b\right)\right\}.$$

Hence

$$B_{\bowtie }\left(P\right)=\left\{\left(1,1\right),\left(1,b\right),\left(e,1\right),\left(f,1\right)\right\}.$$

which is a groupoid with

• vertex set $E\left(B_{\bowtie }\left(P\right)\right)=B_{\bowtie }\left(P\right)=\left\{\left(1,1\right),\left(1,b\right),\left(e,1\right),\left(f,1\right)\right\};$
• arrow set $B_{\bowtie }\left(P\right);$
• the inverse of an arrow $\left(a,b\right)\in B_{\bowtie }\left(P\right)$ is $\left(a,b\right);$
• each arrow $\left(a,b\right)\in B_{\bowtie }\left(P\right)$ starts and finishes at $\left(a,b\right);$ and
• the composite arrow is the same arrow at each vertex $\left(a,b\right)\in E\left(B_{\bowtie }\left(P\right)\right).$

However, we cannot obtain an inductive groupoid from $B_{\bowtie }\left(P\right)$ since the partially ordered set of identities do not form a meet semilattice. The ordering on $E\left(B_{\bowtie }\left(P\right)\right)$ is given by:

$$\left(e,p\right)\le \left(f,q\right)\iff e=e\left(p·f\right),p=p^{f}q.$$

From this, we conclude the following Figure 2 illustrating that $\left(e,1\right)$ and $\left(1,b\right)$ do not have the greatest lower bound. Similarly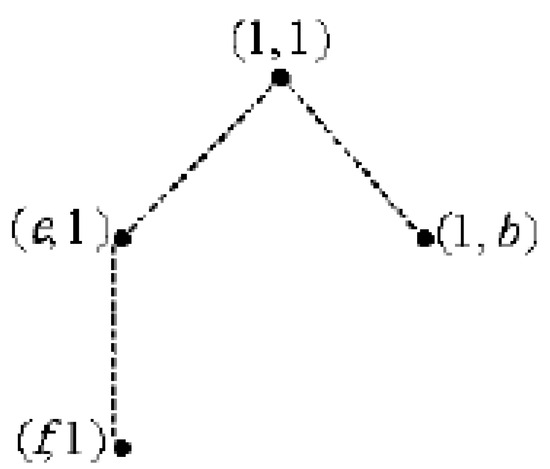, $\left(f,1\right)$ and $\left(1,b\right).$

Figure 2. The set of identities do not form a meet semilattices.

We have

$$\begin{array}{cc}\hfill 1& =1\left(b·1\right),b=b^{1}1\iff \left(1,b\right)\le \left(1,1\right),e=e\left(1·1\right),1=1^{1}1\hfill \\ \hfill & \iff \left(e,1\right)\le \left(1,1\right),f=f\left(1·1\right),1=1^{1}1\iff \left(f,1\right)\le \left(1,1\right)\hfill \end{array}$$

and $f=f\left(1·e\right),1=1^{e}1\iff \left(f,1\right)\le \left(e,1\right).$ However, $\left(e,1\right)\nleqq \left(1,b\right)$ since $1^{1}b=b\ne 1$ ($p\ne p^{f}q)$ or $\left(1,b\right)\nleqq \left(e,1\right)$ because $1\left(b·e\right)=1f=f\ne 1(e\ne e\left(p·f\right)).$ Also $\left(f,1\right)\nleqq \left(1,b\right)$ since $1^{1}b=b\ne 1(p\ne p^{f}q)or\left(1,b\right)\nleqq \left(f,1\right).$ Because $1\left(b·f\right)=1f=f\ne 1$ ($e\ne e\left(p·f\right)).$ Thus, $E\left(B_{\bowtie }\left(P\right)\right)$ is not a semilattice.

5. Conclusions

Extension theory addresses the intricate challenge of constructing inverse semigroups from simpler components, a task that remains complex even in the group context. This complexity often arises because classical semidirect products of two inverse semigroups do not necessarily yield an inverse result. Bernd was able to resolve this issue by redefining semidirect products in inverse cases, naming this new formation as the $\lambda$-semidirect product. His adaptation ensures that the product maintains its inverse nature, thus paving the way for the formulation of a broader theoretical framework. Building upon this foundational work, our objective was to develop an inverse Zappa–Szép product from two inverse semigroups by employing the established correspondence between inverse semigroups and inductive groupoids. In the process, we were able to provide an alternative proof of Billhardt’s $\lambda$-semidirect product by applying the Ehresmann–Schein–Nambooripad theorem. While this work successfully categorized the Zappa–Szép product as a groupoid, advancing it to an inductive groupoid proved more challenging. This unresolved issue sets the stage for future research, where the aim is to refine the methodology and deepen the understanding to transform this groupoid into an inductive groupoid, ultimately achieving an inverse Zappa–Szép product.