The Vehicle-Routing Problem with Satellites Utilization: A Systematic Review of the Literature
Abstract
1. Introduction
2. Materials and Methods
- Research Questions
- Search Strategy
- Selection and Evaluation Process
- Analysis and Synthesis
2.1. Research Questions
2.2. Search Strategy
2.3. Selection and Evaluation Process
2.4. Analysis and Synthesis
- Removing duplicate DOIs found in WoS and Scopus reduced the dataset to 1486 publications.
- By using titles, abstracts, and keywords, a second filter was applied based on the exclusion criteria presented in Table 2.
3. Results
- −
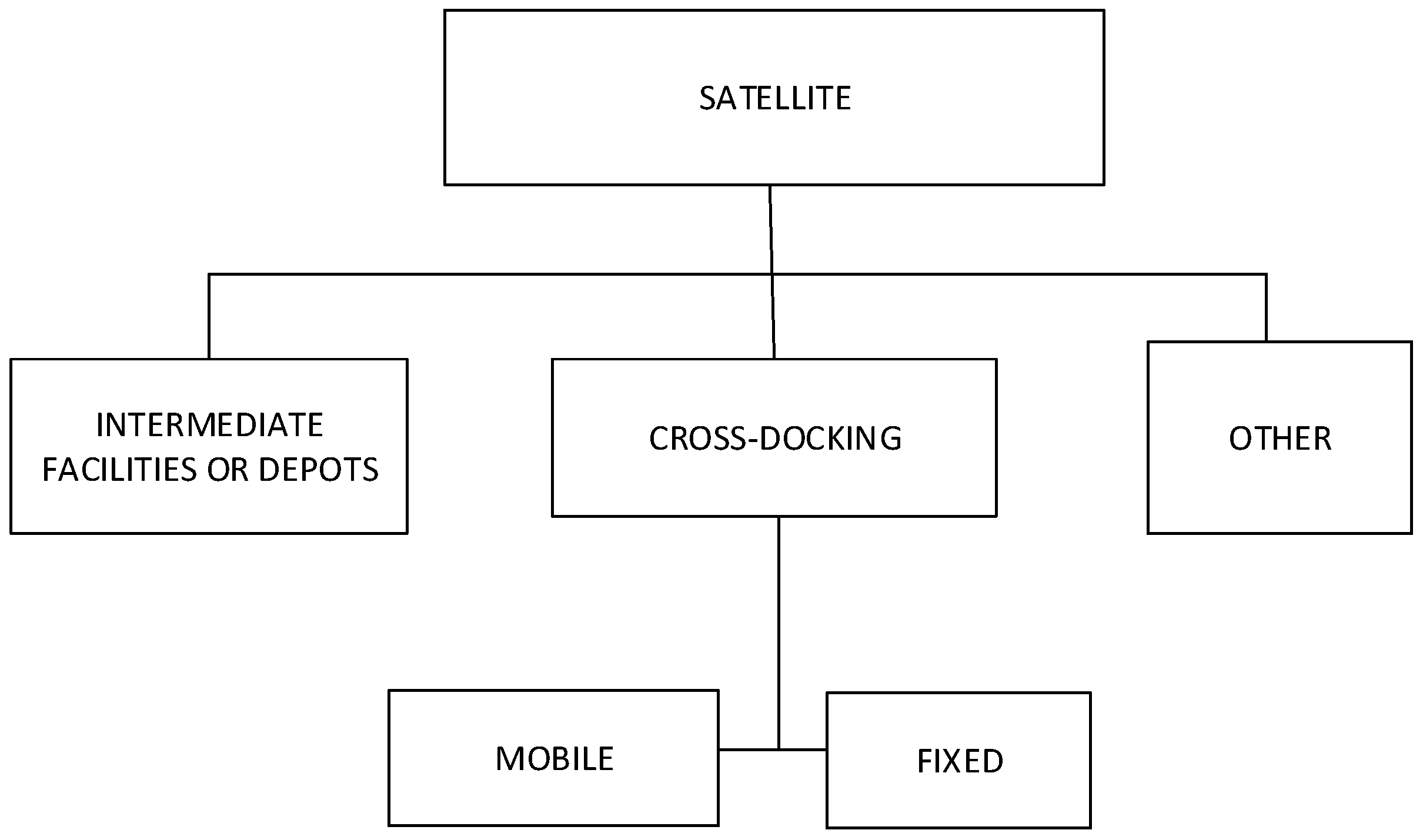
- Intermediate Depots: Intermediate locations for transferring products with capacity for unloading, vehicle replenishment, and storage [19], which can be fixed [13] or mobile [18]. For example, ref. [13] uses parcel lockers as fixed intermediate depots where customers can pick up their goods. In the case of mobile depots, ref. [30] uses parking lots as mobile storage satellites for exchanging containers.
- −
- Cross-Docking: Locations without storage capacity, designed for transferring products from one vehicle to another [19], which can be divided into the following subcategories:
- ∘
- Fixed Sites: Stations located in areas not equipped for transshipment activities, as exemplified by using a gas station parking lot for product exchange between vehicles [31].
- ∘
- Mobile Sites: Delivery points without storage capacity, exemplified by vehicle locations where parcels can be transferred between them [32].
- −
- Satellite Depots: A set of locations where trailers can be detached and products can be transferred between trucks and trailers [33]. Vehicles transporting smaller vehicles are also included in this category, such as [34], which describes a parked van serving as a launch point for drones to make deliveries.
- −
- Satellite Customers: A customer that can be served while the primary vehicle performs an action, either through an alternative means of transport or by a person, such as a customer that can be visited “on foot” while the vehicle is recharging [35].
- −
- Within these categories, the following variants were identified:
- −
- Path Level (o Step): The problem involves two echelons of routing: first, designing routes from depots to a subset of satellites, and second, routing from the satellites to serve customers [36].
- −
- Location: Involves opening specific depots, assigning customers to the open depots, and designing vehicle routes from the depots to the customers [37].
- −
- Trailer Transfer: Applies to a fleet of trucks and trailers with capacity available to serve a set of customers [38].
- −
- Electromobility: Use of electric vehicles with zero-emission energy [39].
- −
- Temporal Synchronization: Coordination of vehicle arrival times at satellites [40].
- −
- Multi Trip: The ability to make multiple trips to visit customers from a satellite, deliver goods, and return empty to the satellite to start another journey or finish at the depot [41].
- −
- Multi-depots: Considers two (or more) depots for deliveries [42].
- −
- Pickup and Delivery: Customers with both pickup and delivery demands, where vehicles must deliver goods to customers, pick up other goods, or perform both [43].
- −
- −
- Time Constraints: Classic time restrictions (time windows) or synchronization constraints [45].
- −
3.1. Description of Articles
3.1.1. Intermediate Depots or Facilities
3.1.2. Cross-Docking—Fixed
3.1.3. Cross-Docking—Mobile
3.1.4. Satellite Depots
3.1.5. Satellite Customers
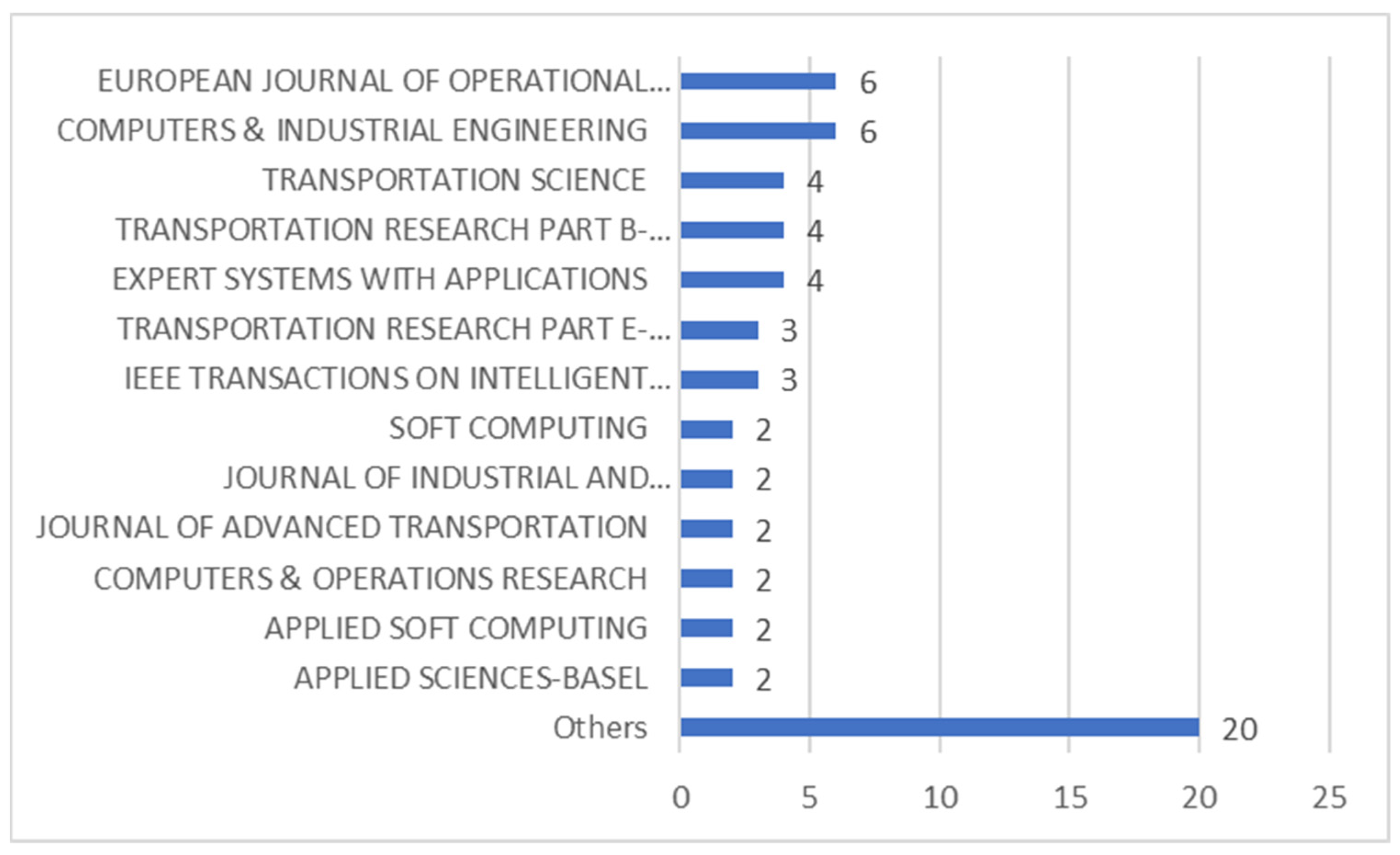
3.2. Used Instances
3.2.1. Literature Instances
3.2.2. Adapted Instances
3.2.3. Created Instances
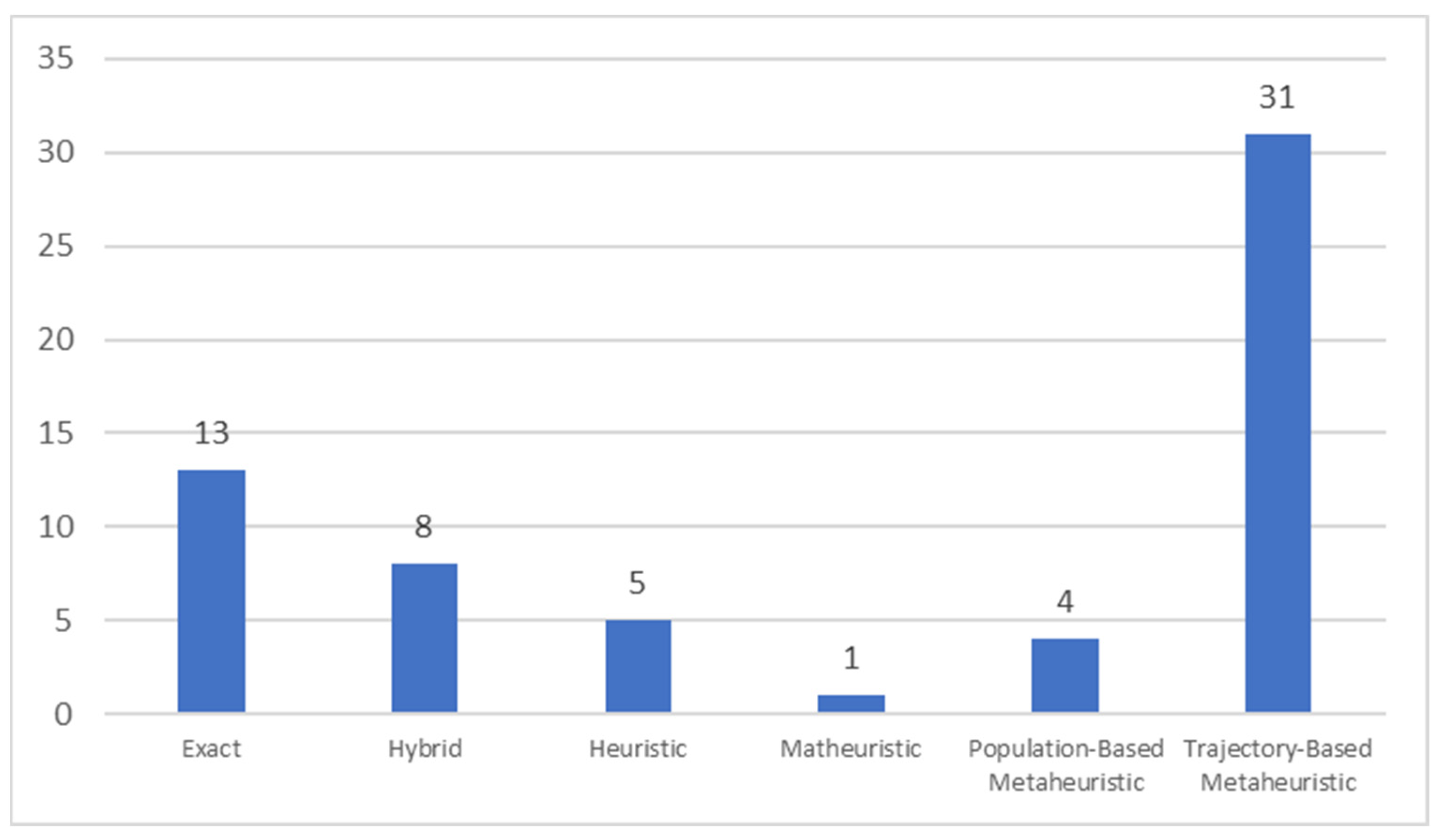
3.2.4. Accessibility of Instances and Trend in VRP Research with Satellites
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mardešić, N.; Erdelić, T.; Carić, T.; Đurasević, M. Review of Stochastic Dynamic Vehicle Routing in the Evolving Urban Logistics Environment. Mathematics 2024, 12, 28. [Google Scholar] [CrossRef]
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-Mile Delivery Concepts: A Survey from an Operational Research Perspective. Springer: Berlin/Heidelberg, Germany, 2021; Volume 43, ISBN 0123456789. [Google Scholar]
- Toth, P.; Vigo, D. Vehicle Routing, Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014; ISBN 9781611973587. [Google Scholar]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Encycl. Oper. Res. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. The Vehicle Routing Problem; SIAM: Philadelphia, PA, USA, 2002; ISBN 0898715792. [Google Scholar]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. Ann. Oper. Res. 2022, 314, 255–275. [Google Scholar] [CrossRef]
- Ulmer, M.W. Anticipation versus reactive reoptimization for dynamic vehicle routing with stochastic requests. Networks 2019, 73, 277–291. [Google Scholar] [CrossRef]
- Zuhanda, M.K.; Suwilo, S.; Sitompul, O.S.; Mardiningsih; Caraka, R.E.; Kim, Y.; Noh, M. Optimization of Vehicle Routing Problem in the Context of E-commerce Logistics Distribution. Eng. Lett. 2023, 31, 279–286. [Google Scholar]
- Chopra, S.; Meindl, P. Supply Chain Management: Strategy, Planning, and Operation; Pearson: New York, NY, USA, 2016; ISBN 9780133800203. [Google Scholar]
- Lo, S.C.; Chuang, Y.L. Vehicle Routing Optimization with Cross-Docking Based on an Artificial Immune System in Logistics Management. Mathematics 2023, 11, 811. [Google Scholar] [CrossRef]
- Neghabadi, P.D.; Samuel, K.E.; Espinouse, M.L. Systematic literature review on city logistics: Overview, classification and analysis. Int. J. Prod. Res. 2019, 57, 865–887. [Google Scholar] [CrossRef]
- Sutrisno, H.; Yang, C.L. A two-echelon location routing problem with mobile satellites for last-mile delivery: Mathematical formulation and clustering-based heuristic method. Ann. Oper. Res. 2023, 323, 203–228. [Google Scholar] [CrossRef]
- Enthoven, D.L.J.U.; Jargalsaikhan, B.; Roodbergen, K.J.; uit het Broek, M.A.J.; Schrotenboer, A.H. The two-echelon vehicle routing problem with covering options: City logistics with cargo bikes and parcel lockers. Comput. Oper. Res. 2020, 118, 104919. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Chen, J.; Bai, M. Two-echelon vehicle routing problem with satellite bi-synchronization. Eur. J. Oper. Res. 2021, 288, 775–793. [Google Scholar] [CrossRef]
- Dellaert, N.; Saridarq, F.D.; Van Woensel, T.; Crainic, T.G. Branch-and-price-based algorithms for the two-echelon vehicle routing problem with time windows. Transp. Sci. 2019, 53, 463–479. [Google Scholar] [CrossRef]
- Mühlbauer, F.; Fontaine, P. A parallelised large neighbourhood search heuristic for the asymmetric two-echelon vehicle routing problem with swap containers for cargo-bicycles. Eur. J. Oper. Res. 2021, 289, 742–757. [Google Scholar] [CrossRef]
- He, P.; Li, J. The two-echelon multi-trip vehicle routing problem with dynamic satellites for crop harvesting and transportation. Appl. Soft Comput. J. 2019, 77, 387–398. [Google Scholar] [CrossRef]
- Xue, G.; Wang, Y.; Guan, X.; Wang, Z. A combined GA-TS algorithm for two-echelon dynamic vehicle routing with proactive satellite stations. Comput. Ind. Eng. 2022, 164, 107899. [Google Scholar] [CrossRef]
- Dumez, D.; Tilk, C.; Irnich, S.; Lehuédé, F.; Olkis, K.; Péton, O. A matheuristic for a 2-echelon vehicle routing problem with capacitated satellites and reverse flows. Eur. J. Oper. Res. 2023, 305, 64–84. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, J. A branch-and-price algorithm for two-echelon electric vehicle routing problem. Complex Intell. Syst. 2023, 9, 2475–2490. [Google Scholar] [CrossRef]
- Grangier, P.; Gendreau, M.; Lehuédé, F.; Rousseau, L.M. An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization. Eur. J. Oper. Res. 2016, 254, 80–91. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Chen, K.; Lin, Q. The two-echelon city logistics system with on-street satellites. Comput. Ind. Eng. 2020, 139, 105577. [Google Scholar] [CrossRef]
- Yuan, P.; Wang, Y.; Su, M.; Yang, Z.; Zhang, Q. Markov decision process-based routing algorithm in hybrid Satellites/UAVs disruption-tolerant sensing networks. IET Commun. 2019, 13, 1415–1424. [Google Scholar] [CrossRef]
- Deng, X.; Zeng, S.; Chang, L.; Wang, Y.; Wu, X.; Liang, J.; Ou, J.; Fan, C. An Ant Colony Optimization-Based Routing Algorithm for Load Balancing in LEO Satellite Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 3032997. [Google Scholar] [CrossRef]
- Barkaoui, M.; Berger, J. A new hybrid genetic algorithm for the collection scheduling problem for a satellite constellation. J. Oper. Res. Soc. 2020, 71, 1390–1410. [Google Scholar] [CrossRef]
- Sluijk, N.; Florio, A.M.; Kinable, J.; Dellaert, N.; Van Woensel, T. Two-echelon vehicle routing problems: A literature review. Eur. J. Oper. Res. 2023, 304, 865–886. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Wang, F.; Bai, M. Ground-vehicle and unmanned-aerial-vehicle routing problems from two-echelon scheme perspective: A review. Eur. J. Oper. Res. 2021, 294, 1078–1095. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef]
- Mena-Reyes, J.F.; Vergara, F.; Linfati, R.; Escobar, J.W. Quantitative Techniques for Sustainable Decision Making in Forest-to-Lumber Supply Chain: A Systematic Review. Forests 2024, 15, 297. [Google Scholar] [CrossRef]
- Sina Mohri, S.; Mohammadi, M.; Van Woensel, T. Designing zero-emissions containerized last-mile delivery systems: A case study for melbourne. Transp. Res. Part C Emerg. Technol. 2024, 159, 104492. [Google Scholar] [CrossRef]
- Bevilaqua, A.; Bevilaqua, D.; Yamanaka, K. Parallel island based Memetic Algorithm with Lin–Kernighan local search for a real-life Two-Echelon Heterogeneous Vehicle Routing Problem based on Brazilian wholesale companies. Appl. Soft Comput. J. 2019, 76, 697–711. [Google Scholar] [CrossRef]
- Bayliss, C.; Bektaş, T.; Tjon-Soei-Len, V.; Rohner, R. Designing a multi-modal and variable-echelon delivery system for last-mile logistics. Eur. J. Oper. Res. 2023, 307, 645–662. [Google Scholar] [CrossRef]
- Villegas, J.G.; Prins, C.; Prodhon, C.; Medaglia, A.L.; Velasco, N. GRASP/VND and multi-start evolutionary local search for the single truck and trailer routing problem with satellite depots. Eng. Appl. Artif. Intell. 2010, 23, 780–794. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Chen, J.; Bai, M. Two-echelon vehicle routing problem with time windows and mobile satellites. Transp. Res. Part B Methodol. 2020, 138, 179–201. [Google Scholar] [CrossRef]
- Cortés-Murcia, D.L.; Prodhon, C.; Murat Afsar, H. The electric vehicle routing problem with time windows, partial recharges and satellite customers. Transp. Res. Part E Logist. Transp. Rev. 2019, 130, 184–206. [Google Scholar] [CrossRef]
- Zhou, L.; Baldacci, R.; Vigo, D.; Wang, X. A Multi-Depot Two-Echelon Vehicle Routing Problem with Delivery Options Arising in the Last Mile Distribution. Eur. J. Oper. Res. 2018, 265, 765–778. [Google Scholar] [CrossRef]
- Veenstra, M.; Roodbergen, K.J.; Coelho, L.C.; Zhu, S.X. A simultaneous facility location and vehicle routing problem arising in health care logistics in the Netherlands. Eur. J. Oper. Res. 2018, 268, 703–715. [Google Scholar] [CrossRef]
- Bartolini, E.; Schneider, M. A two-commodity flow formulation for the capacitated truck-and-trailer routing problem. Discret. Appl. Math. 2020, 275, 3–18. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, H.; Hu, R.; Qiu, Y. Location of electric vehicle charging stations: A perspective using the grey decision-making model. Energy 2019, 173, 548–553. [Google Scholar] [CrossRef]
- Jia, S.; Deng, L.; Zhao, Q.; Chen, Y. an Adaptive Large Neighborhood Search Heuristic for Multi-Commodity Two-Echelon Vehicle Routing Problem With Satellite Synchronization. J. Ind. Manag. Optim. 2023, 19, 1187–1210. [Google Scholar] [CrossRef]
- Marques, G.; Sadykov, R.; Deschamps, J.-C. A branch-cut-and-price approach for the single-trip and multi-trip two-echelon vehicle routing problem with time windows. Transp. Sci. 2022, 56, 1598–1617. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. Multi-depot Two-Echelon Fuel Minimizing Routing Problem with Heterogeneous Fleets: Model and Heuristic. Netw. Spat. Econ. 2019, 19, 969–1005. [Google Scholar] [CrossRef]
- Li, J.; Xu, M.; Sun, P. Two-echelon capacitated vehicle routing problem with grouping constraints and simultaneous pickup and delivery. Transp. Res. Part B Methodol. 2022, 162, 261–291. [Google Scholar] [CrossRef]
- Zhang, M.; Xiong, G.; Bao, S.; Meng, C. A Time-Division Distribution Strategy for the Two-Echelon Vehicle Routing Problem With Demand Blowout. J. Ind. Manag. Optim. 2022, 18, 2847–2872. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Lv, T.; Chang, X. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems. Transp. Res. Part B Methodol. 2016, 94, 169–188. [Google Scholar] [CrossRef]
- Yu, V.F.; Lin, S.W.; Zhou, L.; Baldacci, R. A fast simulated annealing heuristic for the multi-depot two-echelon vehicle routing problem with delivery options. Transp. Lett. 2024, 16, 921–932. [Google Scholar] [CrossRef]
- Marques, G.; Sadykov, R.; Deschamps, J.C.; Dupas, R. An improved branch-cut-and-price algorithm for the two-echelon capacitated vehicle routing problem. Comput. Oper. Res. 2020, 114, 104833. [Google Scholar] [CrossRef]
- Guimarães, J.C.F.; da Cunha, C.B. Math-Heuristic for the Capacitated Two-Echelon Vehicle Routing Problem. Pesqui. Operacional 2023, 43, e270829. [Google Scholar] [CrossRef]
- Huang, H.; Yang, S.; Li, X.; Hao, Z. An Embedded Hamiltonian Graph-Guided Heuristic Algorithm for Two-Echelon Vehicle Routing Problem. IEEE Trans. Cybern. 2022, 52, 5695–5707. [Google Scholar] [CrossRef]
- Zuhanda, M.K.; Suwilo, S.; Sitompul, O.S.; Mardiningsih. A Combination K-Means Clustering and 2-Opt Algorithm for Solving the Two Echelon E-Commerce Logistic Distribution. Logforum 2022, 18, 213–225. [Google Scholar] [CrossRef]
- Yu, V.F.; Nguyen, M.P.K.; Putra, K.; Gunawan, A.; Dharma, I.G.B.B. The Two-Echelon Vehicle Routing Problem with Transshipment Nodes and Occasional Drivers: Formulation and Adaptive Large Neighborhood Search Heuristic. J. Adv. Transp. 2022, 2022, 5603956. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Fan, J.; Wang, Z.; Zhen, L. Emergency logistics network optimization with time window assignment. Expert Syst. Appl. 2023, 214, 119145. [Google Scholar] [CrossRef]
- Jiang, D.; Li, X. Order fulfilment problem with time windows and synchronisation arising in the online retailing. Int. J. Prod. Res. 2021, 59, 1187–1215. [Google Scholar] [CrossRef]
- Li, H.; Bai, M.; Zhao, Y.; Dai, C. Vehicle flow formulation for two-echelon time-constrained vehicle routing problem. J. Manag. Sci. Eng. 2019, 4, 75–90. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, D.; Ji, B.; Li, S. Two-echelon vehicle routing problem with direct deliveries and access time windows. Expert Syst. Appl. 2024, 244, 121150. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, S. A variable neighborhood search algorithm with constraint relaxation for the two-echelon vehicle routing problem with simultaneous delivery and pickup demands. Soft Comput. 2022, 26, 8879–8896. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Xiong, Y.; Zhang, S.; Zhou, Y. Machine learning-based optimisation in a two-echelon logistics network for the dry port operation in China. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2252321. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Zhang, Z.; Li, J. Two-echelon vehicle routing problem with time windows and simultaneous pickup and delivery. Soft Comput. 2022, 26, 3345–3360. [Google Scholar] [CrossRef]
- Paul, A.; Kumar, R.S.; Rout, C.; Goswami, A. A bi-objective two-echelon pollution routing problem with simultaneous pickup and delivery under multiple time windows constraint. Opsearch 2021, 58, 962–993. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, C.; Lian, K.; Ren, Y.; Meng, L. A two-echelon fuzzy clustering based heuristic for large-scale bike sharing repositioning problem. Transp. Res. Part B Methodol. 2022, 160, 54–75. [Google Scholar] [CrossRef]
- Agárdi, A.; Kovács, L.; Bányai, T. Two-Echelon Vehicle Routing Problem with Recharge Stations. Transp. Telecommun. 2019, 20, 305–317. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, H. A two-echelon electric vehicle routing problem with time windows and battery swapping stations. Appl. Sci. 2021, 11, 10779. [Google Scholar] [CrossRef]
- Akbay, M.A.; Kalayci, C.B.; Blum, C.; Polat, O. Variable Neighborhood Search for the Two-Echelon Electric Vehicle Routing Problem with Time Windows. Appl. Sci. 2022, 12, 1014. [Google Scholar] [CrossRef]
- Ramírez-Villamil, A.; Montoya-Torres, J.R.; Jaegler, A.; Cuevas-Torres, J.M. Reconfiguration of last-mile supply chain for parcel delivery using machine learning and routing optimization. Comput. Ind. Eng. 2023, 184, 109604. [Google Scholar] [CrossRef]
- Yu, V.F.; Jodiawan, P.; Schrotenboer, A.H.; Hou, M.L. The two-echelon vehicle routing problem with time windows, intermediate facilities, and occasional drivers. Expert Syst. Appl. 2023, 234, 120945. [Google Scholar] [CrossRef]
- Liu, D.; Deng, Z.; Zhang, W.; Wang, Y.; Kaisar, E.I. Design of sustainable urban electronic grocery distribution network. Alex. Eng. J. 2021, 60, 145–157. [Google Scholar] [CrossRef]
- Liu, D.; Liu, D.; Deng, Z.; Mao, X.; Yang, Y.; Yang, Y.; Kaisar, E.I. Two-Echelon Vehicle-Routing Problem: Optimization of Autonomous Delivery Vehicle-Assisted E-Grocery Distribution. IEEE Access 2020, 8, 108705–108719. [Google Scholar] [CrossRef]
- Tian, X.D.; Hu, Z.H. A branch-and-price method for a two-echelon location routing problem with recommended satellites. Comput. Ind. Eng. 2023, 184, 109593. [Google Scholar] [CrossRef]
- Yıldız, E.A.; Karaoğlan, İ.; Altiparmak, F. An exact algorithm for Two-Echelon Location-Routing problem with simultaneous pickup and delivery. Expert Syst. Appl. 2023, 231, 120598. [Google Scholar] [CrossRef]
- Ramirez-Villamil, A.; Jaegler, A.; Montoya-Torres, J.R. Sustainable local pickup and delivery: The case of Paris. Res. Transp. Bus. Manag. 2022, 45, 100692. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, D.; Du, Y.; Liu, J.; Pardalos, P.M.; Qiao, J. The two-echelon production routing problem with cross-docking satellites. Transp. Res. Part E Logist. Transp. Rev. 2021, 147, 102210. [Google Scholar] [CrossRef]
- Mhamedi, T.; Andersson, H.; Cherkesly, M.; Desaulniers, G. A Branch-Price-and-Cut Algorithm for the Two-Echelon Vehicle Routing Problem with Time Windows. Transp. Sci. 2022, 56, 245–264. [Google Scholar] [CrossRef]
- Schmidt, J.; Tilk, C.; Irnich, S. Using public transport in a 2-echelon last-mile delivery network. Eur. J. Oper. Res. 2022, 317, 827–840. [Google Scholar] [CrossRef]
- Agnimo, V.; Ouhimmou, M.; Paquet, M.; Montecinos, J. Integrated strategic and tactical design of multi-echelon city distribution systems with vehicles synchronization: A case of the Greater Montréal area. Comput. Ind. Eng. 2023, 183, 109458. [Google Scholar] [CrossRef]
- Escobar-Vargas, D.; Crainic, T.G. Multi-attribute two-echelon location routing: Formulation and dynamic discretization discovery approach. Eur. J. Oper. Res. 2024, 314, 66–78. [Google Scholar] [CrossRef]
- Groß, P.O.; Ehmke, J.F.; Mattfeld, D.C. Interval travel times for robust synchronization in city logistics vehicle routing. Transp. Res. Part E Logist. Transp. Rev. 2020, 143, 102058. [Google Scholar] [CrossRef]
- Lan, Y.L.; Liu, F.; Ng, W.W.Y.; Gui, M.; Lai, C. Multi-Objective Two-Echelon City Dispatching Problem With Mobile Satellites and Crowd-Shipping. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15340–15353. [Google Scholar] [CrossRef]
- Lan, Y.L.; Liu, F.G.; Huang, Z.; Ng, W.W.Y.; Zhong, J. Two-Echelon Dispatching Problem with Mobile Satellites in City Logistics. IEEE Trans. Intell. Transp. Syst. 2022, 23, 84–96. [Google Scholar] [CrossRef]
- Yan, X.; Huang, H.; Hao, Z.; Wang, J. A Graph-Based Fuzzy Evolutionary Algorithm for Solving Two-Echelon Vehicle Routing Problems. IEEE Trans. Evol. Comput. 2020, 24, 129–141. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, S.; Ji, B.; Li, S. A Two-Echelon Capacitated Vehicle Routing Problem with Sharing Satellite Resources. IEEE Trans. Intell. Transp. Syst. 2024, 25, 12216–12227. [Google Scholar] [CrossRef]
- Accorsi, L.; Vigo, D. A hybrid metaheuristic for single truck and trailer routing problems. Transp. Sci. 2020, 54, 1351–1371. [Google Scholar] [CrossRef]
- da Cruz, H.F.A.; Salles da Cunha, A. The Profitable Single Truck and Trailer Routing Problem with Time Windows: Formulation, valid inequalities and branch-and-cut algorithms. Comput. Ind. Eng. 2023, 180, 109238. [Google Scholar] [CrossRef]
- Li, H.; Wang, F. Branch-price-and-cut for the truck–drone routing problem with time windows. Nav. Res. Logist. 2023, 70, 184–204. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Zhan, Z. Truck and Unmanned Vehicle Routing Problem with Time Windows: A Satellite Synchronization Perspective. J. Adv. Transp. 2022, 2022, 6599089. [Google Scholar] [CrossRef]
- Scherr, Y.O.; Hewitt, M.; Neumann Saavedra, B.A.; Mattfeld, D.C. Dynamic discretization discovery for the service network design problem with mixed autonomous fleets. Transp. Res. Part B Methodol. 2020, 141, 164–195. [Google Scholar] [CrossRef]
- Issi, G.C.; Linfati, R.; Escobar, J.W. Mathematical optimization model for truck scheduling in a distribution center with a mixed service-mode dock area. J. Adv. Transp. 2020, 2020, 8813372. [Google Scholar] [CrossRef]
- Perboli, G.; Tadei, R.; Vigo, D. The two-echelon capacitated vehicle routing problem: Models and math-based heuristics. Transp. Sci. 2011, 45, 364–380. [Google Scholar] [CrossRef]
- Crainic, T.G.; Perboli, G.; Mancini, S.; Tadei, R. Two-Echelon Vehicle Routing Problem: A satellite location analysis. Procedia-Soc. Behav. Sci. 2010, 2, 5944–5955. [Google Scholar] [CrossRef]
- Hemmelmayr, V.C.; Cordeau, J.F.; Crainic, T.G. An adaptive large neighborhood search heuristic for Two-Echelon Vehicle Routing Problems arising in city logistics. Comput. Oper. Res. 2012, 39, 3215–3228. [Google Scholar] [CrossRef]
- Chao, I.M. A tabu search method for the truck and trailer routing problem. Comput. Oper. Res. 2002, 29, 33–51. [Google Scholar] [CrossRef]
- Lin, S.W.; Yu, V.F.; Chou, S.Y. A note on the truck and trailer routing problem. Expert Syst. Appl. 2010, 37, 899–903. [Google Scholar] [CrossRef]
- Voigt, S.; Frank, M.; Fontaine, P.; Kuhn, H. Hybrid adaptive large neighborhood search for vehicle routing problems with depot location decisions. Comput. Oper. Res. 2022, 146, 105856. [Google Scholar] [CrossRef]
- Archetti, C.; Savelsbergh, M.; Speranza, M.G. The Vehicle Routing Problem with Occasional Drivers. Eur. J. Oper. Res. 2016, 254, 472–480. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Lahrichi, N.; Rei, W. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems. Oper. Res. 2012, 60, 611–624. [Google Scholar] [CrossRef]
- Huang, Y.; Savelsbergh, M.; Zhao, L. Designing logistics systems for home delivery in densely populated urban areas. Transp. Res. Part B Methodol. 2018, 115, 95–125. [Google Scholar] [CrossRef]
- Yu, V.F.; Jodiawan, P.; Hou, M.L.; Gunawan, A. Design of a two-echelon freight distribution system in last-mile logistics considering covering locations and occasional drivers. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102461. [Google Scholar] [CrossRef]
- Baldacci, R.; Mingozzi, A.; Roberti, R.; Calvo, R.W. An exact algorithm for the two-echelon capacitated vehicle routing problem. Oper. Res. 2013, 61, 298–314. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Tuzun, D.; Burke, L.I. Two-phase tabu search approach to the location routing problem. Eur. J. Oper. Res. 1999, 116, 87–99. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Gendreau, M.; Laporte, G. A tabu search heuristic for periodic and multi-depot vehicle routing problems. Networks 1997, 30, 105–119. [Google Scholar] [CrossRef]
- Breunig, U.; Baldacci, R.; Hartl, R.F.; Vidal, T. The electric two-echelon vehicle routing problem. Comput. Oper. Res. 2019, 103, 198–210. [Google Scholar] [CrossRef]
- Adulyasak, Y.; Cordeau, J.F.; Jans, R. Formulations and branch-and-cut algorithms for multivehicle production and inventory routing problems. INFORMS J. Comput. 2014, 26, 103–120. [Google Scholar] [CrossRef]
- Lin, S.W.; Yu, V.F.; Lu, C.C. A simulated annealing heuristic for the truck and trailer routing problem with time windows. Expert Syst. Appl. 2011, 38, 15244–15252. [Google Scholar] [CrossRef]
- Desaulniers, G.; Errico, F.; Irnich, S.; Schneider, M. Exact Algorithms for Electric Vehicle-Routing Problems with Time Windows. Oper. Res. 2016, 64, 1388–1405. [Google Scholar] [CrossRef]
- Taillard, É.D. A heuristic column generation method for the heterogeneous fleet VRP. RAIRO-Oper. Res. 1999, 33, 1–14. [Google Scholar] [CrossRef]
- Schneider, M.; Löffler, M. Large composite neighborhoods for the capacitated location-routing problem. Transp. Sci. 2019, 53, 301–318. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Prins, C.; Prodhon, C. Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking. Eur. J. Oper. Res. 2012, 216, 113–126. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Prins, C.; Prodhon, C. A multi-start evolutionary local search for the two-echelon location routing problem. In Hybrid Metaheuristics, Processings of the 7th International Workshop, HM 2010, Vienna, Austria, 1–2 October 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 88–102. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Guan, X.; Xu, M.; Liu, Y.; Wang, H. Two-echelon collaborative multi-depot multi-period vehicle routing problem. Expert Syst. Appl. 2021, 167, 114201. [Google Scholar] [CrossRef]
- Breunig, U.; Schmid, V.; Hartl, R.F.; Vidal, T. A large neighbourhood based heuristic for two-echelon routing problems. Comput. Oper. Res. 2016, 76, 208–225. [Google Scholar] [CrossRef]
- Liu, T.; Luo, Z.; Qin, H.; Lim, A. A branch-and-cut algorithm for the two-echelon capacitated vehicle routing problem with grouping constraints. Eur. J. Oper. Res. 2018, 266, 487–497. [Google Scholar] [CrossRef]
- Crainic, T.G.; Mancini, S.; Perboli, G.; Tadei, R. Clustering-Based Heuristics for the Two-Echelon Vehicle Routing Problem; CIRRELT Publ.: Montréal, QC, USA, 2008; pp. 179–190. [Google Scholar]
- Xu, P.; Lan, D.A.N.; Yang, H.; Kim, H.; Shin, I. Ship Formation and Route Optimization Design Based on Improved PSO and D-P Algorithm. IEEE Access 2025, 13, 15529–15546. [Google Scholar] [CrossRef]
- Li, J.; Liu, R.; Wang, R. Handling dynamic capacitated vehicle routing problems based on adaptive genetic algorithm with elastic strategy. Swarm Evol. Comput. 2024, 86, 101529. [Google Scholar] [CrossRef]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. J. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
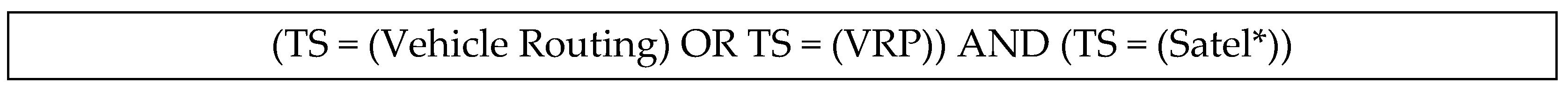


| Criteria | Description |
|---|---|
| Language | English |
| Publication year | Between 2019 and 2024 (Closed June 19) |
| Publication Type | Peer-reviewed journal article |
| Subject/content | Research related to the Vehicle-Routing Problem with the use of satellites. The articles must relate the use of the satellite keyword in some VRP variants. |
| Database | Scopus, Web of Science Core Collections |
| Criteria | Description |
|---|---|
| Publication Type | Journal papers Survey/Review papers |
| Subject/content | All applications of the satellite concept belonging to VRP. Applications only considering the non-model satellite concept. Research topic with quantitative techniques for decision-making. |
| Access | Papers only with full access. |
| Stage Identification | Process | Number of Papers |
|---|---|---|
| Screening | Scopus and WoS database search sting downloading | 2593 |
| Screening | Review of papers published in Scopus and WoS | −1107 |
| Sub-total | 1486 | |
| Screening | Papers excluided for not being VRP, for example, low earth orbit (LEO) and others | −1413 |
| Sub-total | 73 | |
| Screening | Papers excluded by other criteria, such as the following:
| −11 |
| Included | Total | 62 |
| Categories | |||||
|---|---|---|---|---|---|
| Intermediate Facilities or Depots | Cross-Docking | Satellite Depots | Satellite Customer | ||
| Variants | Fixed | Mobile | |||
| Path Splitting | [13,15,18,19,20,30,40,41,42,43,44,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69] | [8,14,16,31,70,71,72,73,74,75] | [17,22,32,76,77,78,79,80] | [12,34] | |
| Location | [66,68,69] | [74,75] | [12] | ||
| Trailer Transfer | [38,81,82,83] | [84] | |||
| Electromobility | [20,61,62,63,66,67] | [85] | [34,83,84] | [35,84] | |
| Temporal Synchronization | [40] | [14,74,75] | [34,83] | ||
| Multi Trip | [19,41] | [17] | |||
| Multi-depot | [40,42,46,64] | [8,75] | [32] | ||
| Pickup and Delivery | [19,43,56,57,58,59,69] | ||||
| Random demands | [18,44] | ||||
| Time Constraints | [15,19,41,52,53,54,55,58,59,62,63,65] | [14,72,73,75] | [32,76] | [34,82,83] | [35,84] |
| Delivery Options | [13,30,43,46,50,57,60,64,66] | [8,16] | [32,78] | [12] | |
| Instance | Frequency | Research | Usage Percentage |
|---|---|---|---|
| [87] | 5 | [49,51,64,67,79] | 5.95 |
| [88] | 4 | [49,59,67,79] | 4.76 |
| [89] | 4 | [49,51,65,79] | 4.76 |
| [15] | 3 | [41,55,72] | 3.57 |
| [26] | 2 | [48,80] | 2.38 |
| [90] | 2 | [38,81] | 2.38 |
| [91] | 2 | [38,81] | 2.38 |
| [92] | 1 | [48] | 1.19 |
| [93] | 1 | [51] | 1.19 |
| [94] | 1 | [52] | 1.19 |
| [95] | 1 | [65] | 1.19 |
| [96] | 1 | [65] | 1.19 |
| [21] | 1 | [41] | 1.19 |
| [37] | 1 | [13] | 1.19 |
| [41] | 1 | [19] | 1.19 |
| [97] | 1 | [65] | 1.19 |
| [98] | 1 | [52] | 1.19 |
| [99] | 1 | [35] | 1.19 |
| [100] | 1 | [81] | 1.19 |
| [33] | 1 | [81] | 1.19 |
| [38] | 1 | [81] | 1.19 |
| [101] | 1 | [81] | 1.19 |
| http://www.bernabe.dorronsoro.es/vrp/ (accessed on 24 January 2025) | 1 | [18] | 1.19 |
| http://prodhonc.free.fr/Instances/instancesLRP2E_us.htm (accessed on 24 January 2025) | 1 | [12] | 1.19 |
| http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/ (accessed on 24 January 2025) | 1 | [18] | 1.19 |
| https://prolog.univie.ac.at/research/TwoEVRP/ (accessed on 24 January 2025) | 1 | [49] | 1.19 |
| Instance | Frencuency | Research | Usage Percentage |
|---|---|---|---|
| [15] | 3 | [55,58,75] | 3.57 |
| [98] | 3 | [34,83,84] | 3.57 |
| [87] | 2 | [42,67] | 2.38 |
| [102] | 2 | [20,62] | 2.38 |
| [103] | 1 | [71] | 1.19 |
| [104] | 1 | [82] | 1.19 |
| [105] | 1 | [20] | 1.19 |
| [106] | 1 | [31] | 1.19 |
| [107] | 1 | [47] | 1.19 |
| [108] | 1 | [78] | 1.19 |
| [109] | 1 | [69] | 1.19 |
| [36] | 1 | [46] | 1.19 |
| [110] | 1 | [57] | 1.19 |
| [111] | 1 | [56] | 1.19 |
| [89] | 1 | [58] | 1.19 |
| [112] | 1 | [43] | 1.19 |
| [113] | 1 | [53] | 1.19 |
| [99] | 1 | [63] | 1.19 |
| https://www.bernabe.dorronsoro.es/vrp/ (accessed on 24 January 2025) | 1 | [77] | 1.19 |
| http://vrp.galgos.inf.puc-rio.br/ (accessed on 24 January 2025) | 1 | [68] | 1.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto-Concha, R.; Escobar, J.W.; Morillo-Torres, D.; Linfati, R. The Vehicle-Routing Problem with Satellites Utilization: A Systematic Review of the Literature. Mathematics 2025, 13, 1092. https://doi.org/10.3390/math13071092
Soto-Concha R, Escobar JW, Morillo-Torres D, Linfati R. The Vehicle-Routing Problem with Satellites Utilization: A Systematic Review of the Literature. Mathematics. 2025; 13(7):1092. https://doi.org/10.3390/math13071092
Chicago/Turabian StyleSoto-Concha, Raúl, John Willmer Escobar, Daniel Morillo-Torres, and Rodrigo Linfati. 2025. "The Vehicle-Routing Problem with Satellites Utilization: A Systematic Review of the Literature" Mathematics 13, no. 7: 1092. https://doi.org/10.3390/math13071092
APA StyleSoto-Concha, R., Escobar, J. W., Morillo-Torres, D., & Linfati, R. (2025). The Vehicle-Routing Problem with Satellites Utilization: A Systematic Review of the Literature. Mathematics, 13(7), 1092. https://doi.org/10.3390/math13071092







