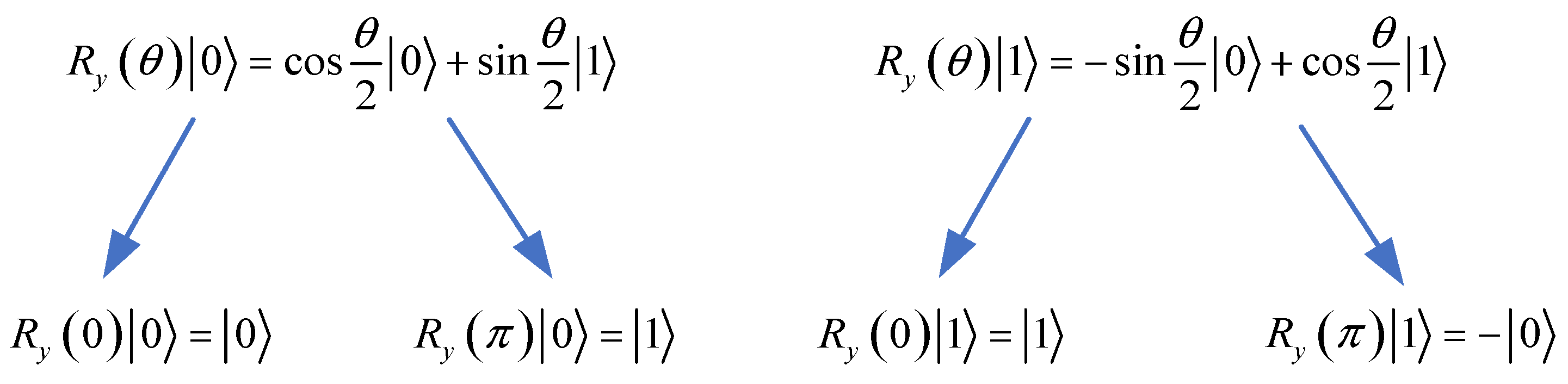Quantum Privacy Comparison with R_y Rotation Operation

Abstract

This paper presents a novel quantum privacy comparison (QPC) protocol that employs R_y rotation operations to enable two participants to securely compare their binary secrets without disclosing the actual data to any party except for the comparison result. In this protocol, classical bits 0 and 1 are encoded as rotation angles 0 and π, respectively, using the R_y rotation operation. The participants apply these rotations to quantum sequences received from a semi-honest third party (TP) and return the encoded sequences to the TP. The TP then performs quantum measurements to determine the comparison result and announces it to the participants, ensuring fairness and privacy throughout the process. By leveraging the principles of quantum mechanics, the protocol is resistant to various quantum attack strategies, providing robust security against both external adversaries and insider threats. The protocol utilizes Bell states as quantum resources, R_y rotation operations for encoding classical information, and quantum measurements to derive the comparison result, making it experimentally feasible with current quantum technologies. Simulations conducted on a quantum platform validate the protocol’s practicality. Furthermore, each Bell state is used to compare one bit of binary information, achieving a qubit efficiency of 50%.

1. Introduction

As quantum computing technology advances at an unprecedented rate, it raises significant concerns about the security and privacy of traditional encryption methods. These methods, which have long been the foundation of data security, are increasingly viewed as inadequate in the face of quantum algorithms. Notably, the Shor algorithm [1] can efficiently factor large integers, rendering widely used encryption schemes like RSA insecure. Similarly, the Grover algorithm [2] provides a quadratic speedup for searching unsorted databases, posing a threat to symmetric cryptographic systems. These developments highlight the urgent need for more secure alternatives to classical cryptography.

Quantum cryptography has emerged as a promising solution, leveraging the principles of quantum mechanics to provide theoretically unbreakable security. Unlike classical methods, which depend on mathematical complexity, quantum cryptography ensures security through physical principles such as the no-cloning theorem and the uncertainty principle. This has led to the development of various quantum cryptographic applications, including quantum key distribution (QKD) [3,4,5,6], quantum secret sharing (QSS) [7,8,9,10], quantum private set intersection (QPSI) [11,12,13], and quantum secure direct communication (QSDC) [14,15,16].

A foundational problem in secure multi-party computation (MPC) is the millionaire problem introduced by Andrew Yao in 1982 [17]. This problem illustrates how two parties can compare their private inputs (e.g., wealth) without revealing the actual values. Building on the millionaire problem, Boudot et al. [18] proposed the socialist millionaire problem, which focuses on determining whether two private inputs are equal rather than comparing their magnitudes. However, as Lo [19] pointed out, securely computing equality in a two-party setting introduces vulnerabilities. To address this issue, a semi-honest third party (TP) is introduced to facilitate the comparison while ensuring privacy.

Traditional privacy comparison protocols rely on the computational complexity of mathematical problems, such as factoring integers or computing discrete logarithms. However, the advent of quantum computing has rendered these assumptions obsolete, as quantum algorithms can efficiently solve these problems. To address these challenges, quantum privacy comparison (QPC) protocols have been developed, leveraging quantum mechanics to ensure secure comparisons.

The first QPC protocol [20] is designed by utilizing EPR (Einstein–Podolsky–Rosen) pairs as quantum resources and incorporating decoy photons to detect potential eavesdropping. The qubit efficiency of this initial QPC protocol is reported to be 25%. Chen et al. [21] proposed a QPC protocol that leverages Greenberger–Horne–Zeilinger (GHZ) states, which are a type of entangled quantum state involving multiple particles. The protocol employs single-particle measurements, which simplify the measurement process, and achieves a qubit efficiency of 33%. Ju et al. [22] utilized four-particle entangled states and single-particle measurements for developing their QPC protocol, and this protocol can achieve a qubit efficiency of 25% with one four-particle entangled state comparing one classical bit. Ye and Ji [23] utilized five-particle entangled states, Bell measurements, and single-particle measurements for developing their QPC protocol, and this protocol can achieve a qubit efficiency of 40% with one five-particle entangled state comparing two classical bits. Sun [24] utilized six-particle entangled states and Bell measurements for developing the QPC protocol, and this protocol can achieve a qubit efficiency of 33% with one six-particle entangled state comparing two classical bits. Ji et al. [25] utilized seven-particle entangled states, Bell measurements, and single-particle measurements for developing their QPC protocol, and this protocol can achieve a qubit efficiency of 29% with one seven-particle entangled state comparing two classical bits. Fan et al. [26] utilized eight-particle entangled states and single-particle measurements for developing their QPC protocol, and this protocol can achieve a qubit efficiency of 25% with one eight-particle entangled state comparing two classical bits. To date, numerous QPC protocols [27,28,29,30,31,32] have been developed utilizing a variety of quantum states, reflecting the diverse approaches being taken to facilitate comparison.

While multi-particle entangled states are crucial for the design of QPC protocols, the preparation and manipulation of multi-particle entangled states remain experimentally challenging, limiting their practicality. Exploring simpler quantum states, such as Bell states and single photons, presents promising avenues for enhancing the practicality of quantum cryptographic systems, ensuring they can meet the demands of real-world applications. Additionally, many existing protocols achieve suboptimal qubit efficiencies, often below 50%, which increases resource demands and implementation costs.

In this paper, we propose a QPC protocol that utilizes R_y rotation operations to securely compare binary secrets between two participants, demonstrating improved performance in both practicality and efficiency. The main contributions of this work are as follows:

(1)

We propose a QPC protocol that employs R_y rotation operations, enabling two participants to securely compare their binary secrets without disclosing the actual data to any party other than the comparison result.

(2)

By leveraging the principles of quantum mechanics, the protocol is designed to resist various quantum attack strategies, including external eavesdropping and insider threats.

(3)

The proposed protocol utilizes Bell states as quantum resources and R_y rotation operations to encode classical bits into quantum states, which are easier to implement. Simulations conducted on a quantum platform validate the protocol’s feasibility.

(4)

Our protocol achieves a qubit efficiency of 50%, as each Bell state in the protocol compares one bit of binary information.

The remainder of this paper is organized as follows. Section 2 introduces the properties of R_y rotation operation and Bell states. Section 3 details the proposed QPC protocol. Section 4 presents the simulation results conducted on a quantum platform. Section 5 analyzes the protocol’s security against external and insider attacks. Section 6 provides a discussion of the protocol’s qubit efficiency. Finally, Section 7 concludes the paper by summarizing the key findings.

2. Properties of Rotation Operation and Bell States

The rotation operation $R_y\left(\theta \right)$ [33] around the y-basis is given by

$$R_y\left(\theta \right)=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)$$

(1)

The $R_y\left(\theta \right)$ is a unitary operation, satisfying ${R_y}^{†}\left(\theta \right)R_y\left(\theta \right)=R_y\left(-\theta \right)R_y\left(\theta \right)=I$, where I is the identity matrix. This operation can be viewed as an encryption method, with the secret key $\theta$ serving as the encryption key. For instance, when applied to the basis states $\left|1\right.⟩$ or $\left|0\right.⟩$, the rotation operation yields the following:

$$R_y\left(\theta \right)\left|1\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}-\sin {\displaystyle \frac{\theta }{2}}\\ \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)=-\sin {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\cos {\displaystyle \frac{\theta }{2}}\left|1\right.〉$$

(2)

$$R_y\left(\theta \right)\left|0\right.〉=\left(\begin{array}{cc}\cos {\displaystyle \frac{\theta }{2}}& -\sin {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}& \cos {\displaystyle \frac{\theta }{2}}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\cos {\displaystyle \frac{\theta }{2}}\\ \sin {\displaystyle \frac{\theta }{2}}\end{array}\right)=\cos {\displaystyle \frac{\theta }{2}}\left|0\right.〉+\sin {\displaystyle \frac{\theta }{2}}\left|1\right.〉$$

(3)

We can conclude that the rotation operation performed on the quantum states $\left|1\right.⟩$ or $\left|0\right.⟩$ transforms them into unknown quantum states, thereby masking the original states $\left|1\right.⟩$ or $\left|0\right.⟩$.

For $\theta =\pi$, we have $R_y\left(\pi \right)\left|0\right.⟩=\left|1\right.⟩$ and $R_y\left(\pi \right)\left|1\right.⟩=\left|0\right.⟩$, ignoring the global phase, which has no observable effect. The effect of $R_y\left(\theta \right)$ on qubits $\left|0\right.⟩$ and $\left|1\right.⟩$ is shown in Figure 1.

For any two rotation angles ${\theta }_1$ and ${\theta }_2$, the following relationship holds:

$$R_y\left({\theta }_2\right)R_y\left({\theta }_1\right)=\left(\begin{array}{cc}\cos {\displaystyle \frac{{\theta }_2}{2}}& -\sin {\displaystyle \frac{{\theta }_2}{2}}\\ \sin {\displaystyle \frac{{\theta }_2}{2}}& \cos {\displaystyle \frac{{\theta }_2}{2}}\end{array}\right)\left(\begin{array}{cc}\cos {\displaystyle \frac{{\theta }_1}{2}}& -\sin {\displaystyle \frac{{\theta }_1}{2}}\\ \sin {\displaystyle \frac{{\theta }_1}{2}}& \cos {\displaystyle \frac{{\theta }_1}{2}}\end{array}\right)=\left(\begin{array}{cc}\cos \left({\displaystyle \frac{{\theta }_2}{2}}+{\displaystyle \frac{{\theta }_1}{2}}\right)& -\sin \left({\displaystyle \frac{{\theta }_2}{2}}+{\displaystyle \frac{{\theta }_1}{2}}\right)\\ \sin \left({\displaystyle \frac{{\theta }_2}{2}}+{\displaystyle \frac{{\theta }_1}{2}}\right)& \cos \left({\displaystyle \frac{{\theta }_2}{2}}+{\displaystyle \frac{{\theta }_1}{2}}\right)\end{array}\right)=R_y\left({\theta }_2+{\theta }_1\right)$$

(4)

Notably, applying $R_y\left(\theta \right)$ followed by $R_y\left(-\theta \right)$ to any single-qubit state $\left|\psi \right.⟩$ retrieves the original state $\left|\psi \right.⟩$.

The four Bell states, which represent maximally entangled states of two qubits, are defined as follows:

$$\left|{\Phi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.〉+\left|11\right.〉\right)$$

(5)

$$\left|{\Phi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|00\right.〉-\left|11\right.〉\right)$$

(6)

$$\left|{\Psi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|01\right.〉+\left|10\right.〉\right)$$

(7)

$$\left|{\Psi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|01\right.〉-\left|10\right.〉\right)$$

(8)

When two rotation operations $R_y\left(0\right)$ or $R_y\left(\pi \right)$ are successively applied to the first particle of a Bell state, the resulting states are summarized in

Table 1. Resulting Bell states after applying two rotation operations.

Two Rotation Operations	$\left|{\mathit{\Phi }}^{+}\right.⟩$	$\left|{\mathit{\Phi }}^{-}\right.⟩$	$\left|{\mathit{\Psi }}^{+}\right.⟩$	$\left|{\mathit{\Psi }}^{-}\right.⟩$
$R_y\left(0\right)R_y\left(0\right)$	$\left|{\Phi }^{+}\right.⟩$	$\left|{\Phi }^{-}\right.⟩$	$\left|{\Psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$
$R_y\left(0\right)R_y\left(\pi \right)$	$\left|{\Psi }^{-}\right.⟩$	$\left|{\Psi }^{+}\right.⟩$	$\left|{\Phi }^{-}\right.⟩$	$\left|{\Phi }^{+}\right.⟩$
$R_y\left(\pi \right)R_y\left(0\right)$	$\left|{\Psi }^{-}\right.⟩$	$\left|{\Psi }^{+}\right.⟩$	$\left|{\Phi }^{-}\right.⟩$	$\left|{\Phi }^{+}\right.⟩$
$R_y\left(\pi \right)R_y\left(\pi \right)$	$\left|{\Phi }^{+}\right.⟩$	$\left|{\Phi }^{-}\right.⟩$	$\left|{\Psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$

.

From Table 1, we observe that the Bell state remains unchanged only when the same two rotation operations are applied successively to the first particle.

3. Two-Party QPC Protocol

The proposed two-party quantum privacy comparison (QPC) protocol involves three entities:

Semi-honest third party (TP): The TP generates and distributes the necessary quantum resources, such as Bell states, to Alice and Bob. The TP obtains the comparison result based on the operations performed by Alice and Bob but does not access their private inputs. Meanwhile, the TP adheres to the protocol and does not collude with the participants.

Alice: Alice encodes her secret X using rotation operations on the shared Bell states, transforming the quantum states to reflect her secret without revealing it.

Bob: similarly, Bob encodes his secret Y using rotation operations on the shared Bell states, ensuring his secret remains confidential.

The goal of the protocol is to determine whether X and Y are equal. The binary representations of X and Y are $X=\left(x_{N-1}, x_{N-2},\cdots ,x_0\right)$ and $Y=\left(y_{N-1}, y_{N-2},\cdots {,y}_0\right)$, where $x_i,y_i\in \left\{\mathrm{0,1}\right\}$ for $i=\mathrm{0,1},\cdots ,N-1$.

Protocol Steps

Step 1. Preparation of Quantum Resources

The TP prepares N Bell states, randomly chosen from Equations (1)–(4), and records their states. She organizes them into two sequences: $S_1$ (composed by all first qubits) and $S_2$(composed by all second qubits). To prevent eavesdropping, the TP inserts m decoy photons, randomly chosen from $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$, into $S_1$ to form a modified sequence ${S^{\prime }}_1$. Finally, she sends ${S^{\prime }}_1$ to Alice and retains $S_2$.

Step 2. Eavesdropping Detection (Alice and TP)

After receiving ${S^{\prime }}_1$, Alice confirms receipt. The TP announces the positions and measurement bases of the decoy photons. Alice measures the decoy photons and reports the results to the TP, who computes the error rate by comparing the consistency of the measurement results with the initially prepared decoy photons. If the error rate exceeds a predefined threshold, the protocol is aborted; otherwise, it proceeds.

Step 3. Encoding by Alice

Alice removes the decoy photons from ${S^{\prime }}_1$ to recover $S_1$, and performs the following operations:

(1)

Encodes her secret X by applying $R_y\left(0\right)$ or $R_y\left(\pi \right)$ on the i-th qubit of $S_1$, depending on the value of $x_i$. If $x_i=0$, then $R_y\left(0\right)$ is applied; otherwise, $R_y\left(\pi \right)$ is used. The new generated sequence is denoted as $S_A$.

(2)

Generates a secret key $K_A=\left(a_{N-1},a_{N-2},\cdots ,a_0\right)$, where $a_i\in \left.[\mathrm{0,2}\pi \right)$.

(3)

Applies $R_y\left(a_i\right)$ to the i-th qubit of $S_A$ to obtain a new sequence $E{S}_A$. This process can be considered an encryption of $S_A$ using $a_i$ as the encryption key.

(4)

Inserts m decoy photons, randomly chosen from $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$, into $E{S}_A$ to form a modified sequence ${ES}_A^{\prime }$.

(5)

Sends ${ES}_A^{\prime }$ to Bob.

Step 4. Encoding by Bob

Bob performs eavesdropping detection on ${ES}_A^{\prime }$ as described in Step 2. If the quantum channel is secure, Alice announces $K_A$. Bob removes the decoy photons from ${ES}_A^{\prime }$ to recover ${ES}_A$, and performs the following operations:

(1)

Applies $R_y\left({-a}_i\right)$ to the i-th qubit of $E{S}_A$ to obtain $S_A$. This process can be considered a decryption of ${ES}_A$ using $-a_i$ as the decryption key.

(2)

Encodes his secret Y using $R_y\left(0\right)$ or $R_y\left(\pi \right)$ on the i-th qubit of $S_A$, depending on the value of $y_i$. If $y_i=0$, then $R_y\left(0\right)$ is applied; otherwise, $R_y\left(\pi \right)$ is used. The new generated sequence is denoted as $S_B$.

(3)

Generates a secret key $K_B=\left(b_{N-1},b_{N-2},\cdots ,b_0\right)$, where $b_i\in \left.[\mathrm{0,2}\pi \right)$.

(4)

Applies $R_y\left(b_i\right)$ to the i-th qubit of $S_B$ to obtain a new sequence $E{S}_B$. This process can be considered an encryption of $S_B$ using $b_i$ as the encryption key.

(5)

Inserts m decoy photons, randomly chosen from $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$, to form a modified sequence ${ES}_B^{\prime }$.

(6)

Sends ${ES}_B^{\prime }$ to the TP.

Step 5. Comparison by TP

The TP performs eavesdropping detection on ${ES\prime }_B$ as described in Step 2. If the quantum channel is secure, Bob announces $K_B$. The TP removes the decoy photons from ${ES\prime }_B$ to recover ${ES}_B$, and performs the following operations:

(1)

Applies $R_y\left({-b}_i\right)$ to the i-th qubit of ${ES}_B$ to obtain $S_B$. This process can be considered a decryption of ${ES}_B$ using $-b_i$ as the decryption key.

(2)

Performs Bell measurements on $S_B$ and $S_2$ to obtain the measurement results.

(3)

Compares all measurement results with the initial Bell states. If they are identical, then $X=Y$; otherwise, $X\ne Y$.

4. Simulation

To validate the feasibility and correctness of the proposed protocol, we consider a scenario where Alice holds a secret $X=5$ and Bob holds a secret $Y=3$. The goal is to determine whether X and Y are equal. It is evident that $X\ne Y$, and this example serves to verify the correctness and practicality of the protocol.

The binary representations of X and Y are $X=\left(\mathrm{1,0,1}\right)$ and $Y=\left(\mathrm{0,1,1}\right)$, respectively. Since both the binary representations of X and Y are 3 bits long, the TP prepares three Bell states: $\left\{\left|{\Phi }^{+}\right.⟩,\left|{\Phi }^{-}\right.⟩,\left|{\Psi }^{+}\right.⟩\right\}$. Assume that Alice’s secret key is $K_A=\left({\displaystyle \frac{\pi }{3}},{\displaystyle \frac{3\pi }{4}},{\displaystyle \frac{\pi }{2}}\right)$ and Bob’s secret key is $K_B=\left({\displaystyle \frac{5\pi }{4}},{\displaystyle \frac{3\pi }{2}},{\displaystyle \frac{7\pi }{6}}\right)$. To perform Bell measurements, we use a combination of Hadamard and CNOT gates, followed by measurements on the computational basis. The outcomes of the measurement provide information about the original state of the two qubits:

(1)

If the measurement yields 00, the state was projected onto $\left|{\Phi }^{+}\right.⟩$.

(2)

If the measurement yields 01, the state was projected onto $\left|{\Phi }^{-}\right.⟩$.

(3)

If the measurement yields 10, the state was projected onto $\left|{\Psi }^{+}\right.⟩$.

(4)

If the measurement yields 11, the state was projected onto $\left|{\Psi }^{-}\right.⟩$.

The three Bell states $\left\{\left|{\Phi }^{+}\right.⟩,\left|{\Phi }^{-}\right.⟩,\left|{\Psi }^{+}\right.⟩\right\}$ are generated by applying the following operations to qubits q[0]–q[5]:

• q[0]: Hadamard (H) and Controlled- NOT (CNOT) as the control bit;
• q[1]: Controlled- NOT (CNOT) as the target bit;
• q[2]: Hadamard (H) and Controlled- NOT (CNOT) as the control bit;
• q[3]: Controlled- NOT (CNOT) as the target bit;
• q[4]: Hadamard (H) and Controlled- NOT (CNOT) as the control bit;
• q[5]: Controlled- NOT (CNOT) as the target bit.

Here, qubits q[0] and q[1] are used to generate $\left|{\Phi }^{+}\right.⟩$, q[2] and q[3] for $\left|{\Phi }^{-}\right.⟩,$ q[4] and q[5] for $\left|{\Psi }^{+}\right.⟩$.

Alice applies the following quantum operations to encode her secret Y and encrypt the encoded states with the secret key $K_A$:

• q[0]: $R_y\left(\pi \right)$ and $R_y\left({\displaystyle \frac{\pi }{3}}\right)$;
• q[1]: Nothing;
• q[2]: $R_y\left(0\right)$ and $R_y\left({\displaystyle \frac{3\pi }{4}}\right)$;
• q[3]: Nothing;
• q[4]: $R_y\left(\pi \right)$ and $R_y\left({\displaystyle \frac{\pi }{2}}\right)$;
• q[5]: Nothing.

Bob applies the following quantum operations to encode his secret X and encrypt the encoded states with the secret key $K_B$:

• q[0]: $R_y\left(-{\displaystyle \frac{\pi }{3}}\right),$ $R_y\left(0\right)$ and $R_y\left({\displaystyle \frac{5\pi }{4}}\right)$;
• q[1]: Nothing;
• q[2]: $R_y\left(-{\displaystyle \frac{3\pi }{4}}\right),$ $R_y\left(\pi \right)$ and $R_y\left({\displaystyle \frac{3\pi }{2}}\right)$;
• q[3]: Nothing;
• q[4]: $R_y\left(-{\displaystyle \frac{\pi }{2}}\right),$ $R_y\left(\pi \right)$ and $R_y\left({\displaystyle \frac{7\pi }{6}}\right)$;
• q[5]: Nothing.

The TP applies the following quantum operations to decrypt the received states and perform Bell measurements:

• q[0]: $R_y\left(-{\displaystyle \frac{5\pi }{4}}\right),$ Controlled- NOT (CNOT) as the control bit and Hadamard (H);
• q[1]: Controlled- NOT (CNOT) as the target bit;
• q[2]: $R_y\left(-{\displaystyle \frac{3\pi }{2}}\right),$ Controlled- NOT (CNOT) as the control bit and Hadamard (H);
• q[3]: Controlled- NOT (CNOT) as the target bit;
• q[4]: $R_y\left(-{\displaystyle \frac{7\pi }{6}}\right),$ Controlled- NOT (CNOT) as the control bit and Hadamard (H);
• q[5]: Controlled- NOT (CNOT) as the target bit.

The actual implementation and results will be presented in Figure 2 and Figure 3, respectively, which depict the quantum circuit for comparing secrets X and Y, as well as the measurement outcomes obtained from executing it on the IBM Quantum Composer. For more details, please visit https://quantum.ibm.com/composer (accessed on 11 March 2025). The IBM Quantum Composer is a graphical quantum programming tool that lets you drag and drop operations to build quantum circuits and run them on real quantum hardware or simulators.

Based on the measurement results presented in Figure 3, the outcomes yield the sequence 11,10,10 from right to left, which corresponds to the Bell states $\left\{\left|{\Phi }^{-}\right.⟩,\left|{\Psi }^{+}\right.⟩,\left|{\Psi }^{+}\right.⟩\right\}$. According to the proposed protocol, we can determine that if all measurement results are identical to the initially prepared Bell states, then $X=Y$; otherwise, $X\ne Y$. However, the measurement results presented in Figure 3 do not match the initially prepared Bell states $\left\{\left|{\Phi }^{+}\right.⟩,\left|{\Phi }^{-}\right.⟩,\left|{\Psi }^{+}\right.⟩\right\}$, confirming that $X\ne Y$. This simulation demonstrates the feasibility and correctness of the protocol.

5. Security Analysis

The proposed protocol must ensure security against both external eavesdroppers and insider participants (TP, Alice, and Bob). Specifically, the protocol satisfies the following security properties:

(1)

Security against outsider eavesdroppers: an external adversary cannot access the private inputs X and Y, even when employing various quantum attack strategies.

(2)

Security against semi-honest TP: The TP cannot learn X and Y, beyond the comparison result, even if it attempts to exploit intermediate results.

(3)

Alice’s privacy: Alice cannot access Bob’s private input Y.

(4)

Bob’s privacy: Bob cannot access Alice’s private input X.

Theorem 1. 

An external adversary cannot access the private inputs X and Y, even when employing various quantum attack strategies.

Proof. 

An external eavesdropper, referred to as “Eve”, may employ quantum attack strategies such as intercept–resend, entangle–measure, and Trojan horse attacks to steal the private inputs X and Y. We demonstrate that the proposed protocol is secure against these threats.

In the intercept–resend attack [34], Eve intercepts the quantum sequences sent between Alice, Bob, and the TP, replacing them with fake sequences. After Alice or Bob announces the positions and bases of the decoy photons, Eve measures the intercepted particles to deduce the private inputs. However, the protocol includes decoy photons to detect eavesdropping. The presence of these decoy photons allows the legitimate participants to verify the security of the quantum channel. When Eve performs the intercept–resend attack, the probability of detecting Eve’s attack is $1-{\left({\displaystyle \frac{3}{4}}\right)}^m$, where m is the number of decoy photons. As m increases, this probability approaches 1, making it nearly impossible for Eve to succeed without detection. Additionally, the rotation operation conceals the encoded private inputs, preventing Eve from accurately determining the original quantum states. Thus, the intercept–resend attack is thwarted.

When Eve performs the entangle–measurement attack, she entangles decoy photons with an ancillary quantum state using a unitary operator U. This process can be outlined as follows:

$$U\left|0\right.〉\left|\epsilon \right.〉={\delta }_{00}\left|0\right.〉\left|{\epsilon }_{00}\right.〉+{\delta }_{01}\left|1\right.〉\left|{\epsilon }_{01}\right.〉$$

(9)

$$U\left|1\right.〉\left|\epsilon \right.〉={\delta }_{10}\left|0\right.〉\left|{\epsilon }_{10}\right.〉+{\delta }_{11}\left|1\right.〉\left|{\epsilon }_{11}\right.〉$$

(10)

$$\begin{array}{l}U\left|+\right.〉\left|\epsilon \right.〉={\displaystyle \frac{1}{2}}\left|+\right.〉\left({\delta }_{00}\left|{\epsilon }_{00}\right.〉+{\delta }_{01}\left|{\epsilon }_{01}\right.〉+{\delta }_{10}\left|{\epsilon }_{10}\right.〉+{\delta }_{11}\left|{\epsilon }_{11}\right.〉\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{1}{2}}\left|-\right.〉\left({\delta }_{00}\left|{\epsilon }_{00}\right.〉-{\delta }_{01}\left|{\epsilon }_{01}\right.〉+{\delta }_{10}\left|{\epsilon }_{10}\right.〉-{\delta }_{11}\left|{\epsilon }_{11}\right.〉\right)\end{array}$$

(11)

$$\begin{array}{l}U\left|-\right.〉\left|\epsilon \right.〉={\displaystyle \frac{1}{2}}\left|+\right.〉\left({\delta }_{00}\left|{\epsilon }_{00}\right.〉+{\delta }_{01}\left|{\epsilon }_{01}\right.〉-{\delta }_{10}\left|{\epsilon }_{10}\right.〉-{\delta }_{11}\left|{\epsilon }_{11}\right.〉\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{1}{2}}\left|-\right.〉\left({\delta }_{00}\left|{\epsilon }_{00}\right.〉-{\delta }_{01}\left|{\epsilon }_{01}\right.〉-{\delta }_{10}\left|{\epsilon }_{10}\right.〉+{\delta }_{11}\left|{\epsilon }_{11}\right.〉\right)\end{array}$$

(12)

where $\epsilon$ is an ancillary quantum state. The four quantum states $\left|{\epsilon }_{00}\right.⟩,\left|{\epsilon }_{01}\right.⟩,\left|{\epsilon }_{10}\right.⟩,\left|{\epsilon }_{11}\right.⟩$ are determined uniquely by U and satisfy the following condition:

$${\displaystyle \sum _{\alpha ,\beta \in \left\{0,1\right\}}〈{\epsilon }_{\alpha ,\beta }|{\epsilon }_{\alpha ,\beta }〉}=1$$

(13)

The parameters ${\delta }_{00},{\delta }_{01},{\delta }_{10},{\delta }_{11}$ should satisfy the following condition:

$${\left|{\delta }_{00}\right|}^2+{\left|{\delta }_{01}\right|}^2=1$$

(14)

$${\left|{\delta }_{10}\right|}^2+{\left|{\delta }_{11}\right|}^2=1$$

(15)

If Eve aims to perform this attack successfully, she must pass the eavesdropping detection process. This involves ensuring that her actions go undetected by the legitimate participants (Alice, Bob, and TP). For her to do this, certain conditions must be met:

$$\left\{\begin{array}{l}{\delta }_{00}={\delta }_{11}=1\\ {\delta }_{01}={\delta }_{10}=0\\ {\delta }_{00}\left|{\epsilon }_{00}\right.〉-{\delta }_{01}\left|{\epsilon }_{01}\right.〉+{\delta }_{10}\left|{\epsilon }_{10}\right.〉-{\delta }_{11}\left|{\epsilon }_{11}\right.〉=0\\ {\delta }_{00}\left|{\epsilon }_{00}\right.〉+{\delta }_{01}\left|{\epsilon }_{01}\right.〉-{\delta }_{10}\left|{\epsilon }_{10}\right.〉-{\delta }_{11}\left|{\epsilon }_{11}\right.〉=0\end{array}\right.$$

(16)

From Equation (16), we derive $\left|{\epsilon }_{00}\right.⟩=\left|{\epsilon }_{11}\right.⟩$. Therefore, we have

$$U\left|0\right.〉\left|\epsilon \right.〉=\left|0\right.〉\left|{\epsilon }_{00}\right.〉$$

(17)

$$U\left|1\right.〉\left|\epsilon \right.〉=\left|1\right.〉\left|{\epsilon }_{00}\right.〉$$

(18)

$$U\left|+\right.〉\left|\epsilon \right.〉=\left|+\right.〉\left|{\epsilon }_{00}\right.〉$$

(19)

$$U\left|-\right.〉\left|\epsilon \right.〉=\left|-\right.〉\left|{\epsilon }_{00}\right.〉$$

(20)

As shown in Equations (17)–(20), if Eve can pass the eavesdropping check under the condition that the particles and ancillary states are in a product state, then the entangle–measurement attack does not succeed.

Eve may attempt Trojan horse attacks, such as the delay-photon attack and the invisible photon attack [35], to deduce private inputs. These attacks threaten the security of the two-way quantum protocol by compromising the transmission of quantum sequences from Alice or Bob to the TP. To mitigate this risk, it is recommended to implement a wavelength quantum filter and a photon number splitter, which would enhance the system’s resistance to such attacks.

In conclusion, an external adversary cannot access the private inputs X and Y, even when employing various quantum attack strategies. □

Theorem 2. 

The TP cannot learn X and Y, beyond the comparison result, even if it attempts to exploit intermediate results.

Proof. 

The TP acts as a semi-honest intermediary and cannot collude with Alice or Bob. The TP’s knowledge is limited to the prepared and final Bell states, which allow computation of $X\oplus Y$, but do not provide the individual values of $X \mathrm{a}\mathrm{n}\mathrm{d} Y$. The operation $X\oplus Y$ allows for the comparison of the two inputs, but it does not enable the TP to extract the individual inputs themselves. If the TP attempts to perform an intercept–resend attack on the sequence ${ES}_A^{\prime }$ to derive Alice’s private input X, the protocol’s detection mechanisms will identify and terminate the attack. Even if the TP manages to intercept the encoded quantum sequence, the rotation operation applied to conceal the private inputs complicates her efforts. Without knowledge of the rotation angles used in these rotation operations, the TP cannot determine the value of X.

For the TP to learn Bob’s private input Y, she must know the sequence $S_A$ that Alice sent. However, there is no opportunity for the TP to acquire $S_A$ unless she intercepts ${ES}_A^{\prime }$. Yet, any such interception would trigger the eavesdropping detection mechanisms built into the protocol, leading to its termination.

To conclude, the TP does not gain any information about the private inputs X and Y, apart from the comparison results. This holds true even if the TP utilizes immediate results to deduce the private inputs. □

Theorem 3. 

Alice cannot access Bob’s private input Y.

Proof. 

Bob’s private input Y is encoded into the sequence $S_A$. While Alice might consider sending a fake sequence $S_A$ (for example, by using states $\left|0\right.⟩$ for all photons), this does not provide her with access to Bob’s actual input. If Bob sends ${ES}_B^{\prime }$ to the TP, and Alice intercepts it to replace it with another fake sequence, this action would typically allow her to manipulate the communication. However, the protocol is designed to detect such interception attempts. If Bob announces his secret key $K_B$, it would imply that he has not detected any eavesdropping. However, due to the detection mechanisms in place, if Alice intercepts any communication, Bob will not publish $K_B$. The protocol ensures that no secret key is announced in the presence of an eavesdropper. Without access to $K_B$, Alice cannot deduce Bob’s private input Y.

Therefore, Alice cannot access Bob’s private input Y. □

Theorem 4. 

Bob cannot access Alice’s private input X.

Proof. 

Alice’s private input X is encoded into the sequence $S_1$. Since the initially prepared Bell states are unknown to Bob, he lacks the necessary information to directly infer X. The only method for Bob to potentially learn Alice’s private input X would be to intercept the sequence $S_1$ and replace it with a fake sequence (for example, using states $\left|0\right.⟩$ for all photons). If Bob intercepts $S_1$ and sends a fake sequence to Alice, this behavior would be detected by both TP and Alice. Once any eavesdropping is detected, the protocol is designed to terminate and restart. This means that Bob’s attempt to intercept and manipulate the sequence would ultimately fail.

Therefore, Bob cannot access Alice’s private input X. □

6. Discussion

The qubit efficiency [36,37] is a crucial metric for assessing the utilization ratio of qubits in quantum cryptographic protocols. It can be defined as follows:

$$q_e={\displaystyle \frac{q_c}{q_t}}$$

(21)

where $q_c$ and $q_t$ are the numbers of private bits compared and the total number of qubits consumed during the comparison process, respectively. The qubits used in the security check process are excluded from this calculation, as this process is considered an independent procedure in quantum cryptography. In our protocol, the binary representations of inputs X and Y have lengths of N, resulting in $q_c=N$. The third party (TP) prepares N Bell states as quantum information carriers for the comparison. Since each Bell state consists of two qubits, the total number of qubits consumed is $q_t=2N$. Consequently, the qubit efficiency is calculated as $q_e=N/2N=50\%$. A comparative analysis of our protocol with other existing QPC protocols is presented in

Table 2. Comparison between our protocol and other existing QPC protocols.

Protocol	Quantum Source	The Need for Entanglement Swapping	The Need for Unitary Operations	The Need for QKD	Measurement Manner	Qubit Efficiency
Ref. [21]	GHZ states	No	Yes	No	X-basis	33%
Ref. [22]	Four-particle entangled states	No	No	Yes	Z-basis	25%
Ref. [23]	Five-particle entangled states	No	No	Yes	Bell-basis and Z-basis	40%
Ref. [24]	Six-particle entangled states	No	No	Yes	Bell-basis	33%
Ref. [25]	Seven-particle entangled states	No	No	Yes	Bell-basis and Z-basis	29%
Ref. [26]	Eight-particle entangled states	No	Yes	No	Z-basis	25%
Ours	Bell states	No	Yes	No	Bell-basis	50%

.

Ref. [21] employed GHZ states as quantum resources, utilizing unitary operations for state conversion and X-basis measurements in the QPC protocol. This approach achieved a qubit efficiency of 33%, relying on one GHZ state to compare one bit of classical information.

Ref. [22] used four-particle entangled states as quantum resources, implementing QKD technologies to protect privacy and Z-basis measurements for the QPC protocol. This resulted in a qubit efficiency of 25%, with one four-particle entangled state used for comparing one bit of classical information.

Ref. [23] utilized five-particle entangled states as quantum resources, also leveraging QKD technologies for privacy protection, along with Bell-basis and Z-basis measurements in the QPC protocol. This method achieved a qubit efficiency of 40%, employing one five-particle entangled state to compare two classical bits.

Ref. [24] incorporated six-particle entangled states as quantum resources, utilizing QKD technologies for privacy protection and Bell-basis measurements for the QPC protocol. This setup achieved a qubit efficiency of 33%, using one six-particle entangled state to compare two classical bits.

Ref. [25] utilized seven-particle entangled states as quantum resources, employing QKD technologies for privacy protection and both Bell-basis and Z-basis measurements in the QPC protocol. This protocol achieved a qubit efficiency of 29%, using one seven-particle entangled state to compare two classical bits.

Ref. [26] leveraged eight-particle entangled states as quantum resources, utilizing unitary operations for state conversion and Z-basis measurements for the QPC protocol. This approach achieved a qubit efficiency of 25%, relying on one eight-particle entangled state to compare two classical bits.

Our protocol offers several advantages over those referenced in studies [20,21,22,23,24,25,26]. Firstly, it utilizes Bell states as quantum resources, employs unitary operations for encoding private inputs, and implements Bell-basis measurements to obtain the results. This approach is more feasible to realize compared to protocols based on multi-qubit states. Secondly, unlike several protocols in [22,23,24,25], our protocol does not require additional quantum resources for key distribution, thereby reducing the overall consumption of quantum resources. Finally, our protocol achieves a qubit efficiency of 50%, surpassing many existing QPC protocols as noted in Refs. [21,22,23,24,25,26].

7. Conclusions

In this study, we introduce a two-party quantum privacy comparison (QPC) protocol that utilizes R_y rotation operations to enable secure equality comparison of private inputs from two participants without disclosing their information. The feasibility of the proposed protocol is confirmed through simulations on a quantum platform. Security analysis demonstrates that the protocol is resilient against both external eavesdropping and internal participant attacks, ensuring the confidentiality of the participants’ private inputs. The protocol employs Bell states as quantum resources, unitary operations for encoding private inputs, and Bell-basis measurements to derive the comparison results. This methodology is more straightforward to implement compared to QPC protocols that rely on multi-qubit states. Notably, our protocol eliminates the need for a separate quantum key distribution process, thereby minimizing the consumption of additional quantum resources. Furthermore, it achieves a qubit efficiency of 50%, as it uses one Bell state to compare one bit of binary information, outperforming many existing QPC protocols.