Abstract
In real-world logistics scenarios, the complexities often surpass what traditional Capacitated Vehicle Routing Problem (CVRP) models can effectively address. For instance, when there is an excess of goods and limited vehicles, traditional CVRP models frequently fail to yield feasible solutions. Additionally, the time sensitivity of goods and the large scale of vehicles and goods in practical logistics scenarios present significant challenges for efficient problem-solving. This underscores the urgent need to develop a novel CVRP model that is better suited for logistics scenarios and enhances the scalability of CVRP. To address these limitations, we propose a flexible CVRP model, referred to as Flexible CVRP, which modifies the optimization objectives and constraints. This allows CVRP to provide a sensible solution even when no feasible solution exists in the traditional sense. To tackle the challenges posed by large-scale problems, we leverage the Memory Pointer Network (MemPtrN). This approach enables the modeling of solution strategies, offering strong generalization capabilities and mitigating the explosive growth in complexity to some extent. Compared to commonly used heuristic algorithms, our method achieves superior solution quality for large-scale problems. Specifically, when addressing large-scale scenarios, the MemPtrN outperforms Google’s OR-Tools solver, heuristic algorithms, enhanced evolutionary algorithms, and other reinforcement learning methods in terms of both solution speed and quality.
Keywords:
memory pointer network; deep reinforcement learning; flexible CVRP; combinatorial optimization problem; actor–critic algorithm MSC:
35A01; 65L10; 65L12; 65L20; 65L70
1. Introduction
In the logistics scenario, it is often necessary to deal with the matching problem between vehicles and goods. The traditional Capacitated Vehicle Routing Problem (CVRP) model is commonly used in such scenarios. However, this model is often too simple to be well applied to actual logistics scenario. For example, in the traditional CVRP model, in order to simplify the expression, it is considered that all vehicles have the same capacity. In an actual logistics scenario, the distribution center may have different models of vehicles, and the capacity of the vehicles is not the same. In addition, the traditional CVRP requires all the nodes to be visited and the vehicle to not be overweight, but this scenario is elusive. If the transportation demand increases rapidly but the number of vehicles is limited, the traditional CVRP modeling and solving method may have no feasible solution. Therefore, the problem cannot be solved, and the distribution center cannot be stopped at this time. According to the above analysis, the CVRP model in the actual logistics scenario faces two problems: (1) The scale of the problem is usually large. (2) There are many different constraints and different ways of calculating them when quantified as mathematical constraints. Therefore, it is necessary to think of a CVRP solution that can challenge the very large scale in a very short time; at the same time, this scheme can support all kinds of extensibility constraint computation, and we call it Flexible CVRP. The core innovation of Flexible CVRP lies in transforming the traditional binary feasible/infeasible problem into a multi-objective optimization by relaxing the “all customers must be served” constraint. This mathematical reformulation enables solving scenarios where demand temporarily exceeds capacity—a common situation in real-world logistics where managers need optimal resource allocation strategies rather than simply “no solution” responses. Our approach aligns with practical business decision-making processes where service prioritization is essential during resource constraints.
For the traditional CVRP problem, the author finds that the following mainstream solutions exist: heuristic search, industrial solver, and deep reinforcement learning (DRL). We will introduce the development in recent years.
Yodwangjai et al. [1] proposed an improved Whale Optimization Algorithm (WOA) by introducing an adaptive weighting strategy and a local search mechanism to enhance the algorithm’s global search capability, achieving excellent results on Solomon benchmark instances. Souza et al. [2] combined the advantages of the differential evolution (DE) algorithm to develop a hybrid algorithm called CDELS, which is based on differential evolution meta-heuristics and discrete adaptive techniques. This approach balances the algorithm’s exploration and exploitation capabilities through discrete adaptive control parameters. To address the tendency of traditional meta-heuristic algorithms to become trapped in local optima when solving the Capacitated Vehicle Routing Problem (CVRP), Rezaei et al. [3] integrated genetic local search with multi-population evolutionary algorithms to propose a hybrid algorithm named ICAHGS. This algorithm employs dynamic crossover and mutation operators to maintain population diversity and incorporates local search strategies to enhance solution quality. Frías et al. [4] designed a hybrid algorithm based on Ant Colony Optimization (ACO) and integrated clustering methods, such as K-means and K-Medoids, enabling both free ants and constrained ants to effectively solve the Energy Minimization Vehicle Routing Problem (EMVRP). Altabeb A. M. et al. [5] improved the Firefly Algorithm (FA) to make it suitable for CVRP, naming the enhanced version CVRP-FA. This algorithm utilizes two different local searches to improve solution quality, achieving excellent results. Despite their widespread adoption, these heuristic approaches face fundamental limitations. The iterative update process for parameters, environment states, and objective functions introduces computational complexity that grows exponentially with problem size. This computational burden makes these methods increasingly impractical for large-scale CVRP instances, where the transition from initial to optimal solutions becomes prohibitively time-consuming.
In practical scenarios, to address these computational challenges, practitioners are increasingly turning to commercial and open-source mathematical optimization solvers. These solvers implement exact methods and complex mathematical programming techniques, enabling them to effectively handle various types of vehicle routing problems. While they may not guarantee the optimal solution for all large-scale instances, they often provide high-quality solutions with verified optimality gaps. Table 1 summarizes the widely used optimization solvers and their corresponding solving capabilities.

Table 1.
Comparison of various commercial solvers.
While these industrial solvers demonstrate excellent performance in solving linear/nonlinear mixed-integer programming and small-scale constrained programming, they exhibit two critical limitations: (1) computational efficiency deteriorates significantly with problem scale, particularly for problems exceeding 1000 nodes [14], and (2) they struggle to handle scenarios without feasible solutions—a common occurrence in dynamic logistics environments where demand may temporarily exceed capacity constraints. To deal with large-scale optimization problems, reinforcement learning first appeared in the field of solving CVRPs, where the pioneer was Irwan Bello [15], who first tried to combine the gradient strategy method with combinatorial optimization, giving a deep learning idea to traditional optimization problems and achieving a better spontaneous optimization search effect for sample starvation situations through prior knowledge of historical samples. Tsai Y L et al. [16] adopted deep neural networks and reinforcement learning to realize the optimal CVRP with a fixed time. Li J et al. [17] adopted a deep reinforcement learning method based on the attention mechanism, in which the vehicle selection decoder considers the heterogeneous vehicle fleet constraints, and the node selection decoder considers the route construction. The results show that the performance and generalization are ideal. Xu Y et al. [18] used multi-relational attention reinforcement learning to solve VRP. Recently, Fan et al. [19] proposed a novel algorithm that integrates Convolutional Neural Networks (CNNs) with Double Deep Q-Learning, enabling the coordinated learning of maps and agents. Zou et al. [20] introduced an improved Transformer model (TAOA) that combines Multi-Head Attention (MHA) and Attention on Attention (AOA) mechanisms, applying it to the Multi-Depot Vehicle Routing Problem (MDVRP) with low-carbon objectives. Si et al. [21] developed a multi-agent hierarchical reinforcement learning method to schedule discrete and segmented Capacitated Vehicle Routing Problems (CVRPs). Their model demonstrates better generalization performance for solving larger-scale optimization problems with different data distributions, thus enabling the idea of small sample training, i.e., training on small-scale problems and introducing this experience to the solution of large-scale problems. Among these advancements, adding the attention mechanism is the most effective for improving the optimization ability of reinforcement learning.
Although the Vehicle Routing Problem (VRP) has many variants, such as the Vehicle Routing Problem with Time Windows (VRPTWs) and the Vehicle Routing Problem with Load Balancing (VRP-LB), this paper addresses the limitations of traditional CVRP models in meeting the high scalability and flexibility requirements of real-world logistics scenarios. To this end, we propose an enhanced Flexible CVRP model, which is more suitable for real-world applications, and treat it as a Seq2Seq problem to better reflect the complexities and uncertainties present in real-world logistics environments. The model involves vehicles with different capacities and introduces two optimization objectives: minimizing the total vehicle travel distance and maximizing the number of serviceable nodes, leading to a multi-objective optimization problem. To solve the large-scale CVRP problem, which is urgently needed, we propose a Memory Pointer Network method trained via reinforcement learning. This approach helps mitigate the exponential growth of complexity to some extent. The model can be trained on smaller-scale problems to acquire a priori knowledge that can be applied to solve large-scale problems. This generalizability enables the training of large-scale problems and thus makes it suitable for solving ultra-complex Flexible CVRP. The MemPtrN uses an attention mechanism (inspired by pointer networks [22]) to make decisions and improves the original GAT [23] mechanism, making it more suitable for Flexible CVRP.
In the design of the algorithm, we focus on improving the flexibility and practicality of the CVRP model to better address the diverse demands and uncertainty constraints in real-world logistics scenarios. Building on this foundation, we introduce a new memory module, which, combined with the improved GAT mechanism and attention mechanism, leads to the development of the Memory Pointer Network (MemPtrN). This approach redefines memory updating and output, enabling a more adaptable problem-solving framework. Furthermore, we explore methods that not only generate feasible solutions for programming problems but also provide approximate or tolerant solutions when constraints are especially strict or when no feasible solutions exist. This ensures the algorithm’s robustness and applicability across various scenarios. The detailed methodology is elaborated in Section 3.
In our Flexible CVRP benchmark, we compare the MemPtrN with OR-Tools [13], recently proposed new search algorithms [4,5], reinforcement learning methods [20], and classical heuristic algorithms [24]. OR-Tools performs well in the optimization of complex CVRP and the solution speed is relatively fast. Compared with OR-Tools, heuristic algorithms are more flexible and can design heuristic strategies for problems. However, from our point of view, these two methods are inefficient when dealing with large-scale problems and need to provide sufficient time or multiple iterations to obtain a better solution. If the problem is very large but the calculation time for OR-Tools and heuristic algorithms is very limited, the tool cannot search for a feasible solution. The results show that for large-scale CVRP problems, the solution quality of the MemPtrN is 21.46% higher than OR-Tools, 28.5% better than CPLEX, 27.3% better than Gurobi, 17.2% better than the best heuristic algorithm, and 61.11% better than the most classic combinatorial optimization algorithm.
The main objectives of this paper are as follows:
- Identify the limitations of traditional CVRP models in addressing real-world logistics scenarios with heterogeneous vehicle fleets and demand fluctuations.
- Propose a Flexible CVRP model that accommodates different vehicle capacities and provides sensible solutions even when traditional CVRP constraints cannot be satisfied.
- Design a novel Memory Pointer Network (MemPtrN) that combines an improved Graph Attention Network with a memory module to effectively model complex routing strategies.
- Demonstrate the strong generalization capabilities of the MemPtrN, allowing models trained on small-scale problems to successfully solve ultra-large-scale instances.
- Evaluate the proposed approach through comprehensive experiments comparing the MemPtrN with commercial solvers, heuristic algorithms, and other reinforcement learning methods.
- Demonstrate significant performance improvements over state-of-the-art approaches, with the MemPtrN outperforming Google’s OR-Tools solver by 21.46%, the best heuristic algorithm by 17.2%, and classical optimization algorithms by 61.11% for large-scale CVRP problems.
The remaining parts of this paper are arranged as follows: Section 2 describes and models Flexible CVRP. The algorithm architecture is introduced in Section 3, and the Memory Pointer Network (MemPtrN) is proposed. In Section 4, the data preprocessing and experimental design are described, and the experimental results of the MemPtrN are compared with a series of heuristic algorithms, as well as OR-Tools. In Section 5, the advantages of the MemPtrN are summarized and orientation for further research, and experiments are given.
2. Flexible CVRP Model
The traditional CVRP model is introduced in this section, and then the Flexible CVRP is derived from the traditional CVRP model. The relevant symbols of the model are as shown in Table 2.

Table 2.
Symbol convention table.
The solution of the optimization problem can be represented by variables and , which are defined as follows:
The traditional CVRP is characterized by a homogeneous fleet of vehicles with identical capacity (formally expressed as ). The problem involves a set of geographically dispersed customer nodes, each with specific transportation requirements. Each vehicle must originate from the depot, serve a subset of customers without exceeding its capacity, and return to the depot upon completion of its route. The model enforces several critical constraints: (1) all customer nodes must be visited exactly once, (2) no vehicle may be overloaded beyond its capacity, and (3) each vehicle must complete a closed route beginning and ending at the depot. The objective function typically minimizes either the total travel distance across all vehicles, the number of vehicles required, or some combination thereof. This formulation, while elegant, often proves inadequate for real-world logistics scenarios with fluctuating demand patterns:
The objective of the optimization problem is to minimize the path cost. Constraint (4) is that each user must be served by only one vehicle. Constraint (5) is that each user must be served by the same vehicle. Constraint (6) is the capacity constraint. Constraint (7) is to prevent loops from forming on the vehicle path.
In the Flexible CVRP problem, the capacity of all vehicles is not the same, and the optimization goal is to maximize the number of users served and minimize the driving distance of all vehicles. The formulaic description of the model is as follows:
Flexible CVRP models use completely different optimization objectives than traditional CVRP models, allowing the CVRP to produce common sense solutions. Additionally, constraint (4) is removed to tolerate the presence of unserved users.
3. Algorithm Design
3.1. Algorithm Overview
In this paper, we transform the CVRP into a decision problem with two related sequences. A MemPtrN model for the sequential decision-making of CVRP is proposed to express the strategy in the sequential decision-making model. There are two parts in the process of solving CVRP with the MemPtrN: (1) Training the MemPtrN. (2) Using a trained MemPtrN to solve CVRP. The overall solution is shown in Figure 1.
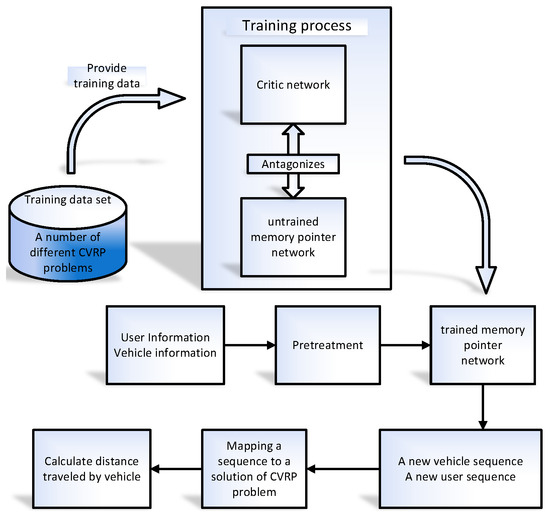
Figure 1.
Solution of CVRP based on the MemPtrN.
The input of the MemPtrN has two parts: target portion and additional portion. The output of the network results in a reordering of the target portion. Figure 2 shows how the Flexible CVRP is solved by the MemPtrN.
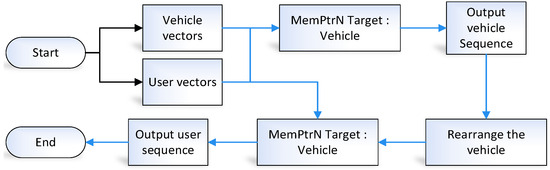
Figure 2.
Collaboration between two MemPtrNs.
The vehicle sequence and user sequence are respectively generated by two MemPtrNs. There are two parts in the MemPtrN, the part that needs to be generated for the new sequence is the target part, and the other information as the additional part. The two parts of the MemPtrN in Figure 2 correspond to opposite contents.
3.2. Pretreatment
In order to simplify the programming, Node 0 is considered the distribution center and located at the origin of coordinates, and the user is located in the rectangular range of , and any vehicle needs to return to the distribution center after serving the user. User i is represented as a four-dimensional vector as the input to the MemPtrN, where is the transportation demand of user i, , are the coordinates given by the user, and is the distance from user i to the distribution center. For the MemPtrN that generates the vehicle sequence, its input uses the maximum vehicle capacity in Section 2 as the input. In addition, according to the characteristics of the neural network, the user vector and the vehicle maximum capacity are treated as follows:
Let be a matrix of n rows and 4 columns, where line i is the user vector , and is the matrix of t rows and one column, where line i is the vehicle capacity . The four-dimensional vectors of the input network are extended by a fully connected layer transformation, where and are the high-dimensional vectors obtained by and through the fully connected layer. The dimensions of the higher-dimensional space, mentioned above, are represented by g.
The distance between users in CVRP can be naturally regarded as a fully connected graph with weights. Based on this scenario, inspired by the ant colony algorithm, this paper fuses the adjacency matrix between users on the GAT mechanism to realize the user relative position encoding. In this paper, the distance matrix between two users is transformed as heuristic information combined with the GAT mechanism. Assuming that the distance matrix between the two users is D, the transformation steps are as follows:
- Compute the distance between the vectors in the matrix, denoted as the symmetric matrix D.
- Let be the result of setting the diagonal of the matrix D to infinity.
- Let insMat be the result of the transformation, insMat .
The above calculation process is performed for the user and vehicle vector groups C and T, and the calculation results are input into the improved GAT encoder of the vehicle and the user, respectively. The matrix insMat, which abstracts the distance between users, is used as heuristic information to participate in the process of improving the GAT encoder to calculate the attention weight between two nodes and is fused with the attention weight between the user or vehicle information. Finally, the encoding result of the user or vehicle information is obtained.
Since the MemPtrN trained by reinforcement learning can only deal with sequential decision-making models, it is necessary to transform the mathematical programming model into a sequential decision-making model in order to make full use of the advantages of reinforcement learning in solving such problems. In this paper, an algorithm is designed to uniquely map the vehicle and user sequences to a solution of the above planning problem. Considering that the second optimization goal is to serve as many users as possible, the algorithm adopts a greedy mapping strategy. Let the capacity sequence of the vehicle sequence be and the transportation demand sequence corresponding to the user sequence be . The algorithm for mapping a sequence to a solution of a programming problem is as shown in Algorithm 1 below:
| Algorithm 1: Sequence to solution mapping. |
 |
The above algorithm can uniquely map a vehicle sequence and a user sequence as a solution to the Flexible CVRP. Using the above greedy algorithm, the order of the vehicle and cargo is mapped to the solution of the CVRP problem, thus transforming the combinatorial optimization problem into a decision problem of two related sequences. According to the sequential decision model and network structure, two sequences are needed to solve a CVRP. In this paper, two MemPtrNs are stacked to generate vehicle sequences and user sequences.
3.3. Design of MemPtrN
The MemPtrN first encodes the problem using an improved GAT mechanism that aggregates relative positions between users, and then uses a novel memory module to remember the current decision state. The new mechanism can fully explore the characteristics of problem description information, and the complex environment interaction design work can be abandoned. This paper uses the A2C training framework to train the MemPtrN.
3.3.1. MemPtrN Architecture
An encoder, memory module, and decoder are the main components of the MemPtrN. The working mode of the MemPtrN is shown in Figure 3.
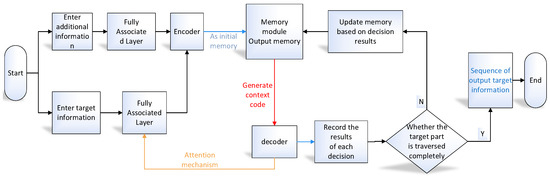
Figure 3.
Main frame of the MemPtrN.
In the MemPtrN, the fully connected layer is first used to transform the vector describing the problem into a vector in a higher-dimensional space. Then, the improved GAT mechanism, which combines the idea of the ant colony algorithm [25] and general GAT [23], can be used to encode the relative positions between users, and the Transformer structure [26] can transform the description of the problem into a semantic vector. The semantic vectors will be provided for use by the memory module, and the encoder is designed in detail as shown in Section 3.3.2. The decoder then uses the attention mechanism to make decisions to generate the sequence. The memory module connects the encoder with the decoder. The module saves the semantic vector generated by the encoder and generates the context encoding vector according to the current solving condition. Finally, the memory content can be updated according to the decision of the decoder.
The decoder generates the sequence by iterating, with the number of iterations equal to the number of elements in the target portion. The attention mechanism [22] is used to calculate the probability of selecting an element in the target part in each iteration, which is described as follows:
The above expression is where Q is the matrix formed by copying the context encoding vector q, where a is the length of the target portion, R is the matrix formed by the target portion, and v, , and are model parameters participating in gradient descent. Through multiple iterations, the decoder generates a sequence of the same length as the target portion, which is a new ordering of the target portion. In training, the decoder randomly samples according to the probability calculated by the above formula. When using the model to solve the problem, it selects the node number with the highest probability to output.
In each iteration, the decision made by the decoder is output as a part of the result. On the other hand, it is used as the basis for updating the memory content to realize the update of memory, to guide the next decision of the decoder.
3.3.2. Encoder
The input of the MemPtrN is the target part and the additional part, respectively. The workflow is shown in Figure 4. The MemPtrN encoder uses an improved GAT mechanism to learn relative positions between users, uses LSTM to capture rank information in the sequence, and uses Transformer to capture the associations between all vectors.
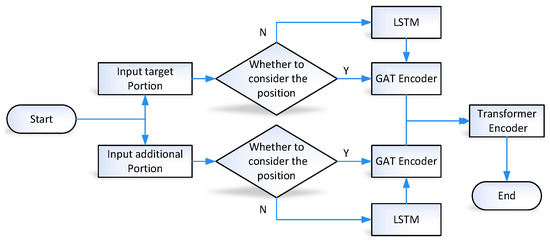
Figure 4.
Encoder structure.
The encoder first judges whether a piece of certain information is position-sensitive information, and if it is, it uses LSTM [27] to process this part of the information to realize the encoding of the order information. The information of the two parts of the first MemPtrN in Figure 2 does not need to consider the order. The vehicle information of the second MemPtrN is the additional portion, and the new user is the target portion. Currently, the vehicle information is the result of rearrangement according to the vehicle sequence. It is necessary to pay attention to the ranking information of the vehicle. The additional part of the second MemPtrN requires the consideration of ranking information, which is why LSTM is needed. However, the target portion does not need to consider the rank.
The GAT part of the encoder in Figure 4 uses multiple improved GAT modules with residual connections [28] as shown in Figure 5. The improved GAT module also uses the multi-head graph attention mechanism.
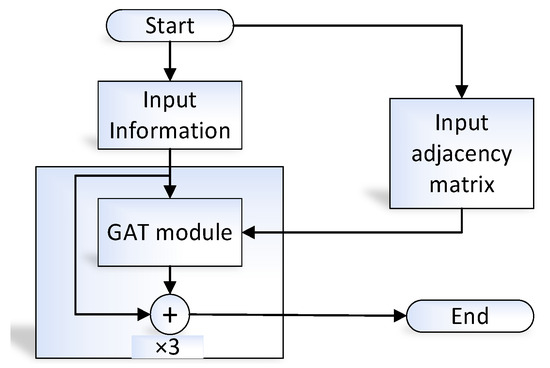
Figure 5.
Main structure of the GAT encoder.
The original GAT mechanism first calculates the attention weight between the vectors and then shields the attention weight distribution according to the adjacency matrix so that the attention mechanism is only operated on the neighbors. Therefore, the traditional GAT mechanism cannot integrate the side-weighted situation, that is, it does not apply to directed graphs and undirected graphs with weighted edges. The improved GAT mechanism superimposes the adjacency matrix on the attention matrix of the original GAT so that the original GAT mechanism can use the weight of edges. In this paper, the insMat in Section 3.2 is used as the adjacency matrix of the graph, superimposed with the original attention matrix, to realize the ability to capture the relative distance between users.
First assume that there are R nodes on the undirected graph G. If a g-dimensional vector is defined on each node, the vector of the i-th node is . Based on the above symbols, one head of the attention coefficient between any two nodes (node i and node j) in the improved GAT mechanism is calculated according to the following formula:
In the above equation, is the parameter involved in training. represents the combination of two vectors, where the combined vector dimension is the sum of the dimensions of the original two vectors. After combination, the result is multiplied by , which also participates in training, to obtain the attention weight of the first part. Next, represents the element of row i and column j of the adjacency matrix, which is insMat mentioned in Section 3.2 when solving the Flexible CVRP problem. Similarly, are also the model norms involved in training. Leaky ReLU corresponds to the activation function f in Formula (18). Based on the calculation method of , can be obtained by using improved GAT encoding for the vector of the i-th node as follows:
Among them, “‖” denotes the vector concatenation, represents the GAT mechanism with -head, and indicates stacking vectors into a matrix row-wise. w is a model parameter used to combine the matrices into a vector, and is the activation function Elu.
3.3.3. Memory Module
The memory module accepts the semantic vector output by the encoder as the initial memory content. On the one hand, it can output the context encoding vector according to the memory content to guide the decoder’s work; on the other hand, it can dynamically update the memory content according to the decision of the decoder. So, the memory module can be called the bridge between the encoder and the decoder. The memory module in this paper improves the memory network in the literature [29]. A new memory updating mechanism and a new memory segmentation mechanism are adopted, and the memory output process is also improved.
In this paper, we propose an innovative mechanism of segmented memory, which divides the memory into multiple segments according to semantic meaning. The memory update, the output algorithm, and the model parameters required by the algorithm are shared between different segments. The difference of each segment is reflected in the memory content and memory combination weight a. The number of memory module segments can be set according to the problem. In the Flexible CVRP problem, there are two entities, vehicles and goods, so the memory is divided into two segments, corresponding to the semantic vector of vehicles and goods, respectively.
Multi-Head Attention [26] mechanisms are used for memory output. If the number of segments is m, the matrix with o rows and g columns represents the memory content of segment i. The total memory length is , and the dimension of the memory vector is g (the high-dimensional space dimension in Section 3.2). The memory output method is described as follows:
The model parameters involved in training are , , , , and v. The hyperparameter is the number of components of Multi-Head Attention (-head attention). The splicing of the matrix is represented by ‘∥’, and the result is a matrix with rows and g columns, denoted as M. In order to comply with the calculation rules, the matrix P has a shape of n rows and g columns. The parameter v is the memory query vector, which is shared across multiple iterations and participates in training. The model parameter , a -dimensional vector, is the aggregation parameter of the Multi-Head Attention. The above memory output process is abbreviated as .
The decision results of the decoder guide the update of the memory module. The update of the memory is shown in Figure 6. First, the decision result is mapped to the memory space to generate new memory content, then the memory retention coefficient is calculated, and finally the original memory is retained and superimposed with the newly generated memory according to the above retention coefficient.
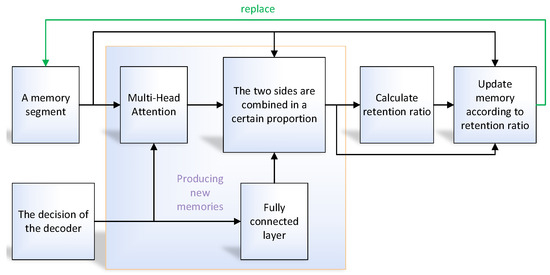
Figure 6.
Memory update process.
Suppose the target part is denoted by g-dimensional vector , and the i-th element of the target part is selected in a certain decoder iteration. For a memory segment, the algorithm to generate a new memory is as follows:
The new memory NewMem is a g-dimensional vector. Part of the new memory is directly generated by the vector selected by the decoder, and the other part is the output of the current memory content. The combination coefficient of the two parts is determined by a model parameter shared by all memory segments. The calculation method of the retention coefficient between old and new memories is as follows:
According to Formulas (26)–(28), NewMem can be obtained, and its dimension is g. Copy NewMem times to obtain a matrix of rows and g columns as , which can be written as According to the definition of , the final update calculation of a memory segment is as follows:
According to Formula (29), the retention coefficient of each memory vector in a memory segment constitutes a vector . The multiplication of the elements in with the corresponding rows of being expressed by in Equation (30). The meaning is that the i-th element in is multiplied by the i-th row vector in .
3.4. Complexity Analysis
This paper solves the CVRP using a stack of two MemPtrNs. We use a MemPtrN to obtain the vehicle sequence, and then use a MemPtrN to generate the user sequence based on the vehicle sequence. Finally, an algorithm is used to convert the two sequences into a solution to the Flexible CVRP.
The decoder of the MemPtrN uses the attention mechanism mentioned in Section 3.3.1 for multiple iterations to generate a sequence, that is, the formula in Section 3.3.1 needs to be calculated multiple times. The time complexity of each iteration is , where is the number of target portion vectors, is the dimension of the query vector q, and is the dimension of the target portion vector.
The time complexity of calculating the attention weight in the improved GAT coding in Section 3.3.2 is , where is the number of heads of the attention mechanism, g is the high-dimensional vector dimension in Section 3.2, and is the number of input vectors to the GAT encoder. Here, is the time complexity of calculating , and is the time complexity required to add the two parts. After the memory weight calculation is completed, the original vector needs to be transformed and output, and the time complexity of this part is . Finally, it can be concluded that the time complexity of the improved GAT encoder is .
According to the time complexity of Multi-Head Attention, it can be concluded that the time complexity of the memory output operation is denoted as , where is the number of query vectors. According to the memory output calculation formula in Section 3.3.3, the number of query vectors is 1. Then, .
The input of the memory updating process is a vector, which updates all memory segments according to the information of the input vector. The first part of the new memory is obtained by linear transformation of the input vector, and the time complexity of this operation is . The other part is obtained by querying all the current memories by the Multi-Head Attention mechanism, and the time complexity of this part is . Since the memory update formula in Section 3.3.3 indicates there is only one query vector, this part of time is . This operation needs to operate on all memory segments, so the time complexity of the memory update operation is .
The vehicle sequence and cargo sequence are generated by two MemPtrNs, respectively. There is no need to care about the sequence information when generating the vehicle sequence. Currently, the encoder does not perform LSTM encoding. The second MemPtrN needs to generate the user sequence from the vehicle sequence, so the encoder in the second MemPtrN needs to perform an LSTM encoding. The time complexity of using LSTM encoding is , where and are the sequence length and input vector dimension entering the LSTM, respectively, and is the LSTM hidden layer vector dimension. If the time complexity of the encoder with one LSTM and the encoder without LSTM is and , respectively, and s is assumed to be the number of layers of the GAT encoding stack, then since , and s are constants after the model is determined, the following conclusions can be drawn:
Combining the two cases of the encoder, the time complexity of the encoder can be obtained, where is the number of target portion vectors, and is the number of additional portion vectors.
One iteration of the decoder has three steps: (1) generate a context encoding vector through the query vector and memory module; (2) generate a sequence number through the attention mechanism in Section 3.3.1 using the context encoding vector and target portion; (3) according to the sequence number, a vector in the target portion is selected, and the memory module is updated with this vector. The number of iterations is equal to the number of vectors of the target portion, and the time complexity of the decoder through the above process is
The calculation of the MemPtrN requires two steps: (1) encoder encoding and (2) decoder iteration. According to the above process, the number of memory paragraphs in the memory module in this paper is two, which are the target portion and additional portion, respectively. After the model is determined, the high-dimensional vector dimensions g, , are all constants, and the time complexity of the MemPtrN can be obtained. is
The target parts of the two MemPtrNs used in this article are the opposite of the target portion and the additional portion. In summary, the time complexity of the two MemPtrNs used in this paper to solve the CVRP is , where n is the number of users and t is the number of vehicles.
4. Experimental Design and Results
This section describes the physical and virtual environments, the design process, and the parameter details of the experiment, and then evaluates the results of the experimental model for different problem sizes. At present, there is no public standard benchmark of CVRPs with different vehicle capability, so this paper generates some CVRPs with different vehicle capabilities.
4.1. Experimental Design
The CPU used in the experiment is Ryzen 5800H (AMD, Santa Clara, CA, USA), the GPU used is RTX 3070 Laptop GPU (NVIDIA, Santa Clara, CA, USA), and the memory is DDR4 3200 Mhz 32G (Kingston, Fountain Valley, CA, USA). The language used in the software environment is Python 3.8, PyTorch 1.10.0, the CPU computing environment is NumPy 1.20.3, the GPU computing environment is CUDA 11.3.1, and cudnn 8.2.1.
In this paper, the dimension of the low-dimensional problem description vector is extended to 128 dimensions through the fully connected layer (the constant g mentioned in Section 3.2 and Section 3.3.2 adopts 128). Four-head attention is the main form of multi-headed attention mechanism in this paper. The problem size of 200 users and 50 cars is used during the MemPtrN training in this article. Since the vehicle capabilities in the currently public standard benchmark are all the same, this paper attempts to generate CVRPs with different vehicle capabilities. Since there is no standard benchmark for Flexible CVRP at present, this paper generates problem examples based on the following rules. The problems are generated to ensure that feasible solutions exist under the traditional CVRP model.
- Multiple random user coordinates are generated in a rectangular range of , and the number of users is denoted as n.
- A uniform distribution between 1 and 4 is used to randomly generate the transportation demands of each user. For each user, demand variables for their shipments are generated.
- A load capacity of 4, 8, 16, and 32 tons is randomly selected for each vehicle.
- Verify that the sum of all vehicle capacities exceeds the sum of all customer demands. If this condition is met, save the problem instance; otherwise, regenerate the problem.
In the above problem generation steps, the randomly generated and selected numbers are integers. In addition, this article tests the performance of the model trained on a larger scale problem, such as 800 users and 200 cars, or even 1600 users and 400 cars. Large-scale problem generation still uses the above-mentioned problem generation method. This paper generates 512 samples for each problem scale as examples. Each example utilizes a comprehensive comparative analysis between the MemPtrN proposed in this paper and multiple state-of-the-art methods, including two recently introduced heuristic methods (improved ACO [4], CVRP-FA [5]), one reinforcement learning method (TAOA [20]), three commercial optimization solvers (OR-Tools [13], IBM CPLEX [6], and Gurobi [7]), and one classic unenhanced search algorithm (SA [4]). This selection of comparison methods provides a thorough evaluation across different algorithmic paradigms. The selection criteria ensure that the various methods differ in their core concepts and exhibit significant structural differences from the algorithm presented in this paper. This approach minimizes result imbalances caused by similarities in the component connections and encoding among homogeneous methods, thereby enabling a robust evaluation of the strengths and weaknesses of different approaches on the Flexible Capacitated Vehicle Routing Problem (Flexible CVRP). The mean of the reward function for the 512 question samples is then calculated as the experimental result for each question scale. For each problem scale, 512 sample questions are taken. Then, taking the vehicle driving distance as the optimization objective, the above methods are used to solve the problem. Finally, the mean value of the solution result of each problem scale is calculated and used as the experimental result of the problem scale.
In the experiment, the A2C reinforcement learning framework is used to train the MemPtrN, the distance is the reward, and the training goal is to minimize the reward. Before the MemPtrN starts training, we first randomly generate a sequence mapping to a solution of the CVRP, and calculate the reward of these solutions. According to the above reward, the critic network is trained for 64 rounds, and then the A2C training process is started.
4.2. Experimental Result
This section gives the comparative experiments as well as the solutions for a large-scale CVRP. In this set of comparative experiments, the problem is set at the scale of “m × n”, which represents the problem with m users and n vehicles, e.g., “200 × 50” represents the problem size with 200 users and 50 vehicles. The results of comparative experiments show that that the MemPtrN has advantages in some aspects compared with OR-Tools. In large-scale solutions, the MemPtrN shows better calculation performance and solution quality than OR-Tools. The time consumption of the improved ACO is shorter, followed by SA, and finally CVRP-FA. The MemPtrN can use GPU acceleration. In the case of GPU acceleration, the time-consuming advantage is more obvious. Because the solving ability of OR-Tools becomes stronger with the increase in time consumption, the time consumption of OR-Tools is set to be the same as that of the model in this paper. Among them, the solution time delay (unit: second) of various algorithms and solvers when solving different problem sizes is shown in Figure 7.
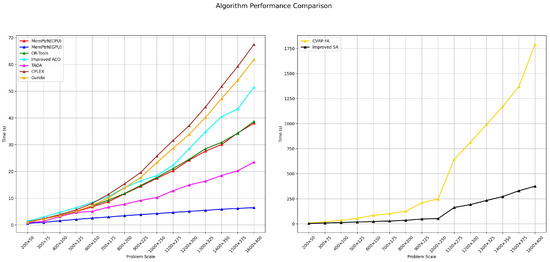
Figure 7.
Time consumption.
The improved ACO is the shortest time-consuming heuristic algorithm, which is better than the MemPtrN using CPU. Another advantage of the MemPtrN is that it is easy to use GPU acceleration, and the solution cost is much less than other solutions. Under the premise of the time-consuming solution shown in Figure 7, compared with the heuristic algorithm and solver, the solution quality of the method in this paper is also better. The solution results in Table 3 show the driving distance of the vehicle in units of 104 km.

Table 3.
Solution results.
According to the analysis in Section 3.4, the time complexity of the MemPtrN is ), so the quality of the solution of the MemPtrN is better than commercial solvers, including OR-Tools, CPLEX, and Gurobi, under the same solution time. Our results show that while CPLEX and Gurobi excel in smaller problem instances (200 × 50 to 400 × 100), their performance deteriorates as the problem scale increases. In addition, compared to heuristic algorithms, the MemPtrN algorithm has advantages both in time consumption and in solution quality, especially in the face of large-scale problems. The quality of the solution obtained by the method in this paper is almost the same as that obtained by the solver and heuristic algorithm when faced with the “200 × 50” problem size, which is used for training. It can be seen from the figure that when the problem scale increases, the solution quality of OR-Tools and other heuristic algorithms has a significant gap compared with the MemPtrN.
The goal of the MemPtrN is to solve the Flexible CVRP in Section 2. The problems generated in the experiment are all problems with feasible solutions in the traditional CVRP model, which is a necessary condition for running OR-Tools. Since the MemPtrN adopts an elastic vehicle–customer matching mechanism, the following situations may occur when solving the traditional CVRP. If a problem has a feasible solution as a traditional CVRP but there may be unsuspecting customers obtained by using the MemPtrN, this situation reduces the driving distance of the vehicle. Among the 512 questions, if there are n users in a question, and n’ users are not served, the average number of unserved users is defined as follows:
where i in Formula (38) is the index of problems. The meaning of this metric is that, on average, each question has users not served. In the above problem scenario of a rectangular space of 1000 km × 1000 km, in the solution process, if there is a user who is not served, then when the user is included in the service, the maximum travel distance is , which is the situation as shown in Figure 8 and Figure 9.
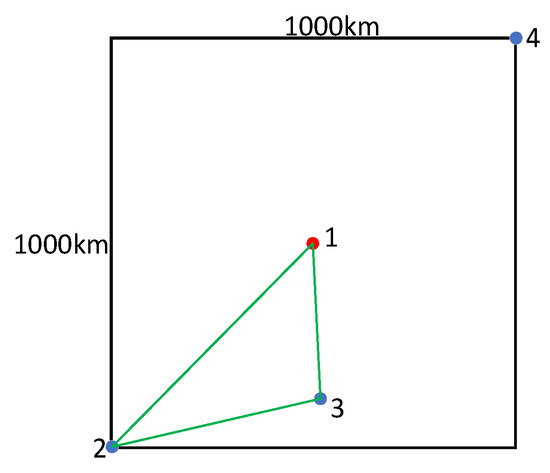
Figure 8.
Original path.
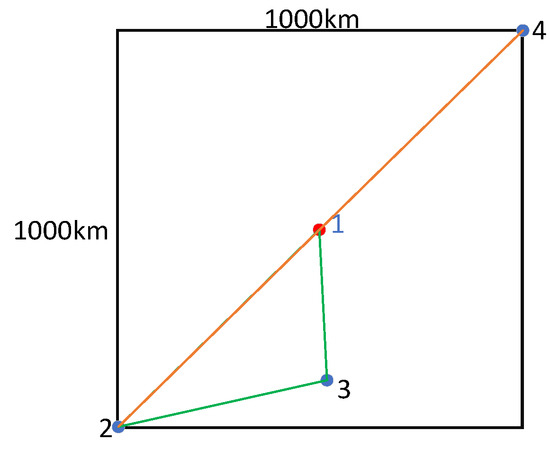
Figure 9.
Add user longest path.
As shown in Figure 8, suppose that the original path is 1-2-3-1, in which the fourth user is not served. At this time, the maximum travel distance of a newly connected node is shown in Figure 9. The new path is 1-2-4-2-3-1. This case represents the maximum travel distance to include a new user on the route. In summary, the distance to add a node increases by km at most, which is approximately km. If unserved users are considered, the solution results in Table 3 need to be revised. The statistics of the average number of unserved users are shown in Table 4.

Table 4.
Average number of unserved users.
Currently, only the MemPtrN and improved ACO algorithms have unserved users. Therefore, the solution results of these two algorithms need to be revised. The revised solution results in the case of unserved users are considered as shown in Table 5.

Table 5.
Corrected solution results.
Table 5 gives an upper bound: the maximum travel distance after adding unserved users to the path solved by the MemPtrN under each problem scale. The added distance for all users to be served will be less than . Even in the worst case, the solution quality of the MemPtrN is still better than OR-Tools and other heuristic algorithms for large-scale problems.
5. Conclusions
In terms of models, we identified and addressed two critical limitations in the traditional CVRP model when applied to real logistics scenarios: the uniform vehicle capacity assumption and the inability to handle scenarios without feasible solutions. Our Flexible CVRP transforms the traditional binary feasible/infeasible problem into a multi-objective optimization by relaxing the “all customers must be served” constraint. This enables meaningful solutions in scenarios where traditional methods would fail completely. Our experimental results confirm that the MemPtrN outperforms existing methods even when accounting for unserved users, validating that this design is not a limitation but a practical advantage that more accurately represents real-world logistics environments where demand fluctuations often require prioritization decisions. In terms of problem-solving, with the current commonly used heuristic algorithms and solvers, it is difficult to solve large-scale CVRPs quickly. Aiming at the challenge of a very large-scale CVRP, the Memory Pointer Network (MemPtrN) is proposed in this paper, which is trained by reinforcement learning. Based on the above two aspects of the work, a common-sense solution can be obtained when the traditional CVRP has no feasible solution, and the large-scale Flexible CVRP can be effectively dealt with.
Our comprehensive experimental results demonstrate the effectiveness of the MemPtrN across different problem scales. For small-scale problems, the MemPtrN achieves comparable solution quality to state-of-the-art commercial solvers like OR-Tools, while outperforming both recent and classical heuristic algorithms. In large-scale scenarios, the MemPtrN exhibits superior performance with significantly better solution quality and reduced computational time compared to existing approaches. With GPU acceleration, the computational advantage of the MemPtrN becomes even more pronounced. Notably, our experiments validate that the MemPtrN trained on small-scale problems successfully generalizes to large-scale instances, demonstrating its scalability and practical applicability.
While our reinforcement learning approach significantly reduces the solution time, several limitations should be noted. First, although the model demonstrates good generalization across different problem scales, its performance may vary when the ratio between vehicles and goods changes significantly. Second, while our greedy strategy-based mapping method improves the computational efficiency, it potentially restricts the solution search space, which might affect the solution quality in certain scenarios. Additionally, the current model’s generalization capability is primarily demonstrated within different problem scales of CVRP; for different types of routing problems, the problem representation needs to be redesigned, and the model requires retraining.
Future research directions include several promising avenues. Investigating the MemPtrN performance under varying vehicle-to-goods ratios could provide valuable insights into the model’s robustness. Evaluating the MemPtrN on the established CVRP benchmarks would facilitate direct comparison with other state-of-the-art methods. Extending this methodology to other combinatorial optimization problems, such as TSP and VRPTW, could help validate its broader applicability. Additionally, exploring alternative memory expression forms and memory update mechanisms may enhance the solution quality while further reducing the computational overhead. These extensions would contribute to the development of more versatile and efficient approaches for solving complex routing problems in real-world logistics applications.
Author Contributions
E.W.: Conceptualization, Methodology, Formal analysis, Writing—original draft, Writing—review and editing, Visualization. Y.C.: Methodology, Formal analysis, Software, Writing—original draft, Writing—review and editing. Z.S.: Conceptualization, Data curation, Writing—review and editing, Supervision, Project administration, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China under Grant 61972208, 62272239; Jiangsu Agriculture Science and Technology Innovation Fund (JASTIF) CX(22)1007.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors of this article declare that there are no direct group or individual interests, or competitive relationships.
References
- Yodwangjai, S.; Malampong, K. An Improved Whale Optimization Algorithm for Vehicle Routing Problem with Time Windows. J. Ind. Technol. 2022, 18, 104–122. [Google Scholar]
- Souza, I.P.; Boeres, M.C.S.; Moraes, R.E.N. A robust algorithm based on differential evolution with local search for the capacitated vehicle routing problem. Swarm Evol. Comput. 2023, 77, 101245. [Google Scholar]
- Rezaei, B. Combining genetic local search into multi-population evolutionary algorithms for the capacitated vehicle routing problem. Appl. Soft Comput. 2023, 142, 110309. [Google Scholar] [CrossRef]
- Frías, N.; Johnson, F.; Valle, C. Hybrid Algorithms for energy minimizing vehicle routing problem: Integrating clusterization and ant colony optimization. IEEE Access 2023, 11, 125800–125821. [Google Scholar]
- Altabeeb, A.M.; Mohsen, A.M.; Ghallab, A. An improved hybrid firefly algorithm for capacitated vehicle routing problem. Appl. Soft Comput. 2019, 84, 105728. [Google Scholar]
- Lazarev, A.A.; Grishin, E.M.; Galakhov, S.A.; Tarasov, G.V. Algorithms for locomotives maintenance schedule. IFAC-PapersOnLine 2019, 52, 951–956. [Google Scholar]
- Xiao, L.; Dridi, M.; Hassani, A.H.E.; Lin, W.; Fei, H. A solution method for treatment scheduling in rehabilitation hospitals with real-life requirements. IMA J. Manag. Math. 2019, 30, 367–386. [Google Scholar] [CrossRef]
- Shinano, Y.; Berthold, T.; Heinz, S. ParaXpress: An experimental extension of the FICO Xpress-Optimizer to solve hard MIPs on supercomputers. Optim. Methods Softw. 2018, 33, 530–539. [Google Scholar]
- Vo-Minh, T. Calculation of Bearing Capacity Factors of Strip Footing Using the Node-based Smoothed Finite Element Method (NS-FEM). Geotech. Sustain. Infrastruct. Dev. 2020, 62, 1127–1134. [Google Scholar]
- Gamrath, G.; Koch, T.; Maher, S.J.; Rehfeldt, D.; Shinano, Y. SCIP-Jack—A solver for STP and variants with parallelization extensions. Math. Program. Comput. 2017, 9, 231–296. [Google Scholar]
- Gurung, A.; Ray, R. Simultaneous solving of batched linear programs on a GPU. In Proceedings of the ACM/SPEC International Conference on Performance Engineering, Mumbai, India, 7–11 April 2019. [Google Scholar]
- Boas, M.; Santos, H.G.; Merschmann, L.; Berghe, G.V. Optimal decision trees for the algorithm selection problem: Integer programming based approaches. Int. Trans. Oper. Res. 2021, 28, 2759–2781. [Google Scholar]
- Hamzehi, S.; Bogenberger, K.; Kaltenhäuser, B.; Tian, J.; Chin, A.; Cao, Y. Distance-Based Neural Combinatorial Optimization for Context-based Route Planning. In Proceedings of the IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25–28 April 2021. [Google Scholar]
- Khor, C.S. Recent Advancements in Commercial Integer Optimization Solvers for Business Intelligence Applications. In E-Business-Higher Education and Intelligence Applications; IntechOpen: London, UK, 2021. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural combinatorial optimization with reinforcement learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Tsai, Y.L.; Rastogi, C.; Kitanidis, P.K.; Field, C.B. Routing algorithms as tools for integrating social distancing with emergency evacuation. arXiv 2021, arXiv:2103.03413. [Google Scholar]
- Li, J.; Ma, Y.; Gao, R.; Cao, Z.; Lim, A.; Song, W.; Zhang, J. Deep reinforcement learning for solving the heterogeneous capacitated vehicle routing problem. IEEE Trans. Cybern. 2021, 52, 13572–13585. [Google Scholar]
- Xu, Y.; Fang, M.; Chen, L.; Xu, G.; Du, Y.; Zhang, C. Reinforcement Learning with Multiple Relational Attention for Solving Vehicle Routing Problems. IEEE Trans. Cybern. 2021, 52, 11107–11120. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Zhou, Y.; Liu, C.Y. Trajectory Planning for Capacitated Vehicle Routing Problem: A Deep Reinforcement Learning Approach. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 6–9 August 2023; pp. 760–765. [Google Scholar]
- Zou, Y.; Wu, H.; Yin, Y.; Dhamotharan, L.; Chen, D.; Tiwari, A.K. An improved transformer model with multi-head attention and attention to attention for low-carbon multi-depot vehicle routing problem. Ann. Oper. Res. 2024, 339, 517–536. [Google Scholar]
- Si, J.; He, F.; Lin, X.; Tang, X. Vehicle dispatching and routing of on-demand intercity ride-pooling services: A multi-agent hierarchical reinforcement learning approach. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103551. [Google Scholar]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. In Proceedings of the Advances in Neural Information Processing Systems 28, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar]
- Mazzeo, S.; Loiseau, I. An ant colony algorithm for the capacitated vehicle routing. Electron. Notes Discret. Math. 2004, 18, 181–186. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems 30, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Sukhbaatar, S.; Szlam, A.; Weston, J.; Fergus, R. End-to-end memory networks. In Proceedings of the Advances in Neural Information Processing Systems 28, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).