To demonstrate and evaluate our automated FUN3D–LASTRAC coupling approach, we examine three different canonical flow configurations: a zero-pressure-gradient flat plate, the NLF-0416 airfoil, and the 6:1 prolate spheroid. Collectively, these cases feature transition due to TS waves, separation bubbles, and crossflow instability. The computational predictions for these cases are evaluated via comparisons with experimental measurements as well as other computational predictions, including transport-equation-based models and results from similar iterative approaches for transition prediction.
3.1. Zero-Pressure-Gradient Flat Plate
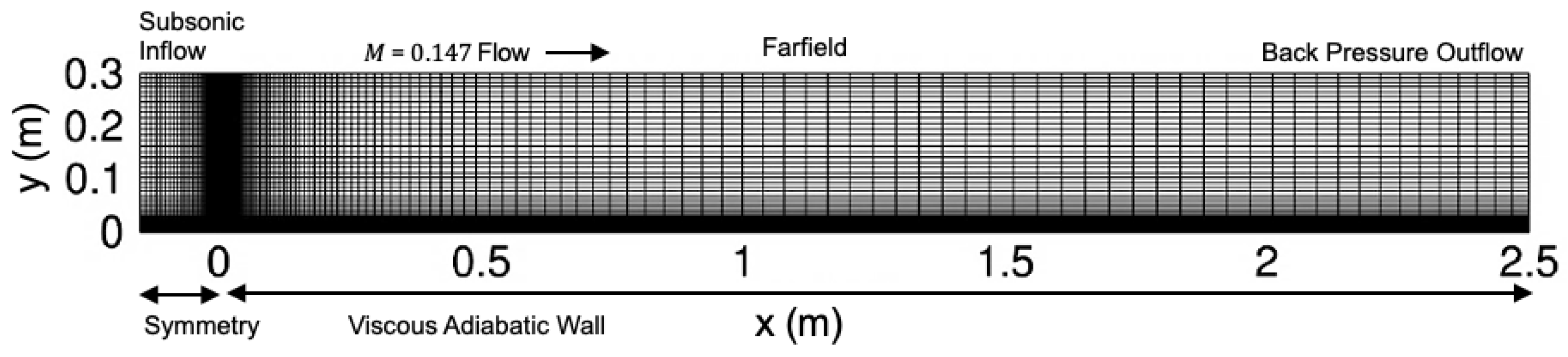
The first case we consider is low-speed flow over a two-dimensional zero-pressure-gradient flat plate with a sharp leading edge. This flat plate starts at
m and extends to
m. We select the flow conditions to match those from experiments by Schubauer and Skramstad [
38]. The freestream density, velocity, and temperature are
kg/m
3,
m/s, and
K, respectively. This yields a freestream unit Reynolds number of
m) and Mach number of
. We assume a perfect gas such that
, where
J/K/kg is the specific gas constant for air. Here,
is the constant ratio of specific heats. The Prandtl number is set to a constant value of
. To compute the dynamic viscosity
, we use Sutherland’s law
with
kg/(ms
) and
K. A freestream turbulence intensity of
is used for this case. The left edge of the computational domain at
m is a subsonic inflow, and the right edge is a back-pressure outflow. Furthermore, the flat plate has adiabatic and no-slip boundary conditions, and the small portion before the flat plate is set to a wall-normal-symmetry boundary condition. A farfield boundary condition is used at the top edge of the domain at
m.
We use a computational grid with 961 and 513 points in the streamwise and wall-normal directions, respectively. The 961 points also include the 257 points upstream of the leading edge of the flat plate. We place the first grid point above the flat plate at a distance of
m, which satisfies
regardless of the boundary-layer state, and the wall-normal grid spacing increases gradually from there to the freestream. This computational grid is designed to have more than 150 points within the boundary layer. Furthermore, the streamwise grid spacing is the smallest near the leading edge of the flat plate at
m. This exact computational grid is depicted as level 6 herein, and others in the family were used in previous work by Venkatachari et al. [
39]. For grids in this family, the resolution doubles between consecutive even or odd levels. Grid level 7 has 1441 and 769 points in the streamwise and wall-normal directions, respectively, while grid level 8 has 1921 and 1025 points.
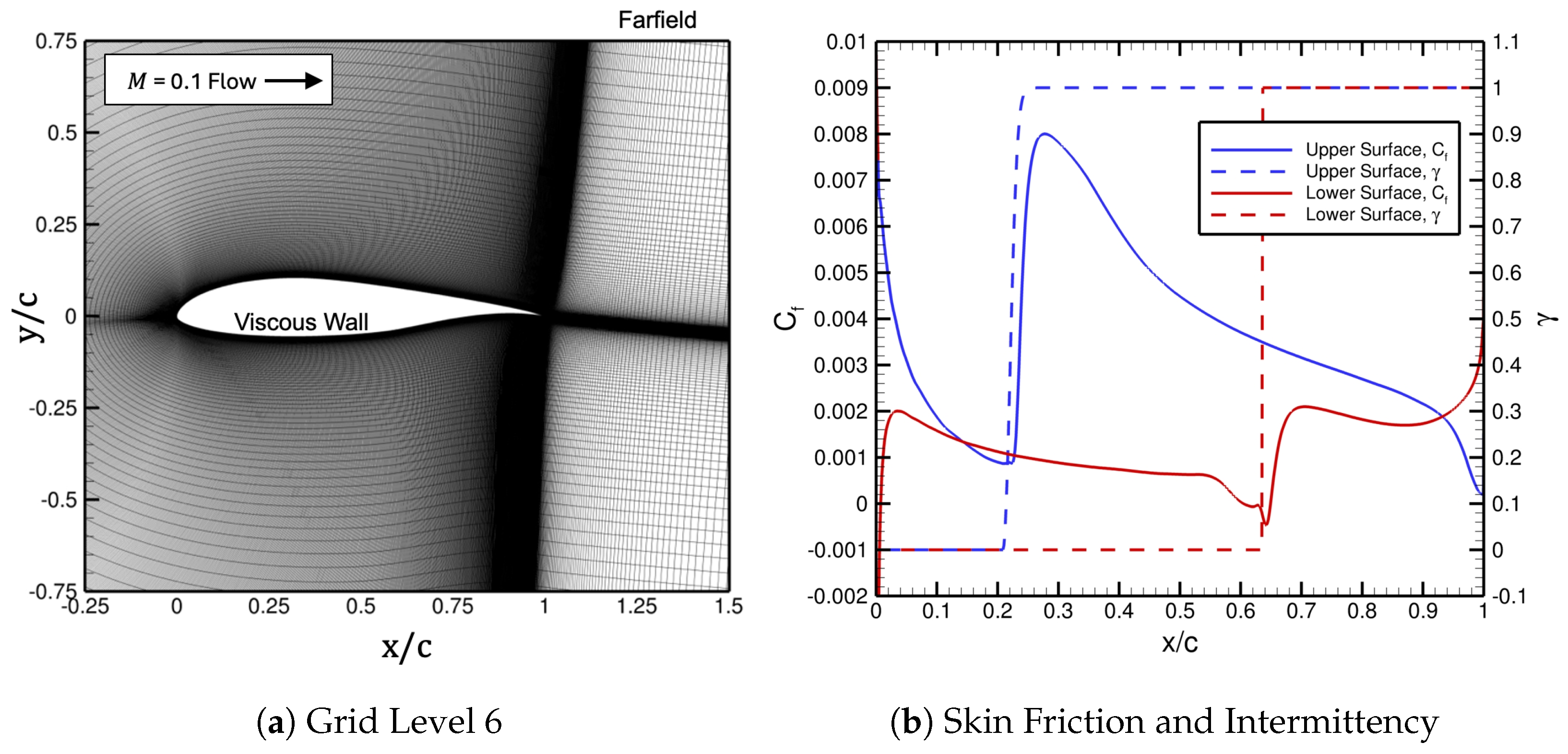
Figure 2 displays grid level 1 in this family and the corresponding boundary conditions.
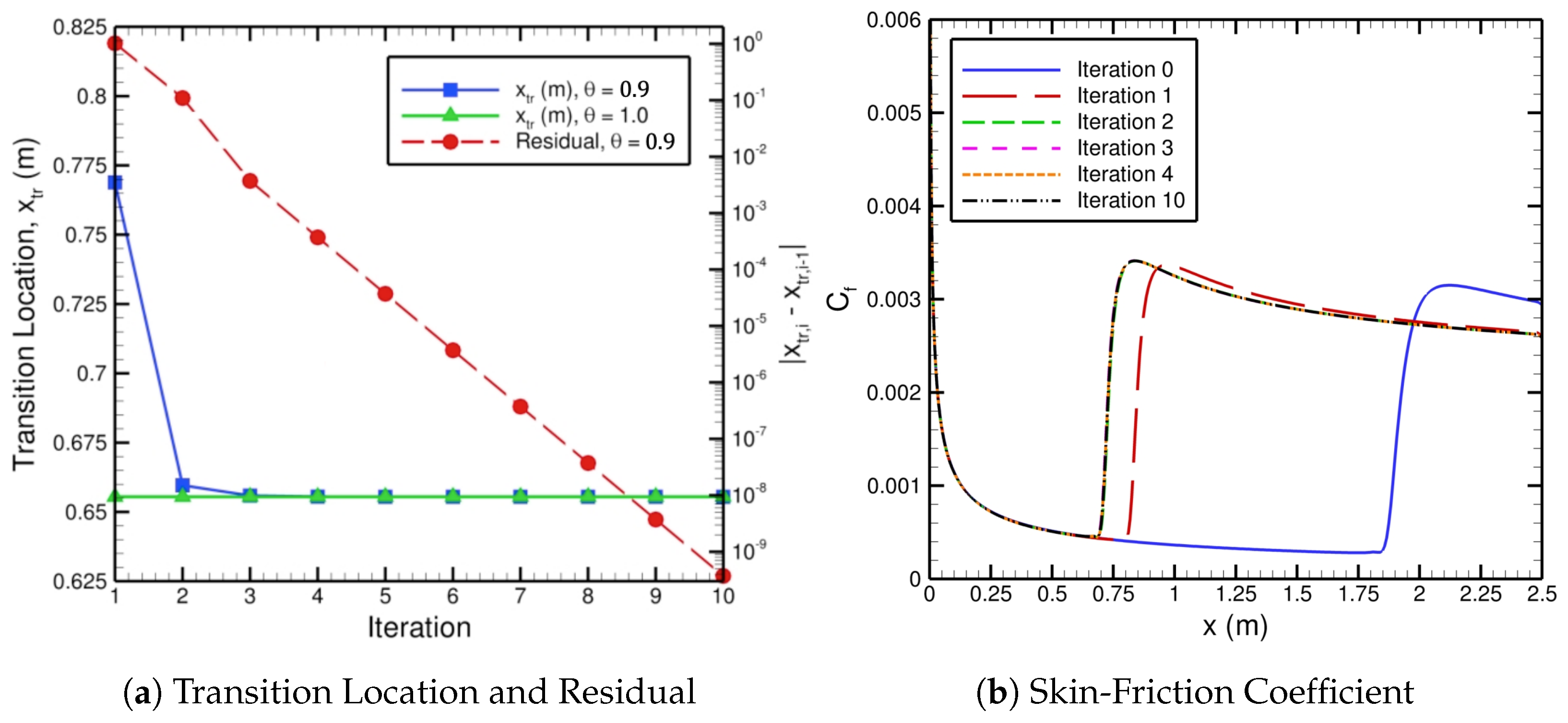
Figure 3 displays the streamwise distributions of the skin-friction coefficient and the intermittency along the plate for iterations 1 and 10 of the automated coupling approach with FUN3D and LASTRAC pertaining to grid level 6. There is a significant difference between the results from iterations 1 and 10 after transition occurs, but, upstream in the laminar portion, the solutions are the exact same. Moreover, the intermittency varies smoothly from 0 to 1 in the region of transition as the skin-friction coefficient also rises from approximately
to
. A closeup view of both the skin-friction coefficient and the intermittency near transition to turbulence are shown in
Figure 3 on the right. As indicated in
Figure 3, the intermittency function helps the flow to shift from laminar to fully turbulent over a finite streamwise extent (instead of happening very abruptly) to better match the physics and the experiments. Although not shown, it also improves the iterative convergence of the automated FUN3D–LASTRAC transition-prediction method.
The iterative convergence of the imposed transition location with the corresponding residual and the skin-friction coefficient are displayed in
Figure 4. For the initial basic state, i.e., the zeroth iteration, we imposed transition far downstream at
m. The skin-friction distribution from the initial basic state is shown in
Figure 4b. Once the initial FUN3D basic state has been obtained, it is converted by the solver-independent module to a format that LASTRAC is able to read. That mean flow file is used to determine the
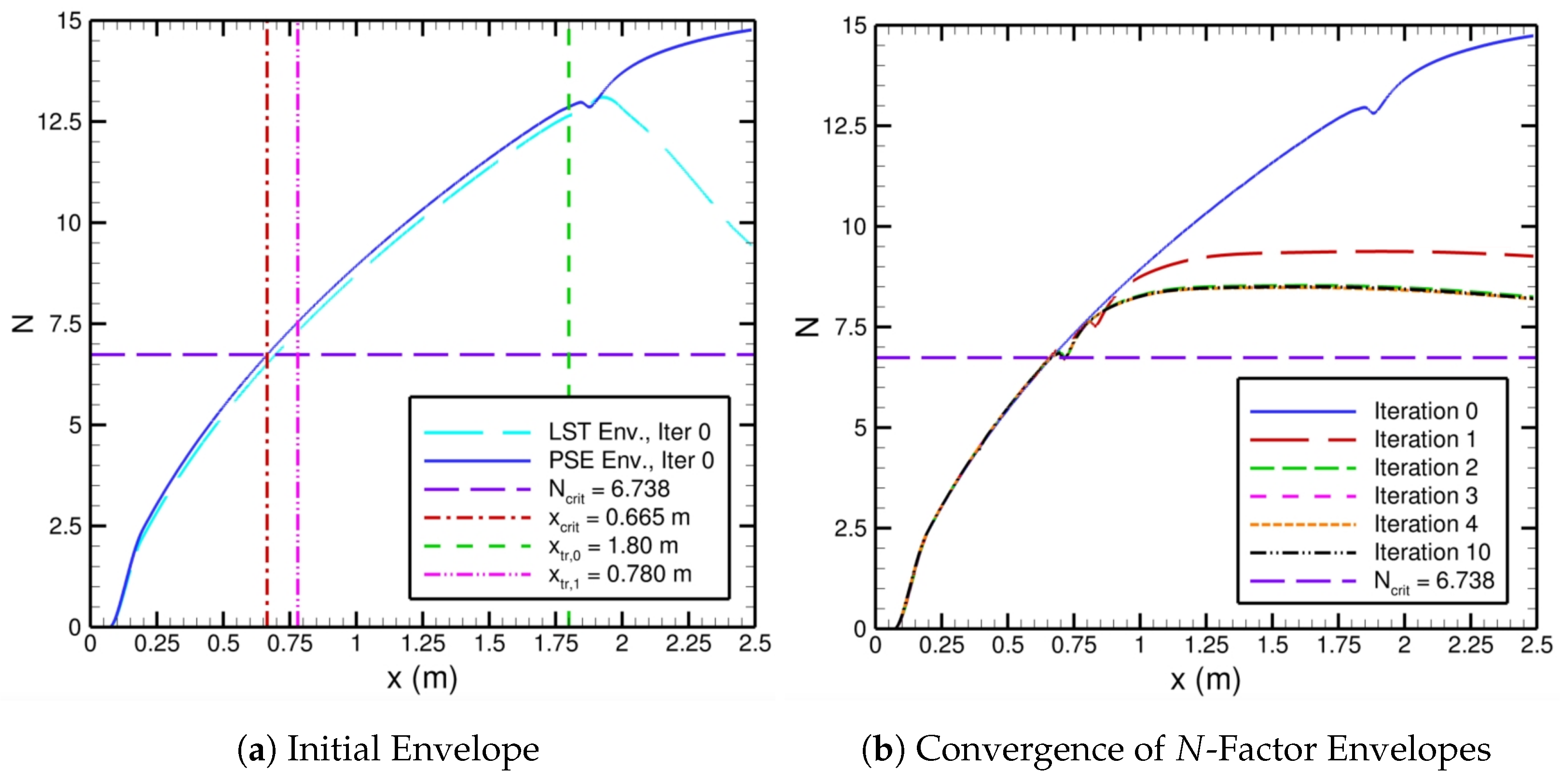
N-factor envelope based on PSE computations. The
N-factor envelope of the initial basic state is depicted in
Figure 5, along with the
N-factor envelopes pertaining to iterations 1 through 10. The value of
in
Figure 5 comes from the expression
via Mack [
8] for TS waves in 2D flows with
. Note that Mack’s correlation of
is based on LST results, but, since nonparallel effects for the flat plate are rather small, the same expression may be used for the PSE as well. The location where
crosses the
N-factor envelope yields
, which, in turn, is used to determine the next transition location,
, with Equation (
7) using
and an appropriate under-relaxation factor. This results in the values of
m and
m in
Figure 5 with
m and
for iteration 0. The new transition location,
m, is prescribed in the next FUN3D basic-state computation pertaining to iteration 1. As the iteration number increases from 0 to 10, the
N-factor envelopes converge in
Figure 5b, and the skin-friction distributions converge in
Figure 4b. The resulting change in the location of transition onset from each iteration decreases exponentially, or in a straight line on a logarithmic scale, to machine zero according to
Figure 4a. Moreover, if the under-relaxation factor is set to unity (i.e., zero under-relaxation), then after just one iteration the location of transition onset converges for this flat-plate case. This means the flow does not have significant viscous–inviscid interactions and is not overly sensitive to changes in the location of transition onset. For cases with stronger viscous–inviscid interactions, under-relaxation is necessary to achieve robust convergence, especially during the early iterations, but can be increased afterwards to reduce the number of overall iterations. Similar iterative convergence of the automated FUN3D–LASTRAC method is obtained for different initially imposed transition locations of the initial basic state from
m to
m. If the imposed transition location is considerably upstream of the final converged transition location, then extrapolation is used to predict the next imposed transition location.
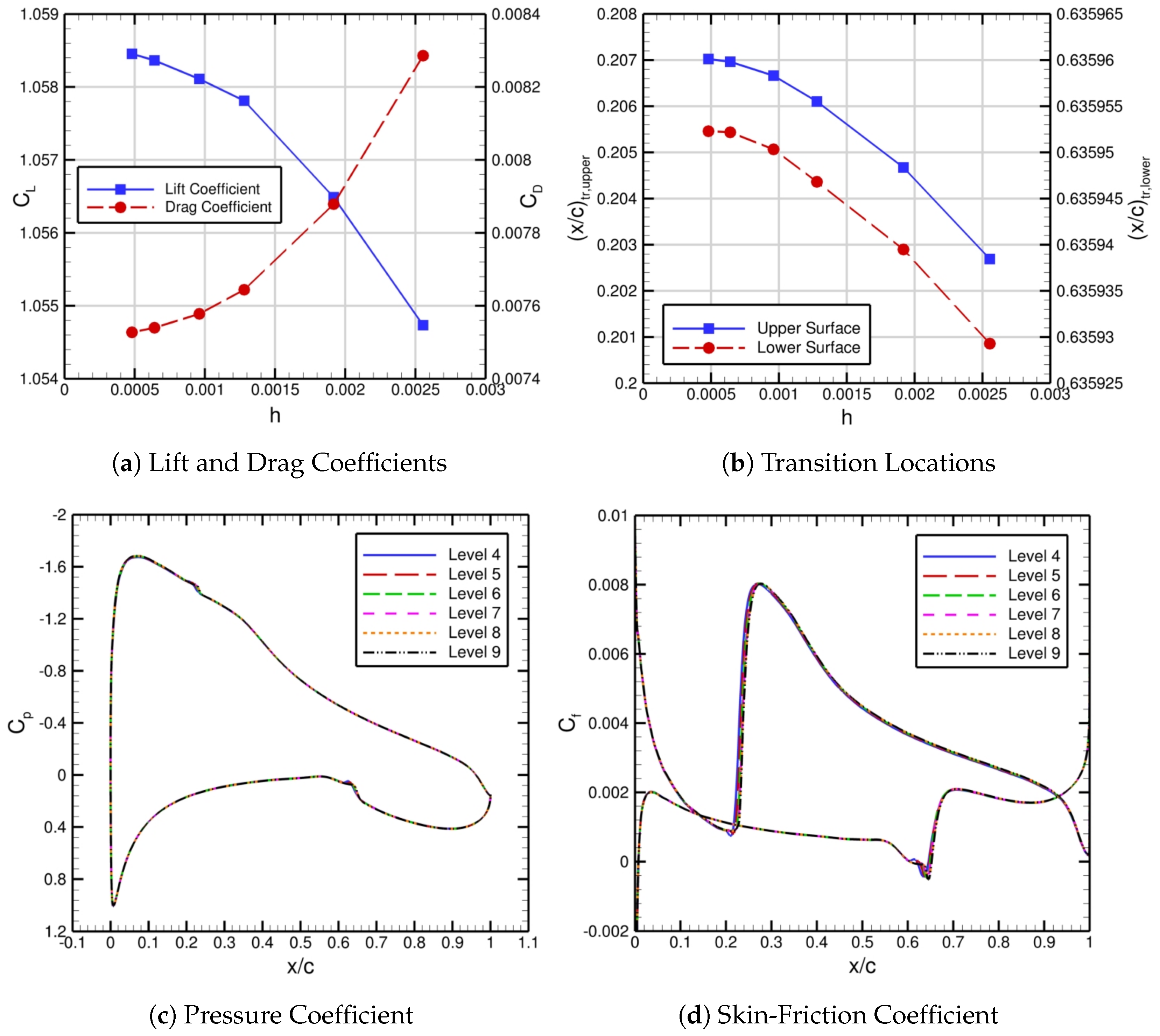
After showing iterative convergence of the automated FUN3D–LASTRAC transition-prediction method for the zero-pressure-gradient flat plate, we focus on grid convergence for the same case.
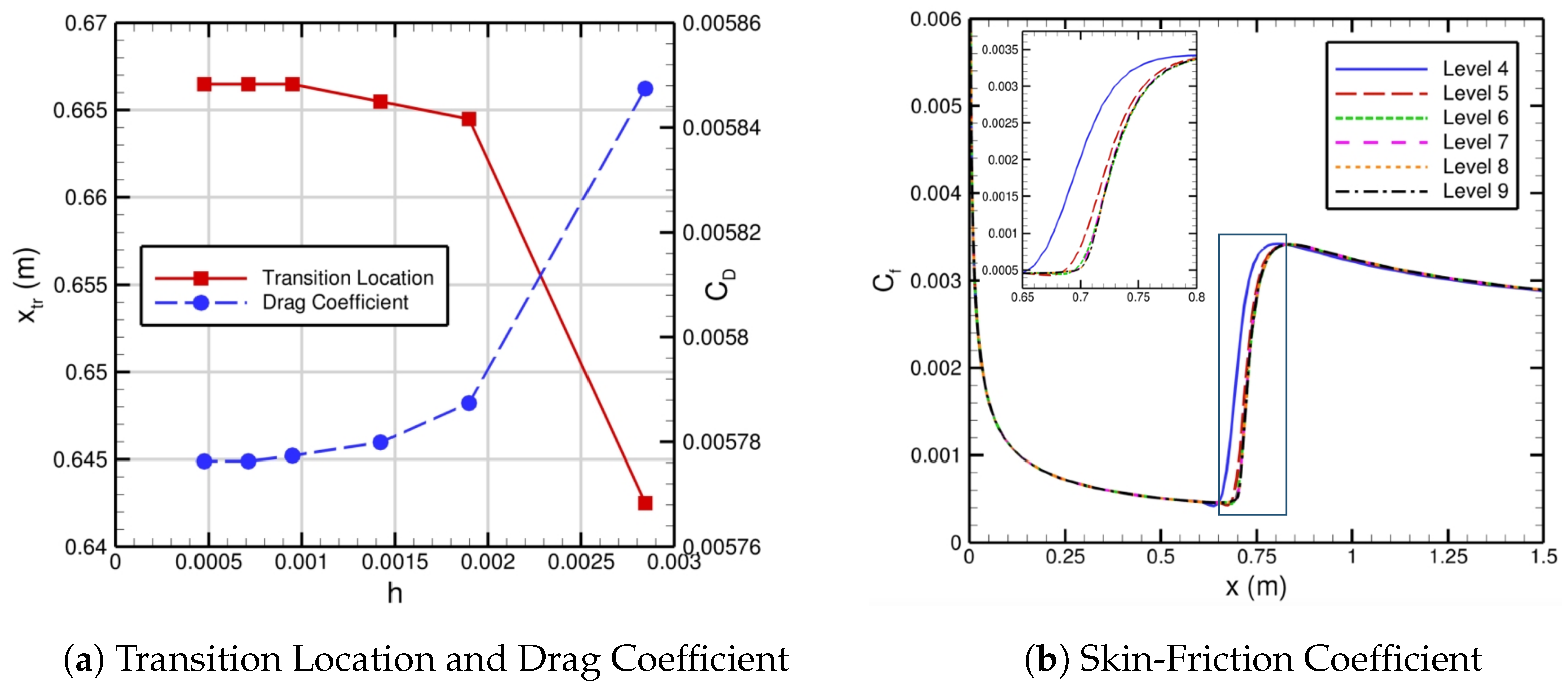
Figure 6 shows the grid convergence of the drag coefficient, transition location, and skin-friction coefficient for this flat-plate case across levels 4 through 9. The level 4 grid has 123,616 points, and the level 9 grid has 4,428,097 points, where the resolution doubles along each spatial direction every other grid level. In
Figure 6a, both the drag coefficient and transition location plateau for levels 8 and 9 as the grid spacing parameter
approaches zero. The skin-friction distribution also converges as the resolution increases (or the grid spacing decreases) in
Figure 6b. Hence, our automated FUN3D–LASTRAC transition-prediction method converges with respect to both the iteration number and grid resolution.
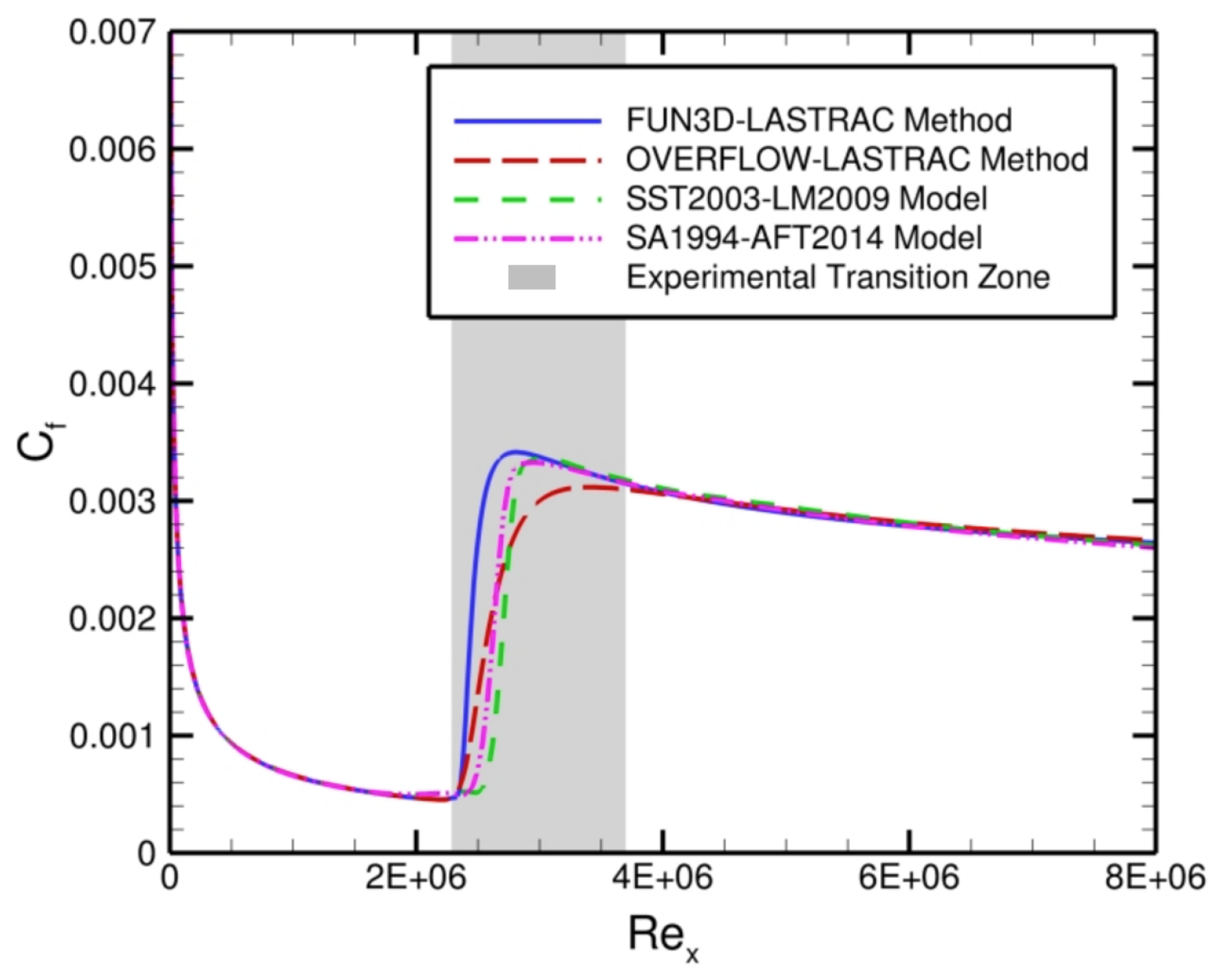
To validate our automated FUN3D–LASTRAC transition-prediction method, we compare the skin-friction distributions between our method, the OVERFLOW–LASTRAC method [
29], the SST2003-LM2009 model [
5], and the SA1994-AFT2014 model [
14] in
Figure 7. The experimentally observed transition zone [
38] is also included as part of
Figure 7 to validate our method. All the different computational skin-friction distributions begin to quickly rise in the experimentally observed transition zone [
38], which indicates good agreement between the computations and experiments. The relative agreement between the skin-friction distributions computed with the FUN3D–LASTRAC and OVERFLOW–LASTRAC methods indicates that transition occurs at the exact same value of
(the laminar and turbulent skin-friction coefficients also match); the only deviation is limited to the intermittent region between laminar and fully turbulent flow because the coupling methods use different intermittency functions. There is also relatively good agreement between the RANS-based transition models (i.e., SST2003-LM2009 and SA1994-AFT2014) and the automated FUN3D–LASTRAC transition-prediction method in terms of the skin-friction coefficient and the location of transition onset. These successful comparisons provide verification and validation of the FUN3D–LASTRAC approach for modeling transition for this 2D zero-pressure-gradient flat-plate case.
3.2. NLF-0416 Airfoil
To help validate the automated FUN3D–LASTRAC iterative method for strong viscous–inviscid interaction and transition due to a separation bubble, we consider the NLF-0416 airfoil that is a natural-laminar-flow configuration developed at the NASA Langley Research Center by Somers [
40]. This particular airfoil is designed to achieve a large value of the maximum lift coefficient and a low value of the cruise drag coefficient. An angle of attack equal to 5 degrees is considered, which leads to natural boundary-layer transition in a fully attached boundary layer over the upper surface and separation-bubble-induced transition across the lower surface. A moderate Reynolds number based on the chord length is prescribed,
, and the freestream Mach number is
. The freestream density, velocity, and temperature are
kg/m
3,
m/s, and
K, respectively. A freestream turbulence intensity of
is used based on the benchmark problem from the 1st AIAA Transition Modeling Workshop (
https://transitionmodeling.larc.nasa.gov/workshop_i/, accessed on 20 March 2025). The farfield boundaries are placed 1000 chord lengths away from the airfoil surface. Freestream boundary conditions are enforced at the left, right, top, and bottom edges of the computational domain. Adiabatic and no-slip boundary conditions are employed at the airfoil surface. This case is significantly more challenging than the flat plate because multiple applications of stability analysis for the basic states are required to capture the strong influence of the recirculation bubble on transition due to an interaction that occurs between the separation-reattachment characteristics and the location of transition onset.
We use a C-type mesh generated with conformal mapping for the NLF-0416 airfoil. The coarser levels of this mesh are based on the grids provided by the 1st AIAA Transition Modeling Workshop. Here, the level 6 grid has 2113 and 289 points along the chordwise and wall-normal directions, respectively. There are 289 points in the wake cut of the grid. It has a near-wall spacing of
based on the chord length that yields a nondimensional wall spacing of approximately
based on turbulent flat-plate estimates at the quarter-chord location. Furthermore, this exact computational grid (level 6) and others in the family were used in the previous work by Venkatachari et al. [
39]. For grids in this family, the resolution doubles with every other level. Grid level 8 has 4225 and 577 points in the chordwise and wall-normal directions, respectively.
Figure 8a displays grid level 6 in this family and the corresponding boundary conditions. There is a clustering of grid points near the airfoil surface and in the wake region.
The streamwise distribution of the skin-friction coefficient and the intermittency along the upper and lower surfaces of the NLF-04146 airfoil for the final iteration of the automated FUN3D–LASTRAC method computed on grid level 6 are shown in
Figure 8b. The intermittency increases smoothly from 0 to 1 in the regions of boundary-layer transition occurring on the upper and lower surfaces of the NLF-0416 airfoil, while the skin friction also rises sharply in these regions. For the lower airfoil surface, there is negative skin friction within a separation bubble that causes transition, while the boundary layer on the upper airfoil surface undergoes a natural transition.
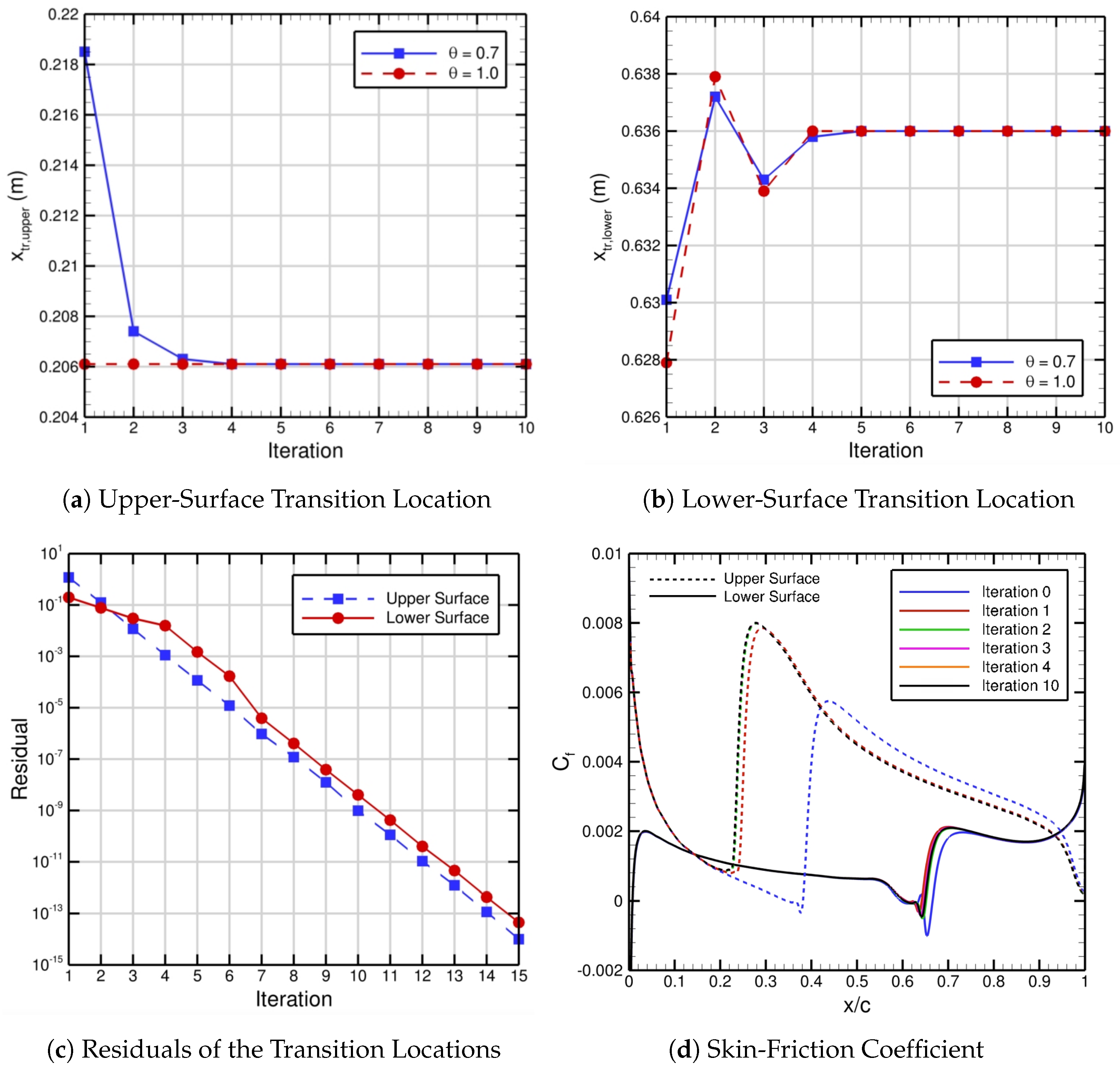
Figure 9 depicts the iterative convergence of the imposed transition locations with the associated residuals and the skin-friction distributions. For the initial basic state, i.e., the zeroth iteration, we imposed transitions at
and
. Note that this choice is arbitrary, and, if we imposed transition further upstream or downstream on either the upper or lower surfaces for the zeroth iteration, the final converged transition locations would be the same. The skin friction of the initial basic state is shown in
Figure 9d. After the initial FUN3D basic state has been obtained, we perform the same iterative procedure conducted for the zero-pressure-gradient flat-plate case and outlined in
Figure 1. Both transition locations on the upper and lower surfaces of the NLF-0416 airfoil converge in
Figure 9, with values of
and
. In this case, we consider the flow to be converged at iteration 5 because the associated change in the locations of transition onset for the upper and lower surfaces after iteration 5 is less than
m, but we also show convergence to machine zero (i.e.,
m) or to iteration 15 in
Figure 9c. Also, the skin friction in
Figure 9d is essentially identical for iterations 4 through 10. The lower under-relaxation factor of 0.7 does not have a significant benefit in this particular case, but, for initially imposed transition locations far away from their converged values and for more complex flow configurations, it helps the automated FUN3D–LASTRAC iterative method to smoothly approach the final solution. The upper-surface transition location converges similarly to the flat-plate case, but the lower-surface transition location has oscillatory convergence because of the strong influence of the separation bubble on transition to turbulence. In other words, for the lower airfoil surface, there is an interaction that occurs between the separation-reattachment characteristics and the location of transition onset. This causes the imposed transition location for the lower surface to be upstream and downstream of the final converged transition location at different iterations of the automated FUN3D–LASTRAC process.
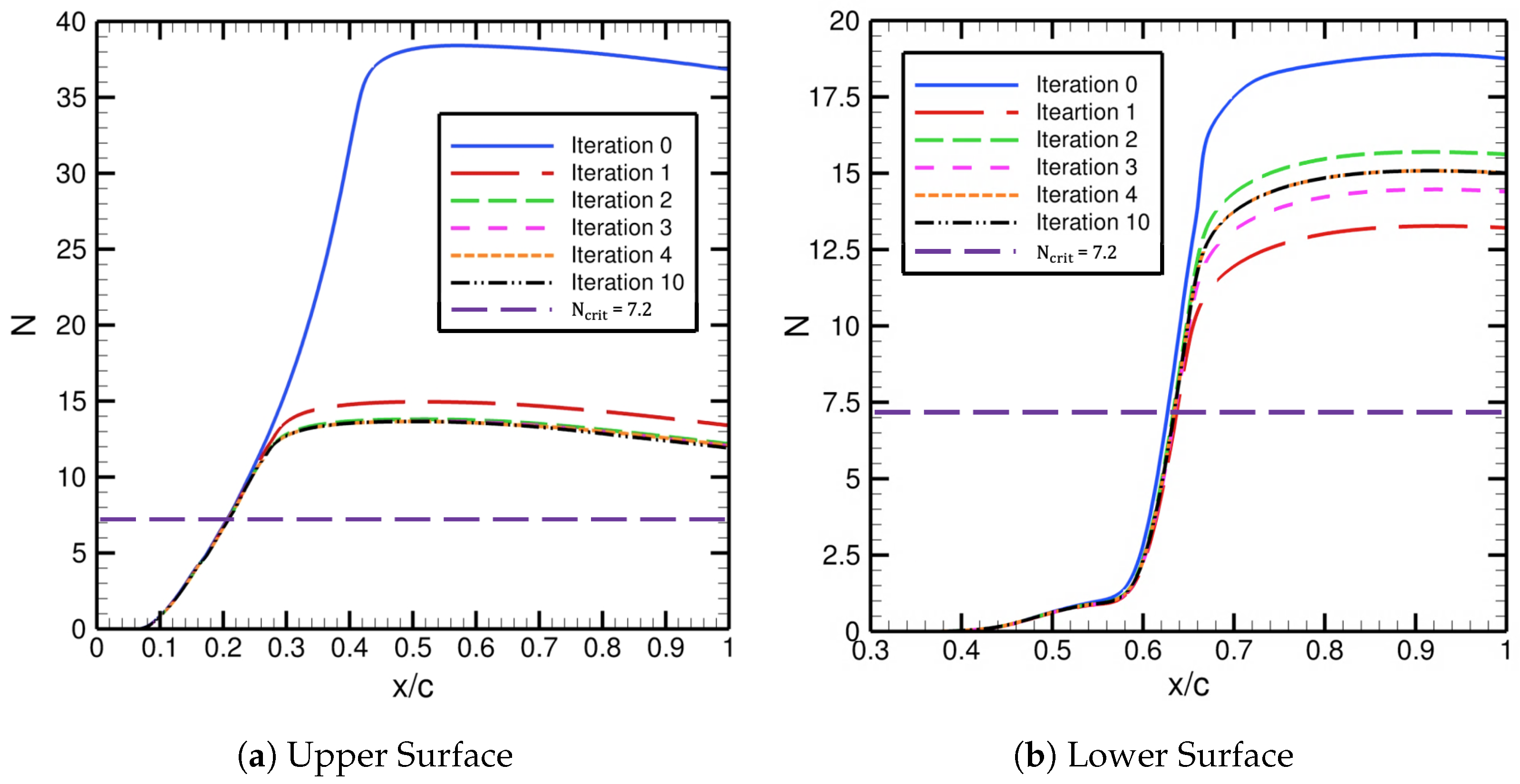
Figure 10 shows the iterative convergence of the
N-factor envelopes that are computed with PSE using LASTRAC for iterations 0, 1, 3, 4, and 10. Since the value of
is 0.15%, we obtain
. Again, this expression from Mack [
8] is based on flat-plate computations with LST (i.e., TS growth in attached boundary layers). Thus, it applies for natural transition along the upper surface, but, for the lower surface, its use for separation bubbles is somewhat arbitrary. It will be demonstrated that values based on Mack’s correlation lead to reasonable flow behavior and yield a good match with the limited available experimental measurements for this case. For the upper airfoil surface, the
N-factor envelopes decrease from a maximum value of approximately 38 to 15 until convergence by about iteration 5. Moreover, for the lower airfoil surface, the maximum values of the
N-factor envelopes oscillate around the final converged maximum value of 15 by iteration 4. This reaffirms the interaction that occurs between the separation-reattachment characteristics and the location of transition onset on the lower surface. Regardless of the visible influence of the separation bubble on the lower-surface transition location, the automated FUN3D–LASTRAC transition-prediction method iteratively converges quickly by iteration 4 in terms of both the skin-friction coefficient and the location of transition onset.
Similar to the flat-plate case, after demonstrating iterative convergence of the automated FUN3D–LASTRAC transition-prediction method for the NLF-0416 airfoil, we focus on showing grid convergence for the
case.
Figure 11 shows the grid convergence of the lift and drag coefficients, transition locations, and the skin-friction coefficient for the NLF-0416 airfoil via levels 4 through 9. The level 4 grid has 153,265 points, and the level 9 grid has 4,331,777 points. In
Figure 11a, the lift and drag coefficients are converging as the grid spacing parameter
approaches zero. Both the upper and lower transition locations in
Figure 11b also converge with respect to grid resolution. Furthermore, the skin-friction distribution in
Figure 11d is also grid-converged by level 9.
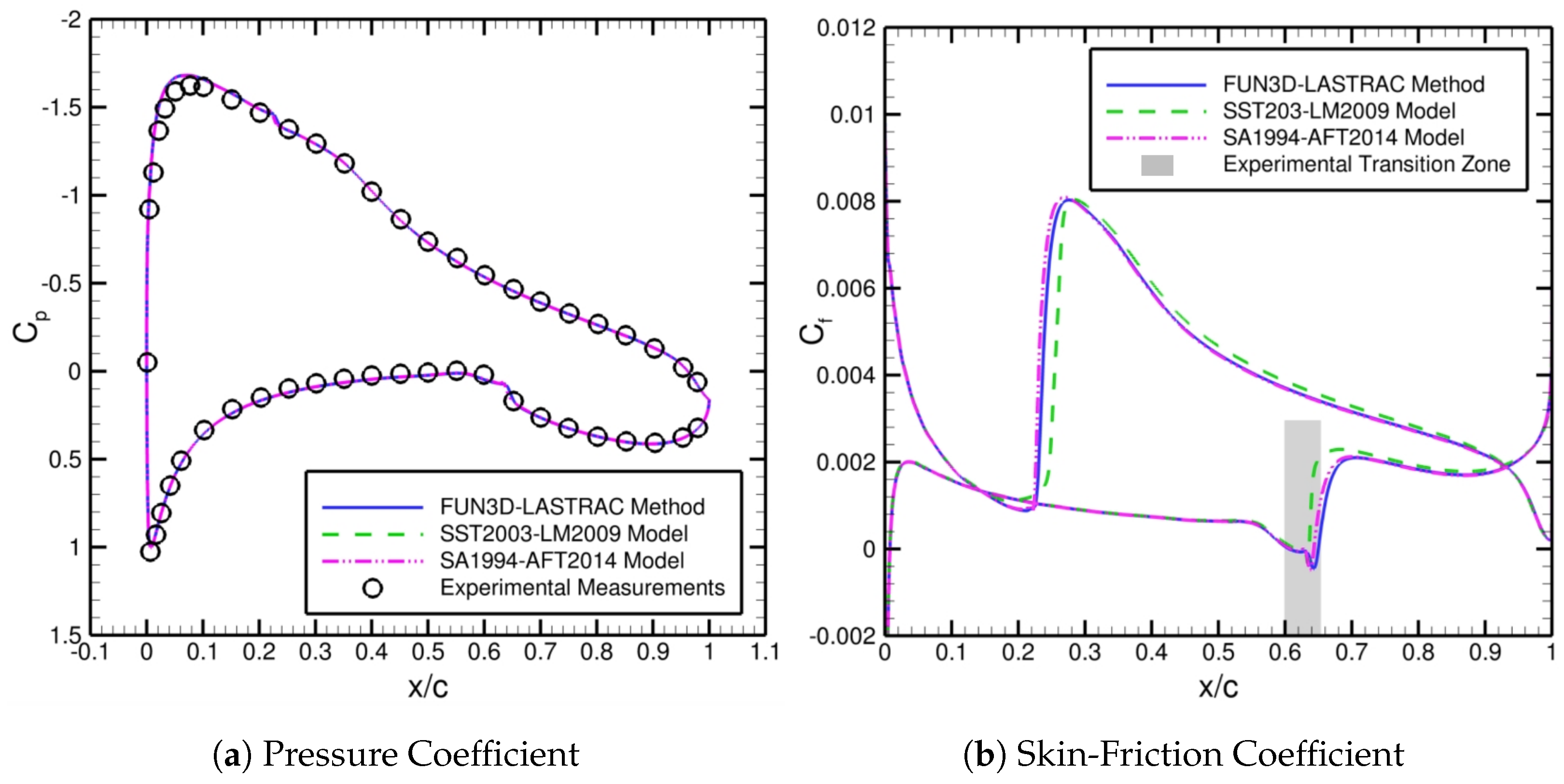
To validate our automated FUN3D–LASTRAC transition-prediction method, we compare the pressure and skin-friction coefficients between our method, the SST2003-LM2009 model [
5], the SA1994-AFT2014 model [
14], and experimental measurements [
40] in
Figure 12. There is excellent agreement between the computational and experimental results in terms of the pressure coefficient in
Figure 12a. All the different computational skin-friction distributions begin to quickly rise in the experimentally observed transition zone [
40] for the lower airfoil surface, which indicates good agreement between the computations and experiments in
Figure 12b. Note that there are no measurements of the experimental transition zone on the upper surface. There is also good agreement between the different computational predictions (i.e., our automated FUN3D–LASTRAC transition-prediction method and two RANS-based transition models) of the skin-friction distributions and transition locations.
3.3. The 6:1 Prolate Spheroid
The last case we consider to validate our automated FUN3D–LASTRAC transition-prediction method is the 6:1 prolate spheroid. This geometry was experimentally investigated by Kreplin et al. [
41]. Stability analysis for the 6:1 prolate spheroid has been performed by Spall and Malik [
42], Stock [
43], and Krimmelbein et al. [
44]. The spheroid is representative of a simplified fuselage of a commercial aircraft. This flow configuration is a part of both the AIAA Transition Modeling Workshop and the AVT-313 Incompressible Flow Transition Comparison Workshop (
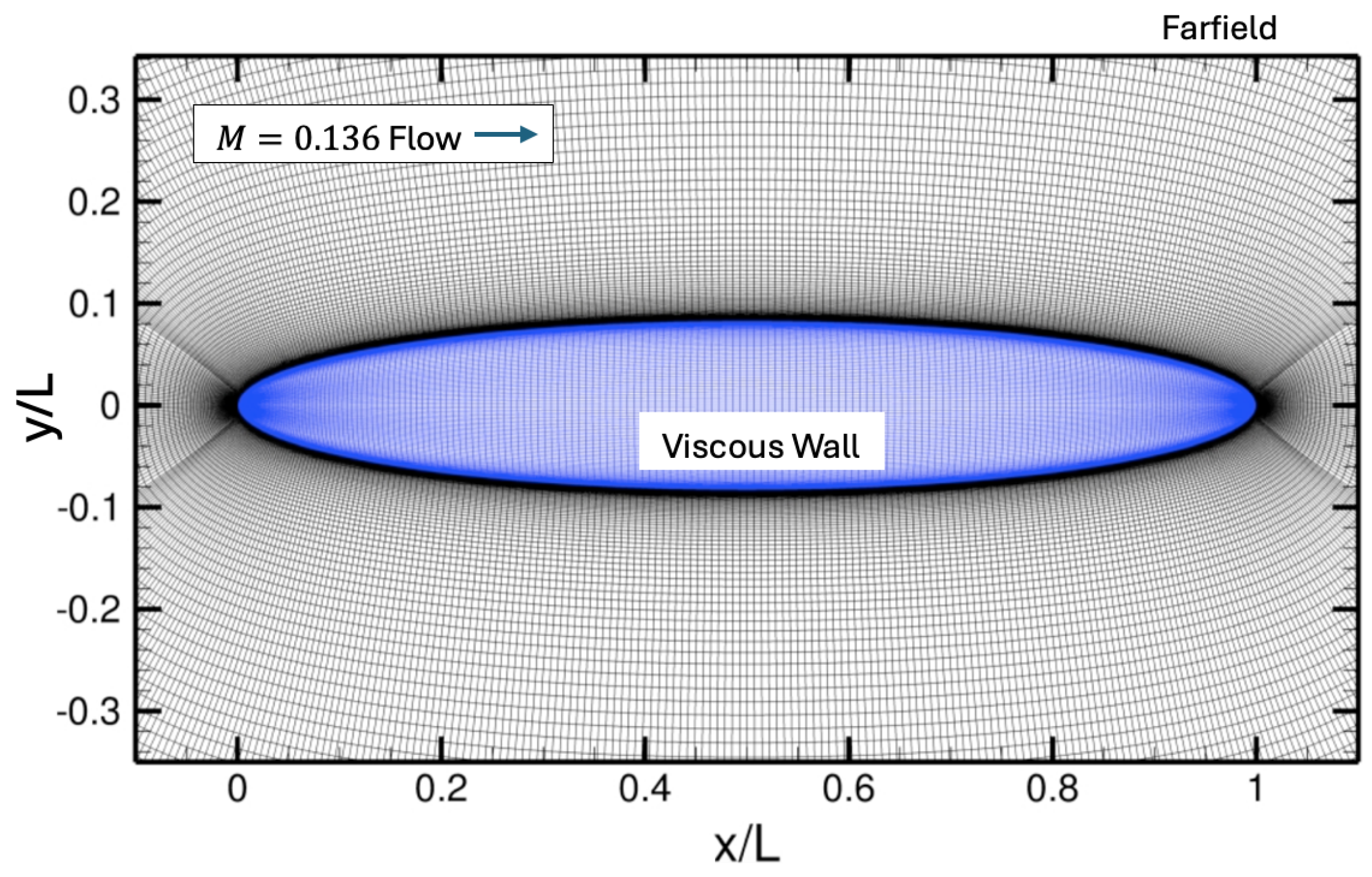
http://web.tecnico.ulisboa.pt/ist12278/Workshop_AVT_313_2D_cases/Workshop_AVT_313_2D_cases.htm, accessed on 20 March 2025). We consider an angle of attack equal to 24 degrees. The freestream Mach number, temperature, and Reynolds number based on the spheroid length are 0.136, 300 K, and
, respectively. A freestream turbulence intensity of
is used for this case. The spheroid length is equal to 2.4 m. Transition can occur via TS waves and crossflow instability. Farfield boundary conditions are employed at the domain edges approximately 100 spheroid lengths away from the viscous surface, except for a symmetry boundary condition that is employed on the
plane at
. Adiabatic and no-slip boundary conditions are enforced on the spheroid surface. We have run a few representative cases using our coupled iterative approach for the 6:1 prolate spheroid with the entire geometry and flow field, i.e., no symmetry assumption, and the results are identical to simplified cases with the symmetry assumption.
Figure 13 depicts the lowest-resolution (i.e., level 3) computational grid on the spheroid surface and within the
plane for better visibility. We use a multiblock structured grid to avoid singularities along the major axis of the spheroid model near the nose and the aft end of the geometry. Totals of 65, 65, and 257 points are used in the streamwise, azimuthal, and wall-normal directions to resolve the nose and aft blocks. For the central portion of the grid, we use 321, 193, and 257 points along the streamwise, azimuthal, and wall-normal directions, respectively. This grid is designed to contain at least 100 points within the boundary layer. Moreover, the first grid point away from the viscous surface is located at
, which yields
at the location of
. For mesh level 5, totals of 97, 97, and 385 points are used in the streamwise, azimuthal, and wall-normal directions to resolve the nose and aft blocks, while 481, 289, and 385 points in the same respective directions are used to resolve the central portion of the grid.
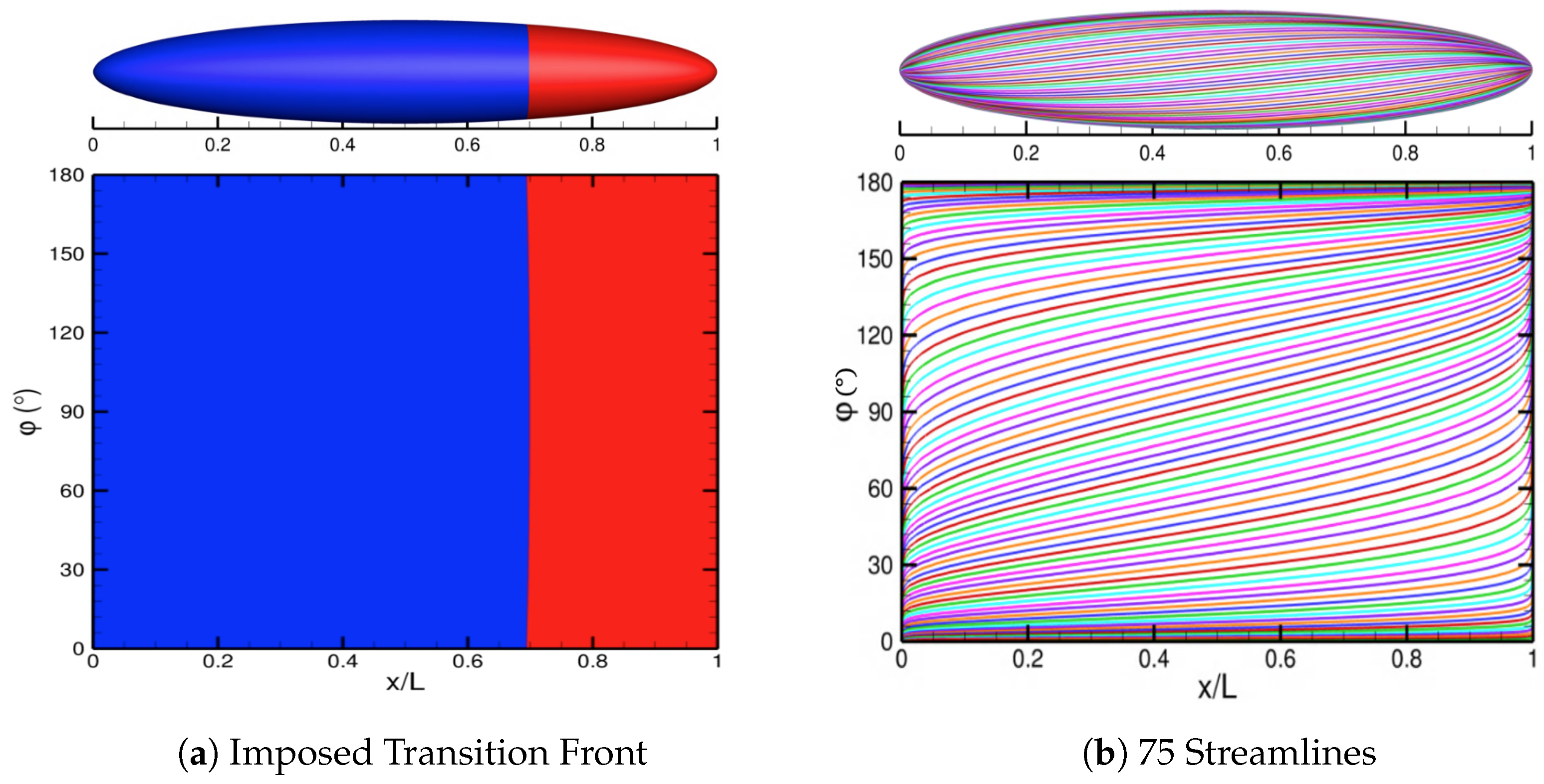
To initiate the automated FUN3D–LASTRAC method, we impose a transition front downstream at
. This initial transition front is shown in
Figure 14a, where the blue contours indicate a laminar region and the red contours indicate a turbulent region. For the LASTRAC stability analysis, we use 75 vertex seeds on the spheroid surface. The solver-independent module creates the streamlines for stability analysis from these vertex seeds.
Figure 14b displays the 75 streamlines on the spheroid surface. We employ under-relaxation by using Equation (
7) at each point along the azimuthal or
plane with
We use the dual
–
criterion [
45,
46,
47] to determine where transition occurs from the TS and crossflow
N-factor values. Refer to Choudhari et al. [
2] for more information on calibrating the dual
–
criterion for multiple aerodynamic configurations. To illustrate the automated transition modeling for a 3D flow configuration, we use the simple criterion
. In a real-world application, the criterion would be tuned for a specific facility using a broad range of data. Unlike for the 2D cases, we use point transition or an intermittency zone with zero length, which is a convenient option for 3D cases with mixed-mode transition where intermittency models have not been developed.
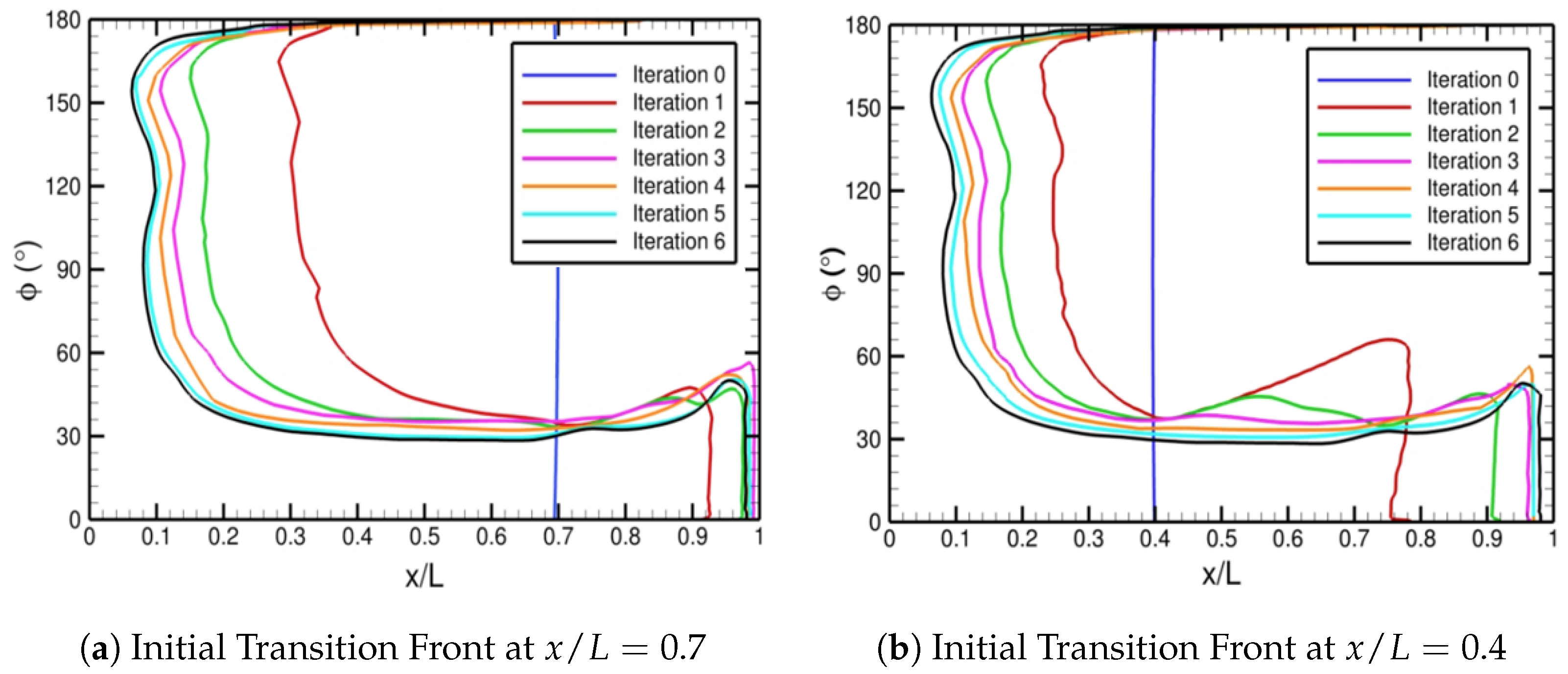
Figure 15 displays the transition fronts corresponding to iterations 0 through 6 for two different initially imposed transition fronts. Notice that, by iteration 6, the automated FUN3D–LASTRAC method converges for both initial conditions.
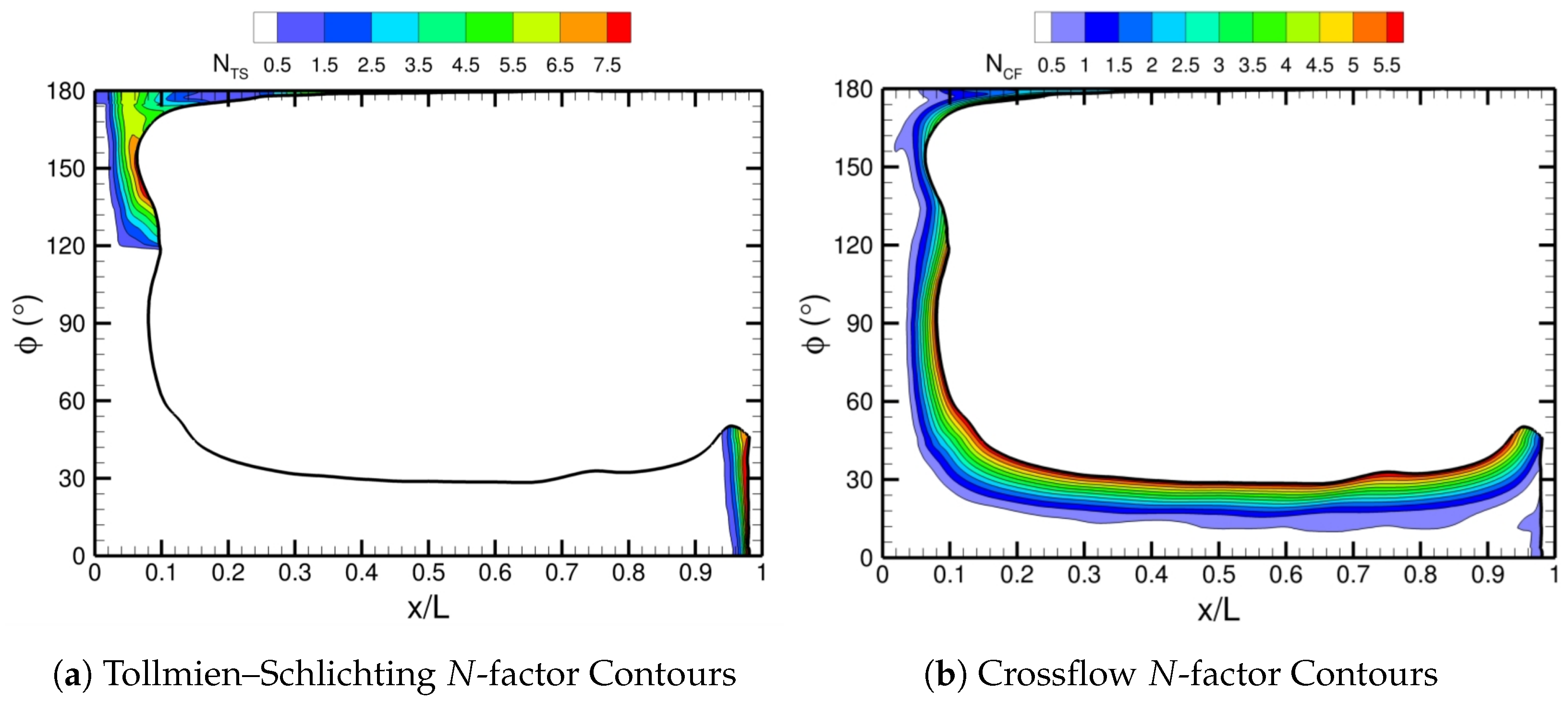
Figure 16 depicts the
N-factor contours of TS and crossflow instability from PSE with LASTRAC. The final imposed transition front is also shown in
Figure 16, downstream of which the
N-factor contours are removed or set to zero because the flow has already transitioned to turbulence. For this case where
, the
N-factor values associated with TS waves are relatively small and do not significantly influence transition, except for
far downstream near
and
in
Figure 16a. Crossflow vortices are important for this angle of attack because the associated
N-factor values are appreciably large and are likely to dominate transition for
. We show the final solution of the automated FUN3D–LASTRAC method in
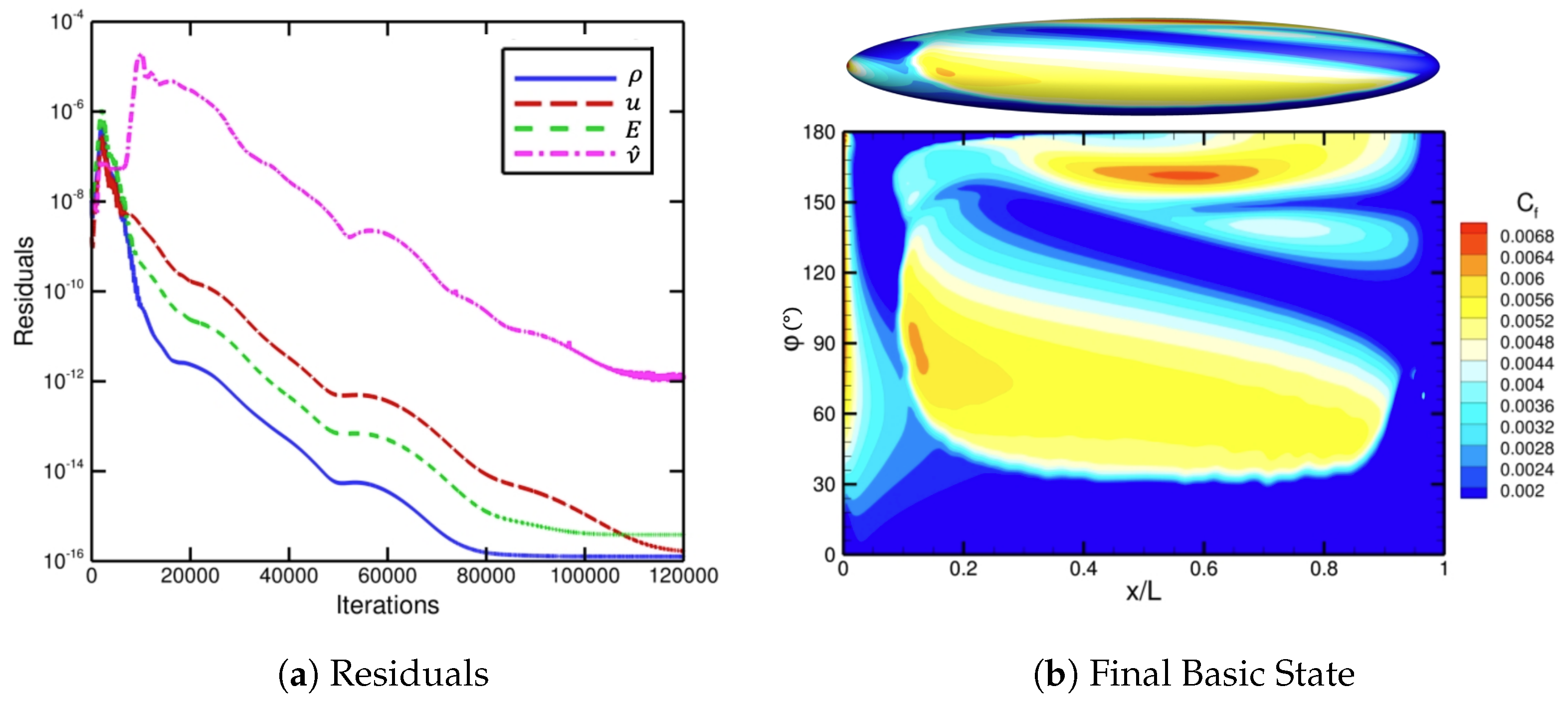
Figure 17, along with the mean-flow basic-state residuals. Notice in
Figure 17a that the mean-flow basic-state residuals drop approximately 10 orders of magnitude to machine zero and level out. The skin-friction contours of the final converged solution in
Figure 17b are smooth and match the final transition front in
Figure 15. Also, the results in
Figure 17b agree with the skin-friction contours in
Figure 11d of Krimmelbein et al. [
44] for the 6:1 prolate spheroid at
, computed using a coupled iterative approach (i.e., SST model [
48] with a similar dual
N-factor strategy).
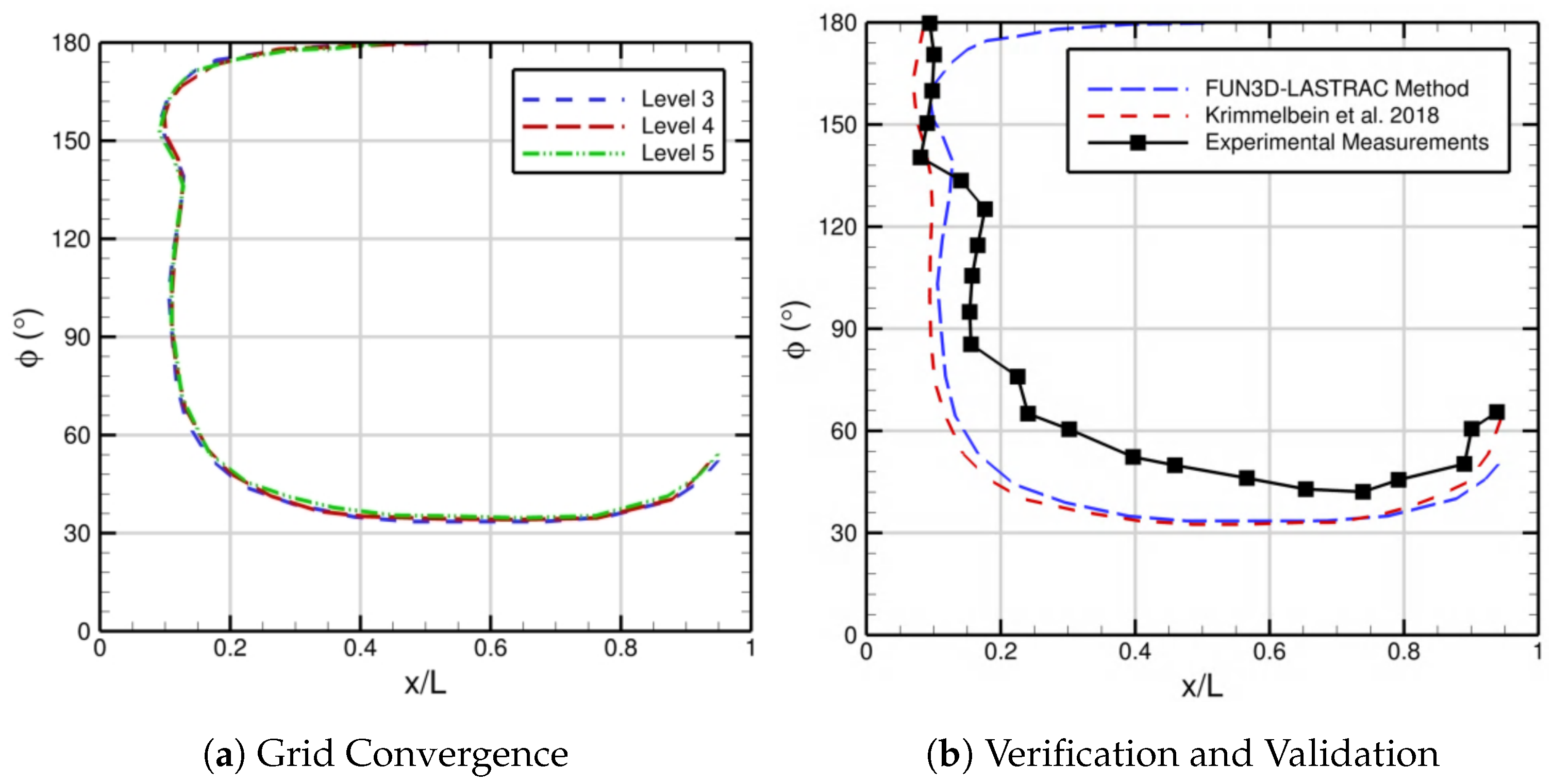
The grid convergence of the automated FUN3D–LASTRAC transition-prediction method is displayed in
Figure 18a. Comparisons with the results from our method, the experimental measurements in Kreplin et al. [
41], and the computational results from Krimmelbein et al. [
44] based on the SST model paired with a similar dual
N-factor strategy are depicted in
Figure 18b. For the results in
Figure 18, the extracted transition front comes from the skin-friction contours, more specifically
. This is conducted for better comparison with the measurements by Kreplin et al. [
41] and Krimmelbein et al. [
44]. In
Figure 18a, the converged transition front is relatively insensitive to changes in the grid resolution across levels three, four, and five. The agreement between our computational results and those of Krimmelbein et al. [
44] is very good. The comparison between our predictions and the experimental measurements by Kreplin et al. [
41] is also reasonable, except that the predicted transition front is more upstream across the crossflow-dominated region from
, highlighting the need for calibrating the dual
N-factor criterion in actual applications, similar to Krimmelbein et al. [
44] and Choudhari et al. [
2]. Overall, the sufficient iterative and grid convergence, along with the successful validation of the automated iterative coupled approach with FUN3D and LASTRAC for a 3D flow configuration, demonstrate that it can be applied to more complex problems and maintain accuracy, robustness, and efficiency.