Effects of Diffusion and Delays on the Dynamic Behavior of a Competition and Cooperation Model
Abstract
:1. Introduction and Preliminaries
- (i)
- To investigate the effects of three different cases of delay terms on stability and Hopf bifurcation areas, in order to understand how these delays interact with the diffusion parameters, growth rates, and other free rates in the model.
- (ii)
- To illustrate the theoretical properties of the DDEs using the Galerkin method, which provides accurate approximate solutions for delay PDEs.
- (iii)
- To explore analytically a condition for the existence of Hopf bifurcation points.
- (iv)
- To construct bifurcation diagrams, limit cycle plots, and 2-D phase portraits, in order to verify the theoretical findings.
- (v)
- To explain how these results relate to real-world scenarios and the potential benefits of applying them to practical situations.
2. Methodology and Framework
2.1. The Galerkin Technique
2.2. The Dynamical Theoretical Formulations
3. Stability and Bifurcation Analysis
3.1. Hopf Bifurcation with No Delay ()
3.2. Hopf Bifurcation with One Delay Time ()
3.3. Hopf Bifurcation with Two Different Delays ()
4. Bifurcation Diagrams and Numerical Examples
4.1. Bifurcation Diagrams and Periodic Solutions
4.2. Numerical Simulation Examples
5. Conclusions, Economic Implications, and Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1-D | One-dimensional |
| 2-D | Two-dimensional |
| CN-FDM | Crank–Nicolson finite-difference scheme |
| ODE | Ordinary differential equation |
| PDE | Partial differential equation |
| RK4 | Fourth-order Runge–Kutta |
Appendix A
References
- Alfifi, H.Y. Stability and Hopf bifurcation analysis for the diffusive delay logistic population model with spatially heterogeneous environment. Appl. Math. Comput. 2021, 408, 126362. [Google Scholar]
- Alfifi, H.Y. Semi analytical solutions for the diffusive logistic equation with mixed instantaneous and delayed density dependencel. Adv. Differ. Equ. 2020, 2020, 162. [Google Scholar]
- Feng, W.; Lu, X. On diffusive population models with toxicants and time delays. J. Math. Anal. Appl. 1999, 233, 374–386. [Google Scholar]
- Noufaey, K.S.A.; Marchant, T.R.; Edwards, M.P. The diffusive Lotka-Volterra predator-prey system with delay. Math. Biosci. 2015, 270, 30–40. [Google Scholar] [CrossRef]
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Semi-analytical solutions for the 1- and 2-D diffusive Nicholson’s blowflies equation. IMA J. Appl. Math. 2014, 79, 175–199. [Google Scholar]
- Taylor, M.P.; Kobiler, O.; Enquist, L.W. Alphaherpesvirus axon-to-cell spread involves limited virion transmission. Proc. Natl. Acad. Sci. USA 2012, 109, 17046–17051. [Google Scholar]
- Alfifi, H.Y. Effects of diffusion and delayed immune response on dynamic behavior in a viral model. Appl. Math. Comput. 2023, 441, 127714. [Google Scholar]
- Gu, Y.; Ullah, S.; Khan, M.A.; Alshahrani, M.Y.; Abohassan, M.; Riaz, M.B. Mathematical modeling and stability analysis of the COVID-19 with quarantine and isolation. Results Phys. 2022, 34, 105284. [Google Scholar] [CrossRef] [PubMed]
- Manna, K. A non-standard finite difference scheme for a diffusive HBV infection model with capsids and time delay. J. Differ. Equ. Appl. 2017, 23, 1901–1911. [Google Scholar]
- Noufaey, K.S.A.; Marchant, T.R. Semi-analytical solutions for the reversible Selkov model with feedback delay. Appl. Math. Comput. 2014, 232, 49–59. [Google Scholar]
- Marchant, T.R. Cubic autocatalytic reaction diffusion equations: Semi-analytical solutions. Proc. R. Soc. Lond. 2002, A458, 873–888. [Google Scholar]
- Alfifi, H.Y. Semi-analytical solutions for the diffusive Kaldor-Kalecki business cycle model with a time delay for gross product and capital stock. Complexity 2021, 2021, 9998756. [Google Scholar]
- Fang, Y.; Xu, H.; Perc, M.; Tan, Q. Dynamic evolution of economic networks under the influence of mergers and divestitures. Phys. A Stat. Mech. Its Appl. 2019, 524, 89–99. [Google Scholar]
- Kalecki, M. A macrodynamic theory of business cycles. Econometrica 1935, 3, 327–344. [Google Scholar]
- Liao, M.; Xu, C.; Tang, X. Dynamical behaviors for a competition and cooperation model of enterprises with two delays. Nonlinear Dyn. 2014, 75, 257–266. [Google Scholar]
- Hua, H.; Gashi, B.; Zhang, M. Robust risk-sensitive control. Int. J. Robust Nonlinear Control. 2023, 33, 5484–5509. [Google Scholar]
- Hu, W.; Dong, T.; Zhao, H. Dynamic analysis of a competition-cooperation enterprise cluster with core-satellite structure and time delay. Complexity 2021, 2021, 6644292. [Google Scholar]
- Li, L.; Zhang, C.; Yan, X. Stability and Hopf bifurcation analysis for a two-enterprise interaction model with delays. Commun. Nonlinear Sci. Numer. Simul. 2015, 30, 70–83. [Google Scholar]
- Liao, M.; Xu, C.; Tang, X. Stability and Hopf bifurcation for a competition and cooperation model of two enterprises with delay. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3845–3856. [Google Scholar]
- Feng, C.; Pogue, O. The existence of periodic solutions for a two-enterprise interaction model with delays. Asian Res. J. Math. 2022, 9, 108–115. [Google Scholar]
- Lu, L.; Lian, Y.; Li, C. Dynamics for a discrete competition and cooperation model of two enterprises with multiple delays and feedback controls. Open Math. 2017, 15, 218–232. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L. Dynamic analysis on a diffusive two-enterprise interaction model with two delays. J. Math. 2022, 2022, 3466954. [Google Scholar] [CrossRef]
- Xu, C. Periodic behavior of competition and corporation dynamical model of two enterprises on time scales. J. Quant. Econ. 2012, 29, 1–4. [Google Scholar]
- Muhammadhaji, A.; Abdurahman, X. Dynamics in a competition and cooperation model of two enterprises with delays. Preprint, 2022. [Google Scholar] [CrossRef]
- Szydłowski, M.; Krawiec, A. The Kaldor-Kalecki model of business cycle as a two-dimensional dynamical system. J. Nonlinear Math. Phys. 2001, 8 (Suppl. S1), 266–271. [Google Scholar] [CrossRef]
- Guerrini, L. Small delays in a competition and cooperation model of enterprises. Appl. Math. Sci. 2016, 10, 2571–2574. [Google Scholar] [CrossRef]
- Wang, Y. Permanence and stability for a competition and cooperation model of two enterprises with feedback controls on time scales. IAENG Int. J. Appl. Math. 2021, 51, 630–636. [Google Scholar]
- Fletcher, C.A. Computational Galerkin Methods; Springer: New York, NY, USA, 1984. [Google Scholar]
- Alfifi, H.Y.; Almuaddi, S.M. Stability analysis and hopf bifurcation for the Brusselator reaction—Diffusion system with gene expression time delay. Mathematics 2024, 12, 1170. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Semi-analytical solutions for the delayed diffusive food-limited model. In Proceedings of the 2017 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, United Arab Emirates, 4–6 April 2017; pp. 1–5. [Google Scholar]
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Non-smooth feedback control for Belousov-Zhabotinskii reaction-diffusion equations: Semi-analytical solutions. J. Math. Chem. 2016, 57, 157–178. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Stability analysis and hopf bifurcation for two-species reaction-diffusion-advection competition systems with two time delays. Appl. Math. Comput. 2024, 474, 128684. [Google Scholar] [CrossRef]
- Marchant, T.R.; Nelson, M.I. Semi-analytical solution for one-and two-dimensional pellet problems. Proc. R. Soc. Lond. 2004, A460, 2381–2394. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Stability analysis for schnakenberg reaction-diffusion model with gene expression time delay. Chaos Solitons Fractals 2022, 155, 111730. [Google Scholar]
- Noufaey, K.S.A. Stability analysis for Selkov-Schnakenberg reaction-diffusion system. Open Math. 2021, 19, 46–62. [Google Scholar]
- Erneux, T. Applied Delay Differential Equations; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hale, J. Theory of Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- Looss, G.; Joseph, D.D. Elementary Stability and Bifurcation Theory, 2nd ed.; Springer: New York, NY, USA, 1990. [Google Scholar]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods, 3rd ed.; Oxford: New York, NY, USA, 1985. [Google Scholar]
- Verwer, J.; Hundsdorfer, W.; Sommeijer, B. Convergence properties of the Runge-Kutta-Chebyshev method. Numer. Math. 1990, 57, 157–178. [Google Scholar]
- Maplesoft, a Division of Waterloo Maple Inc. Maple; Maplesoft: Waterloo, ON, Canada, 2019. [Google Scholar]
- Noufaey, K.S.A. Stability analysis of a diffusive three-species ecological system with time delays. Symmetry 2021, 13, 2217. [Google Scholar] [CrossRef]
- Burić, N.; Mudrinic, M.; Vasović, N. Time delay in a basic model of the immune response. Chaos Solitons Fractals 2001, 12, 483–489. [Google Scholar] [CrossRef]
- Canabarro, A.A.; Gléria, I.M.; Lyra, M.L. Periodic solutions and chaos in a non-linear model for the delayed cellular immune response. Phys. A Stat. Mech. Its Appl. 2004, 342, 234–241. [Google Scholar]
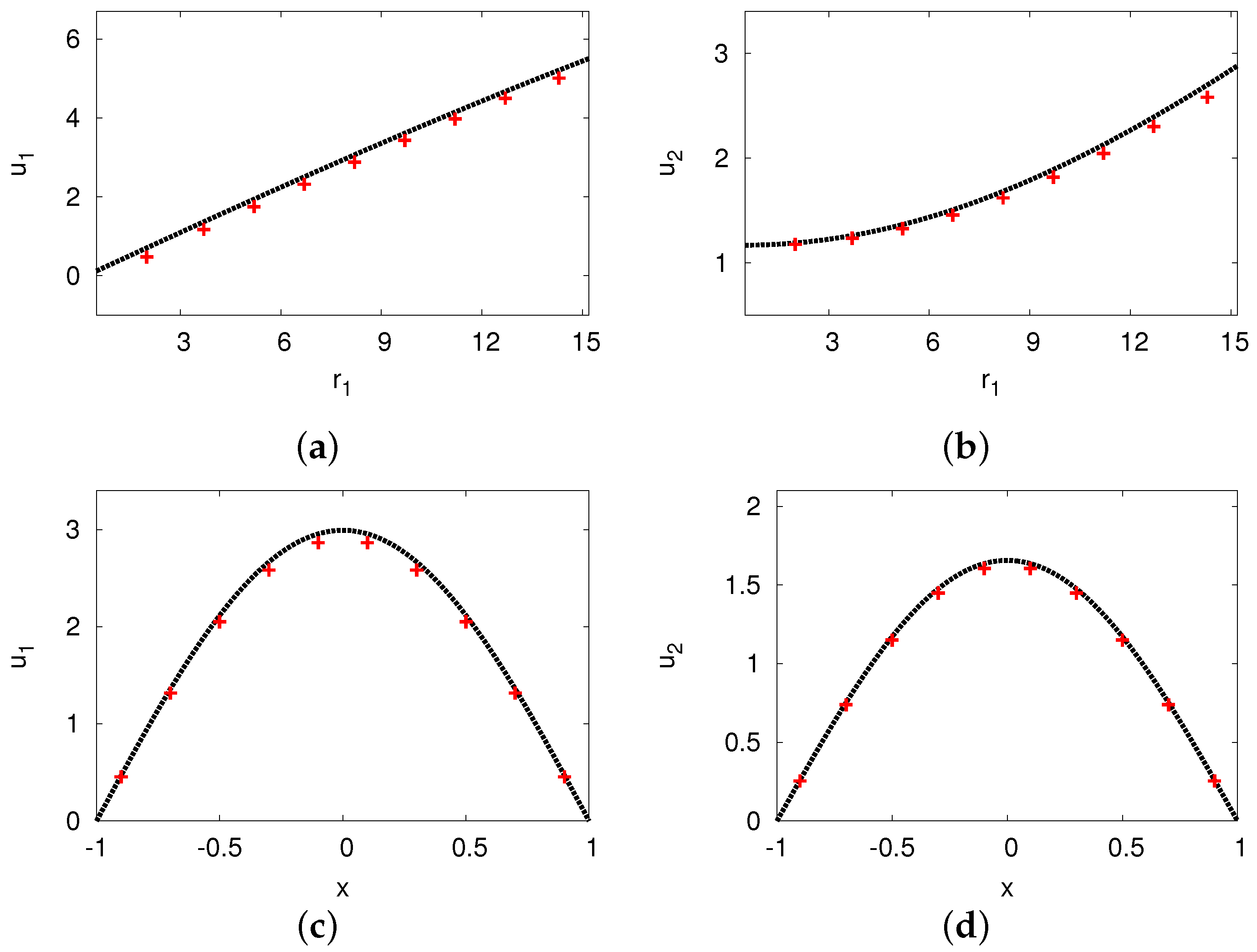
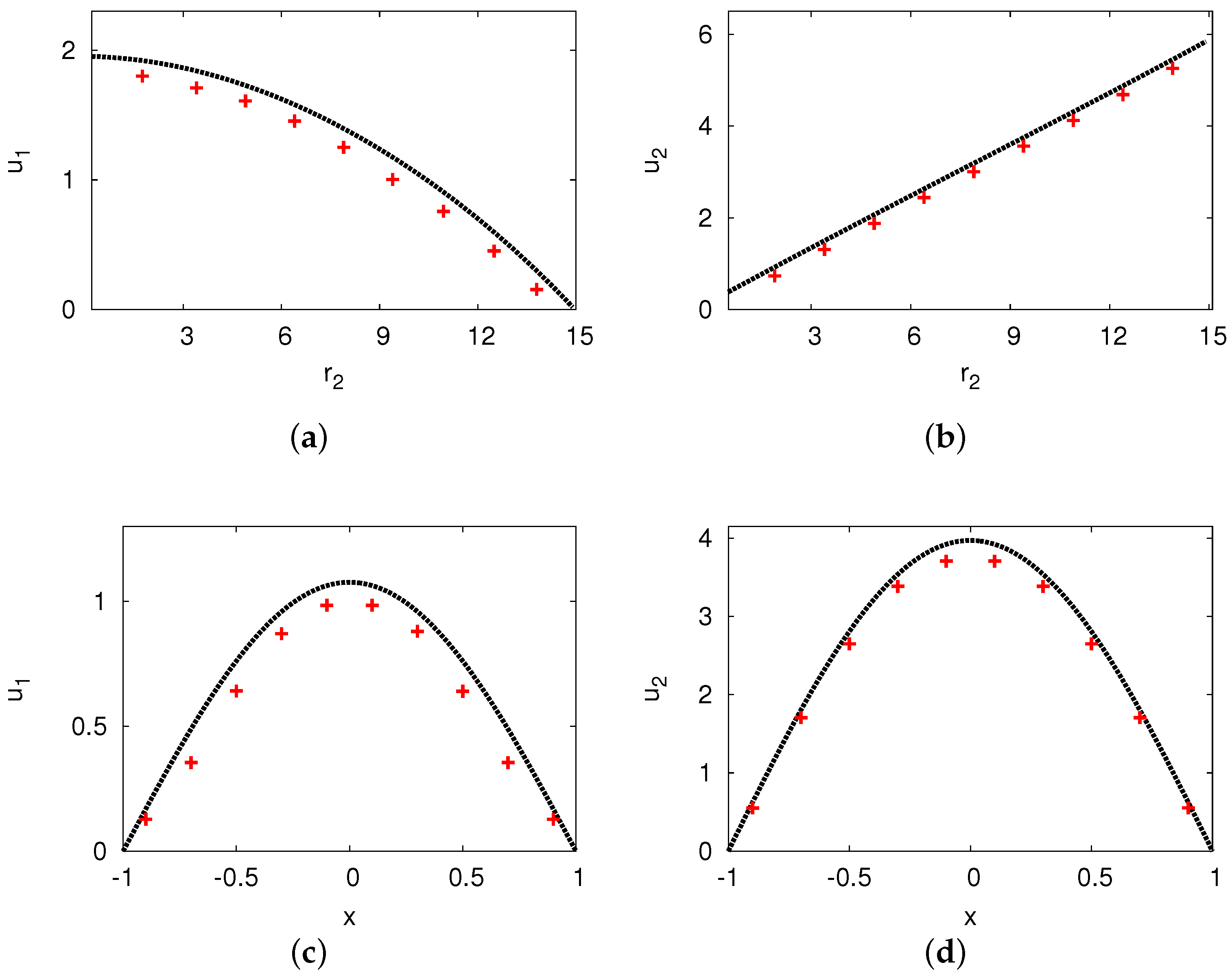

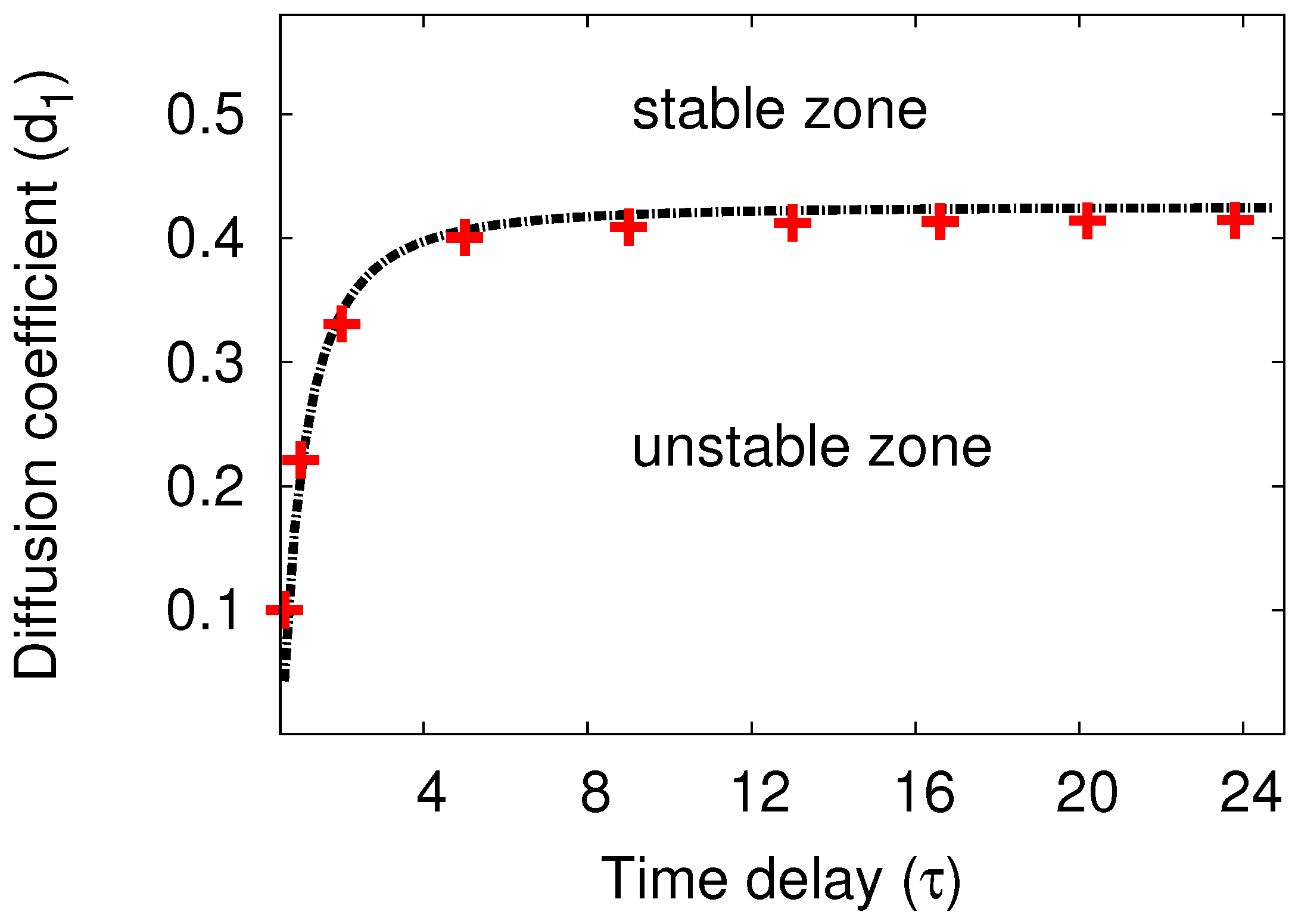
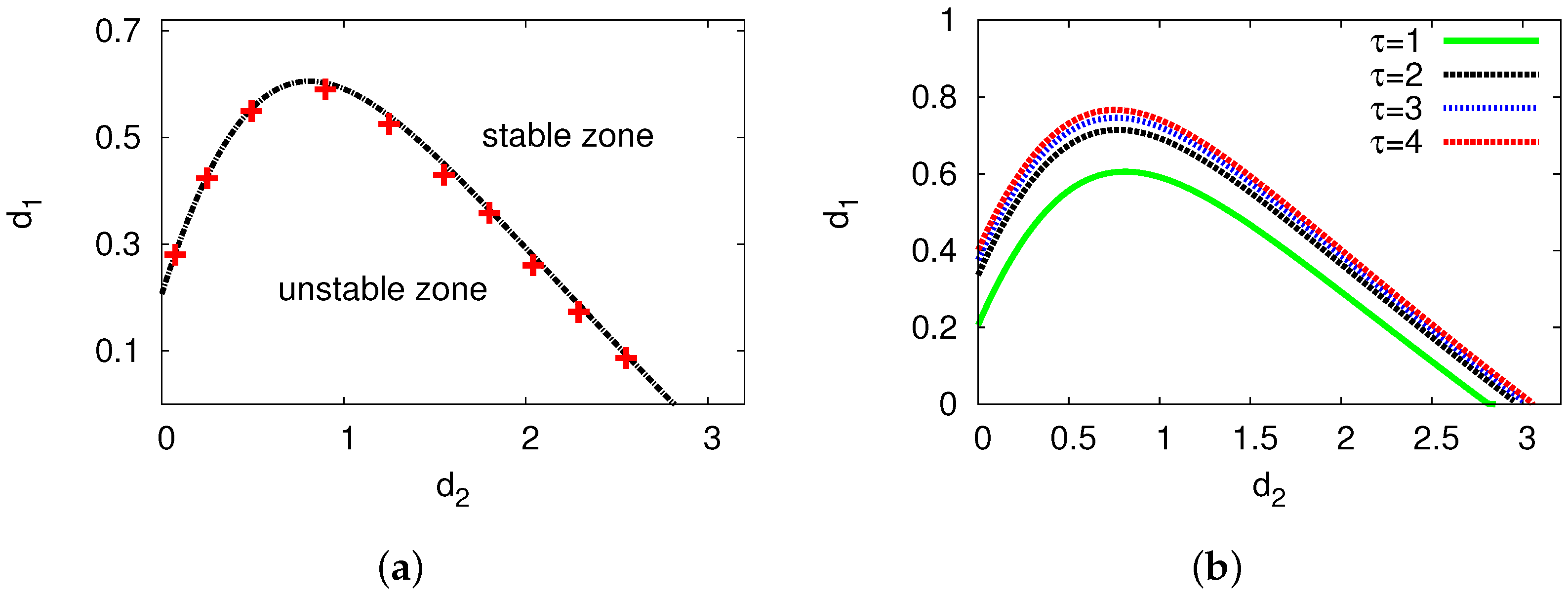
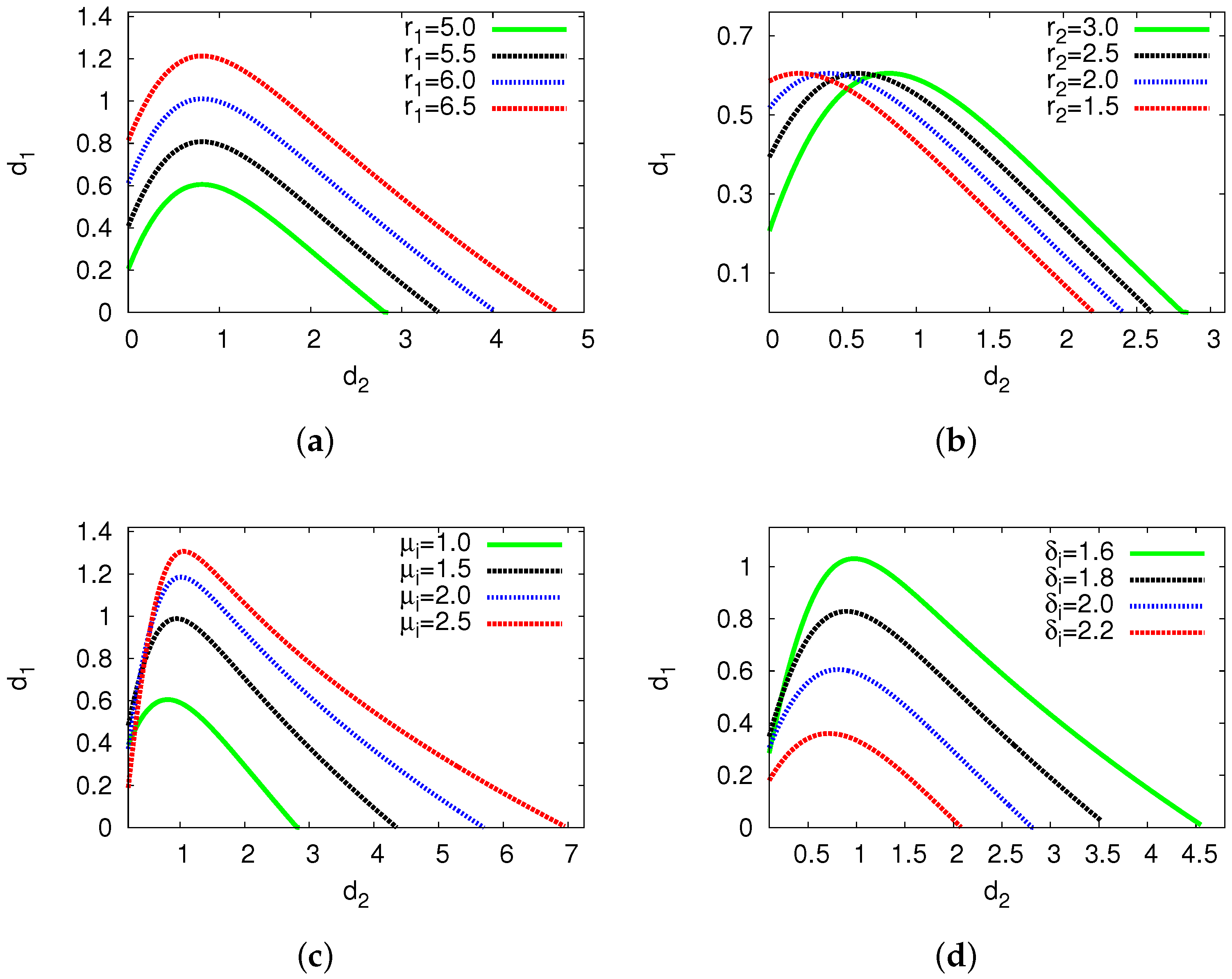
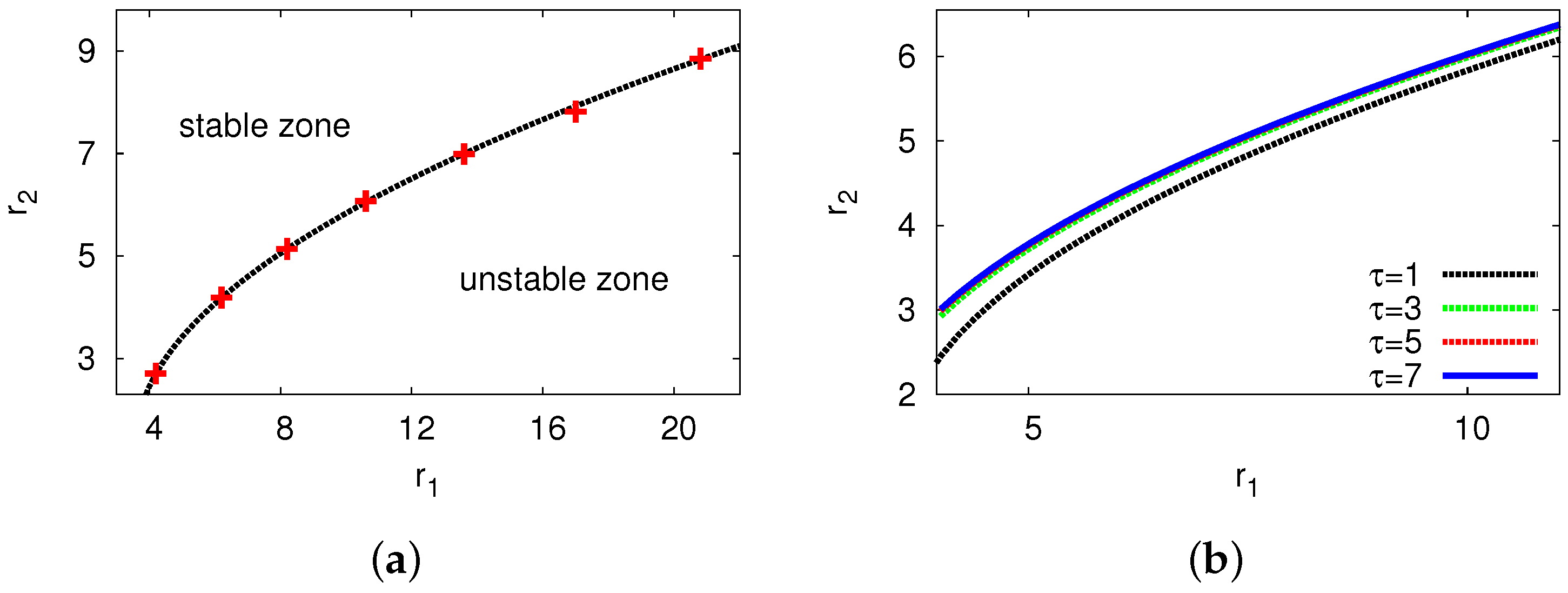
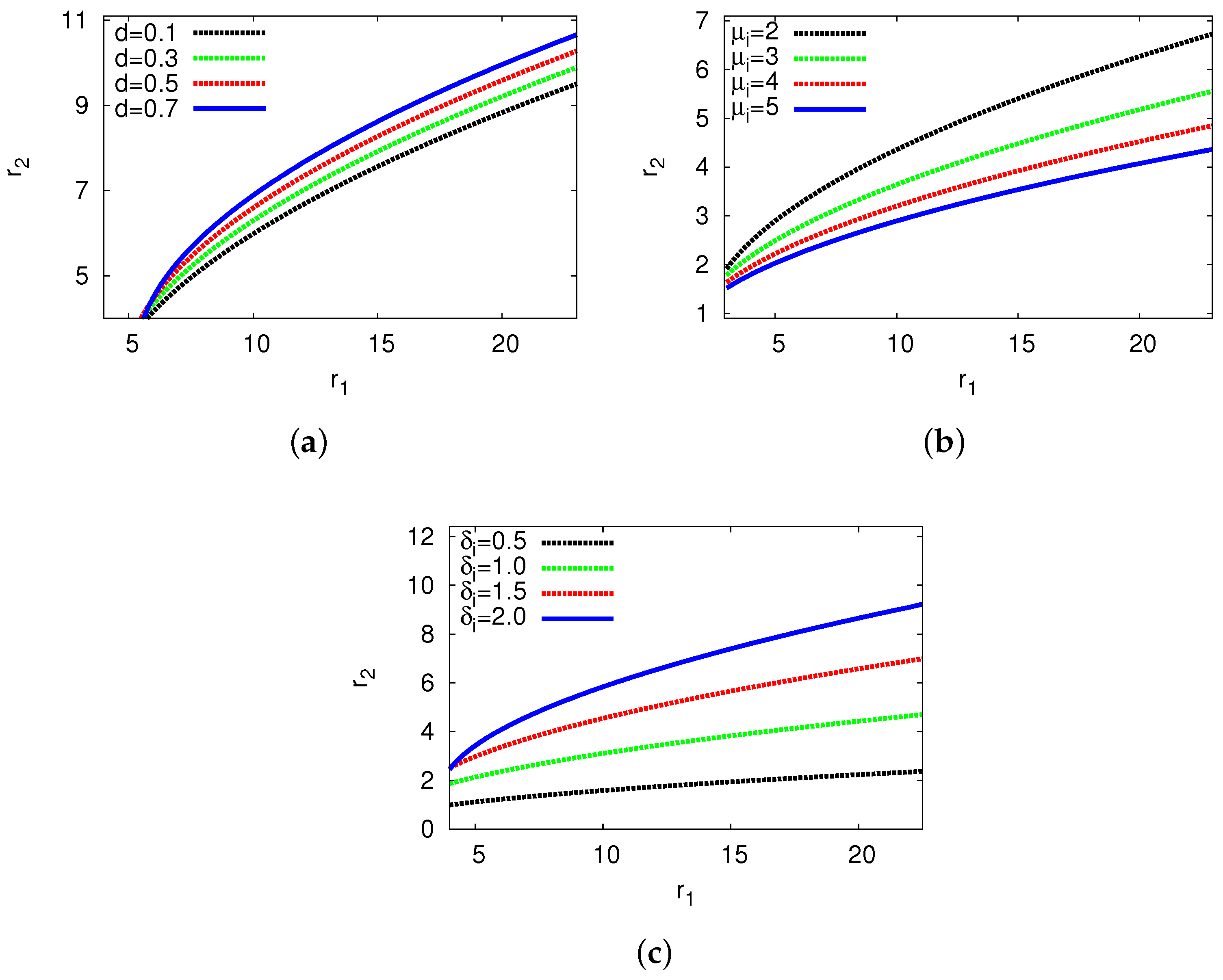
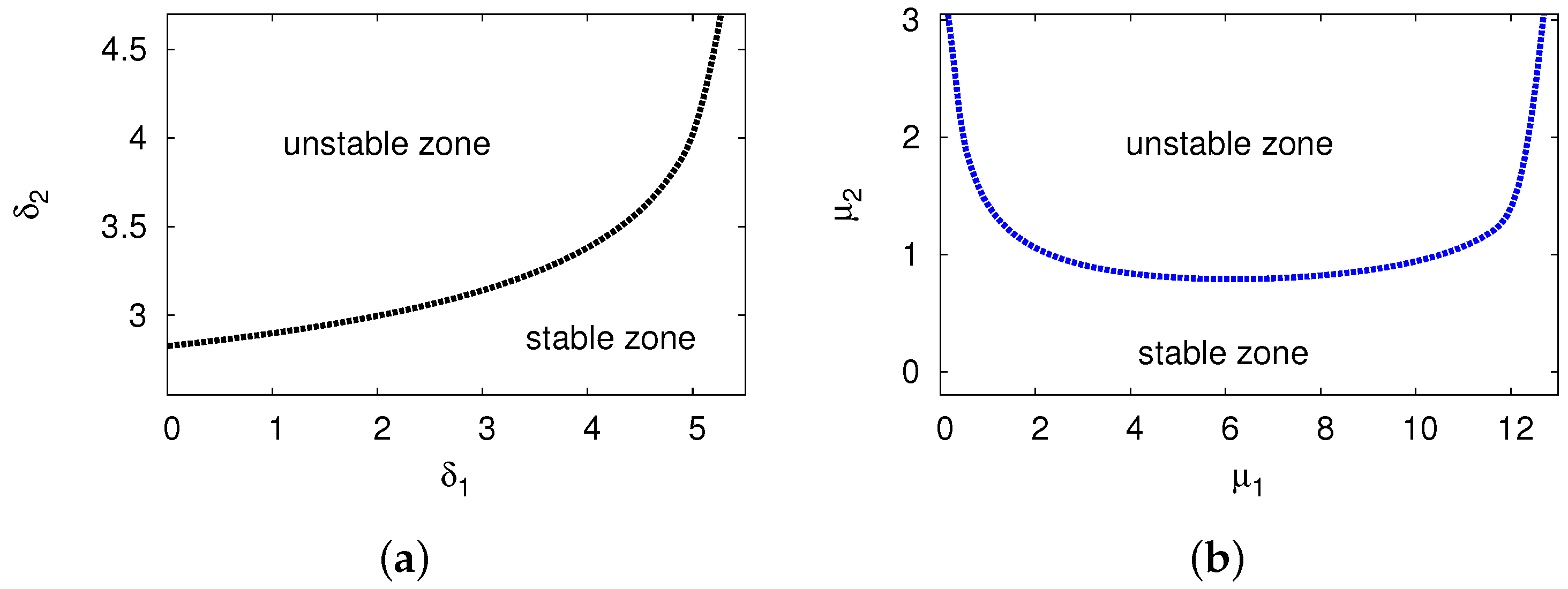
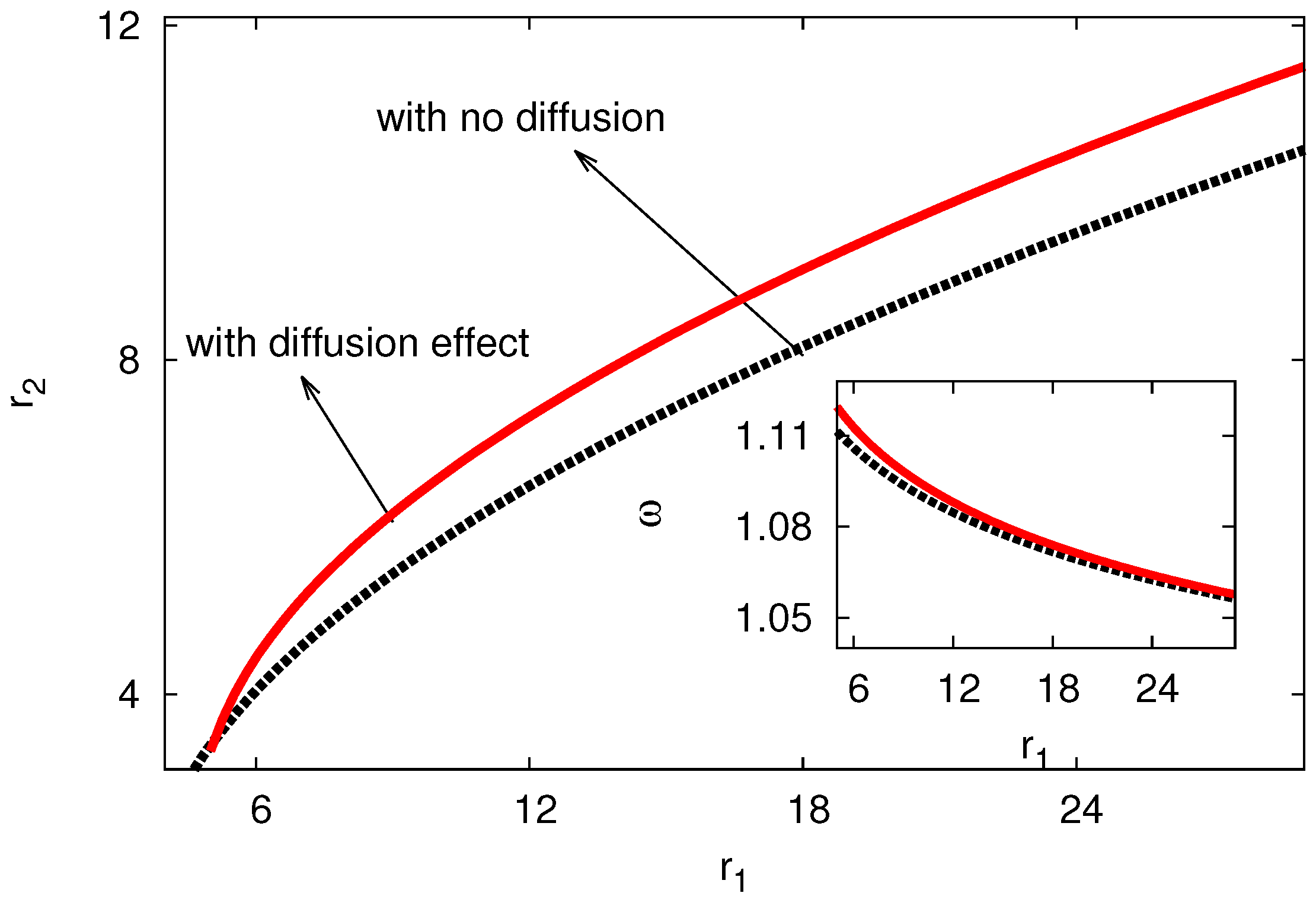
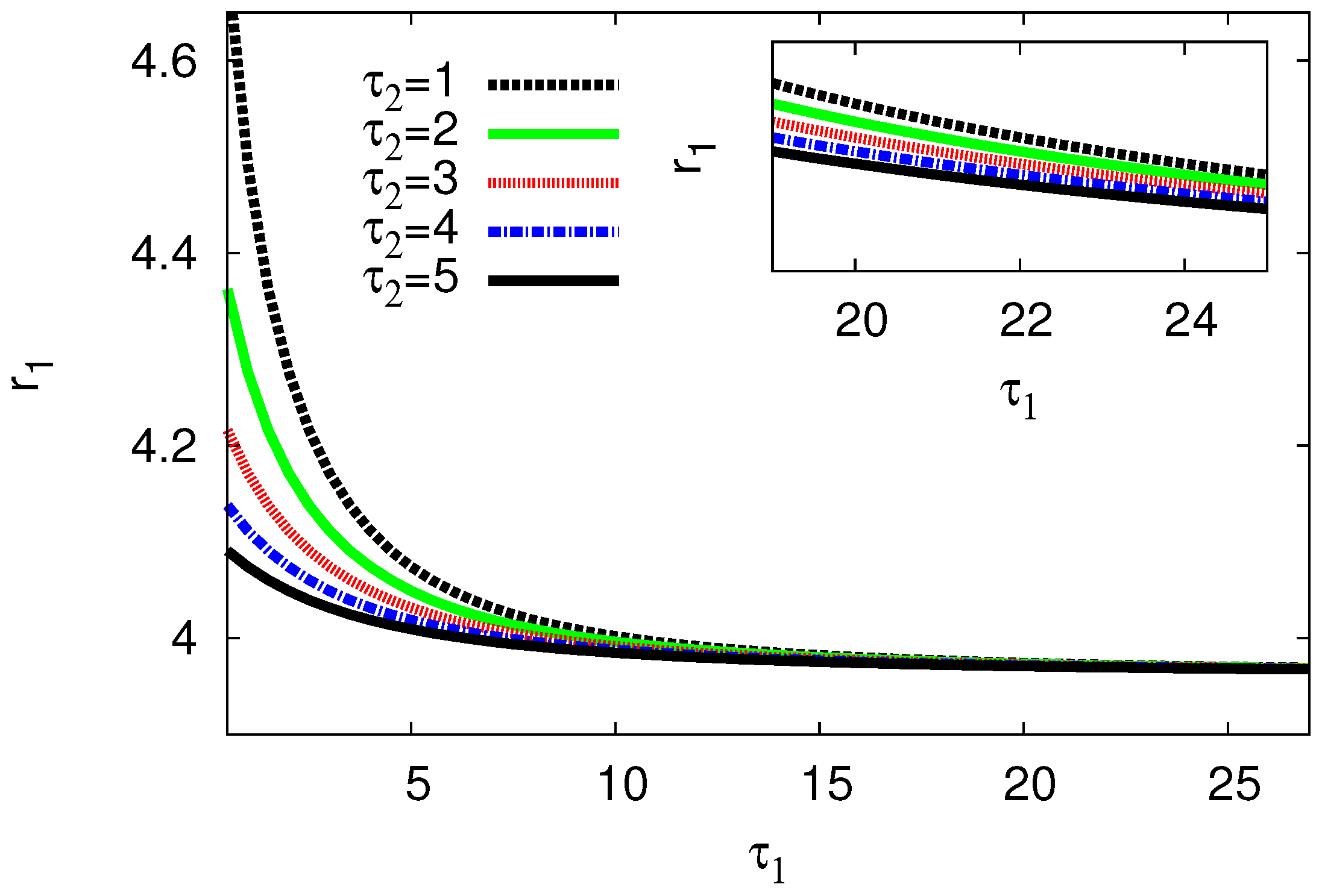
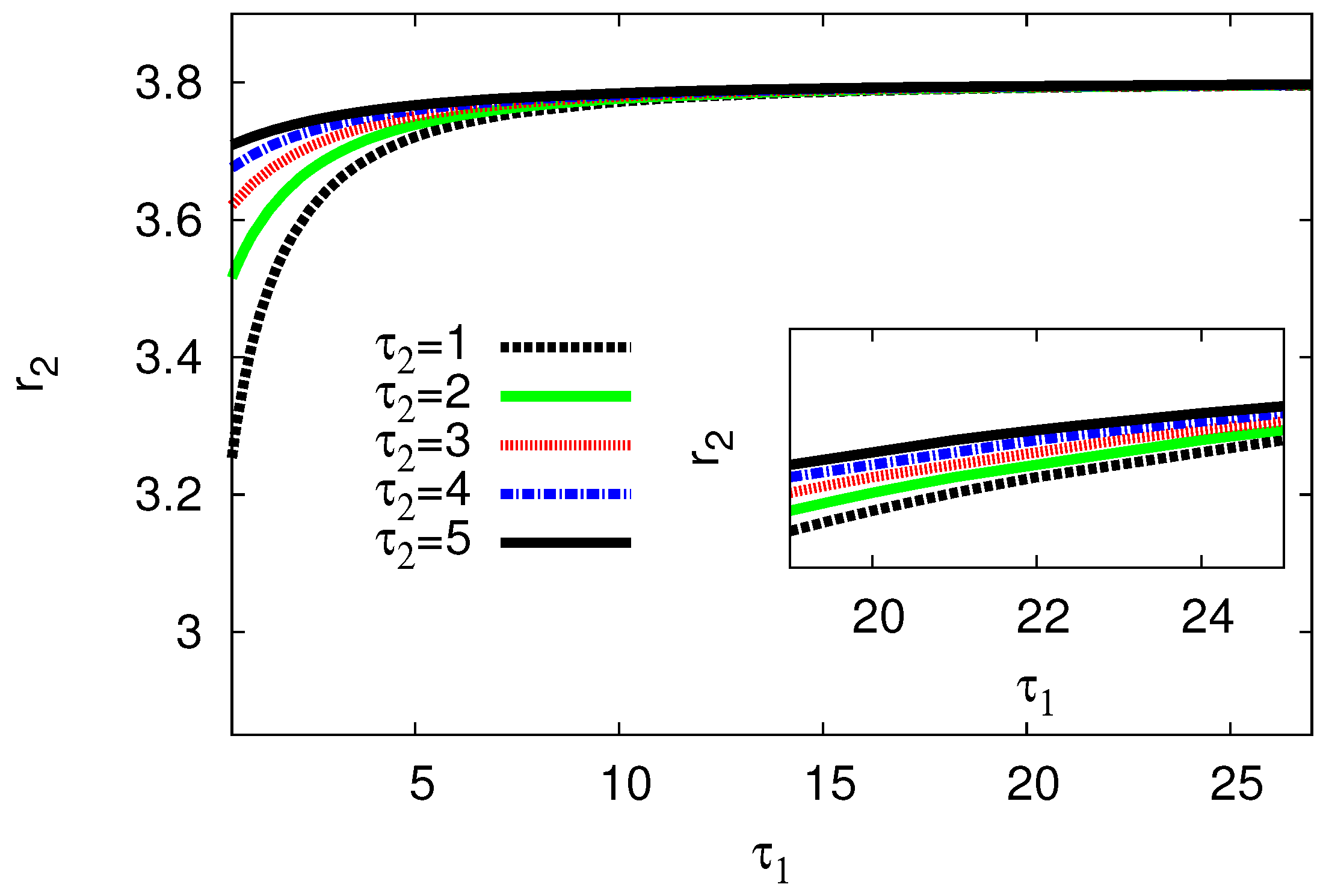
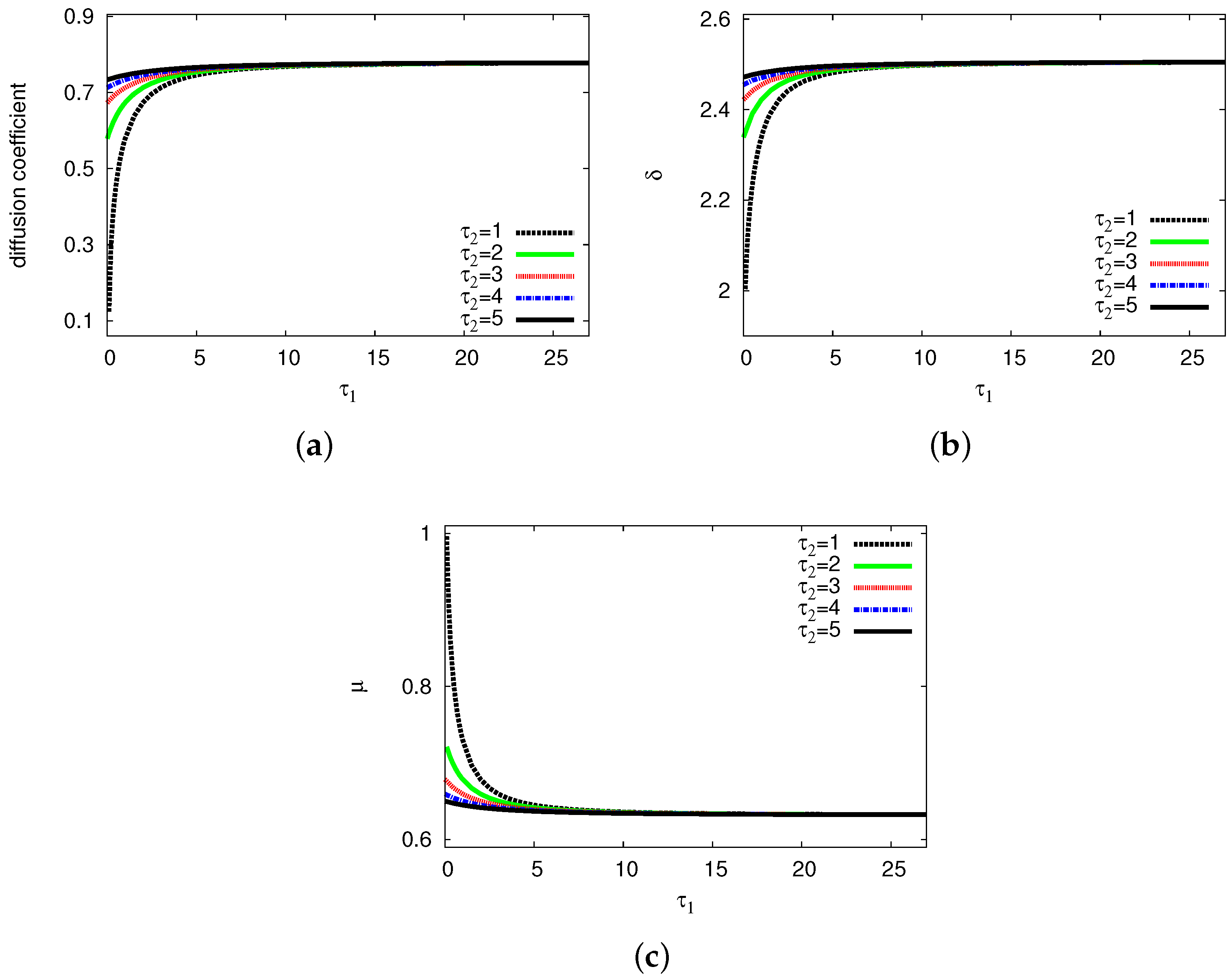
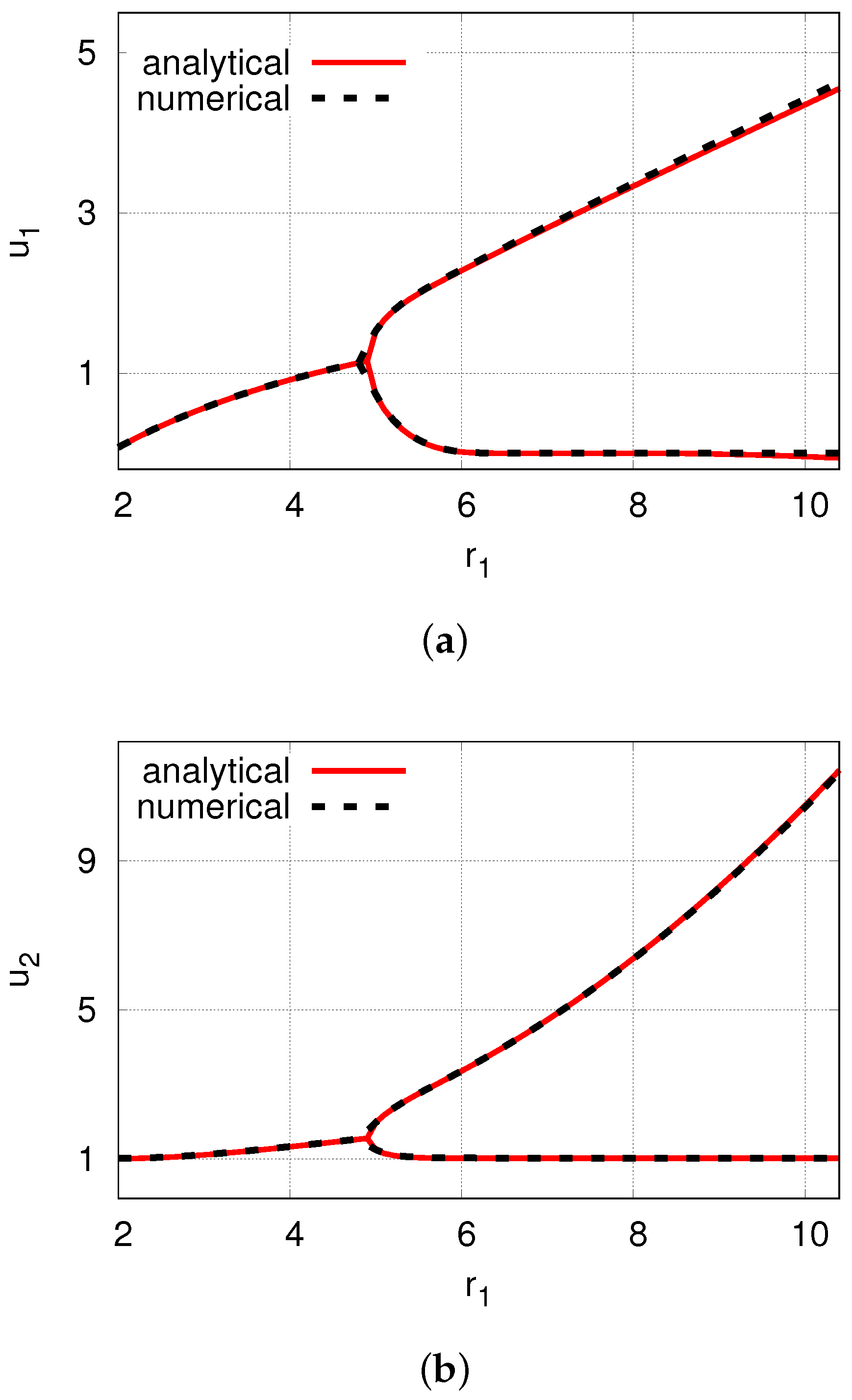
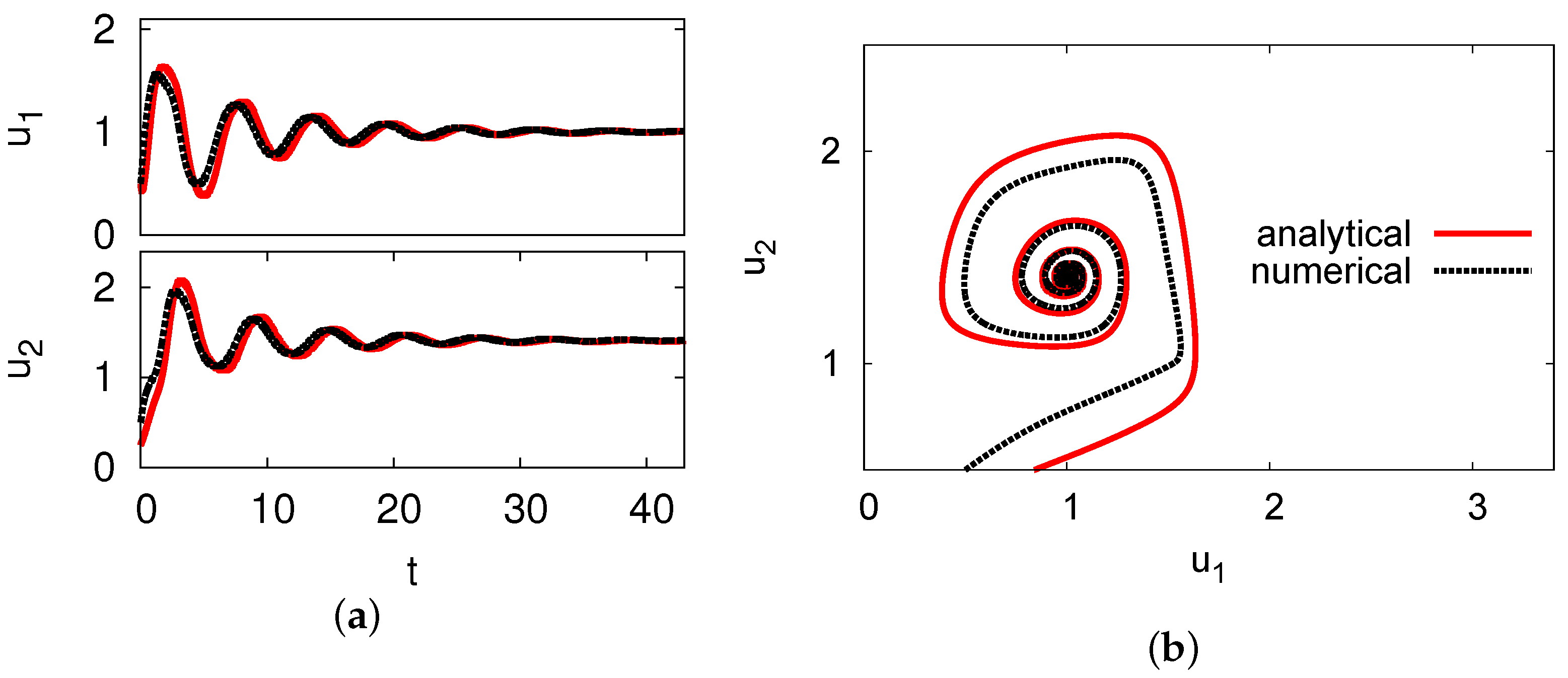

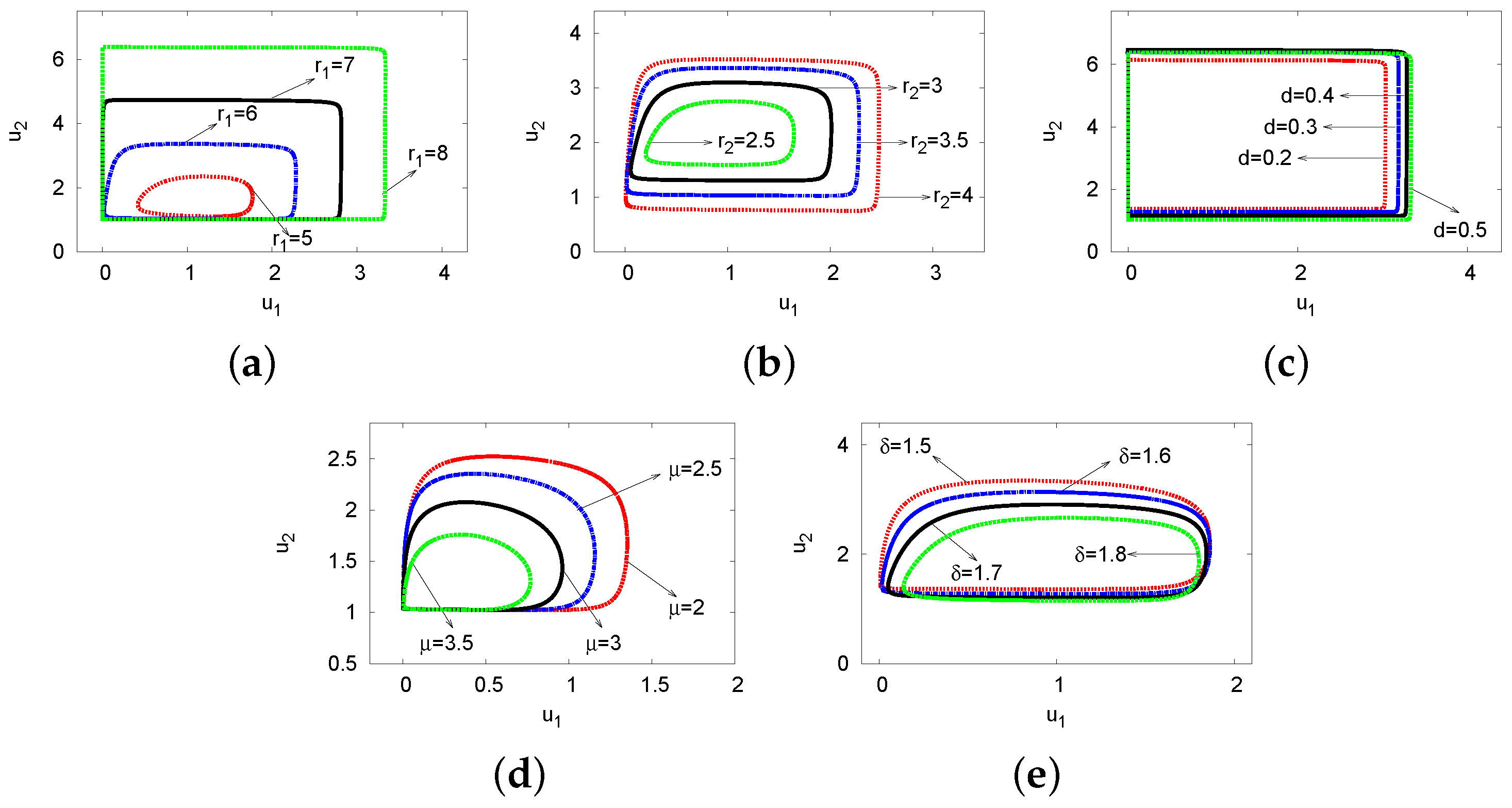
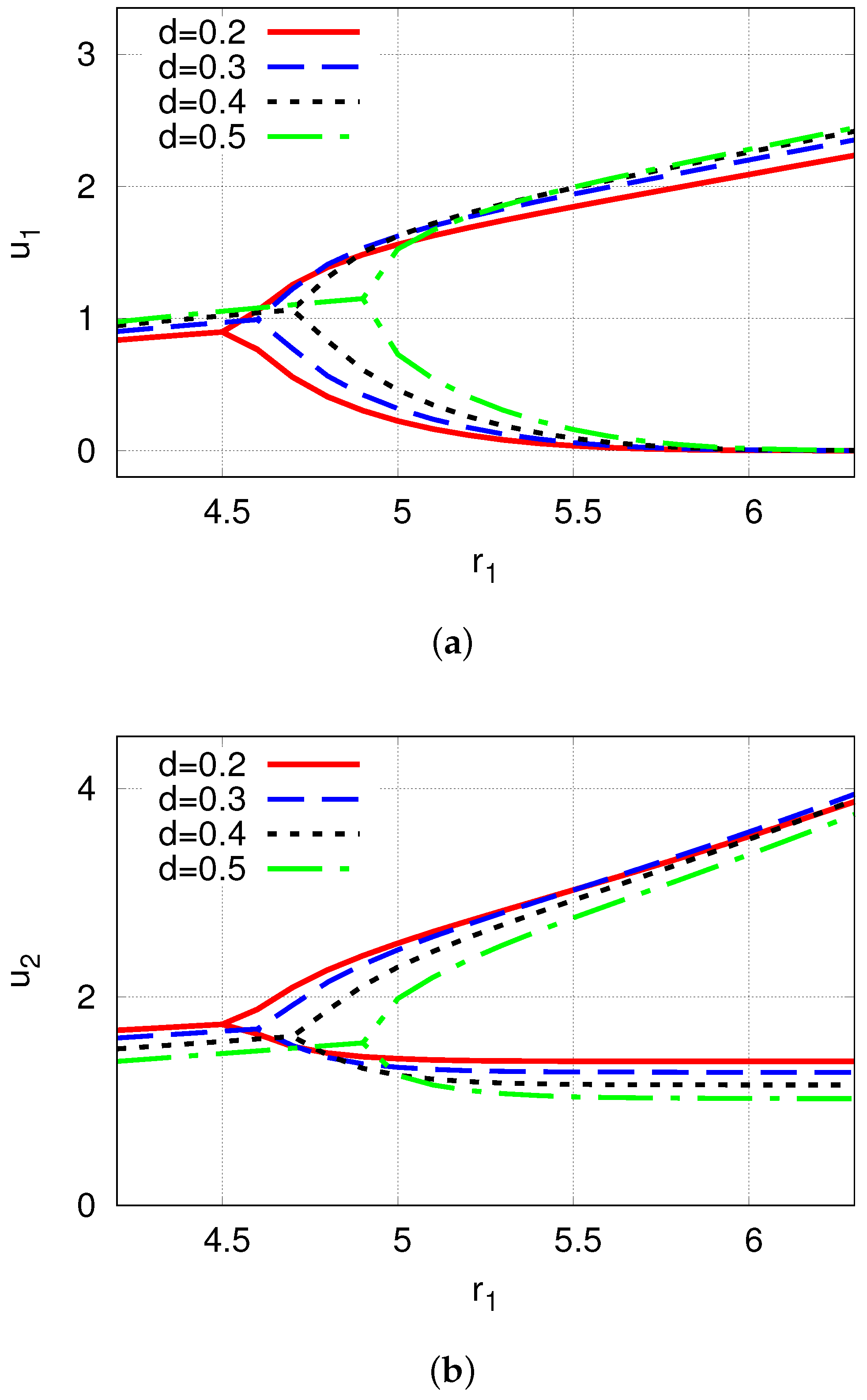
| Growth rate () | Frequency () | |||||
|---|---|---|---|---|---|---|
| Case | Theoretical | Numerical | Error (%) | Theoretical | Numerical | Error (%) |
| 5.491 | 5.578 | ≃1.56 | 1.116 | 1.159 | ≃3.71 | |
| 5.447 | 5.455 | ≃0.15 | 1.056 | 1.072 | ≃1.49 | |
| 5.407 | 5.411 | ≃0.07 | 0.999 | 1.006 | ≃0.60 | |
| 5.394 | 5.397 | ≃0.06 | 0.981 | 0.985 | ≃0.40 | |
| 5.387 | 5.389 | ≃0.04 | 0.971 | 0.974 | ≃0.30 | |
| 5.383 | 5.384 | ≃0.02 | 0.966 | 0.968 | ≃0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfifi, H.Y. Effects of Diffusion and Delays on the Dynamic Behavior of a Competition and Cooperation Model. Mathematics 2025, 13, 1026. https://doi.org/10.3390/math13071026
Alfifi HY. Effects of Diffusion and Delays on the Dynamic Behavior of a Competition and Cooperation Model. Mathematics. 2025; 13(7):1026. https://doi.org/10.3390/math13071026
Chicago/Turabian StyleAlfifi, Hassan Y. 2025. "Effects of Diffusion and Delays on the Dynamic Behavior of a Competition and Cooperation Model" Mathematics 13, no. 7: 1026. https://doi.org/10.3390/math13071026
APA StyleAlfifi, H. Y. (2025). Effects of Diffusion and Delays on the Dynamic Behavior of a Competition and Cooperation Model. Mathematics, 13(7), 1026. https://doi.org/10.3390/math13071026







