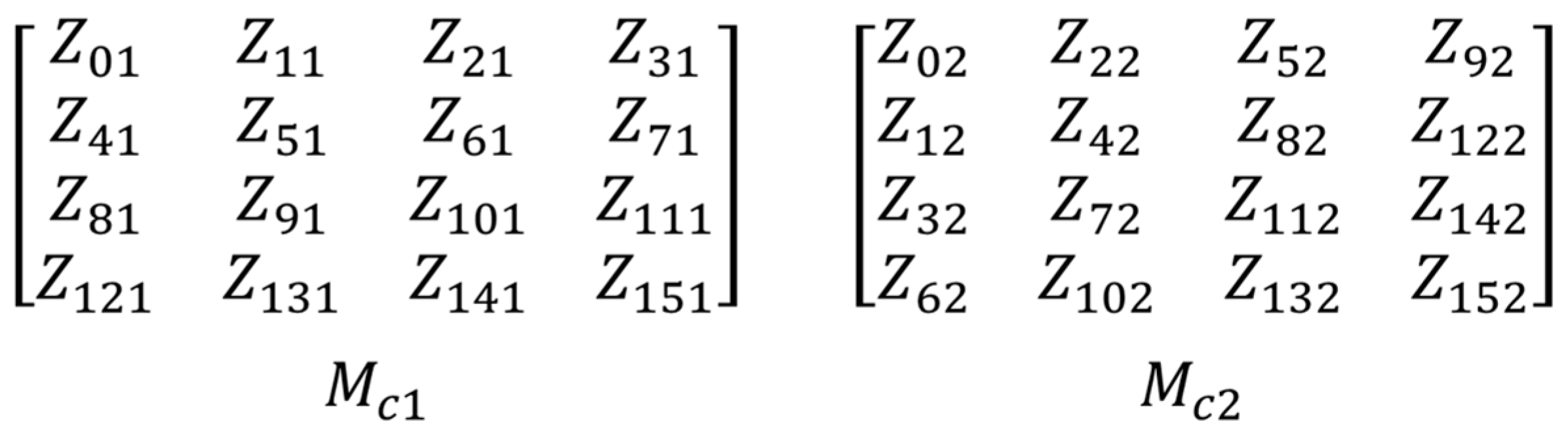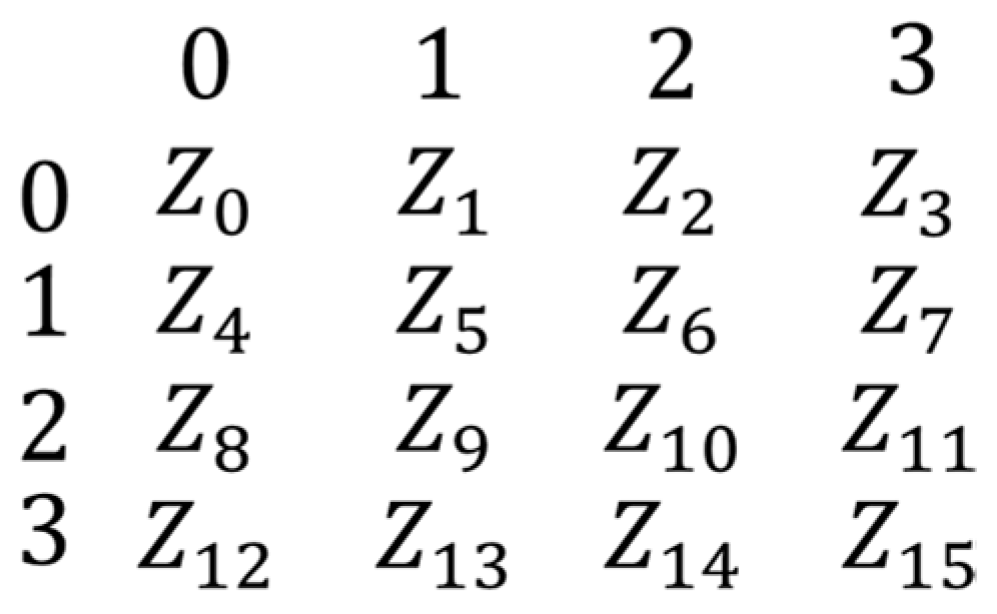Symmetric Grayscale Image Encryption Based on Quantum Operators with Dynamic Matrices

Abstract

Image encryption is crucial for ensuring the confidentiality and integrity of digital images, preventing unauthorized access and alterations. However, existing encryption algorithms often involve complex mathematical operations or require specialized hardware, which limits their efficiency and practicality. To address these challenges, we propose a novel image encryption scheme based on the emulation of fundamental quantum operators from a multi-braided quantum group in the sense of Durdevich. These operators—coproduct, product, and braiding—are derived from quantum differential geometry and enable the dynamic generation of encryption values, avoiding the need for computationally intensive processes. Unlike quantum encryption methods that rely on physical quantum hardware, our approach simulates quantum behavior through classical computation, enhancing accessibility and efficiency. The proposed method is applied to grayscale images with 8-, 10-, and 12-bit depth per pixel. To validate its effectiveness, we conducted extensive experiments, including visual quality metrics (PSNR, SSIM), randomness evaluation using NIST 800-22, entropy and correlation analysis, key sensitivity tests, and execution time measurements. Additionally, comparative tests against AES encryption demonstrate the advantages of our approach in terms of performance and security. The results show that the proposed method provides a high level of security while maintaining computational efficiency.

1. Introduction

The development of new technologies and the exchange of information have created new challenges in how data are shared and in ensuring that images exchanged over the internet correspond to their original versions. To preserve their integrity, various cryptographic techniques have been developed to hide or protect sensitive information within images. Current encryption algorithms are classified into two categories, namely stream and block ciphers. Stream ciphers process information one bit or one byte at a time [1,2]. Today, the most widely used symmetric block cipher standard is the Advanced Encryption Standard (AES) [3].

In broad terms, the AES operates through three fundamental invertible transformations. The first is a linear mixing transformation that ensures diffusion across multiple rounds. The second is a nonlinear transformation, implemented using substitution matrices. The third involves adding a subkey, derived from the initial key, to enhance security by improving both diffusion and nonlinearity.

Meanwhile, researchers have explored new encryption methods, leading to various innovative approaches. These include encryption techniques based on DNA computing [4,5,6], neural networks [7,8,9], chaotic systems [10,11,12,13,14,15,16,17,18], and methods inspired by quantum phenomena.

Regarding the use of quantum systems, two main applications can be highlighted, quantum key distribution (QKD) [19,20] and quantum secure direct communication (QSDC). QKD, introduced by Charles H. Bennett and Gilles Brassard in 1984 [20], enables two parties to generate a shared secret key securely, even in the presence of an eavesdropper. In recent years, several new QKD proposals have emerged, exploring enhancements in security, efficiency, and implementation techniques [21,22,23].

Introduced by Deng et al. in 2003 [24], quantum direct communication (QDC) protocols are a class of quantum communication protocols that enable secure information transmission without the need for pre-shared encryption keys. Unlike quantum key distribution (QKD), which is used to establish a shared secret key for classical encryption, QDC allows for the direct transmission of secret messages through quantum states. Specifically, QDC encodes messages into quantum states using Einstein–Podolsky–Rosen (EPR) pairs to ensure secure transmission.

Building on the foundations of QDC, several innovative proposals have emerged. For example, Panda et al. [25] introduced a protocol based on quantum walks. Additionally, QDC has been applied in various domains, such as a quantum blockchain scheme proposed by Xu et al. [26] and a QDC-based framework for quantum cloud computing [27].

Although quantum key distribution (QKD) and quantum digital certificates (QDCs) promise significant security advantages, their practical implementation is constrained by the requirement for specialized quantum hardware to handle and transmit quantum states. To address this, we propose a novel encryption method grounded in the diagrammatic framework of multi-braided quantum groups. This technique leverages the sophisticated algebraic properties of quantum groups, as originally developed by Micho Durdevich [28,29].

This paper is organized as follows: Section 2 provides a mathematical background about multi-braided quantum groups. Section 3 provides a comprehensive overview of the cipher’s stages, explaining the operation of each constituent quantum operator. Section 4 presents the experimental results of our proposed method, accompanied by an analysis of visual quality metrics applied to encrypted images and randomization tests for thorough algorithm evaluation. The paper concludes with a discussion of the results, followed by concluding remarks and a roadmap for future research directions.

In summary, our research contributes to the following aspects:

• Quantum operator-based encryption: We propose an image encryption algorithm that leverages quantum operator characteristics to encrypt images with depths of 8, 10, and 12 bits or higher resolutions, enabled by hexadecimal-by-hexadecimal encryption.
• Finite field processing: The algorithm employs finite fields to ensure proper linkage between operators when processing the hexadecimal values of each pixel.
• Dynamic random matrices: Encryption keys generate random matrices dynamically, preventing the use of fixed matrices and ensuring that each encryption process is unique.
• Computational efficiency: The properties of the creation, annihilation, and crossover operators reduce the computational burden by minimizing the number of required mathematical operations. This enhances the overall efficiency of the encryption process.

Enhanced security and performance: Quantum cipher operations provide exceptional security and encryption efficiency. Experimental results and performance analyses demonstrate that the proposed algorithm offers significant advantages, particularly in the efficiency of encryption.

2. Background

In this section, we present brief descriptions of the Abelian groups and Galois field. Also, the multi-braided quantum groups are described as the performance of the quantum operators.

2.1. Abelian Groups and Galois Field

A binary operation in a non-empty set $M$ is a mapping from $M\times M$ to $M$. For $a,b\in M$, a binary operation, is called a commutative monoid if the commutative law is satisfied, $ab=ba$ for all $a,b\in M$ and the associative law is $\left(ab\right)c=a\left(bc\right)$ for all $a,b,c\in M$.

In a monoid $M$, there exists an element $e\in M$ such that $eg=g=ge$ for all $g\in M$, called a neutral element. In an additive monoid, the element is known as a zero element. On the other hand, for a multiplicative monoid, the element is called a unit element.

For a multiplicatively written monoid ($M,·,1$), there is an element $u\in M$ and $v\in M$ such that $uv=1=vu$, and $u$ is called invertible element. In the case where every element of $M$ has an invertible element, it is called a group. Moreover, if the group is conmutative, it is called an Abelian group.

The theory of modules is a central tool in the study of finite fields, which need to be defined over commutative rings. A ring ($R,+,·,0,1)$ is a set $R$ with two binary operations, $(R,+,0)$, in an Abelian group. If the ring is commutative with all non-zero elements having multiplicative inverses, it is said to be a field.

A set ${\mathbb{Z}}_n$ (the integer modulo $n$) forms a field under addition and multiplication modulo n if and only if $n$ is a prime number.

The cryptosystems rely on hard computational problems, such as the prime factorization of large numbers used in RSA [30]. Similarly, in private-key cryptography, transformations are performed over a finite field ${Ϝ}_2^8$ [31], also known as the Galois field. A finite field is an algebraic structure consisting of a finite set $Z_p$, defined as

$$Z/p Z=Z_p=\{0,1,2,3,\dots ,p-1\}$$

(1)

The proposed encryption method employs two finite fields, defined as $Z_4=\{0, 1, 2, 3\}$ and $Z_{16}=\{0, 1, 2, 3, \dots , 14, 15\}$, to define the interaction of our version of the quantum operators. These rings provide a structured algebraic framework that facilitates controlled transitions between different modular arithmetic domains, ensuring the coherence of the encryption process.

2.2. Multi-Braided Quantum Groups

This framework extends the conventional algebraic structures of quantum groups by incorporating categorical and topological features that enable the non-trivial transformations of encoded data. Our encryption scheme exploits the interplay between fundamental quantum operators—namely the product, coproduct, and braiding operator—to define encryption and decryption processes within a quantum algebraic setting. Quantum groups, in the sense of Woronowicz, provide a powerful generalization of classical symmetry structures, where commutative and non-cocommutative properties arise naturally [32]. The diagrammatic formulation introduced by Durdevich offers an intuitive yet rigorous way to manipulate these structures, making it particularly well-suited for encoding transformations in an encryption system.

The key algebraic components that form the backbone of our approach are as follows:

(A)

Product Operator $m:A\otimes A\to A$ (Multiplication/Annihilation Operator): The product defines an associative binary operation that combines two elements within the quantum algebra. In the context of braided quantum groups, this operation respects the braiding constraints, ensuring compatibility with the underlying categorical structure.

(B)

Coproduct Operator $\varphi :A\to A\otimes A$ (Comultiplication/Creation Operator): The coproduct is a co-associative map that encodes the decomposition of algebraic elements, playing a crucial role in comultiplicative structures. It satisfies the compatibility condition with the antipode in Hopf algebraic settings and enables hierarchical encoding in encryption schemes.

(C)

Braiding Operator $\sigma :A\otimes A\to A\otimes A$ (Exchange/Crossover Operator): In multi-braided quantum groups, the braiding operator introduces a controlled exchange mechanism that preserves the non-commutative structure of the algebra. The braiding map satisfies the Yang–Baxter equation [33], ensuring coherence in multiple exchanges.

The proposed encryption method is inspired by previously introduced operators and their interactions. This approach leverages algebraic structures to define encryption operations, which introduce non-trivial symmetries, contributing to the robustness of the encryption scheme. Unlike traditional quantum groups, the operators in this method are specifically adapted for bijective mappings, making them suitable for encryption and decryption tasks. This adaptation enables secure encryption with reduced computational complexity.

3. Proposed Algorithm

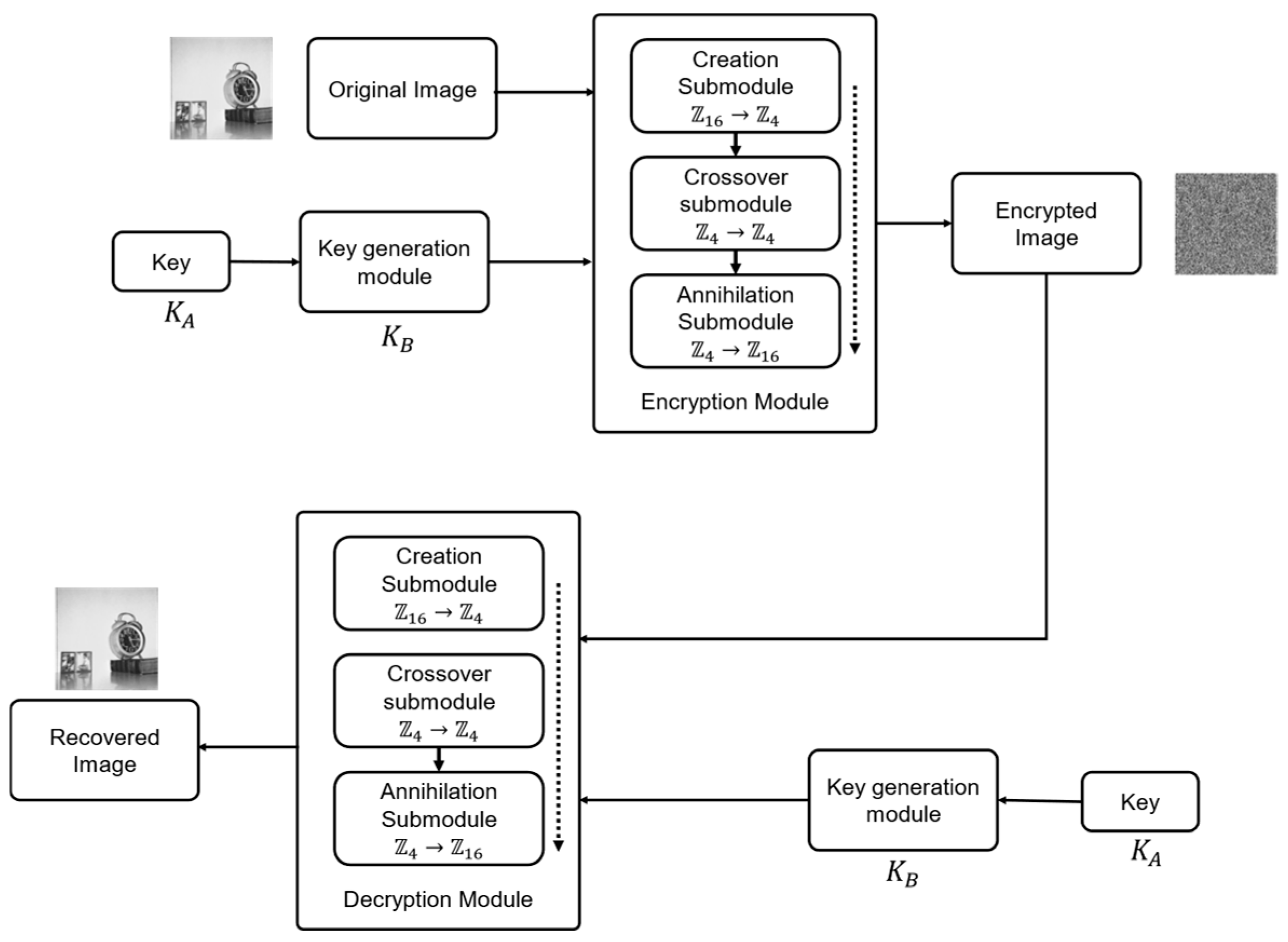
This section outlines the encryption steps and the complete decryption process of our proposed encryption scheme based on quantum operators with dynamic matrices.

The proposed algorithm consists of two phases, which are described in a general manner as follows: The first phase involves generating a new key $K_B$ from a given key $K_A$, which is separated into its hexadecimal components. Through a series of modular operations and predetermined matrices, the new key $K_B$ is constructed. The second phase involves encrypting the image; this phase comprises three essential stages of the encryption process, involving a creation module, a crossover module, and an annihilation module. The general structure of the encryption system is depicted in Figure 1.

3.1. Key Generation Module

The key generation module processes a 128-bit (16-ASCII character or 32 hexadecimal) key $K_A$ by separating it into its hexadecimal components. The key $K_A$ is then divided into two strings, with $Z_{n1}$ containing the most significant hexadecimals and $Z_{n2}$ containing the least significant hexadecimals, where n denotes the position of each ASCII-character of the key, as shown in Figure 2.

Once both strings are generated, the hexadecimal values are arranged into two different matrices denoted as $M_{C1}$ and $M_{C2}$ of 4 × 4 in size, according to the distribution shown in Figure 3.

Subsequently, a specific modular addition and modular multiplication are performed, as shown in (2).

This process aims to generate two new matrices, referred to as $M_{C3}$ and $M_{C4}$.

$$\begin{gathered} M_{C3}=mod \left(\right(M_{C1}+M_{C2}),16) \\ {M}_{C4}=mod \left(\right(M_{C1}\ast M_{C2}),16) \end{gathered}$$

(2)

Once both matrices are obtained, the new key $K_B$ is created by considering the order of values displayed in the matrices $M_{C3}$ and $M_{C4}$ in Figure 4, where $M_{C3}$ represents the most significant and $M_{C4}$ the least significant hexadecimals.

The key $K_B$ will consist of two vectors composed of $Z_{n3}$ and $Z_{n4}$, where $Z_{n3}$ corresponds to the most significant hexadecimals and $Z_{n4}$ to the least significant hexadecimals, as illustrated in Figure 5.

The new key $K_B$ is a vector composed of 32 hexadecimals arranged in the following order: $Z_{03}, Z_{04}, Z_{13}, Z_{14}, \dots Z_{n3}, Z_{n4}$.

3.2. Encryption Module

The module allows for processing images of dimensions $N\times M$, which can be either grayscale or medical images. Additionally, it can receive an encryption key $K_B$ composed of 32 hexadecimal characters. The input image is processed into an array $A=[a_1, a_2,\dots ,a_n]$, where $n=N\times M\times 2$, the array contains the hexadecimal values of each pixel, and this array undergoes a rightward rotation. Following a stream cipher approach, one hexadecimal $a_n$ from the image array is encrypted in parallel with one hexadecimal $Z_{nj}$ from the key $K_B$ array.

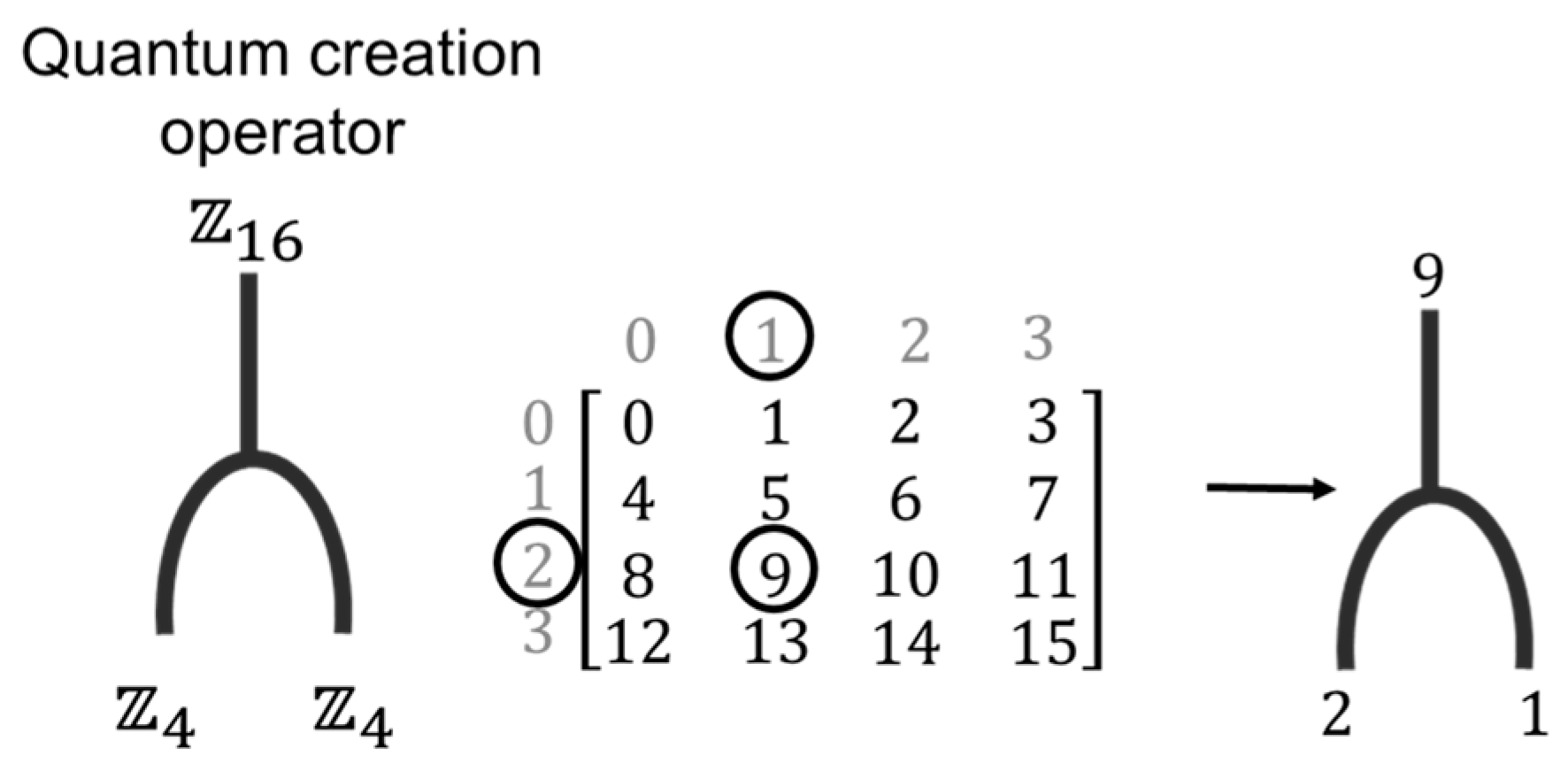
3.2.1. Creation Operator Module

The module utilizes a set of four configurable matrices to map elements from $Z_{16}$ to $Z_4$ using a 4 $\times$ 4 matrix configuration. These matrices are composed of hexadecimal values ranging from 0 to F arranged in a random order, and a base matrix exists, as shown in Figure 6. The four configurable matrices are generated by applying rotations to the rows and columns of the base matrix. Each rotation is guided by eight hexadecimal values derived from the key $K_B$. Specifically, each hexadecimal value determines the rotation position for a corresponding row or column; rows are rotated upward, while columns are shifted to the right.

Each matrix configuration that was generated is selected according to the two least significant bits (LSBs) of the hexadecimal value of the encryption key $K_B$ being used at that moment. For instance, if the two LSBs are (00), the matrix will use the first configuration; if they are (01), the second; if (10), the third; and if (11), the last configuration will be used. The creation operators split an element into two parts. To achieve this, the hexadecimal value of the pixel is in the selected matrix, and the row and column values where it is found are obtained, as shown in Figure 7; assuming that the value to be encrypted is nine, the row and column values are determined. Consequently, the resulting values from the crossover operator will be {2, 1}. The resulting values are selected using the matrix determined by the key $K_B$.

The two resulting values from the mapping of ${\mathbb{Z}}_{16}$ to ${\mathbb{Z}}_4$ are obtained according to the position of the hexadecimal within the selected matrix. These values, which are in ${\mathbb{Z}}_4$, are then sent to the crossover module connected in the cryptosystem.

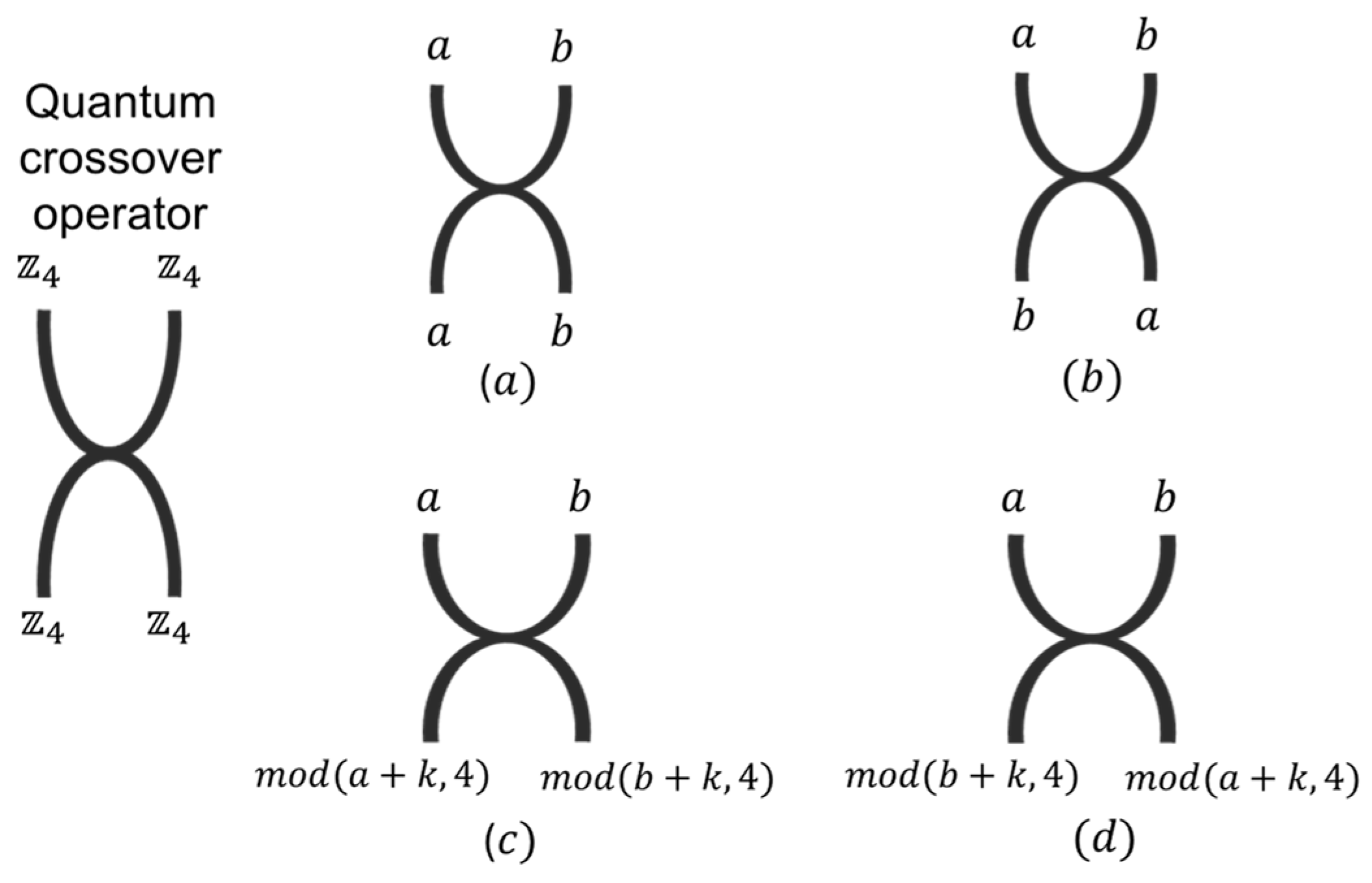
3.2.2. Crossover Operator Module

Like the creation operator, the crossover operator works through various configurations, including direct crossover, inverse crossover, inverse modular additive crossover, or direct modular additive crossover. These can be applied to both ends or just one end of the operator, as shown in Figure 8.

The module operates on the two values within a field from $Z_4$ to $Z_4$. The operation assigned to each submodule is determined by the hexadecimal value of the key $K_B$ being used at that moment. In direct crossover, the input values retain their original positions. In inverse crossover, the positions are swapped. In the inverse modular additive crossover, the positions are swapped, and a modulo-4 addition with $k=\{1, 2, 3\}$ is performed on both digits or just one. Finally, in direct modular additive, a modulo-4 addition is performed with $k=\{1, 2, 3\}$ on both digits or just one. The output values from the crossover module are passed to the next encryption stage, which is the annihilation operator’s module.

3.2.3. Annihilation Operator Module

This operator performs a mapping in a field from $Z_4$ to $Z_{16}$. Unlike the creation operator, it receives the two values from the crossover operator and returns a single value, which is associated with the numbers using the matrix shown in Figure 6.

The module operates through a series of four configurable matrices that perform a mapping from $Z_4$ to $Z_{16}$ using a 4 $\times$ 4 matrix configuration, created using the key $K_B$. This matrix has four different configuration possibilities, like the creation operators module. Each configuration is selected based on the two most significant bits (MSBs) of the first hexadecimal of the encryption key $K_B$, e.g., if the two MSBs are (00), the matrix will use the first configuration; if (01), the second; if (10), the third; and if (11), the last configuration. The annihilation operator takes two values from a crossover operator and generates a new one using the selected matrix as shown in Figure 9.

The value resulting from the annihilation operator represents a hexadecimal value for a pixel in the output image, meaning each resulting pair of hexadecimal digits corresponds to a new pixel. For the generated key $K_B$, once its 32 hexadecimal digits are processed with the 32 hexadecimal digits of the original image, a left rotation of seven positions is performed in $K_B$. This is then followed by further processing with the next 32 hexadecimal digits of the original image. Processing the image on a hexadecimal-by-hexadecimal basis allows the proposed method to behave as a stream cipher. Additionally, this approach eliminates restrictions related to the dimensions of the image, as the need to process complete blocks of data is removed through this methodology. Once the image has been fully processed, the system performs four additional encryption rounds, meaning that each image undergoes a total of five rounds, like the AES algorithm.

3.3. Decryption Module

The entire encryption process is reversible because the quantum operation satisfies the unitary property, allowing for the exact recovery of the original image. The decryption process involves two modules, namely a key generation module $K_B$ and a decryption module, where quantum operators function in reverse. The $K_B$ key generation module follows the same process described in Section 2.1. However, the decryption module undergoes slight modifications. The creation and annihilation operators, as well as the matrix selection process, maintain the same behavior. In contrast, the crossover operator changes by performing additive four sums differently. Specifically, when summing values of $k=\{1, 2, 3\}$, the operation is carried out with their opposite values, i.e.,$k=\{3, 2, 1\}$, respectively.

4. Results

This section presents the experimental and theoretical verification of various aspects of the proposed encryption algorithm. The evaluation includes key sensitivity, adjacent pixel correlation, information entropy, encryption/decryption time, and analysis using the NIST 800-22 test suite. The proposed method was implemented on a personal computer with a Microsoft Windows 11 © operating system, Intel© core i7 processor, and 16 GB of RAM. MATLAB R2024a serves as the simulation software.

Tests were conducted on grayscale images with 8, 10, and 12 bit/pixel in depth and different spatial resolutions, denoted as I_res8, I_res10, and I_res12; its dimensions are 256 × 256, 256 × 256, and 512 × 512, respectively. The test images used are from common databases, I_res8 from USC-SIPI (http://sipi.usc.edu/database/ (accessed on 28 February 2025)) and I_res10 and I_res12 constituting the set of medical images that corresponds to a dataset provided by Instituto Mexicano del Seguro Social (IMSS) for research purposes.

The images, along with their corresponding histograms, are shown in Figure 10, Figure 11, and Figure 12, respectively. By applying the proposed methodology, the encrypted images shown in these figures were obtained. As observed, the encrypted images do not visually exhibit any patterns related to the original versions, resulting in images that appear to be pure noise.

In the histograms of medical and grayscale images, several well-defined peaks can be observed, indicating distinct intensity concentrations. These peaks correspond to regions where specific intensity ranges predominate, reflecting variations in illumination or the presence of multiple objects with similar characteristics. In contrast, when the histogram of an encrypted image is uniform, it signifies that the distribution of pixel intensity values is nearly homogeneous. This suggests that the encryption process has eliminated the statistical correlations present in the original image, making the encrypted image resemble random noise. As a result, it becomes challenging to identify patterns or correlations with the original image, thereby reducing its susceptibility to cryptanalysis, including statistical attacks.

4.1. Visual Quality Assessment

It is crucial that an encrypted image differs significantly from its original version to ensure its security and protect it against potential attacks. The visual difference between the original image and its encrypted counterpart should be pronounced, making it nearly impossible to identify recognizable patterns or features that could facilitate data recovery.

To assess the similarity between the original and encrypted images, the peak signal-to-noise ratio (PSNR) and the structural similarity index metric (SSIM) were used [33,34], both defined by (3) and (4), respectively. These metrics provide a quantitative evaluation of the quality of the encrypted image in comparison to the original, allowing for an accurate measurement of the encryption’s effectiveness.

$$PSNR(dB)=10{\log }_{10}\left({\displaystyle \frac{{Max Pixel Value}^2}{\frac{1}{N·M}\left({\displaystyle \sum _{x=1}^N}{\displaystyle \sum _{y=1}^M{\left(I_O(x,y)-I_E(x,y)\right)}^2}\right)}}\right),$$

(3)

where N × M are the original dimensions, I_O and I_E are the original and encrypted images, and $Max Pixel Value$ is the maximum value a pixel can take (e.g., 255 in 8-bit images), respectively.

$$SSIM(I_O,I_E)={\displaystyle \frac{(2{\mu }_{I_O}{\mu }_{I_E}+C_1)(2{\sigma }_{I_O I_E}+C_2)}{({\mu }_{I_O}^2+{\mu }_{I_E}^2+C_1)({\sigma }_{I_O}^2+{\sigma }_{I_E}^2+C_2)}}.$$

(4)

From (4), µ_I and µ_I’ denote mean intensity (luminance); the term ${\sigma }_{I_O{I}_E}$ denotes a correlation coefficient between I_O and I_E with structure comparison purposes, ${\sigma }_{I_O}^2$ and ${\sigma }_{I_E}^2$ denote variance, and C₁, C₂ are small constant values [33,34]. SSIM separates the task of similarity measurements into three comparisons, including luminance, contrast, and structure. The range of SSIM values is [0, 1], where a value of one indicates that the original and the reference image are the same [35]. A comparison was conducted with the AES cipher in ECB mode, and the corresponding values are presented in

Table 1. Evaluation with quality metrics PSNR and SSIM.

	Proposed Method		AES
Image	PSNR	SSIM	PSNR	SSIM
Ires8	7.3068	0.0100	8.5218	0.0091
Ires10	1.2921	0.0207	1.2073	0.0528
Ires12	4.5577	0.0853	4.5862	0.0743

.

4.2. Efficiency Analysis

As is widely recognized, one of the main objectives in developing encryption algorithms in addition to ensuring security is to improve the efficiency of the encryption process. Therefore, a well-designed encryption algorithm should not only provide a high level of security but also ensure high execution efficiency. To evaluate the efficiency of the proposed algorithm, timing tests were conducted on both the proposed and AES algorithms, with the results presented in

Table 2. Evaluation of execution times (in seconds).

Image	Proposed Method	AES
Ires8	15.634 s	38.572 s
Ires10	16.755 s	43.963 s
Ires12	64.112 s	179.465 s

. As shown, the proposed algorithm requires less processing time compared to AES. It is important to note that the AES implementation used was the built-in MATLAB© algorithm [36,37].

4.3. Statistical Randomness Test

To assess the quality of the numbers generated by the system in terms of their randomness, several tests can be conducted. These tests are crucial to ensure that the generated numbers are sufficiently unpredictable, making them suitable for critical applications such as cryptography.

An evaluation was conducted using the NIST 800-22 standard [38], which assesses the statistical properties of uniformity and independence in randomness for sequences generated by RNGs and PRNGs. Ten tests were applied to an output sequence of 1,000,000 bits, generating p-values that provide a metric to classify the sequence as random or non-random. The evaluated tests are frequency tests (1), a frequency block (2), a runs test (3), the longest run (4), non-overlapping matching (5), overlapping matching (6), Maurer’s test (7), cumulative sums forward (8), cumulative sums backward (9), and the random excursions test (10). The p-value serves as an indicator of whether a test is passed or failed. To qualify as random, the p-value must be greater than 0.01. The results of the NIST 800-22 statistical tests for both the proposed algorithm and AES are summarized in

Table 3. p-values of the proposed method and AES.

	Ires8		Ires10		Ires12
Test	Proposed Method	AES	Proposed Method	Test	Proposed Method	Test
1	0.463	0.337	0.597	0.627	0.449	0.345
2	0.358	0.895	0.124	0.826	0.502	0.250
3	0.972	0.776	0.615	0.561	0.015	0.032
4	0.742	0.077	0.684	0.091	0.209	0.063
5	0.138	0.773	0.609	0.053	0.311	0.373
6	0.656	0.300	0.680	0.324	0.539	0.296
7	0.944	0.242	0.148	0.386	0.546	0.104
8	0.732	0.540	0.403	0.855	0.388	0.268
9	0.316	0.150	0.859	0.565	0.835	0.317
10	0.882	0.454	0.597	0.627	0.449	0.345

.

This analysis significantly contributes to validating the quality of the random sequences generated during the encryption process based on quantum operators, ensuring that the results meet the necessary randomness standards for a secure and efficient cryptosystem implementation. As observed in the results from the NIST test, all tests yielded values greater than 0.01, indicating that the test was passed and confirming the presence of randomness in the results produced by the cipher. Furthermore, in most tests, the value obtained by the proposed method exceeds that of the AES, demonstrating its effectiveness in encrypting information.

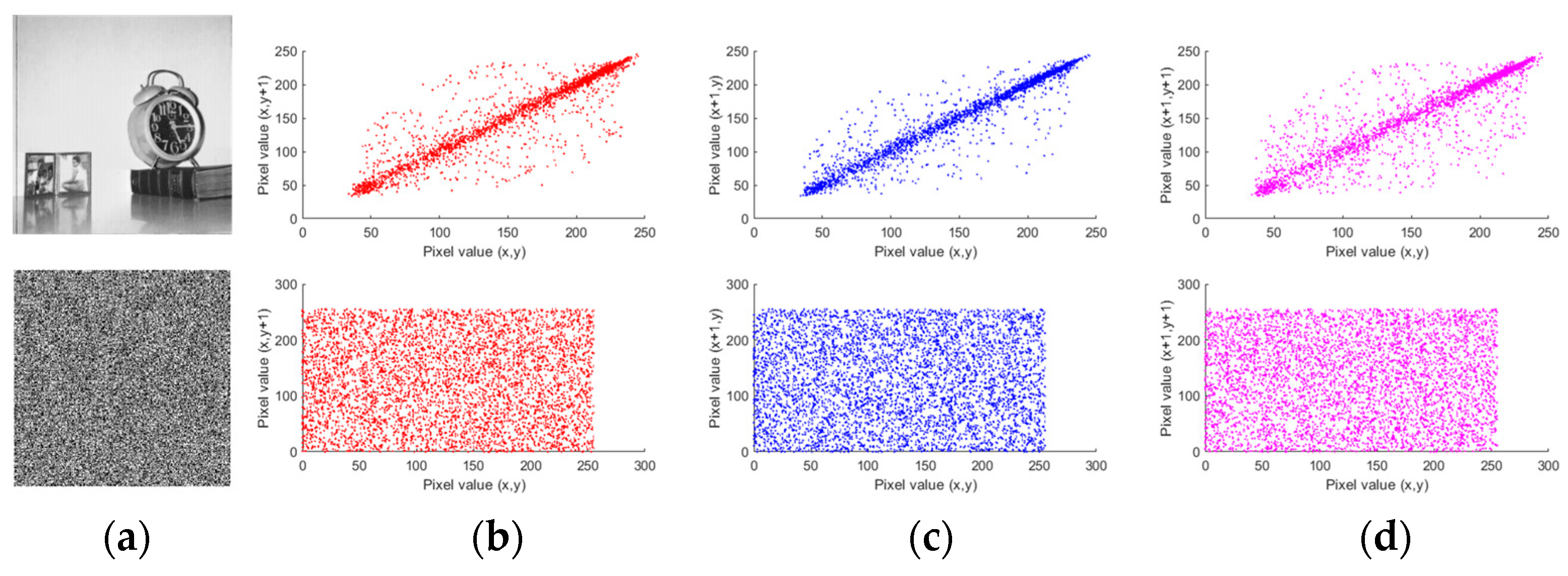
4.4. Correlation Analysis

Digital images inherently exhibit significant correlations between adjacent pixels. To address the security risks associated with these dependencies, robust encryption algorithms must effectively disrupt such correlations [39,40], as shown in Figure 13.

To quantitatively evaluate the performance of the proposed encryption method in diminishing pixel correlation, the correlation coefficient (CC) was introduced as an analytical metric. The correlation coefficient can be expressed as follows:

$$CC={\displaystyle \frac{E\left(\left(v_x-E\left(v_x\right)\right)\times \left(v_y-E\left(v_y\right)\right)\right)}{\sqrt{D\left(v_x\right)\times D\left(v_y\right)}}}$$

(5)

where E(v) and D(v) are the expectation and variance of the grayscale value; $v, v_x$, and $v_x$ are the gray values of two adjacent pixels in a certain direction.

In plain images, the correlation coefficient (CC) exhibits very high absolute values. However, after encryption, these values decrease significantly, often becoming negative. In encrypted images, CC values close to zero or negative indicate that the encrypted image has little to no correlation with the original one, which is desirable. The results for each image are presented in

Table 4. CC values of encrypted images.

Image	CC
	Horizontal	Vertical	Diagonal
Ires8	−0.00007	−0.00007	0.0826
Ires10	−0.0026	−0.0026	−0.00039
Ires12	−0.0029	−0.0029	−0.00147

.

4.5. Plain Image Sensivity

Compared to brute-force attacks, differential attacks are more common and powerful. To ensure the security of an image encryption algorithm, it is crucial that the algorithm exhibits extremely high sensitivity to the key, meaning that small changes in the key should result in drastic variations in the encrypted image. This behavior, known as the “avalanche” principle [41], ensures that a differential attack cannot exploit the minimal differences caused by key alterations.

To evaluate the key sensitivity of our proposal, a random key was generated $K_{A^1}$ and a new key was created $K_{A^2}$ from $K_{A^1}$ that differed by just one bit from the original.

$$K_{A^1}=26302566572\mathrm{F}516233744\mathrm{C}593931233\mathbf{3}$$

$$K_{A^2}=26302566572\mathrm{F}516233744\mathrm{C}593931233\mathbf{4}$$

As shown in Figure 14, encrypting the same image with a small change in just one bit in the key results in a completely different encrypted image. This demonstrates a significant transformation, indicating that the algorithm responds effectively to small key modifications and is resistant to differential attacks. Therefore, the encryption algorithm exhibits extremely high key sensitivity.

4.6. Information Entropy

Information entropy is an indicator that effectively measures the randomness and uniformity of a signal’s distribution. It is commonly used to assess the randomness of encrypted images and, consequently, evaluate the security of an encryption algorithm [42,43,44,45]. Mathematically, the definition of information entropy can be expressed as follows:

$$H^{\left(s\right)}={\sum }_{i=1}^T{p}^{{(s}_t)}{\log }_2{\displaystyle \frac{1}{p^{\left(s_i\right)}}}$$

(6)

where the total number of symbols $s_i$ is $T$ and the occurrence probability of symbol $s_i$ is $p^{\left(s_i\right)}.$ For an 8-bit grayscale image, the ideal value of its information entropy is eight and for a 12-bit grayscale image, it is 12. Therefore, the information entropy of the encrypted image should be close to these values. As shown in

Table 5. Information entropy values of test and corresponding encrypted images.

Image	Information Entropy Value
	Original Image	Encrypted Image
Ires8	6.7057	7.9972
Ires10	5.3885	11.9506
Ires12	9.2399	11.9887

, the information entropy of the encrypted images generated by the proposed algorithm is very close to 8 and 12, respectively, indicating excellent randomness.

The information entropy values of the encrypted images generated by the proposed cipher are very close to the ideal entropy value, indicating extremely high randomness. Additionally, we compare the information entropy test results of our method with those of other encryption algorithms with Figure 10a. The test results are presented in

Table 6. Information entropy values of test with Figure 10a and corresponding encrypted images.

Method	[46]	[47]	[48]	[49]	Our Method
Information entropy	7.9971	7.9980	7.9909	7.9976	7.9991

.

5. Discussion

The results demonstrate that the proposed encryption algorithm maintains high security while requiring lower computational resources compared to AES. The use of creation, crossover, and annihilation operators enables the system to effectively obfuscate image data, minimizing correlation between the encrypted and original images. Furthermore, the NIST randomness tests strengthen the cryptographic robustness of the method, confirming the absence of patterns that could undermine security. While both algorithms yielded competitive results, the proposed algorithm showed comparable—and in most cases superior—performance to AES. The observed differences suggest potential advantages in specific cryptographic scenarios where enhanced randomness is crucial. These findings validate the proposed algorithm’s effectiveness and position it as a promising alternative to the AES for applications demanding high randomness and stringent security standards.

Since the proposed methodology encrypts the hexadecimal values of each pixel in the image, it allows the encryptor to operate with higher-resolution images. For instance, if an image consists of 16 bits or more, its corresponding hexadecimal values will be extracted, and the encryption process will proceed accordingly. Similarly, this approach can be applied to color images, where each RGB channel is encrypted as a grayscale image and then recombined to produce the encrypted color image.

6. Conclusions

To address security and efficiency challenges in image encryption, we have proposed a novel encryption scheme based on the emulation of quantum operators from a multi-braided quantum group. This approach leverages the properties of the creation, annihilation, and crossover operators to dynamically generate encryption values while avoiding the need for complex mathematical computations. The creation operator produces two new values from one, while the annihilation operator reduces two values into one. The crossover operator enables position exchange, ensuring an effective diffusion process. By combining these operations, the proposed algorithm achieves encryption with no discernible correlation to the original data, enhancing security.

To evaluate the performance of our approach, extensive experiments were conducted, including visual quality metrics (SSIM and PSNR), randomness testing (NIST 800-22), entropy analysis, key sensitivity assessment, coefficient evaluation, and execution time measurement. The results demonstrate that our method achieves a lower computational load and faster processing times compared to AES while maintaining high encryption quality. Additionally, the NIST 800-22 tests confirm the high randomness of the generated sequences, ensuring cryptographic robustness by eliminating detectable patterns that could compromise security. The sensitivity analysis further validates those minor changes in the input that lead to significant variations in the encrypted output, reinforcing resistance against differential attacks.

In future work, we aim to enhance the proposed methodology by introducing dynamic structures that modify the order of operators and extend their interactions beyond three-operator chains. By operating within different fields of $Z_n$, we seek to further minimize correlations between input and encrypted data, ensuring greater randomness and improving security metrics. Additionally, we plan to expand the application of this encryption model to other types of multimedia data, such as audio and video, to assess its adaptability and robustness across different formats.