Zero-Error Prescribed-Time Tracking Control for Switched Non-Square MIMO Nonlinear Systems Subject to Asymmetric Time-Varying Output Constraints
Abstract
1. Introduction
- (1)
- The conservatism in initial conditions inherent to BLF-based control methods, as observed in [24,25,26,27], poses significant challenges for practical implementation. Although the integral BLF approach proposed in [29] alleviates this issue to some extent, it remains ineffective in addressing time-varying asymmetric output constraints. To address this limitation, we employ the ANM method, effectively alleviating the conservatism in the system’s initial output constraints.
- (2)
- The proposed ANM method is applicable to asymmetric time-varying output constraints, including unilateral constraints, unconstrained cases, and constant constraints, offering greater generality compared to the nonlinear transferred function approach discussed in [28]. Our approach permits the constraint functions to be arbitrary smooth time-varying functions, in contrast to [27,28,30], where they are required to have opposite signs.
- (3)
2. Problem Formulation
2.1. System and Assumptions
2.2. Preliminaries
3. Control Design and Stability Analysis
3.1. State-Constrained Transformation
3.2. Controller Design
3.3. Stability Analysis
- (1)
- the prescribed output constraint is not violated, i.e., the output satisfies
- (2)
- all signals of the closed-loop system are bounded on ;
- (3)
- the tracking error possesses the following property:where represents the first time derivative of .
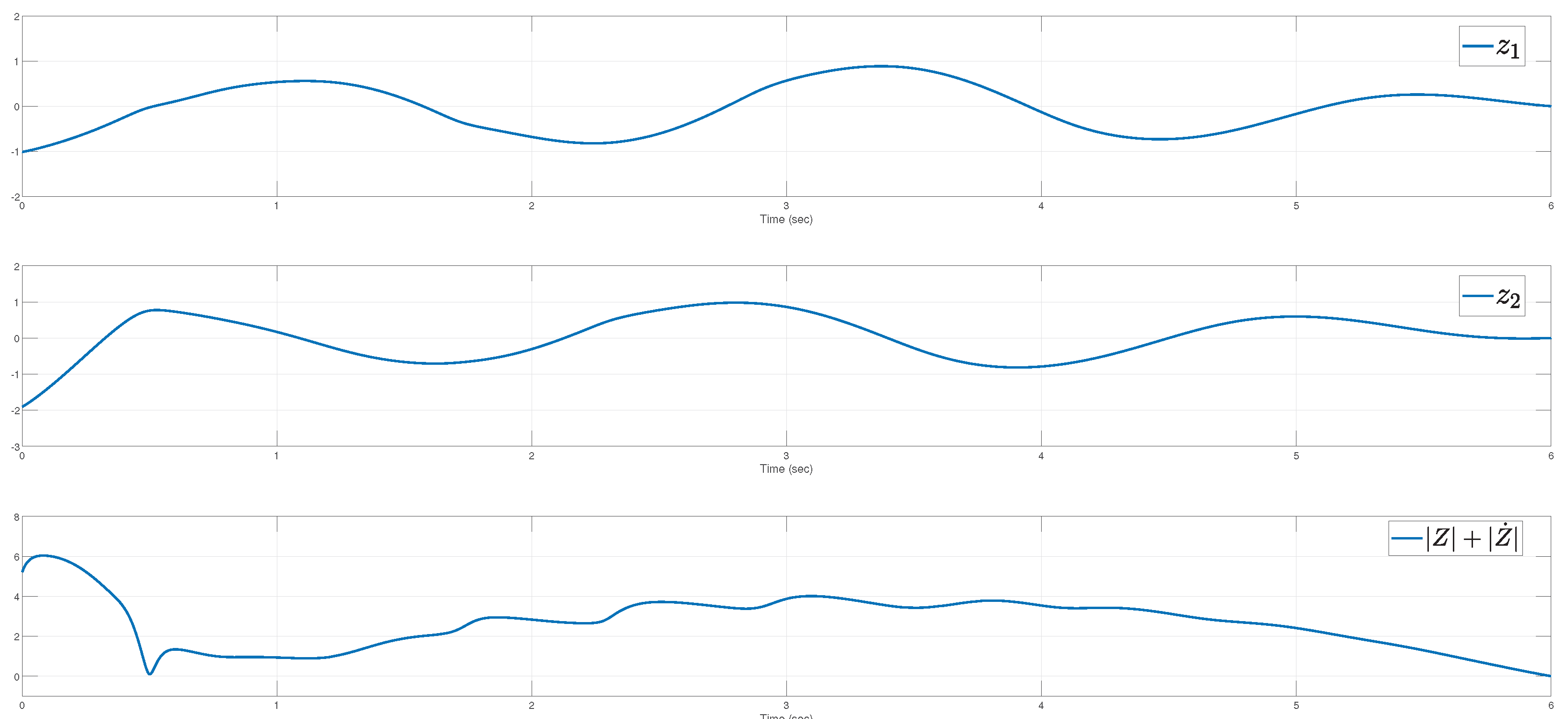
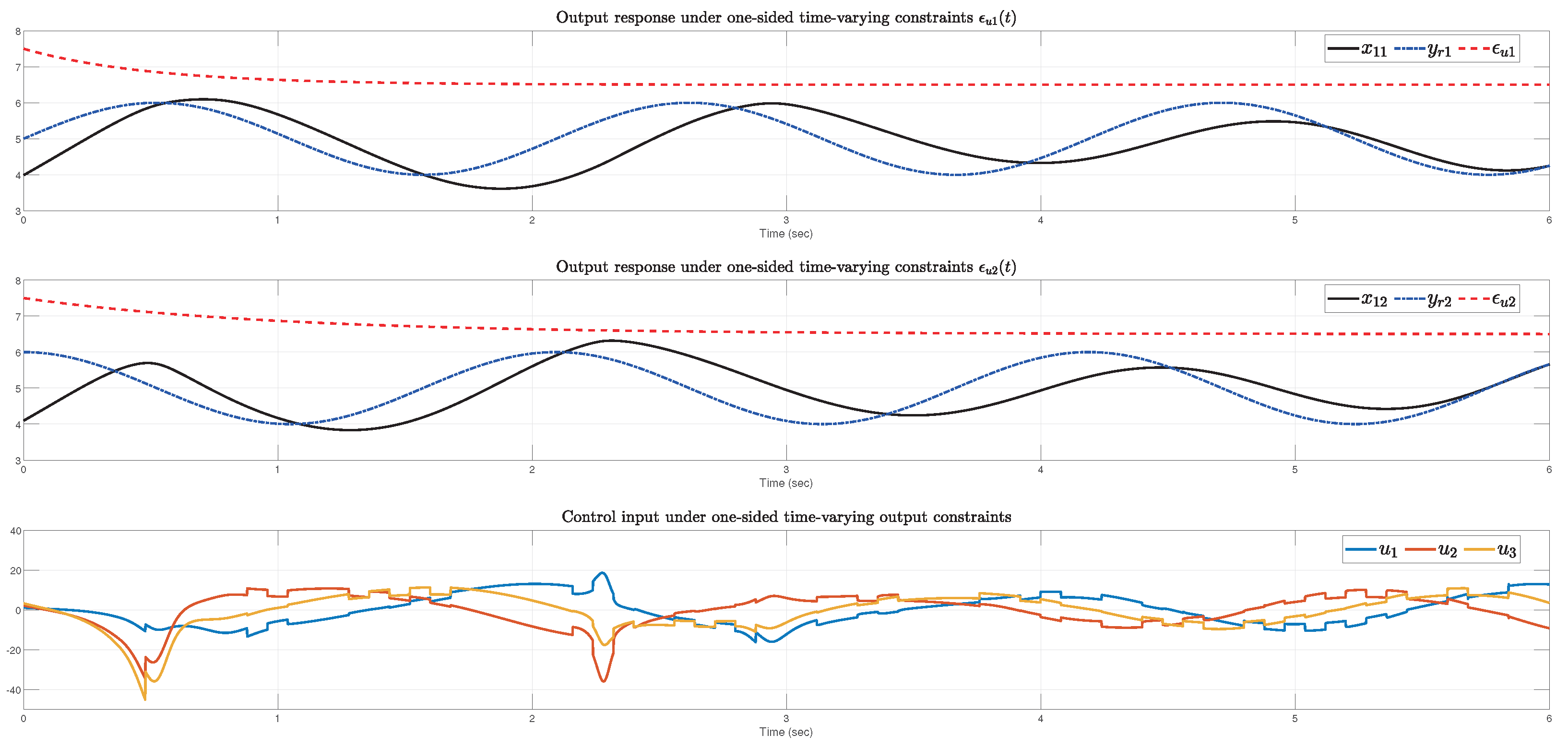
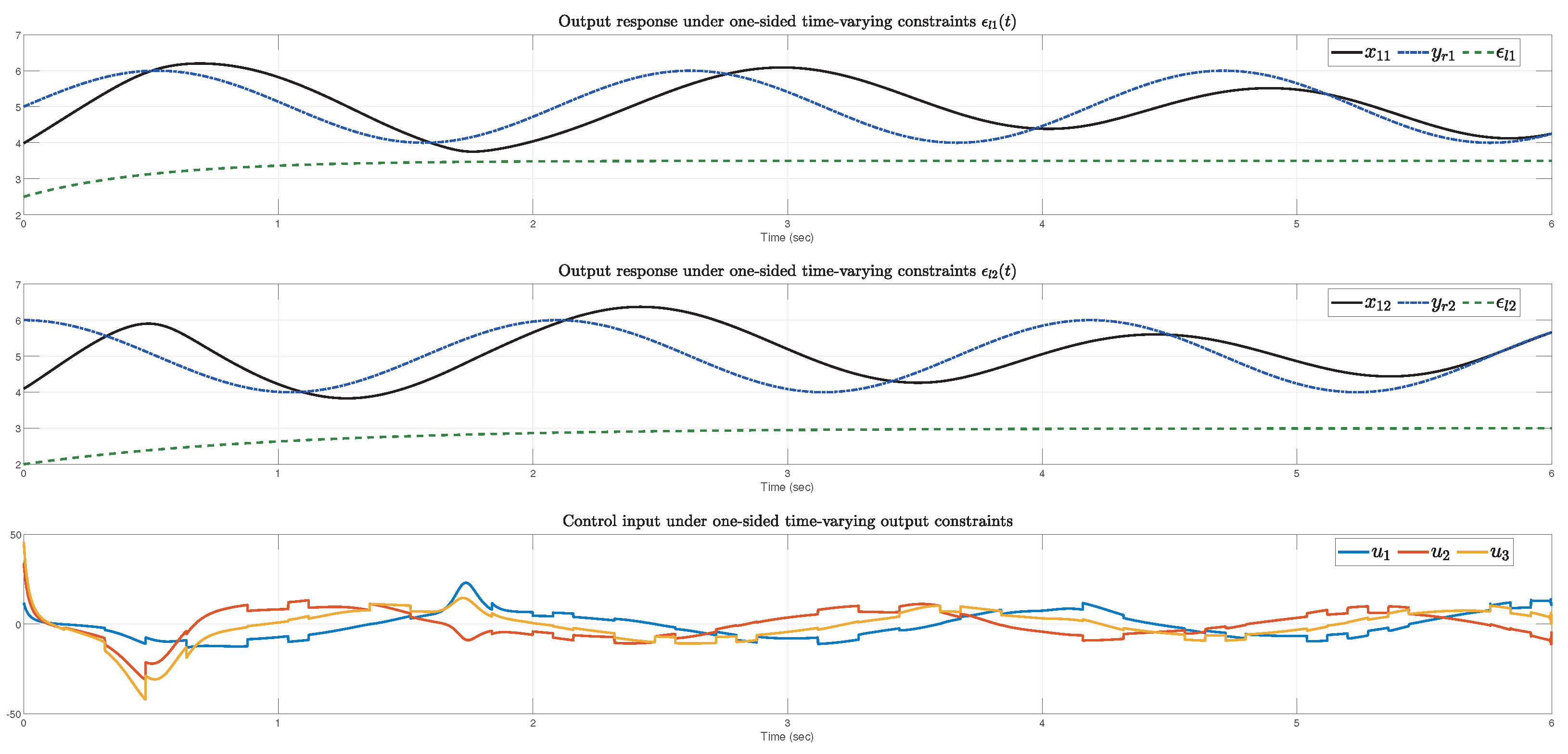
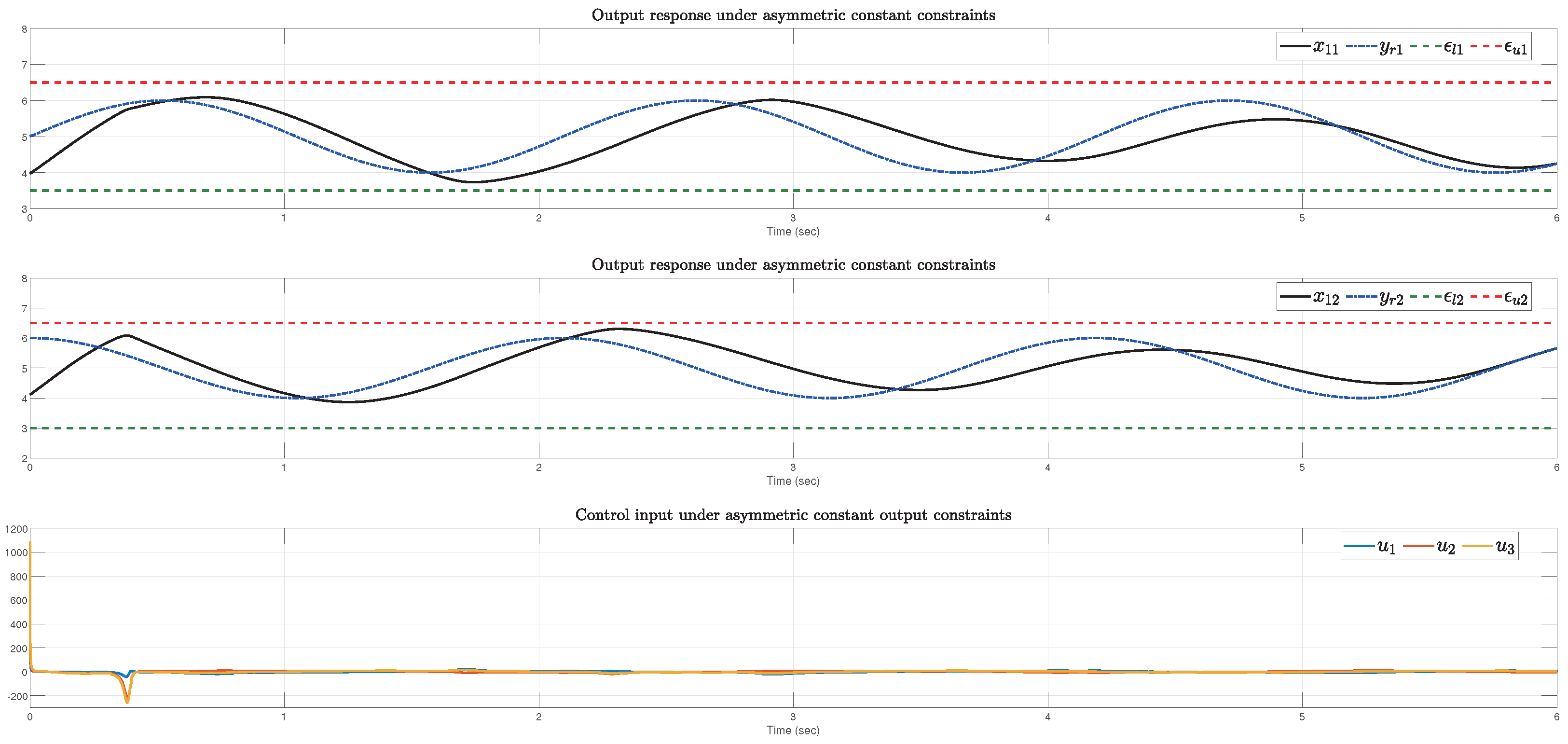
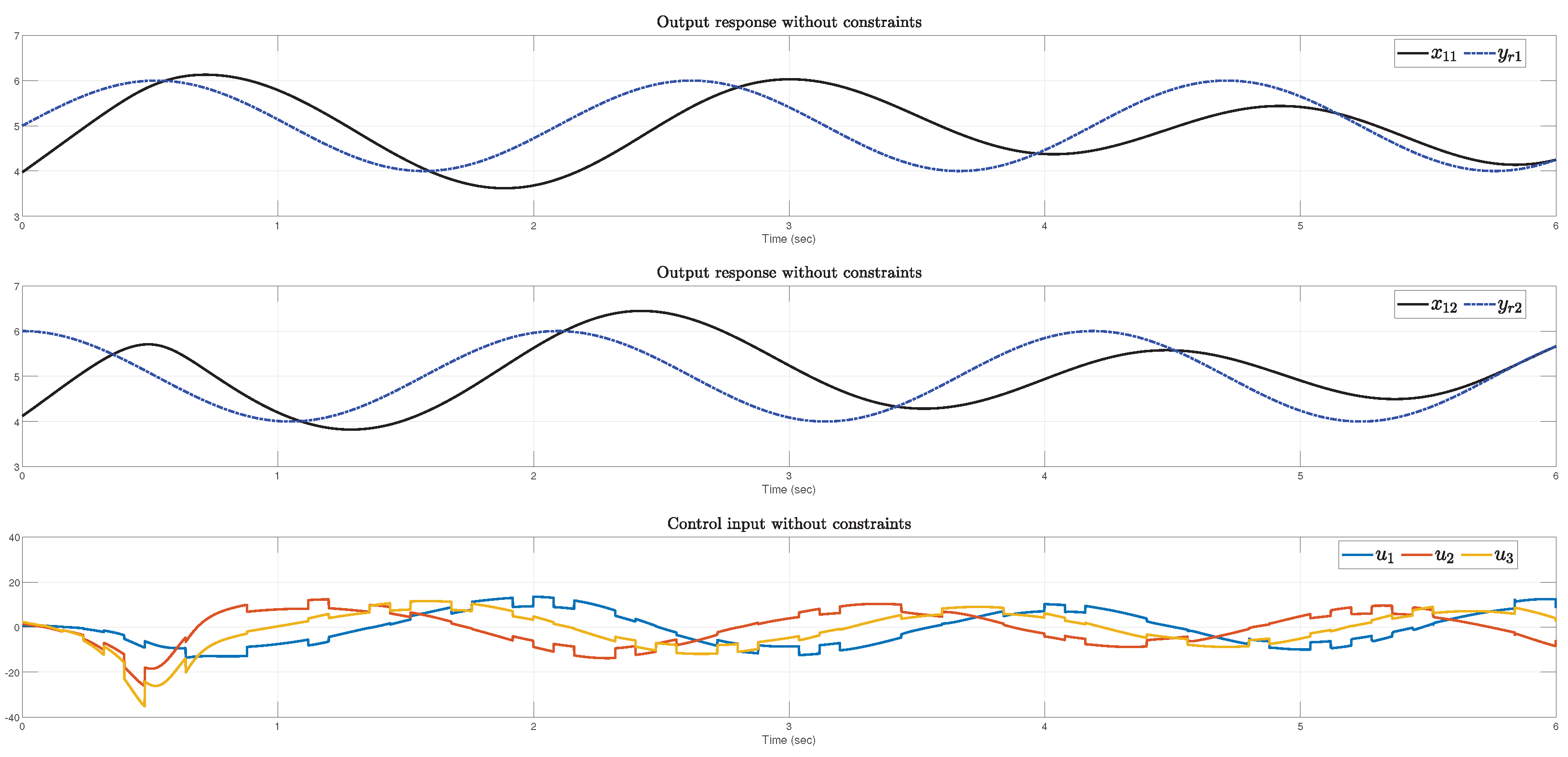
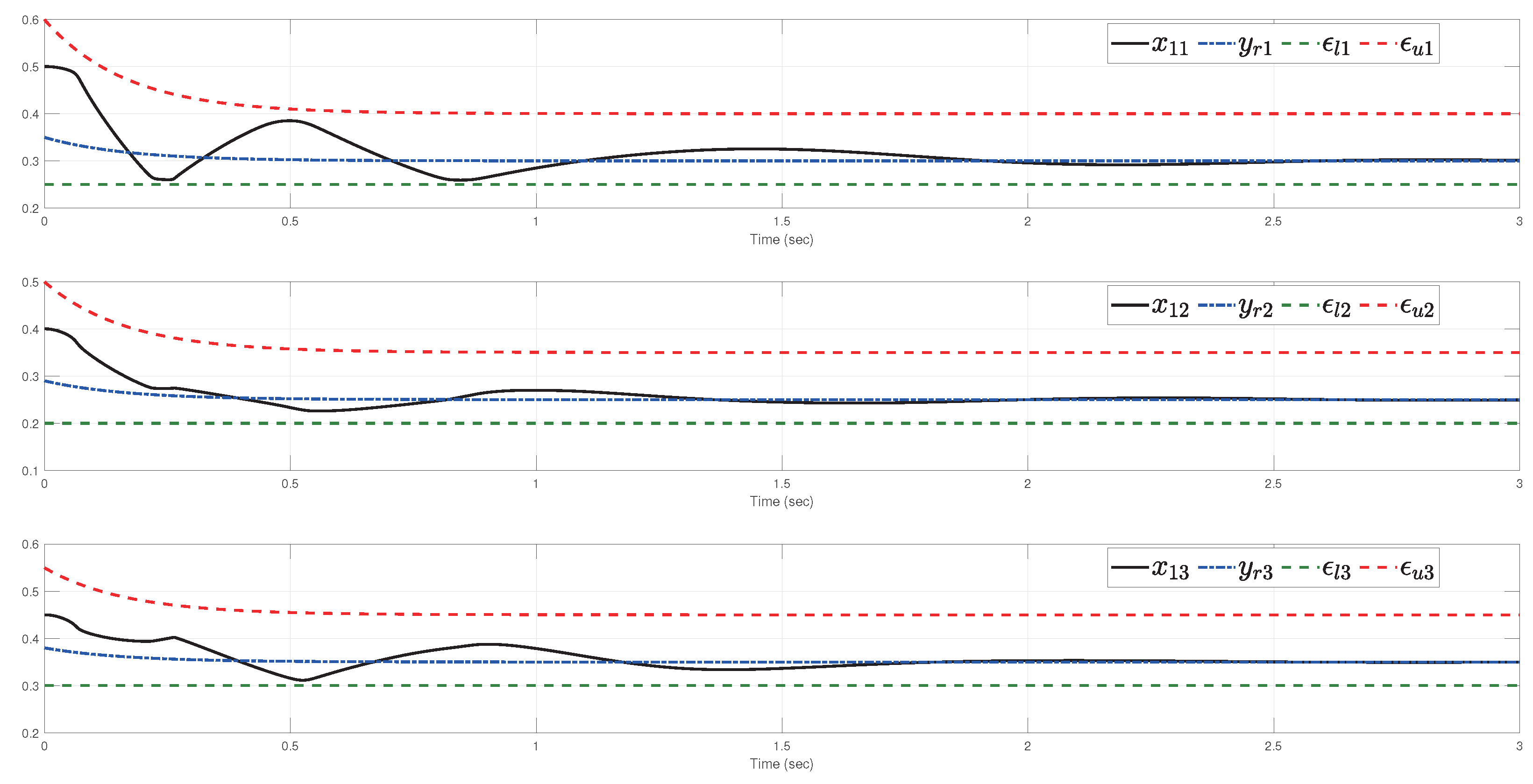
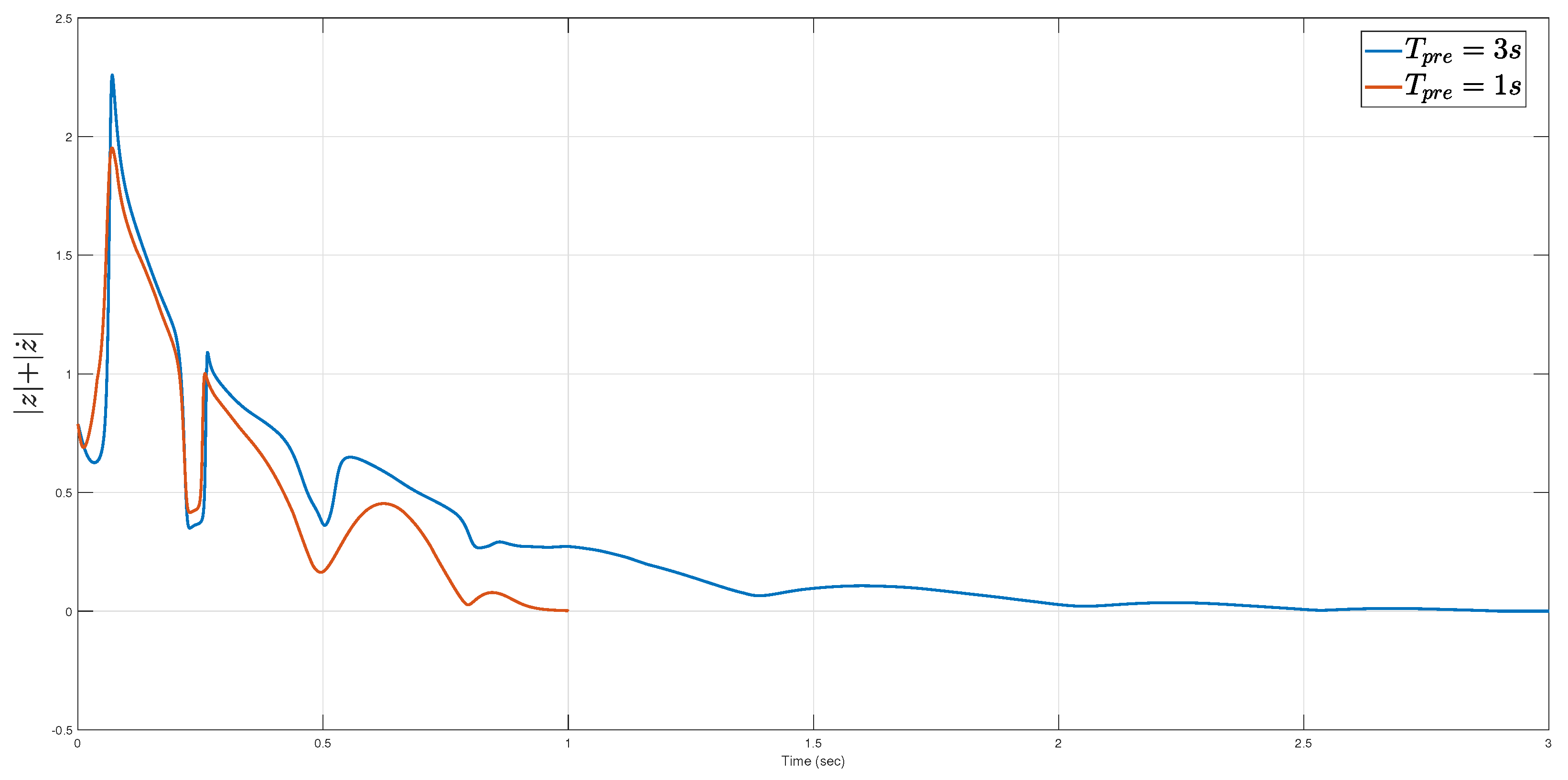
4. Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Ahn, C.K.; Guo, J.; Xiang, Z.R. Global output feedback sampled-data stabilization of a class of switched nonlinear systems in the p-normal form. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1075–1084. [Google Scholar] [CrossRef]
- Liberzon, D. Finite data-rate feedback stabilization of switched and hybrid linear systems. Automatica 2014, 50, 409–420. [Google Scholar] [CrossRef]
- Pavlichkov, S.S.; Dashkovskiy, S.N.; Pang, C.K. Uniform stabilization of nonlinear systems with arbitrary switchings and dynamic uncertainties. IEEE Trans. Autom. Control 2016, 62, 2207–2222. [Google Scholar] [CrossRef]
- Kong, L.H.; He, W.; Liu, Z.J.; Yu, X.B.; Silvestre, C. Adaptive tracking control with global performance for output-constrained MIMO nonlinear systems. IEEE Trans. Autom. Control 2022, 68, 3760–3767. [Google Scholar] [CrossRef]
- Liu, Y.C.; Zhu, Q.D. Adaptive neural network asymptotic control design for MIMO nonlinear systems based on event-triggered mechanism. Inf. Sci. 2022, 603, 91–105. [Google Scholar] [CrossRef]
- Xu, H.; Yu, D.; Sui, S.; Zhao, Y.P.; Chen, C.L.P.; Wang, Z. Nonsingular practical fixed-time adaptive output feedback control of MIMO nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7222–7234. [Google Scholar] [CrossRef]
- Ye, H.F.; Song, Y.D. Prescribed-time tracking control of MIMO nonlinear systems with nonvanishing uncertainties. IEEE Trans. Autom. Control 2022, 68, 3664–3671. [Google Scholar] [CrossRef]
- Shao, X.D.; Hu, Q.L.; Shi, Y.; Zhang, Y.M. Fault-tolerant control for full-state error constrained attitude tracking of uncertain spacecraft. Automatica 2023, 151, 110907. [Google Scholar] [CrossRef]
- Song, Y.D.; Huang, X.C.; Wen, C.Y. Tracking control for a class of unknown non-square MIMO nonaffine systems: A deep-rooted information based robust adaptive approach. IEEE Trans. Autom. Control 2015, 61, 3227–3233. [Google Scholar] [CrossRef]
- Xin, X.; Kaneda, M. Swing-up control for a 3-DOF gymnastic robot with passive first joint: Design and analysis. IEEE Trans. Robot. 2007, 23, 1277–1285. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity approach to high-order sliding mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Du, H.B.; Qian, C.J.; Yang, S.Z.; Li, S.H. Recursive design of finite-time convergent observers for a class of time-varying nonlinear systems. Automatica 2013, 49, 601–609. [Google Scholar] [CrossRef]
- Zhang, X.F.; Feng, G.; Sun, Y.H. Finite-time stabilization by state feedback control for a class of time-varying nonlinear systems. Automatica 2012, 48, 499–504. [Google Scholar] [CrossRef]
- Hong, Y.G.; Wang, J.K.; Cheng, D.Z. Adaptive finite-time control of nonlinear systems with parametric uncertainty. IEEE Trans. Autom. Control 2006, 51, 858–862. [Google Scholar] [CrossRef]
- Song, X.N.; Wu, C.L.; Song, S.; Stojanovic, V.; Tejado, I. Fuzzy wavelet neural adaptive finite-time self-triggered fault-tolerant control for a quadrotor unmanned aerial vehicle with scheduled performance. Eng. Appl. Artif. Intell. 2024, 131, 107832. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Finite-time and fixed-time stabilization: Implicit Lyapunov function approach. Automatica 2015, 51, 332–340. [Google Scholar] [CrossRef]
- Ning, B.D.; Han, Q.L.; Zuo, Z.Y.; Ding, L.; Lu, Q.; Ge, X.H. Fixed-time and prescribed-time consensus control of multi-agent systems and its applications: A survey of recent trends and methodologies. IEEE Trans. Ind. Inform. 2022, 19, 1121–1135. [Google Scholar] [CrossRef]
- Chen, C.C.; Sun, Z.Y. Fixed-time stabilisation for a class of high-order non-linear systems. IET Control Theory Appl. 2018, 12, 2578–2587. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Zhang, K.; Xie, X.P.; Stojanovic, V. ADP-based prescribed-time control for nonlinear time-varying delay systems with uncertain parameters. IEEE Trans. Autom. Sci. Eng. 2024, 22, 3086–3096. [Google Scholar] [CrossRef]
- Xie, H.X.; Jing, Y.W.; Dimirovski, G.M.; Chen, J.Q. Adaptive fuzzy prescribed-time tracking control for nonlinear systems with input saturation. ISA Trans. 2023, 143, 370–384. [Google Scholar] [CrossRef] [PubMed]
- Cui, Q.; Cao, H.W.; Wang, Y.J.; Song, Y.D. Prescribed-time tracking control of constrained Euler-Lagrange systems: An adaptive proportional-integral solution. Int. J. Robust Nonlinear Control 2022, 32, 9723–9741. [Google Scholar] [CrossRef]
- Li, J.J.; Xiang, X.B.; Dong, D.L.; Yang, S.L. Prescribed-time observer based trajectory tracking control of autonomous underwater vehicles with tracking error constraints. Ocean Eng. 2023, 274, 114018. [Google Scholar] [CrossRef]
- Gao, Y.; Tong, S.C.; Li, Y.M. Observer-based adaptive fuzzy output constrained control for MIMO nonlinear systems with unknown control directions. Fuzzy Sets Syst. 2016, 290, 79–99. [Google Scholar] [CrossRef]
- Zhang, T.P.; Liu, H.Q.; Xia, M.Z.; Yi, Y. Adaptive neural control of MIMO uncertain nonlinear systems with unmodeled dynamics and output constraint. Int. J. Adapt. Control Signal Process. 2018, 32, 1731–1747. [Google Scholar] [CrossRef]
- Tian, X.Y.; Li, Y.C.; Ma, R.C. Prescribed-time stabilization with time-varying output constraints for switched nonlinear systems. Int. J. Control Autom. Syst. 2023, 21, 1538–1546. [Google Scholar] [CrossRef]
- Ling, S.; Wang, H.Q.; Liu, P.X. Adaptive tracking control of high-order nonlinear systems under asymmetric output constraint. Automatica 2020, 122, 109281. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.D.; Chen, C.L.P.; Chen, L. Control of nonlinear systems under dynamic constraints: A unified barrier function-based approach. Automatica 2020, 119, 109102. [Google Scholar] [CrossRef]
- Tang, Z.L.; Ge, S.Z.S.; Tee, K.P.; He, W. Robust adaptive neural tracking control for a class of perturbed uncertain nonlinear systems with state constraints. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1618–1629. [Google Scholar] [CrossRef]
- Fan, B.; Yang, Q.M.; Tang, X.Y.; Sun, Y.X. Robust ADP design for continuous-time nonlinear systems with output constraints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2127–2138. [Google Scholar] [CrossRef]
- Song, X.N.; Sun, P.; Song, S.; Stojanovic, V. Saturated-threshold event-triggered adaptive global prescribed performance control for nonlinear Markov jumping systems and application to a chemical reactor model. Expert Syst. Appl. 2024, 249, 123490. [Google Scholar] [CrossRef]
- Song, Y.D.; Ye, H.F.; Lewis, F.L. Prescribed-time control and its latest developments. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4102–4116. [Google Scholar] [CrossRef]
- Song, Y.D.; Wang, Y.J.; Holloway, J.; Krstic, M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F.; Krstic, M. A dynamic high-gain design for prescribed-time regulation of nonlinear systems. Automatica 2020, 115, 108860. [Google Scholar] [CrossRef]
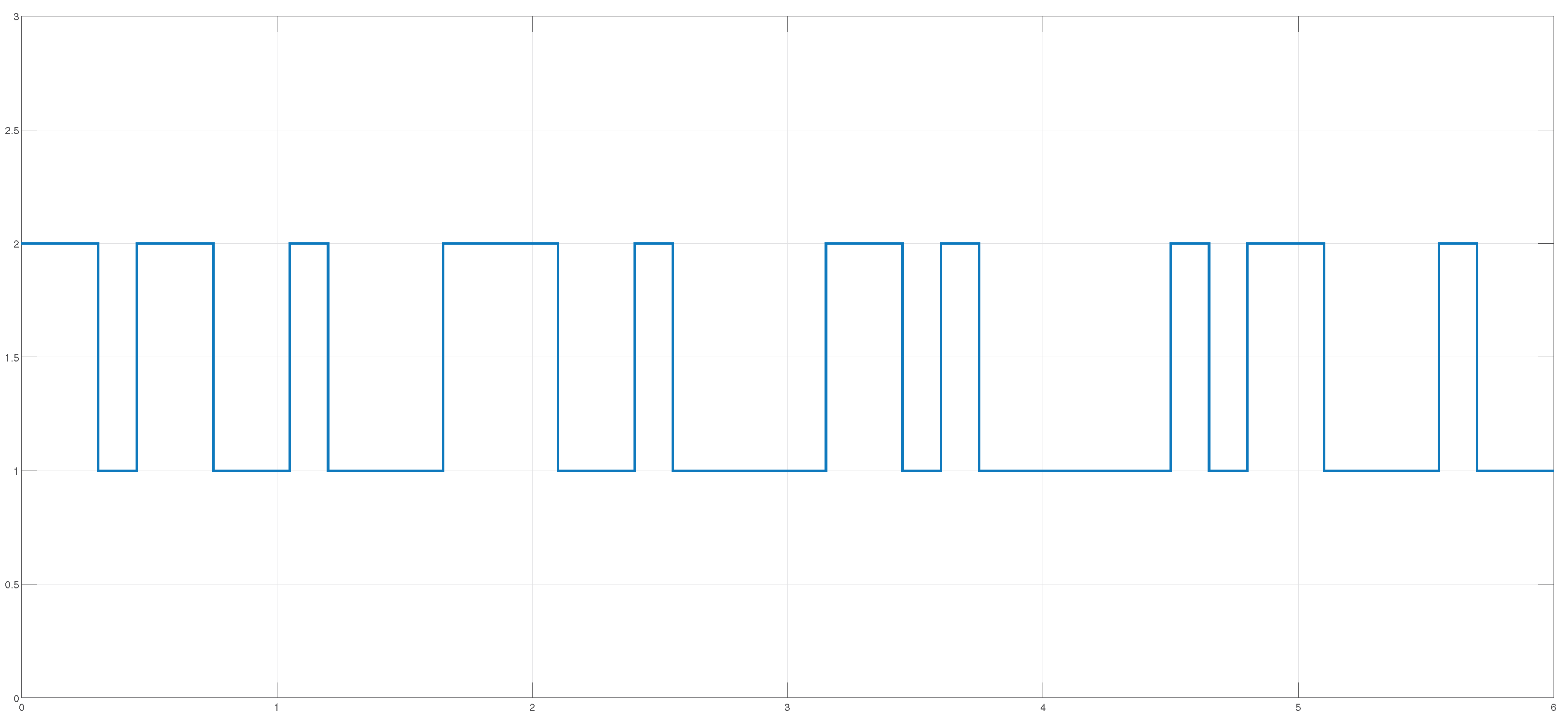

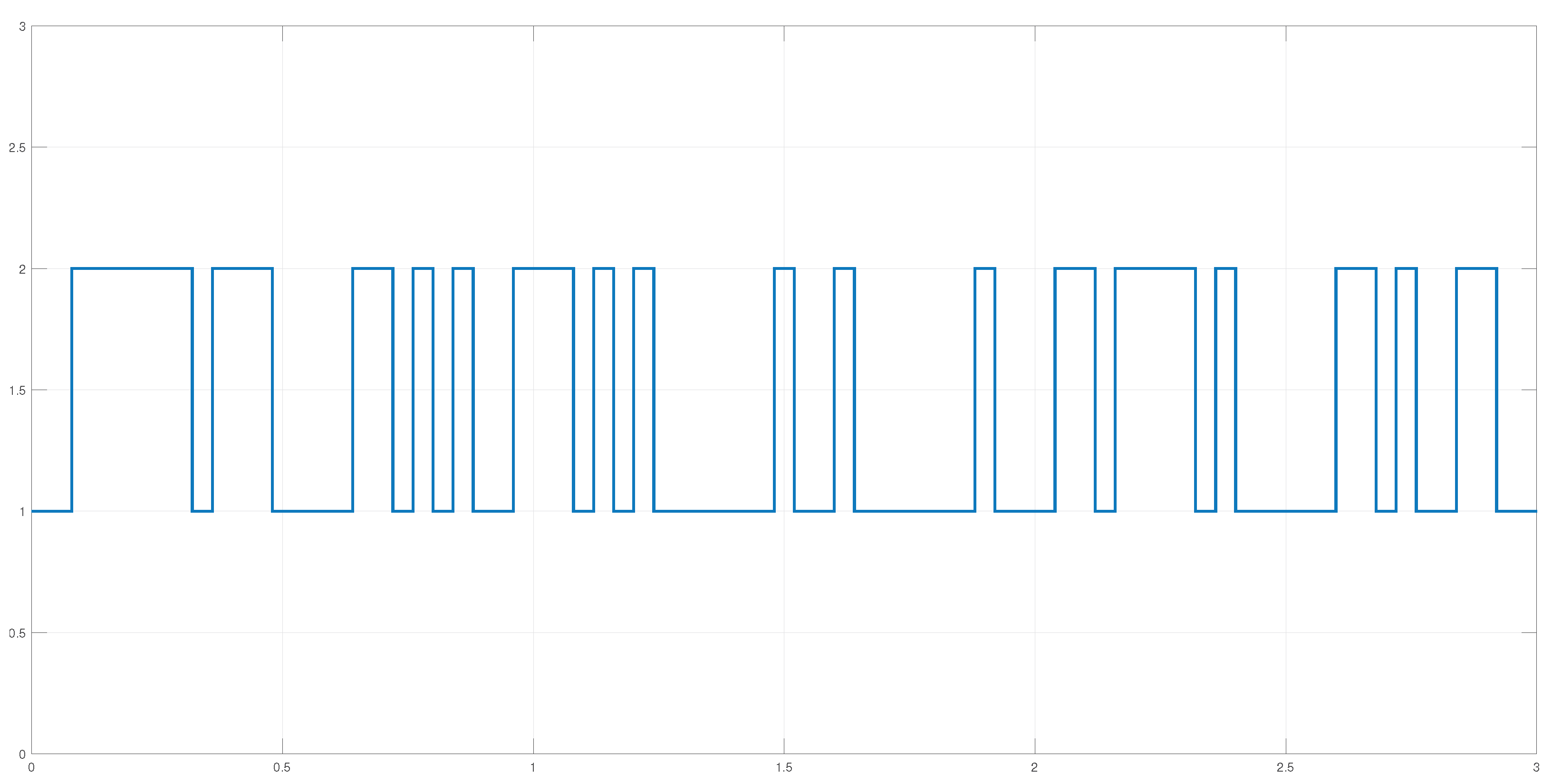


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, H.; Zhu, Q.; Jia, F. Zero-Error Prescribed-Time Tracking Control for Switched Non-Square MIMO Nonlinear Systems Subject to Asymmetric Time-Varying Output Constraints. Mathematics 2025, 13, 986. https://doi.org/10.3390/math13060986
Liu Y, Wang H, Zhu Q, Jia F. Zero-Error Prescribed-Time Tracking Control for Switched Non-Square MIMO Nonlinear Systems Subject to Asymmetric Time-Varying Output Constraints. Mathematics. 2025; 13(6):986. https://doi.org/10.3390/math13060986
Chicago/Turabian StyleLiu, Ying, Hui Wang, Quanxin Zhu, and Fujin Jia. 2025. "Zero-Error Prescribed-Time Tracking Control for Switched Non-Square MIMO Nonlinear Systems Subject to Asymmetric Time-Varying Output Constraints" Mathematics 13, no. 6: 986. https://doi.org/10.3390/math13060986
APA StyleLiu, Y., Wang, H., Zhu, Q., & Jia, F. (2025). Zero-Error Prescribed-Time Tracking Control for Switched Non-Square MIMO Nonlinear Systems Subject to Asymmetric Time-Varying Output Constraints. Mathematics, 13(6), 986. https://doi.org/10.3390/math13060986






