Abstract
Image encryption plays a critical role in ensuring the confidentiality and integrity of visual information, particularly in applications involving secure transmission and storage. While traditional cryptographic algorithms like AES are widely used, they may not fully exploit the properties of image data, such as high redundancy and spatial correlation. In recent years, chaotic systems have emerged as promising candidates for lightweight and secure encryption schemes, but comprehensive comparisons between different chaotic maps and standardized methods are still lacking. This study investigates the use of three classical chaotic systems—Henon, tent, and logistic maps—for image encryption, and evaluates their performance both visually and statistically. The research is motivated by the need to assess whether these well-known chaotic systems, when used with proper statistical sampling, can match or surpass conventional methods in terms of encryption robustness and complexity. We propose a key generation method based on chaotic iterations, statistically filtered for independence, and apply it to a one-time-pad-like encryption scheme. The encryption quality is validated over a dataset of 100 JPEG images of size , using multiple evaluation metrics, including MSE, PSNR, NPCR, EQ, and UACI. Results are benchmarked against the AES algorithm to ensure interpretability and reproducibility. Our findings reveal that while the AES algorithm remains the fastest and most uniform in histogram flattening, certain chaotic systems, such as the tent and logistic maps, offer comparable or superior results in visual encryption quality and pixel-level unpredictability. The analysis highlights that visual encryption performance does not always align with statistical metrics, underlining the importance of multi-faceted evaluation. These results contribute to the growing body of research in chaos-based image encryption and provide practical guidelines for selecting encryption schemes tailored to specific application requirements, such as efficiency, visual secrecy, or implementation simplicity.
Keywords:
image encryption; chaotic maps; statistical independence; security analysis; key generation; AES benchmark MSC:
37-11
1. Introduction
Chaos refers to a seemingly random and unpredictable behavior observed within a deterministic dynamical system, stemming from its high sensitivity to initial conditions and parameters. The exploration of chaos theory finds its roots in the examination of the three-body problem conducted by H. Poincaré in 1913 [1]. The exploration of chaotic systems has emerged as a crucial domain within nonlinear dynamics due to their intricate behaviors, posing challenges for prediction and control. These systems find diverse applications across various fields, including finance [2], machine learning [3], medicine [4], and many others [5,6,7,8,9,10].
In addition to chaotic systems, the recent literature has explored advanced image encryption techniques leveraging neural networks, DNA encoding, compressive sensing, and quantum cryptography. However, many such methods are computationally intensive or lack standardized evaluation benchmarks, motivating a systematic re-evaluation of simpler chaotic maps under rigorous statistical scrutiny.
In recent years, image encryption has evolved through the integration of various paradigms, including chaotic systems, optical transformations, neural networks, and quantum techniques. Notable proposals involve the use of fractional-order Hopfield neural networks for medical data protection [11], dynamic vector-level operations with 2D-enhanced logistic modular maps [12], and robust polynomial hyperchaotic maps combined with pixel fusion [13]. While innovative, these methods often come with trade-offs in terms of computational cost, interpretability, and robustness under statistical attacks.
Storing image data generally requires more space than text due to its inherent redundancy and the strong correlation between adjacent pixels, though this redundancy can often be reduced through compression techniques. Traditional encryption methods might not handle these characteristics effectively, potentially leaving patterns or structures that could be exploited. However, chaos theory offers a new solution. Chaotic systems, which are highly sensitive to initial conditions, produce vastly different trajectories even with minor differences at . Long-term prediction without exact initial conditions is impossible. They also exhibit high ergodic-like behaviours, and pseudo-randomness, essential for image encryption [14].
Chaos-based image encryption has proven to be a resilient and flexible approach for safeguarding digital images. A recent review paper [1] delves into the intricacies of chaos-based encryption, encompassing both symmetric and asymmetric schemes. A comprehensive evaluation of existing encryption algorithms is provided, along with an exploration of the integration of emerging technologies such as neural networks or DNA encoding [15,16,17,18,19].
However, many of these approaches are not evaluated using rigorous statistical criteria. Weak key diffusion, dependency between key elements, or poor resistance to noise can reduce practical robustness. Moreover, as shown in cryptanalytic works such as [20], schemes based only on chaotic or biological encoding are often susceptible to differential or chosen-plaintext attacks if their key generation mechanisms are not sufficiently random or independent.
Building on such analyses, recent cryptanalytic studies have targeted hybrid encryption schemes. For example, recent works like [21] investigate a scheme based on Feistel networks and dynamic DNA encoding, revealing vulnerabilities related to predictable diffusion and weak key generation. Their findings reinforce the importance of statistically validated designs and motivate our inclusion of independence testing and comparative benchmarking in the proposed method.
Despite its advantages, chaos-based encryption can face challenges, such as resistance to cryptanalysis (patterns can emerge under specific conditions/set of parameters) and the processing of encrypted images. Chaos-based encryption algorithms often involve complex mathematical operations, such as iterating chaotic maps, which can be computationally intensive. This can lead to slower encryption and decryption processes, particularly for high-resolution images. While the sensitivity to initial conditions is a strength in chaos-based systems, it can also be a challenge. Small errors in parameter settings during decryption can lead to incorrect image reconstruction. These challenges serve as catalysts for further research aimed at addressing current limitations and ensuring the continued viability of this promising technique. By tackling these obstacles and exploring emerging opportunities, we can safeguard the integrity and confidentiality of sensitive information in an increasingly digital world [1].
Recent cryptanalysis efforts [20] have revealed weaknesses in many proposed image encryption schemes, particularly those that rely solely on chaotic or DNA-based encoding without rigorous statistical validation. These findings highlight the need for secure designs backed by empirical testing and motivate our use of statistical independence analysis and multiple encryption quality metrics to ensure practical robustness.
To address these limitations, our work proposes a systematic and statistically grounded evaluation of three classical chaotic maps—Henon, tent, and logistic—used as key generators in an image encryption framework. By filtering chaotic sequences through a statistical independence test before use in encryption, we aim to improve the unpredictability and quality of the resulting cipher.
Furthermore, our study benchmarks encryption quality using both perceptual (visual) and quantitative metrics such as NPCR, UACI, MSE, and entropy. The results are compared against AES (Advanced Encryption Standard), a well-established symmetric encryption standard, to contextualize the performance and highlight the trade-offs between complexity and security.
The novelty of our contribution lies in the rigorous statistical evaluation of classical chaotic systems in practical encryption scenarios, a domain often overshadowed by overly complex or untested schemes.
This paper aims to systematically analyze the performance of several chaotic systems for image encryption, both visually and statistically, and to assess their practicality by comparing them with a widely adopted standard algorithm, AES. A structured comparison is carried out between well-established industry-standard systems and lesser-known chaotic maps.
- Section 2 establishes the analytical framework by describing the dynamical systems and the statistical independence test used to assess and generate pseudo-random numbers from the chaotic maps [22,23,24,25,26,27,28]. These numbers are then used to construct the encryption key for the algorithm.
- Section 3 introduces the proposed image encryption scheme in detail, including the preprocessing steps, chaotic key generation, encryption and decryption procedures, and implementation specifics. A flowchart is provided to illustrate the full process.
- Section 4 builds on this foundation by introducing new insights into image encryption and comparing the results for each chaotic system using the same set of metrics. Additionally, the results of the chaos-based image encryption are compared to those obtained using AES (Advanced Encryption Standard), serving as a reference system for computational efficiency and data protection.
- Section 5 summarizes the main findings and explores potential directions for further research.
In contrast to recent proposals involving complex architectures or novel chaotic maps, our work revisits classical chaotic systems (Henon, tent, logistic) through a statistically robust evaluation framework. The key novelty lies in the use of independence-verified chaotic sequences for encryption and in the comparative benchmarking against AES on a large, labeled image dataset.
Main contributions of this work:
- We perform a structured comparative analysis of three classical chaotic systems (Henon, tent, and logistic maps) applied to image encryption.
- We generate encryption keys based on chaotic sequences filtered through a statistical independence test to enhance unpredictability.
- We benchmark the performance of these systems both visually and quantitatively using metrics such as MSE, PSNR, NPCR, EQ, and UACI.
- We provide a side-by-side comparison with the AES standard to contextualize the results within established cryptographic practices.
- We propose practical insights regarding the trade-offs between statistical encryption strength and perceptual (visual) encryption quality.
2. Theoretical Background
This section provides the theoretical foundation for our analysis of chaos-based image encryption. We begin by introducing the chaotic systems used to generate pseudo-random numbers, which are crucial for constructing encryption keys. These systems are then discussed in detail, along with their mathematical descriptions. Following this, we describe the methodology employed to ensure the statistical independence of the generated pseudo-random numbers, which is essential for effective encryption. Finally, we outline the metrics used to evaluate the performance of the encryption algorithms.
2.1. Chaotic Systems
Let us start the analysis by detailing out the systems used to generate pseudo-random numbers which were subsequently used to generate the key for image encryption. The algorithm used for image encryption will be explained in detail in Section 4.
The selection of the Henon map, the logistic map, and the asymmetric tent map for this study was driven by their extensive prior analysis and well-established characteristics in the literature [26,27]. Each of these three topologies of chaotic systems has been thoroughly investigated for their pseudo-random properties and applicability in cryptographic applications. These systems were chosen for their proven performance and their detailed analysis in earlier studies, ensuring a solid ground for their application in the current encryption framework. Their well-documented behavior and established theoretical underpinnings make them reliable choices for generating encryption keys in image encryption applications.
The first chaotic system used is the Henon map. The equations that describe it are detailed out in (1).
where and ensure the chaotic behaviour of the system.
An alternative to the Henon map is the logistic map which is another discrete dynamic system depicted by (2).
where parameter r between 3.57 and 4 ensures chaotic behaviour [29].
The third discrete chaotic system used is represented by the asymmetric tent map (3), another simple, yet powerful, tool [30].
where p is a number between 0 and 1.
The common aspect about the above systems is that they can be used to iterate different chaotic trajectories starting from a set of initial conditions. At the end of the iteration, one is left with a long array of real numbers of any length desired. These numbers will be the basis for the secret keys used for image encryption (and decryption). Furthermore, the numbers used for the key generations are not selected from consecutive states of the solution space, but a further sampling is performed in order to ensure statistical independence of the data and decrease the chance that the cipher is broken, in case parts of the key and/or the clear message are captured. It is thus very relevant to briefly describe the algorithm and procedure used to sample the solution space and collect the data needed for the experimental analysis.
2.2. Statistical Independence
The approach summarized below determines the statistical independence of two continuous random variables (X and Y) by employing a chi-square test on transformed data (U and V). It eliminates the need for visual inspection [22,23,26]. X and Y are selected at different moments in time from the trajectories/iterations of the chaotic systems.
The following steps are involved:
- Step 1—Data Transformation: X and Y are transformed into U and V, ensuring they follow a standard normal distribution.
- Step 2—Chi-Square Test: the chi-square test is applied to U and V to assess their conformity with a specific uncorrelated, jointly normal probability law (4). This conformity is evaluated against the standard Gaussian bivariate probability law represented by the following equation:
- Step 3—Decision-Making: if U and V comply with the standard Gaussian bivariate probability law (Equation (4)), then X and Y are considered statistically independent. Conversely, a deviation from this distribution suggests dependence between X and Y.
As a final remark before proceeding and discussing the experimental results, apart from encrypting images by making use of the different chaotic maps described above, we also considered a standard algorithm as a baseline, i.e., the AES [31]. All the results and metrics used will be shown as a comparison between the chaotic systems and the AES standard image encryption.
2.3. Metrics Used to Evaluate the Encryption Results
Several metrics were monitored for the different encryption algorithms, including the following:
- The execution time was the difference between the start and end time of the simulation, which included the key generation and encrypting/decrypting of the image. The computer used contained an Intel i5 processor (8th Gen) and 8 GB of RAM memory.
- MSE (mean-squared error) is the mean of the squared differences between the original image and the encrypted image. The squared difference is calculated for each pixel and color plane and the values are averaged over image size and color planes. The bigger the MSE, the harder it is to understand/decrypt the encrypted image.
- PSNR (peak signal-to-noise ratio) is calculated based on the MSE (5).If the MSE needs to be large to ensure a good encryption, this means that a small PSNR value is desired.
- EQ (encryption quality) is calculated based on (6). The encryption quality of an image, is calculated by comparing the pixels of the encrypted image with those of the original image. It is considered better when the difference between the pixel values of the two images is larger. The larger the EQ parameter value, the higher the encryption security.The encryption quality can be determined as follows: and represent the values of the pixel at row i and column j, in the encrypted image and the original image, respectively, each image having dimensions with L pixel levels. and are defined as the number of occurrences of each level L in the original image and the encrypted image, respectively. EQ represents the average number of changes for each level and considering all color planes of the image.
- NPCR (number of pixel (bit) change rate) calculates the percentage of bits that differ between two images with respect to the total number of bits in the images. It is desirable that the NPCR between the original and the encrypted image is as high as possible to 50%. Note that the acronym NPCR was preserved to maintain consistency with the well-known parameter from image processing, but in fact it could have been referred to as NBCR, being a bit by bit comparison.To calculate NPCR at the bit level, two images are considered—one corresponding to the original image and the other to the encrypted image, denoted as X and Y, respectively. Each pixel value is converted to its binary representation, and the bit strings of the original and encrypted images are compared. A bipolar matrix D, with the same dimensions as X and Y, is used to calculate the difference. The value of is determined by comparing and . If the bit strings of and differ, then ; otherwise, .The formula for calculating NPCR is as follows:where:The larger the NPCR value, the more significant the differences between the original and encrypted images at the bit level.
- UACI (unified average changing intensity) measures the average change in pixel intensity between the two images (8) and the higher it is, the better it is from an encryption point of view.
3. Proposed Image Encryption Scheme
This section presents a detailed description of the proposed image encryption method based on classical chaotic maps. The process consists of six main stages, as illustrated in the flowchart in Figure 1, and is outlined below, together with the underlying design rationale and implementation details.
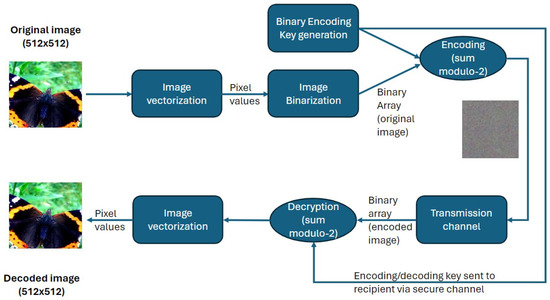
Figure 1.
Flowchart of the proposed image encryption scheme.
- Step 1: Image preprocessing—vectorization and binarization
The input RGB image is converted into a binary sequence. Each pixel is represented using 8 bits per channel, resulting in a total of = 6,291,456 bits for a standard color image. This binary representation is used as the plaintext input for the encryption operation.
- Step 2: Binary encoding key generation
One of three chaotic systems—Henon, tent, or logistic map—is selected as the core generator for the encryption key. The maps are initialized with known parameters and initial conditions, ensuring chaotic behavior (discussed in Section 2). The rationale for using chaotic systems lies in their high sensitivity to initial conditions and ergodicity, which are essential for unpredictability and key variability.
The selected map is iterated to produce a sequence of real numbers. To avoid statistical dependence between consecutive values, the sequence is sampled at regular intervals. The appropriate sampling distance is determined based on statistical independence criteria, as outlined in Section 2.2. This step enhances the randomness and security of the resulting encryption key.
The sampled chaotic values are binarized using a thresholding rule. For the tent map, the threshold is chosen as the map parameter p; for other maps, the mean value of the range is used. The output is a binary key of the same length as the binary image sequence. This key is used in the encryption stage.
- Step 3: XOR-based encryption
Encryption is performed using a bitwise XOR operation between the binary image and the binary key. This approach is conceptually similar to the one-time pad method, where the security relies entirely on the randomness and uniqueness of the key. The XOR operation ensures low computational cost and full reversibility.
- Step 4: Image reconstruction/decryption
We assume a noiseless transmission channel, where both the encrypted image and the chaotic key parameters are received without distortion or error. Under this assumption, decryption is guaranteed to reconstruct the original image exactly, provided that the chaotic map and sampling parameters are synchronized at the receiver.
Decryption is achieved by applying the same XOR operation using the identical chaotic key, thus recovering the original image without loss, assuming correct parameter synchronization.
- Hardware and Software Configuration
All simulations and image encryption experiments were conducted on a standard laptop equipped with an Intel Core i5-8265U CPU (1.60 GHz, 8th Gen) and 8 GB of DDR4 RAM, running Windows 10 (64-bit). The implementation was carried out using MATLAB R2021a, with additional Python 3.9 scripts for image preprocessing and encryption result visualization. No GPU acceleration was used during testing, in order to reflect performance under standard consumer hardware.
- Dataset Description
To ensure generality and allow for statistical comparisons, we used a benchmark dataset of 100 RGB images, each of size pixels. The images were selected from publicly available Kaggle datasets [32], spanning five object classes: albatross, airliner, admiral butterfly, African elephant, and American lobster. The dataset was not augmented or compressed prior to encryption. All experiments were performed using the full-resolution versions of the images to preserve structural complexity and pixel-level entropy. The original images were encrypted without performing any further dimensionality and redundancy reduction, even though that would have been possible.
- Implementation notes and key synchronization
For all experiments, the encryption keys were generated using the methodology described above, with sampling distances chosen based on prior statistical independence studies [22,23,24]. This ensured that the resulting binary sequences used for encryption were pseudo-random and uncorrelated.
As shown in the flowchart (Figure 1), the binary key was applied directly to the image bitstream using XOR. The decryption process simply repeated the same operation with the same key, resulting in perfect recovery of the original image, assuming identical initial conditions and parameters on both ends.
4. Experimental Results and Encryption Performance Analysis
This section evaluates the performance of various chaotic systems (Henon map, tent map, logistic map) and the AES algorithm in the context of image encryption. It covers the following aspects:
- Encryption scheme: describes the process of encrypting an image using different chaotic systems and AES. This includes converting pixel values into binary arrays and applying encryption keys.
- Visual analysis: provides visual comparisons of the original, encrypted, and decrypted images for each encryption method, highlighting their effectiveness and any observable weaknesses.
- Histograms: analyzes the histograms of the original and encrypted images to assess how well each encryption method disperses pixel value distributions.
- Quantitative metrics: evaluates the encryption methods using metrics such as execution time, mean-squared error (MSE), peak signal-to-noise ratio (PSNR), encryption quality (EQ), number of pixel change rate (NPCR), and unified average changing intensity (UACI) to determine the overall effectiveness of each encryption technique.
To strengthen the security evaluation of the proposed scheme, we included several standard criteria used in the image encryption literature. These include visual irreversibility of the encrypted image, entropy and correlation analysis, NPCR and UACI for plaintext sensitivity, and runtime performance. Each of these aspects confirms the effectiveness of the proposed method from both statistical and practical perspectives.
The encryption procedure is illustrated below for the first chaotic system analyzed, Henon map. Figure 2 shows the original image on the left, the encrypted image in the middle, and the decrypted image on the right side. As expected, the decrypted and the original image are identical because no information should be lost if the key is known by the encrypted image recipient. It is easy to notice that the encrypted image hides the information contained in the original image quite well. At the end of this section, we will include a comparison between the different chaotic systems/algorithms based on quantitative measures, but for now, we will discuss only the qualitative results.
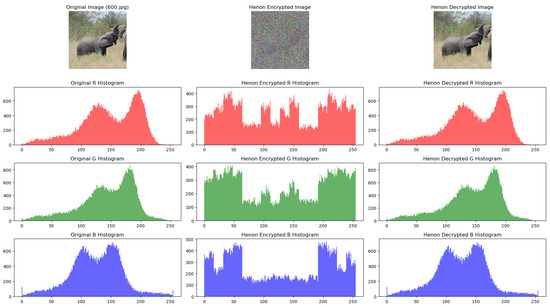
Figure 2.
Original, encrypted, and decrypted image using the Henon map.
It is useful to also check the histograms of the original and the encrypted image with the different algorithms and correlate them with the visual results of the encryption. In Figure 2, it can be noticed that through encryption with the Henon map, the R, G, and B histograms become more uniform compared to the original distribution, which is desirable from a cryptography point of view. Nevertheless, the uniformity of the histograms is not perfect, and other chaotic systems can be better from an encryption perspective, as will be noticed in the following results.
There is also a dependency of the encrypted image. Figure 3 shows another image which is encrypted with the same procedure and making use of the Henon map. The visual result obtained in this case is not as good as in Figure 2. A potential workaround would be to apply the Henon map encryption multiple times and the visual aspect of the image will become less similar to the original. Applying the Henon map multiple times is different from applying an equivalent Henon map with a specific set of parameters, due to the higher-order terms which appear in the equations after several Henon applications/iterations.
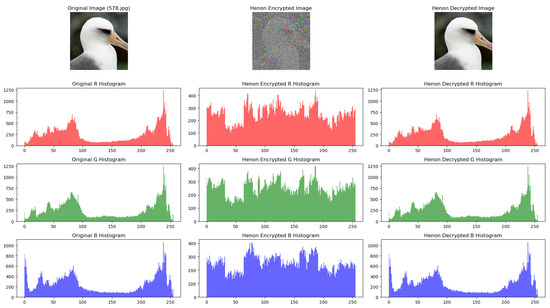
Figure 3.
Original, encrypted, and decrypted image using the Henon map.
The next system analyzed was the tent map. The visual results of the encryption (Figure 4) are better compared to the Henon map, because the encrypted image does not resemble the original image.
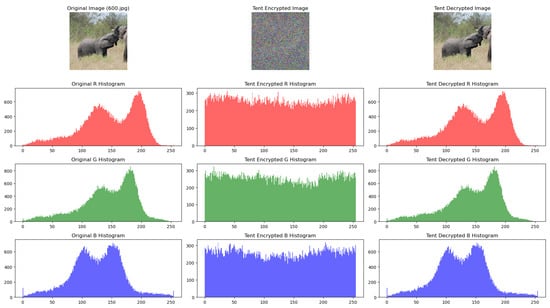
Figure 4.
Original, encrypted, and decrypted image using the tent map.
The third chaotic system included in the comparison was the logistic map. The results obtained after encryption are shown in Figure 5.
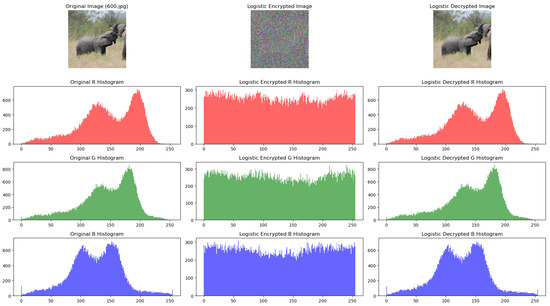
Figure 5.
Original, encrypted, and decrypted image using the logistic map.
AES is a state-of-the-art system and was used as a baseline in comparison with the above chaos-based systems. The results for the image encryption based on AES are shown in Figure 6. The “most” uniform histograms are obtained for AES and the tent map, and the logistic map is not far behind. The “worst” from this point of view is the one based on the Henon map, and this was also noticeable in the visual quality of the encrypted image.
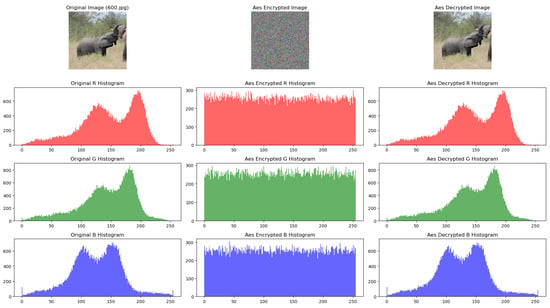
Figure 6.
Original, encrypted and decrypted image using AES.
It is useful to compare the quality of the encryption in the different algorithms/chaotic systems using the metrics introduced in Section 2. The results are presented in Table 1 and Table 2. It may be worthwhile to visualize the results in Table 1 and Table 2 in form of box plots for the analyzed parameters.

Table 1.
Encryption metrics summary (Part 1).

Table 2.
Encryption metrics summary (Part 2).
As anticipated, the AES algorithm demonstrates the best performance across metrics; however, the primary aim of this paper is to evaluate chaotic systems in image encryption, necessitating an analysis of the performance across four chaotic maps to identify those producing satisfactory results.
From an efficiency perspective, the logistic map algorithm stands out, with the shortest execution time among the chaotic systems tested.
An inverse relationship between PSNR and MSE is observed, which is typical in image processing metrics. PSNR indicates the similarity between the original and encrypted images. Lower PSNR values are preferred in encryption since they signify a greater deviation from the original image, thereby enhancing data security. Conversely, higher MSE values indicate more substantial distortion. Although PSNR and MSE offer quantifiable insights (Figure 7 and Figure 8), they do not always correlate directly with visual encryption effectiveness. For instance, although the Henon algorithm exhibits the lowest PSNR, visually, other algorithms yield more satisfactory encryption outcomes.
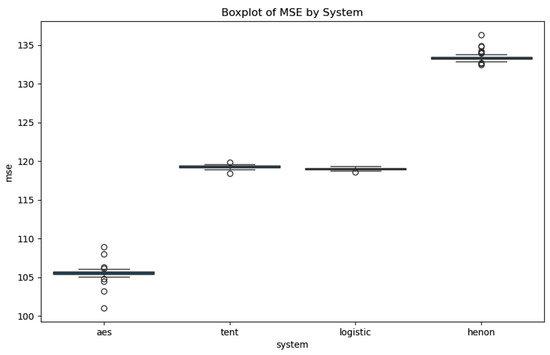
Figure 7.
The MSE variation across the different systems.
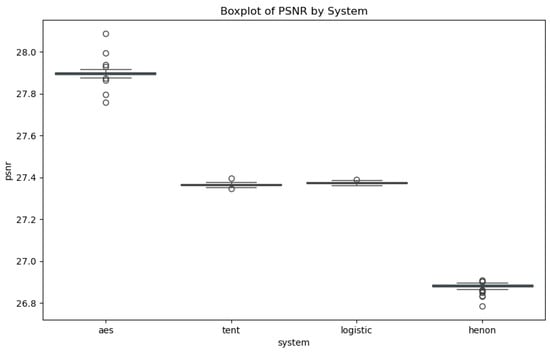
Figure 8.
The PSNR variation across the different systems.
NPCR (number of pixels–bit change rate) is another critical measure of encryption efficacy, evaluating the proportion of pixel alterations between the original and encrypted images. A high NPCR value indicates extensive pixel–bit changes, which is beneficial for robust encryption. Despite this, a high NPCR alone does not guarantee satisfactory visual encryption results. For example, both Henon and tent algorithms achieve NPCR values near 100%, but the tent algorithm produces a significantly better visual result, rendering the encrypted image almost unrecognizable (Figure 9).
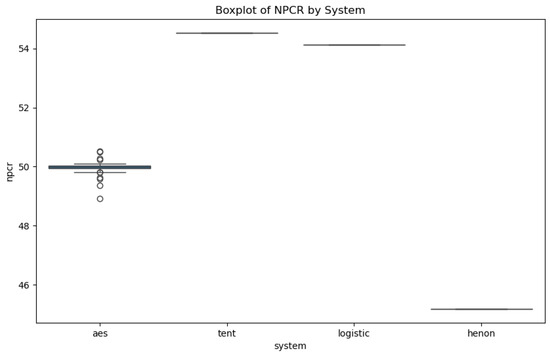
Figure 9.
The NPCR variation across the different systems.
UACI (unified average changing intensity) measures the average intensity variation, which is desirable for confounding potential adversaries. Although the Henon map performs best in terms of UACI (Figure 10), it does not consistently ensure an effective visual result, as its encrypted images may remain partially interpretable.
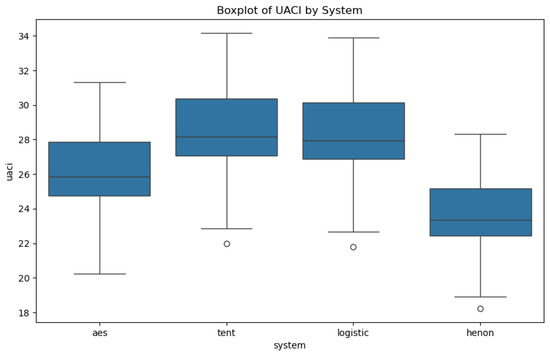
Figure 10.
The UACI variation across the different systems.
The EQ (encryption quality) metric assesses how thoroughly pixel values differ between the original and encrypted images, with higher EQ values signifying stronger encryption (Figure 11). In this context, the tent algorithm achieves the highest EQ value, reflecting an almost random, highly secure encrypted image that is effectively indecipherable.
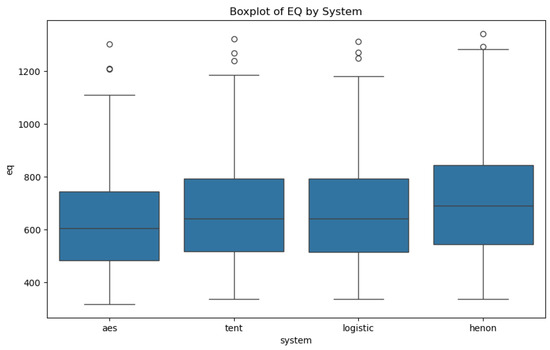
Figure 11.
The EQ variation across the different systems.
The metrics analyzed provide valuable insights into the robustness of encryption algorithms. Generally, favorable values across these parameters reflect effective encryption with high data protection. Visual evaluation, however, emphasizes the encrypted image’s perceptual quality. Notably, an algorithm that excels in security metrics may not always yield visually optimal results. For example, the Henon algorithm scores well across mean, MSE, PSNR, NPCR, and UACI metrics, suggesting strong data protection, yet visually, other algorithms outperform it.
Striking a balance between data protection and visual encryption quality is crucial. The tent algorithm’s parameters are competitive with Henon’s while providing superior visual outcomes. In contrast, the logistic map offers lower execution time (Figure 12), enhancing both efficiency and security. Each algorithm presents distinct advantages and limitations, suggesting that algorithm selection should be guided by the specific requirements of the intended application.
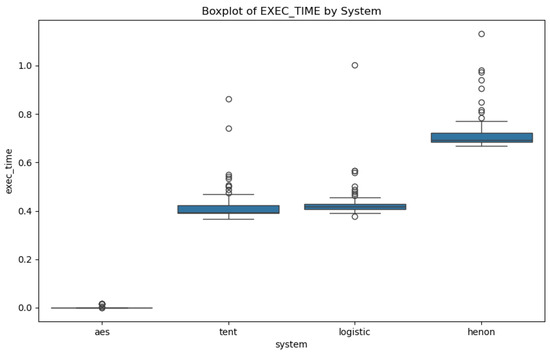
Figure 12.
The execution time variation across the different systems.
5. Conclusions
This paper addressed the need for a systematic and reproducible evaluation of classical chaotic maps used in image encryption, while many recent studies propose novel chaotic or hyperchaotic encryption schemes, relatively few conduct comparative analyses based on statistical independence, standardized datasets, and baseline cryptographic benchmarks. Our work aims to fill this gap by exploring how classical maps such as Henon, tent, and logistic perform under a unified evaluation protocol.
The experiments conducted revealed that there is not always a direct correlation between quantitative performance metrics (such as MSE, PSNR) and the visual strength of encryption. This highlights the importance of applying multi-dimensional evaluation criteria when selecting or designing encryption algorithms.
Key findings of this study include the following:
- The tent and logistic maps achieved strong encryption quality and pixel randomness, often outperforming Henon in visual encryption clarity and NPCR/UACI scores.
- The AES algorithm remained the most efficient in terms of execution time and histogram uniformity, validating its role as a performance benchmark.
- Classical chaotic maps can produce satisfactory results when used with statistically independent sampling and binary key derivation.
These results support the idea that simple chaotic systems, when properly sampled and evaluated, can offer viable alternatives to traditional encryption schemes in certain contexts, particularly in lightweight or resource-constrained applications.
This comparative analysis focuses primarily on statistical and visual performance metrics. In future work, we aim to extend the evaluation to include complete security profiling of chaotic encryption schemes, including key space estimation, key sensitivity analysis, correlation analysis, and entropy measurement. These additions will provide a more comprehensive understanding of cryptographic resilience in real-world deployment.
Future research directions could also explore the following:
- The integration of hyperchaotic systems and hybrid encryption structures;
- Robustness testing under noise, compression, and partial image loss;
- Energy-efficient implementations for embedded or real-time systems;
- Applying machine learning models to optimize chaotic parameter tuning dynamically.
Author Contributions
Methodology, A.D.; software, A.D.; formal analysis, A.D.; investigation, A.D.; writing—original draft, A.D.; writing—review and editing, A.D. and M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by UEFISCDI and the National University of Science and Technology Politehnica Bucharest through project PN-IV-P7-7.1-PTE-2024-0505.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, B.; Liu, L. Chaos-Based Image Encryption: Review, Application, and Challenges. Mathematics 2023, 11, 2585. [Google Scholar] [CrossRef]
- Tusset, A.M.; Fuziki, M.E.K.; Balthazar, J.M.; Andrade, D.I.; Lenzi, G.G. Dynamic Analysis and Control of a Financial System with Chaotic Behavior Including Fractional Order. Fractal Fract. 2023, 7, 535. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Zhu, Z.; Zhao, L.; Wang, H.; Song, C.; Chen, Y.; Zhao, Q.; Yang, J.; Pei, Y. A Comprehensive Review on Synergy of Multi-Modal Data and AI Technologies in Medical Diagnosis. Bioengineering 2024, 11, 219. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-F.; Lin, Y.-X.; Chang, S.-H. Medical Image Encryption Using Chaotic Mechanisms: A Study. Bioengineering 2025, 12, 734. [Google Scholar] [CrossRef]
- Hou, Y.-Y. Synchronization of Chaotic Systems and Its Application in Security Terminal Sensing Node of Internet of Things. Micromachines 2022, 13, 1993. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, Y.; Munir, A. Image Encryption Algorithms: A Survey of Design and Evaluation Metrics. J. Cybersecur. Priv. 2024, 4, 126–152. [Google Scholar] [CrossRef]
- Lawnik, M.; Moysis, L.; Volos, C. Chaos-Based Cryptography: Text Encryption Using Image Algorithms. Electronics 2022, 11, 3156. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Ramadoss, J.; Abd-El-Atty, B.; Khalifa, H.S.; Nazarimehr, F. A Novel Chaos-Based Cryptography Algorithm and Its Performance Analysis. Mathematics 2022, 10, 2434. [Google Scholar] [CrossRef]
- Hamida Alrekaby, S.N.; Khodher, M.A.A.; Adday, L.K.; Aljuaidi, R. Secure Image Transmission Using Multilevel Chaotic Encryption and Video Steganography. Algorithms 2025, 18, 406. [Google Scholar] [CrossRef]
- Zolfaghari, B.; Koshiba, T. Chaotic Image Encryption: State-of-the-Art, Ecosystem, and Future Roadmap. Appl. Syst. Innov. 2022, 5, 57. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, K.; Zhang, J.; Zhao, X.; Chen, Y.; Cai, B.; Zhu, Z.; Wen, H.; Ye, C. Integrating Fractional-Order Hopfield Neural Network with Differentiated Encryption: Achieving High-Performance Privacy Protection for Medical Images. Fractal Fract. 2025, 9, 426. [Google Scholar] [CrossRef]
- Li, H.; Yu, S.; Feng, W.; Chen, Y.; Zhang, J.; Qin, Z.; Zhu, Z.; Wozniak, M. Exploiting Dynamic Vector-Level Operations and a 2D-Enhanced Logistic Modular Map for Efficient Chaotic Image Encryption. Entropy 2023, 25, 1147. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Wozniak, M. Exploiting Robust Quadratic Polynomial Hyperchaotic Map and Pixel Fusion Strategy for Efficient Image Encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Shi, L.; Li, X.; Jin, B.; Li, Y. A Chaos-Based Encryption Algorithm to Protect the Security of Digital Artwork Images. Mathematics 2024, 12, 3162. [Google Scholar] [CrossRef]
- Chang, H.; Wang, E.; Liu, J. Research on Image Encryption Based on Fractional Seed Chaos Generator and Fractal Theory. Fractal Fract. 2023, 7, 221. [Google Scholar] [CrossRef]
- Huang, L.; Huang, Q.; Chen, H.; Cai, S.; Xiong, X.; Yang, J. A Novel One-Dimensional Chaotic System for Image Encryption in Network Transmission Through Base64 Encoding. Entropy 2025, 27, 513. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, X.; Sun, J.; Yan, P. Chaotic Image Security Techniques and Developments: A Review. Mathematics 2025, 13, 1976. [Google Scholar] [CrossRef]
- Premkumar, R.; Mahdal, M.; Elangovan, M. An Efficient Chaos-Based Image Encryption Technique Using Bitplane Decay and Genetic Operators. Sensors 2022, 22, 8044. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Shi, Q.; Ding, Q. Cryptanalysis of an Image Encryption Algorithm Using DNA Coding and Chaos. Entropy 2025, 27, 40. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Improved Cryptanalysis and Enhancements of an Image Encryption Scheme Using Combined 1D Chaotic Maps. Entropy 2018, 20, 843. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Cryptanalysis and Improvement on an Image Encryption Algorithm Design Using a Novel Chaos Based S-Box. Symmetry 2018, 10, 399. [Google Scholar] [CrossRef]
- Badea, B.; Vlad, A. Revealing Statistical Independence of Two Experimental Data Sets. In An Improvement on Spearman’s Algorithm, Lecture Notes in Computer Science, Vol. 3980 (ICCSA 2006); Springer: Berlin/Heidelberg, Germany, 2006; pp. 1166–1176. ISSN 0302-9743. [Google Scholar]
- Vaduva, A.; Vlad, A.; Badea, B. Evaluating the Performance of a Test-Method for Statistical Independence Decision in the Context of Chaotic Signals. In Proceedings of the 2016 International Conference on Communications (COMM), Bucharest, Romania, 9–11 June 2016; pp. 417–422. [Google Scholar] [CrossRef]
- Dinu, A.; Frunzete, M. The Lorenz Chaotic System, Statistical Independence and Sampling Frequency. In Proceedings of the 2021 International Symposium on Signals, Circuits and Systems (ISSCS), Iasi, Romania, 15–16 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Dinu, A.; Frunzete, M. Singularity, Observability and Statistical Independence in the Context of Chaotic Systems. Mathematics 2023, 11, 305. [Google Scholar] [CrossRef]
- Luca, A.; Vlad, A.; Badea, B.; Frunzete, M. A Study on Statistical Independence in the Tent Map. In Proceedings of the IEEE International Symposium on Signals, Circuits and Systems (ISSCS 2009), Iasi, Romania, 9–10 July 2009; IEEE: New York, NY, USA; pp. 1–4. [Google Scholar] [CrossRef]
- Vlad, A.; Ilyas, A.; Luca, A. Unifying Running-Key Approach and Logistic Map to Generate Enciphering Sequences. Ann. Telecommun. 2013, 68, 179–186. [Google Scholar] [CrossRef]
- Dinu, A.; Vlad, A. The Compound Tent Map and the Connection Between Gray Codes and the Initial Condition Recovery. UPB Sci. Bull. Ser. A Appl. Math. Phys. 2014, 76, 17–28. Available online: https://www.scientificbulletin.upb.ro/rev_docs_arhiva/full72a_882955.pdf (accessed on 20 July 2024).
- Khairullah, M.K.; Alkahtani, A.A.; Bin Baharuddin, M.Z.; Al-Jubari, A.M. Designing 1D Chaotic Maps for Fast Chaotic Image Encryption. Electronics 2021, 10, 2116. [Google Scholar] [CrossRef]
- Daoui, A.; Yamni, M.; Chelloug, S.A.; Wani, M.A.; El-Latif, A.A.A. Efficient Image Encryption Scheme Using Novel 1D Multiparametric Dynamical Tent Map and Parallel Computing. Mathematics 2023, 11, 1589. [Google Scholar] [CrossRef]
- Abikoye, O.C.; Haruna, A.D.; Abubakar, A.; Akande, N.O.; Asani, E.O. Modified Advanced Encryption Standard Algorithm for Information Security. Symmetry 2019, 11, 1484. [Google Scholar] [CrossRef]
- Kaggle. Available online: https://www.kaggle.com/ (accessed on 21 December 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).