The Kelvin–Voigt–Brinkman–Forchheimer Equations with Non-Homogeneous Boundary Conditions
Abstract
1. Introduction
- is the velocity field, ;
- is the pressure, ;
- is the external force field; ;
- is a dimensionless parameter included in the convective term; ;
- is a parameter characterizing the elasticity of the media, ;
- is the viscosity function, ;
- is a function describing hereditary effects (memory), ;
- is a parameter characterizing the permeability of the media, ;
- the symbol ⊗ denotes the tensor product of vectors, that is, for any vectors ;
- the symbol ∇ denotes for the gradient with respect to the space variables , that is, ;
- the differential operators div, and are defined as follows:for a vector-valued function and a matrix-valued function .
2. Preliminaries
2.1. Isomorphisms and Some Related Results
2.2. Local Solvability of Equations with Fréchet Differentiable Operators
- (1)
- The inclusions and hold.
- (2)
- The operator norms and obey the following relation
- (3)
- The mapping is continuously Fréchet differentiable.
- (4)
- The equality holds.
- (5)
- The Fréchet derivative is equal to the zero operator.
2.3. Notation for Scalar Product and Euclidean Norm in and
2.4. Spaces of Time-Independent Functions
- ;
- ;
- the Lebesgue space , and the Sobolev space , .
2.5. Spaces of Time-Dependent Functions
2.6. Helmholtz–Weyl Decomposition and Leray Projection
2.7. Quotient of Sobolev Space by Constants
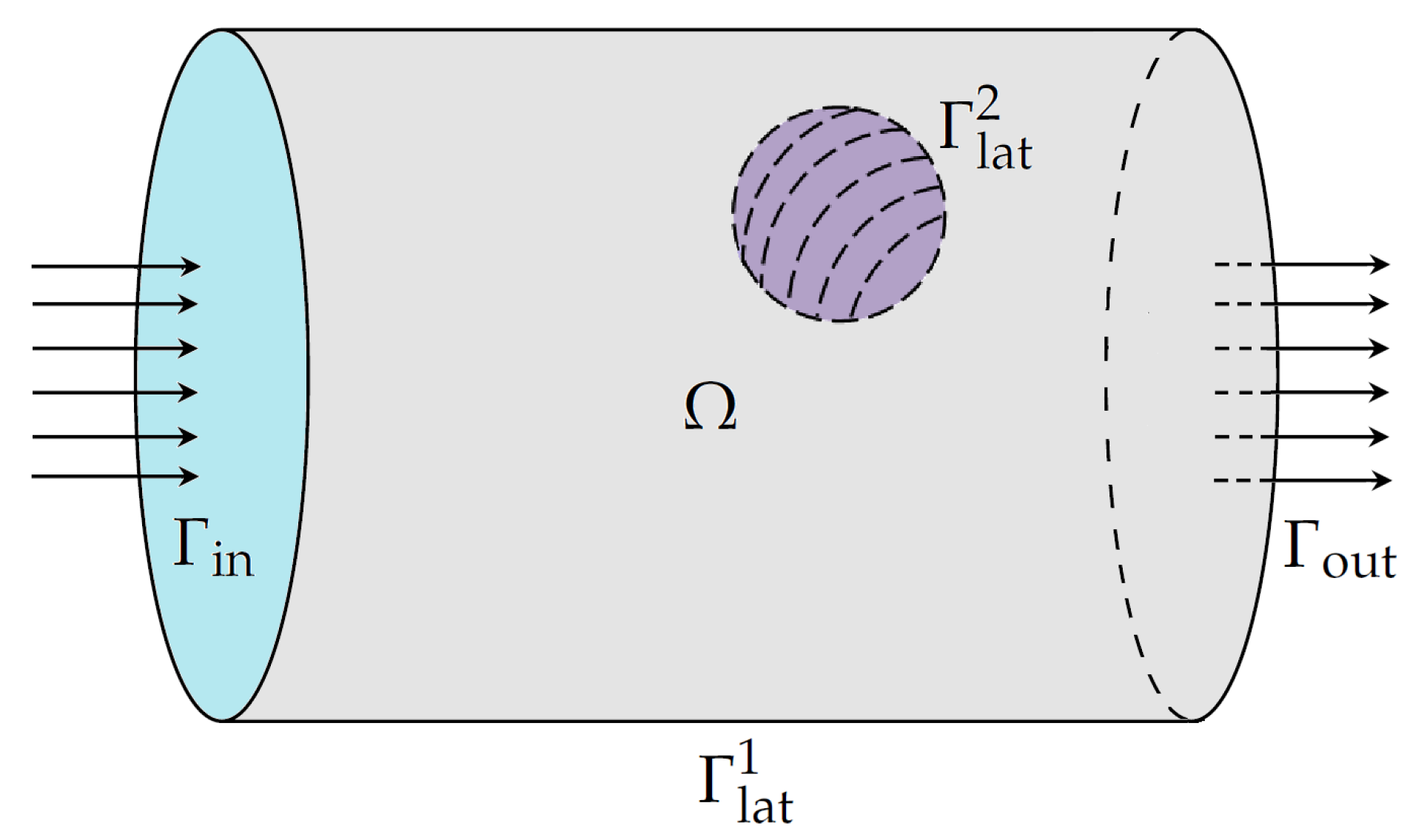
3. Strong Formulation of Problem
- the vector function and the equivalence class satisfy the system
4. Main Results
- Ω is a bounded domain in space , where or 3, and
- , and
- all inclusions in (13) are valid;
- the vector functions and satisfy the compatibility condition
- (a)
- (b)
5. Auxiliary Propositions
5.1. Boundary Trace and Divergence-Free Lifting
5.2. Two Linear Operators Associated with Kelvin–Voigt–Brinkman–Forchheimer System
6. Proof of Main Theorem
7. Final Comments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987. [Google Scholar] [CrossRef]
- Chorin, A.J.; Marsden, J.E. A Mathematical Introduction to Fluid Mechanics, 3rd ed.; Springer: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Marchioro, C.; Pulvirenti, M. Mathematical Theory of Incompressible Nonviscous Fluids; Springer: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Glass, O. Exact boundary controllability of 3-D Euler equation. ESAIM Control Optim. Calc. Var. 2000, 5, 1–44. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Shamin, R.V. A Riccati-type solution of 3D Euler equations for incompressible flow. J. King Saud Univ. 2020, 32, 125–130. [Google Scholar] [CrossRef]
- Ladyzhenskaya, O.A. The Mathematical Theory of Viscous Incompressible Flow, 2nd ed.; Gordon and Breach: New York, NY, USA, 1969. [Google Scholar]
- Temam, R. Navier–Stokes Equations: Theory and Numerical Analysis; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Tartar, L. An Introduction to Navier–Stokes Equation and Oceanography; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Boyer, F.; Fabrie, P. Mathematical Tools for the Study of the Incompressible Navier–Stokes Equations and Related Models; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Varnhorn, W. The Stokes Equations; Akademie Verlag: Berlin, Germany, 1994. [Google Scholar]
- Damazio, P.D.; Manholi, P.; Silvestre, A.L. Lq-theory of the Kelvin–Voigt equations in bounded domains. J. Differ. Equ. 2016, 260, 8242–8260. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Mixed initial–boundary value problem for equations of motion of Kelvin–Voigt fluids. Comput. Math. Math. Phys. 2016, 56, 1363–1371. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Strong solutions of the incompressible Navier–Stokes–Voigt model. Mathematics 2020, 8, 181. [Google Scholar] [CrossRef]
- Khompysh, K.; Kenzhebai, K. An inverse problem for Kelvin–Voigt equations perturbed by isotropic diffusion and damping. Math. Meth. Appl. Sci. 2022, 45, 3817–3842. [Google Scholar] [CrossRef]
- Straughan, B. Stability problems with generalized Navier–Stokes–Voigt theories. Ann. Univ. Ferrara 2024, 70, 1747–1766. [Google Scholar] [CrossRef]
- Straughan, B. Double diffusion in a Navier–Stokes–Voigt fluid with a Christov heat law. Ann. Univ. Ferrara 2025, 71, 23. [Google Scholar] [CrossRef]
- Anh, C.T.; Trang, P.T. On the 3D Kelvin–Voigt–Brinkman–Forchheimer equations in some unbounded domains. Nonlinear Anal. 2013, 89, 36–54. [Google Scholar] [CrossRef]
- Mohan, M.T. Global and exponential attractors for the 3D Kelvin–Voigt–Brinkman–Forchheimer equations. Discret. Contin. Dyn. Syst. Ser. B 2020, 25, 9. [Google Scholar] [CrossRef]
- Gentile, M.; Straughan, B. Stabilization estimates for the Brinkman–Forchheimer–Kelvin–Voigt equation backward in time. Acta Mech. 2023, 234, 4001–4009. [Google Scholar] [CrossRef]
- Badday, A.J.; Harfash, A.J. Thermosolutal convection in a Brinkman–Darcy–Kelvin–Voigt fluid with a bidisperse porous medium. Phys. Fluids 2024, 36, 014119. [Google Scholar] [CrossRef]
- Caucao, S.; Yotov, I. Velocity-vorticity-pressure mixed formulation for the Kelvin–Voigt–Brinkman–Forchheimer equations. arXiv 2024, arXiv:2406.16703. [Google Scholar] [CrossRef]
- Shivaraj Kumar, D.L.; Basavaraj, M.S.; Aruna, A.S. Linear stability analysis of the viscoelastic Navier–Stokes–Voigt fluid model through Brinkman porous media: Modal and non-modal approaches. Int. J. Non-Linear Mech. 2024, 167, 104885. [Google Scholar] [CrossRef]
- Straughan, B. Kelvin–Voigt fluid models in double-diffusive porous convection. Transp. Porous Media 2025, 152, 11. [Google Scholar] [CrossRef]
- Oskolkov, A.P.; Shadiev, R. Towards a theory of global solvability on [0, ∞) of initial-boundary value problems for the equations of motion of Oldroyd and Kelvin–Voight fluids. J. Math. Sci. 1994, 68, 240–253. [Google Scholar] [CrossRef]
- Doubova, A.; Fernandez-Cara, E. On the control of viscoelastic Jeffreys fluids. Syst. Control Lett. 2012, 61, 573–579. [Google Scholar] [CrossRef]
- Zafar, A.A.; Fetecau, C.; Mirza, I.A. On the flow of Oldroyd-B fluids with fractional derivatives over a plate that applies shear stress to the fluid. Math. Rep. 2016, 18, 85–108. [Google Scholar]
- Baranovskii, E.S.; Artemov, M.A. Global existence results for Oldroyd fluids with wall slip. Acta Appl. Math. 2017, 147, 197–210. [Google Scholar] [CrossRef]
- Bir, B.; Goswami, D. On a three step two-grid finite element method for the Oldroyd model of order one. Z. Angew. Math. Mech. 2021, 101, e202000373. [Google Scholar] [CrossRef]
- Oskolkov, A.P. Unsteady flows of viscoelastic fluids. Proc. Steklov Inst. Math. 1984, 159, 105–134. [Google Scholar]
- Oskolkov, A.P. Theory of nonstationary flows of Kelvin–Voigt fluids. J. Math. Sci. 1985, 28, 751–758. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Artemov, M.A. Generalized Navier–Stokes equations with non-homogeneous boundary conditions. Fractal Fract. 2022, 6, 373. [Google Scholar] [CrossRef]
- Deteix, J.; Yakoubi, D. Improving the pressure accuracy in a projection scheme for incompressible fluids with variable viscosity. Appl. Math. Lett. 2018, 79, 111–117. [Google Scholar] [CrossRef]
- Plasman, L.; Deteix, J.; Yakoubi, D. A projection scheme for Navier–Stokes with variable viscosity and natural boundary condition. Int. J. Numer. Methods Fluids 2020, 92, 1845–1865. [Google Scholar] [CrossRef]
- Tartaglione, A. Regularity of weak solutions to the inhomogeneous stationary Navier–Stokes equations. Symmetry 2021, 13, 1336. [Google Scholar] [CrossRef]
- Russo, R.; Tartaglione, A. The plane exterior boundary-value problem for nonhomogeneous fluids. J. Math. Fluid Mech. 2020, 22, 14. [Google Scholar] [CrossRef]
- Korobkov, M.V.; Pileckas, K.; Pukhnachov, V.V.; Russo, R. The flux problem for the Navier–Stokes equations. Russ. Math. Surv. 2014, 69, 1065–1122. [Google Scholar] [CrossRef]
- Pukhnachev, V.V. Three dimensional flux problem for the Navier–Stokes equations. Vestn. Yuzhno-Ural. Univ. Ser. Mat. Model. Program. 2015, 8, 95–104. [Google Scholar] [CrossRef]
- Korobkov, M.; Pileckas, K.; Russo, R. The Steady Navier–Stokes System: Basics of the Theory and the Leray Problem; Birkhäuser: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Di Plinio, F.; Giorgini, A.; Pata, V.; Temam, R. Navier–Stokes–Voigt equations with memory in 3D lacking instantaneous kinematic viscosity. J. Nonlinear Sci. 2018, 28, 653–686. [Google Scholar] [CrossRef]
- Yushkov, E.V. On the blow-up of a solution of a non-local system of equations of hydrodynamic type. Izv. Math. 2012, 76, 190–213. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. , Fomin, S.V. Introductory Real Analysis; Dover Publications: New York, NY, USA, 1975. [Google Scholar]
- Renardy, M.; Rogers, R. An Introduction to Partial Differential Equations, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Adams, R.A.; Fournier, J.J.F. Sobolev Spaces, Vol. 40 of Pure and Applied Mathematics; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Antontsev, S.N.; Khompysh, K. Inverse problems for a Boussinesq system for incompressible viscoelastic fluids. Math. Methods Appl. Sci. 2023, 46, 11130–11156. [Google Scholar] [CrossRef]
- Rajagopal, K.R. On some unresolved issues in non-linear fluid dynamics. Russ. Math. Surv. 2003, 58, 319–330. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. The first problem of Stokes for an Oldroyd-B fluid. Int. J. Non-Linear Mech. 2003, 38, 1539–1544. [Google Scholar] [CrossRef]
- Pukhnachev, V.V. Mathematical model of an incompressible viscoelastic Maxwell medium. J. Appl. Mech. Tech. Phys. 2010, 51, 546–554. [Google Scholar] [CrossRef]
- Baranovskii, E.S. On steady motion of viscoelastic fluid of Oldroyd type. Sb. Math. 2014, 205, 763–776. [Google Scholar] [CrossRef]
- Artemov, M.A.; Baranovskii, E.S. Mixed boundary-value problems for motion equations of a viscoelastic medium. Electron. J. Differ. Equ. 2015, 2015, 252. [Google Scholar]
- Ershkov, S.V.; Christianto, V.; Shamin, R.V.; Giniyatullin, A.R. About analytical ansatz to the solving procedure for Kelvin–Kirchhoff equations. Eur. J. Mech. B Fluids 2020, 79, 87–91. [Google Scholar] [CrossRef]
- Ye, Z. Global regularity of the high-dimensional Oldroyd-B model in the corotational case. J. Math. Anal. Appl. 2020, 486, 123867. [Google Scholar] [CrossRef]
- Fetecau, C.; Bridges, C. Analytical solutions for some unsteady flows of fluids with linear dependence of viscosity on the pressure. Inverse Probl. Sci. Eng. 2021, 29, 378–395. [Google Scholar] [CrossRef]
- Mallea-Zepeda, E.; Ortega-Torres, E.; Villamizar-Roa, É.J. An optimal control problem for the Navier–Stokes-α system. J. Dyn. Control Syst. 2023, 29, 129–156. [Google Scholar] [CrossRef]
- Sirota, D.D.; Gushchin, K.A.; Khan, S.A.; Kostikov, S.L.; Butov, K.A. Neural operators for hydrodynamic modeling of underground gas storage facilities. Russ. Tech. J. 2024, 12, 102–112. [Google Scholar] [CrossRef]
- Mallea-Zepeda, E.; Lenes, E.; Valero, E. Boundary control problem for heat convection equations with slip boundary condition. Math. Probl. Eng. 2018, 2018, 7959761. [Google Scholar] [CrossRef]
- Brizitskii, R.V.; Saritskaya, Z.Y. Control problem for generalized Boussinesq model. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1268, p. 012011. [Google Scholar] [CrossRef]
- Boldrini, J.L.; Mallea-Zepeda, E.; Rojas-Medar, M.A. Optimal boundary control for the stationary Boussinesq equations with variable density. Commun. Contemp. Math. 2020, 22, 1950031. [Google Scholar] [CrossRef]
- Brizitskii, R.V.; Saritskaia, Z.Y. Analysis of inhomogeneous boundary value problems for generalized Boussinesq model of mass transfer. J. Dyn. Control Syst. 2023, 29, 1809–1828. [Google Scholar] [CrossRef]
- Chebotarev, A.Y.; Pak, N.M.; Kovtanyuk, A.E. Analysis and numerical simulation of the initial-boundary value problem for quasilinear equations of complex heat transfer. J. Appl. Ind. Math. 2023, 17, 698–709. [Google Scholar] [CrossRef]
- Chebotarev, A.Y. Optimal control of quasi-stationary equations of complex heat transfer with reflection and refraction conditions. Comput. Math. Math. Phys. 2023, 63, 2050–2059. [Google Scholar] [CrossRef]
- Chebotarev, A.Y. Inhomogeneous problem for quasi-stationary equations of complex heat transfer with reflection and refraction conditions. Comput. Math. Math. Phys. 2023, 63, 441–449. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Exact solutions for non-isothermal flows of second grade fluid between parallel plates. Nanomaterials 2023, 13, 1409. [Google Scholar] [CrossRef]
- Brizitskii, R.V. Generalised Boussinesq model with variable coefficients. Sib. Electron. Math. Rep. 2024, 21, 213–227. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Brizitskii, R.V.; Saritskaia, Z.Y. Optimal control problems for the reaction–diffusion–convection equation with variable coefficients. Nonlinear Anal. Real World Appl. 2024, 75, 103979. [Google Scholar] [CrossRef]
- Davidson, P.A. Introduction to Magnetohydrodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Galtier, S. Introduction to Modern Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Xiros, N. Mathematical Magnetohydrodynamics; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Brizitskii, R.V. Boundary value and control problems for the stationary magnetic hydrodynamic equations of heat conducting fluid with variable coefficients. J. Dyn. Control Syst. 2024, 30, 39. [Google Scholar] [CrossRef]
| Values of Parameters | Flow Model |
|---|---|
| , , , , | The incompressible Euler equations for describing unsteady flows of an inviscid fluid [1,2,3,4,5] |
| , , , , | The standard Navier–Stokes equations for describing Newtonian fluids motion [6,7,8,9] |
| , , , , | The non-stationary Stokes equations for describing the creeping flows of an incompressible viscous fluid [6,7,8,9,10] |
| , , , , | The incompressible Navier–Stokes–Voigt equations for describing the flows of Kelvin–Voigt-type viscoelastic fluids [11,12,13,14,15,16] |
| , , , , | The Kelvin–Voigt–Brinkman–Forchheimer equations (without an integral memory term) for describing the dynamics of incompressible viscoelastic fluids in a porous medium [17,18,19,20,21,22,23] |
| , , , , | The model for describing flows of Jeffreys–Oldroyd-type viscoelastic fluids [24,25,26,27,28] |
| , , , , | The Oskolkov integro-differential system for describing the motion of non-Newtonian fluids with memory [29,30,31] |
| , , , , | The generalized Navier–Stokes system for describing flows of non-homogeneous incompressible viscous fluids [32,33,34] |
| , , , , | The generalized Stokes system for describing creeping flows of non-homogeneous incompressible viscous fluids [35] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baranovskii, E.S.; Artemov, M.A.; Ershkov, S.V.; Yudin, A.V. The Kelvin–Voigt–Brinkman–Forchheimer Equations with Non-Homogeneous Boundary Conditions. Mathematics 2025, 13, 967. https://doi.org/10.3390/math13060967
Baranovskii ES, Artemov MA, Ershkov SV, Yudin AV. The Kelvin–Voigt–Brinkman–Forchheimer Equations with Non-Homogeneous Boundary Conditions. Mathematics. 2025; 13(6):967. https://doi.org/10.3390/math13060967
Chicago/Turabian StyleBaranovskii, Evgenii S., Mikhail A. Artemov, Sergey V. Ershkov, and Alexander V. Yudin. 2025. "The Kelvin–Voigt–Brinkman–Forchheimer Equations with Non-Homogeneous Boundary Conditions" Mathematics 13, no. 6: 967. https://doi.org/10.3390/math13060967
APA StyleBaranovskii, E. S., Artemov, M. A., Ershkov, S. V., & Yudin, A. V. (2025). The Kelvin–Voigt–Brinkman–Forchheimer Equations with Non-Homogeneous Boundary Conditions. Mathematics, 13(6), 967. https://doi.org/10.3390/math13060967







