Weakly Ricci-Symmetric Space-Times and f (R,G) Gravity

Abstract

In the present article, we classify conformally flat weakly Ricci-symmetric space-times and obtain that they represent Robertson–Walker space-times. Furthermore, we provethat a Ricci-recurrent weakly Ricci-symmetric space-time is static and a Ricci-semi-symmetric weakly Ricci-symmetric space-time does not exist. Further, we acquire the conditions under which a weakly Ricci-symmetric twisted space-time becomes a generalized Robertson–Walker space-time. Also, we examine the effect of conformally flat weakly Ricci-symmetric space-time solutions in $f(R,G)$ gravity by considering two models, and we see that the null, weak and strong energy conditions are verified, but the dominant energy condition fails, which is also consistent with present observational studies that reveal the universe is expanding. Finally, we apply the flat Friedmann–Robertson–Walker metric to deduce a relation between deceleration, jerk and snap parameters.

1. Introduction

From the theory of general relativity, we know that a space-time is a Lorentzian manifold $(M^4,g)$ having the signature $(+,+,+,-)$ and that it allows a globally time-oriented vector. Perfect fluids perform a fascinating role in general relativity, being the root of Einstein’s field equations. Recently, physicists have used perfect fluid models to investigate plasma physics, nuclear physics and astrophysics. Many geometers have examined space-times using a variety of methodologies, such as in [1,2,3] and many others.

$M^n$$(n\ge 4)$ is called a generalized Robertson–Walker space-time [4] if it can be expressed by $-\mathcal{I}\times {\varphi }^2\tilde{M}$, in which $\mathcal{I}$ indicates an open subset of $\mathbb{R}$ and $\tilde{M}$ indicates an $(n-1)$-dimensional Riemannian manifold. Specifically, a generalized Robertson–Walker space-time represents Robertson–Walker space-time if $\tilde{M}$ is of dimension three and of constant curvature.

Among other limitations, Robertson–Walker space-times and generalized Robertson–Walker space-times are characterized by the presence of a torse-forming unit and a time-like vector [5]. They illustrate that the presence of a single, unique vector may still define twisted manifolds without any additional constraints. Twisted manifolds generalize Robertson–Walker and generalized Robertson–Walker space-times because they include a scale function that depends on both space and time.

This leads to the definition of twisted space-times. Twisted space-times are significantly more general than warped space-times, which involve periodic alterations to the world. Twisted space-times were initially conceptualized by Chen [6], who defined them as a Lorentzian manifold $M^n$ with the metric (in local form)

$$d{s}^2=g_{jk}d{z}^{j}d{z}^k=-{\left(dt\right)}^2+{\varphi }^2(z,t)g_{jk}^{*}d{z}^{j}d{z}^k,$$

(1)

where $g^{*}$ indicates the metric tensor of an (n-1)-dimensional Riemannian manifold. If $\varphi$ is only a function of t, then the twisted space-time becomes a generalized Robertson–Walker space-time. For further details about generalized Robertson–Walker, Robertson–Walker, and other space-times, see [1,5,6,7,8,9,10,11,12,13].

If $M^4$ is a perfect fluid space-time, then the non-zero Ricci tensor $R_{jk}$ fulfills

$$R_{jk}=a{g}_{jk}+b{u}_j{u}_k,$$

(2)

in which a and b stand for scalars and u denotes the unit time-like vector, that is, $u_j{u}^j=-1$. u is also known as the velocity vector or flow vector.

For a perfect fluid space-time [14], the energy momentum tensor is demonstrated by

$$T_{jk}=p{g}_{jk}+\left(p+\mu \right)u_j{u}_k,$$

(3)

where p and $\mu$ indicate isotropic pressure and energy density. Also, the state equation $p=p\left(\mu \right)$ relates $\mu$ and p. Here, the perfect fluid space-time is called isentropic. Also, for $p=\mu$, the space-time reveals stiff matter [15]. According to the Einstein field equations without a cosmological constant,

$$R_{jk}-{\displaystyle \frac{1}{2}}{g}_{jk}R=\kappa T_{jk},$$

(4)

where $\kappa$ is the gravitational constant and R is the Ricci scalar. The Equations (3) and (4) together yield the Equation (2) [13].

Sen and Chaki [16] investigated certain curvature constraints on a particular type of class one conformally flat spaces in 1967, and derived the covariant derivative of the Ricci tensor as follows:

$${\nabla }_l{R}_{hi}=2{\alpha }_l{R}_{hi}+{\alpha }_h{R}_{li}+{\alpha }_i{R}_{hl},$$

(5)

where ${\alpha }_i$ is the covariant vector and ∇ indicates the covariant derivative.

In 1988, Chaki [17] defined a non-flat Riemannian manifold as a pseudo-Ricci-symmetric manifold where the Ricci tensor satisfies (5). Generalizing this notion, Tamássy and Binh [18], in 1993, developed the concept of n-dimensional weakly Ricci-symmetric manifolds. If an n (≥3)-dimensional Riemannian or semi-Riemannian manifold has a non-zero $R_{hk}$, and the following condition is satisfied:

$${\nabla }_l{R}_{hi}={\alpha }_l{R}_{hi}+{\beta }_h{R}_{li}+{\gamma }_i{R}_{hl},$$

(6)

where ${\alpha }_i$, ${\beta }_i$ and ${\gamma }_i$ are the covariant vectors (not simultaneously zero) and ∇ is the covariant derivative, then the manifold is said to be weakly Ricci-symmetric. If $\alpha =\beta =\gamma =0$, then this manifold turns into a Ricci-symmetric manifold [19]. According to Chaki and Koley, the manifold is referred to as a generalized pseudo-Ricci-symmetric manifold [20] if the vector $\alpha$ in (6) is replaced with $2\alpha$. Hence, the defining condition of a weakly Ricci-symmetric manifold is a little weaker than that of a generalized pseudo-Ricci-symmetric manifold.

Throughout the paper, we assume that ${\lambda }_i={\beta }_i-{\gamma }_i$. Since, by hypothesis, ${\beta }_i$ and ${\gamma }_i$ are unit time-like vectors, ${\lambda }_i$ is also a unit time-like vector. Here, ${\alpha }_i$, ${\beta }_i$ and ${\gamma }_i$ were chosen as unit time–like vectors for physical reasons.

Definition 1.

A four-dimensional Lorentzian manifold is named a weakly Ricci-symmetric space-time if the covariant derivative of the Ricci tensor satisfies Equation (6), where ${\alpha }_i$, ${\beta }_i$ and ${\gamma }_i$ are the unit time-like vectors.

In a Lorentzian manifold $\mathrm{M}$, the Weyl tensor $\mathcal{C}$ is described by

$${\mathcal{C}}_{hijk}=R_{hijk}-{\displaystyle \frac{1}{2}}\left\{g_{ij}{R}_{hk}-g_{ik}{R}_{hj}+g_{hk}{R}_{ij}-g_{hj}{R}_{ik}\right\}+{\displaystyle \frac{R}{6}}\left\{g_{ij}{g}_{hk}-g_{ik}{g}_{hj}\right\},$$

(7)

where $R_{hijk}$ indicates the curvature tensor.

Definition 2.

In M, if the Ricci tensor obeys the following relation

$$R_{lk}=-R{u}_l{u}_k,$$

(8)

where $u_l$ denotes a unit time-like vector, then M is called Ricci-simple [21].

The inquiry of weakly Ricci-symmetric space-times is important because this kind of space-time describes how the universe has evolved. In general relativity, the matter tensor of a space-time is the most important component. It is known that the universe’s material content behaves as a perfect fluid space-time in typical cosmological models [13].

A space-time is considered static in general relativity if it is irrotational and does not vary over time. A static space-time is a particular instance of a stationary space-time, which is a space-time with a rotational axis but no change in time. The non-rotating Schwarzschild solution is a static example of a stationary space-time, whereas the Kerr solution is an example of a stationary space-time that is not static. In [22], it is proved that if $(M,g)$ be a static space-time and g is complete, then both the static vector field K and the integral hypersurfaces of $K^{\perp }$ are complete, with the restriction of the metric g and also the compact static space-time being complete. Birkhoff’s theorem [23] demonstrates that a spherically symmetric vacuum solution is necessarily static. Thus, the Schwarzschild solution is the only solution for any spherical symmetric vacuum field equation. The vector field is time-like Killing and is also a gradient.

Agreement. Throughout the paper, we consider a four-dimensional weakly Ricci-symmetric space-time.

Patterson [24] introduced the notion of Ricci-recurrent manifolds in 1952. According to [24], for a non-zero vector ${\alpha }_l$, a space-time is named Ricci-recurrent if it obeys the relation

$${\nabla }_l{R}_{ij}={\alpha }_l{R}_{ij}.$$

(9)

From (6), it is clear that if $\beta =\gamma =0$, then a weakly Ricci-symmetric space-time reduces to a Ricci-recurrent space-time. In the present article we prove the following.

Theorem 1.

A Ricci-recurrent weakly Ricci-symmetric space-time is static.

Ricci semi-symmetry is well known to be weaker than Ricci-recurrent space-times. If a space-time satisfies the condition

$${\nabla }_l{\nabla }_m{R}_{ij}-{\nabla }_m{\nabla }_l{R}_{ij}=0,$$

(10)

it is called Ricci-semi-symmetric [25]. Again, the class of Ricci-symmetric spaces is a proper subset of Ricci-semi-symmetric spaces. Every semi-symmetric space is known to be Ricci-semi-symmetric, but the converse is usually not true. In a Riemannian space, they are equivalent for dimension three.

In this article, we choose a Ricci-semi-symmetric weakly Ricci-symmetric space-time and provethe following:

Theorem 2.

A Ricci-semi-symmetric weakly Ricci-symmetric space-time does not exist.

In [13], it is illustrated that an n ($n\ge 3$)-dimensional Lorentzian manifold M represents a generalized Robertson–Walker space-time if it allows a time-like and unit torse-forming vector ${\nabla }_j{u}_k=\phi \{g_{jk}+u_j{u}_k\}$ which is also an eigenvector of the Ricci tensor; $\phi$ denotes a scalar. Also, in [5] it is demonstrated that M becomes a twisted space-time if it allows a time-like and unit torse-forming vector, that is, ${\nabla }_j{u}_k=\phi \{g_{jk}+u_j{u}_k\}$ and $u^j{u}_j=-1$. In [7], Chen establish the following:

Theorem I. A necessary and sufficient condition for a Lorentzian manifold to be a generalized Robertson–Walker space-time is that the space-time has a time-like concircular vector $v_i$: ${\nabla }_k{v}_i=\Psi g_{ik}$, $\Psi$ being a scalar.

Then, we acquire under what condition a weakly Ricci-symmetric twisted space-time becomes a generalized Robertson–Walker space-time and establish the following:

Theorem 3.

A weakly Ricci-symmetric twisted space-time whose associated vector $u_j$ is irrotational becomes a generalized Robertson–Walker space-time.

In general relativity, to examine black holes and wormholes, energy conditions are pivotal tools in various modified gravities [26]. Energy conditions were produced in [27] by applying Raychaudhuri equations and demonstrate the character of gravity with the positivity condition $R_{kj}{u}^k{u}^j\ge 0$, where $u^j$ denotes the null vector. The very last criterion is equal to the null energy condition $T_{kj}{u}^k{u}^j\ge 0$. Furthermore, for every time-like vector $u^j$, the weak energy condition asserts that $T_{kj}{u}^k{u}^j\ge 0,$ presuming a positive local energy density. Also, a space-time obeys the dominant energy condition if $T_{kj}{u}^k{v}^j\ge 0$ satisfies for all two co-oriented time-like vectors u and v and the strong energy condition [28] if $R_{kj}{u}^k{u}^j\ge 0$ fulfills for every time-like vector u.

$f(R,G)$ gravity was evolved by substituting a function of R and G for the original Ricci scalar R [29]. In this modified theory, the authors of [30] examined de Sitter’s solutions and power-law stability and discovered that both are dependent on the model’s parameters and the structure of the $f(R,G)$ gravity. They also discovered that gravitational action performs a significant role in the stability of the solution. The authors of [31] investigated the weak-field limit of this gravity by selecting post-Newtonian formalism. Also, in [32], the likelihood of inflation was shown by this gravity theory. We would like to highlight that one of the most possible theories to account for the accelerated expansion of the universe today is $f(R,G)$ gravity. For numerous outcomes in this approach, see [33,34,35,36].

The foregoing mentioned research works gave inspiration for the current study, which aims to explore energy conditions in terms of R and G in a conformally flat weakly Ricci-symmetric space-time that fulfills the $f(R,G)$ gravity condition.

2. Proof of the Main Results

By interchanging h and i in Equation (6), we reveal

$${\nabla }_l{R}_{ih}={\alpha }_l{R}_{ih}+{\beta }_i{R}_{lh}+{\gamma }_h{R}_{il}.$$

(11)

Subtracting (11) from (6), we obtain

$${\beta }_h{R}_{li}+{\gamma }_i{R}_{hl}-{\beta }_i{R}_{lh}-{\gamma }_h{R}_{il}=0,$$

(12)

that is,

$${\lambda }_h{R}_{li}={\lambda }_i{R}_{lh},$$

(13)

where ${\lambda }_i={\beta }_i-{\gamma }_i$.

Multiplying Equation (13) by $g^{li}$ produces

$${\lambda }_{h}R=R_{lh}{\lambda }^l,\sin \mathrm{ce}{R}_{li}{g}^{li}=R.$$

(14)

Again multiplying Equation (13) by ${\lambda }^h$ gives

$$-R_{li}={\lambda }_i{R}_{lh}{\lambda }^h,\sin \mathrm{ce}{\lambda }_h{\lambda }^h=-1.$$

(15)

Using Equations (14) in (15), we infer

$$R_{li}=-R{\lambda }_l{\lambda }_i,$$

(16)

which means the space-time is Ricci-simple.

In [13], the authors provide the physical interpretation of Equation (16). It is proved that the Equation (16) represents a stiff matter fluid [21], that is, a perfect fluid space-time with $p=\mu$, in which ${\lambda }_i$ is the velocity vector or flow vector of the fluid. Thus, we write the following:

Proposition 1.

A weakly Ricci-symmetric space-time represents a stiff matter fluid.

Mantica et al. [21] proved that in an n-dimensional Lorentzian manifold, if the Ricci tensor is of the form $R_{li}=-R{u}_l{u}_i$, where $u_l$ is a unit time-like vector and with null divergence of the Weyl tensor, then the space-time becomes a generalized Robertson–Walker space-time. Assuming that the weakly Ricci-symmetric space-time is conformally flat, then ${\nabla }_i{\mathcal{C}}_{jkl}^i=0$. Thus, a conformally flat weakly Ricci-symmetric space-time is a generalized Robertson–Walker space-time. Again, a generalized Robertson–Walker space-time has been found to be conformally flat if it is a Robertson–Walker space-time [37]. Hence, we state the following:

Proposition 2.

A conformally flat weakly Ricci-symmetric space-time is a Robertson–Walker space-time.

Remark 1.

For $R=0$, from Equation (16) we acquire $R_{li}=0$, which contradicts the definition of a weakly Ricci-symmetric space-time. Therefore, in a weakly Ricci-symmetric space-time, R is non-zero.

Remark 2.

In stiff matter, the velocity of sound equals the velocity of light in a vacuum. In the early universe, the dark fluid behaved as a stiff fluid and the internal energy dominated. Historically, the Zel’dovich cosmological model, which postulates that the primordial cosmos was composed of a cold gas of baryons, was the first to raise the prospect of a primordial stiff matter epoch. Recent cosmological models that use relativistic self-gravitating Bose–Einstein condensates as dark matter also exhibit a primordial stiff matter epoch.

Proof of Theorem 1.

Let a weakly Ricci-symmetric space-time be Ricci-recurrent. Then,

$${\nabla }_k{R}_{ij}={\nu }_k{R}_{ij},$$

(17)

with ${\nu }_k$ being a covariant vector.

Multiplying the above equation with $g^{ij}$, we infer

$${\nabla }_{k}R={\nu }_{k}R,\sin \mathrm{ce}{R}_{ij}{g}^{ij}=R.$$

(18)

Taking the covariant differentiation of Equation (16), we acquire

$${\nabla }_k{R}_{ij}=-{\nabla }_{k}R{\lambda }_i{\lambda }_j-R({\lambda }_j{\nabla }_k{\lambda }_i+{\lambda }_i{\nabla }_k{\lambda }_j).$$

(19)

Using Equation (17) in the foregoing equation, we get

$${\nu }_k{R}_{ij}=-{\nabla }_{k}R{\lambda }_i{\lambda }_j-R({\lambda }_j{\nabla }_k{\lambda }_i+{\lambda }_i{\nabla }_k{\lambda }_j).$$

(20)

Therefore, using the Equations (16) and (18) in Equation (20) gives

$$-R\left\{{\lambda }_j{\nabla }_k{\lambda }_i+{\lambda }_i{\nabla }_k{\lambda }_j\right\}=0.$$

(21)

As $R\ne 0$,

$${\lambda }_j{\nabla }_k{\lambda }_i+{\lambda }_i{\nabla }_k{\lambda }_j=0.$$

(22)

Since ${\lambda }_i{\lambda }^i=-1$, taking the covariant derivative, we get ${\lambda }^i{\nabla }_k{\lambda }_i=0$.

Multiplying (22) with ${\lambda }^i$ and applying ${\lambda }^i{\nabla }_k{\lambda }_i=0$, we provide

$${\nabla }_k{\lambda }_j=0.$$

(23)

If a space-time allows a Killing time-like vector ${\lambda }_j$, then it is called a stationary space-time and if, in addition, ${\lambda }_j$ is irrotational, then it is named a static space-time ([22,38], p. 283).

If v is a smooth vector, then the Lie derivative £ is expressed by

$${\pounds }_v{g}_{lj}={\nabla }_l{v}_j+{\nabla }_j{v}_l.$$

Now, ${\nabla }_h{\lambda }_j=0$ produces ${\pounds }_{\lambda }{g}_{lj}=0$, which proves that ${\lambda }_j$ is Killing. Further, ${\nabla }_l{\lambda }_j=0$ tells us that ${\lambda }_j$ is irrotational. Therefore, the space-time is static.

Hence, the proof is over. □

Remark 3.

It is commonly known that every static space-time is always of Petrov type I, D or O ([39], Section 10.7). Therefore, the space-time of concern is of Petrov classification I, D or O.

Proof of Theorem 2.

Choose a Ricci-semi-symmetric weakly Ricci-symmetric space-time, that is,

$${\nabla }_l{\nabla }_m{R}_{ij}-{\nabla }_m{\nabla }_l{R}_{ij}=0.$$

(24)

Therefore, using (16) in the foregoing equation, we infer

$$R\{{\lambda }_j\left({\nabla }_l{\nabla }_m{\lambda }_i\right)-{\lambda }_j\left({\nabla }_m{\nabla }_l{\lambda }_i\right)+{\lambda }_i\left({\nabla }_l{\nabla }_m{\lambda }_j\right)-{\lambda }_i\left({\nabla }_m{\nabla }_l{\lambda }_j\right)\}=0.$$

(25)

Then, making use of the Ricci identity, that is, ${\nabla }_l{\nabla }_m{\lambda }_i-{\nabla }_m{\nabla }_l{\lambda }_i={\lambda }_h{R}_{iml}^h$, we acquire

$${\lambda }_h{R}_{iml}^h{\lambda }_j+{\lambda }_h{R}_{jml}^h{\lambda }_i=0,$$

(26)

in which $R_{iml}^h$ denotes a Riemann curvature tensor of (1,3) type.

Multiplying by $g^{im}$, the above equation provides

$${\lambda }_h{R}_l^h{\lambda }_j+{\lambda }_h{R}_{jml}^h{\lambda }^m=0,\sin \mathrm{ce}{R}_{iml}^h{g}^{im}=R_l^h,g^{im}{\lambda }_i={\lambda }^m.$$

(27)

Multiplying by ${\lambda }^j$ immediately gives

$$-{\lambda }_h{R}_l^h+{\lambda }_h{\lambda }^j{\lambda }^m{R}_{jml}^h=0,\sin \mathrm{ce}{\lambda }_j{\lambda }^j=-1,$$

which implies that

$${\lambda }_h{R}_l^h=0,\sin \mathrm{ce}{\lambda }_h{\lambda }^j{\lambda }^m{R}_{jml}^h=0,\mathrm{as}{R}_{hjml}=-R_{jhml}.$$

(28)

Now, multiplying the Equation (16) by ${\lambda }^l$ gives ${\lambda }^l{R}_{il}=R{\lambda }_i$ and using the previous equation, we achieve $R{\lambda }_i=0$, which implies $R=0$, which contradicts Remark 1. □

Proof of Theorem 3.

In a twisted space-time, we have [5]

$${\nabla }_j{u}_k=\phi \{g_{jk}+u_j{u}_k\}$$

(29)

where $u_j$ is a torse-forming unit time-like vector and $\phi$ indicates scalars (non-zero).

The covariant derivative of Equation (29) yields

$${\nabla }_i\left({\nabla }_j{u}_k\right)={\phi }_i\{g_{jk}+u_j{u}_k\}+{\phi }^2\{g_{ji}{u}_k+g_{ki}{u}_j+2u_j{u}_k{u}_i\}.$$

(30)

From the last equation, one can easily acquire

$${\nabla }_i\left({\nabla }_j{u}_k\right)-{\nabla }_j\left({\nabla }_i{u}_k\right)={\phi }_i\{g_{jk}+u_j{u}_k\}-{\phi }_j\{g_{ik}+u_i{u}_k\}+{\phi }^2\{g_{ki}{u}_j-g_{kj}{u}_i\}.$$

(31)

Using the Ricci identity in Equation (31), we produce

$$u_h{R}_{kji}^h={\phi }_i\{g_{jk}+u_j{u}_k\}-{\phi }_j\{g_{ik}+u_i{u}_k\}+{\phi }^2\{g_{ki}{u}_j-g_{kj}{u}_i\}.$$

(32)

We multiply Equation (32) with $g^{kj}$ and obtain

$$R_{hi}{u}^h=(n-2){\phi }_i-{\phi }_j{u}^j{u}_i+{\phi }^2(1-n)u_i.$$

(33)

In a weakly Ricci-symmetric space-time from Equation (14), we infer

$$R_{hi}{u}^h=R{u}_i.$$

(34)

Using the last equation in Equation (33), we have

$${\phi }_i=f_1{u}_i,$$

(35)

in which $f_1={\displaystyle \frac{1}{n-2}}\{R+{\phi }_j{u}^j-{\phi }^2(1-n)\}$ and, hence, $f_1$ is a scalar.

Now,

$${\nabla }_k\left(\phi u_j\right)-{\nabla }_j\left(\phi u_k\right)={\phi }_k{u}_j+\phi {\nabla }_k{u}_j-{\phi }_j{u}_k-\phi {\nabla }_j{u}_k.$$

(36)

Let $u_j$ be irrotational (that is, ${\nabla }_k{u}_j-{\nabla }_j{u}_k=0$) and then, using (35), we acquire

$${\nabla }_k\left(\phi u_j\right)-{\nabla }_j\left(\phi u_k\right)=f_1{u}_k{u}_j-f_1{u}_j{u}_k+\phi ({\nabla }_k{u}_j-{\nabla }_j{u}_k),$$

which implies that

$${\nabla }_k\left(\phi u_j\right)-{\nabla }_j\left(\phi u_k\right)=0.$$

(37)

Hence, $\phi u_j$ is the gradient. Thus, we can write $\phi u_j={\nabla }_j\lambda$, where $\lambda$ is a scalar.

Putting $V_j=u_j{e}^{-\lambda }$, we obtain

$${\nabla }_k{V}_j=e^{-\lambda }\{\left({\nabla }_k{u}_j\right)-u_j\left({\nabla }_k\lambda \right)\}.$$

(38)

Equations (29) and (38) reflect that

$${\nabla }_k{V}_j=e^{-\lambda }(\phi \{g_{jk}+u_j{u}_k\}-\phi u_j{u}_k)=\left(e^{-\lambda }\phi \right)g_{jk}.$$

(39)

Now, $V_j{V}^j=\left(u_j{e}^{-\lambda }\right)\left(u^j{e}^{-\lambda }\right)=-e^{-2\lambda }<0$. So, $V_j$ is a time-like concircular vector.

Thus, we conclude our result. □

3. Conformally Flat Weakly Ricci-Symmetric Space-Time Satisfying $\mathbf{f}(\mathbf{R},\mathbf{G})$ Gravity

We now spotlight $f(R,G)$ gravity, which is a specified subclass of modified gravity. The Gauss–Bonnet invariant G is expressed as

$$G=R^2+R_{hijk}{R}^{hijk}-4R_{hk}{R}^{hk},$$

(40)

and the gravitational force formula is demonstrated by

$$S={\displaystyle \frac{1}{2\kappa }}\int \sqrt{-g}f(R,G)d^{4}x+S_{\mathrm{mat}},$$

(41)

in which $S_{\mathrm{mat}}$ denotes the action term. The field equations are given by

$$\begin{array}{ccc}\hfill & & 0=\kappa T_{ik}^{\left(m\right)}+{\displaystyle \frac{1}{2}}{g}_{ik}+f_G(-2R_{ik}R+4R_{mink}{R}^{mn}-2R_{impq}{R}_k^{mpq}+4R_i^m{R}_{mk})\hfill \\ & & +(2R{\nabla }_k{\nabla }_i-2g_{ik}R\square -4R_i^m{\nabla }_m{\nabla }_k-4R_k^m{\nabla }_m{\nabla }_i+4R_{ik}\square )f_G\hfill \\ & & -(R_{ik}-{\nabla }_i{\nabla }_k+g_{ik}\square )f_R+(4g_{ik}{R}_{mn}{\nabla }^n{\nabla }^m-4R_{nimk}{\nabla }^n{\nabla }^m)f_G,\hfill \end{array}$$

(42)

in which the term $T_{ik}^{\left(m\right)}$ arises from $S_{\mathrm{mat}}$ and $f_G\equiv {\displaystyle \frac{\partial f}{\partial G}}$, $f_R\equiv {\displaystyle \frac{\partial f}{\partial R}}$, and □ denotes the d’Alembert operator.

In most cases, $T_{ij}$ is contemplated as the perfect fluid shape

$$T_{ij}^{\left(m\right)}=p^{\left(m\right)}{g}_{ij}+(p^{\left(m\right)}+{\mu }^{\left(m\right)})u_i{u}_j,$$

(43)

in which $p^{\left(m\right)}$ indicates the isotropic pressure and ${\mu }^{\left(m\right)}$ denotes the energy density of the perfect fluid.

Particularly for a conformally flat space-time, Equation (42) can be reframed as

$$R_{ik}-{\displaystyle \frac{R}{2}}{g}_{ik}=\kappa (T_{ik}^m+T_{ik}^{curv})=\kappa T_{ik}^{\mathrm{eff}},$$

(44)

where the term $T_{ik}^{curv}$ results from the space-time geometry and is written by

$$\begin{array}{cc}\hfill \kappa T_{ik}^{curv}& ={\nabla }_i{\nabla }_k{f}_R-g_{ik}\square f_R+2R{\nabla }_i{\nabla }_k{f}_G-2g_{ik}R\square f_G-4R_i^h{\nabla }_h{\nabla }_k{f}_G\hfill \\ \hfill & -4R_k^h{\nabla }_h{\nabla }_i{f}_G+4R_{ik}\square f_G+4g_{ik}{R}^{hk}{\nabla }_h{\nabla }_k{f}_G+4R_{ihkk}{\nabla }^h{\nabla }^k{f}_G\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{g}_{ik}\left(f-G{f}_G-R{f}_R\right)-\left(f_R-1\right)\left(R_{ik}-{\displaystyle \frac{1}{2}}{g}_{ik}R\right)\hfill \end{array}$$

(45)

in which $T_{ij}^{\mathrm{eff}}$ indicates the effective energy momentum tensor.

From Equation (16), we provide

$$R^{lk}=-R{\lambda }^l{\lambda }^k.$$

(46)

Equations (16) and (46) together imply

$$R_{lk}{R}^{lk}=R^2.$$

(47)

Since the space-time is conformally flat, then Equation (7) yields

$$R_{hijk}={\displaystyle \frac{1}{2}}\left\{g_{ij}{R}_{hk}-g_{ik}{R}_{hj}+g_{hk}{R}_{ij}-g_{hj}{R}_{ik}\right\}-{\displaystyle \frac{R}{6}}\left\{g_{ij}{g}_{hk}-g_{ik}{g}_{hj}\right\}.$$

(48)

From (48), we acquire

$$R^{hijk}={\displaystyle \frac{1}{2}}\left\{g^{ij}{R}^{hk}-g^{ik}{R}^{hj}+g^{hk}{R}^{ij}-g^{hj}{R}^{ik}\right\}-{\displaystyle \frac{R}{6}}\left\{g^{ij}{g}^{hk}-g^{ik}{g}^{hj}\right\}.$$

(49)

Multiplying (48) and (49), one arrives at

$$R_{hijk}{R}^{hijk}={\displaystyle \frac{23}{6}}{R}^2.$$

(50)

Jointly using the Equations (40), (47) and (50), the Gauss–Bonnet invariant is given by

$$G={\displaystyle \frac{5R^2}{6}}.$$

(51)

In a conformally flat weakly Ricci-symmetric space-time, let the Ricci scalar be constant, and then Equation (45) reduces to

$$\kappa T_{ik}^{curv}={\displaystyle \frac{1}{2}}{g}_{ik}(f-G{f}_G-R{f}_R)-(f_R-1)(R_{ik}-{\displaystyle \frac{1}{2}}{g}_{ik}R).$$

(52)

Using Equation (51) in the above equation yields

$$\kappa T_{ik}^{curv}=({\displaystyle \frac{f}{2}}-{\displaystyle \frac{5R^2}{12}}{f}_G-{\displaystyle \frac{R}{2}})g_{ik}-(R{f}_R-R){\lambda }_i{\lambda }_k.$$

(53)

From Equations (43), (44) and (53), we acquire

$$\begin{array}{ccc}\hfill & & \kappa p^{\left(m\right)}{g}_{ij}+\kappa (p^{\left(m\right)}+{\mu }^{\left(m\right)}){\lambda }_i{\lambda }_k\hfill \\ & & +({\displaystyle \frac{f}{2}}-{\displaystyle \frac{5R^2}{12}}{f}_G-{\displaystyle \frac{R}{2}})g_{ik}-(R{f}_R-R){\lambda }_i{\lambda }_k\hfill \\ & & =\kappa p^{\mathrm{eff}}{g}_{ij}+\kappa (p^{\mathrm{eff}}+{\mu }^{\mathrm{eff}}){\lambda }_i{\lambda }_k,\hfill \end{array}$$

(54)

Multiplying the last equation with ${\lambda }^i$, we infer that

$${\mu }^{\mathrm{eff}}-{\mu }^{\left(m\right)}=-{\displaystyle \frac{1}{\kappa }}({\displaystyle \frac{f}{2}}-R{f}_R-{\displaystyle \frac{5R^2}{12}}{f}_G+{\displaystyle \frac{R}{2}}).$$

(55)

Multiplying Equation (54) with $g^{ik}$ and using the last equation, we obtain

$$p^{\mathrm{eff}}-p^{\left(m\right)}={\displaystyle \frac{1}{\kappa }}({\displaystyle \frac{f}{2}}-{\displaystyle \frac{5R^2}{12}}{f}_G-{\displaystyle \frac{R}{2}}).$$

(56)

In the literature, many models of $f(R,G)$ theory have been presented. We examine our findings using two distinct, well-known models in this part. For the sake of simplicity, we will analyse the various energy conditions for both models using the vacuum scenario in [26], which is $p^{\left(m\right)}={\mu }^{\left(m\right)}=0$.

We are now focusing on the following models:

• A. $f(R,G)=\sqrt{G}+R$

This type of $f(R,G)$ model was also taken into consideration by Myrzakulov et al. [40]. For this instance, the effective pressure and the effective energy density for a perfect fluid matter is given by

$$p^{\mathrm{eff}}={\displaystyle \frac{1}{\kappa }}[{\displaystyle \frac{\sqrt{G}+R}{2}}-{\displaystyle \frac{5R^2}{24\sqrt{G}}}-{\displaystyle \frac{R}{2}}].$$

(57)

$${\mu }^{\mathrm{eff}}={\displaystyle \frac{1}{\kappa }}[-{\displaystyle \frac{\sqrt{G}+R}{2}}+{\displaystyle \frac{5R^2}{24\sqrt{G}}}+{\displaystyle \frac{3R}{2}}].$$

(58)

Now, we demonstrate the ECs for this setup using Equations (57) and (58). To draw the following figures, we set $\kappa =1$, $G\in [1.5,3]$ and $R\in [0,2]$.

Figure 1 illustrates that the energy density is positive for the ranges of parameters $G\in [1.5,3]$ and $R\in [0,2]$. The $p^{\mathrm{eff}}+{\mu }^{\mathrm{eff}}$ profile, which produces a positive value, is shown in Figure 2. Hence, the null energy condition and weak energy condition are verified. From the ${\mu }^{\mathrm{eff}}-\left|p^{\mathrm{eff}}\right|$ profile in Figure 3, we can see that the dominant energy condition is failed. We can see from Figure 4 that the strong energy condition is also verified.

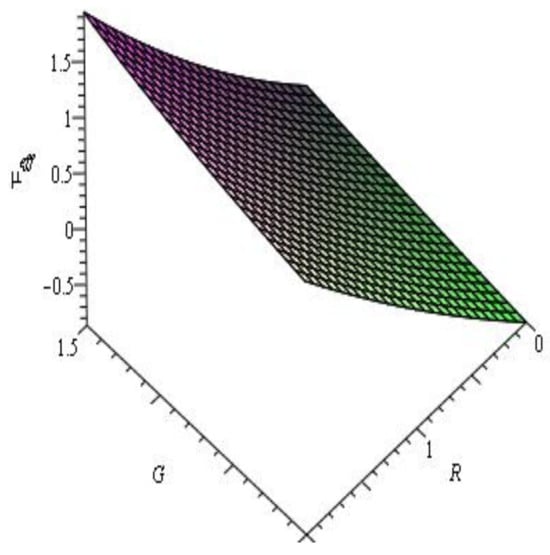
Figure 1. Evolution of ${\mu }^{\mathrm{eff}}$.

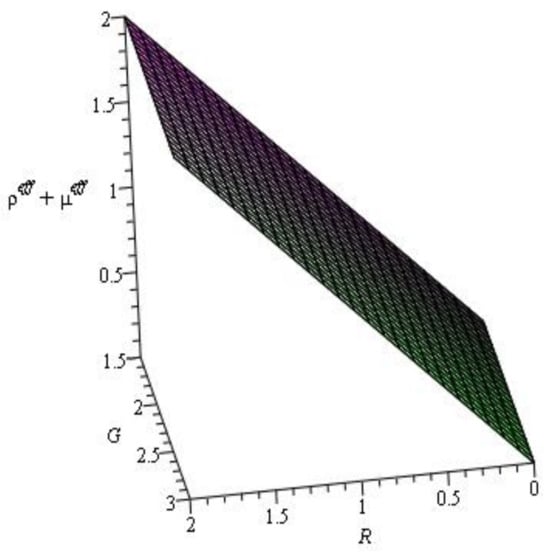
Figure 2. Evolution of $p^{\mathrm{eff}}+{\mu }^{\mathrm{eff}}$.

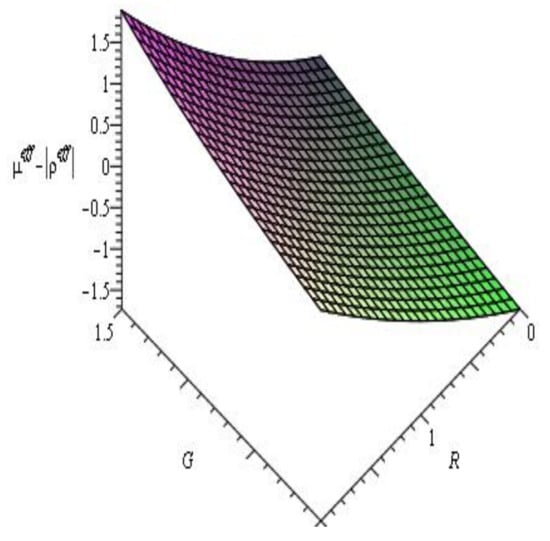
Figure 3. Evolution of ${\mu }^{\mathrm{eff}}-\left|p^{\mathrm{eff}}\right|$.

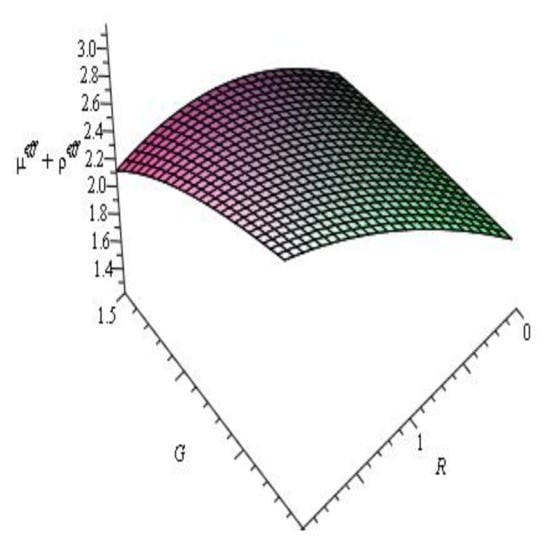
Figure 4. Evolution of $3p^{\mathrm{eff}}+{\mu }^{\mathrm{eff}}$.

• B. $f(R,G)=GlnG+R^2$

This type of $f(R,G)$ model was also considered by Sebastian Bahamonde et al. [41]. Here, the effective pressure and the effective energy density for a perfect fluid matter are written by

$$p^{\mathrm{eff}}={\displaystyle \frac{1}{\kappa }}[{\displaystyle \frac{GlnG+R^2}{2}}-{\displaystyle \frac{5R^2}{12}}(1+lnG)-{\displaystyle \frac{R}{2}}].$$

(59)

$${\mu }^{\mathrm{eff}}={\displaystyle \frac{1}{\kappa }}[-{\displaystyle \frac{GlnG+R^2}{2}}+{\displaystyle \frac{5R^2}{12}}(1+lnG)+2R^2-{\displaystyle \frac{R}{2}}].$$

(60)

We are now able to discuss the energy conditions for this setup using Equations (59) and (60). To draw the following figures, we set $\kappa =1$, $G\in [1.5,3]$ and $R\in [0,2]$.

Figure 5 shows that the behavior of the energy density is positive for the ranges of parameters $G\in [1.5,3]$ and $R\in [0,2]$. Figure 6 shows the ${\mu }^{\mathrm{eff}}-\left|p^{\mathrm{eff}}\right|$ profile, which also produces a positive value. Therefore, the null energy condition and weak energy condition are satisfied. From Figure 7, we can conclude that the dominant energy condition is violated. Figure 8 shows that the strong energy condition is also verified.

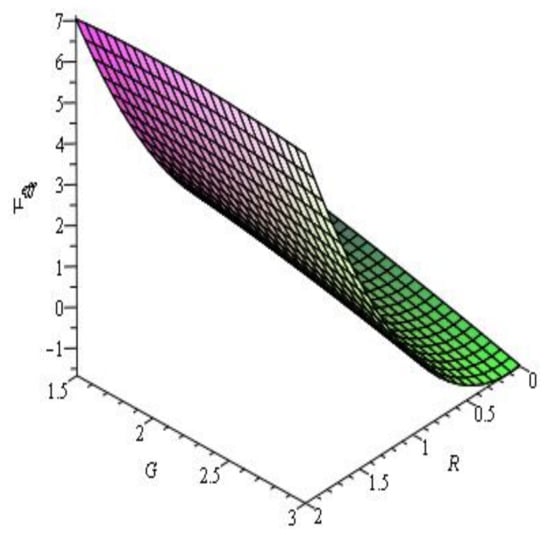
Figure 5. Evolution of ${\mu }^{\mathrm{eff}}$.

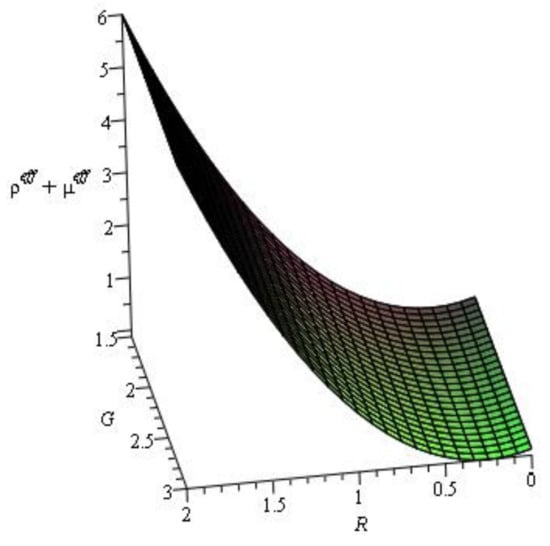
Figure 6. Evolution of $p^{\mathrm{eff}}+{\mu }^{\mathrm{eff}}$.

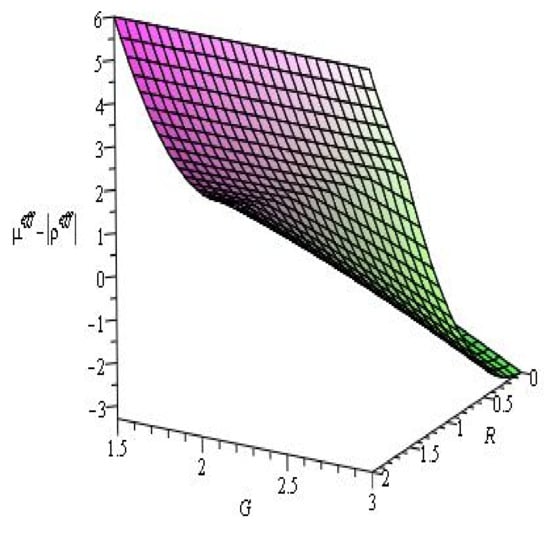
Figure 7. Evolution of ${\mu }^{\mathrm{eff}}-\left|p^{\mathrm{eff}}\right|$.

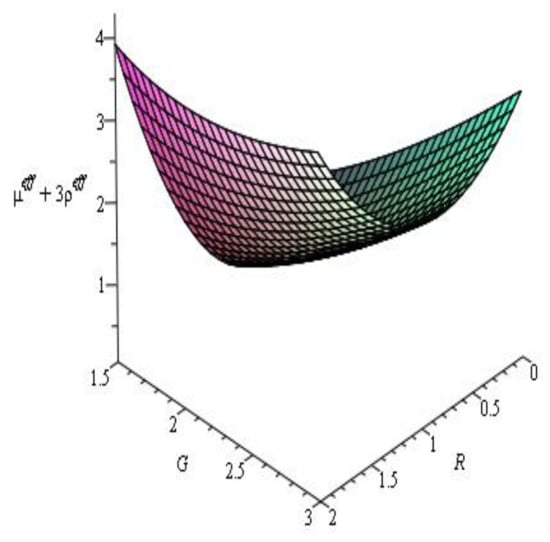
Figure 8. Evolution of $3p^{\mathrm{eff}}+{\mu }^{\mathrm{eff}}$.

Lastly, we choose the well-known flat Friedmann–Robertson–Walker metric

$$d{s}^2=a^2\left(t\right)\left(d{x}_1^2+d{x}_2^2+d{x}_3^2\right)-d{t}^2,$$

(61)

where the universe’s scale factor is denoted by $a\left(t\right)$. The cosmological parameters—Hubble ($\mathcal{H}$), jerk (j), deceleration (q) and snap (s)—are found in Taylor’s series expansion of a(t). Analysing these parameters helps us to understand the cosmic structure better. The accelerated expansion is investigated in [11], on the assumption that unique deceleration parameters emerge throughout the universe. The self-stability of cosmological models in the present universe is examined using these parameters in [12]. From the Friedmann–Robertson–Walker background, the field equations for $f(R,G)$ gravity are shown by

$$8\mathcal{H}\dot{\mathcal{H}}\dot{f_G}+2\dot{\mathcal{H}}{f}_R=\mathcal{H}\dot{f_R}+4{\mathcal{H}}^3\dot{f_G}-\ddot{f_R}-4{\mathcal{H}}^2\ddot{f_G},$$

(62)

$$24{\mathcal{H}}^3\dot{f_G}+6{\mathcal{H}}^2{f}_R=f_{R}R+G{f}_G-6\mathcal{H}\dot{f_R}-f(R,G),$$

(63)

where $\mathcal{H}={\displaystyle \frac{\dot{a}}{a}}$ and overdot $\equiv {\displaystyle \frac{d}{dt}}$. Further, we infer that

$$R=6(\dot{\mathcal{H}}+2{\mathcal{H}}^2)$$

(64)

and

$$G=24{\mathcal{H}}^2(\dot{\mathcal{H}}+{\mathcal{H}}^2).$$

(65)

Using the Equations (51), (64) and (65), we acquire

$${\mathcal{H}}^2={\displaystyle \frac{5R}{36}}\mathrm{and}\dot{\mathcal{H}}={\displaystyle \frac{R}{9}}.$$

(66)

Since $\mathcal{H}={\displaystyle \frac{\dot{a}}{a}}$, then ${\displaystyle \frac{\dot{a}}{a}}={\displaystyle \frac{\sqrt{5R}}{6}}$. From these, we can easily calculate

$$\ddot{a}=a(\dot{\mathcal{H}}-{\mathcal{H}}^2),$$

(67)

$$\stackrel{⃛}{a}=a(\ddot{\mathcal{H}}-\mathcal{H}\dot{\mathcal{H}}-{\mathcal{H}}^3)$$

(68)

and

$$\stackrel{⃜}{a}=a(\stackrel{⃛}{\mathcal{H}}-{\dot{\mathcal{H}}}^2-4{\mathcal{H}}^2\dot{\mathcal{H}}-{\mathcal{H}}^4)$$

(69)

We then describe acceleration, velocity, jerk and snap in the context of cosmology using an analogy to classical mechanics. The deceleration, jerk and snap parameters are written by

$$q=-{\displaystyle \frac{1}{{\mathcal{H}}^2}}{\displaystyle \frac{\ddot{a}}{a}},j={\displaystyle \frac{1}{{\mathcal{H}}^3}}{\displaystyle \frac{\stackrel{⃛}{a}}{a}}\mathrm{and}s={\displaystyle \frac{1}{{\mathcal{H}}^4}}{\displaystyle \frac{\stackrel{⃜}{a}}{a}},$$

(70)

respectively. Making use of Equations (67)–(69) in (70), we provide $q={\displaystyle \frac{1}{5}}$, $j=-{\displaystyle \frac{9}{5}}$ and $s=-{\displaystyle \frac{89}{25}}$, and hence we get

$$40q-20j+25s+13=0.$$

(71)

Therefore, for a conformally flat weakly Ricci-symmetric space-time fulfilling $f(R,G)$ gravity, the jerk, deceleration and snap parameters are connected by (71).

4. Discussion

Modified gravitational theories are considered as the most exciting and promising approach to examine the current cosmic expansion since they include extra higher-order curvature terms. Here, we study $f(R,G)$ gravity models with the geometric constraint of a conformally flat weakly Ricci-symmetric space-time. The various energy conditions are good candidates to investigate the self-consistency of the modified gravity, and these energy conditions may be found using the well-known Raychaudhuri equation. The null, weak, dominant and strong energy conditions under $f(R,G)$ gravity in a conformally flat weakly Ricci-symmetric space-time have all been examined in this work. Two distinct $f(R,G)$ models have been considered: $f(R,G)=\sqrt{G}+R$ and $f(R,G)=GlnG+R^2$. We conclude that in the current scenario, the dominant energy condition exhibits negative behavior for both models, but the null energy condition is always fulfilled. The weak and strong energy requirements are satisfied when $G\in [1.5,3]$ and $R\in [0,2]$ for the two models. The present observational data show the universe’s accelerated expansion, and are thus strongly consistent with both models.

It is possible to investigate modified gravity theories in order to find new theoretical predictions and behaviors that are not present in more conventional general relativity theories. This enables better comprehension of the fundamental laws governing the cosmos. They could provide a different explanation for late-time cosmic acceleration than the generally accepted general relativity theory. This variety of theories is necessary to build a comprehensive knowledge of cosmic acceleration. We examine energy conditions in this setting to assess the validity of the $f(R,G)$ gravity theory. Verifying that the theory fulfills a number of energy conditions is crucial to demonstrating its validity. For late-time cosmology, comprehending the energy conditions and the effects of $f(R,G)$ gravity can have more significant consequences for cosmological models and our comprehension of the universe’s evolution. Using a logarithm and exponential function, this new study will undoubtedly provide some support for research into the cosmos’ late-time acceleration.