Darwiche and Pearl’s Iterated Belief Revision: Not Always Spohn-Expressible

Abstract

The problem of iterated belief revision, which concerns how rational agents modify their beliefs in response to new information over time, lies at the core of understanding rational belief change. This article examines the interplay between the following two prominent frameworks for iterated belief revision: the qualitative Darwiche and Pearl’s approach (abbrev. DP approach) and the quantitative Spohn conditionalization. In particular, we prove that the DP approach is too liberal (under-constrained) to capture Spohn’s conditionalization (confined to revision scenarios); hence, the former cannot be regarded as a precise qualitative counterpart of the latter. Against this background, we provide insights into the essential semantic constraints on total preorders over the possible worlds needed to strengthen the DP approach and achieve alignment with Spohn’s method.

1. Introduction

The seminal work of Alchourrón, Gärdenfors, and Makinson [1], gave rise to a versatile and widely-accepted formal framework, the so-called AGM paradigm, which studies the dynamics of knowledge, a cornerstone subject of Artificial Intelligence. Within the AGM paradigm [1], the belief corpus of an agent is modelled as a logical theory K of an underlying logic language, also referred to as a belief set; the epistemic input (i.e., new information) is represented as a logical sentence $\phi$ of the language; and the revision of K by $\phi$ is encoded into a revision function * that maps K and $\phi$ to a (revised) belief set $K\ast \phi$. A set of eight postulates, known as the AGM postulates for revision, circumscribes the territory of all rational revision functions, named AGM revision functions.

It has been concretely shown that iterated revision is not properly addressed by the AGM paradigm; see [2,3,4]. One of the first proposals dealing with this important issue is Spohn’s conditionalization, a natural shifting process that operates on quantitative structures that represent preference information, the so-called ordinal conditional functions (OCFs) [5]. (As a matter of fact, Spohn’s conditionalization was proposed by Spohn as a general belief-change method, which implements both revision and contraction. It proves to be the case, however, that it inherently solves the iterated-revision problem.) Inspired by Spohn’s work, which slightly deviates from the spirit of the AGM paradigm, Darwiche and Pearl introduced four new postulates, called the DP postulates, that supplement the AGM postulates for revision in regulating successive revisions [6]; in a sense, the DP postulates are “trying to imitate” the transitions dictated by Spohn’s conditionalization. The well-accepted framework developed by Darwiche and Pearl is typically referred to as the DP approach. For a survey on the iterated-revision problem, the interested reader is referred to [7], in which, beyond a concrete demonstration of this issue, a number of other notable proposals addressing it are reported.

It turned out that not all the DP postulates, as originally introduced in [6], were consistent with the AGM postulates for revision [8]. The inconsistency was resolved in a subsequent work by Darwiche and Pearl [2], in which revision functions do not operate on belief sets (as it was the case in [6]), but on some richer structures, called belief states (also referred to as epistemic states). It is noteworthy that Darwiche and Pearl claim that the shift from belief sets to belief states is not necessitated by technical reasons alone, as conceptual considerations also point to the same direction. Although several properties of belief states were identified by Darwiche and Pearl in [2] (such as that each belief state is associated with a belief set), no explicit definition of this concept was provided. Nevertheless, the nature of belief states has been the focus of recent studies [9,10,11,12], which delve into the suitability of structures such as total preorders over possible worlds and OCFs for effectively representing belief states. In order to reflect the switch from belief sets to belief states, Darwiche and Pearl modified the AGM postulates for revision accordingly; we shall refer to the revision functions satisfying these modified postulates as modified AGM revision functions and to the modified AGM revision functions that satisfy the DP postulates as DP revision functions.

The aim of this article is a detailed investigation of the relationship between the qualitative DP approach and the quantitative Spohn conditionalization. In particular, the following contributions are made:

• First, we define a special type of modified AGM revision functions, which we call Spohn-expressible revision functions, that are perfectly aligned with the shifting process of Spohn’s conditionalization, confined to revision scenarios.
• We prove that there are DP revision functions that are not Spohn-expressible, meaning that they cannot be encoded/emulated through Spohn’s conditionalization. Hence, we show that the DP approach is too liberal (under-constrained) to capture the latter mechanism, and therefore, the DP approach is not a precise qualitative counterpart of Spohn’s proposal.
• Against this background, we introduce two new semantic postulates that every Spohn-expressible revision function respects, constituting the necessary conditions for Spohn expressibility. The proposed postulates impose constraints on the total preorders over possible worlds, and in doing so, strengthen the DP approach.

The interplay between aspects of the DP approach and Spohn’s proposal has not been left unattended in the literature, most notably in recent works [13,14,15]. In [13], Haldimann and Kern-Isberner examine a collection of mappings between OCFs and total preorders over possible worlds, proposing postulates to preserve key properties such as syntax splitting, and enabling a seamless method transfer between these frameworks. Kern-Isberner et al. in [14] generalize the kinematics principle—a well-known and powerful principle which ensures that changing the probabilities of facts does not unnecessarily change conditional probabilities—a qualitative iterated revision, when belief states are represented by total preorders over possible worlds. To study the kinematics principle, the authors defined a conditionalization for the total preorders which inherit essential features from the conditionalization of OCFs. Lastly, Kern-Isberner et al. in [15] shed light on the significance of empty layers in OCFs, proposing concepts like revision equivalence, which postulate the equivalence of OCFs after (most general) revision operations.

The rest of this article is structured as follows: The next section introduces the basic terminology and notation that we shall use throughout our exposition, followed by a brief overview of the AGM paradigm (Section 3). Section 4 and Section 5 introduce Spohn’s conditionalization and the DP approach, respectively. Section 6 is devoted to the definition of Spohn-expressible revision functions, whereas, Section 7 studies the connection between Spohn-expressible and DP revision functions. Thereafter, Section 8 provides the necessary conditions for Spohn expressibility. The article closes with a brief conclusion, reporting interesting avenues for future research.

2. Formal Preliminaries

This section is devoted to the introduction of the required formal background of the study.

• Language. We shall work with a propositional language $\mathcal{L}$, built over a finite, non-empty set $\mathcal{P}$ of atoms (propositional variables), using the standard Boolean connectives ∧ (conjunction), ∨ (disjunction), → (implication), ↔ (equivalence), ¬ (negation), and governed by classical propositional logic. The classical consequence relation is denoted by ⊧.
• Belief Sets. For a set of sentences $\mathrm{\Gamma }$ of $\mathcal{L}$, $Cn\left(\mathrm{\Gamma }\right)$ denotes the set of all logical consequences of $\mathrm{\Gamma }$, i.e., $Cn\left(\mathrm{\Gamma }\right)=\left\{\phi \in \mathcal{L}:\mathrm{\Gamma }\vDash \phi \right\}$. An agent’s set of beliefs will be modelled by a theory, also referred to as a belief set. A theory K of $\mathcal{L}$ is a deductively closed set of sentences of $\mathcal{L}$, meaning that $K=Cn\left(K\right)$. For a theory K and a sentence $\phi$ of $\mathcal{L}$, $K+\phi$ denotes the expansion of K by $\phi$, which is defined as $K+\phi =Cn\left(K\cup \left\{\phi \right\}\right)$.
• Possible Worlds. A literal is an atom $p\in \mathcal{P}$ or its negation $\neg p$. A possible world (abbrev. world) r is a consistent set of literals, such that, for each atom $p\in \mathcal{P}$, either $p\in r$ or $\neg p\in r$. The set of all possible worlds is denoted by $\mathbb{M}$. For a sentence or set of sentences $\phi$ of $\mathcal{L}$, $\left[\phi \right]$ is the set of worlds at which $\phi$ is true. For a set of worlds $V\subseteq \mathbb{M}$, we denote by $th\left(V\right)$ the set of sentences (theory) satisfied by all worlds in V. If $V=⌀$, then, vacuously, $th\left(V\right)=\mathcal{L}$.
• Binary Relations. A partial preorder (abbrev. preorder) over a set V is any reflexive, transitive binary relation on V. A preorder ⪯ over V is called total iff any two elements of V are ⪯-comparable; i.e., for all $r,r^{\prime }\in V$, $r⪯r^{\prime }$, or $r^{\prime }⪯r$. The strict part of ⪯ is denoted by ≺, i.e., $r\prec r^{\prime }$ iff $r⪯r^{\prime }$ and $r^{\prime }r$. The indifference part of ⪯ is denoted by ≈, i.e., $r\approx r^{\prime }$ iff $r⪯r^{\prime }$ and $r^{\prime }⪯r$. Furthermore, min$(V,⪯)$ denotes the set of all ⪯-minimal elements in V; that is, min$(V,⪯)=\{r\in V:$ for all $r^{\prime }\in V$, $r^{\prime }⪯r$ entails $r⪯r^{\prime }\}$. Whenever the set V contains (natural) numbers, we shall simply write min$\left(V\right)$ to denote the minimum number in V. Lastly, for a binary relation R, $tr\left(R\right)$ denotes the transitive closure of R.

3. The AGM Paradigm

Within the AGM paradigm [1], a revision function * is modelled as a binary function that maps a theory K and a sentence $\phi \in \mathcal{L}$ to a revised theory $K\ast \phi$. The AGM postulates for revision, presented subsequently, circumscribe the territory of all rational revision functions, the so-called AGM revision functions.

$(\mathbf{K}\ast \mathbf{1})$	$K\ast \phi$ is a belief set.
$(\mathbf{K}\ast \mathbf{2})$	$\phi \in K\ast \phi$.
$(\mathbf{K}\ast \mathbf{3})$	$K\ast \phi \subseteq K+\phi$.
$(\mathbf{K}\ast \mathbf{4})$	If $\neg \phi \notin K$, then $K+\phi \subseteq K\ast \phi$.
$(\mathbf{K}\ast \mathbf{5})$	If $\phi$ is consistent, then $K\ast \phi$ is also consistent.
$(\mathbf{K}\ast \mathbf{6})$	If $Cn\left(\left\{\phi \right\}\right)=Cn\left(\left\{\psi \right\}\right)$, then $K\ast \phi =K\ast \psi$.
$(\mathbf{K}\ast \mathbf{7})$	$K\ast (\phi \wedge \psi )\subseteq (K\ast \phi )+\psi$.

$(\mathbf{K}\ast \mathbf{8})$

If $\neg \psi \notin K\ast \phi$, then $(K\ast \phi )+\psi \subseteq K\ast (\phi \wedge \psi )$.

A detailed discussion on the AGM postulates for revision $(K\ast 1)$–$(K\ast 8)$ can be found in [16,17]. Herein, we only state that, in the limiting case where the new information $\phi$ does not contradict the initial belief set K (i.e., $\neg \phi \notin K$), the conjunction of postulates $(K\ast 3)$ and $(K\ast 4)$ entails that revision reduces to expansion, and therefore, $K\ast \phi =K+\phi$. To avoid a cumbersome presentation, we shall focus our subsequent analysis on the principal case of revision of consistent belief sets by consistent epistemic input $\phi$, which contradicts the initial belief set K (i.e., $\neg \phi \in K$).

As demonstrated by Katsuno and Mendelzon [18], any AGM revision function can be semantically constructed through a special kind of total preorders over all possible worlds, called faithful preorders.

Definition 1 

(Faithful Assignment Over Belief Sets [18]). A function that maps each belief set K to a total preorder ${⪯}_K$ over the possible worlds of $\mathbb{M}$ is a faithful assignment over belief sets iff $\left[K\right]\ne ⌀$ entails $\left[K\right]=min(\mathbb{M},{⪯}_K)$.

The total preorder ${⪯}_K$ of Definition 1 is typically referred to as a preorder faithful to K. Intuitively, the assertion $r{⪯}_K{r}^{\prime }$ states that the world r is at least as plausible as the world $r^{\prime }$ relative to K.

The following theorem characterizes the class of revision functions induced from faithful assignments over belief sets.

Theorem 1 

([18]). A revision function * satisfies postulates $(K\ast 1)$–$(K\ast 8)$ iff there exists a faithful assignment over belief sets that maps each belief set K to a total preorder ${⪯}_K$ over $\mathbb{M}$, such that, for any $\phi \in \mathcal{L}$, the following holds:

$$(\mathbf{F}\ast )\hspace{1em}K\ast \phi =th\left(min\right(\left[\phi \right],{⪯}_K\left)\right).$$

The AGM paradigm is undoubtedly a prominent framework for implementing rational belief change. Nevertheless, convincing examples have illustrated that the AGM postulates for revision are liberal in their treatment of successive revisions, as they allow unreasonable revision behaviours [2,3,4]. The next two sections discuss two well-accepted methods addressing this significant issue, namely, the quantitative Spohn conditionalization (Section 4) and the qualitative DP approach (Section 5).

4. Spohn’s Conditionalization

Spohn argues that the iterated-revision problem “[i]s not just some important problem; it is vital to belief revision theory” ([3], p. 2). His proposal addressing this issue is a natural shifting process that operates on quantitative structures that represent preference information, the so-called ordinal conditional functions (OCFs) [5].

Definition 2 

(OCF [5]). An OCF κ is a function from the set $\mathbb{M}$ of possible worlds to the class of ordinals, such that at least one world is assigned the ordinal 0.

Like in [19], for mathematical simplicity, we take the range of an OCF $\kappa$ to be the non-negative integers. For a world r, we call $\kappa \left(r\right)$ the rank of r. Intuitively, $\kappa$ assigns a plausibility grading to worlds; the larger the $\kappa \left(r\right)$ is for some world r, the less plausible r is. This plausibility grading can easily be extended to sentences of $\mathcal{L}$ by requiring that the rank of a sentence be the smallest rank assigned to a world that satisfies the sentence.

Definition 3 

(Rank of a Sentence [5]). For a consistent sentence $\phi \in \mathcal{L}$, $\kappa \left(\phi \right)$ is the κ-rank of the most plausible φ-world, i.e., $\kappa \left(\phi \right)=min\left(\left\{\kappa \left(r\right):r\in \left[\phi \right]\right\}\right)$.

The most plausible worlds (i.e., those whose $\kappa$-rank is zero) define the belief set with which $\kappa$ is associated. In particular, this can be expressed as follows:

Definition 4 

(Belief Set of an OCF [5]). The belief set associated with an OCF κ is denoted by $B\left(\kappa \right)$ and is defined as $B\left(\kappa \right)=th\left(\left\{r\in \mathbb{M}:\kappa \left(r\right)=0\right\}\right)$.

Given an OCF $\kappa$, a sentence $\phi$ of $\mathcal{L}$, and a non-negative integer d expressing the degree of firmness by which an agent accepts $\phi$, the $\langle \phi ,d\rangle$-conditionalization of $\kappa$ produces a new OCF, which is denoted by $\kappa •\langle \phi ,d\rangle$ and is defined as follows:

$$\kappa •\langle \phi ,d\rangle \left(r\right)=\left\{\begin{array}{cc}\kappa \left(r\right)-\kappa \left(\phi \right)\hfill & \mathrm{if}r\in \left[\phi \right]\hfill \\ \\ \kappa \left(r\right)-\kappa (\neg \phi )+d\hfill & \mathrm{if}r\in [\neg \phi ]\hfill \end{array}\right.$$

From the above definition, a number of major differences between Spohn’s conditionalization and the revision policies dictated by the AGM paradigm is evident. First, Spohn’s construction quantitatively defines both revision (when $d>0$) and contraction (when $d=0$) operators; on the contrary, the AGM postulates that for revision there are purely qualitative constraints for revision operators. Second, Spohn’s approach demands enriched epistemic input, namely, a logical formula accompanied by its degree of firmness, whereas, an AGM revision function works with a mere logical formula. Despite those important distinctions, Spohn’s conditionalization, confined to revision scenarios, is compliant with the AGM postulates for revision, in the sense that, for any degree of firmness $d>0$, the revision function * defined as $B\left(\kappa \right)\ast \phi =th\left(\left\{r\in \mathbb{M}:\kappa •\langle \phi ,d\rangle \left(r\right)=0\right\}\right)$ satisfies postulates $(K\ast 1)$–$(K\ast 8)$, as outlined in [5,16].

The next concrete example illustrates the shifting process of Spohn’s conditionalization.

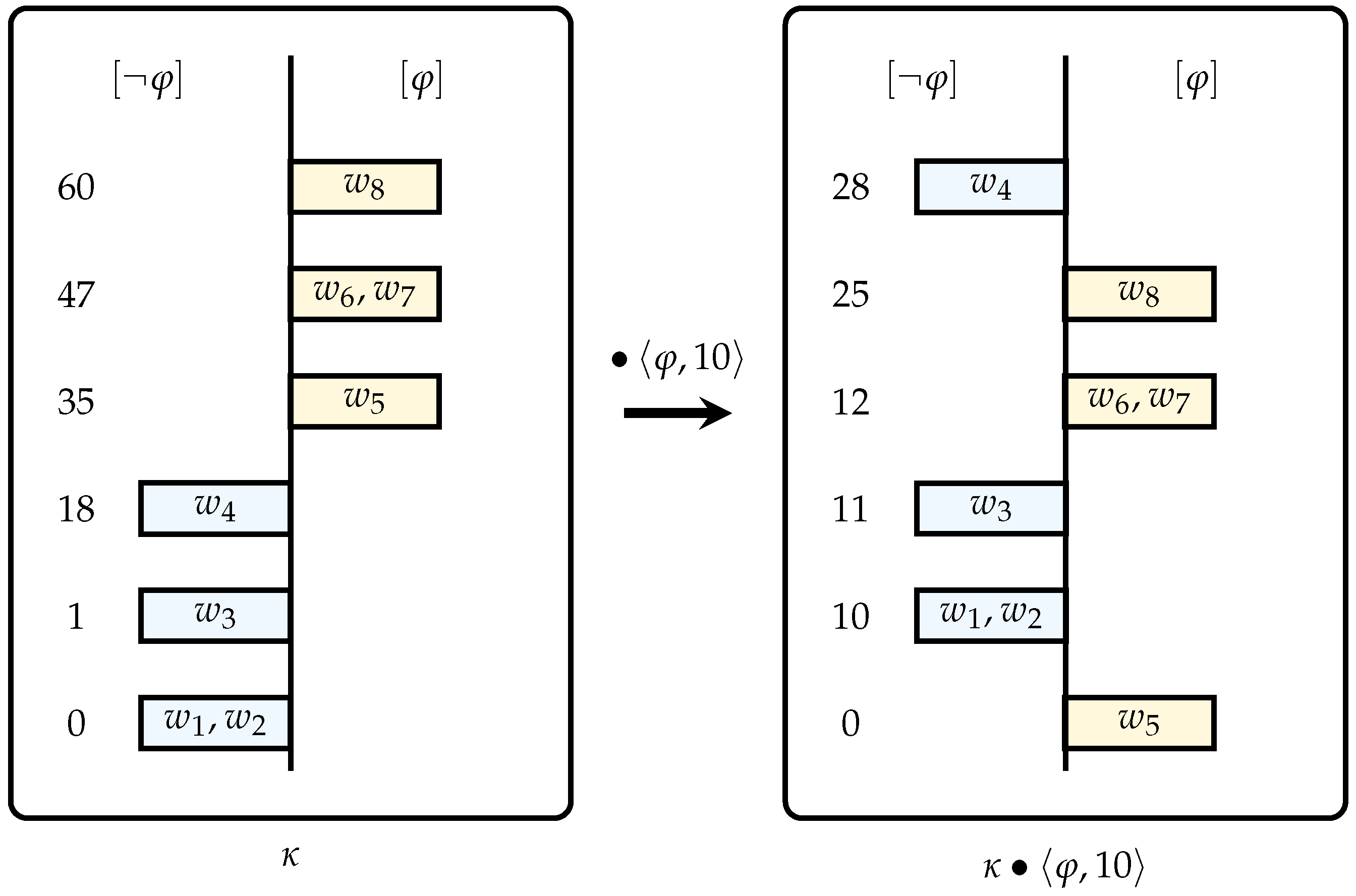
Example 1 

(Spohn’s Conditionalization). Suppose that $\mathcal{L}$ is built from only four atoms, let $\mathbb{M}=\{w_1,w_2,\dots ,w_8\}$ be the set of the eight possible worlds, and let φ be a sentence of $\mathcal{L}$ such that $\left[\phi \right]=\{w_5,w_6,w_7,w_8\}$. Moreover, let κ be the OCF depicted in Figure 1; clearly, $B\left(\kappa \right)=th\left(\{w_1,w_2\}\right)$. Assuming a degree of firmness $d=10$ for φ, the $\langle \phi ,d\rangle$-conditionalization of κ produces the OCF $\kappa •\langle \phi ,d\rangle$ of Figure 1. For producing $\kappa •\langle \phi ,d\rangle$ from κ, all φ-worlds are uniformly shifted “downwards” against all $\neg \phi$-worlds, until the most κ-plausible of them hit the bottom of the rank. On the other hand, all $\neg \phi$-worlds are uniformly shifted “upwards”, until the most κ-plausible of them are at a distance d from the bottom.

Recall that we have restricted our study to the interesting case of revision by epistemic input $\phi$ that contradicts the initial state of belief. In the context of revising OCFs, this sets the assumption that $\kappa \left(\phi \right)>0$, $\kappa (\neg \phi )=0$ and $d>0$; hence, in that case, the agent initially believes $\neg \phi$ and, after revision, the agent ends up believing $\phi$ with a degree of firmness $\kappa •\langle \phi ,d\rangle (\neg \phi )=d$ (see Example 1).

5. Darwiche and Pearl’s Approach

Darwiche and Pearl, drawing inspiration from Spohn’s quantitative construction, developed a qualitative framework aligned with the AGM paradigm, the so-called DP approach, which is perhaps one of the most influential models addressing the iterated-revision problem [2,6]. In the core of the DP approach lies a set of four postulates, typically referred to as the DP postulates, regulating successive revisions.

5.1. Modified AGM Postulates for Revision

Darwiche and Pearl originally proposed their approach for iterated belief revision in [6]. Nevertheless, partially in response to a problem identified by Lehmann [8]—who showed that the second DP postulate, as originally stated, was inconsistent with the AGM postulates for revision—the DP approach was later modified in [2]. In the modified version, Darwiche and Pearl defined revision functions to operate on belief states (also referred to as epistemic states), rather than on belief sets. Accordingly, for the modified revision functions of the DP approach that operate on belief states, we shall use the symbol ∘ to differentiate them from the revision function * of the original AGM paradigm. Hence, a modified revision function ∘ is a binary function that maps a belief state S and a sentence $\phi \in \mathcal{L}$ to a revised belief state $S\circ \phi$.

While Darwiche and Pearl did not provide an explicit definition of belief states, their exposition made clear that to each belief state S corresponds a total preorder over all possible worlds. From this total preorder over possible worlds, one can in turn determine the (unique) belief set that is associated with S, denoted by $B\left(S\right)$.

In order to reflect the shift from belief sets to belief states, Darwiche and Pearl recast the AGM postulates for revision $(K\ast 1)$–$(K\ast 8)$ into the following set of postulates $(S\circ 1)$–$(S\circ 8)$, which, except from postulate $(S\circ 1)$, constrain only the belief sets of the involved belief states.

$(\mathbf{S}\circ \mathbf{1})$	$S\circ \phi$ is a belief state.
$(\mathbf{S}\circ \mathbf{2})$	$\phi \in B(S\circ \phi )$.
$(\mathbf{S}\circ \mathbf{3})$	$B(S\circ \phi )\subseteq B\left(S\right)+\phi$.
$(\mathbf{S}\circ \mathbf{4})$	If $\neg \phi \notin B\left(S\right)$, then $B\left(S\right)+\phi \subseteq B(S\circ \phi )$.
$(\mathbf{S}\circ \mathbf{5})$	If $\phi$ is consistent, then $B(S\circ \phi )$ is also consistent.
$(\mathbf{S}\circ \mathbf{6})$	If $Cn\left(\left\{\phi \right\}\right)=Cn\left(\left\{\psi \right\}\right)$, then $B(S\circ \phi )=B(S\circ \psi )$.
$(\mathbf{S}\circ \mathbf{7})$	$B\left(S\circ (\phi \wedge \psi )\right)\subseteq B(S\circ \phi )+\psi$.
$(\mathbf{S}\circ \mathbf{8})$	If $\neg \psi \notin B(S\circ \phi )$, then $B(S\circ \phi )+\psi \subseteq B\left(S\circ (\phi \wedge \psi )\right)$.

Postulates $(S\circ 1)$–$(S\circ 8)$, as well as the DP postulates that will follow, have been rephrased in the AGM notation. Note that the original version of $(S\circ 6)$ is slightly different from the one presented herein—see postulate (R*4) of [2]. In this article, we adopt the approach of Jin and Thielscher [4], and reformulate the original version of $(S\circ 6)$ so that it faithfully reflects the intuition of postulate $(K\ast 6)$ of the AGM paradigm. We shall call a modified revision function ∘modified AGM revision function iff it satisfies the modified AGM postulates for revision $(S\circ 1)$–$(S\circ 8)$. Analogously to Definition 1 of Section 3, Darwiche and Pearl proceed to the following definition.

Definition 5 

(Faithful Assignment over Belief States [2]). A function that maps each belief state S to a total preorder ${⪯}_S$ over the possible worlds of $\mathbb{M}$ is a faithful assignment over belief states iff $\left[B\right(S\left)\right]\ne ⌀$ entails $\left[B\left(S\right)\right]=min(\mathbb{M},{⪯}_S)$.

As stated, the belief set $B\left(S\right)$ associated with a belief state S can be extracted from the total preorder ${⪯}_S$ assigned at S. This is implied by Definition 5, according to which $B\left(S\right)$ is the theory corresponding to the ${⪯}_S$-minimal worlds, i.e., $B\left(S\right)=th\left(min(\mathbb{M},{⪯}_S)\right)$. Evidently, a belief state is a richer structure than a belief set, as two different belief states may be associated with the same belief set. This feature of belief states is crucial for resolving the original inconsistency of the DP approach with the AGM postulates for revision, identified by Lehmann [8].

Analogously to Theorem 1 of Section 3, the following theorem characterizes the class of modified revision functions induced from faithful assignments over belief states.

Theorem 2 

([2]). A modified revision function ∘ satisfies postulates $(S\circ 1)$–$(S\circ 8)$ iff there exists a faithful assignment over belief states that maps each belief state S to a total preorder ${⪯}_S$ over $\mathbb{M}$, such that, for any $\phi \in \mathcal{L}$, the following holds:

$$(\mathbf{F}\circ )\hspace{1em}B(S\circ \phi )=th\left(min(\left[\phi \right],{⪯}_S).\right)$$

The next remark is derived directly from Theorem 2.

Remark 1. 

Let ∘ be a modified AGM revision function, and let φ be an arbitrary sentence of $\mathcal{L}$. Given two distinct belief states S and $S^{\prime }$ such that $B\left(S\right)=B\left(S^{\prime }\right)$, it may be the case that $S\circ \phi \ne S^{\prime }\circ \phi$. That is to say, a modified AGM revision function may φ-revise differently two distinct belief states that are associated with the same belief set.

5.2. DP Postulates

To regulate successive revisions, Darwiche and Pearl introduced four additional postulates (DP1)–(DP4), known as the DP postulates and presented below, which supplement postulates $(S\circ 1)$–$(S\circ 8)$.

(DP1)	If $\phi \vDash \psi$, then $B\left(\right(S\circ \psi )\circ \phi )=B(S\circ \phi )$.
(DP2)	If $\phi \vDash \neg \psi$, then $B\left(\right(S\circ \psi )\circ \phi )=B(S\circ \phi )$.
(DP3)	If $\psi \in B(S\circ \phi )$, then $\psi \in B\left(\right(S\circ \psi )\circ \phi )$.
(DP4)	If $\neg \psi \notin B(S\circ \phi )$, then $\neg \psi \notin B\left(\right(S\circ \psi )\circ \phi )$.

The DP postulates—a discussion of which can be found in [2,7]—have a nice semantic characterization in terms of total preorders over possible worlds. In particular, Darwiche and Pearl proved that there is a one-to-one correspondence between (DP1)–(DP4) and the following constraints on possible worlds (R1)–(R4).

(R1)	If $r,r^{\prime }\in \left[\phi \right]$, then $r{⪯}_S{r}^{\prime }$ iff $r{⪯}_{S\circ \phi }{r}^{\prime }$.
(R2)	If $r,r^{\prime }\in [\neg \phi ]$, then $r{⪯}_S{r}^{\prime }$ iff $r{⪯}_{S\circ \phi }{r}^{\prime }$.
(R3)	If $r\in \left[\phi \right]$ and $r^{\prime }\in [\neg \phi ]$, then $r{\prec }_S{r}^{\prime }$ entails $r{\prec }_{S\circ \phi }{r}^{\prime }$.
(R4)	If $r\in \left[\phi \right]$ and $r^{\prime }\in [\neg \phi ]$, then $r{⪯}_S{r}^{\prime }$ entails $r{⪯}_{S\circ \phi }{r}^{\prime }$.

Constraints (R1)–(R4) associate the total preorder ${⪯}_S$, corresponding to the initial belief state S, with the total preorder ${⪯}_{S\circ \phi }$, corresponding to the belief state that results from the revision of S by $\phi$. Specifically, when S is revised by $\phi$, conditions (R1) and (R2) require that the comparative plausibility of $\phi$-worlds and $\neg \phi$-worlds, respectively, is not changed. Conditions (R3) and (R4), on the other hand, require that, if a $\phi$-world r is (strictly) more plausible than a $\neg \phi$-world $r^{\prime }$ at the initial state of belief, then r continues to be (strictly) more plausible than $r^{\prime }$ at the revised state of belief [4].

We shall call a modified AGM revision function that satisfies postulates (DP1)–(DP4) a DP revision function.

5.3. Independence Postulate

Jin and Thielscher argued that the DP postulates are quite liberal in certain revision scenarios [4,20]. On that basis, they proposed a new postulate, called the Independence postulate (Ind), which blocks the counter-intuitive behaviours allowed by the DP postulates.

(Ind)

If $\neg \psi \notin B(S\circ \phi )$, then $\psi \in B\left(\right(S\circ \psi )\circ \phi )$.

Interestingly, postulate (Ind) was studied independently in [21,22] as well. The semantic counterpart of postulate (Ind) in terms of total preorders over possible worlds is the following condition (IndR).

(IndR)

If $r\in \left[\phi \right]$ and $r^{\prime }\in [\neg \phi ]$, then $r{⪯}_S{r}^{\prime }$ entails $r{\prec }_{S\circ \phi }{r}^{\prime }$.

Jin and Thielscher proved that the Independence postulate is consistent with the conjunction of postulates $(S\circ 1)$–$(S\circ 8)$ and (DP1)–(DP4), as well as that it is strictly stronger than both (DP3) and (DP4). They also claimed that any rational modified AGM revision function ought to respect postulates (DP1), (DP2), and (Ind) [4,20].

6. Spohn-Expressible Revision Functions

For studying the relationship between the qualitative DP approach and the quantitative Spohn construction, we first proceed with the definition of a special type of modified AGM revision functions that are perfectly aligned with the shifting process of Spohn’s conditionalization. This is accomplished with the aid of the notion of imitation, defined subsequently.

Definition 6 

(Imitation). Let ∘ be a modified revision function, and let κ be an OCF. We shall say that κ imitates ∘ at a belief state S iff, for all finite sequences of sentences ${\phi }_1,\dots ,{\phi }_n\in \mathcal{L}$, there exist positive integers $d_1,\dots ,d_n$, such that the following holds:

$$B\left(\kappa •\langle {\phi }_1,d_1\rangle •\cdots •\langle {\phi }_n,d_n\rangle \right)=B\left(S\circ {\phi }_1\circ \cdots \circ {\phi }_n.\right)$$

Roughly speaking, an OCF $\kappa$ imitates a modified revision function ∘ at a belief state S whenever the ∘-revision of S by any finite sequence of sentences can be “mimicked” by the revision of $\kappa$ by the same sequence of sentences, in the sense that the resulting states of belief encompass identical belief content. This ensures that the OCF $\kappa$ is able to “track” the outcomes of ∘ step by step, leading to convergence between Spohn’s conditionalization and revision under ∘ on the same revised belief set. Observe that, if $\kappa$ imitates ∘ at S, then $B\left(\kappa \right)=B\left(S\right)$ (simply replace ${\phi }_1,\dots ,{\phi }_n$ in Definition 6 with a tautology).

Definition 7 

(Spohn-Expressible Revision Function). Let ∘ be a modified revision function. We shall say that ∘ is Spohn-expressible iff, for every belief state S, there exists an OCF that imitates ∘ at S. Otherwise, we shall say that ∘ is Spohn-inexpressible.

Essentially, Spohn-expressible revision functions can be considered as a qualitative analogue of Spohn’s conditionalization. As it is shown in the next section, the class of Spohn-expressible revision functions is a proper subclass of the class of DP revision functions that also respect postulate (Ind), as there exist DP revision functions satisfying (Ind) that are Spohn-inexpressible.

We close this section with Remark 2 that points out an important observation related to the Spohn expressibility of revision functions, when multiple belief states are associated with a single total preorder over worlds.

Remark 2. 

Suppose that multiple belief states are associated with each total preorder over the possible worlds. Even if an OCF κ imitates a modified AGM revision function ∘ at one particular belief state S, it may not imitate ∘ at another distinct belief state $S^{\prime }$, even if S and $S^{\prime }$ are both associated with the same total preorder over worlds. This is due to the fact that ∘ may revise differently the distinct belief states S and $S^{\prime }$, for the same epistemic input (compare with Remark 1 of Section 5).

7. Spohn-Expressible Revision Functions and DP Revision Functions

In this section, we take a closer look at the relation between Spohn-expressible and DP revision functions. To that end, we first prove, in Theorem 3 below, that all Spohn-expressible revision functions are DP revision functions that respect postulate (Ind).

Theorem 3. 

If a modified revision function ∘ is Spohn-expressible, then ∘ is a DP revision function that satisfies postulate (Ind).

Proof. 

Assume that a modified revision function ∘ is Spohn-expressible, and let S be an arbitrary belief state. Hence, there exists an OCF $\kappa$ that imitates ∘ at S. Let $\phi$ be any sentence of $\mathcal{L}$. Firstly, observe that, for any $d>0$, it is true that $B(\kappa •\langle \phi ,d\rangle )$=$th\left(\left\{r\in \left[\phi \right]:\kappa \left(r\right)=\kappa \left(\phi \right)\right\}\right)$. It follows, then, that there is a total preorder ${⪯}_S$ over $\mathbb{M}$, defined, for any $r,r^{\prime }\in \mathbb{M}$, as $r{⪯}_S{r}^{\prime }$ iff $\kappa \left(r\right)⩽\kappa \left(r^{\prime }\right)$, which is faithful to S (since $B\left(\kappa \right)=B\left(S\right)$), and for some $d>0$, $B(S\circ \phi )=B\left(\kappa •\langle \phi ,d\rangle \right)$=$th\left(\left\{r\in \left[\phi \right]:\kappa \left(r\right)=\kappa \left(\phi \right)\right\}\right)$=$th\left(min\right(\left[\phi \right],{⪯}_S\left)\right)$. Therefore, we derive from Theorem 2 that ∘ satisfies postulates $(S\circ 1)$–$(S\circ 8)$; thus, ∘ is a modified AGM revision function.

With an analogous line of reasoning, we can show that, for the total preorder ${⪯}_{S\circ \phi }$ corresponding to ∘ via (F∘), there exists a positive integer d such that, for any $r,r^{\prime }\in \mathbb{M}$, $r{⪯}_{S\circ \phi }{r}^{\prime }$ iff $\kappa •\langle \phi ,d\rangle \left(r\right)⩽\kappa •\langle \phi ,d\rangle \left(r^{\prime }\right)$. On the other hand, from the process of Spohn’s conditionalization (under our assumption that $\kappa \left(\phi \right)>0$, $\kappa (\neg \phi )=0$ and $d>0$), we derive the following:

(i) 

If $r,r^{\prime }\in \left[\phi \right]$, then $\kappa \left(r\right)⩽\kappa \left(r^{\prime }\right)$ iff $\kappa •\langle \phi ,d\rangle \left(r\right)⩽\kappa •\langle \phi ,d\rangle \left(r^{\prime }\right)$.

(ii) 

If $r,r^{\prime }\in [\neg \phi ]$, then $\kappa \left(r\right)⩽\kappa \left(r^{\prime }\right)$ iff $\kappa •\langle \phi ,d\rangle \left(r\right)⩽\kappa •\langle \phi ,d\rangle \left(r^{\prime }\right)$.

(iii) 

If $r\in \left[\phi \right]$ and $r^{\prime }\in [\neg \phi ]$, then $\kappa \left(r\right)⩽\kappa \left(r^{\prime }\right)$ entails $\kappa •\langle \phi ,d\rangle \left(r\right)<\kappa •\langle \phi ,d\rangle \left(r^{\prime }\right)$.

Then, conditions (i), (ii), and (iii) imply that ${⪯}_S$ and ${⪯}_{S\circ \phi }$ respect conditions (R1), (R2), and (IndR), respectively. This again entails that ∘ satisfies (DP1), (DP2), and (Ind), respectively. Since (Ind) implies both (DP3) and (DP4), we derive that ∘ is a DP revision function that satisfies (Ind), as desired. □

The inverse of Theorem 3 does not generally hold. That is to say, there exist DP revision functions that respect postulate (Ind) which are Spohn-inexpressible, and thus, they cannot be encoded/emulated by means of Spohn’s conditionalization. Theorem 4 proves the alluded result and essentially shows that the DP postulates are not a precise qualitative analogue of Spohn’s conditionalization, as expressed in its qualitative form through Spohn-expressible revision functions. Theorem 4 also proves that the Independence postulate (Ind) does not sufficiently constrain the class of DP revision functions so that it coincides with the class of Spohn-expressible revision functions.

Theorem 4. 

There exists a Spohn-inexpressible DP revision function ∘ that satisfies postulate (Ind).

Proof. 

We shall construct a revision scenario that exploits the ability of DP revision functions satisfying postulate (Ind) to permit “non-uniform” shifts in the plausibility of possible worlds—a behaviour not allowed by Spohn’s conditionalization.

In the context of this proof, we shall occasionally treat a set of literals as a sentence, i.e., the conjunction of all its literals, leaving it to the context to resolve any ambiguity; thus for example, in the expression “$\neg (w_1\vee w_2)$”, $w_1$ and $w_2$ are sentences of $\mathcal{L}$, whereas, in “$w_1{\prec }_S{w}_2$”, $w_1$ and $w_2$ are worlds of $\mathbb{M}$.

Assume that the set of atoms $\mathcal{P}$ contains at least three atoms, and let K be any theory such that $\left[K\right]=\left\{w_1\right\}$. Given that $\mathcal{P}$ contains at least three atoms, beyond $w_1$, there exist at least four other distinct worlds in $\mathbb{M}$; call these $w_2,w_3,w_4,w_5$. Let S be a belief state such that $B\left(S\right)=K$, and let ∘ be a DP revision function that satisfies postulate (Ind), which assigns at S (via (F∘)) the following faithful preorder ${⪯}_S$ over $\mathbb{M}$:

-

$w_1{\prec }_S{w}_2{\approx }_S{w}_3{\prec }_S{w}_4{\prec }_S{w}_5$.

-

$w_5{\prec }_{S}z$, for all $z\in \mathbb{M}-\{w_1,w_2,w_3,w_4,w_5\}$.

-

$z{\approx }_S{z}^{\prime }$, for all $z,z^{\prime }\in \mathbb{M}-\{w_1,w_2,w_3,w_4,w_5\}$.

Suppose that ∘ also assigns at the belief states $S\circ \neg (w_1\vee w_2)$ and $S\circ \neg (w_1\vee w_3)$ (via (F∘)) the following faithful preorders ${⪯}_1$ and ${⪯}_2$, respectively (see Figure 2):

-

$w_3{\prec }_1{w}_4{\prec }_1{w}_1{\prec }_1{w}_2{\prec }_1{w}_5$.

-

$w_5{\prec }_{1}z$, for all $z\in \mathbb{M}-\{w_1,w_2,w_3,w_4,w_5\}$.

-

$z{\approx }_1{z}^{\prime }$, for all $z,z^{\prime }\in \mathbb{M}-\{w_1,w_2,w_3,w_4,w_5\}$.

and

-

$w_2{\prec }_2{w}_1{\prec }_2{w}_4{\prec }_2{w}_5{\prec }_2{w}_3$.

-

$w_3{\prec }_{2}z$, for all $z\in \mathbb{M}-\{w_1,w_2,w_3,w_4,w_5\}$.

-

$z{\approx }_2{z}^{\prime }$, for all $z,z^{\prime }\in \mathbb{M}-\{w_1,w_2,w_3,w_4,w_5\}$.

As expected from the fact that ∘ is a DP revision function that satisfies postulate (Ind), the transition from ${⪯}_S$ to ${⪯}_1$, through the ∘-revision of S by $\neg (w_1\vee w_2)$, respects conditions (R1)–(R4) and (IndR). So does the transition from ${⪯}_S$ to ${⪯}_2$, through the ∘-revision of S by $\neg (w_1\vee w_3)$.

Next, we show that ∘ is Spohn-inexpressible. Assume on the contrary that there exists an OCF $\kappa$ that imitates ∘ at S. Then, for all $r,r^{\prime }\in \mathbb{M}$, $\kappa \left(r\right)⩽\kappa \left(r^{\prime }\right)$ iff $r{⪯}_S{r}^{\prime }$. To verify this, assume on the contrary that, for some $r,r^{\prime }\in \mathbb{M}$, $\kappa \left(r\right)⩽\kappa \left(r^{\prime }\right)$ and $r^{\prime }{\prec }_{S}r$. Then, for some $d>0$, $r\in \left[B\left(\kappa •\langle r\vee r^{\prime },d\rangle \right)\right]$, whereas, $r\notin \left[B\left(S\circ (r\vee r^{\prime })\right)\right]$. This of course contradicts our assumption that $\kappa$ imitates ∘ at S. An analogous argument can be asserted for the case where $r{⪯}_S{r}^{\prime }$ and $\kappa \left(r^{\prime }\right)<\kappa \left(r\right)$.

Moreover, since $\kappa$ imitates ∘ at S, revision preserves this relationship; that is, there exist $d_1>0$ and $d_2>0$, such that, for all $r,r^{\prime }\in \mathbb{M}$, as follows:

$$\kappa •〈\neg (w_1\vee w_2),d_1〉\left(r\right)⩽\kappa •〈\neg (w_1\vee w_2),d_1〉\left(r^{\prime }\right)\mathrm{iff}r{⪯}_1{r}^{\prime }$$

and

$$\kappa •〈\neg (w_1\vee w_3),d_2〉\left(r\right)⩽\kappa •〈\neg (w_1\vee w_3),d_2〉\left(r^{\prime }\right)\mathrm{iff}r{⪯}_2{r}^{\prime }.$$

Let ${\kappa }_1=\kappa •〈\neg (w_1\vee w_2),d_1〉$ and ${\kappa }_2=\kappa •〈\neg (w_1\vee w_3),d_2〉$. By the process of Spohn’s conditionalization, we have that

$$\begin{array}{c}{\kappa }_1\left(w_5\right)=\kappa \left(w_5\right)-\kappa \left(w_3\right),\hfill \\ {\kappa }_1\left(w_4\right)=\kappa \left(w_4\right)-\kappa \left(w_3\right),\hfill \\ {\kappa }_1\left(w_2\right)=\kappa \left(w_2\right)+d_1,\mathrm{and}\hfill \\ {\kappa }_1\left(w_1\right)=d_1.\hfill \end{array}$$

Moreover, from $w_4{\prec }_1{w}_1{\prec }_1{w}_2{\prec }_1{w}_5$, we derive that ${\kappa }_1\left(w_4\right)<{\kappa }_1\left(w_1\right)<{\kappa }_1\left(w_2\right)<{\kappa }_1\left(w_5\right)$. Hence, ${\kappa }_1\left(w_2\right)-{\kappa }_1\left(w_1\right)<{\kappa }_1\left(w_5\right)-{\kappa }_1\left(w_4\right)$, and therefore

$$\begin{array}{c}\kappa \left(w_2\right)<\kappa \left(w_5\right)-\kappa \left(w_4\right).\end{array}$$

(1)

Likewise, from Spohn’s conditionalization, we have that

$$\begin{array}{c}{\kappa }_2\left(w_5\right)=\kappa \left(w_5\right)-\kappa \left(w_2\right),\hfill \\ {\kappa }_2\left(w_4\right)=\kappa \left(w_4\right)-\kappa \left(w_2\right),\hfill \\ {\kappa }_2\left(w_3\right)=\kappa \left(w_3\right)+d_2,\mathrm{and}\hfill \\ {\kappa }_2\left(w_1\right)=d_2.\hfill \end{array}$$

Moreover, from $w_1{\prec }_2{w}_4{\prec }_2{w}_5{\prec }_2{w}_3$, we derive that ${\kappa }_2\left(w_1\right)<{\kappa }_2\left(w_4\right)<{\kappa }_2\left(w_5\right)<{\kappa }_2\left(w_3\right)$. Hence, ${\kappa }_2\left(w_5\right)-{\kappa }_2\left(w_4\right)<{\kappa }_2\left(w_3\right)-{\kappa }_2\left(w_1\right)$, and therefore

$$\begin{array}{c}\kappa \left(w_5\right)-\kappa \left(w_4\right)<\kappa \left(w_3\right).\end{array}$$

(2)

Finally, from $w_2{\approx }_S{w}_3$, we derive that

$$\begin{array}{c}\kappa \left(w_2\right)=\kappa \left(w_3\right).\end{array}$$

(3)

Combining relations (1), (2), and (3), we conclude that $\kappa \left(w_5\right)-\kappa \left(w_4\right)<\kappa \left(w_3\right)=\kappa \left(w_2\right)<\kappa \left(w_5\right)-\kappa \left(w_4\right)$, which is a contradiction. □

As it is evident from the proof of Theorem 4, the reason that Spohn’s conditionalization fails to capture the entire class of modified AGM revision functions defined by the DP approach is, roughly speaking, that the DP postulates allow transitions from an initial belief state to (revised) belief states, such that the $\phi$-worlds and/or the $\neg \phi$-worlds are shifting “non-uniformly”—even though the relative order of the worlds in $\left[\phi \right]$ and $[\neg \phi ]$ remains unchanged due to (R1) and (R2), respectively.

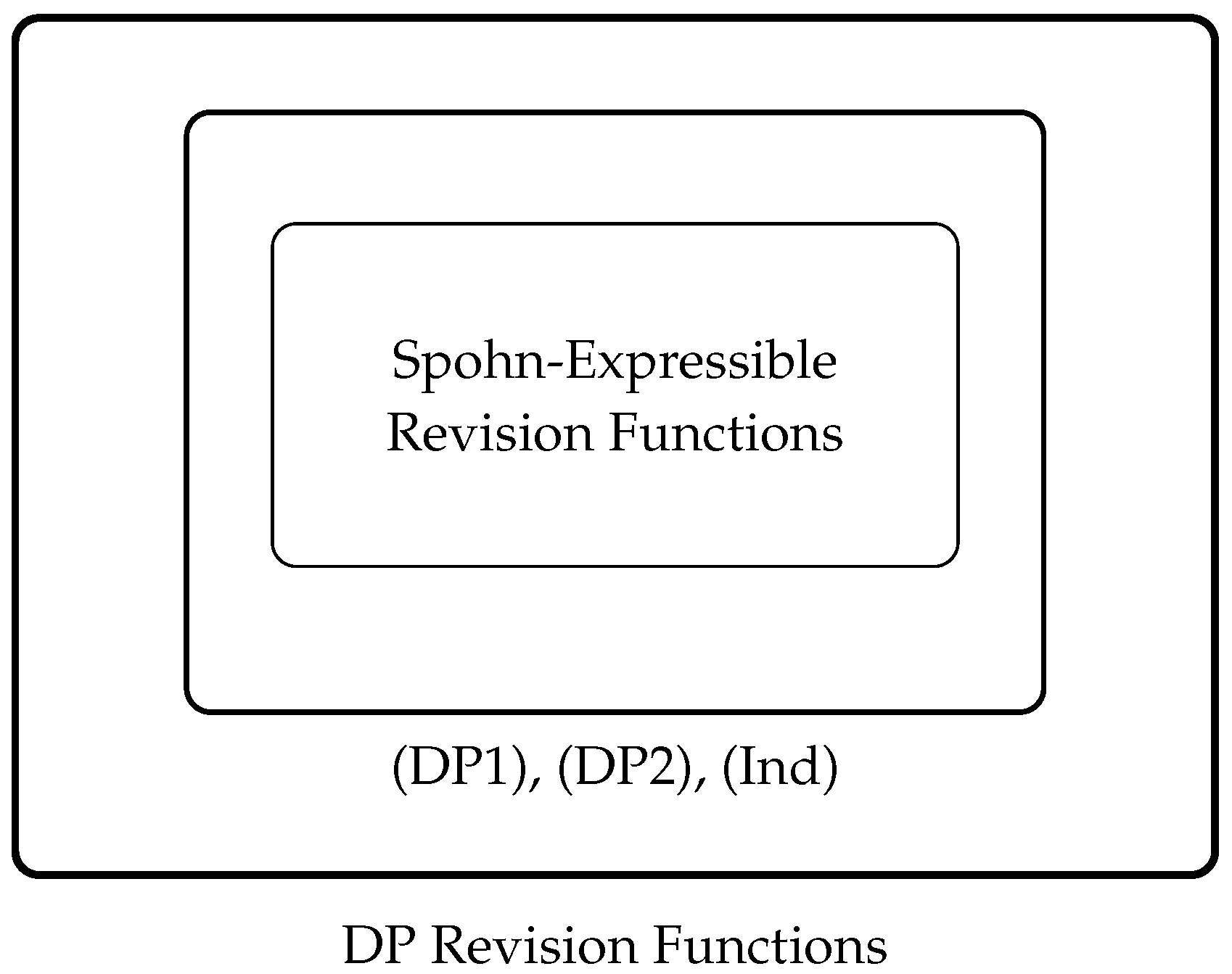
The conjunction of Theorems 3 and 4 entails that the class of Spohn-expressible revision functions is a proper subclass of the class of modified AGM revision functions identified by the conjunction of postulates (DP1), (DP2), and (Ind), which are in turn a proper subclass of the class of DP revision functions, as depicted in Figure 3.

The identified differences between DP and Spohn-expressible revision functions are particularly relevant in scenarios where the gradual accumulation of evidence must respect highly uniform shifts in the plausibility of possible worlds. For instance, in diagnostic reasoning (e.g., medical diagnosis or fault detection in engineering), new evidence can dictate uniform “rank adjustments” that, unlike the DP approach, Spohn’s conditionalization strictly enforces. Similarly, in real-time strategic decision-making—such as multi-step planning or iterative negotiation protocols—a Spohn-expressible revision function ensures consistent plausibility modifications in line with OCFs, whereas certain DP revision functions may produce plausibility shifts that are not globally uniform. In any case, recognizing that the DP approach and Spohn’s conditionalization occupy distinct but overlapping regions of iterated revision could inspire new revision operators that permit partially uniform shifts, while retaining some of the DP approach’s flexibility. For example, an operator that employs OCFs to process evidence in a Spohn-like manner, yet allows for non-uniform adjustments under carefully circumscribed conditions, could offer a middle ground.

We conclude this section with a note on the consequences of the established results. In a recent work by the authors (co-authored by Pavlos Peppas and Mary-Anne Williams) of [9,23], it has been shown that each one of the DP postulates is, in a strong sense, incompatible with Parikh’s relevance-sensitive axiom for belief revision [24,25,26]. Parikh’s axiom is a well-studied constraint that addresses the weakness of the AGM postulates for revision in capturing relevant change. On that basis, Theorems 3 and 4 imply the following important corollary.

Corollary 1. 

Spohn-expressible revision functions are incompatible with Parikh’s relevance-sensitive axiom.

Corollary 1 essentially points out that Spohn’s conditionalization, as qualitatively expressed through Spohn-expressible revision functions, does not respect Parikh’s notion of relevance (a result in the spirit of Corollary 1 is Corollary 4 of ([9], p. 1513)).

Corollary 2 is also an implication of Theorems 3 and 4.

Corollary 2. 

The counter-examples illustrating that the DP postulates produce unintuitive results apply to Spohn’s method for belief change as well—see [27], pp. 205–206, for counter-examples on (DP1); [28], p. 352, and [27], pp. 206–208, for counter-examples on (DP2); and [29], pp. 437–438, for counter-examples on (DP3) and (DP4).

8. Strengthening the DP Approach: New Necessary Conditions for Spohn Expressibility

Having established that the DP approach is overly liberal to serve as a qualitative analogue of Spohn’s conditionalization, this section introduces two new semantic postulates on total preorders over possible worlds, which strengthen the DP approach, and constitute necessary conditions for Spohn expressibility.

8.1. Initial Considerations

In this subsection, we introduce the formal concepts required for the alluded semantic postulates.

Definition 8 

(Biased Worlds towards Sequence of Sentences). Let $r,r^{\prime }$ be two worlds of $\mathbb{M}$, and let ${\phi }_1,\dots ,{\phi }_n$ be a finite sequence of sentences of $\mathcal{L}$. We shall say that $r,r^{\prime }$ are biased towards ${\phi }_1,\dots ,{\phi }_n$, which we denote by $\{r,r^{\prime }\}\twoheadrightarrow {\phi }_1,\dots ,{\phi }_n$, iff, for all $i\in \{1,\dots ,n\}$, either $r,r^{\prime }\in \left[{\phi }_i\right]$ or $r,r^{\prime }\in [\neg {\phi }_i]$.

Clearly, each sentence ${\phi }_i$ of the sequence ${\phi }_1,\dots ,{\phi }_n$ “splits” the set of all possible worlds $\mathbb{M}$ into two (disjoint) parts; namely, $\left[{\phi }_i\right]$ and $[\neg {\phi }_i]$. Hence, two worlds are biased towards ${\phi }_1,\dots ,{\phi }_n$ iff, for each ${\phi }_i$, they both belong to only one of these parts (either $\left[{\phi }_i\right]$ or $[\neg {\phi }_i]$). In what follows, notation $\{z,z^{\prime }\},\{r,r^{\prime }\}\twoheadrightarrow {\phi }_1,\dots ,{\phi }_n$ shall be an abbreviation of $\{z,z^{\prime }\}\twoheadrightarrow {\phi }_i$ and $\{r,r^{\prime }\}\twoheadrightarrow {\phi }_i$, for every ${\phi }_i$ of the sequence ${\phi }_1,\dots ,{\phi }_n$.

Thereafter, let $\mathbb{W}$ be the (finite) set of all pair sets of possible worlds of $\mathbb{M}$; namely, $\mathbb{W}=\left\{\{r,r^{\prime }\}:\mathrm{for}\mathrm{all}r,r^{\prime }\in \mathbb{M}\right\}$. Since $r=r^{\prime }$ is permitted in the specification of $\mathbb{W}$, the set $\mathbb{W}$ also contains singleton sets.

On that premises, Definitions 9–11 introduce a collection of binary relations over the set $\mathbb{W}$, which essentially encode forms of a qualitative distance between possible worlds, relative to a belief state S. We start by defining an indifference–distance relation.

Definition 9 

(Indifference Distance between Worlds, ${\simeq }_S$). Let ∘ be a modified AGM revision function, let S be a belief state, and let ${⪯}_S$ be the total preorder over $\mathbb{M}$ that corresponds to ∘, via (F∘). Moreover, let $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ be any two elements of $\mathbb{W}$. Define ${\simeq }_S^{\prime }$ to be a binary relation over $\mathbb{W}$ such that the following holds:

$\{z,z^{\prime }\}{\simeq }_S^{\prime }\{r,r^{\prime }\}$

iff

there is a finite sequence of sentences ${\phi }_1,\dots ,{\phi }_n\in \mathcal{L}$,such that $z{\approx }_{S\circ {\phi }_1\circ \cdots \circ {\phi }_n}r$ ,$z^{\prime }{\approx }_{S\circ {\phi }_1\circ \cdots \circ {\phi }_n}{r}^{\prime }$, and $\{z,z^{\prime }\},\{r,r^{\prime }\}\twoheadrightarrow {\phi }_1,\dots ,{\phi }_n.$

Then, the indifference distance between $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ is encoded into the binary relation ${\simeq }_S=tr\left({\simeq }_S^{\prime }\right)$ over $\mathbb{W}$.

Remark 3. 

The binary relation ${\simeq }_S$ over $\mathbb{W}$ is reflexive, symmetric, and transitive. Hence, ${\simeq }_S$ is an equivalence relation over $\mathbb{W}$.

Building on the indifference–distance relation, we proceed to a more general form of the distance.

Definition 10 

(Distance between Worlds, ${⊑}_S$). Let ∘ be a modified AGM revision function, let S be a belief state, and let ${⪯}_S$ be the total preorder over $\mathbb{M}$ that corresponds to ∘, via (F∘). Moreover, let ${\simeq }_S$ be the relation over $\mathbb{W}$ that corresponds to ∘, via Definition 9, and let $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ be any two elements of $\mathbb{W}$. Define ${⊏}_S^{\prime }$ to be a binary relation over $\mathbb{W}$ such that the following holds:

$\{z,z^{\prime }\}{⊏}_S^{\prime }\{r,r^{\prime }\}$

iff

there is a finite sequence of sentences ${\phi }_1,\dots ,{\phi }_n\in \mathcal{L}$, such that $r{\prec }_{S\circ {\phi }_1\circ \cdots \circ {\phi }_n}z{⪯}_{S\circ {\phi }_1\circ \cdots \circ {\phi }_n}{r}^{\prime }$, $r{⪯}_{S\circ {\phi }_1\circ \cdots \circ {\phi }_n}{z}^{\prime }{⪯}_{S\circ {\phi }_1\circ \cdots \circ {\phi }_n}{r}^{\prime }$, and $\{z,z^{\prime }\},\{r,r^{\prime }\}\twoheadrightarrow {\phi }_1,\dots ,{\phi }_n$

Then, the distance between $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ is encoded into the binary relation ${⊑}_S=tr\left({⊏}_S^{\prime }\cup {\simeq }_S\right)$ over $\mathbb{W}$.

Remark 4. 

The binary relation ${⊑}_S$ over $\mathbb{W}$ is reflexive and transitive. Hence, ${⊑}_S$ is a partial preorder over $\mathbb{W}$.

Finally, we formalize the strict version of the relation ${⊑}_S$.

Definition 11 

(Strict Distance between Worlds, ${⊏}_S$). Let ∘ be a modified AGM revision function, let S be a belief state, and let ${⪯}_S$ be the total preorder over $\mathbb{M}$ that corresponds to ∘, via (F∘). Moreover, let ${\simeq }_S$ and ${⊑}_S$ be the relations over $\mathbb{W}$ that correspond to ∘, via Definitions 9 and 10, respectively. The strict distance between any two elements $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ of $\mathbb{W}$ is encoded into a binary relation ${⊏}_S$ over $\mathbb{W}$, such that $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$ iff $\{z,z^{\prime }\}{⊑}_S\{r,r^{\prime }\}$ and $\{z,z^{\prime }\}\neg {\simeq }_S\{r,r^{\prime }\}$.

Remark 5. 

In Definitions 9 and 10, the involved sentences ${\phi }_1,\dots ,{\phi }_n$ may be tautological as well. This implies that the relations ${\simeq }_S$, ${⊑}_S$, and ${⊏}_S$ are also determined by the total preorder ${⪯}_S$ over $\mathbb{M}$, i.e., by the comparative plausibility of the possible worlds at the belief state S.

Remark 6. 

The binary relation ${⊏}_S$ over $\mathbb{W}$ is transitive, but not necessarily reflexive or irreflexive.

As stated, each one of the relations ${\simeq }_S$, ${⊑}_S$, and ${⊏}_S$ can be intuitively interpreted as an encoding of a qualitative distance between worlds, relative to a belief state S. In this sense, we can interpret the relations as follows. For two elements $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ of $\mathbb{W}$, the following holds:

• $\{z,z^{\prime }\}{\simeq }_S\{r,r^{\prime }\}$ holds whenever the qualitative distance between $z,z^{\prime }$ is equal to the qualitative distance between $r,r^{\prime }$ at S.
• $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$ holds whenever the qualitative distance between $z,z^{\prime }$ is strictly shorter than the qualitative distance between $r,r^{\prime }$ at S.
• $\{z,z^{\prime }\}{⊑}_S\{r,r^{\prime }\}$ holds whenever the qualitative distance between $z,z^{\prime }$ is shorter than or equal to the qualitative distance between $r,r^{\prime }$ at S.

8.2. Distance-Based Constraints on Total Preorders over Possible Worlds

Let ∘ be a modified AGM revision function. Moreover, let S be a belief state, and let ${\simeq }_S$, ${⊑}_S$ and ${⊏}_S$ be the relations over $\mathbb{W}$ that correspond to ∘, via Definitions 9–11, respectively. While, as previously stated, the aforementioned binary relations over $\mathbb{W}$ can be interpreted as encoding a qualitative distance between worlds, they do not inherently guarantee the necessary coherence. For instance, the revision process through ∘ may result in two elements $\{z,z^{\prime }\}$, $\{r,r^{\prime }\}$ of $\mathbb{W}$ simultaneously satisfying $\{z,z^{\prime }\}{\simeq }_S\{r,r^{\prime }\}$ and $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$, or even $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$ and $\{r,r^{\prime }\}{⊏}_S\{z,z^{\prime }\}$, at the same time. Obviously, such incoherences undermine the intended interpretation of a (qualitative) distance. To avoid such absurd circumstances, we can impose the following two constraints, (SPN1) and (SPN2), on the relations ${\simeq }_S$ and ${⊏}_S$, which ensure a coherent representation of the qualitative distance between worlds.

(SPN1)	If $\{z,z^{\prime }\}{\simeq }_S\{r,r^{\prime }\}$, then $\{z,z^{\prime }\}\neg {⊏}_S\{r,r^{\prime }\}$.
(SPN2)	If $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$, then $\{r,r^{\prime }\}\neg {⊏}_S\{z,z^{\prime }\}$.

Condition (SPN1) ensures that, if $\{z,z^{\prime }\}{\simeq }_S\{r,r^{\prime }\}$ holds, then it cannot be the case that $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$ or $\{r,r^{\prime }\}{⊏}_S\{z,z^{\prime }\}$. In a similar vein, condition (SPN2) guarantees that, if $\{z,z^{\prime }\}{⊏}_S\{r,r^{\prime }\}$ holds, then it cannot be the case that $\{r,r^{\prime }\}{⊏}_S\{z,z^{\prime }\}$. Thus, both conditions (SPN1) and (SPN2) impose constraints on the modified AGM revision function ∘, ensuring that the qualitative distance (at S) between worlds biased toward any finite sequence of sentences remains unchanged during the ∘-revision of S. This restriction preserves coherence in the qualitative comparisons of worlds during the revision process.

Remarks 7 and 8 follow immediately from Definitions 9–11.

Remark 7. 

In the presence of condition (SPN2), $\{z,z^{\prime }\}{⊑}_S\{r,r^{\prime }\}$ and $\{r,r^{\prime }\}{⊑}_S\{z,z^{\prime }\}$ entails $\{z,z^{\prime }\}{\simeq }_S\{r,r^{\prime }\}$.

Remark 8. 

Condition (SPN2) makes the binary relation ${⊏}_S$ over $\mathbb{W}$ asymmetric—or equivalently irreflexive—given that a transitive binary relation is asymmetric iff it is irreflexive, and ${⊏}_S$ is transitive (irrespectively of (SPN2)). Hence, ${⊏}_S$ is a strict partial order over $\mathbb{W}$. Notably, in the absence of condition (SPN2), ${⊏}_S$ is not necessarily a strict partial order over $\mathbb{W}$, as asymmetry may no longer be guaranteed (see Remark 6).

Remark 9 follows from the proof of Theorem 4 of Section 7.

Remark 9. 

The DP revision function ∘ (satisfying postulate (Ind)) constructed in the proof of Theorem 4 violates both conditions (SPN1) and (SPN2).

Proof. 

It is deduced from (Figure 2 of) the proof of Theorem 4 that $\{w_1,w_2\}{\simeq }_S\{w_1,w_3\}$, $\{w_1,w_2\}{⊏}_S\{w_4,w_5\}$, and $\{w_4,w_5\}{⊏}_S\{w_1,w_3\}$. From $\{w_1,w_2\}{\simeq }_S\{w_1,w_3\}$ and $\{w_1,w_2\}{⊏}_S\{w_4,w_5\}$, we derive that $\{w_1,w_3\}{⊑}_S\{w_4,w_5\}$. However, this is a contradiction in the presence of the semantic conditions (SPN1) and (SPN2). □

Interestingly, the semantic constraints (R2) and (SPN2) ensure that the Independence postulate (Ind) is respected, as Proposition 1 proves below. The converse is obviously not true, in view of Remark 9.

Proposition 1. 

Let ∘ be a modified AGM revision function, let S be a belief state, and let ${⪯}_S$ be the total preorder over $\mathbb{M}$ that corresponds to ∘, via (F∘). Moreover, let ${⊏}_S$ be the relation over $\mathbb{W}$ that corresponds to ∘, via Definition 11. If ${⪯}_S$ and ${⊏}_S$ satisfy the semantic constraints (R2) and (SPN2), then ∘ satisfies postulate (Ind).

Proof. 

Suppose that ${⪯}_S$ and ${⊏}_S$ satisfy conditions (R2) and (SPN2). It suffices to show that ${⪯}_S$ satisfies condition (IndR) as well. To that end, let $\phi$ be any sentence of $\mathcal{L}$, such that $\neg \phi \in B\left(S\right)$. Consider any worlds $r,r^{\prime }\in \mathbb{M}$, such that $r\in \left[\phi \right]$, $r^{\prime }\in [\neg \phi ]$, and $r{⪯}_S{r}^{\prime }$. We need to show that $r{\prec }_{S\circ \phi }{r}^{\prime }$.

Suppose that z is any ${⪯}_S$-minimal $\phi$-world and $z^{\prime }$ is any ${⪯}_S$-minimal $\neg \phi$-world. Since $\neg \phi \in B\left(S\right)$, it holds that $z^{\prime }\in \left[B\left(S\right)\right]$ and $z^{\prime }{\prec }_{S}z$. Hence, we derive that $\{r,z\}{⊏}_S\{r^{\prime },z^{\prime }\}$.

Now, since $\phi \in B(S\circ \phi )$ (from $(S\circ 2)$), it follows that $z\in \left[B(S\circ \phi )\right]$ and $z{\prec }_{S\circ \phi }{z}^{\prime }$. Furthermore, condition (SPN2) entails that $\{r^{\prime },z^{\prime }\}\neg {⊏}_S\{r,z\}$; thus, $\{r^{\prime },z^{\prime }\}\neg {⊏}_{S\circ \phi }\{r,z\}$ as well. From $z^{\prime }{⪯}_S{r}^{\prime }$ and (R2), we derive that $z^{\prime }{⪯}_{S\circ \phi }{r}^{\prime }$. Combining the above, we conclude that it must be the case that $r{\prec }_{S\circ \phi }{r}^{\prime }$, as desired. □

8.3. The Necessity of (SPN1) and (SPN2) for Spohn Expressibility

In view of the introduced formal background, we proceed to Theorem 5 below, which proves that the new semantic conditions (SPN1) and (SPN2) are necessary conditions for Spohn expressibility.

Theorem 5. 

Let ∘ be a modified AGM revision function, and let S be a belief state. Moreover, let ${\simeq }_S$ and ${⊏}_S$ be the relations over $\mathbb{W}$ that correspond to ∘, via Definitions 9 and 11, respectively. If ∘ is Spohn-expressible, then ${\simeq }_S$ and ${⊏}_S$ satisfy conditions (SPN1) and (SPN2).

Proof. 

The proof is straightforward, since, if ∘ is Spohn-expressible, then there exists an OCF $\kappa$ that imitates ∘ at S. □

9. Conclusions

This article investigated the relationship between two prominent proposals addressing the problem of iterated belief revision; namely, the qualitative DP approach and the quantitative Spohn conditionalization. As a first contribution, we proved that the DP postulates—even when supplemented by postulate (Ind)—do not precisely encode the shifting process of Spohn’s conditionalization (restricted to revision scenarios), since the latter is overly strict to capture the whole class of DP revision functions. This is essentially demonstrated through Theorem 4 of Section 7, which presents a DP revision function ∘ satisfying postulate (Ind) that is not Spohn-expressible. Against this background, two new semantic postulates, (SPN1) and (SPN2), were introduced, and any Spohn-expressible revision function necessarily satisfies these (Theorem 5); however, the aforementioned DP revision function ∘ of Theorem 4 violates (Remark 9). The proposed semantic postulates constrain the total preorders over possible worlds corresponding to DP revision functions and, in doing so, strengthen the DP approach.

Future work will be devoted to the precise characterization of the class of Spohn-expressible revision functions, that is, to the formulation of the required sound and complete constraints to which any Spohn-expressible revision function adheres. An intriguing open question, for instance, is whether the semantic conditions (R1), (R2), (SPN1), and (SPN2)—shown to be necessary—are also sufficient to guarantee Spohn expressibility.