Abstract
Accurate tumor segmentation is crucial for clinical diagnosis, treatment planning, and efficacy evaluation in medical imaging. Although traditional image processing techniques have been widely applied in tumor segmentation, they often perform poorly when dealing with tumors that have low contrast, irregular shapes, or varying sizes. With the rise of deep learning, particularly the application of convolutional neural networks (CNNs) in medical image segmentation, significant progress has been made, especially in handling multimodal data such as positron emission tomography (PET) and computed tomography (CT). However, the “black-box” nature of CNNs presents challenges for interpretability, which is particularly important in clinical applications. To address this, we propose a tumor segmentation framework based on a multi-scale interpretability module (MSIM). Through ablation experiments and comparisons on three public datasets, we evaluate the performance of the proposed method. The ablation results show that the proposed method achieves an improvement of 1.6, 1.62, and 2.36 in the Dice Similarity Coefficient (DSC) on the Melanoma, Lymphoma, and Lung Cancer datasets, respectively, highlighting the benefits of the interpretability module. Furthermore, the method outperforms the best comparative methods on all three datasets, achieving DSC improvements of 1.46, 1.27, and 1.93, respectively. Finally, visualization and perturbation experiments further validate the effectiveness of our method in emphasizing critical features.
MSC:
68T45
1. Introduction
Cancer has long been one of the major challenges in the history of medicine. According to the 2024 global cancer statistics published by the International Agency for Research on Cancer (IARC) for 2022 [1], there were approximately 20 million new cancer cases and 9.7 million cancer-related deaths worldwide. Medical imaging plays a critical role in clinical diagnosis and treatment, particularly in tumor detection and assessment. Accurate tumor localization and segmentation not only enhance clinical decision-making but also enable personalized treatment planning for patients. Positron emission tomography (PET) and computed tomography (CT) are two commonly used imaging techniques that are widely applied in tumor diagnosis and monitoring. PET detects metabolic activity by imaging radiotracers, such as 18F-FDG, injected into the body, identifying active tumor tissue [2]. Due to their higher metabolic activity, tumor regions often exhibit higher standardized uptake values (SUV) on PET images, contrasting with surrounding normal tissue [3,4], as shown in Figure 1b. CT provides high-resolution anatomical structural information, clearly showing tumors and their surrounding anatomical details, as shown in Figure 1a. However, using PET or CT images alone for tumor segmentation has limitations: PET imaging suffers from low spatial resolution and issues such as blurred boundaries and uneven intensity, while CT images have poor contrast between lesions and normal tissues, making it difficult to fully capture the pathological features of tumors. Therefore, combining PET and CT images to leverage the strengths of both modalities has proven to be an effective way to improve tumor segmentation accuracy and reliability [5,6,7].
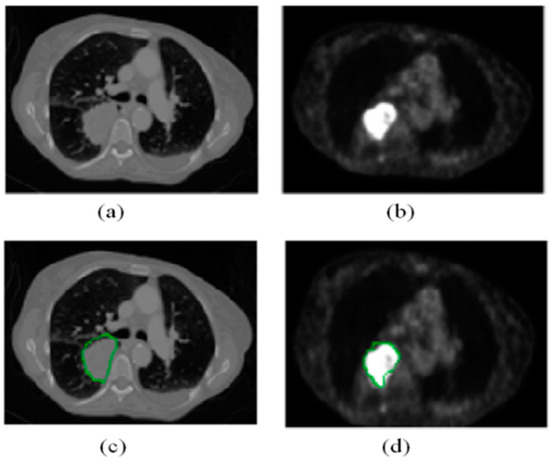
Figure 1.
(a,b) are the original CT and PET images of the same patient, respectively. The green contours in images (c,d) represent the corresponding contour labels from (a,b).
In recent years, deep learning techniques have made significant progress in the field of medical image analysis. By training large neural networks, deep learning models are able to automatically learn and extract complex features from images, achieving high-accuracy image classification, detection, and segmentation. In particular, the UNet model based on convolutional neural networks (CNNs) and its variants have achieved remarkable success in medical image segmentation tasks [8]. However, when dealing with multimodal images such as PET-CT, the UNet model still faces some challenges. The standard UNet model, with its symmetric encoder-decoder structure, can effectively capture multi-scale features in images, but it still struggles to fully utilize the complementary information between PET and CT images. Traditional multimodal processing methods typically handle each modality independently or perform simple fusion at the feature or decision level [9]. This approach limits the effective use of complementary information between PET and CT images, impacting the precision and consistency of segmentation results. Furthermore, in practical applications, model interpretability is a critical issue, particularly in clinical settings. Clinicians need to understand the reasoning behind the model’s decisions to ensure its reliability and safety. However, deep learning models are often seen as “black boxes”, especially when fusing multimodal images, because of a lack of transparency [10,11]. Improving model interpretability and making the decision-making process more transparent is an important direction for enhancing the clinical application value of deep learning models. To address these challenges, this study proposes a tumor segmentation method based on a multi-scale interpretability approach. By integrating a multi-scale interpretative mask generation mechanism, we have designed a multi-scale interpretability module (MSIM) aimed at improving both the precision and interpretability of PET-CT image tumor segmentation. This module extracts and integrates complementary information from both PET and CT images across different scales, significantly enhancing the segmentation accuracy of tumor regions while providing clear decision-making support for clinicians. Additionally, the design of an interpretability loss function further enhances the model’s focus on key features during training, boosting its interpretability.
The remainder of this paper is organized as follows: Section 2 reviews related work on PET-CT segmentation. Section 3 introduces the proposed method. Section 4 details the experimental setup. Section 5 presents the experimental results and analysis. Section 6 discusses the findings. Section 7 concludes the paper.
2. Related Work
Over the past decade, medical image segmentation has been a popular research topic in the fields of computer vision and medical image processing, especially in tumor segmentation, where accurate segmentation results are critical for disease diagnosis, treatment planning, and efficacy evaluation. PET-CT imaging is widely used in tumor segmentation research because it provides both metabolic activity and anatomical structural information about tumors. Before the widespread application of deep learning techniques in medical image analysis, many studies on lung tumor segmentation relied on traditional image processing methods, which typically included techniques such as thresholding segmentation [12], region growing [13], edge detection [14], and graph cuts [15]. However, these methods often require manual parameter setting, and their segmentation performance is suboptimal when tumors have indistinct contrast with normal tissues, irregular shapes, or varying sizes. With the advent of deep learning, significant progress has been made in the field of medical image segmentation, particularly through CNNs, which have demonstrated powerful capabilities in automatically extracting complex image features [16,17]. These models use deep network structures to automatically learn complex features within images, thereby achieving high precision in tumor recognition and localization.
In clinical diagnosis, combining multimodal data provides different perspectives and richer information. Therefore, many multimodal PET-CT-based segmentation methods have been proposed. For instance, Kumar et al. [18] introduced a joint learning module to obtain an attention fusion map, which quantifies the relative importance of features at different spatial locations, thereby acquiring complementary multimodal information. Fu et al. [19] proposed a framework with two branches, where one branch introduces a multimodal spatial attention module to capture spatial changes in the PET images, and the other branch captures CT features and segmentation results. Huang et al. [20] proposed an improved spatial attention network that highlights tumor location information while suppressing non-tumor regions. Similarly, Zhao et al. [21] used two V-NET networks to extract semantic features from PET and CT images, followed by multiple cascaded convolutions to fuse PET and CT feature maps for tumor segmentation. In EFNet [22], an evidence loss function is used to capture the uncertainty in segmentation results, and evidence fusion is applied to reduce the uncertainty in the results from each modality. While these methods have shown good results in multimodal segmentation, the “black-box” nature of CNNs leads to a lack of transparency and interpretability in the decision-making process [23], which is especially critical in medical image segmentation, where the model’s decision logic must be understandable to clinicians to ensure the reliability of the diagnosis.
In recent years, researchers have proposed various interpretability methods to improve the transparency of deep learning models, particularly in decision-making processes for classification or segmentation tasks. For example, Dabkowski et al. [24] proposed an interpretability method that uses CNNs to generate interpretable masks, which effectively identify significant regions in input images. The process of generating and applying these masks not only reveals the key regions upon which the model relies for decision-making but also provides a visualization tool that allows researchers and clinicians to better understand the model’s behavior and rationale. Li et al. [25] proposed a guided attention reasoning network where the interpretable masks are explored through the network itself and guide the network to focus on the regions of interest. Fong et al. [26] introduced several meaningful perturbation methods to explain the “black-box” nature of models by removing regions from input images to interpret the network’s decision-making process. While many researchers have proposed various interpretability techniques for image segmentation, there has been limited research on combining interpretability methods with PET-CT images. Kang et al. [27] proposed an interpretable multimodal image segmentation method that attempts to enhance feature fusion transparency by generating interpretable images. While this method somewhat improves model interpretability, it primarily relies on post-processing steps, which fail to directly embed the interpretability mechanism into the model architecture. This post-processing approach may lead to discrepancies between the interpretability results and the actual segmentation process, thus affecting the accuracy and reliability of the interpretation. To address this issue, the present study proposes a segmentation method based on multi-scale interpretability. We build upon the traditional UNet model by incorporating a multi-scale interpretive mask generation mechanism and designing an MSIM to enhance the accuracy and interpretability of tumor segmentation in PET-CT images. Specifically, we extract multi-scale features from the UNet down-sampling process and input them into the multi-scale interpretability module to generate multi-scale interpretive masks, which better highlight key features from each modality during the segmentation process. By embedding the interpretability mechanism directly into the model structure and conducting experiments on publicly available datasets, the experimental results show that our method not only significantly improves segmentation performance but also enhances the model’s interpretability. Additionally, to supervise the generation of reasonable interpretable masks, we also design an interpretability loss function.
Main Contributions of This Study:
- Proposing a Multi-Scale Interpretability-Based Segmentation Model: This model not only significantly improves segmentation performance but also provides valuable interpretability information for the decision-making process of the segmentation network.
- Introducing an Interpretability Loss Function: This loss function provides clear supervisory signals during training, encouraging the network to focus on informative features and further enhancing segmentation performance.
3. Methods
This study proposes a PET-CT segmentation model based on a multi-scale interpretability approach for tumor segmentation in PET-CT images. The core innovation of the model lies in the introduction of a multi-scale interpretive mask mechanism, upon which a multi-scale feature interpretability module is constructed. First, we extract multi-scale features from the down-sampling process of the UNet network and input them into the MSIM for processing. These feature maps not only cover information at different levels but also provide richer contextual information, enhancing the model’s sensitivity to tumor features at multiple scales.
Next, based on these multi-scale feature maps, we generate multi-scale interpretive masks through the mask mechanism. These masks effectively highlight the critical areas in PET and CT images that are essential for tumor segmentation. Each mask focuses on different levels of tumor features, ensuring that the model can concentrate on the tumor regions at different image scales and avoid missing critical features. The core advantage of this process is that it not only improves segmentation accuracy but also enhances the interpretability of the segmentation results by explicitly highlighting key areas. To further improve the performance of the interpretability module, we design an interpretability loss function. This loss function provides clear supervisory signals to guide the model in effectively integrating key information from both PET and CT images. This mechanism ensures that, during training, the model optimizes tumor segmentation accuracy and provides a reasonable explanation for each decision, making the final segmentation result more transparent and reliable. Through this approach, our model not only improves tumor segmentation performance but also significantly enhances model interpretability, ensuring its reliability in clinical applications.
The proposed model architecture is illustrated in Figure 2, showing the overall structure of the network, including the integration process of the feature extraction, interpretability module, and segmentation module. The outputs of each module are fused through weighted integration to obtain accurate tumor segmentation results.
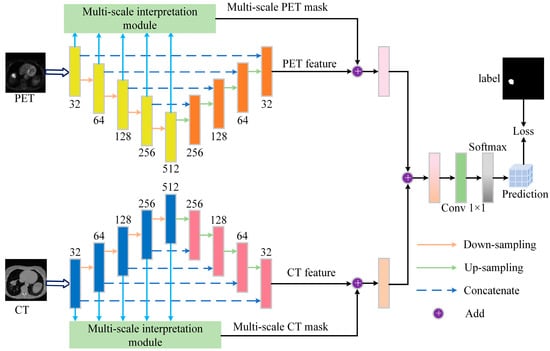
Figure 2.
Overview of the proposed segmentation framework, which consists of the segmentation backbone and interpretability module. The backbone uses the UNet network, and the interpretability module includes a multi-scale feature processing module and a mask generation module, each with PET and CT branches. The features extracted through the down-sampling process are input into the feature processing module to generate feature maps at different scales, which are then input into the mask generation branch to create different interpretive masks. Finally, the weighted fused masks are combined with the feature maps output by the segmentation backbone, and the final segmentation result is obtained through 1 × 1 convolution and softmax operation.
3.1. Segmentation Backbone
In this study, we aim to validate the effectiveness of the proposed interpretability method in multimodal segmentation tasks. To ensure the method’s generalization capability, we chose to use the generic UNet [16] as the backbone for segmentation rather than designing a specialized and complex segmentation model. The segmentation network consists of two parallel feature extraction branches (PET branch and CT branch) and a segmentation branch that generates the final segmentation result. Both the PET and CT branches share the same encoder-decoder architecture, as shown in Figure 2. In the encoder path, each layer compresses the input to generate higher-dimensional representations with lower resolution. In the decoder path, these representations are gradually expanded, ultimately recovering to a size close to the original input.
3.2. The Network Structure of MSIM
The MSIM is a core component of the tumor segmentation model and is designed to effectively integrate multimodal PET and CT information to improve segmentation accuracy and enhance model interpretability. The module consists of the multi-scale feature processing module and the mask generation module. First, the multi-scale feature maps extracted during the UNet down-sampling process are input into the multi-scale feature processing module. This module processes features at different scales to ensure effective information fusion. Next, the mask generation module uses a specific mask mechanism to generate interpretive masks that emphasize critical areas for tumor segmentation. Finally, the masks at multiple scales are fused through weighted integration to generate the final multi-scale fusion mask, which guides the model to achieve more accurate segmentation predictions. The structure of the MSIM is shown in Figure 3.
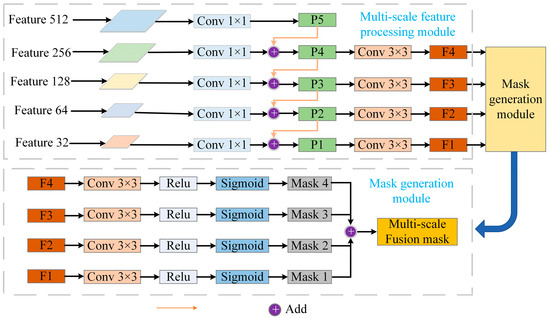
Figure 3.
Overview of the MSIM. The module is divided into two parts: the multi-scale feature processing module and the mask generation module. First, the feature maps at different layers extracted from the UNet down-sampling process are input into the multi-scale feature processing module, which processes each scale’s feature map. Subsequently, the mask generation module computes interpretive masks at each scale to highlight important regions relevant to tumor segmentation. Finally, through a weighted fusion of masks from different scales, a multi-scale fusion mask is generated to guide the model’s segmentation predictions.
3.2.1. Multi-Scale Feature Processing Module
The primary objective of the multi-scale feature processing module is to efficiently extract and integrate multi-level feature information from PET and CT images, ensuring the comprehensive utilization of feature data. This module first extracts feature maps from different levels during the down-sampling process of the UNet, with each feature map containing multi-scale information ranging from fine details to global context. Each feature map is processed independently, with convolution operations applied to extract features while maintaining the integrity of information across scales. This design draws on the core idea of the Feature Pyramid Network [28], integrating multi-level features through top-down and lateral connections. Lower-level features contain high-resolution details, enabling precise localization of tumor boundaries, while higher-level features encode global context, aiding in the recognition of the overall distribution of tumors. Through the weighted fusion strategy in Equation (2), the model dynamically adjusts the contribution ratio of features at different scales. For instance, it assigns higher weights to metabolically active regions in PET images while enhancing boundary responses of anatomical structures in CT images. This mechanism can be mathematically interpreted as a multi-task optimization problem, where the objective function improves the robustness of segmentation results by minimizing the reconstruction error between local features and global semantics [29]. Specifically, the module first applies a 1 × 1 convolution operation to each scale’s feature map to normalize the channel number and standardize these data:
where represents the normalized feature, denotes the input feature, refers to the convolution operation. This operation ensures that the features at all scales remain consistent in the channel dimension, thus laying the foundation for subsequent feature fusion. To further enhance the model’s ability to leverage information across different scales, the multi-scale feature processing module employs a layer-wise weighted fusion strategy. Specifically, features at lower scales (higher resolution) are combined with those at higher scales (lower resolution) to improve the global representation of information. Therefore, for each scale , its feature is weighted and summed with the feature from the previous scale:
In this context represents a learnable weight that dynamically balances the contribution of local details and global semantics. refers to the up-sampling operation applied to the higher-level feature, resizing it to match the dimensions of for pixel-wise summation. This process ensures that features across different scales complement each other, allowing lower-level features to benefit from a richer global context. After feature fusion is completed, to further capture local information and enhance the representational power of features, each scale undergoes a 3 × 3 convolution operation to improve fine-grained feature representation. The network structure parameters of the multi-scale feature processing module are shown in Table 1.

Table 1.
The network structure parameters of the multi-scale feature processing module, with the input and output dimensions represented by width, height, and channels, respectively.
3.2.2. Mask Generation Module
The core objective of the mask generation module is to create multi-scale interpretable masks that highlight the most critical regions in PET-CT images for tumor segmentation. In our model, the interpretable masks are generated through the multi-scale feature extraction module. This module first applies a 3 × 3 convolution operation to the feature map of each scale, followed by activation using the ReLU function. After convolution and activation, the feature maps are weighted and summed based on learnable weights to generate intermediate feature representations of the masks. These intermediate features are then processed through a Sigmoid activation function to ensure that the mask values fall within the (0, 1) range, effectively highlighting regions that contribute significantly to the segmentation task. Specifically, the formula for generating the interpretable mask at scale is:
where represents the input feature at scale , is the learnable weight for that scale, is the Sigmoid activation function, and is the interpretable mask generated at scale . This process ensures that the features at each scale are effectively extracted and generate interpretable masks relevant to the segmentation task. To ensure the effective integration of multi-scale information, the masks from different scales are weighted and summed to generate the final multi-scale fused mask. The fusion process is as follows:
where is the final multi-scale fused mask, and is the fusion weight of the i-th scale mask, controlling the contribution of each scale in the final fused result. This weighted fusion strategy allows the model to integrate feature information from various scales, highlight the key features of the tumor region, and improve segmentation accuracy. It is noteworthy that, compared with traditional attention mechanisms such as SENet [30], the mask generation process of MSIM offers stronger interpretability and controllability. SENet learns channel weights through global pooling, but its decision-making process lacks transparency in spatial localization. In contrast, MSIM generates masks through local convolution and explicit supervision, which can directly map to key regions of the input image. This difference is mathematically reflected in the fact that SENet’s attention weights are implicit scalars (), while MSIM’s masks are explicit spatial matrices (), and their generation process can be traced through backpropagation [31]. This explicitness makes MSIM more suitable for medical image analysis tasks that require clinical validation. The network structure parameters of the mask generation module are shown in Table 2.

Table 2.
The network structure parameters of the mask generation module, with the input and output dimensions represented by width, height, and channels, respectively.
3.3. Loss Functions
3.3.1. Segmentation Backbone Loss
The segmentation backbone loss uses the Dice loss, which directly focuses on the overlap between the predicted and ground truth regions. To further improve the segmentation performance of the model, we introduce deep supervision loss [32] in each branch to ensure full utilization of information from all layers during training:
where represents the Dice similarity coefficient loss, which directly measures the overlap between the predicted region and the ground truth region. In this equation, denotes the predicted value, denotes the ground truth label, is the total number of pixels, and is a smoothing term to prevent division by zero. To better leverage the complementary information between the PET and CT modalities, we calculate the Dice loss for both the PET and CT branches and their combined loss:
where and represent the features extracted from the PET and CT branches, respectively, and denotes the ground truth. The term represents the segmentation loss calculated on the final fused feature map, where is the fused feature map. The total backbone loss aggregates all individual loss terms with being a hyperparameter that controls the weight of the segmentation loss.
3.3.2. Interpretability Loss
To ensure that the interpretability module generates reasonable interpretability masks and prevents excessive concentration of attention weights, this study designs an interpretability loss function that includes mask loss and regularization loss. The mask loss constrains the model to focus on key tumor regions in the PET and CT modalities through the Dice similarity coefficient, with the mathematical formulation as follows:
where and represent the mask losses for the CT and PET branches, respectively, and represents the ground truth. To prevent the excessive concentration of attention weights, a regularization term is introduced to constrain the mask distribution. The design of the regularization term is based on the principle of maximizing information entropy [33]. Its essence is to force the model to distribute attention weights across multiple potentially relevant features, avoiding overfitting caused by excessive reliance on a single modality or local feature, with the mathematical formulation as follows:
The total interpretability loss is defined as:
The theoretical advantage of the designed interpretability loss lies in its explicit supervision mechanism: unlike traditional attention mechanisms, the mask 1oss directly constrains the model to focus on spatial regions consistent with the ground truth through pixel-level supervision (Equations (10) and (11)). Its gradients can be mapped back to the input image via backpropagation, providing a visual basis for clinical interpretation. Additionally, the regularization loss (Equation (13)) balances the weight distribution of PET and CT masks, forcing the model to integrate metabolic information with anatomical structures, thereby enhancing the robustness of low-contrast tumors. Experiments show that the model achieves an optimal balance in the DSC when = 0.5, = 1.5, and = 0.5 (Appendix A).
3.3.3. Total Loss Function
The total loss function combines the segmentation loss, mask loss, and regularization loss:
4. Experimental Setup
4.1. Dataset
To validate the proposed model, we used the AutoPET [34] dataset for evaluation. The AutoPET dataset contains data from melanoma, lymphoma, and lung cancer patients who underwent whole-body FDG-PET/CT scans between 2014 and 2018 at the University Hospital Tübingen. Specifically, there are 174 lung cancer patients, 132 lymphoma patients, and 166 melanoma patients. All scans were conducted using a state-of-the-art PET/CT scanner (Siemens Biograph mCT). The PET images were reconstructed using Gaussian reconstruction with a full width at half maximum of 2 mm, followed by iterative smoothing, and the enhanced CT slices had a thickness of 2 or 3 mm. We conducted experiments on data from these three types of patients, extracting slices containing tumors and resizing them to 128 × 128. Ultimately, the datasets for these three cancers contain 7176, 8201, and 8807 paired PET and CT slices, respectively. Five-fold cross-validation was performed on all three datasets.
4.2. Experiment Details
The proposed method was implemented using Python 3.7 and the PyTorch 2.0.0 on a system equipped with an NVIDIA GeForce RTX 4090 GPU. During the training phase, data augmentation strategies were applied to increase the number of training samples and enhance the network’s generalization capability. These strategies include random rotation (0°, 45°) with a probability of 0.5, Gaussian noise contamination (, ), and mix-up (with a probability of 0.2). The mix-up strategy involves randomly selecting two training samples and blending them together according to a certain ratio, with both input data and the labels being fused, as shown in Figure 4. The model uses the Adam optimizer with the first momentum factor set to 0.9 and the second momentum factor set to 0.99. The initial learning rate is set based on empirical values, and the learning rate update strategy uses simulated annealing, with a decay every 25 epochs, to avoid becoming stuck in local optima. The number of training epochs is set to 300, and early stopping is applied, terminating the training if the validation performance does not improve after 30 epochs. The baseline model requires approximately 120 s per epoch for a single round of training, while the introduction of MSIM increases this to 135 s per epoch, representing a relative increase of about 12.5%. This increase primarily stems from the additional computations required for multi-scale feature fusion.
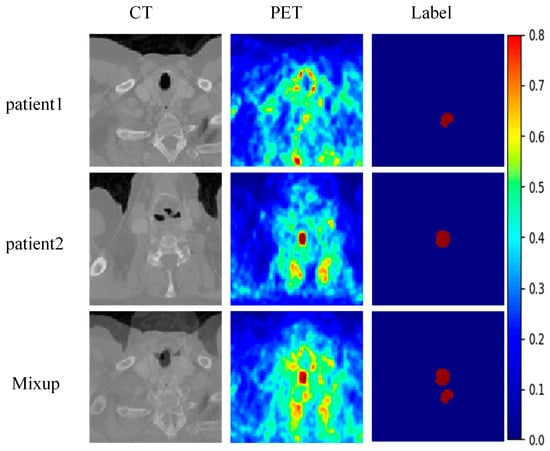
Figure 4.
An example of mix-up data enhancement.
4.3. Evaluation Metrics
4.3.1. Dice Similarity Coefficient
The Dice Similarity Coefficient (DSC) [35] is one of the most commonly used metrics in medical image segmentation. It is a similarity measure that is typically used to compute the similarity between two samples. The DSC value ranges from [0, 1], with higher values indicating a higher degree of overlap between the two sets and, therefore, higher segmentation accuracy. In this paper, the Dice coefficient is used as the primary evaluation metric, calculated as follows:
where and represent the predicted and ground truth sets, respectively, and denotes the size of their intersection. The DSC is an important indicator for assessing segmentation quality, especially in imbalanced data scenarios, where it provides a more accurate evaluation.
4.3.2. Classification Error
Classification Error (CE) [36] is another commonly used metric for evaluating the performance of segmentation models. It calculates the ratio of the number of false negatives () and false positives () predicted by the model to the total number of pixels, representing the classification error. A lower CE value indicates better performance in correctly classifying pixels. The formula for calculating CE is as follows:
where represents the number of pixels incorrectly classified as negative, represents the number of pixels incorrectly classified as positive, and represents the pixel sets of the ground truth.
4.3.3. Volume Error
Volume Error (VE) [37] is used to evaluate the relative error between the predicted segmentation volume and the ground truth volume. The formula is as follows:
where represents the actual volume of the positive class, and represents the predicted volume of the positive class. and are the volumes of the ground truth and predicted segmentation, respectively.
4.3.4. Volume Overlap Error
Volume Overlap Error (VOE) [38] is an evaluation metric that measures the error in the overlapping regions between the predicted segmentation results and the ground truth labels. VOE quantifies the difference between the predicted segmentation and the ground truth by calculating the error in their overlapping regions. The value of VOE ranges from [0, 1], with smaller values indicating higher overlap between the predicted results and the ground truth, implying better segmentation performance. The formula is as follows:
where represents the predicted segmentation results and represents the ground truth labels. denotes the intersection of the predicted and ground truth regions, i.e., the overlapping portion. represents the union of the predicted and ground truth regions, which includes all regions from both the predicted segmentation and the ground truth labels.
4.3.5. Hausdorff Distance
Hausdorff Distance (HD) [39] is a measure of shape similarity, defined as the maximum of the shortest distances from an element in one set to the other set. HD primarily focuses on the segmentation boundaries and serves as a complement to the Dice Similarity Coefficient (DSC). While DSC emphasizes evaluating the overlap within the region of interest (ROI), HD focuses more on boundary information, providing a better evaluation of the model’s ability to capture structural boundaries. The formula is as follows:
where represents the volume (or area) of the ground truth region, and represents the volume (or area) of the predicted segmentation result.
where denotes the distance norm between sets and , typically the L2 norm or Euclidean distance, which is used in this paper.
5. Experimental Results and Analysis
5.1. Ablation Experiment
In this study, we conducted ablation experiments to evaluate the impact of the interpretation module and interpretation loss on the performance of the tumor segmentation model. Table 3 presents the results of these ablation experiments. As shown in the results, compared with the baseline model, the introduction of the interpretation module slightly improved the segmentation performance across all three datasets. However, without explicit supervision to highlight key feature regions from different modalities, the fusion masks may emphasize unimportant areas or overlook critical regions. To address this issue, we introduced interpretation loss to provide explicit supervisory signals to the interpretation module, guiding the model to integrate key features from both PET and CT modalities effectively. The results demonstrate that incorporating interpretation loss improved the DSC by 1.6, 1.62, and 1.36 on the Melanoma, Lymphoma, and Lung cancer datasets, respectively. These findings confirm the effectiveness of the proposed interpretability approach in multimodal segmentation.

Table 3.
The DSC, CE, VE, VOE, and HD of the proposed method with different modules on the Melanoma, Lymphoma, and Lung cancer datasets.
5.2. Comparison Experiment
In this section, we compare the proposed method with four state-of-the-art methods. The results of the comparison are presented in Table 4. The experimental results show that our method exhibits significant advantages across the Melanoma, Lymphoma, and Lung cancer datasets. Specifically, on the Melanoma dataset, our method achieved the highest DSC value of 82.36% and the lowest HD value of 21.0937, indicating superior segmentation accuracy and boundary handling capabilities. Additionally, our method achieved the lowest CE and VOE, further highlighting its effectiveness in reducing classification errors and overlap discrepancies, thus demonstrating its outstanding performance in capturing and segmenting target regions.

Table 4.
The DSC, CE, VE, VOE, and HD of the proposed method and multimodality segmentation baselines on Melanoma, Lymphoma, and Lung cancer datasets.
On the Lymphoma dataset, our method continued to outperform the other methods, achieving a DSC of 83.18% and an HD of 20.6478 while also reducing VOE to 18.89%. These results demonstrate the method’s ability to segment complex structures accurately. The results for the Lung cancer dataset further support this conclusion, with our method reaching a DSC of 84.80% and significantly reducing CE, VE, and VOE, indicating that it effectively reduces segmentation errors and ensures the accuracy and consistency of the results. Figure 5 provides visual examples of segmentation results on the Lung cancer dataset using different segmentation methods. The visual results show that our method excels in tumor recognition and segmentation. In comparison, methods such as MSAM, ISANet, EFNet, and LFFI, while able to detect the main lesion areas in some cases, exhibit certain shortcomings in boundary processing and detail preservation. For example, in the first row, other methods show noticeable under-segmentation or mis-segmentation at the lesion edges, whereas our method aligns better with the ground truth (GT). In the second and third rows, where the lesion areas are more complex and include smaller lesions, our method again demonstrates its ability to capture these intricate structures, especially excelling in the segmentation of small lesions, avoiding both over-segmentation and missed detection. In contrast, EFNet and LFFI show insufficient recognition capabilities for small lesions in these scenarios, leading to more under-segmentation and artifacts in their outputs. The case in the fourth row further validates the robustness of our method in complex scenarios. The lesion area in this image has an irregular shape, and the contrast in both CT and PET images is relatively low, which increases the difficulty of segmentation. Despite these challenges, our method still accurately segments the lesion area and maintains high precision in boundary processing.
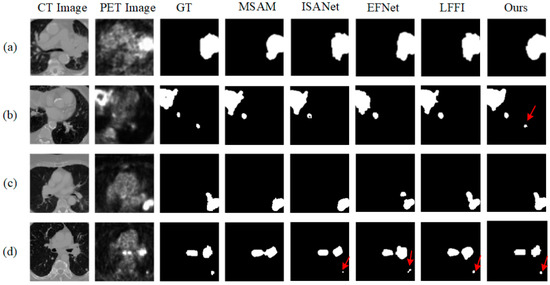
Figure 5.
The tumor segmentation visualization results of the five methods on the LUNG dataset, with (a–d) representing four different slices. GT stands for Ground Truth.
5.3. Visualization Experiments
5.3.1. Mask Visualization
Figure 6 presents the features, corresponding masks, ground truth (GT), and predicted results of our proposed method on CT and PET images from the LUNG dataset, with the channel names indicated in white text at the top right corner of each image. The first row of images shows the original CT image, feature map, and mask. In the original image, the anatomical structures of the lungs are clearly visible. The feature map reveals regions inside the lungs identified by the network, which may indicate potential tumor locations. The mask highlights key regions in the feature map that contribute the most to the segmentation result, with brighter colors (such as yellow and red) indicating higher importance. The ground truth annotation represents the tumor regions manually marked by radiologists as a reference. The model’s predictions closely align with the ground truth, demonstrating that the interpretation module effectively guides the network to focus on crucial features in a CT image, thus improving segmentation accuracy.
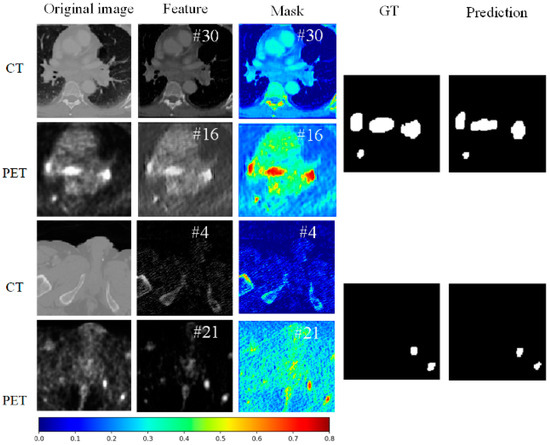
Figure 6.
The visualization of the PET and CT features for two samples, along with their corresponding interpretive masks and original image, is presented with the channel names indicated in white font in the top right corner.
The second row shows the corresponding PET image for the same slice. The original PET image displays metabolic activity, with brighter areas indicating regions of higher metabolic activity, often associated with tumors. The feature map captures these high-activity regions in the PET scan. The mask highlights these critical areas, marking regions with high metabolic activity (e.g., red areas), which are essential for the segmentation result. The comparison of the ground truth and the model’s predictions further confirms that the model accurately identifies the tumor regions in high-metabolism areas, indicating excellent segmentation performance in PET images.
The third row presents another CT image slice. The original image again shows the anatomical structure. The highlighted regions in the feature map show the important areas recognized by the network. The mask further emphasizes these key regions, with the most contributive parts to the segmentation result prominently displayed. The comparison between the ground truth and predictions shows that the model accurately segments the tumor region, verifying the consistency and reliability of the interpretation module across different slices.
The fourth row shows the corresponding PET image slice. The original image demonstrates the distribution of metabolic activity. The feature map captures the areas of high metabolic activity within the PET image. The mask highlights these critical regions, underscoring their importance to the segmentation result. The comparison of the ground truth and the model’s predictions further validates the model’s predictive ability, showing that it accurately identifies tumor regions across different slices in PET images.
5.3.2. LIME Visualization
In multimodal tumor segmentation research, LIME (Local Interpretable Model-agnostic Explanations) [40] serves as an important tool for revealing the rationale behind the model’s decisions. Figure 7 presents the LIME explanation results, ground truth (GT), and predicted results of our proposed method on CT and PET images. In the LIME_CT and LIME_PET images, the white regions represent the areas the model focuses on most during prediction, while the yellow areas indicate secondary areas of attention. These color annotations allow LIME to reveal the degree to which the model relies on features in different modalities. From the figure, it is evident that, for each row of CT images, the LIME_CT explanation results show that the model mainly focuses on high-intensity edge features in the image, which are typically related to anatomical structures. The white areas cover broader edge information, and the regions highlighted by LIME show good overlap with the GT, indicating that the model is able to identify key tumor-related features in CT images effectively. For each row of PET images, the LIME_PET explanation results show that the model primarily focuses on regions of high metabolic activity (white areas), which typically correspond to tumor locations. The yellow areas highlight secondary metabolic features to which the model attends. The white areas from the LIME explanation overlap well with the tumor regions annotated in the GT, indicating that the model can accurately capture important tumor-related features in PET images as well. Moreover, the model’s predictions align closely with the GT, further validating its accuracy.
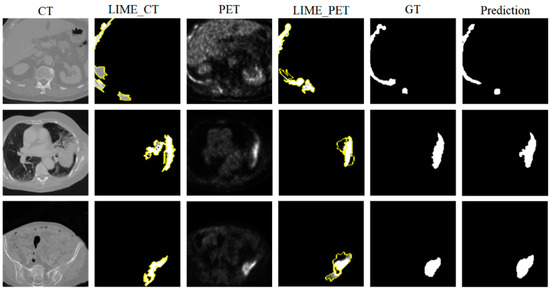
Figure 7.
LIME Explanation Diagram Overview: This diagram illustrates the decision-making rationale of our proposed method on CT and PET images from the LUNG dataset. The left column displays the original CT images and their corresponding LIME explanation results, the middle column shows the original PET images along with their LIME explanations, and the right column presents the ground truth (GT) and model segmentation predictions. The highlighted areas in the LIME explanations represent the feature regions that the model focuses on most in each modality.
5.4. Perturbation Experiments
In this section, we explain the “black-box” decision-making process of neural networks through feature perturbation experiments. Specifically, the experiment involves removing certain regions from the input images and observing the impact of these removals on the model’s decisions, thus gaining a better understanding of the model’s behavior in the tumor segmentation task. We assess the impact of removing features related to the tumor regions on segmentation performance. To accomplish this, we employed two perturbation strategies: random perturbation and explanation-based perturbation. Figure 8 presents the results of the feature perturbation experiment. As shown in the figure, the explanation-based perturbation method demonstrates clear advantages over the random perturbation method. In the random perturbation experiment, as the removal ratio increases, the DSC gradually decreases, indicating that the random removal of features significantly weakens the model’s segmentation performance. Particularly, when the removal ratio approaches 1, the segmentation ability of the model is almost completely lost, with the DSC coefficient dropping close to 0, verifying the importance of features for model performance. In contrast, in the explanation-based perturbation experiment, when removing features indicated by the interpretability mask with relatively low importance, the performance degradation is significantly reduced. This phenomenon demonstrates the effectiveness of the explanation module in identifying and retaining key features. The model is able to prioritize preserving the regions of features that are crucial to the segmentation task. When the removal ratio is low (e.g., between 0 and 40%), the model maintains high segmentation accuracy, exhibiting strong robustness. This indicates that the model has minimal reliance on non-critical features and possesses a degree of fault tolerance. However, when the removal ratio exceeds 40%, the segmentation performance starts to decline significantly, especially when the removal ratio nears 1, where segmentation performance is nearly lost, indicating the model’s high dependency on these key features. This further confirms that the explanation module successfully highlights the critical features that play a decisive role in segmentation performance.
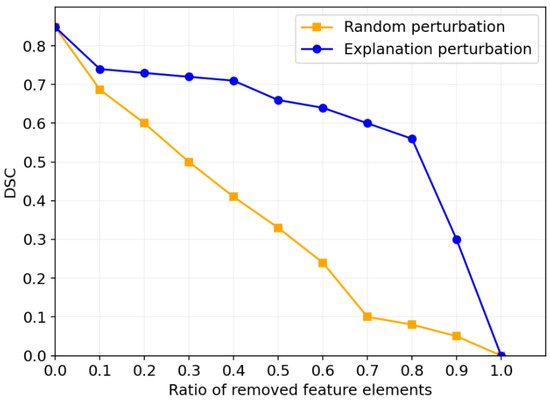
Figure 8.
Segmentation performance after removing a certain proportion of features on the LUNG dataset.
6. Discussion
6.1. Results Analysis
The tumor segmentation framework based on MSIM proposed in this paper generates multi-scale interpretive masks by incorporating a multi-scale feature processing module and an interpretation module. Specifically, the interpretation loss function we designed provides explicit supervisory signals to the interpretation module, which helps improve the model’s performance in the multimodal feature integration process. Our experimental results show that the proposed method outperforms several mainstream tumor segmentation methods on multiple datasets. In the ablation experiments, we validated the effectiveness of the multi-scale interpretability module and interpretation loss in improving segmentation performance (as shown in Table 3. The results demonstrate that, compared with the baseline methods, our approach improves the DSC by 1.6, 1.62, and 2.36 on three datasets, indicating that the introduction of the interpretation module and loss function effectively enhanced the model’s segmentation ability. Additionally, the comparison experiments with four mainstream methods (as shown in Table 4 also demonstrate the advantages of our method in tumor segmentation tasks. Notably, in the visualization analysis, the interpretive masks generated by the interpretation module successfully highlighted the key features of the tumor region. By visualizing the PET and CT features and their corresponding masks (as shown in Figure 6), we were able to clearly see the key regions the model focused on during the decision-making process, which further validated the role of our interpretation module in enhancing model transparency and reliability. Additionally, through LIME visualization results, we were able to clearly observe the key regions the model focused on when making segmentation decisions. The model primarily concentrated on edge features in CT images (usually related to anatomical structures) and high metabolic activity regions in PET images (associated with tumors). These visual results provide strong support for our method, validating the model’s decision-making rationale and enhancing model transparency and trustworthiness. Finally, the feature perturbation experiments further proved the ability of our method to identify and retain critical features. As the removal ratio increased, the segmentation performance significantly declined, especially in the explanation-based perturbation method, where the performance degradation was significantly reduced when removing features of relatively low importance, as indicated by interpretive masks. When the removal ratio exceeded 40%, the segmentation performance began to decline significantly (as shown in Figure 8. This result shows that our method can effectively identify and emphasize the most informative regions in tumor segmentation, thereby improving the model’s accuracy and stability.
6.2. Limitations and Future Work
Although this study has achieved excellent performance, there are still some limitations: (1) The current framework is designed for PET-CT imaging, leveraging the complementary nature of PET and CT information. Its generalizability to other multimodal combinations (such as MRI-CT) has not yet been validated. Differences in intensity distribution or spatial resolution between modalities may require adjustments to the fusion strategy. (2) While the computational overhead of MSIM is moderate (a 12–15% increase in FLOPs and a 10–12% increase in training time), the real-time processing requirements for data in clinical environments still need further optimization to adapt to hardware deployments with limited resources. (3) The interpretability analysis only employs LIME, lacking consistency comparisons with other mainstream methods (such as Shapley values and Grad-CAM), which may introduce methodological bias. Future studies might integrate these techniques to strengthen the explanatory power of the model. Additionally, although the visualization results align with clinical intuition, quantitative alignment with radiologists’ cognitive logic (e.g., through scoring to evaluate the overlap between saliency maps and manually annotated regions) remains to be explored. To address these limitations, future work will focus on the following aspects: (1) Extending the framework to other modality combinations by designing adaptive fusion mechanisms that dynamically adjust feature weights based on modality reliability. (2) Exploring model compression techniques (such as knowledge distillation) to reduce computational costs while maintaining accuracy. (3) Collaborating with radiologists to evaluate the model’s attention regions through double-masked experiments, ensuring consistency with clinical decision-making. Introducing causal inference frameworks can further distinguish spurious associations from causally relevant features.
7. Conclusions
This paper presents a multimodal tumor segmentation framework based on a multi-scale interpretability approach, which effectively leverages the high sensitivity of PET for tumor detection and the high precision of CT for tumor boundary delineation, significantly improving lung tumor segmentation accuracy. By introducing the MSIM, we generate multi-scale feature maps and interpretive masks that effectively highlight the critical regions in tumor segmentation. Additionally, we designed an interpretation loss function to provide explicit supervisory signals to the model’s interpretability module. The experimental results demonstrate that our method outperforms existing mainstream methods across multiple datasets, achieving improvements of 1.6, 1.62, and 2.36 in DSC on three datasets. Ablation and comparison experiments further validate the enhancement in model performance due to the proposed interpretability module. Visualization and perturbation experiments also confirm that our method can successfully identify and retain key features, improving the stability and accuracy of tumor segmentation. Although the current work focuses on PET-CT, future research will aim to achieve cross-modal generalization, optimize computational efficiency, and conduct more in-depth clinical validation to promote the application of trustworthy AI in oncology.
Author Contributions
This work was conducted in collaboration with all authors. Conceptualization, H.Y. and D.Y.; methodology, D.Y.; validation, D.Y.; formal analysis, D.Y.; investigation, D.Y.; resources, Y.W.; data curation, Y.M. and Y.W.; writing—original draft preparation, D.Y. and Y.W.; writing—review and editing, H.Y. and D.Y.; visualization, Y.M. and Y.W.; supervision, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the Haikou Science and Technology Plan Project under Grant 2022-007 and Hainan Engineering Research Center for Virtual Reality Technology and Systems (QiongfaGaigaoji [2023] No. 818). (Corresponding author: Houqun Yang).
Data Availability Statement
We used the publicly available datasets at https://www.cancerimagingarchive.net/collection/fdg-pet-ct-lesions/ (accessed on 21 July 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Figure A1 shows the DSC results under different combinations of hyperparameters (, , ), where these hyperparameters correspond to the weights of the segmentation loss, mask loss, and regularization loss, respectively. The analysis reveals that as increases, the overall DSC stabilizes, with the highest DSC score achieved when = 0.5. For , lower values of typically result in lower DSC scores, indicating that mask loss plays a key role in model performance. However, excessively high values of may lead to suboptimal results, possibly due to the overemphasis on mask prediction at the expense of overall segmentation quality. For the regularization term , segmentation performance is closely linked to . When = 0.5, the best performance occurs at = 0.5. We observe that the combination of = 0.5, = 1.5, and = 0.5 achieves the best DSC score.
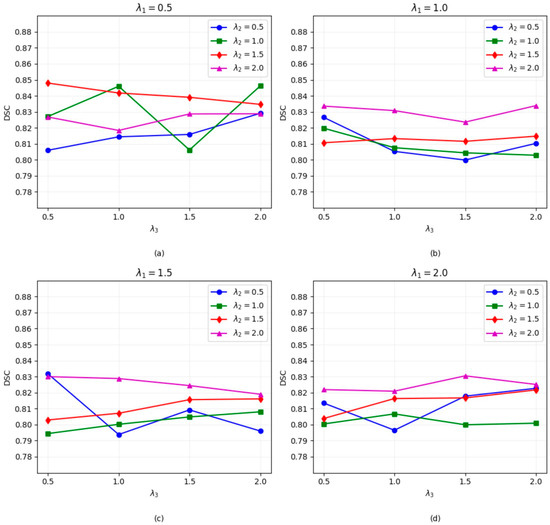
Figure A1.
The DSC coefficients of the models trained with different hyperparameters (, and ) on the LUNG dataset. (a–d) represent the DSC segmentation performance figure under different parameter combinations of , , and .
References
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: Globocan estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef] [PubMed]
- Coleman, R.E. Pet in lung cancer. J. Nucl. Med. 1999, 40, 814–820. [Google Scholar] [PubMed]
- Khalaf, M.; Abdel-Nabi, H.; Baker, J.; Shao, Y.; Lamonica, D.; Gona, J. Relation between nodule size and 18 f-fdg-pet suv for malignant and benign pulmonary nodules. J. Hematol. Oncol. 2008, 1, 1–8. [Google Scholar] [CrossRef]
- Grgic, A.; Yüksel, Y.; Gröschel, A.; Schäfers, H.-J.; Sybrecht, G.W.; Kirsch, C.M.; Hellwig, D. Risk stratification of solitary pulmonary nodules by means of pet using 18 f-fluorodeoxyglucose and suv quantification. Eur. J. Nucl. Med. Mol. Imaging 2010, 37, 1087–1094. [Google Scholar] [CrossRef]
- Li, L.; Lu, W.; Tan, Y.; Tan, S. Variational pet/ct tumor co-segmentation integrated with pet restoration. IEEE Trans. Radiat. Plasma Med. Sci. 2019, 4, 37–49. [Google Scholar] [CrossRef]
- Xu, L.; Tetteh, G.; Lipkova, J.; Zhao, Y.; Li, H.; Christ, P.; Piraud, M.; Buck, A.; Shi, K.; Menze, B.H. Automated whole-body bone lesion detection for multiple myeloma on 68ga-pentixafor pet/ct imaging using deep learning methods. Contrast Media Mol. Imaging 2018, 2018, 2391925. [Google Scholar] [CrossRef]
- Zhong, Z.; Kim, Y.; Zhou, L.; Plichta, K.; Allen, B.; Buatti, J.; Wu, X. 3D fully convolutional networks for co-segmentation of tumors on pet-ct images. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 228–231. [Google Scholar]
- Mall, P.K.; Singh, P.K.; Srivastav, S.; Narayan, V.; Paprzycki, M.; Jaworska, T.; Ganzha, M. A comprehensive review of deep neural networks for medical image processing: Recent developments and future opportunities. Healthc. Anal. 2023, 4, 100216. [Google Scholar] [CrossRef]
- Rahaman, M.A.; Chen, J.; Fu, Z.; Lewis, N.; Iraji, A.; Calhoun, V.D. Multi-modal deep learning of functional and structural neuroimaging and genomic data to predict mental illness. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Virtual Conference, 1–5 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 3267–3272. [Google Scholar]
- Li, L.; Zhao, X.; Lu, W.; Tan, S. Deep learning for variational multimodality tumor segmentation in pet/ct. Neurocomputing 2020, 392, 277–295. [Google Scholar] [CrossRef]
- Van der Velden, B.H.; Kuijf, H.J.; Gilhuijs, K.G.; Viergever, M.A. Explainable artificial intelligence (xai) in deep learning-based medical image analysis. Med. Image Anal. 2022, 79, 102470. [Google Scholar] [CrossRef]
- Tseng, L.-Y.; Huang, L.-C. An adaptive thresholding method for automatic lung segmentation in ct images. In Proceedings of the AFRICON 2009, Nairobi, Kenya, 23–25 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–5. [Google Scholar]
- El Hassani, A.; Skourt, B.A.; Majda, A. Efficient lung ct image segmentation using mathematical morphology and the region growing algorithm. In Proceedings of the 2019 International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), Taza, Morocco, 26–27 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Chandrashekar, N.; Natraj, K. Detection of lung cancer by canny edge detector for performance in area, latency. In Proceedings of the 2018 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT), Msyuru, India, 14–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 690–696. [Google Scholar]
- Yu, K.; Chen, X.; Shi, F.; Zhu, W.; Zhang, B.; Xiang, D. A novel 3d graph cut based co-segmentation of lung tumor on pet-ct images with gaussian mixture models. In Medical Imaging 2016: Image Processing; SPIE: Bellingham, WA, USA, 2016; Volume 9784, pp. 787–793. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 565–571. [Google Scholar]
- Kumar, A.; Fulham, M.; Feng, D.; Kim, J. Co-learning feature fusion maps from pet-ct images of lung cancer. IEEE Trans. Med. Imaging 2019, 39, 204–217. [Google Scholar] [CrossRef]
- Fu, X.; Bi, L.; Kumar, A.; Fulham, M.; Kim, J. Multimodal spatial attention module for targeting multimodal pet-ct lung tumor segmentation. IEEE J. Biomed. Health Inform. 2021, 25, 3507–3516. [Google Scholar] [PubMed]
- Huang, Z.; Zou, S.; Wang, G.; Chen, Z.; Shen, H.; Wang, H.; Zhang, N.; Zhang, L.; Yang, F.; Wang, H.; et al. Isa-net: Improved spatial attention network for pet-ct tumor segmentation. Comput. Methods Programs Biomed. 2022, 226, 107129. [Google Scholar]
- Zhao, X.; Li, L.; Lu, W.; Tan, S. Tumor co-segmentation in pet/ct using multi-modality fully convolutional neural network. Phys. Med. Biol. 2018, 64, 015011. [Google Scholar]
- Diao, Z.; Jiang, H.; Han, X.-H.; Yao, Y.-D.; Shi, T. Efnet: Evidence fusion network for tumor segmentation from pet-ct volumes. Phys. Med. Biol. 2021, 66, 205005. [Google Scholar]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar]
- Dabkowski, P.; Gal, Y. Real time image saliency for black box classifiers. Adv. Neural Inf. Process. Syst. 2017, 30, 6970–6979. [Google Scholar]
- Li, K.; Wu, Z.; Peng, K.-C.; Ernst, J.; Fu, Y. Tell me where to look: Guided attention inference network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9215–9223. [Google Scholar]
- Fong, R.C.; Vedaldi, A. Interpretable explanations of black boxes by meaningful perturbation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3429–3437. [Google Scholar]
- Kang, S.; Chen, Z.; Li, L.; Lu, W.; Qi, X.S.; Tan, S. Learning feature fusion via an interpretation method for tumor segmentation on pet/ct. Appl. Soft Comput. 2023, 148, 110825. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Wang, L.; Lee, C.-Y.; Tu, Z.; Lazebnik, S. Training deeper convolutional networks with deep supervision. arXiv 2015, arXiv:1505.02496. [Google Scholar]
- Moradi, R.; Berangi, R.; Minaei, B. A survey of regularization strategies for deep models. Artif. Intell. Rev. 2020, 53, 3947–3986. [Google Scholar]
- Gatidis, S.; Hepp, T.; Früh, M.; La Fougère, C.; Nikolaou, K.; Pfannenberg, C.; Schölkopf, B.; Künstner, T.; Cyran, C.; Rubin, D. A whole-body fdg-pet/ct dataset with manually annotated tumor lesions. Sci. Data 2022, 9, 601. [Google Scholar]
- Li, L.; Wang, J.; Lu, W.; Tan, S. Simultaneous tumor segmentation, image restoration, and blur kernel estimation in pet using multiple regularizations. Comput. Vis. Image Underst. 2017, 155, 173–194. [Google Scholar] [PubMed]
- Hatt, M.; Le Rest, C.C.; Turzo, A.; Roux, C.; Visvikis, D. A fuzzy locally adaptive bayesian segmentation approach for volume determination in pet. IEEE Trans. Med. Imaging 2009, 28, 881–893. [Google Scholar] [PubMed]
- Dewalle-Vignion, A.-S.; Betrouni, N.; Lopes, R.; Huglo, D.; Stute, S.; Vermandel, M. A new method for volume segmentation of pet images, based on possibility theory. IEEE Trans. Med. Imaging 2010, 30, 409–423. [Google Scholar]
- Christ, P.F.; Ettlinger, F.; Grün, F.; Elshaera, M.E.A.; Lipkova, J.; Schlecht, S.; Ahmaddy, F.; Tatavarty, S.; Bickel, M.; Bilic, P.; et al. Automatic liver and tumor segmentation of ct and mri volumes using cascaded fully convolutional neural networks. arXiv 2017, arXiv:1702.05970. [Google Scholar]
- Aydin, O.U.; Taha, A.A.; Hilbert, A.; Khalil, A.A.; Galinovic, I.; Fiebach, J.B.; Frey, D.; Madai, V.I. An evaluation of performance measures for arterial brain vessel segmentation. BMC Med. Imaging 2021, 21, 1–12. [Google Scholar]
- Palatnik de Sousa, I.; Maria Bernardes Rebuzzi Vellasco, M.; Costa da Silva, E. Local interpretable model-agnostic explanations for classification of lymph node metastases. Sensors 2019, 19, 2969. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).