Abstract
Signifiable computability aims to separate what is theoretically computable from what is computable through performable processes on computers with finite amounts of memory. Mathematical objects are signifiable in a formalism on an alphabet if they can be written as spatiotemporally finite texts in on . In a previous article, we formalized the signification and reference of real numbers and showed that data structures representable as multidimensional matrices of discretely finite real numbers are signifiable. In this investigation, we continue to formulate our theory of signifiable computability by offering an axiomatization of signifiable computation on discretely finite real numbers. The axiomatization implies an ontology of functions on discretely finite real numbers that classifies them as signifiable, signifiably computable, and signifiably partially computable. Relative to and , signification is performed with two formal systems: the Former that forms texts in on and the Transformer that transforms texts formed by into other texts in on . Singifiable computation is defined relative to on as a finite sequence of signifiable program states, the first of which is generated by and each subsequent state is deterministically obtained from the previous one by . We define a debugger function to investigate signifiable computation on finite-memory devices and to prove two theorems, which we call the Debugger Theorems. The first theorem shows that, for a singifiably partially computable function signified by a program on a finite-memory device , the memory capacity of is exceeded when running the program on signifiable discretely finite real numbers outside of the function’s domain. The second theorem shows that there are functions signifiably computable in general that become partially signifiably computable when signified by programs on insomuch as the memory capacity of can be exceeded even when the programs are executed on some signifiable discretely finite real numbers in the domains of these functions.
Keywords:
computability theory; recursion theory; signifiable computability; axiomatization; debugger theorems; discretely finite real numbers; number theory MSC:
03D75; 03D80
1. Introduction
While general computability describes functions computable on devices without any memory limitations [1], or, equivalently, computable in principle [2], actual computability aims to characterize functions computable on devices with finite amounts of memory available for computation. We call such devices finite-memory devices (FMD) [3]. In a previous article [4], we began to formulate a theory of signifiable computability (or, equivalently, a signifiable computability theory (SCT)). The SCT separates general computability investigated in the classical computability theory (CCT) from actual computability when computation occurs within a finite amount of memory, as is the the case in many areas of applied computer science. In signifiable computability, names of intuitive objects, such as numbers, functions, data types and structures (i.e., instances of data types), programs, and program states are treated as spatiotemporally finite texts constructed with formal languages (or, equivalently, formalisms) on specific alphabets. Thus, these texts signify (or, equivalently, designate or name) intuitive objects, such as numbers, functions, data types and structures, programs, and program states in a given universe of discourse described by a formalism on an alphabet (e.g., Lisp on Unicode). When the texts are stored within the available memory units on an FMD , they signify the corresponding objects in the finite memory of , thereby making the universe of discourse conditional not only on and , but also on . E.g., a human programmer using Lisp on Unicode on a computer with 5 terabytes (TB) of combined RAM and hard disk space cannot signify an intuitive object on this FMD if the storage size of the signifying text (i.e., the name of the object in Lisp on Unicode) exceeds 5 TB.
In a previous investigation [4], we defined the concepts of signification and reference of real numbers and extended signification to number tuples and data types and structures. We showed that data structures representable as tuples of discretely finite real numbers are signifiable. The signification of multidimensional matrices was introduced to show that data structures representable as multidimensional matrices of discretely finite real numbers are also signifiable. We argued that, in order to be sufficiently expressive, on must be not only decimal-sufficient (i.e., should contain finitely many rules to signify discretely finite real numbers in the standard decimal notation or an equivalent thereof) but also tuple-sufficient (i.e., should have finitely many rules to signify sequences of such numbers).
In this investigation, we continue to formulate the SCT by offering an axiomatization of signifiable computation on discretely finite real numbers. We show how a sufficiently expressive on can be extended with instruction types and how these types can be signified with texts and arranged into sequences. Signified instructions in a text sequence can be executed (or, equivalently, performed) one-by-one in order to carry out the prescribed numerical computation. If the computation exists (i.e., the execution finishes), its result (or, equivalently, output) is signified with a text in on . An independent party can verify the computation from (1) the input text; (2) the text of the instruction sequence; and (3) the text with the sequences of the numerals of the individual instructions used in the computation.
This investigation is motivated by the following limitations of the CCT reflected in its axioms: (1) what is computable in principle (general computability) is indistinguishable from what is actually computable on computers with finite amounts of memory (actual computability); (2) the investigation of computability properties is confined to functions on natural numbers; (3) the formation of programs is insufficiently axiomatized insomuch as it is unclear how programs are formed (or, equivalently, generated or produced); (4) the transformation of programs to obtain a computation in the form of a finite sequence of program states is insufficiently axiomatized in that there is no concept of error or cost; (5) interpretation of input and output texts is unresolved to the extent that no position is taken on whether interpretation (e.g., a denotational or operational semantics) is part of computation or not. While the SCT is grounded in the CCT, it extends the CCT, because it (1) separates general computability from actual; (2) extends the investigation of computability properties to functions on discretely finite real numbers; (3) makes actual computability properties of functions explicitly dependent on formalisms, alphabets, and FMDs on which those functions are signified and computed; (4) introduces error and cost into computation; (5) takes a position that interpretation is not part of computation and as such belongs to metacomputability. As we formulate the SCT in this article, we reference, when appropriate, the CCT axioms summarized for the reader’s convenience in the Appendix A.
The remainder of this article is organized as follows. In Section 2, we review the basic ontology of the CCT presented in [1,2] and the formalism in [4] that we continue to use in this article. In Section 3, we axiomatize the formation and transformation of texts. Signification is actualized with two formal systems: the Former that generates texts in on , and the Transformer that transforms texts formed by into other texts in on . In Section 4, we define formable and transformable instructions and axiomatize the formation and transformation of program instructions and formation of programs. In Section 5, we axiomatize program states and computations. Computation is defined relative to on as a finite sequence of signifiable program states, the first of which is generated by and each subsequent state is deterministically obtained from the previous one by . In Section 6, we axiomatize the transformation of programs and discuss whether it is possible for to transform program states that are not generated by . In Section 7, we offer an ontology of functions on discretely finite real numbers that classifies functions as signifiable, signifiably computable, and signifiably partially computable. In Section 8, we introduce memory limitations on signifiable computation to characterize functions as signifiably computable and partially computable on FMDs. Section 2, Section 3, Section 4, Section 5, Section 6, Section 7 and Section 8 can be viewed as the preliminary, auxiliary steps to Section 9, where we present our main results. In particular, we define a debugger function to actualize signifiable computation on FMDs and use it to prove two theorems, which we call the Debugger Theorems, to investigate some of the effects of finite memory on signifiable computation. In Section 10, we discuss our results. In Section 11, we summarize our findings and outline the scope of the next part of our investigation of signifiable computability.
2. Prolegomena
The reader may skip this section on first reading and return to it as necessary. Here, we review the basic concepts of the CCT and the basic formal apparatus in [4] that we continue to use in this article.
The CCT ontology used in this article is based on [1,2] and includes the following concepts:
- function—a mathematical object, i.e., a mapping from a given domain to a given range;
- alphabet—a finite set of symbols (or, equivalently, signs) (e.g., );
- formalism—a formal language on a specific alphabet defined with a finite set of syntactic rules used to name (or, equivalently, signify or designate) intuitive mathematical objects (e.g., numbers, functions, sequences, etc.);
- model—a formal model to compute functions, such as a Turing machine (TM) (cf., e.g., Ch. 6 in [1]);
- program—a signified finite sequence of instructions in on that specifies how a function named by the program can be computed, i.e., how a signified sequence of inputs in on can be mapped (or, equivalently, transformed) to a signified sequence of outputs by a computer capable of performing instructions in on ;
- computer—a device or an agent, physical or abstract, that executes programs in on on given inputs according to a specific model;
- program state—a state of a program in on signified by a spatiotemporally finite text in on that, at a minimum, signifies the value of every variable used by the program and the next instruction in the program for a computer to perform;
- computation—a finite sequence of program states signified by a spatiotemporally finite text in on that a computer goes through in order to compute the signified values of a function designated by a program in on on a signified input (or, equivalently, to transform a signified input to a signified output);
- class of functions—a set of functions; in the CCT, the three most prominent classes are: primitive recursive; computable; and partially computable.
Finite automata (cf., e.g., [5]) such as finite state machines (FSA), stack machines (also known as push-down automata (PDA)), and TMs are formal models signifiable with different formalisms on different alphabets to compute different classes of functions. A formalism is necessarily paired with an alphabet . E.g., a programming language, such as Lisp, Perl, C/C++, etc., can be defined on Unicode or ASCII. Computability is a property of functions. E.g., a primitive recursive function (e.g., ) is signifiable in different formalisms on different alphabets and is computable by an FSA, a PDA, or a TM. There are functions signifiable with context-free formalisms and computable by PDAs that are not computable by FSAs (e.g., = ën, , where ën and denote n consecutive occurences of ë and ?, respectively). There are functions signifiable with context-sensitive formalisms that are computable by TMs but not by PDAs (e.g., = ën, ) (cf., e.g., [6]). In formal logic, some texts in on are referred to as names and the named classes of those objects are called extensions (cf. p. 94 and pp. 268–269 in [7]). If a text signifies a unique object, it signifies a singleton.
The statements and mean that is a proper subset and a subset of the set , respectively; ∅ denotes the empty set. , , , , , respectively denote the infinite sets of natural numbers (), of whole numbers (), of negative whole numbers (), of positive whole numbers (), of rational numbers ( ), and of real numbers that include the whole numbers, the rational numbers, and the irrational numbers. If , are sets, then
where is called a k-tuple, i.e., a finite sequence of k elements.
A finite-memory device (FMD) is a computational device with a finite number of memory units (or, equivalently, memory cells) available for computation. An FMD is not a model of computation insomuch as it can perform computations according to different models so long as each computation can be signified within its memory capacity. If is the set of all FMDs, then the function maps each FMD to the number of its memory cells. Thus, each FMD has a strictly positive memory capacity. It should be noted that if a device is an FSA, a PDA, or a TM, then
On the other hand, if D is an FMD, then
Thus, if and are two TMs, the predicates , , are, respectively, equivalent to , , , of which the first statement is vacuously true, whereas the second and third statements have no immediate logical satisfaction without a reinterpretation of < and > (e.g., along the lines of Cantor’s set theory, where < ). On the other hand, if and are FMDs, then the three CCAP statements above can be assigned the Boolean values of True and False under the standard interpretation of the three comparison operators on natural numbers.
If is an FSA, a PDA, or a TM, then can be turned into an FMD if, and only if, one of the two conditions holds. First, , i.e., an explicit upper bound in the form of a concrete positive integer is placed on the combined size of the the text that signifies the finite control of and the size of the input tape. Second, is signified in a specific formalism on a specific alphabet (e.g., Lisp, Perl, C/C++ on Unicode) on a specific FMD (e.g., a computer with 5 TB of RAM and hard disk space). In the latter case, is an FMD, because its memory capacity is bounded by the memory capacity of the device on which it runs, i.e., TB.
An elementary sign is that which can be written in exactly one memory cell. We enclose all elementary signs in pairs of matching " (e.g., "0", "1", "+"). The elementary sign "" is the empty sign. An alphabet is an enumerably finite, non-empty set of non-empty elementary signs. A text is a spatiotemporally finite sequences of elementary signs of . We intentionally use the term text instead of the term string to avoid allusions to the modern string theory in physics or to the classical finite automata theory of theoretical computer science. All texts are also enclosed in matching pairs of ". An alphabet is decimal-sufficient if, and only if, contains the signs of the standard decimal notation or their isomorphic equivalents. on is decimal-sufficient if, and only if, it allows, via a finite set of rules, for the mechanical formation of texts on in the characteristic-mantissa form of the standard decimal notation.
A basic text formation operation in on is concatenation, denoted as . The order of the sign concatenation in the formation of a text is arbitrarily assumed to be left to right, i.e., for ,
Two enumerably infinite sets, denoted as
are associated with on . The first set includes all signs of and all non-empty texts in on formed according to the finite set of rules of . The second set is defined as
For , , , we let
If , then is the number of the elementary signs from in t. If , then and . If , then , , designate the consecutive elementary signs of from the leftmost to the rightmost, where .
If f is a function, and denote the domain and the range of f, respectively; abbreviates , where ∧ denotes the logical and. E.g., if = ën, , then and ë, ëë, ëëë, or, equivalently, ë, ëë, ëëë, . If and , then f is defined on or, in symbols, if, and only if, there exists such that or, equivalently, , where ∃ designates the logical existential quantifier. If , where ¬ designates the logical not, then f is undefined on or, in symbols, . If and
where ∀ designates the logical universal quantifier, f is total on . If
then f is partial on . It should be noted that while the notation is used for partial and total functions, total functions on are defined for all , whereas partial functions on may not be defined for some . Thus, every total function on is partial on , but not vice versa.
Let . Then, r is discretely finite in on if, and only if, there exists
where each t signifies (or, equivalently, designates or names) r and no other number, or, in symbols,
If , then t signifies r in on , or, in symbols,
and are symmetric.
Let such that . Then, r is finite-memory signifiable (FM-signifiable) or, equivalently, FM-designatable in on on an FMD if, and only if, there exists such that , in which case,
holds. If , then t FM-signifies or, equivalently, FM-designates r in on on , or, in symbols,
and are symmetric. In general, the subscript when added to the right of the subscripts and means that a relationship is defined not only relative to and but also to , and, in particular, relative to .
A numeral is that designates a real number. A decimal-sufficient alphabet can be extended with the unique signs ⊴, ⊵, ∓ that designate the beginning of a tuple, the end of a tuple, and a number separator inside a tuple, respectively. E.g., let
be a decimal-sufficient alphabet and let
consists of the standard decimal notation signs in and the signs in that can be used to signify number tuples, data types, and data instances. Specifically, in in (7), we let ⊴ = "", ⊵ = "a", and ∓ = ";". Alphabets that contain these unique signs are tuple-sufficient. Thus, is tuple-sufficient. on a tuple-sufficient is tuple-sufficient if, and only if, contains finitely many rules that allow for the signification of k-tuples of discretely finite real numbers on . For brevity, we will say that on is tuple-sufficient to mean that both and are tuple-sufficient. E.g., Lisp, Perl, C/C++ on Unicode are tuple-sufficient.
Let , , , , , . Then,
is the unmarked concatenation of in on and
is the marked concatenation of in on . E.g., in a tuple-sufficient on , "1;2;3" is the unmarked concatenation of "1", "2", and "3", whereas "1;2;3a" is the marked concatenation of "1", "2", and "3".
A k-tuple , , is signifiable or, equivalently, designatable in on if, and only if, (a) is of type and is signifiable in on , or, in symbols, ; and (b) , , . If (a) and (b) hold, then is signifiable in on by
or, in symbols,
If is not signifiable in on , then ""; is symmetric.
A k-tuple , , is finite-memory signifiable (FM-signifiable) or, equivalently, FM-designatable in on on if, and only if, (a) and (b) . If (a) and (b) hold, then . If is not FM-signifiable in on on , then ""; is symmetric.
Let be the i-th prime so that , , , etc., and let
Let be a k-tuple such that . The Gödel number (G-number) of is
Let be such that . The j-shifted Gödel number (denoted as , ) of this k-tuple is
The G-number and -number of are defined to be 1.
Let be a 1–1 function that maps each sign of to a unique odd prime, i.e.,
E.g., for in (7), we have
The 1–1 function in (12) maps (i.e., , , , ) to a unique positive integer and maps "" to 0 (cf. Theorem 4 in [4]).
3. Formation, Transformation, Metacomputability
A programming formalism on is a formalism by which one formal system generates texts in on that signify sequences of numerical instructions that another formal system can perform. Hence,
Definition 1 (Programming Formalism).
Let be tuple-sufficient on . Then, on is a programming formalism if it is used by two formal systems: the Former and the Transformer .
A formal system in (1) is specified by a finite set of formal rules and a rule application mechanism to form texts or to transform texts into other texts. The rules and rule application mechanisms have no meaning inside the systems and, in that sense, are purely syntactic (cf. Ch. IV in [8]).
Definition 2 (The Former).
The formal text formation system, denoted as , is a finite set of rules
and a rule application mechanism to form texts in .
Each formation rule is assigned a unique name (i.e., signified with a unique ). Since is a unique natural number, we have
so that each formation rule is mapped to a unique natural number signifiable in on , which we abbreviate as
If uses the rule sequence , , to form from "", then, by convention, the first argument of each rule takes the output of the previous rule and the first argument of is "", whence
where "" and , , . E.g., if is tuple-sufficient on
and contains the rule for , then
designates the concatenation of the signs in separated with . E.g., if "♡", then, for in (15), we have
Definition 3 (Text Formation).
A mechanical formation or, simply, formation of by is a finite sequence of formation rules , such that
where
Each rule has access to .
Definition 4 (Formation Signature).
Let , , , be a formation of by , where, for ,
Then,
where , , , , …, , for , , , is a formation signature of by , whence
and is a signed formation of by designated by s.
E.g., let be tuple-sufficient on in (7), where ⊴ = "", ⊵ = "", ∓ = ";", and
Then, if we keep the matching pairs of " only in "" and "." for clarity and omit them elsewhere for brevity, then
designates the formation signature of "3.14" by .
Thus, any formed by exists as a spatiotemporally finite entity constructed from a finite number of signs of by finitely many rules signified in the formation signature of t. Hence, our first two axioms.
SCT Axiom 1.
A signed formation of by takes a finite amount of physical time, and t occupies a finite amount of physical space.
SCT Axiom 2.
If s designates a formation signature of t by , then, given , s, and , another formal system can deterministically verify the formation of t by within a finite amount of physical time and space.
No a priori knowledge is assumed on how time and space are physically measured (e.g., sun cycles, turns of a sand clock, nanoseconds, meters, centimeters, cubic meters, bits, bytes, megabytes, etc.). SCT Axioms 1 and 2 concretize CCT Axiom A1 (cf. Appendix A) by taking a definite position on the origin of texts that designate programs: (1) these texts are produced by one formal system for another formal system; (2) their production can be deterministically verified; and (3) the produced texts are spatiotemporally finite objects.
For , the predicate
holds if, and only if, t is formed by through a signed formation. We let vacuously hold and define
to be the enumerably infinite set of texts formed by . E.g., if is Unicode and is Lisp and includes the finitely many Common Lisp program formation rules in [9], then
Definition 5 (The Transformer).
The formal text transformation system, denoted as , is a finite set of rules
and a deterministic rule application mechanism to transform texts in into texts in .
Each transformation rule is assigned a unique name (i.e., signified with a unique ). Since is a unique natural number,
so that each transformation rule is mapped to a unique natural number signifiable in on , which we abbreviate as
Associated with every tuple is a finite, non-empty set of error messages
that the transformation rules of can output to signal that specific transformations are impossible. E.g., if cannot verify the formation of by , then issues an error message.
Suppose that uses the rule sequence , , to transform to . By convention, the first argument of each subsequent rule takes the output of the previous rule and the first argument of is t, whence we have the following definition:
Definition 6 (Text Transformation).
A mechanical transformation, or simply transformation, of by into , , is a finite sequence of transformation rules , , , , where
An example of a transformation rule is substitution which can use to substitute for all occurrences of in so long as the texts satisfy a finite set of syntactic requirements (cf., e.g., Ch. 18, p. 558 in [1]; Ch. IX, § 44 in [8]; Ch. 14, pp. 402–403 in [9]); Ch. 4, p. 66 in [10], for various definitions of substitution in different formal systems).
Definition 7 (Transformation Signature).
Let , , , be a transformation of by , where
Then,
where , , is a transformation signature of the transformation of t into by , in which case
holds, and is a signed transformation, designated by s, of t into by .
Let , , . The predicate
holds if, and only if, there exists a signed transformation of t into by . The relation is clearly transitive, i.e., if
then
E.g., if is Unicode, is Lisp, and is the standard transformation rules of Common Lisp applied deterministically by the rule application mechanism known as the read-eval-print loop (cf., e.g., Ch. 20 in [9]), then
holds, because uses the Lisp progn construct that defines a sequence of Lisp operations to transform "(defun g (n) (+ n 1)) (g 2.14))" into a text of a procedure associated with the symbol named "g", substitutes "2.14" for the variable named "n" in "(+ n 1)" to obtain "(+ 2.14 1)", and then uses the transformation rules associated with the function named "+" to transform "(+ 2.14 1)" to "3.14". One can easily verify this transformation in any Lisp system that implements the Common Lisp formation and transformation rules in [9]. E.g., if is GNU CLISP 2.49.60+ on Linux 18.04 LTS, and is used to form
"(progn (defun g (n) (+ n 1)) (g 2.14))"
- on Unicode, then the following transformation is produced in the GNU CLISP 2.49.60+ Linux terminal, where ">" is the CLISP prompt.
- "> (progn (defun g (n) (+ n 1)) (g 2.14))
- 3.14"
Suppose generates and signs
"(loop while (= 3.14 3.14) do (+ 13.7 13.7))"
The next axiom states that spatiotemporally finite transformations are verifiable. If a transformation and its signature are available, another formal system can independently and deterministically verify the transformation from its signature and the set of transformation rules.
SCT Axiom 3.
If , where , , and , holds and s designates the transformation signature of the transformation of t into by , then, given t, , s, and , another formal system can deterministically verify the transformation of t into by within finite amounts of physical time and space.
SCT Axiom 3 extends the CCT axioms by introducing the concept of deterministic verifiability of transformation. We should note here that SCT Axioms 1, 2, and 3 take no position with respect to computing agents that use and or computing devices on which these systems are signified. Thus, neither nor are identical to the computing agent L in CCT Axioms A2, A4, A5, A9, and A10.
By interpretation of a program P in on , we will mean the application of a denotational or operational semantics of on to P with respect to the input text t and, when applicable, to the output text (cf., e.g., Chapters 17, 18 in [1]; Ch. 2 in [10])). We will use the term metacomputability to refer to a denotational and operational semantics of on and the interpretation of programs with respect to given input and output texts and assume that metacomputability is captured by neither the formation nor the transformation rules. We will not tackle the question of whether metacomputability is algorithmic in nature and leave it outside of the scope of this article. Hence,
SCT Axiom 4.
Metacomputability occurs outside of and .
4. Formation and Transformation of Instructions and Formation of Programs
Some texts formed by and transformed by designate instructions from a finite set of instruction types
The elements of denote operations of a specific type, e.g., addition or subtraction of finitely many discretely finite real numbers. E.g., is Lisp on Unicode, then
designate the same numerical operation type of addition applied to numerals designated by specific variable names. If we switch to Perl on Unicode, then we obtain
designating the same numerical operation type.
Definition 8 (Signifiable Instruction).
If and , then the predicate holds if, and only if, t signifies in on , in which case is a signifiable or, equivalently, designatable instruction in on . is symmetric.
E.g., let and L stand for Lisp, P for Perl, and U for Unicode. We have the following relations hold.
The elements of vary from alphabet to alphabet and from programming formalism to programming formalism due to the software-hardware duality principle of computer science: specific instructions are written to run on devices designed to perform those and only those instructions. E.g., while one formalism may restrict its set of instructions to addition and subtraction of natural numbers, another formalism may be designed for a device that adds, subtracts, multiplies, and divides discretely finite real numbers.
Definition 9 (Formable Instruction).
If , then
in which case is an instruction in on formable or, equivalently, generatable by . is symmetric.
Definition 10 (Transformable Instruction).
If , then
in which case, is an instruction in on transformable by .
The next axiom is rooted in the existence of general programming languages such as Lisp and Perl.
SCT Axiom 5.
There exists on in which the instruction types in Table A1 in the Appendix A are spatiotemporally finitely formable and transformable.
SCT Axiom 5 agrees with CCT Axiom A9 in that the computational capacity of the computing agent is always finite, i.e., any agent, physical or abstract, can execute only a finite number of instruction types. However, SCT Axiom 5 differs from CCT Axiom A9, because it makes it explicit that the computational capacity of a computing agent is a characteristic of not just the computing agent, but also of on . In this sense, SCT Axiom 5 offers yet another take on the software-hardware duality principle: programming formalisms are designed for computational devices and computational devices are constructed to perform computations prescribed by programs signified with specific formalisms. We will hereafter refer to a tuple-sufficient on that satisfies SCT Axiom 5 as minimally adequate. E.g., Lisp, Perl, and C/C++ Unicode are minimally adequate.
Definition 11 (Formable Program).
Let on be minimally adequate. Let , . If , …, and , then
where , is a program formable by . The function denotes the number of the instructions in . The predicate
holds if, and only if, is formable by . The set
is the enumerably infinite set of programs in on formable by .
Thus, is formable by or, in symbols, if, and only if, it is a finite concatenation of the enumerated formable and transformable instruction texts in on . E.g., in Figure 1 is a Lisp program on Unicode formable by the GNU CLISP 2.49.60+ disassembler.
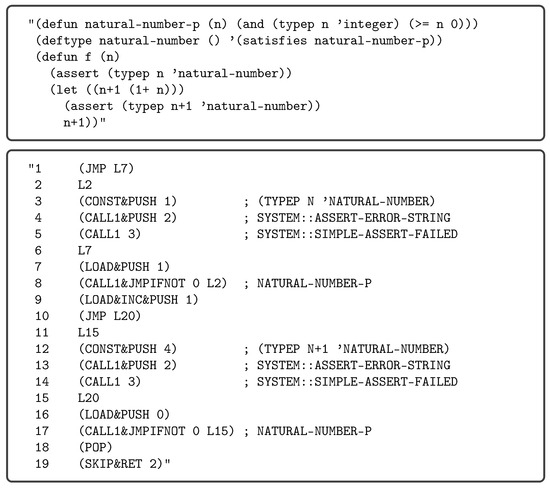
Figure 1.
(Top box) A definition in Lisp on Unicode of a strongly typed function on natural numbers, from which in the bottom box is automatically formed by the GNU CLISP 2.49.60+ disassembler. (Bottom box) The program in Lisp on Unicode is a concatenation of enumerated instruction texts generated from the definition of the function f in the top box by the GNU CLISP 2.49.60+ disassembler. The statements to the right of the semicolons, which are single line comment markers in Lisp, are comments automatically generated by the disassembler.
Definition 11 allows us to give a programmatic illustration of SCT Axiom 3 in Figure 2, where the bottom box contains a Lisp program on Unicode formed by the GNU CLISP 2.49.60+ disassembler that no Lisp transformer whose consists of the standard transformation rules of the Lisp read-eval-print loop can transform into a text on Unicode within a finite amount of physical time. However, each individual enumerated instruction text of in Figure 2, is transformable by within a finite amount of physical time.

Figure 2.
(Top box) A definition in Lisp on Unicode of an infinite loop, from which the Lisp program in the bottom box is automatically formed by the GNU CLISP 2.49.60+ disassembler. (Bottom box) The program in Lisp on Unicode is a concatenation of enumerated instruction texts formed from the definition of the loop in the top box by the GNU CLISP 2.49.60+ disassembler. The statements to the right of the semicolons, which are single line comment markers in Lisp, are comments automatically generated by the disassembler.
5. Program States and Computations
To transform deterministically into an output text designating the result of the computation formalized in on a singified input, goes through a sequence of states of . Hence,
Definition 12 (Program State).
Let . Then, is a valid state of if, and only if, can determine from σ: (a) the numeral designating the number of the instruction in to perform; (b) the numeral designating the total number of the instructions of already performed; (c) the texts designating the type and value of every variable name in , including the type and value of the unique output variable denoted by ; (d) the text ; and (e) for every variable name in σ, can assign exactly one type and exactly one value. If σ is a valid state, then contained in σ is referred to as of σ, while σ is referred to as σ of .
E.g., a valid state of in Figure 1, constructed according to the Common Lisp syntactic conventions, is given in (23), where the symbol "…" in the right-hand side of the equality designates the text of the lines 2–18 and , i.e., "2" is the numeral designating the number of the output register in this case.
mechanically obtains from in (23) the following elements:
- "1" — designates the instruction number to perform;
- "0" — designates the total number of instructions already performed;
- "(natural-number-p n)" — designates the type of the input variable "n";
- "(n 12)" — designates that the current value of "n" is "12" that, according to the standard decimal notation in Lisp on Unicode, designates the natural number 12;
- "(natural-number-p 2)"—designates the type specification of the output variable;
- "(2 0)" — designates that the current value of the output variable named "2" is "0";
- "(1 (JMP L7) ... 19 (SKIP&RET 2))"— designates that the nineteen instructions of are enumerated with "1", "2", …, "19" that designate the natural numbers 1, 2, …, 19 in Lisp on Unicode.
Definition 12 and valid program states like the state in (23) imply the existence of several predicates and functions that we now proceed to define to subsequently formalize the concept of transformation of programs in .
The function in (24) (VLDS abbreviates Valid State) returns "1", if is a valid program state, and "0" otherwise.
where "1" is arbitrarily interpreted as True and "0" as False. E.g., if is a valid program state and is not, then
which can be, respectively, abbreviated as
The function in (27) (PROG abbreviates Program) returns the text of the program of , if the latter is valid, and otherwise.
where t is the program of , . For example, if is given in (23) and is given in Figure 1, then = .
The function in (28) (NPIS abbreviates Number of Program Instructions) returns the numeral designating the number of the instructions in if is valid and otherwise.
The function in (29) (CINS abbreviates Current Instruction) returns the numeral designating the number of the instruction to execute in , if is valid, and otherwise.
E.g., for in (23), = or, more succinctly, .
The function in (31) (TOTI abbreviates Total Instructions) returns the numeral designating the total number of the transformed (or, equivalently, performed or executed) instruction texts in if is valid and otherwise.
E.g., for in (23), = . If, for some valid , and , we abbreviate to .
The next function in (32) (VVRS abbreviates Values of Variables) returns a marked concatenation designating a tuple of 2-tuples, each of which designates a variable and its numerical value. Toward that end, we let be valid and let contain variables, including the unique output variable designated by . We let , , designate the i-th variable and , , designate the variable’s numerical value, i.e., , . We let ⊴, ⊵, designate the beginning of a tuple, the end of a tuple, and the separator sign, respectively. With these conventions in place, the function in (32) returns the text designating the tuple of 2-tuples, each of which designates a variable and its numerical value in , when is valid, and otherwise.
E.g., if we recall that in Lisp , , and ∓ is any non-empty sequence of white space Unicode characters, then = .
The function in (33) (OUTV abbreviates Output Value) returns the numeral designating the value of the output variable of , if is valid, and otherwise.
E.g., = . If, for some valid , and , we abbreviate to . takes the output of (i.e., ) and returns the numeral designating the value of the output variable in the tuple so long as is valid.
The function in (34) (VV abbreviates Variable Value) returns the text designating the value of the i-th variable in and otherwise.
We now define a useful variant of to obtain the numerals designating the values of the input variables for any program that takes input texts. If contain variable-value tuples, of which the first tuples, by convention, designate the names and values of the input variables. The function in (35) (IVV abbreviates Input Variable Value) returns the numeral designating the value of the i-th input variable in , if is valid, and otherwise.
The function in (36) (NXTS abbreviates Next State) returns the next valid program state of if is valid and an error message otherwise.
This function looks at the current instruction and deterministically constructs the next valid state from the type of the instruction and the variables used in the instruction in the current program state so long as that latter is valid, or, equivalently, it transforms into . The choice of the transformation rule is determined by . Since the next valid state (the notation denotes the application of to to compute ) necessarily depends on the specifics of on , we offer an intuitive and abstract outline of how uses to transform to .
transforms the text of the instruction whose number is designated by according to its type (cf. Table A1) and then (1) updates, if necessary, the value numerals of the variable names involved in this instruction, i.e., updates the text returned by ; (2) updates the numeral designating the number of the instruction to execute in ; and (3) updates the numeral designating the total number of the instructions (or, to be more exact, instruction texts) of transformed thus far to the numeral designating the value of the total number incremented by 1. Per Definition 6, if is valid, then we define and, for , define
Thus, we have
Lemma 1.
Let on be minimally adequate and let contain the signs of the standard decimal notation. If , then n and , .
Let us assume that a minimally adequate on , like many modern programming languages, has at least four types of numerical instructions on the numerals in the standard decimal notation: addition, multiplication, subtraction, and division applicable to finitely many discretely finite real numbers. Then, if the current instruction is addition, the numerals designating the values of two or more variable names are added and the numeral of the sum is assigned to a variable name, the numeral value of which is accordingly updated in . The numerals designating the values of the variable names that are not affected by the instruction text, remain in exactly as they are in . The transformation of the multiplication and subtraction instruction types is performed analogously. The transformation of the division instructions is performed with the convention that the division by zero (or, to be more exact, by the numeral designating 0 in on ) results in an error message.
If on has the assignment instruction type whereby the value of a variable is set to a value, then the numeral value of that variable’s name is accordingly updated in . If has a GOTO/JUMP instruction type and the current instruction prescribes a jump to a label (e.g., "(JMP L7)" in in Figure 1 prescribes a jump to the label "L7"), then no updates of the variable numeral values are performed, and the numeral of the next instruction to execute in is set to the numeral of the program line with that label. If multiple instruction texts of have the same label, the numeral of the instruction to execute in is set to the numeral designating the smallest such number. If the current instruction calls for a jump to a label that does not exist in , then the numeral designating the number of the instruction to execute in is set to the numeral designating . The transformation of a dispatch to a numeral designating an instruction number is performed analogously to the transformation of a dispatch to a label. Thus,
Lemma 2.
If = , then .
Associated with the execution of are two states: a program start state and a program end state. The predicate in (38) (STARTS abbreviates Start State) returns "1" if is a valid program start state and "0" otherwise.
The predicate in (39) (ENDS abbreviates End State) returns "1" if is a valid end state and "0" otherwise.
Suppose that starts in a valid start state such that , and then uses a sequence of its transformation rules through (cf. Equation (37)) to transform into , and so on, thus generating a finite sequence of states , , where and are valid start and end states of , respectively, then . Hence,
Definition 13 (Signifiable Computation).
A signifiable computation of is a finite sequence of valid program states , , , , such that
The predicate
holds if, and only if, is a signifiable computation of in on .
Hence,
Lemma 3.
Let . Then, , and .
6. Transformation of Programs
Definition 14 (Transformation of Programs).
Let , , , , and . Then, is transformable by from , which is denoted as , if, and only if, .
The next lemma follows from Definition 14 and Lemmas 2 and 3.
Lemma 4.
and , . Then, the following statements are equivalent, for :
- ;
- ;
- ;
- .
A question naturally arises whether it is possible for to transform, in finitely many steps, a valid start state of a program into another valid state of when is not formed by . In other words, can hold if but ? Definition 11 implies a negative answer, because for the program to be transformable by from a valid start state , every enumerated instruction text in must be transformable. and are co-dependent in that cannot place in a program an instruction text that cannot transform.
E.g., consider a Lisp program by Steele in Figure 3. This text is formally impeccable insomuch as it is formed according to the Lisp syntactic conventions. However, the program is not transformable unless one supplies the definitions of the functions stroke, stuck, make-oar, winded, and dream, all of which, in turn, can be converted by the Lisp disassembler into finite sequences of instruction texts that can transform with the rules of the read-eval-print loop from a valid start state for this program. For example, if is GNU CLISP 2.49.60+, then the attempted transformation of "(life)" results in
whence

Figure 3.
(Top box) A Lisp program by Guy Steele on p. 191 in [9] to illustrate the operational semantics of catch and throw with unwind-protect. (Bottom box) The program generated from the definition of the Lisp function in the top box by the GNU CLISP 2.49.60+ disassembler. The statements to the right of the semicolons, which are single line comment markers in Lisp, are comments automatically generated by the disassembler.
The above observations lead to the next axiom.
SCT Axiom 6.
There exists a minimally adequate on , where any is reducible to an enumerated sequence of instruction texts from a finite set of transformable instruction types that are irreducible to any other instruction types.
SCT Axiom 6 does not appear to have a direct equivalent among the CCT axioms. It is related to CCT Axiom A9 insomuch as it reflects the fact that the computational capacity of any computing agent is finite. This axiom reflects a common fact of modern compiler theory: all higher level constructs (e.g., function definitions and macros) of programming languages are reduced to a finite set of irreducible (also known as primitive) instructions (cf., e.g., Ch. 3 in [1]). Therefore, for any on compliant with SCT Axiom 6, we can assume that a is a concatenation of enumerated instruction texts, each of which designates an irreducible instruction type. We will hereafter assume that on is minimally adequate and satisfies SCT Axiom 6.
7. Signifiable Computability of Functions
To characterize functions that are signifiably computable in principle, we remove memory limitations imposed on computation by an FMD , which is formalized in our next definition.
Definition 15 (Signifiably Computable Function).
A total function is signifiably computable in on if, and only if, there exists and, for , , ,
if, and only if,
The predicate holds if, and only if, f is signifiably computable in on and is a program that signifies f in on .
We proceed to characterize functions that are signifiably partially computable in principle.
Definition 16 (Signifiably Partially Computable Function).
A partial function is signifiably partially computable in on if, and only if, there exists and, for , , ,
if, and only if,
The predicate holds if, and only if, f is signifiably partially computable in on and is a program that signifies f in on .
Definitions 15 and 16 imply
Lemma 5.
If , then .
Definitions 15 and 16 and Lemma 5 broaden the scope of CCT Axiom A0 by making the properties computable and partially computable apply to functions on discretely finite real numbers. The next definition states that signifiable functions are those functions that can be signified with texts in on .
Definition 17 (Signifiable Function).
A function f is signifiable in on , which is denoted as , if, and only if, there exists such that
If , for some FMD , then f is signifiable in on on , which is denoted as .
E.g., , , then
where that signifies f is given in Figure 1.
Lemma 6.
There exist on and a function f such that
Proof.
where "(halts-p p x)" returns the text in designating the Boolean value True if a Lisp funcallable object designated by halts on the real number designated by . Since , we have
Let such that . Let such that . Let
where and , . Take , , and consider the following
"(defun f (x p) (if (halts-p p x) 1 0))",
However, since the predicate halts-p is not signifiably computable in Lisp on Unicode,
□
8. Signifiable Computability of Functions on Finite Memory Devices
We now proceed to modify some of the definitions in Section 5 for situations when functions signifiable by programs in on are computed on an FMD . We associate with every triplet a non-empty set of error messages
where , , , is a unique error message whose size does not exceed the memory capacity of . An important difference between the functions and predicates in Section 5 and the functions and predicates in this section is that the latter return when the memory capacity of is exceeded.
The function in (42) returns if the size of does not exceed the memory capacity of . Otherwise, the function returns .
The function in (43) returns , if is a valid program state and the size of does not exceed the memory capacity of . Otherwise, or are returned.
The function in (44) returns , if is valid and the size of does not exceed the memory capacity of . Otherwise, or are returned.
The function in (45) returns , if is valid and the size of does not exceed the memory capacity of . Otherwise, or are returned.
The function in (46) , if is valid and the size of does not exceed the memory capacity of . Otherwise, the function returns or .
The function in (47) returns , if is valid and the size of does not exceed . Otherwise, or is returned.
The function in (48) returns , if is a valid program state and the size of does not exceed the memory capacity of . Otherwise, it returns or .
The function in (49) returns , if is valid and the size of does not exceed the memory capacity of . Otherwise, or are returned.
We now define memory-dependent signifiable computation on discretely finte real numbers in (18). This definition is similar to its memory-independent counterpart in (13), but is defined in terms of memory-dependent functions and predicates defined above in this section.
Definition 18 (Signifiable Computation on Finite Memory).
A signifiable computation of on an FMD is a finite sequence of valid program states , , , such that
The predicate
holds if, and only if, is a signifiable computation of in on on .
Definition 19 (Signifiably Computable Function on Finite Memory).
A total function is signifiably computable in on on if, and only if, there exists and, for , , ,
if, and only if,
The predicate
holds if, and only if, f is signifiably computable in on on and is a program that signifies f in on on .
The next definition formalizes signifiably computable partial functions when the memory available for computation is confined to the memory capacity of on which the signifiable computation is performed.
Definition 20 (Signifiably Partially Computable Function on Finite Memory).
A partial function is signifiably partially computable in on on if, and only if, there exists and, for , , , ,
if, and only if,
The predicate
holds if, and only if, f is signifiably partially computable in on on and is a program that signifies f in on on .
The above definitions imply that can hold in its memory. In other words, the text that signifies two consecutive valid program states in a signifiable computation does not exceed the memory capacity of . We will hereafter state that such an FMD has a sufficiently large memory capacity, whence the next definition.
Definition 21 (Sufficient Memory Capacity).
Let be an FMD and . Then, has a sufficient memory capacity relative to if, for any sequence of states such that
The predicate
holds if, and only if, has a sufficient memory capacity relative to .
We now axiomatize the signifiable computability of .
SCT Axiom 7.
SCT Axiom 7 concretizes CCT Axiom A3 by formalizing a facility (i.e., ) to move a computation forward step-by-step when a step is identical to a valid program state. SCT Axiom 7 also broadens CCT Axiom A8 by stating that there is an explicit finite bound (i.e., ) on the amount of memory available for signifiable computation whenever signifiable computation is carried out by a computing agent (e.g., an operating system or a virtual machine) on .
Since the functions (43), (44), (45), (46), (47), (48), (49), and (18) are defined in terms of , we have
Definition 22 (Sufficiently Powerful Finite Memory Device).
An FMD is sufficiently powerful relative to on if, for any f, such that
9. Main Results
We now present the two theorems, which we refer to as the Debugger Theorems, that constitute the main results of this investigation. The theorems are so called, because they characterize some properties of the debugger (DBGR) function defined as
We define a debuggable FMD relative to on as
Definition 23 (Debuggable Finite Memory Device).
An FMD is debuggable relative to on if
We now prove
Lemma 7.
Let be an FMD debuggable relative to on . Let such that, for ,
Then,
if, and only if, for ,
Proof.
We omit the subscripts for brevity and let . If and, for , and , then , for . Conversely, assume that . Since = ,
If , then and . Otherwise, we proceed from and examine each consecutive pair , in the same fashion as the pair , to find and such that = and = . □
Corollary 7.1.
Let be an FMD debuggable relative to on . Let such that, for ,
Then,
if, and only if, for ,
We now prove
Theorem 1.
Let be an FMD debuggable relative to and . Let such that
Then, if
then
Proof.
We omit the subscripts for brevity. Let be such that , , and , , . Let be such that .
Since , we have
whence
We observe that if, for some , , , , , and , then, by Lemma 1,
Let . If , then . Otherwise, we run to compute , , whereby computes
If , then . Otherwise, we continue incrementing the natural number corresponding to the previous state counter numeral by 1 and running on and
(i.e., the numerals corresponding to the natural numbers ). After a finite number of such iterations, we necessarily reach and such that
because in the standard decimal notation the numeral encoding contains more digit signs than the numeral encoding , whence
□
We now prove
Theorem 2.
Let be an FMD debuggable relative to and . Then, there exists such that , , and, for some , if
Then,
Proof.
We omit the subscripts , , for brevity. Let such that . Then, , (cf., e.g., in Figure 1). Let be the smallest positive integer such that and . Let
Since , then, by (50),
□
Corollary 2.1.
Let be an FMD debuggable relative to and . Let f in Theorem (2) be such that if and , then . Then, for some , if
then
10. Discussion
The proposed axiomatization broadens the scope of CCT Axiom A0 in that it makes the properties computable and partially computable apply to functions on discretely finite real numbers (cf. Definitions 15 and 16 and Lemma 5). The ontology of functions on discretely finite real numbers implied by the proposed axiomatization distinguishes three classes of functions: signifiable, signifiably computable, and signifiably partially computable. Per Lemma 5, signifiably computable functions are signifiably partially computable, but not vice versa. Per Lemma 6, there are signifiable functions that are not signifiably partially computable.
The proposed axiomatization characterizes signifiable computation on discretely finite real numbers in terms of two formal systems: the Former that generates texts in in and the Transformer that transforms texts formed by into other texts in on . These systems are co-dependent on each other and cannot exist in isolation. Neither system is involved in the interpretation of the results insomuch as such interpretation is outside of their scope. Both systems can be signified as programs in minimally adequate formalisms and those programs can be executed by different computing agents, such as human programmers or automated program synthesizers and debuggers. Consequently, and are not identical to the computing agent L of CCT Axioms A4, A5, A9 and A10. All texts produced by these two formal systems are spatiotemporally finite. While always takes a finite amount of physical time, regardless of how time is measured, to form a text, is not guaranteed to take a finite amount of physical time to transform a text into another text. The formation and transformation of texts can be signed by both systems and verified by third parties.
Programs that use continuous, random or analogue methods are evidently inconsistent with CCT Axioms A4 and A5. However, they are consistent with the proposed axiomatization in the following sense. If such programs are signified in a minimally adequate formalism, then their formation and transformation can be deterministically verified at least on some inputs in the domains of functions that those programs designate. Furthermore, if those programs are executed on an FMD debuggable relative to the said formalism, then, per the two Debugger Theorems, the programs can be effectively debugged on all signifiable inputs. It should be noted that this debugging is effective, because on any signifiable input, the program that signifies the debugger function in (50) on the said FMD returns either the output signifying a discretely finite real number, an error message, or a message that the computation cannot be carried forward, because the FMD’s memory capacity is exceeded. This integration of error into computation makes the proposed axiomatization different from the CCT axiomatization.
SCT Axiom 5 of the proposed axiomatization concretizes CCT Axiom A9, because it states that the computational capacity of a computing agent is a characteristic of not just the computing agent but also of the programming formalism. SCT Axiom 7 of the proposed axiomatization also concretizes CCT Axiom A8 by stating that there is an explicit finite bound on the memory available for signifiable computation whenever the computation is carried out by a computing agent on an FMD. Furthermore, the Debugger Theorems (cf. Section 9) indicate that CCT Axioms A6, A7, A8, and A10 do not apply to actual computability, i.e., situations when the signification of computation is performed on FMDs.
The concept of Debuggable FMD (cf. Definition 23) also bears on CCT Axiom A9 and distinguishes the proposed axiomatization from the CCT axiomatization. Debuggable FMDs are FMDs on which the debugger function (cf. Equation (50)) can be signified by a program in a minimally adequate on . Intuitively, debuggable FMDs are computational devices with finite amounts of memory available for computation that can be effectively debugged. Thus, the computational capacity of a computing agent is limited not only by a finite number of instruction types the agent can perform but also by a concrete finite amount of memory available for signifiable computation.
A fundamental difference between the proposed axiomatization and the CCT axiomatization is the explicit integration of cost into computation through the function TOTI (cf. Equations (31) and (45)). Cost is different from the standard Big-O analysis of computer science (cf., e.g., Ch. 2 in [11]). The Big-O analysis is based on two assumptions: (1) the number of steps can be known ahead of computation as a function of the size of the input, and (2) constant factors do not matter (e.g., , for , even when , i.e., the estimated number of photons in the observable universe). A consequence of the second assumption, almost never explicitly stated, is that the energy is available on demand to carry forward the prescribed computation. The function TOTI is not based on either assumption. It simply states that the cost of computation increases by one abstract unit (e.g., one unit of energy required to obtain a result, one unit of hardware maintenance cost, one unit of economic unavailability of computed results for decision making, etc.) with every signified instruction performed by a computing agent. To put it differently, per Lemma 1, the cost of signifiable computation monotonically increases by one abstract unit with every new signifiable program state.
Our approach to typed instructions (cf., e.g., Equation (22) and Definition 8) is inspired by the approach originally proposed by Church in [12]. However, our end objective is different. We do not aim to integrate -calculus (or any other formalism) into Russell’s hierarchical theory of logical types (cf., e.g., [13,14]). Rather, we aim to formally characterize what is computable in principle and what is computable with performable processes on computational devices with finite amounts of memory.
The usage of logically quantified variables in our formalism makes no ontological commitment that assertions containing the said variables imply that the ranges of the variables actually exist [15] or that designating texts serve as senses of names [16]. While our formal apparatus (cf. Section 2) relies on the axiom of choice of the Zermelo–Fraenkel set theory, the proposed axioms, definitions, lemmas, theorems, and implications thereof should not be viewed as arguments for or against replacing the Zermelo–Fraenkel set theory with the axiom of choice with the modern type theory as the foundation of mathematics (cf., e.g., [17]). The alternative foundations of mathematics are beyond the scope of our article.
Finally, we make no claim that the proposed axiomatization has no alternatives. Rather, it is our hope that this investigation will motivate other computability theory and recursion theory researchers to take a closer look at the differences between general and actual computabilities and to seek alternative axiomatizations of computability to gain deeper insights into the theory and practice of computer science.
11. Conclusions
In our previous investigation [4], we formalized the signification and reference of real numbers and showed that discretely finite structures representable as tuples of discretely finite numbers are signifiable on finite memory devices. In this investigation, we offered an axiomatization of signifiable computation on discretely finite real numbers and proved two theorems to investigate the computability properties of signifiably and partially signifiably computable functions on finite memory devices. For the next part of our investigation of significable computability, which we intend to cover in our next article, we plan to further investigate connections between signifiable computability and the theory of primitive recursive functions (cf., e.g., [18,19]) and, if and when possible, to connect signifiable computability to formal approaches to symbolic AI [10].
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Below are the 11 axioms of the classical computability theory (CCT) based on Chapters 1–3 in [2]. CCT Axiom A0 is based on footnote 2 on p. 2 in [2] that states that the concepts function and partial function are restricted to mappings on non-negative integers. The ordinal numbers in the CCT Axioms A1–A10 correspond to the ordinals in the 10-item list of statements or questions to which affirmative or negative answers are given in Section 1.1 in [2], pp. 2–5. The assumptions reflected in the CCT axioms below are apparent in Chapters 2–8 in [1], another classical text on computability and recursion theory.
CCT Axiom A0.
Functions map natural numbers to natural numbers.
CCT Axiom A1.
An algorithm is given as a set of instructions of finite size.
CCT Axiom A2.
There exists a computing agent that can react to the instructions and carry out the computations.
CCT Axiom A3.
There are facilities for making, storing, and retrieving steps in a computation.
CCT Axiom A4.
If P is the set of instructions in an algorithm and L is a computing agent, then, given an input to P, L reacts to P by performing the computation in a discrete, stepwise fashion without using continuous methods or analogue devices.
CCT Axiom A5.
L reacts to P by performing a computation deterministically, without random methods or devices.
CCT Axiom A6.
There is no fixed finite bound on the size of inputs.
CCT Axiom A7.
There is no fixed finite bound on the size of a set of instructions P.
CCT Axiom A8.
There is no fixed finite bound on the amount of memory storage available to L to carry out a computation in P.
CCT Axiom A9.
There is a fixed finite bound on the capacity of the computing agent L.
CCT Axiom A10.
There is no fixed finite bound on the length of the computation performed by L on P; it is only required that the computation terminate after some finite number of steps.

Table A1.
Instruction types in spatiotemporally finitely formable and transformable in programming formalisms that satisfy SCT Axiom 5. The subscripts and in the right column are omitted for brevity.
Table A1.
Instruction types in spatiotemporally finitely formable and transformable in programming formalisms that satisfy SCT Axiom 5. The subscripts and in the right column are omitted for brevity.
| Instruction Type | Semantics |
|---|---|
| , , | set the value of the variable named v to t |
| , , , | ∧ , t) ∧∧ |
| , ,, | ∧ ∧ ∧ |
| , , , | ∧ ∧ ∧ |
| , , | ∧ ∧∧ ∧∧ |
| , ,, | ∧ ∧ |
| , , , | return the text obtained by substituting in t for , …, for . |
References
- Davis, M.; Sigal, R.; Weyuker, E. Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science, 2nd ed.; Harcourt, Brace & Company: Boston, MA, USA, 1994. [Google Scholar]
- Rogers, H., Jr. Theory of Recursive Functions and Effective Computability; The MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Kulyukin, V. On Correspondences between feedforward artificial neural networks on finite memory automata and classes of primitive recursive functions. Mathematics 2023, 11, 2620. [Google Scholar] [CrossRef]
- Kulyukin, V.A. On Signifiable Computability: Part I: Signification of Real Numbers, Sequences, and Types. Mathematics 2024, 12, 2881. [Google Scholar] [CrossRef]
- Hopcroft, J.E.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation; Narosa Publishing Hourse: New Delhi, India, 2002. [Google Scholar]
- Kuroda, S.Y. Classes of languages and linear-bounded automata. Inf. Control 1964, 7, 207–223. [Google Scholar] [CrossRef]
- Quine, W.V. Methods of Logic; Harvard University Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Kleene, S.C. Introduction to Metamathematics; D. Van Nostrand: New York, NY, USA, 1952. [Google Scholar]
- Steele, G.L. Common Lisp: The Language, 2nd ed.; Digital Press: Bedform, MA, USA, 1990. [Google Scholar]
- Genesereth, M.R.; Nilsson, N.J. Logical Foundations of Artificial Intelligence; Morgan Kaufmann: Los Altos, CA, USA, 1987. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Church, A. A formulation of the simple theory of types. J. Symb. Log. 1940, 5, 56–68. [Google Scholar] [CrossRef]
- Russell, B. Mathematical logic as based on the theory of types. Am. J. Math. 1908, 30, 222–262. [Google Scholar] [CrossRef]
- Kamareddine, F.; Laan, T.; Nederpelt, R. Types in logic and mathematics before 1940. Bull. Symb. Log. 2002, 8, 185–245. [Google Scholar] [CrossRef]
- Church, A. Ontological commitment. J. Philos. 1958, 55, 1008–1014. [Google Scholar] [CrossRef]
- Church, A. A revised formulation of the logic of sense and denotation. Alternative (1). Nous 1993, 27, 141–157. [Google Scholar]
- Altenkirch, T. Should type theory replace set theory as the foundation of mathematics? Glob. Philos. 2023, 33, 21. [Google Scholar] [CrossRef]
- Petersen, U. Induction and primitive recursion in a resource conscious logic—With a new suggestion of how to assign a measure of complexity to primitive recursive functions. Dilemmata Jahrb. Asfpg 2008, 3, 49–106. [Google Scholar]
- Paolini, L.; Piccolo, M.; Roversi, L. A class of recursive permutations which is primitive recursive complete. Theor. Comput. Sci. 2020, 813, 218–233. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).