Abstract
Autonomous vehicles (AVs) are increasingly operating in complex traffic environments where safe and efficient decision-making is crucial. Merging into roundabouts is a key interaction scenario. This paper introduces a decision-making approach for roundabout merging that combines human driving behavior with advanced reinforcement learning (RL) techniques to enhance both safety and efficiency. The proposed framework models the decision-making process of AVs at roundabouts as a Markov decision process (MDP), optimizing the state, action, and reward spaces to more accurately reflect real-world driving behaviors. It simplifies the state space using relative distance and speed and defines three action profiles based on real traffic data to replicate human-like driving behavior. A force-based reward function, derived from constitutive relations, simulates vehicle-roundabout interactions, offering detailed, physically consistent feedback that enhances learning results. The results showed that this method effectively replicates human-like driving decisions, supporting the integration of AVs into dynamic traffic environments. Future research should address the challenges related to partial observability and further refine the state, action, and reward spaces. This research lays the groundwork for adaptive and interpretable decision-making frameworks for AVs, contributing to safer and more efficient traffic dynamics at roundabouts.
MSC:
68T40; 93E24
1. Introduction
Decision-making for autonomous vehicles (AVs) presents significant challenges in environments with complex traffic participants, dynamic flow conditions, and high interaction levels, as observed in scenarios such as unprotected left turns and uncontrolled intersections. Roundabouts are distinctive intersections with a central island that directs traffic in one direction. This design improves traffic flow and safety by reducing conflict points and controlling vehicle speeds [1,2]. Compared with traditional intersections, roundabouts are preferred because of their greater traffic management efficiency and enhanced safety outcomes [3].
However, navigating roundabouts presents significant challenges for both AVs and human drivers [4]. A key challenge is predicting and understanding the behaviors and intentions of other drivers, which complicates decision-making [5]. Another challenge is ensuring safe and efficient merging into and out of the roundabout, requiring precise judgments of the right moments for entry and exit [6]. These challenges have increased the need for robust decision-making frameworks for AVs.
Scholarly studies on decision-making in roundabouts have explored various methodologies, including rule-based strategies, game theory, and reinforcement learning (RL) paradigms.
Finite state machines (FSM) have been used for defining decision-making rules based on contextual variables [7,8]. While effective in simpler scenarios [9], FSMs struggle with the complexities and uncertainties in dynamic environments like roundabouts [10].
Game theory has been applied to model interactions between vehicles in roundabouts [11]. Tian et al. [12] and Chandra et al. [13] combined different driving styles with game-theoretical models to improve decision-making accuracy. Decentralized game-theoretic planning reduces the computational complexity by limiting interactions with the local area within the agents’ observational range [14]. While game-theoretic analysis of AVs and human-driven vehicles can enhance decision-making in complex settings, it faces limitations in handling multi-agent dynamics and the uncertainty of real-time decision-making in complex environments [15].
Reinforcement learning (RL) offers distinct advantages over traditional methods such as finite state machines (FSM) and game theory by providing enhanced robustness to dynamic environments. Unlike FSM and game theory, which often struggle to handle uncertainties and complex, real-time, multi-objective trade-offs, RL can dynamically adapt to changing conditions, making it more robust in uncertain environments [16]. The Markov decision process (MDP), a key framework in RL, enables the modeling of these challenges, allowing for more flexible and robust decision-making.
This is particularly evident in roundabout merging scenarios where the Markov decision process (MDP) framework enables the following: (1) real-time policy optimization under partial observability, (2) graceful degradation when confronted with unmodeled disturbances (e.g., aggressive driver behaviors), and (3) automatic compensation for measurement errors through reward-shaping techniques. Such characteristics allow RL-based agents to maintain stable performance where traditional model-based approaches would require explicit uncertainty quantification [17].
Table 1 presents the decision content of roundabout autonomous driving based on MDP, focusing on the key components such as state space, action space, and reward function. In general, the traditional MDP modeling method has obvious shortcomings in roundabout merging speed planning. First, the traditional state space usually contains a large number of redundant parameters, such as position, velocity, acceleration, etc., which are often not necessary in traffic circle merging scenarios. Vehicle merging behavior depends more on the relative position and speed of the vehicle and the geometry of the traffic circle, and the redundant state parameters increase the computational complexity and affect the decision-making efficiency and real-time performance. Secondly, the traditional discrete action space cannot accurately simulate the continuous and dynamic change behavior of vehicles in the merging process. The decision-making behavior of human drivers is usually flexible, adjusting speed and acceleration according to the geometric characteristics of the traffic circle, and the discretized, fixed-value action space has difficulty reflecting this process. Finally, traditional reward functions with discrete values, such as collision penalties or target speed rewards, are unable to accurately represent the complexity and continuity of driving behavior and lack a unified evaluation framework for different decision dimensions.

Table 1.
The key design elements of MDP for autonomous driving at roundabouts.
Next, we will further analyze these papers from three aspects: state space, action space, and reward function.
Defining the state space is crucial for representing environmental contexts, as it directly influences the effectiveness of algorithmic learning and the quality of decision-making outcomes. Gritschneder et al. [10] defined the state space using the relative data between vehicles, including their positions, velocities, and heading orientations. This approach highlights the dynamic interaction between the ego vehicle and other traffic entities, thereby enabling a more adaptive strategy that can respond to varying traffic conditions. In contrast, most existing studies focus primarily on the ego vehicle’s state attributes in the state space, such as position, velocity, acceleration, and heading angle [18,19,20]. However, these studies do not address the specific formulation of the state space for roundabout scenarios, particularly the relationship between vehicle states and roundabout geometry. A simplified state space can improve the computational efficiency of the algorithm.
In the action space, speed planning is typically modeled using discrete constant acceleration and deceleration parameters. Trajectory planning also incorporates discrete steering angle data [18,19,20]. Although action space designs based on fixed velocities and steering angles work well for simple driving tasks, they lack flexibility in complex, dynamic driving environments, limiting the agent’s adaptability and control precision. Moreover, this approach overlooks the continuous control aspects inherent in human driving behavior. Notably, Gritschneder et al. [10] recognized the variability in the speed of human drivers as they approached roundabouts. Their action space design replicates human-like behaviors such as “Go”, “Stop”, and “Approach” by clustering speed trajectories from real-world driving data.
The design of reward functions has been one of the most important aspects of reinforcement learning [21], and the reward functions reviewed in these studies exhibit significant variability. Gritschneder et al. [10] and Chandiramani et al. [18] used fixed rewards and penalties linked to specific task objectives. Although this approach is simple and easy to implement, using fixed rewards in complex tasks, such as autonomous driving, often fails to capture the dynamic effects of the agent’s actions on the environment. In addition, it lacks adaptability to multiple objectives, long-term goals, and changing environmental conditions. These limitations can lead to suboptimal learning, impractical strategies, and inconsistent performances.
To address these issues, Bey et al. [19] and Li et al. [20] developed dynamic reward functions that adjust the rewards and penalties, emphasizing safety, efficiency, and comfort in autonomous driving. These functions penalize sudden braking and collisions while rewarding smooth driving and adhering to the target speeds. However, using weighted summation to standardize the evaluation metrics across different dimensions fails to accurately reflect the physical interactions between vehicles and between vehicles and the environment. This framework lacks dynamic adaptability, struggles to resolve conflicts between multiple objectives, and overlooks dynamic constraints, all of which can lead to poor performance in complex environments.
Among them, by combining the reward function with other theories in an interdisciplinary way, it not only helps to better understand the nature of the reward mechanism and increase the interpretability of the reward function. It can also provide a richer explanatory framework from different perspectives, making the decision-making process of the system more transparent and predictable [22]. In addition, by combining multiple theories, the reward function can show higher flexibility and adaptability in more complex situations, thereby optimizing decision-making performance and ensuring the robustness and effectiveness of the system in practical applications. Further, this continuous reward space can effectively alleviate problems similar to sparse rewards [23], and in environments where frequent strategy adjustments are required, it can provide smooth and frequent feedback and promote stable learning of intelligent agents. Among them, the mechanics-based method can intuitively simulate the physical and mechanical interactions of the real world, enabling it to more accurately characterize and handle dynamic and complex environments [24].
The social force model is a widely used mechanics-based framework for simulating interactions and negotiation behaviors between individuals. Helbing et al. [25] first introduced the concept of “social force” to quantify the intrinsic motivation that drives individuals to take specific actions. They showed that the social force model can effectively explain various collective phenomena in pedestrian behavior, showing self-organizing characteristics. Over time, the social force model has been increasingly applied to simulate interactions between pedestrians and non-motorized vehicles [24], pedestrians and motorized vehicles [26], and between motorized vehicles [27]. Delpiano et al. [27] introduced a simple two-dimensional microscopic car-following model based on a social force framework to address traffic flow challenges. This model incorporates continuous lateral distance, offering a more intuitive and natural mathematical representation than traditional car-following models.
Further, inspired by the social force model, Li et al. [28] and Li et al. [29] proposed a car-following model and a lane-changing model to describe the microscopic traffic system based on the physical model in the constitutive relationship. Li et al. [28] proposed a new microscopic traffic model based on a mass-spring-damper clutch system to describe the interaction of vehicles in undisturbed traffic flow. The model can naturally reflect the response of the ego vehicle to the relative speed and expected distance of the preceding vehicle, as well as take into account the influence of the ego vehicle on the preceding vehicle, which is ignored by the existing car-following model. Compared with the existing car-following model, the model provides a physical explanation of the car-following dynamics, and through the nonlinear wave propagation analysis technology, the model has good scalability and can chain multiple systems to study macroscopic traffic flow. Li et al. [29] compared acceleration dynamics to material behavior principles. They combined viscous and elastic components into various models to represent the three types of forces acting on a vehicle and developed a force-based two-dimensional lane-changing dynamics model. The comparison results show that the lane-changing dynamics model can effectively capture the complex lane-changing behavior and its interaction with surrounding vehicles in a simple and unified way.
Therefore, in this paper, we introduce an MDP-based decision-making method for automated driving at ring intersections, focusing on safe merging scenarios. First, we optimize the state space for merging at a roundabout intersection and simplify the design of the state space to improve efficiency and real-time decision-making by considering the relative positional relationship between vehicles and the geometric structure of the roundabout intersection. Then, based on previous studies on typical merging driving behaviors of human drivers, as well as natural driving datasets, we design an action space with humanoid merging characteristics, which in turn can mimic human driving behaviors when merging at a roundabout intersection. Finally, in terms of the reward function, we use viscous and elastic models based on mechanical principles to represent the relative motion relationships between vehicles and traffic circle structures, as well as between vehicles and vehicles, so as to simulate the effects of other factors, such as vehicles, roundabout intersections, and traffic rules, on vehicle merging behaviors positively or negatively.
Last but not least, in order to enhance the interpretability of the reward function while providing more adaptive and physically consistent feedback, this paper introduces a constitutive relationship model based on mechanics, specifically a combination of elastic and viscous components (i.e., a force-based reward function). This model can more accurately simulate vehicle interactions, rather than relying solely on discrete reward values and simple distance or speed parameters. Unlike traditional reward mechanisms that rely on static feedback such as collisions, this method can dynamically adapt to real-time driving interactions based on vehicle behavior and surrounding traffic conditions, achieving more human-like decision-making, thereby more adaptively and accurately reflecting real-world driving behavior and improving learning efficiency in dynamic environments.
The main contributions of this paper are as follows:
- The state space focuses on the distance between the ego vehicle and the yield line, along with the vehicle’s speed, to streamline the policy training for greater efficiency.
- The factors affecting vehicle merging were represented using viscoelastic constitutive relations. A new reward model was introduced within the MDP framework to balance safety, efficiency, and comfort, providing a more adaptive and comprehensive approach to autonomous decision-making at roundabouts.
The remainder of this paper is structured as follows: Section 2 introduces the MDP model, defines the state space applicable to the actual roundabout scenario, the action space with human-like driving characteristics, and the reward space for modeling interactive behaviors using constitutive relations. Section 3 evaluates the rationality and effectiveness of the state, action, and reward mechanism designs through a case study. Section 4 summarizes the study and proposes prospects.
2. Algorithm Construction
2.1. Markov Decision Processes Theory
The decision-making problem in AVs can be viewed as a sequential decision problem that is typically solved using an MDP framework. Formally, an MDP is described by a 5-tuple ⟨S, A, P, R, ⟩ along with the policy . In this context, S represents a finite set of possible environmental states s of the environment. A denotes the action space, which is a finite set of actions a that the agent can perform. P is the state transition probability matrix:
R represents the reward function, which specifies the reward gained in a specific state for taking a certain action :
is the discount factor, which is restricted to to ensure convergence. is the rule or function for how the agent chooses actions in each state, which is usually considered the action distribution in a given state :
In an MDP, the system state transitions based on the current action, and the agent learns the optimal strategy by taking action to maximize the cumulative rewards :
The two relevant quantities that describe the performance of the agent are the state-value function :
and the state–action value function :
Therefore, an agent can choose to find the optimal policy by maximizing the optimal state–action value function :
When the policy reaches the optimal state, the value of the state is equal to the maximum action value in the current state: . The relationship between them can be described using the Bellman optimal equation, as shown in Equation (8).
Within the agent, the policy is implemented using a linear or nonlinear function approximator with adjustable parameters and a specific model. This study employed the Q-learning algorithm, which is a widely used method for solving MDPs. Q-learning is a model-free, online, off-policy, value-based algorithm that estimates cumulative long-term rewards using a critique. If the optimal policy is followed, the action with the highest expected cumulative value is selected.
2.2. State Space
Different from the traditional way of defining vehicle state space, the research scenario of this paper is not just a low-level speed planning model, but a more advanced confluence behavior decision model. Therefore, high-level behavior decisions often do not require the same sophisticated state-space design as low-level decision behaviors. This paper uses the distance of the vehicle relative to the yield line and the speed of the vehicle as state-space parameters, and defines the yield line position as the reference point (zero distance). The specific reasons include the following:
First, from the perspective of humanoid driving decisions, whether a vehicle is located on the left or right side of the merging lane, the driver evaluates his/her entry into the roundabout based on the relative distance to the yielding lane and the position relative to the other vehicles, which is consistent with the way human drivers make merging decisions. Thus, relative distance becomes a central factor influencing merging behavior and is sufficient to model vehicle merging decisions without the need for precise position (x, y) or heading angle.
Second, in terms of traffic rules for traffic-circle merging, the merging decision at a roundabout intersection depends primarily on the relationship between the vehicle and the intersection, not just the absolute position of the vehicle. The yield line defines rules such as “Yield right of way”, so the relative distance between vehicles and the yield line is critical in determining when and how vehicles merge.
Then, in terms of application scenarios, the decision model proposed in this paper focuses only on speed planning with predefined merging paths. Therefore, there is a natural relationship between the more precise absolute state variables (x, y, heading) and the relative distance variables between the autoroute and the yield line [10,30].
Finally, from the perspective of algorithm performance, in this paper, the spatial complexity is reduced from a high-dimensional (x, y, heading) space to a more relevant relative metric by introducing the concept of “relative distance to the yield line”. This reduction not only simplifies the state space, reduces the hardware requirements for model training, and improves the computational efficiency, but also enhances the generalization of the model to different roundabout intersections.
Therefore, the simplified state space of the roundabout merge is defined in . The state-space vector is defined as follows:
where D is a series of ego vehicle distances relative to the yield line of the roundabout, which is accumulated by projecting the actual position coordinates of the vehicle onto the centerline of the lane. V is a series of ego vehicle speeds.
Before using a linear function approximator to estimate the value or policy function by linearly combining state features, the state space must be discretized. In this paper, the starting and ending positions of the roundabout are selected as 35 m before and 5 m after the yield line, with an interval of 0.2 m. The speed range is set from 0 m/s to 10 m/s, with an interval of 0.2 m/s. A two-dimensional grid is used to discretize the expected values of the state-space elements, as shown below:
- D = {−35 m, −34.8 m, −34.6 m, …, 4.8 m, 5 m}
- V = {0 m/s, 0.2 m/s, 0.4 m/s, …, 10 m/s}
Finally, to facilitate predicting the state information of other vehicles at the next moment, it is assumed that they are traveling at a constant speed.
2.3. Action Space
Most scholars studying the driving behavior of merging cars in roundabouts [5,31,32], usually broadly categorize the merging driving behavior based on typical driving styles (conservative, conventional, and aggressive) into the following categories. The following categories include “”, “” and “”.
- : The vehicle stops at the yield line and then accelerates to enter the roundabout. The “” behavior occurs when the vehicle stops at the yield line and waits for a gap in traffic before proceeding. This behavior is a direct result of the vehicle assessing the presence of other vehicles entering the roundabout, and it aims to prevent collisions while waiting for the appropriate time to merge into the flow of traffic. The waiting period can be influenced by factors such as the speed and proximity of approaching vehicles, as well as the rules of priority at the roundabout.
- : The vehicle slows appropriately near the yield line before entering the roundabout; The “” behavior refers to the vehicle moving forward to enter and pass through the roundabout once a sufficient gap is identified. This behavior is based on the vehicle’s analysis of the available space in the traffic flow, as well as its ability to merge safely without disrupting the roundabout’s traffic dynamics. In some cases, this behavior might involve accelerating to match the flow of traffic or maintaining a steady pace to merge without causing abrupt disruptions.
- : The “” driving behavior can be seen as a more aggressive approach compared to “”, where the focus shifts from merely ensuring a safe merge to further prioritizing traffic flow efficiency.
These classifications are not arbitrary, but are specific behavioral strategies extracted from real-world driving scenarios, especially in complex traffic situations such as roundabout intersections. In order to replicate human-like driving behavior, the driving characteristics of a human driver entering a roundabout intersection can be combined with an automated driving strategy. Therefore, in this paper, these human-like driving characteristics are defined as the vehicle maintaining the desired target speed during the merging phase.
Therefore, this paper defines these human drivers’ driving behavior characteristics as the target speeds that the AV needs to maintain at different stages during the merging process. With reference to these three human drivers’ merging driving behaviors, this paper defines three human-like roundabout merging actions corresponding to the three target vectors of the speed planning module. They are named with the symbolic description of the action space A as follows:
Figure 1 illustrates three different speed profiles motivated by three human driving behaviors. In this paper, the speed profiles of the three merging behaviors in the action space are extracted from the rounD natural driving dataset, which provides realistic human driving data for the roundabout intersection scenario. More details about the dataset are given in Section 3.
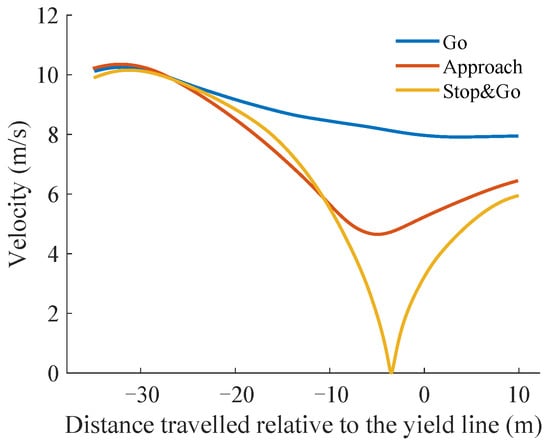
Figure 1.
Velocity profiles approaching a roundabout.
As illustrated in Figure 1, three distinct speed profiles, , , and , vary with distance. These profiles are derived from human driving data and exhibit varying degrees of deceleration. Among them, the profile experiences the least deceleration, maintaining a constant speed as it enters the roundabout. It reflects efficient driving behavior under clear traffic conditions and low roundabout traffic volume. The profile, in contrast, involves initially slowing down before accelerating to enter the roundabout. This profile is typical when roundabout traffic is uncertain, where preemptive slowing allows drivers to better assess the traffic flow. It balances comfort, efficiency, and safety, avoiding a full stop while contributing to smooth overall traffic flow. The profile requires the vehicle to slow to a stop near the entrance, then accelerate when it’s safe to enter the roundabout.
Finally, the discretized state-action space consists of 201 × 51 × 3 = 30,753 sampling points, summarizing the discretization scheme of the state space S and the three actions from action space A.
2.4. Reward Function
The reward function establishes the objective of the decision-making process. When merging into a roundabout, the primary goal is to enter safely, avoid collisions, and maintain a smooth traffic flow. Drawing from mechanical principles and constitutive relationships, our goal is to develop a more comprehensive model of a vehicle’s merging behavior.
The constitutive relation originally described the mathematical expression of material deformation under external forces such as compression or shear. It characterizes the mechanical behavior of materials and defines the relationship between stress (or other physical quantities) and strain (or other state variables). A viscoelastic–plastic constitutive model consists of three basic components: elastic, viscous, and plastic. These components can be combined in series or parallel to simultaneously exhibit viscous, elastic, and plastic properties. Two common types of two-element viscoelastic models are the Maxwell model, which combines elastic and viscous components in series, and the Kelvin–Voigt model, which arranges them in parallel.
Therefore, the application of force and stress concepts to traffic modeling is mainly an analogy between the distance or speed motion state between traffic participants and the behavior of materials under stress, not real forces. For instance, when the relative distance between the ego and host vehicles is large, the ego vehicle tends to accelerate, whereas a smaller distance encourages deceleration, which is akin to the behavior of an elastic component. Likewise, when the speed difference between vehicles is large, the ego vehicle accelerates, whereas a smaller speed difference results in deceleration, similar to the behavior of a viscous component. Thus, the motion of the vehicle can be directly linked to the behavior of the constitutive elements.
Based on the successful application of the constitutive relationship to the car-following model [28] and the lane-changing model [29], this paper further expands the application scenarios of the constitutive relationship. We use a viscoelastic model to simulate the dynamic interaction between the ego vehicle and other vehicles in a roundabout to better capture the real-time dynamics of vehicle interaction.
This study proposes a force-based merging reward model for roundabouts, represented using a parallel viscoelastic constitutive relation, as shown in Figure 2. In this model, and represent the elastic and viscous components, respectively. Meanwhile, k and characterize elastic and viscous properties, respectively. Under parallel conditions, the strains in both the elastic and viscous components were identical, and the total stress was the sum of the individual stresses, as expressed in Equation (11):
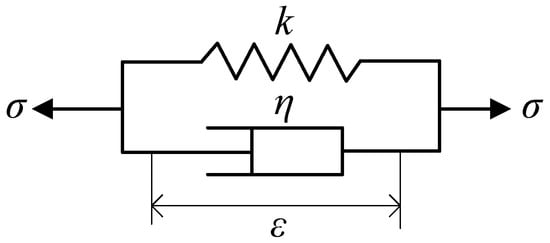
Figure 2.
Viscoelastic model.
In the roundabout merging scenario, the ego vehicle’s driving behavior (, , and ) is influenced not only by the relative distance and speed between the ego vehicle and other vehicles, but also by its current position within the roundabout. As shown in Figure 1, the behavior begins to diverge from the and behaviors at approximately 25 m from the yield line, whereas and start to differ at approximately 10 m. To make human-like driving decisions, the ego vehicle must identify the appropriate driving behavior at critical decision points when entering a roundabout.
Therefore, as shown in Figure 3, the total interaction force when the vehicle enters the roundabout is the difference between the interaction force between the ego vehicle and roundabout , and the interaction force between the ego vehicle and other vehicles in the circulatory road , as expressed below:
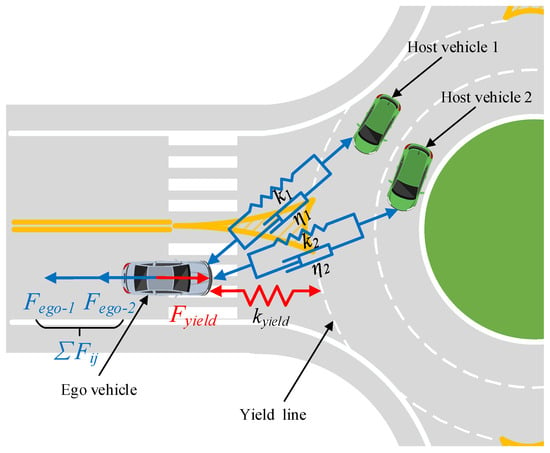
Figure 3.
Schematic diagram of roundabout interaction based on constitutive relationship.
The interaction force between the ego vehicle and roundabout is linked to the decision distances of the three driving behaviors. The objective is to ensure that the interaction forces (reward value) for each driving behavior reach their maximum values near their respective decision distances in sequence. The interaction forces for the three driving behaviors, , , and , are expressed as follows:
where , , and are undetermined coefficients; represents the relative position of the ego vehicle and the yield line; and , , represent the relative position of the three driving behavior decision points and yield line, respectively.
The interaction force represents the influence of a nearby vehicle j on ego vehicle i at time t within the perceptual range of the circulatory road at roundabouts. The magnitude of the interaction force is determined by the differences in the distance and speed between the two vehicles:
where , , and are undetermined coefficients; represents the safety distance between ego and host vehicles [33]; and and represent the relative distance and speed between ego vehicle i and host vehicle j at time t, respectively.
Furthermore, the interaction forces under the three driving behaviors were different. The specific expressions of , , and are as follows:
3. Case Study
This section validates the effectiveness of defining the reward function based on constitutive relationship theory within the MDP framework using the rounD dataset. The main objective of the behavioral decision-making process is to ensure that the vehicle merges safely and efficiently into the roundabout. In this section, we provide a detailed description of the test scenarios, dataset usage, and training parameters, followed by the training results.
3.1. Simulation Scenario and Simulation Parameter Settings
This study utilizes the rounD dataset [34] for model validation, chosen for its high-resolution map data, accurate vehicle location tracking, and geographic reference coordinates, all of which are crucial for studies involving the geometric parameters of roundabouts. Compared to other roundabout datasets [30,35,36], the rounD dataset provides more precise information on vehicle positions and roundabout geometry, allowing for a more accurate representation of real-world driving scenarios.
For the experiments, we selected vehicles entering the roundabout from the east to west direction. This choice was driven by the drone’s limited field of view, ensuring that a sufficiently long validation distance could be captured to observe the vehicle’s merging behavior under different conditions. Based on the visualization tools provided by the dataset itself, we screened the cases where there were no other interfering vehicles in the lane where the vehicle was located when the vehicle was merging, ensuring the rationality of the test samples. The test vehicles’ trajectories were manually annotated to allow for the generation of corresponding state–action pairs used in the MDP model.
To ensure that the training process represents the real scenario, the following parameters were selected for simulation settings, as shown in the Table 2:

Table 2.
Reinforcement learning parameters.
- Discount Factor(): Set to 0.99 to prioritize long-term rewards, promoting safe and efficient merging, similar to real-world decision-making.
- Epsilon () and Epsilon Decay: Initial epsilon set to 0.9 for exploration, decaying at 0.01 to shift towards exploitation as training progresses.
- Optimizer: Stochastic Gradient Descent with Momentum (SGDM) was chosen for its stability and faster convergence by using both current and previous gradients.
- Learning Rate: Set to 0.1 for a balance between learning speed and stability, avoiding overshooting while ensuring steady progress.
- Max Steps Per Episode: 50 steps per episode, providing sufficient decision time without excessively long training.
- Max Episodes: 200 episodes, based on testing, to ensure sufficient learning without overfitting.
- Score Averaging Window Length: A 30-episode moving window for averaging rewards, smoothing performance fluctuations to assess overall effectiveness.
These settings were selected to balance model performance, training time, and convergence stability, ensuring that the model can generalize well to various roundabout merging scenarios.
To facilitate reproducibility, all parameters and configurations were fixed at the values presented here, and the training process was conducted on a dedicated computer with consistent hardware specifications. The configuration of the computer includes the following specifications: CPU: Intel(R) Core(TM) i9-9900K; GPU: NVIDIA GeForce RTX 2080 Ti; Memory: 64 GB.
Finally, referring to the calibration method of constitutive relationship parameters in [29], the calibration results of some parameters involved in the constitutive relationship in the rounD data are as follows: , , , , , , , , , , , .
3.2. Training and Testing
To evaluate the efficacy of the proposed decision-making algorithm across three distinct driving scenarios (, , and ), we selected vehicles ID 271, ID 99, and ID 121 as ego vehicles for the experiments. The spatial relationships between the ego vehicles and host vehicles within the circulatory roadway are shown in Figure 4. The reward trajectories observed during the training phase are presented in Figure 5. After approximately 100 simulation iterations, the reward trajectories for all three scenarios converged to a stable plateau. This indicates that the Q-learning algorithm, combined with the Markov decision process model, effectively meets the agent’s learning criteria, enabling it to extract relevant information from the states and rewards to make accurate decisions. During the initial phases of training, the reward trajectories showed a marked increase, indicating that the force-based interaction reward model provided accurate feedback on the effectiveness of the actions across various states. This accelerates the agent’s learning of the mapping between state transitions and optimal state–action pairs.
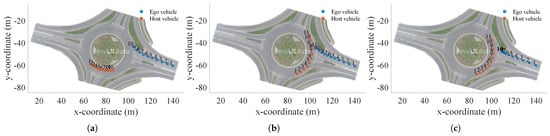
Figure 4.
A bird’s -eye view showing the relative positions of the ego vehicle and the host vehicle in the circulatory roadway for three driving behavior scenarios. (a) shows the scenario with ego vehicle ID 271; (b) shows the scenario with ego vehicle ID 99; (c) shows the scenario with ego vehicle ID 121. Background image from the rounD dataset [34].
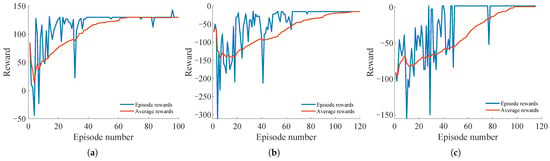
Figure 5.
Illustration of the reward curves for MDP algorithm training in three scenarios: (a) scenario; (b) scenario; (c) scenario.
Figure 6 illustrates the trends in the rewards of three actions (, , and ) as the ego vehicle moves relative to the yield line across three scenarios. In all cases, the reward for the action decreases steadily, indicating that the preference for the behavior diminishes as the ego vehicle approaches the yield line. Nevertheless, in the scenario, the action consistently generates the highest reward across all measured distances. As the vehicle approaches the yield line, the rewards for the and actions steadily increase, eventually surpassing the reward for the action in the and scenarios. This suggests that and behaviors become increasingly preferred near the yield line. In the scenario, the reward for the action gradually surpasses that of the action, peaking at a certain distance. This reflects the situational feasibility of the decision. In the scenario, as the ego vehicle approaches the yield line, the action outperforms both the and actions, emerging as the optimal choice near the yield line. Notably, in all scenarios, the reward curves for the and actions intersect near the yield line. This may reflect the applicability of both relatively aggressive and conservative driving behaviors in complex scenarios such as merging at a roundabout.
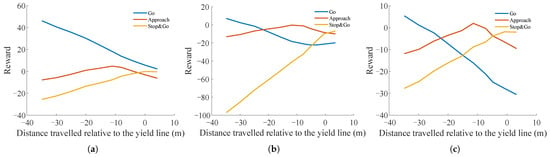
Figure 6.
Reward sequence for the ego vehicle’s action decision vehicle speed curves in three scenarios: (a) scenario; (b) scenario; (c) scenario.
Finally, based on the state and action space proposed in this paper, Figure 7 compares the target merging speed profiles determined by the fixed-value reward function method and the force-based value reward function method with the ground truth speed profiles of human drivers in three scenarios. The results show that the method based on the fixed-value reward function has incorrect decision-making behaviors in all three scenarios, while the method based on the force-based value reward function is more capable of making human-like merging behavior decisions. The target speed determined by the agent’s decision aligns with variations in the actual speed of the vehicle.
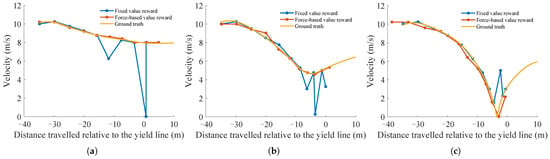
Figure 7.
Velocity profiles of ego vehicle in three scenarios: (a) scenario; (b) scenario; (c) scenario.
4. Conclusions
This study introduces a decision-making method for the safe merging of AVs in roundabout scenarios. By analyzing the vehicle states and driving behaviors of human drivers entering roundabouts, the MDP for this scenario is optimized, including the state, action, and reward spaces. First, the cumulative driving distance relative to the yield line and ego vehicle speed are used as state parameters to define the state space. Compared to traditional methods for general scenarios, this approach simplifies the state-space parameters and enhances the computational efficiency of the algorithm. Second, three representative entry speed curves derived from real traffic datasets are used as action options for the agent, promoting human-like driving behavior and better integration with the surrounding traffic flow. Next, constitutive relationships model the interactions between the ego vehicle and roundabout, as well as with other vehicles. Using the magnitude of forces as the reward function, this method provides immediate, detailed, and physically consistent feedback, addressing the sparse reward problem and enhancing agent performance in complex and dynamic environments. This approach ensures high interpretability and stability.
Future work will explore integrated prediction models to predict the behavior of other vehicles in the roundabout, which can improve safety and decision accuracy in partially observable environments. Additionally, we will investigate how the decision model proposed in this paper can be integrated with traditional control models to enhance optimization and robustness. By combining the adaptive capabilities of reinforcement learning (RL) with classical control approaches, we aim to improve the system’s ability to handle uncertainties and dynamic conditions, leading to better performance in real-world applications. Furthermore, considering the hardware constraints and real-time decision-making requirements, we will continue to refine the design of the state space, action space, and reward function. We will also explore the integration of deep reinforcement learning and incremental learning techniques to further improve the robustness and efficiency of the system in complex dynamic scenarios.
Author Contributions
Conceptualization, Q.S. and H.J.; methodology, Q.S. and A.L.; writing—original draft preparation, Q.S.; writing—review and editing, A.L. and S.M.; supervision, H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Project of Philosophy and Social Science Research in Colleges and Universities in Jiangsu Province (2022SJYB2207), Public Open Project of Automobile Standardization (CATARC-Z-2024-00116) and two Postgraduate Research & Practice Innovation Program of Jiangsu Province (No. KYCX22_3618 and No. KYCX21_3334).
Data Availability Statement
The authors will supply the relevant data in response to reasonable requests.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Retting, R.A.; Mandavilli, S.; McCartt, A.T.; Russell, E.R. Roundabouts, traffic flow and public opinion. Traffic Eng. Control 2006, 47, 268–272. [Google Scholar]
- Patterson, F. Cycling and roundabouts: An Australian perspective. Road Transp. Res. 2010, 19, 4–19. [Google Scholar]
- Rodegerdts, L. Roundabouts Database-kittelson & Associates Inc. 2022. Available online: https://roundabouts.kittelson.com (accessed on 10 May 2024).
- Wang, W.; Jiang, L.; Lin, S.; Fang, H.; Meng, Q. Imitation learning based decision-making for autonomous vehicle control at traffic roundabouts. Multimedia Tools Appl. 2022, 81, 39873–39889. [Google Scholar] [CrossRef]
- Okumura, B.; James, M.R.; Kanzawa, Y.; Derry, M.; Sakai, K.; Nishi, T.; Prokhorov, D. Challenges in perception and decision making for intelligent automotive vehicles: A case study. IEEE Trans. Intell. Vehicles 2016, 1, 20–32. [Google Scholar] [CrossRef]
- Muffert, M.; Pfeiffer, D.; Franke, U. A stereo-vision based object tracking approach at roundabouts. IEEE Intell. Transp. Syst. Mag. 2013, 5, 22–32. [Google Scholar] [CrossRef]
- Wang, X.; Qi, X.; Wang, P.; Yang, J. Decision making framework for autonomous vehicles driving behavior in complex scenarios via hierarchical state machine. Auton. Intell. Syst. 2021, 1, 10. [Google Scholar] [CrossRef]
- Hu, Y.; Yan, L.; Zhan, J.; Yan, F.; Yin, Z.; Peng, F.; Wu, Y. Decision-making system based on finite state machine for low-speed autonomous vehicles in the park. In Proceedings of the 2022 IEEE International Conference on Real-time Computing and Robotics (RCAR), Guiyang, China, 17–22 July 2022; pp. 721–726. [Google Scholar]
- Kurt, A.; Ózgúner, Ú. A probabilistic model of a set of driving decisions. In Proceedings of the 2011 14th International IEEE conference on intelligent transportation systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 570–575. [Google Scholar]
- Gritschneder, F.; Hatzelmann, P.; Thom, M.; Kunz, F.; Dietmayer, K. Adaptive learning based on guided exploration for decision making at roundabouts. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 433–440. [Google Scholar]
- Li, N.; Oyler, D.W.; Zhang, M.; Yildiz, Y.; Kolmanovsky, I.; Girard, A.R. Game theoretic modeling of driver and vehicle interactions for verification and validation of autonomous vehicle control systems. IEEE Trans. Control Syst. Technol. 2017, 26, 1782–1797. [Google Scholar] [CrossRef]
- Tian, R.; Li, S.; Li, N.; Kolmanovsky, I.; Girard, A.; Yildiz, Y. Adaptive game-theoretic decision making for autonomous vehicle control at roundabouts. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 321–326. [Google Scholar]
- Chandra, R.; Manocha, D. Gameplan: Game-theoretic multi-agent planning with human drivers at intersections, roundabouts, and merging. IEEE Robot. Autom. Lett. 2022, 7, 2676–2683. [Google Scholar] [CrossRef]
- Jamgochian, A.; Menda, K.; Kochenderfer, M.J. Multi-Vehicle Control in Roundabouts using Decentralized Game-Theoretic Planning. arXiv 2022, arXiv:2201.02718. [Google Scholar]
- Fan, W. A Comprehensive Analysis of Game theory on Multi-Agent Reinforcement. Highlights Sci. Eng. Technol. 2024, 85, 77–88. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Han, Z.; Sun, W.; He, L. A Decision-Making System for Cotton Irrigation Based on Reinforcement Learning Strategy. Agronomy 2023, 14, 11. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M.; Buscarino, A. Optimal and Robust Control: Advanced Topics with MATLAB®; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Chandiramani, J. Decision Making Under Uncertainty for Automated Vehicles in Urban situations. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Bey, H.; Sackmann, M.; Lange, A.; Thielecke, J. POMDP planning at roundabouts. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium Workshops (IV Workshops), Nagoya, Japan, 11–17 November 2021; pp. 264–271. [Google Scholar]
- Li, X.; Guvenc, L.; Aksun-Guvenc, B. Decision Making for Autonomous Vehicles. arXiv 2023, arXiv:2304.13908. [Google Scholar]
- White, D.; Wu, M.; Novoseller, E.; Lawhern, V.J.; Waytowich, N.; Cao, Y. Rating-based reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 10207–10215. [Google Scholar]
- Wu, M.; Tao, F.; Cao, Y. Value of Potential Field in Reward Specification for Robotic Control via Deep Reinforcement Learning. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MA, USA, 23–27 January 2023; p. 0505. [Google Scholar]
- Wu, M.; Siddique, U.; Sinha, A.; Cao, Y. Offline Reinforcement Learning with Failure Under Sparse Reward Environments. In Proceedings of the 2024 IEEE 3rd International Conference on Computing and Machine Intelligence (ICMI), Mt Pleasant, MI, USA, 13–14 April 2024; pp. 1–5. [Google Scholar]
- Fu, L.; Zhang, Y.; Qin, H.; Shi, Q.; Chen, Q.; Chen, Y.; Shi, Y. A modified social force model for studying nonlinear dynamics of pedestrian-e-bike mixed flow at a signalized crosswalk. Chaos Solitons Fractals 2023, 174, 113813. [Google Scholar] [CrossRef]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Rashid, M.M.; Seyedi, M.; Jung, S. Simulation of pedestrian interaction with autonomous vehicles via social force model. Simul. Model. Pract. Theory 2024, 132, 102901. [Google Scholar] [CrossRef]
- Delpiano, R.; Herrera, J.C.; Laval, J.; Coeymans, J.E. A two-dimensional car-following model for two-dimensional traffic flow problems. Transp. Res. Part C Emerg. Technol. 2020, 114, 504–516. [Google Scholar] [CrossRef]
- Li, Z.; Khasawneh, F.; Yin, X.; Li, A.; Song, Z. A new microscopic traffic model using a spring-mass-damper-clutch system. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3322–3331. [Google Scholar] [CrossRef]
- Li, A.; Su, M.; Jiang, H.; Chen, Y.; Chen, W. A Two-Dimensional Lane-Changing Dynamics Model Based on Force. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20203–20214. [Google Scholar] [CrossRef]
- Zyner, A.; Worrall, S.; Nebot, E.M. ACFR five roundabouts dataset: Naturalistic driving at unsignalized intersections. IEEE Intell. Transp. Syst. Mag. 2019, 11, 8–18. [Google Scholar] [CrossRef]
- Rodrigues, M.; McGordon, A.; Gest, G.; Marco, J. Autonomous navigation in interaction-based environments—A case of non-signalized roundabouts. IEEE Trans. Intell. Vehicles 2018, 3, 425–438. [Google Scholar] [CrossRef]
- Song, Y.; Hu, X.; Lu, J.; Zhou, X. Analytical approximation and calibration of roundabout capacity: A merging state transition-based modeling approach. Transp. Res. Part Methodol. 2022, 163, 232–257. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Ni, D.; Zhang, Y. Comprehensive survival analysis of lane-changing duration. Measurement 2021, 182, 109707. [Google Scholar] [CrossRef]
- Krajewski, R.; Moers, T.; Bock, J.; Vater, L.; Eckstein, L. The round dataset: A drone dataset of road user trajectories at roundabouts in germany. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Robicquet, A.; Sadeghian, A.; Alahi, A.; Savarese, S. Learning Social Etiquette: Human Trajectory Understanding in Crowded Scenes. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VIII 14; Springer: Berlin/Heidelberg, Germany, 2016; pp. 549–565. [Google Scholar]
- Zhan, W.; Sun, L.; Wang, D.; Shi, H.; Clausse, A.; Naumann, M.; Kummerle, J.; Konigshof, H.; Stiller, C.; de La Fortelle, A.; et al. Interaction dataset: An international, adversarial and cooperative motion dataset in interactive driving scenarios with semantic maps. arXiv 2019, arXiv:1910.03088. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).