A Surrogate-Assisted Gray Prediction Evolution Algorithm for High-Dimensional Expensive Optimization Problems
Abstract
1. Introduction
- •
- A gray prediction technique is introduced to solve expensive optimization problems (EOPs). In this work, an even gray model (EGM(1,1)) operator is adopted in concert with a surrogate model to guide the population to search in a promising direction.
- •
- We verified that predictive model operators can be better combined with surrogate models to search for optimal solutions compared to the traditional conventional mutation and crossover operators.
- •
- An inferior individual offspring strategy is proposed to improve the quality of candidate individuals used for true function evaluation.
- •
- We have proposed a surrogate-assisted gray prediction evolution algorithm (SAGPE) for solving EOPs.
2. Related Techniques
2.1. GPE Algorithm
- (i)
- If the maximum Euclidean distance between three individuals in the data sequence is less than a given threshold , the GPE generate offspring by random perturbation.
- (ii)
- If the distance between any two values of the sequence is less than a given threshold , it uses linear fitting to generate offspring.
- (iii)
- Otherwise, it uses EGM(1,1) to generate offspring.
2.2. RBF Model
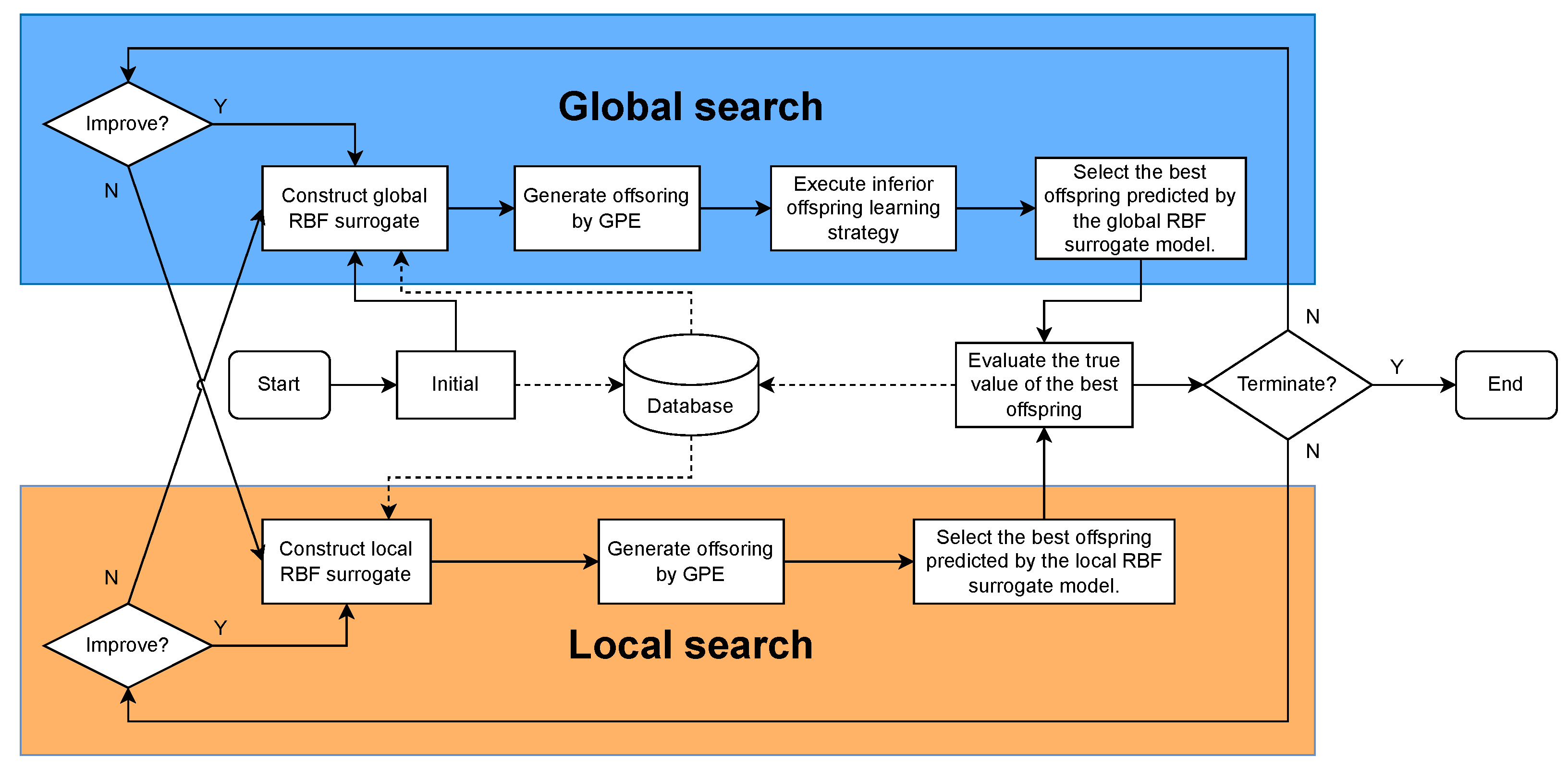
3. Surrogate-Assisted Gray Prediction Evolution Algorithm
3.1. Overall Framework
3.2. Global Search
| Algorithm 1 Pseudo-code of the global search |
|
3.3. Local Search
| Algorithm 2 Pseudo-code of the inferior offspring learning strategy |
|
| Algorithm 3 Pseudo-code of the local search |
|
4. Experimental Studies
4.1. Experimental Setup
4.2. Parameter Sensitivity Analysis
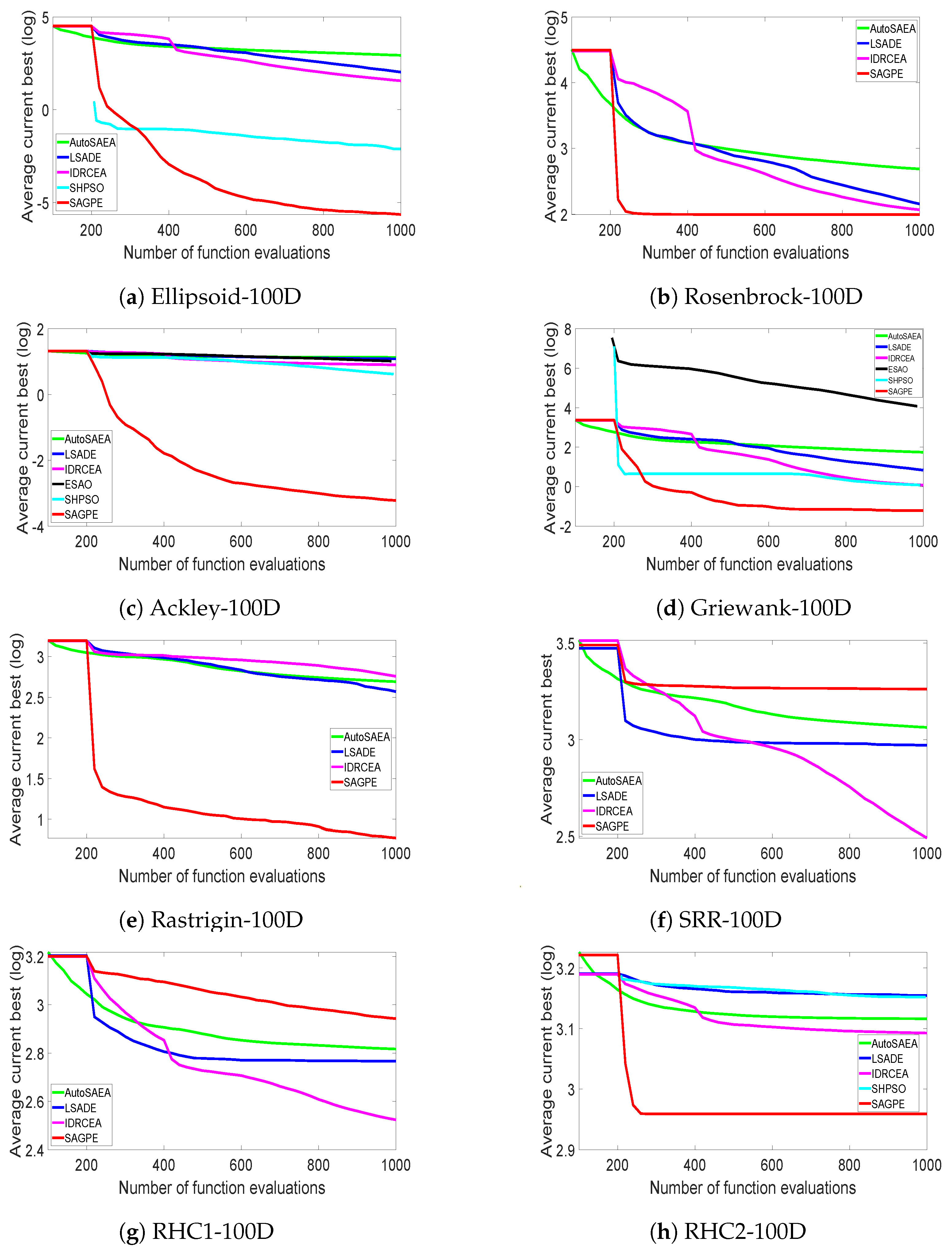
4.3. Experimental Results on 30D, 50D, and 100D Benchmark Functions
4.4. Effects of Inferior Offspring Learning Strategy
4.5. Comparison of Different EAs
4.6. Application on the Speed Reducer Design
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiang, X.; Su, Q.; Huang, G.; Hu, Z. A simplified non-equidistant grey prediction evolution algorithm for global optimization. Appl. Soft Comput. 2022, 125, 109081. [Google Scholar] [CrossRef]
- Zhu, H.; Shi, L.; Hu, Z.; Su, Q. A multi-surrogate multi-tasking genetic algorithm with an adaptive training sample selection strategy for expensive optimization problems. Eng. Appl. Artif. Intell. 2024, 130, 107684. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Chugh, T.; Guo, D.; Miettinen, K. Data-driven evolutionary optimization: An overview and case studies. IEEE Trans. Evol. Comput. 2018, 23, 442–458. [Google Scholar] [CrossRef]
- Zhen, H.; Gong, W.; Wang, L.; Ming, F.; Liao, Z. Two-Stage Data-Driven Evolutionary Optimization for High-Dimensional Expensive Problems. IEEE Trans. Cybern. 2023, 53, 2368–2379. [Google Scholar] [CrossRef]
- Pan, J.S.; Liu, N.; Chu, S.C.; Lai, T. An efficient surrogate-assisted hybrid optimization algorithm for expensive optimization problems. Inf. Sci. 2021, 561, 304–325. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Q.; Gielen, G.G. A Gaussian process surrogate model assisted evolutionary algorithm for medium scale expensive optimization problems. IEEE Trans. Evol. Comput. 2013, 18, 180–192. [Google Scholar] [CrossRef]
- Herrera, M.; Guglielmetti, A.; Xiao, M.; Filomeno Coelho, R. Metamodel-assisted optimization based on multiple kernel regression for mixed variables. Struct. Multidiscip. Optim. 2014, 49, 979–991. [Google Scholar] [CrossRef]
- Huang, K.; Zhen, H.; Gong, W.; Wang, R.; Bian, W. Surrogate-assisted evolutionary sampling particle swarm optimization for high-dimensional expensive optimization. Neural Comput. Appl. 2023, 1–17. [Google Scholar] [CrossRef]
- Tian, J.; Tan, Y.; Zeng, J.; Sun, C.; Jin, Y. Multiobjective infill criterion driven Gaussian process-assisted particle swarm optimization of high-dimensional expensive problems. IEEE Trans. Evol. Comput. 2018, 23, 459–472. [Google Scholar] [CrossRef]
- Xie, L.; Li, G.; Wang, Z.; Cui, L.; Gong, M. Surrogate-Assisted Evolutionary Algorithm with Model and Infill Criterion Auto-Configuration. IEEE Trans. Evol. Comput. 2023, 28, 1114–1126. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Xue, B.; Zhang, M. A constrained competitive swarm optimizer with an SVM-based surrogate model for feature selection. IEEE Trans. Evol. Comput. 2022, 28, 2–16. [Google Scholar] [CrossRef]
- Dong, H.; Dong, Z. Surrogate-assisted grey wolf optimization for high-dimensional, computationally expensive black-box problems. Swarm Evol. Comput. 2020, 57, 100713. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Q.; Lin, Q.; Gao, W. A three-level radial basis function method for expensive optimization. IEEE Trans. Cybern. 2021, 52, 5720–5731. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Gong, M. Expensive optimization via surrogate-assisted and model-free evolutionary optimization. IEEE Trans. Syst. Man. Cybern. Syst. 2022, 53, 2758–2769. [Google Scholar] [CrossRef]
- Wang, H.; Jin, Y.; Doherty, J. Committee-based active learning for surrogate-assisted particle swarm optimization of expensive problems. IEEE Trans. Cybern. 2017, 47, 2664–2677. [Google Scholar] [CrossRef]
- Di Nuovo, A.G.; Ascia, G.; Catania, V. A study on evolutionary multi-objective optimization with fuzzy approximation for computational expensive problems. In Proceedings of the Parallel Problem Solving from Nature-PPSN XII: 12th International Conference, Taormina, Italy, 1–5 September 2012; Springer: Berlin/Heidelberg, Germany, 2012. Part II. pp. 102–111. [Google Scholar] [CrossRef]
- Li, F.; Shen, W.; Cai, X.; Gao, L.; Wang, G.G. A fast surrogate-assisted particle swarm optimization algorithm for computationally expensive problems. Appl. Soft Comput. 2020, 92, 106303. [Google Scholar] [CrossRef]
- Ong, Y.S.; Nair, P.B.; Keane, A.J. Evolutionary optimization of computationally expensive problems via surrogate modeling. AIAA J. 2003, 41, 687–696. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Q. Multiple penalties and multiple local surrogates for expensive constrained optimization. IEEE Trans. Evol. Comput. 2021, 25, 769–778. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.G.; Song, B.; Wang, P.; Wang, Y. A novel evolutionary sampling assisted optimization method for high-dimensional expensive problems. IEEE Trans. Evol. Comput. 2019, 23, 815–827. [Google Scholar] [CrossRef]
- Pan, J.S.; Liang, Q.; Chu, S.C.; Tseng, K.K.; Watada, J. A multi-strategy surrogate-assisted competitive swarm optimizer for expensive optimization problems. Appl. Soft Comput. 2023, 147, 110733. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Z.; Chen, Y.; Ma, G.; Song, L.; Li, J.; Feng, Z. An efficient surrogate-assisted differential evolution algorithm for turbomachinery cascades optimization with more than 100 variables. Aerosp. Sci. Technol. 2023, 142, 108675. [Google Scholar] [CrossRef]
- Zhang, J.; Li, M.; Yue, X.; Wang, X.; Shi, M. A hierarchical surrogate assisted optimization algorithm using teaching-learning-based optimization and differential evolution for high-dimensional expensive problems. Appl. Soft Comput. 2024, 152, 111212. [Google Scholar] [CrossRef]
- Meng, Z.; Yang, C. Hip-DE: Historical population based mutation strategy in differential evolution with parameter adaptive mechanism. Inf. Sci. 2021, 562, 44–77. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, X.; Su, Q.; Zhu, H.; Guo, J. Grey prediction evolution algorithm for global optimization. Appl. Math. Model. 2020, 79, 145–160. [Google Scholar] [CrossRef]
- Li, W.; Su, Q.; Hu, Z. A grey prediction evolutionary algorithm with a surrogate model based on quadratic interpolation. Expert Syst. Appl. 2024, 236, 121261. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Díaz-Manríquez, A.; Toscano, G.; Coello Coello, C.A. Comparison of metamodeling techniques in evolutionary algorithms. Soft Comput. 2017, 21, 5647–5663. [Google Scholar] [CrossRef]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Kuudela, J.; Matousek, R. Combining Lipschitz and RBF surrogate models for high-dimensional computationally expensive problems. Inf. Sci. 2023, 619, 457–477. [Google Scholar] [CrossRef]
- Li, G.; Xie, L.; Wang, Z.; Wang, H.; Gong, M. Evolutionary algorithm with individual-distribution search strategy and regression-classification surrogates for expensive optimization. Inf. Sci. 2023, 634, 423–442. [Google Scholar] [CrossRef]
- Yu, H.; Tan, Y.; Zeng, J.; Sun, C.; Jin, Y. Surrogate-assisted hierarchical particle swarm optimization. Inf. Sci. 2018, 454, 59–72. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.Y.; Suganthan, P.N. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. Comput. Intell. Lab. Zhengzhou Univ. Zhengzhou China Tech. Rep. Nanyang Technol. Univ. Singap. 2013, 635, 2014. [Google Scholar]


| Function | Dimension | Optimun | Property | |
|---|---|---|---|---|
| F1 | Ellipsoid | 30 50 100 | 0 | Unimodal |
| F2 | Rosenbrock | 30 50 100 | 0 | Multimodal with narrow valley |
| F3 | Ackley | 30 50 100 | 0 | Multimodal |
| F4 | Griewank | 30 50 100 | 0 | Multimodal |
| F5 | Rastrigin | 30 50 100 | 0 | Multimodal |
| F6 | Shifted Rotated Rastrigin (SRR) | 30 50 100 | Very complicated multimodal | |
| F7 | Rotated Hybrid Composition function (RHC1) | 30 50 100 | 120 | Very complicated multimodal |
| F8 | Rotated Hybrid Composition function (RHC2) | 30 50 100 | 10 | Very complicated multimodal with a narrow basin |
| Algorithm | AutoSAEA (Mean/Std) | LSADE (Mean/Std) | IDRCEA (Mean/Std) | ESAO (Mean/Std) | SHPSO (Mean/Std) | SAGPE (Mean/Std) | |
|---|---|---|---|---|---|---|---|
| Fun | D | ||||||
| F1 | 30 | 2.01 × /2.03 × (+) | 1.49 × /2.27 × (+) | 4.48 × /4.24 × (+) | 2.75 × /6.96 × (+) | 2.12 × /1.52 × (+) | 9.40 × /5.18 × |
| F2 | 30 | 2.58 × /1.02 × (−) | 2.69 × /1.04 × (−) | 2.64 × /5.56 × (−) | 2.50 × /1.57 × (−) | 2.86 × /4.04 × (+) | 2.73 × /1.89 × |
| F3 | 30 | 1.90 × /4.39 × (+) | 1.57 × /1.07 × (+) | 1.25 × /7.20 × (+) | 2.52 × /8.40 × (+) | 1.44 × /7.74 × (+) | 7.12 × /1.46 × |
| F4 | 30 | 1.40 × /3.10 × (−) | 5.45 × /2.58 × (+) | 4.38 × /6.30 × (−) | 9.53 × /5.04 × (+) | 9.21 × /8.81 × (+) | 2.55 × /4.79 × |
| F5 | 30 | 4.27 × /2.15 × (+) | 8.11 × /1.89 × (+) | 3.54 × /2.13 × (+) | NaN | NaN | 4.67 × /6.15 × |
| F6 | 30 | −2.55 × /2.85 × (−) | −2.11 × /3.75 × (−) | −2.78 × /1.45 × (−) | 6.33 × /2.65 × (−) | −8.25 × /2.25 × (−) | 1.65 × /4.50 × |
| F7 | 30 | 3.82 × /1.56 × (−) | 4.37 × /1.58 × (−) | 3.47 × /1.72 × (−) | NaN | 4.64 × /8.51 × (−) | 6.01 × /7.54 × |
| F8 | 30 | 9.34 × /8.38 × (−) | 9.63 × /4.24 × (+) | 9.50 × /9.00 × (+) | 9.32 × /8.94 × (−) | 9.40 × /9.02 × (−) | 9.48 × /7.24 × |
| F1 | 50 | 8.48 × /7.79 × (+) | 1.26 × /8.75 × (+) | 3.22 × /2.69 × (+) | 7.40 × /5.55 × (+) | 4.03 × /2.06 × (+) | 8.72 × /3.76 × |
| F2 | 50 | 4.95 × /9.73 × (+) | 4.91 × /7.62 × (+) | 4.75 × /7.58 × (−) | 4.74 × /1.71 × (−) | 5.08 × /3.03 × (+) | 4.81 × /4.75 × |
| F3 | 50 | 2.31 × /6.78 × (+) | 7.47 × /3.22 × (+) | 3.78 × /6.46 × (+) | 1.43 × /2.49 × (+) | 1.84 × /5.64 × (+) | 1.51 × /4.56 × |
| F4 | 50 | 2.22 × /7.08 × (+) | 8.11 × /1.36 × (+) | 1.36 × /6.53 × (+) | 9.40 × /4.21 × (+) | 9.45 × /6.14 × (+) | 6.60 × /3.60 × |
| F5 | 50 | 1.01 × /2.73 × (+) | 1.54 × /3.51 × (+) | 8.11 × /4.94 × (+) | Nan | NaN | 1.67 × /3.85 × |
| F6 | 50 | −1.48 × /4.27 × (−) | −1.03 × /5.40 × (−) | −2.19 × /3.08 × (−) | 1.98 × /4.58 × (−) | 1.34 × /3.25 × (−) | 7.06 × /8.12 × |
| F7 | 50 | 3.03 × /8.59 × (−) | 3.64 × /1.07 × (−) | 2.75 × /1.05 × (−) | NaN | 4.74 × /4.20 × (−) | 7.33 × /9.77 × |
| F8 | 50 | 1.04 × /4.38 × (+) | 1.04 × /6.95 × (+) | 1.03 × /2.08 × (+) | 9.57 × /3.71 × (+) | 9.97 × /2.21 × (+) | 9.10 × /4.41 × |
| F1 | 100 | 8.69 × /2.09 × (+) | 1.06 × /2.68 × (+) | 3.66 × /1.37 × (+) | 1.28 × /1.34 × (+) | 7.61 × /2.14 × (+) | 9.29 × /6.83 × |
| F2 | 100 | 4.88 × /7.86 × (+) | 1.42 × /1.88 × (+) | 1.17 × /1.14 × (+) | 5.78 × /4.48 × (+) | 1.66 × /2.64 × (+) | 9.87 × /1.62 × |
| F3 | 100 | 1.35 × /6.03 × (+) | 1.21 × /1.63 × (+) | 7.95 × /7.88 × (+) | 1.04 × /2.11 × (+) | 4.11 × /5.92 × (+) | 6.03 × /1.39 × |
| F4 | 100 | 5.52 × /1.46 × (+) | 6.75 × /1.49 × (+) | 1.21 × /9.80 × (+) | 5.73 × /5.84 × (+) | 1.07 × /2.05 × (+) | 3.32 × /7.27 × |
| F5 | 100 | 4.92 × /7.55 × (+) | 3.71 × /7.54 × (+) | 5.72 × /1.35 × (+) | NaN | NaN | 6.0 × /5.75 × |
| F6 | 100 | 1.16 × /9.96 × (−) | 9.34 × /1.02 × (−) | 3.10 × /8.42 × (−) | 7.13 × /2.65 × (−) | 8.02 × /7.23 × (−) | 1.83 × /6.99 × |
| F7 | 100 | 6.55 × /6.07 × (−) | 5.84 × /3.66 × (−) | 3.34 × /2.60 × (−) | NaN | 5.16 × /3.21 × (−) | 8.76 × /1.21 × |
| F8 | 100 | 1.31 × /2.16 × (+) | 1.43 × /3.44 × (+) | 1.24 × /3.18 × (+) | 1.37 × /2.75 × (+) | 1.42 × /3.82 × (+) | 9.10 × /2.51 × |
| +/−/= | 15/9/0 | 17/7/0 | 15/9/0 | 13/5/0 | 14/7/0 | NaN/NaN/NaN |
| Mothods | D | Avg. Rank | Overall Rank | ||
|---|---|---|---|---|---|
| 30D | 50D | 100D | |||
| AutoSAEA | 1.83 | 3.58 | 4.83 | 3.42 | 3 |
| LSADE | 4.33 | 4.25 | 4.33 | 4.31 | 5 |
| IDRCEA | 2.83 | 2.50 | 2.17 | 2.50 | 2 |
| ESAO | 4.00 | 4.25 | 4.67 | 4.31 | 6 |
| SHPSO | 4.67 | 4.42 | 3.17 | 4.08 | 4 |
| SAGPE | 3.33 | 2.00 | 1.83 | 2.39 | 1 |
| Mothods | SAGPE | SAGPE-W | ||||
|---|---|---|---|---|---|---|
| Fun | Global Search (NFE/NTI) | Local Search (NFE/NTI) | Mean/Std | Global Search (NFE/NTI) | Local Search (NFE/NTI) | Mean/Std |
| F1-30D | 472.9/27.4 | 467.6/22.1 | 9.40 × /5.18 × | 473.1/23.9 | 467.5/18.4 | 8.88 × /4.60 × |
| F2-30D | 486.6/48.4 | 453.9/15.8 | 2.73 × /1.89 × | 474.6/2.73 × | 465.7/18.4 | 2.78 × /3.48 × |
| F3-30D | 470.2/17.9 | 470.3/18.1 | 7.12 × /1.46 × | 468.6/13.7 | 471.9/16.9 | 7.67 × /1.63 × |
| F4-30D | 475.6/22.6 | 464.9/11.8 | 2.55 × /4.79 × | 472.9/16.8 | 467.5/11.4 | 1.79 × /6.09 × |
| F5-30D | 475.2/24.9 | 465.4/15.1 | 4.67 × /6.15 × | 471.4/17.7 | 468.1/15.5 | 3.30 × /5.52 × |
| F6-30D | 474.3/9.00 | 466.4/1.17 | 1.65 × /4.50 × | 471.7/6.30 | 468.8/3.47 | 2.13 × /4.88 × |
| F7-30D | 487.6/37.3 | 452.8/2.43 | 6.01 × /7.54 × | 475.4/25.3 | 465.3/15.3 | 6.82 × /6.74 × |
| F8-30D | 475.6/23.3 | 464.9/12.7 | 9.48 × /7.24 × | 471.0/16.2 | 469.4/14.6 | 9.14 × /2.27 × |
| F1-50D | 451.6/24.4 | 448.7/21.5 | 7.69 × /3.78 × | 450.1/18.7 | 450.5/19.0 | 8.74 × /4.59 × |
| F2-50D | 464.7/45.1 | 435.7/16.1 | 4.76 × /4.10 × | 455.8/31.7 | 444.8/20.7 | 4.81 × /3.12 × |
| F3-50D | 451.2/19.8 | 449.5/18.1 | 1.39 × /3.37 × | 450.7/16.9 | 449.8/15.9 | 1.43 × /4.05 × |
| F4-50D | 459.3/24.6 | 441.1/6.47 | 5.24 × /7.14 × | 456.7/19.6 | 443.8/4.73 | 5.30 × /2.91 × |
| F5-50D | 456.9/20.8 | 443.7/7.63 | 1.99 × /1.97 × | 453.6/15.4 | 446.9/8.77 | 8.57 × /7.22 × |
| F6-50D | 455.2/11.0 | 445.3/1.17 | 6.48 × /7.62 × | 452.4/8.40 | 448.2/4.20 | 7.02 × /8.86 × |
| F7-50D | 466.0/33.3 | 434.7/1.93 | 6.44 × /5.23 × | 453.1/16.8 | 447.5/11.3 | 7.17 × /8.98 × |
| F8-50D | 452.6/23.6 | 447.7/18.7 | 9.10 × /2.92 × | 451.1/18.7 | 449.3/16.9 | 9.10 × /4.28 × |
| F1-100D | 402.2/16.9 | 398.2/12.9 | 9.29 × /6.83 × | 402.4/16.0 | 398.0/11.6 | 1.55 × /9.69 × |
| F2-100D | 405.8/23.3 | 394.7/12.1 | 9.87 × /1.62 × | 401.7/15.3 | 398.7/12.3 | 9.88 × /6.86 × |
| F3-100D | 405.8/24.3 | 394.7/13.2 | 6.03 × /1.39 × | 404.5/18.7 | 396.1/10.4 | 6.45 × /1.67 × |
| F4-100D | 410.7/27.7 | 389.8/6.80 | 3.32 × /7.27 × | 408.0/21.0 | 392.5/5.53 | 1.79 × /3.41 × |
| F5-100D | 404.9/14.4 | 395.6/5.12 | 6.01 × /5.75 × | 405.0/14.3 | 395.5/4.83 | 2.60 × /8.57 × |
| F6-100D | 403.0/7.07 | 397.6/1.70 | 1.83 × /6.99 × | 401.2/5.27 | 399.4/3.50 | 1.90 × /4.89 × |
| F7-100D | 411.3/24.2 | 389.1/1.97 | 8.76 × /1.21 × | 401.6/11.9 | 398.9/9.17 | 9.83 × /1.58 × |
| F8-100D | 406.0/23.3 | 394.7/11.9 | 9.10 × /2.51 × | 4.3.1/16.5 | 397.5/10.9 | 9.10 × /3.00 × |
| Algorithm | GPE (Mean/Std) | DE (Mean/Std) | PSO (Mean/Std) | |
|---|---|---|---|---|
| Fun | D | |||
| F1 | 50 | 7.48 × /1.48 × | 1.76 × /3.14 × (+) | 4.76 × /1.25 × (+) |
| F2 | 50 | 2.34 × /5.57 × | 5.10 × /6.67 × (−) | 1.12 × /9.58 × (+) |
| F3 | 50 | 1.66 × /2.45 × | 3.46 × /5.45 × (+) | 1.45 × /2.49 × (−) |
| F4 | 50 | 3.60 × /1.11 × | 5.40 × /2.16 × (+) | 2.07 × /1.38 × (+) |
| F5 | 50 | 5.21 × /6.46 × | 5.21 × /4.77 × (=) | 5.21 × /5.46 × (=) |
| F6 | 50 | 6.70 × /2.16 × | 6.80 × /1.73 × (+) | 6.69 × /3.10 × (−) |
| F7 | 50 | 9.97 × /8.04 × | 8.40 × /1.10 × (−) | 1.77 × /7.43 × (+) |
| F8 | 50 | 1.47 × /3.94 × | 1.37 × /3.19 × (−) | 1.49 × /3.89 × (+) |
| F9 | 50 | 1.58 × /3.45 × | 1.55 × /3.93 × (−) | 1.60 × /4.69 × (+) |
| F10 | 50 | 1.58 × /6.68 × | 1.62 × /5.12 × (+) | 1.68 × /9.14 × (+) |
| F11 | 50 | 1.62 × /4.91 × | 1.67 × /4.67 × (+) | 1.59 × /7.04 × (−) |
| F12 | 50 | 1.21 × /6.00 × | 1.21 × /5.97 × (=) | 1.21 × /7.64 × (=) |
| F13 | 50 | 1.31 × /1.54 × | 1.31 × /7.90 × (=) | 1.31 × /2.71 × (=) |
| F14 | 50 | 1.65 × /1.69 × | 1.57 × /3.33 × (−) | 1.66 × /2.38 × (+) |
| F15 | 50 | 8.71 × /2.76 × | 2.83 × /1.85 × (+) | 4.75 × /8.36 × (−) |
| F16 | 50 | 1.62 × /2.00 × | 1.62 × /1.81 × (=) | 1.62 × /2.15 × (=) |
| F17 | 50 | 1.86 × /6.01 × | 2.36 × /8.78 × (+) | 6.89 × /2.06 × (+) |
| F18 | 50 | 1.37 × /5.04 × | 3.31 × /8.10 × (+) | 1.71 × /8.30 × (+) |
| F19 | 50 | 2.35 × /5.35 × | 2.59 × /1.29 × (+) | 3.61 × /3.64 × (+) |
| F20 | 50 | 2.32 × /8.91 × | 2.43 × /1.47 × (+) | 2.37 × /1.25 × (+) |
| F21 | 50 | 4.79 × /1.68 × | 1.05 × /2.84 × (+) | 4.22 × /3.89 × (−) |
| F22 | 50 | 2.37 × /1.47 × | 6.13 × /6.57 × (−) | 4.16 × /2.41 × (+) |
| F23 | 50 | 2.53 × /2.78 × | 3.67 × /1.64 × (+) | 3.48 × /2.91 × (+) |
| F24 | 50 | 2.60 × /1.43 × | 3.00 × /2.95 × (+) | 2.73 × /7.86 × (+) |
| F25 | 50 | 2.70 × /8.92 × | 2.97 × /4.22 × (+) | 2.76 × /7.40 × (+) |
| F26 | 50 | 2.77 × /2.53 × | 2.93 × /1.18 × (+) | 2.81 × /1.71 × (+) |
| F27 | 50 | 5.06 × /5.65 × | 5.01 × /5.12 × (−) | 6.02 × /4.32 × (+) |
| F28 | 50 | 7.39 × /1.65 × | 1.12 × /1.27 × (+) | 2.00 × /1.34 × (+) |
| F29 | 50 | 4.05 × /3.43 × | 5.94 × /2.14 × (+) | 2.22 × /4.11 × (+) |
| F30 | 50 | 1.10 × /4.65 × | 6.50 × /2.20 × (+) | 5.65 × /1.63 × (+) |
| +/−/= | NaN/NaN/NaN | 18/8/4 | 21/5/4 |
| Algorithms | Best | Mean | Worst | Std |
|---|---|---|---|---|
| SACSO | 2.2440347 × | 2.5049590 × | 2.3863303 × | 8.7915776 × |
| SA-QUATRE | 2.3946554 × | 2.3946554 × | 2.3946554 × | 7.7292187 × |
| IKAEA | 2.3946554 × | 2.4840309 × | 2.4215750 × | 2.1957428 × |
| FSAPSO | 2.3946554 × | 2.3946555 × | 2.3946554 × | 2.0117613 × |
| SADE-AMSS | 2.3946554 × | 2.5626630 × | 2.4813014 × | 8.0224357 × |
| SAGPE | 2.3524529 × | 2.3524854 × | 2.3525687 × | 2.8563084 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Liu, H.; Zhou, Q.; Su, Q. A Surrogate-Assisted Gray Prediction Evolution Algorithm for High-Dimensional Expensive Optimization Problems. Mathematics 2025, 13, 1007. https://doi.org/10.3390/math13061007
Huang X, Liu H, Zhou Q, Su Q. A Surrogate-Assisted Gray Prediction Evolution Algorithm for High-Dimensional Expensive Optimization Problems. Mathematics. 2025; 13(6):1007. https://doi.org/10.3390/math13061007
Chicago/Turabian StyleHuang, Xiaoliang, Hongbing Liu, Quan Zhou, and Qinghua Su. 2025. "A Surrogate-Assisted Gray Prediction Evolution Algorithm for High-Dimensional Expensive Optimization Problems" Mathematics 13, no. 6: 1007. https://doi.org/10.3390/math13061007
APA StyleHuang, X., Liu, H., Zhou, Q., & Su, Q. (2025). A Surrogate-Assisted Gray Prediction Evolution Algorithm for High-Dimensional Expensive Optimization Problems. Mathematics, 13(6), 1007. https://doi.org/10.3390/math13061007





