Redundant Trees in Bipartite Graphs

Abstract

It has been conjectured that for each positive integer k and each tree T with bipartite $(Z_1,Z_2)$, every k-connected bipartite graph G with $\delta \left(G\right)\ge k+max\left\{\right|Z_1|,|Z_2\left|\right\}$ admits a subgraph $T^{\prime }\cong T$ such that $G-V\left(T^{\prime }\right)$ is still k-connected. In this paper, we generalize the ear decompositions of 2-connected graphs into a $(k,a_k)$-extensible system for a general k-connected graph. As a result, we confirm the conjecture for $k\le 3$ by proving a slightly stronger version of it.

1. Introduction

In this paper, we only consider finite, undirected, and simple graphs (no loops and parallel edges). For a graph G, $V\left(G\right)$ and $E\left(G\right)$ are its vertex set and edge set, respectively. The order of a graph G is the number of its vertices. For a vertex $u\in V\left(G\right)$, the degree $d_G\left(u\right)$ is the number of edges incident with u. For a vertex set U, write ${\delta }_G\left(U\right)=min\{d_G\left(u\right)\mid u\in U\}$, $G\left[U\right]$ is the subgraph induced by U, $G-U=G\left[V\right(G)\setminus U]$ and $G-u=G-\left\{u\right\}$. The neighborhood $N_G\left(U\right)=\{v\notin U\mid uv\in E\left(G\right)$ for some $u\in U\}$. The minimum degree $\delta \left(G\right)={\delta }_G\left(V\left(G\right)\right)$. For two vertices $u,v$ of G, a path connecting u and v is called a $(u,v)$-path. The inner vertices of P is the vertices in $V\left(P\right)\setminus \{u,v\}$. For two vertices $x,y\in V\left(P\right)$, $P[x,y]$ is the $(x,y)$-path contained in P. A set of $(u,v)$-paths $\{P_1,\dots ,P_t\}$ is internally disjoint if $V\left(P_i\right)\cap V\left(P_j\right)\subseteq \{u,v\}$ for any $1\le i<j\le t$. A graph G is k-connected if there are k internally disjoint $(u,v)$-paths for every pair of distinct vertices $u,v$ in G. Chartrand, Kaugars, and Lick [1] gave the following well-known result.

Theorem 1 

(Chartrand, Kaugars, Lick [1]). Every k-connected graph G of minimum degree $\delta \left(G\right)\ge \lfloor {\displaystyle \frac{3k}{2}}\rfloor$ has a vertex x with $\kappa (G-x)\ge k$.

For a k-connected graph G, its subgraph H is called a k-redundant subgraph if $G-V\left(H\right)$ is still k-connected. Furthermore, if H is a tree, then H is called a k-redundant tree. Theorem 1 suggests the existence of a trivial redundant tree. Fujita and Kawarabayashi [2] conjectured that there exists a function $f_k\left(m\right)$ such that every k-connected graph G with $\delta \left(G\right)\ge \lfloor {\displaystyle \frac{3k}{2}}\rfloor +f_k\left(m\right)$ contains a connected k-redundant subgraph of order m. In the same paper, they proved that $f_k\left(2\right)\le 2$, and they also gave examples to show that $f_k\left(m\right)\ge m-1$. Later, Mader [3] confirmed the conjecture and proved that the k-redundant subgraph is, in fact, a path. Based on this result, Mader made the following conjecture.

Conjecture 1 

(Mader [3]). For any tree T of order m, every k-connected graph G with  $\delta \left(G\right)\ge \lfloor {\displaystyle \frac{3k}{2}}\rfloor +m-1$ admits a k-redundant tree isomorphic to T.

Conjecture 1 has been studied by many researchers, but it has not been proven yet. Diwan and Tholiya [4] confirmed the conjecture for the case $k=1$. When $k=2$, many researchers studied special trees [5,6,7,8,9,10]. In [11], we developed a general way to deal with all trees and confirmed the conjecture for arbitrary trees when $k\le 3$. For the general connectivity case, Mader [12] showed the minimum degree condition $\delta \left(G\right)\ge 2{(k+m-1)}^2+m-1$ yields a k-redundant tree isomorphic to each prescribed tree T of order m. Very recently, the lower bound of the minimum degree has been decreased to $3k+4m-6$ in [13].

In [8], Luo, Tian, and Wu generalized the conjecture into a bipartite graph version. For a bipartite graph G, the bipartition is a partition $(U_1,U_2)$ of $V\left(G\right)$ such that $E\left(G\left[U_i\right]\right)=\varnothing$ for $i=1,2$.

Conjecture 2 

(Luo, Tian, Wu [8]). For any tree T with bipartition $(X,Y)$, every k-connected bipartite graph G with $\delta \left(G\right)\ge k+max\left\{\right|X|,|Y\left|\right\}$ admits a k-redundant tree isomorphic to T.

In the same paper, Luo, Tian, and Wu proved Conjecture 2 for paths and stars. Later, Yang and Tian [14] further confirmed the conjecture of caterpillars and spiders in the case $k\le 3$. Very recently, Yang and Tian [15] proved the conjecture for all trees when $k\le 3$ under an additional assumption that the girth of G is not less than the diameter minus 1, where the girth is the minimum length of cycles of a graph and the diameter is the maximum distance between two vertices of a graph. In this paper, we remove the additional assumption and prove the same result. In order to distinguish the two parts of a bipartite graph, we define an embedding $\varphi :T\to G$ of a tree T to G as an injective mapping from $V\left(T\right)$ to $V\left(G\right)$ such that $\varphi \left(u\right)\varphi \left(v\right)\in E\left(G\right)$ as long as $uv\in E\left(T\right)$. For simplicity, we may use $\varphi \left(T\right)$ to denote either the subgraph induced by $\left\{\varphi \right(u\left)\varphi \right(v)\mid uv\in E(T\left)\right\}$ or its vertex set. For a vertex set $U\subseteq V\left(T\right)$ or a subgraph $F\subseteq T$, the image $\varphi \left(U\right)=\left\{\varphi \right(u)\mid u\in U\}$ or $\varphi \left(F\right)=\varphi \left(V\right(F\left)\right)$. In this paper, we generalize the embedding method of [11] into bipartite graphs and prove the following theorem, which confirms the above conjecture for all trees when $k\le 3$.

Theorem 2. 

Let $k\le 3$ be an integer and T be a tree with bipartition $(Z_1,Z_2)$. If G is a k-connected bipartite graph with bipartition $(U_1,U_2)$ such that, for $i=1,2$, ${\delta }_G\left(U_i\right)\ge \left|Z_{3-i}\right|+k$, then there exists an embedding $\varphi :T\to G$ such that $G-\varphi \left(T\right)$ is still k-connected and $\varphi \left(Z_i\right)\subseteq U_i$ for $i=1,2$.

We end this section with some notation used in this paper. For a vertex set U and a vertex $u\notin U$, a $(u,U)$-path P is a $(u,v)$-path with $V\left(P\right)\cap U=\left\{v\right\}$ for some $v\in U$. A family of $(u,U)$-paths $P_1,\dots ,P_k$ are internally disjoint if $V(P_i-u)\cap V(P_j-u)=\varnothing$ for any $i\ne j$. An r-rooted tree is a tree with a special vertex r which is called the root. A leaf of a rooted tree T is a vertex with degree 1 other than the root. The set of leaves of a rooted tree T is denoted by $L\left(T\right)$. An R-rooted forest is the disjoint union of rooted trees, where R is the set of set of roots of all its rooted trees. Write $L\left(F\right)$ be the union of leaves of each of its rooted trees. Let $G,H$ be two graphs. If there exists a bijection from $V\left(H\right)$ to $V\left(G\right)$ such that $uv\in E\left(H\right)$ if and only if $\varphi \left(u\right)\varphi \left(v\right)\in E\left(G\right)$, then we see that H is isomorphic to G, denoted by $H\cong G$. An independent set of a graph G is a vertex set U of G such that $E\left(G\right[U\left]\right)=\varnothing$. In the next section, we shall generalize the embedding lemma of [11] to bipartite graphs, and in the last section, we shall apply the embedding lemma to confirm Conjecture 2 for $k\le 3$.

2. Embedding Lemmas

In [6,11], different sufficient degree conditions for the existence of any trees are obtained. In this section, these sufficient conditions will be generalized into bipartite versions and are stated as follows.

Lemma 1. 

Let T be a tree with bipartition $(Z_1,Z_2)$, $X_1\subseteq L\left(T\right),X_2\subseteq L(T-X_1)$ and $X_3\subseteq V(T-X_1\cup X_2)$ such that $T-X$ is connected, where $X=X_1\cup X_2\cup X_3$. Let G be a bipartite graph with bipartition $(U_1,U_2)$ and ${\varphi }_0:T-X\to G$ be an embedding of $T-X$ such that ${\varphi }_0(Z_i\setminus X)\subseteq U_i$ for $i=1,2$. Denote $X_4=\{x\in V(T-X)\mid N_T\left(x\right)\cap X\ne \varnothing \}$ and $V_4={\varphi }_0\left(X_4\right)$. Suppose $V\left(G\right)\setminus {\varphi }_0(T-X)$ has a partition $(V_1,V_2,V_3)$ such that each of the following holds.

(i) 

for $i=1,2$ and $u\in U_i\cap (V_2\cup V_3\cup V_4)$, $d_G\left(u\right)\ge \left|Z_{3-i}\right|$;

(ii) 

for $i=1,2$ and $u\in U_i\cap (V_3\cup V_4)$, $|N_G\left(u\right)\cap (V_1\cup V_2)|\le |(X_1\cup X_2)\cap Z_{3-i}|$.

Then, there exists an embedding $\varphi :T\to G$ such that $\varphi \left(Z_i\right)\subseteq U_i$ for $i=1,2$, $\varphi \left(X_3\right)\subseteq V_3$ and $\varphi \left(x\right)={\varphi }_0\left(x\right)$ for any $x\in V(T-X)$.

Proof. 

We shall prove a stronger result by replacing (ii) with the following (ii′):

(ii′)

for $i=1,2$ and $u\in U_i\cap (V_3\cup V_4)$, $|N_G\left(u\right)\setminus (V_1\cup V_2)|\ge |Z_{3-i}\setminus (X_1\cup X_2)|$;

The proof is by induction on $\left|X\right|$. If $X=\varnothing$, then $\varphi ={\varphi }_0$ is desired. Thus, we may assume that $X\ne \varnothing$. Let $z_1{z}_2\in E\left(T\right)$ such that $z_1\in X_{i_1}$ for some $1\le i_1\le 3$ and $i_1$ be as small as possible, and subject to this, $d_T\left(z_1\right)$ is as small as possible. Then, $z_1\in L\left(T\right)$. Assume that $z_2\in X_{i_2}$ for some $i_2$. Note that both $X_1$ and $X_2$ are independent sets in T. We see either $i_2>i_1$ or $i_1=i_2=3$. Without loss of generality, we may assume that $z_1\in Z_1\cap X_{i_1}$, and then $z_2\in Z_2\cap X_{i_2}$.

For $i=1,2,3$, let $X_i^{\prime }=X_i\setminus \left\{z_1\right\}$ and let $T^{\prime }=T-z_1$, $X^{\prime }=X\setminus \left\{z_1\right\}$, $Z_1^{\prime }=Z_1\setminus \left\{z_1\right\}$ and $Z_2^{\prime }=Z_2$. Then $|Z_i^{\prime }\setminus (X_1^{\prime }\cup X_2^{\prime })|\le |Z_i\setminus (X_1\cup X_2)|$ for $i=1,2$. Also, let $X_4^{\prime }=N_{T^{\prime }}\left(X^{\prime }\right)$, and then, either $X_4^{\prime }=X_4$ or $X_4^{\prime }=X_4\setminus \left\{z_2\right\}$. Thus, $(X_1^{\prime },X_2^{\prime },X_3^{\prime })$ is a partition of $T^{\prime }-X^{\prime }=T-X$ satisfying (i) and (ii′). By the induction hypothesis, there exists a mapping ${\varphi }_1:T-z_1\to G$ such that ${\varphi }_1\left(Z_i^{\prime }\right)\subseteq U_i$ for $i=1,2$, ${\varphi }_1\left(X_3^{\prime }\right)\subseteq V_3$ and ${\varphi }_1\left(x\right)={\varphi }_0\left(x\right)$ for any $x\in V(T-X)$.

By the choice of $z_1{z}_2$, we see that $X_i=\varnothing$ for each $i<i_1$. Note that $\varphi \left(z_2\right)\in \varphi \left(X_{i_2}^{\prime }\right)\subseteq V_{i_2}\cup \dots \cup V_4$ and $i_2\ge i_1+1\ge 2$. By (i) or (ii′), we see that, if $i_1\le 2$, then by (i), there exists $v\in N_G\left(\varphi \left(z_2\right)\right)\setminus {\varphi }_1(T-z_1)$; and if $i_1\ge 3$ then $i_2\ge 3$ and by (i) and (ii′), $|N_G\left(\varphi \left(z_2\right)\right)\setminus (V_1\cup \dots \cup V_{i_1-1})|\ge |Z_1\setminus (X_1\cup \dots \cup X_{i_1-1})|=|Z_1|>|Z_1^{\prime }|=|{\varphi }_1(T-z_1)\cap U_1|$. This implies that there exists $v\in N_G\left(\varphi \left(z_2\right)\right)\setminus (V_1\cup \dots \cup V_{i_1-1}\cup {\varphi }_1(T-z_1))\subseteq V_{i_1}\cup \dots \cup V_3$. Define $\varphi :T\to G$ by letting $\varphi \left(z_1\right)=v$ and $\varphi \left(x\right)={\varphi }_1\left(x\right)$ for any $x\in V(T-z_1)$. Then, $\varphi$ is desired. Noting that (ii′) is deduced from (i) and (ii), the result is proved. □

If we let $X_1=X_2=\varnothing$, $X_3=V\left(T\right)$ and $V_1=V_2=\varnothing$, $V_3=V\left(G\right)$, then $X_4=\varnothing$ and the conditions in the above corollary are equivalent to those for $i=1,2$, $u\in U_i$, $d_G\left(u\right)\ge \left|Z_{3-i}\right|$. Thus, we have the following corollary.

Corollary 1. 

Let T be a tree with bipartition $(Z_1,Z_2)$ and G be a bipartite graph with bipartition $(U_1,U_2)$. If, for $i=1,2$, ${\delta }_G\left(U_i\right)\ge \left|Z_{3-i}\right|$, then there exists an embedding $\varphi :T\to G$ such that $\varphi \left(Z_i\right)\subseteq U_i$ for $i=1,2$.

For a forest F and $F_0\subseteq F$, every component C of $F-V\left(F_0\right)$ is a rooted tree with root with the only vertex in $N_F\left(V\left(F_0\right)\right)\cap V\left(C\right)$. In this paper, we need the following lemma, which is used to verify the conditions in Lemma 1.

Lemma 2. 

Let F be a $R_0$-rooted forest with bipartite $(Z_1,Z_2)$, $F_0\subseteq F$ be a $R_0$-rooted forest, and $R=N_F\left(F_0\right)$. If $X_0=L\left(F_0\right)$, $X_1=L\left(F\right)$ and $X_2=L(F-X_1)$, then for $i=1,2$, $|(X_1\cup X_2)\cap Z_i|\ge |(X_0\cup R)\cap Z_i|$.

Proof. 

Assume $\left|R\right|=p$ and $T_1,\dots ,T_p$ are the components of $F-V\left(F_0\right)$. For $i=1,\dots ,p$, let $s_i{r}_i\in E\left(F\right)$ such that $s_i\in V\left(F_0\right)$ and $r_i\in V\left(T_i\right)$. For $i=1,\dots ,p$, let $t_i=\left|V\left(T_i\right)\right|$ and it is easy to see that $V\left(T_i\right)\cap (X_1\cup X_2)\cap Z_j\ne \varnothing$ for $j=1,2$ if $t_i\ge 2$.

For $j=1,2$, we shall define a mapping ${\varphi }_j$ from $(X_0\cup R)\cap Z_j$ to $(X_1\cup X_2)\cap Z_j$ as follows: if $z\in (X_0\setminus \{s_1,\dots ,s_p\})\cap Z_j$, then let ${\varphi }_j\left(z\right)=z$; if $z\in \{s_1,\dots ,s_p,r_1,\dots ,r_p\}\cap Z_j$ and ${\varphi }_j\left(z\right)$ is not defined, then $z\in \{s_i,r_i\}$ for some i and let ${\varphi }_j\left(z\right)=z$ if $t_i=1$ and let ${\varphi }_i\left(z\right)$ be one vertex in $V\left(T_i\right)\cap (X_1\cup X_2)\cap Z_i$ if $t_i\ge 2$. We shall show that $\varphi$ is injective. In fact, assume that there exists $z_1,z_2\in (X_0\cup R)\cap Z_j$ such that $z_1\ne z_2$ and ${\varphi }_j\left(z_1\right)={\varphi }_j\left(z_2\right)$. Then, ${\varphi }_j\left(z_1\right)\notin X_0\setminus \{s_1,\dots ,s_p\}$ by the definition, and thus $z_1,z_2\in \{s_1,\dots ,s_p,r_1,\dots ,r_p\}\cap Z_j$. Note that $|\{s_i,r_i\}\cap Z_j|=1$ for $i=1,\dots ,p$ and $j=1,2$, since F is bipartite. Without loss of generality, we may assume that $z_i\in \{s_i,r_i\}$ for $i=1,2$. Then, for $i=1,2$, either ${\varphi }_j\left(z_i\right)\in V\left(T_i\right)$ or ${\varphi }_j\left(z_i\right)=z_i=s_i$. This implies ${\varphi }_j\left(z_1\right)\ne {\varphi }_j\left(z_2\right)$, since $V\left(T_1\right)\cap V\left(T_2\right)=\varnothing$ and $s_1,s_2\notin V(T_1\cup T_2)$, a contradiction. Thus, ${\varphi }_j$ is injective, and the result follows. □

The following lemma is crucial to our main result. The method of our proof is more straightforward than that in [11] and can also be applied to the embedding lemma in [11].

Lemma 3. 

Let $T_0$ be a tree with bipartition $(Z_1,Z_2)$ and G be a bipartite graph with bipartition $(U_1,U_2)$ such that for $i=1,2$, ${\delta }_G\left(U_i\right)\ge {\delta }_i\ge \left|Z_{3-i}\right|+1$. Suppose that ${\varphi }_0:T_0\to G$ is a mapping of $T_0$ on G such that ${\varphi }_0\left(Z_i\right)\subseteq U_i$ for $i=1,2$. Let $T={\varphi }_0\left(T_0\right)$, $B\subseteq G-V\left(T\right)$ and $H=G-(V\left(B\right)\cup {\varphi }_0\left(T_0\right))$. Then, one of the following holds:

(a) 

$N_G\left(H\right)\cap V\left(T\right)=\varnothing$;

(b) 

For $i=1,2$ and $v\in V(H\cup T)\cap U_i$, $|N_G\left(v\right)\cap V\left(B\right)|\le {\delta }_i-\left|Z_{3-i}\right|-1$;

(c) 

There exist $i\in \{1,2\}$ and $v\in V(H\cup T)\cap U_i$ such that $|N_G\left(v\right)\cap V\left(B\right)|\ge {\delta }_i-\left|Z_{3-i}\right|$ and $H\cup T-v$ admits a tree $T^{\prime }\cong T$.

Proof. 

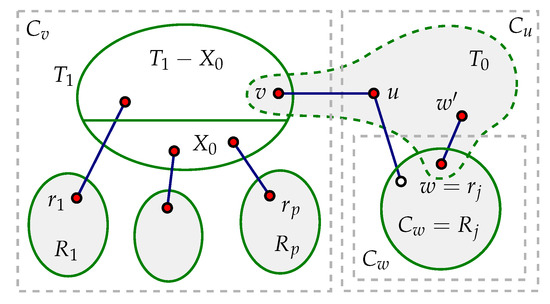
Suppose, to the contrary, that neither (a), (b), nor (c) hold. For $i=1,2$, denote

$$I_i=\{v\in V(T\cup H)\cap U_i\mid |N_G\left(v\right)\cap V\left(B\right)|\ge {\delta }_i-|Z_{3-i}\left|\right\},$$

and $I=I_1\cup I_2$, $J=N_G\left(T\right)\cap V\left(H\right)$. By the assumption that both (a) and (b) fail, we have $I,J\ne \varnothing$. Then, we derive the following claim.

Claim 1. $I\cup J=V\left(T\right)$.

Firstly, we see that $I\subseteq V\left(T\right)$, for otherwise, any vertex in $V\left(H\right)\cap J$ satisfies (c), a contradiction. Suppose that the claim is wrong. Then, there exists a vertex $z\in V\left(T\right)\setminus (I\cup J)$. Without loss of generality, we may assume that $z\in U_1$. Then, by the definitions of $I,J$, we have both $|N_G\left(z\right)\cap V\left(B\right)|\le {\delta }_1-\left|Z_2\right|-1$ and $N_G\left(z\right)\cap V\left(H\right)=\varnothing$. Thus, $d_G\left(z\right)=|N_G\left(z\right)\cap V\left(B\right)|+|N_G\left(z\right)\cap V\left(T\right)|\le ({\delta }_1-|Z_2|-1)+|Z_2|={\delta }_1-1$, a contradiction that proves Claim 1.

For an edge $uv\in E\left(T\right)$, denote by $C_u,C_v$ the two components of $T-uv$ containing $u,v$, respectively. Pick an edge $uv\in E\left(T\right)$ such that $v\in I$ and [$u\in J$ or $u\in N_G\left(V(C_w-w)\right)$ for some $w^{\prime }w\in E\left(T\right)$ with $V(C_w-w)\cap I=\varnothing$], and subject to this, $\left|V\right(C_v\left)\right|$ is as small as possible (see Figure 1). By Claim 1, the edge $uv$ exists, since an edge with $u\in J$ and $v\in I$ exists. Note that $C_w\subseteq C_v$ is allowed. For simplicity, if $u\in J$, then we define $w\in L\left(C_u\right)\setminus \left\{u\right\}$, $w^{\prime }$ is the neighbor of w in $C_u$, and thus $V\left(C_w\right)=\left\{w\right\}$.

Figure 1. Illustration of $T_0,T_1,R_1,\dots ,R_p$.

Let $T_0=T-(V(C_v-v)\cup V(C_w-w))$ and $T_1=T[V\left(C_v\right)\setminus J]$. Then, $V\left(T_1\right)\subseteq I$ by Claim 1. By the choice of $uv$, for any $z\in V\left(T_1\right)$, all the inner vertices on the only $(v,z)$-path in T lie in I and are contained in $V\left(T_1\right)$. This implies that $T_1$ is a subtree of $C_v$. Define two rooted forests F and $F_0$ as follows: if $C_w\subseteq C_v$, then let $F=C_w$ and $F_0=T_1$, and if otherwise, let $F=C_v\cup C_w$ and $F_0=T_1\cup \left\{w\right\}$. Then, F is a rooted forest with root $\left\{v\right\}$ or $\{v,w\}$ and $F_0\subseteq F$. Let $X_0=L\left(F_0\right)=L\left(T_1\right)$, $R_1,\dots ,R_p$ be the components of $F-V\left(F_0\right)$, and for $i=1,\dots ,p$, let $r_i\in V\left(R_i\right)\cap N_T(T_0\cup T_1)$ (see Figure 1). Then, $C_w=R_j$ for some j when $V\left(C_w\right)\cap V\left(C_v\right)=\varnothing$. By the choice of $uv$, we have for $i=1,\dots ,p$,

$$N_G(V\left(H\right)\cup V(R_i-r_i))\cap V(T_1-X_0))=\varnothing ,$$

(1)

for otherwise, for some k, there exists $u_1\in V(T_1-X_0)\cap N_G\left(V(H\cup R_k-r_k)\right)$ such that the only path between $u_1$ and v is as long as possible. By the definition of $X_0$, there exists $v_1\in N_{T_1}\left(u_1\right)$ with a larger distance to v than $u_1$’s in T. Thus, $u_1{v}_1$ is a candidate of $uv$, where $v_1\in I$, either $u_1\in J$ or $u_1=N_G\left(V(C_w-w)\right)$ with $C_w=R_k$ and $w=r_k$, and $|V\left(C_{v_1}\right)|<|V\left(C_v\right)|$, a contradiction.

Define $X_1=L\left(F\right)$, $X_2=L(F-X_1)$, $X_3=V\left(F\right)\setminus (V\left(F_0\right)\cup X_1\cup X_2)$ and $X_4=N_T(X_1\cup X_2\cup X_3)$. Then, $(X_1,X_2,X_3)$ is a partition of $V\left(F\right)\setminus V\left(F_0\right)$ and either $X_4=\left\{v\right\}$ (in this case, $V\left(C_w\right)=\left\{w\right\}$) or $X_4=\{v,w\}$ (in this case, $V\left(C_w\right)\ne \left\{w\right\}$ and $u\in N_G(C_w-w)\setminus N_G\left(H\right)$). Applying Lemma 2 with F and $F_0$, we have $|(X_0\cup \{r_1,...,r_p\})\cap Z_i|\le |(X_1\cup X_2)\cap Z_i|$ for $i=1,2$.

By the choice of $uv$, there exists an $h\in N_G\left(u\right)\cap (V\left(H\right)\cup V(C_w-w))$. Let $G^{\prime }=G-V(B\cup \left\{v\right\})$ and define a mapping ${\varphi }_1:T_0\cup T_1\to G^{\prime }$ by letting ${\varphi }_1\left(v\right)=h$ and ${\varphi }_1\left(z\right)=z$ for any $z\in V(T_0\cup T_1-v)$. Let $V_1=V\left(T_1\right)$, $V_2=N_T(T_0\cup T_1-w)=\{r_1,\dots ,r_p\}$, $V_3=V(T\cup H)\setminus ({\varphi }_1\left(T_0\right)\cup V_1\cup V_2)$ and $V_4={\varphi }_0\left(X_4\right)$. Then, $(V_1,V_2,V_3)$ is a partition of $V(T\cup H)\setminus V\left(T_0\right)$, $V_4=\left\{h\right\}$ or $\{h,w\}$ and $(V_2\cup V_3\cup V_4)\cap I=\varnothing$ by (1). Thus, for any $u\in V_2\cup V_3\cup V_4$, assuming $u\in U_i$, $d_{G^{\prime }}\left(u\right)\ge d_G\left(z\right)-1-|N_G\left(z\right)\cap V\left(B\right)|\ge {\delta }_i-1-({\delta }_i-|Z_{3-i}|-1)=|Z_{3-i}|$. Also, by (1), for any $u\in V_3\cup V_4$, $|N_G\left(u\right)\cap (V_1\cup V_2)|\le |N_G\left(u\right)\cap (X_0\cup \{r_1,...,r_p\})|\le |(X_0\cup \{r_1,...,r_p\})\cap Z_{3-i}|\le |(X_1\cup X_2)\cap Z_{3-i}|$. By Lemma 1, a mapping $\varphi :T\to G^{\prime }$ exists, which implies that v is a vertex satisfying (iii), a contradiction. The proof is complete. □

3. k-Extensible System

It is well known that a graph is 2-connected if and only if it contains an ear decomposition, which is useful for extending a 2-connected graph into a larger one. However, this does not work for k-connected graphs when $k\ge 3$. In this section, we define a system that is used to extend a k-connected graph.

For a positive integer k, let ${\mathcal{G}}_k$ be a family of graphs and ${\psi }_k:{\mathcal{G}}_k\to \mathbb{F}$ be a function that assigns a weight in a totally ordered set $\mathbb{F}$ to each graph in the family. Let $V_k\left(G\right)=\{v\in V\left(G\right)\mid d_G\left(v\right)\ge k\}$ and $a_k$ be an integer. We say that $({\mathcal{G}}_k,{\psi }_k)$ is $(k,a_k)$-extensible (bipartite) system if each of the following holds:

(D1)

For any k-connected (bipartite) graph G, $G\in {\mathcal{G}}_k$;

(D2)

For any $G\in {\mathcal{G}}_k$ and $u,v\in V_k\left(G\right)$, there are at least k internally disjoint $(u,v)$-paths in G;

(D3)

For any $G\in {\mathcal{G}}_k$, construct a (bipartite) graph $G_0$ obtained from G by adding a vertex v and connecting v to at least $a_k$ vertices of G. Then, $G_0$ contains a subgraph $G^{\prime }\in {\mathcal{G}}_k$ such that $V_k\left(G\right)\subseteq V_k\left(G^{\prime }\right)$ and ${\psi }_k\left(G^{\prime }\right)>{\psi }_k\left(G\right)$;

(D4)

For any $G\in {\mathcal{G}}_k$, if there exists a (bipartite) graph $G_0\supseteq G$, a vertex $v\in V\left(G_0\right)\setminus V_k\left(G\right)$ and k internally disjoint $(v,V_k\left(G\right))$-paths $P_1,\dots ,P_k$ in $G_0$ such that $G_0\left[V\left(G\right)\right]=G$ and $|{\bigcup }_{i=1}^{k}V\left(P_i\right)\setminus V\left(G\right)|$ is as small as possible, then $G_0[V\left(G\right)\cup {\bigcup }_{i=1}^{k}V\left(P_i\right)]$ contains a subgraph $G^{\prime }\in {\mathcal{G}}_k$ such that $V_k\left(G\right)\subseteq V_k\left(G^{\prime }\right)$, ${\psi }_k\left(G^{\prime }\right)>{\psi }_k\left(G\right)$ and, furthermore, if $|N_{G_0}\left(u\right)\cap V\left(G\right)|\le a_k-1$ for any $u\in V\left(G_0\right)\setminus V\left(G\right)$, then $|N_{G_0}\left(u\right)\cap V\left(G^{\prime }\right)|\le a_k$ for any $u\notin V\left(G_0\right)\setminus V\left(G^{\prime }\right)$.

(D1) and (D2) ensure that all k-connected (bipartite) graphs belong to ${\mathcal{G}}_k$ and (D3)(D4) give two methods to “enlarge” a graph of ${\mathcal{G}}_k$. From the definition, we see that a $(k,a_k)$-extensible system is a generalization of k-connected graphs. When $k=2$, according to the well-known ear decompositions, it is easy to verify that $({\mathcal{G}}_2,{\psi }_k)$ is (2,2)-extensible system if ${\mathcal{G}}_2$ is the family of all 2-connected graphs and ${\psi }_k\left(G\right)=\left|V\left(G\right)\right|$ for $G\in {\mathcal{G}}_2$. Hence, a $(k,a_k)$-extensible system is also a generalization of ear decompositions. In addition, we have the following conjecture.

Conjecture 3. 

For any positive integer k, there exists a minimum integer $a_k$ and a $(k,a_k)$-extensible bipartite system $({\mathcal{G}}_k,{\psi }_k)$ such that every bipartite graph G with $\delta \left(G\right)\ge a_k$ contains a subgraph $B\in {\mathcal{G}}_k$.

From the definition, a $(k,a_k)$-extensible system is also a $(k,a_k)$-extensible bipartite system. However, the value of $a_k$ might be different. If Conjecture 3 is true then we can prove Conjecture 2.

Theorem 3. 

If Conjecture 3 is true for some $a_k$, then for any tree $T_0$ with bipartition $(Z_1,Z_2)$, every bipartite graph G with bipartition $(U_1,U_2)$ such that ${\delta }_G\left(U_i\right)\ge \left|Z_{3-i}\right|+a_k$ for $i=1,2$ contains a k-redundant tree isomorphic to $T_0$.

Proof. 

By Corollary 1, there exists an embedding $\varphi$: $T_0\to G$ such that $\varphi \left(Z_i\right)\subseteq U_i$ for $i=1,2$. Let $T=\varphi \left(T_0\right)$. By the assumption that Conjecture 3 is true, there exists a $(k,k)$-extensible system $({\mathcal{G}}_k,{\psi }_k)$, and let $B\in {\mathcal{G}}_k$ be an induced subgraph of $G-V\left(T\right)$. Without loss of generality, we can assume that $\varphi$ and B are chosen so that ${\psi }_k\left(B\right)$ is as large as possible.

Let $H=G-V(T\cup B)$. If $V\left(H\right)=\varnothing$, then $G-V\left(T\right)=B$ and for any $v\in V\left(B\right)$, assuming $v\in U_i$, $d_B\left(v\right)\ge d_G\left(v\right)-|N_G\left(v\right)\cap V\left(T\right)|\ge (|Z_{3-i}|+k)-|Z_{3-i}|=k$. By the definition (D2) of $(k,a_k)$-extensible systems, we see that B is k-connected, and we are done. Hence, we may assume that $V\left(H\right)\ne \varnothing$.

Claim 1. For any $u\in V(H\cup T)$, if there exist a vertex u and an embedding ${\varphi }^{\prime }:T_0\to G\left[V(T\cup H-u)\right]$ such that ${\varphi }^{\prime }\left(Z_i\right)\subseteq U_i$ for $i=1,2$, then $|N_G\left(u\right)\cap V\left(B\right)|\le a_k-1$.

To the contrary, suppose that u and ${\varphi }^{\prime }$ are stated as in the claim, but $|N_G\left(u\right)\cap V\left(B\right)|\ge a_k$. By the assumption (3) of $(k,a_k)$-extensible systems, $G\left[V\right(B)\cup \{u\left\}\right]$ contains an induced subgraph $B^{\prime }\in {\mathcal{G}}_k$ such that ${\psi }_k\left(B^{\prime }\right)>{\psi }_k\left(B\right)$ and $B^{\prime }\subseteq G-{\varphi }^{\prime }\left(T_0\right)$, a contradiction to the choice of $\varphi$ and B. The claim is proved.

Claim 2. $N_G\left(H\right)\cap V\left(T\right)\ne \varnothing$.

Suppose, to the contrary, that $N_G\left(H\right)\cap V\left(T\right)=\varnothing$. By Claim 1, we have ${\delta }_H(V\left(H\right)\cap U_i)\ge \left(\right|Z_{3-i}|+a_k)-(a_k-1)=\left|Z_{3-i}\right|+1$. By Lemma 1, H contains a tree isomorphic to $T_0$ and every vertex $u\in V\left(T\right)$ satisfies the condition of Claim 1. Thus, we also have $|N_G\left(u\right)\cap V\left(B\right)|\le a_k-1$ for any $u\in V\left(T\right)$. Assume $u\in U_i$. Then, $d_G\left(u\right)=|N_G\left(u\right)\cap V\left(B\right)|+|N_G\left(u\right)\cap V\left(T\right)|\le a_k-1+\left|Z_{3-i}\right|$, a contradiction to the assumption on ${\delta }_G\left(U_i\right)$. The claim is proved.

Noting that G is k-connected, then there exist a vertex $u\in V\left(G\right)\setminus V_k\left(B\right)$ and k internally disjoint $(u,V_k\left(B\right))$-paths $P_1,\dots ,P_k$ such that $|{\bigcup }_{i=1}^{k}V\left(P_i\right)\setminus V\left(B\right)|$ is as small as possible. By Claim 1 and Claim 2, applying Lemma 3, we see that $|N_G\left(v\right)\cap V\left(B\right)|\le a_k-1$ for any $v\in V(H\cup T)$. Then, according to the definition (D4) of $(k,a_k)$-extensible systems, G contains a subgraph $B^{\prime }\in {\mathcal{G}}_k$ such that ${\psi }_k\left(B^{\prime }\right)>{\psi }_k\left(B\right)$ and $|N_G\left(v\right)\cap V\left(B^{\prime }\right)|\le a_k$. It follows that ${\delta }_{G-V\left(B^{\prime }\right)}(U_i\setminus V\left(B^{\prime }\right))\ge \left(\right|Z_{3-i}|+a_k)-a_k=\left|Z_{3-i}\right|$ for $i=1,2$. By Corollary 1, $G-V\left(B^{\prime }\right)$ contains a subgraph $T^{\prime }\cong T_0$ and thus, $B^{\prime }\in {\mathcal{G}}_k$ is a subgraph of $G-V\left(T^{\prime }\right)$ with ${\psi }_k\left(B^{\prime }\right)>{\psi }_k\left(B\right)$, a contradiction. The proof is complete. □

In view of the above theorem, we believe that the value of $a_k$ in Conjecture 3 should be k. In the next section, we shall confirm the existence of k-redundant trees for $k\le 3$ by using Theorem 3.

4. Redundant Trees

In this section, we confirm Conjecture 2 for $k=2$ and 3 by showing that Conjecture 3 is true for $a_k=k$ when $k\le 3$. For the edge version and the non-bipartite version, see [16] and [11], respectively.

Theorem 4. 

Let ${\mathcal{G}}_2$ be the family of 2-connected bipartite graphs and ${\psi }_2\left(G\right)=\left|V\left(G\right)\right|$ for any $G\in {\mathcal{G}}_2$. Then, $({\mathcal{G}}_2,{\psi }_2)$ is a $(2,2)$-extensible bipartite system such that every graph G with $\delta \left(G\right)\ge 2$ contains a subgraph $B\in {\mathcal{G}}_2$.

Proof. 

First, it is easy to see that every graph with a minimum degree of at least 2 contains a cycle, which belongs to ${\mathcal{G}}_2$. Hence, it suffices to verify (D1)–(D4) in the definition of $(2,2)$-extensible systems. In fact, (D1), (D2), and (D3) can be easily verified from the definition of 2-connected graphs. For (D4), if there exist a graph $G_0\supseteq G$ and two $(u,V_2\left(G\right))$-paths $P_1,P_2$ such that $|V(P_1\cup P_2)\setminus V\left(G\right)|$ is as small as possible, then $G^{\prime }=G\cup P_1\cup P_2\in {\mathcal{G}}_2$ is 2-connected and ${\psi }_2\left(G^{\prime }\right)>{\psi }_2\left(G\right)$. Furthermore, if $|N_{G_0}\left(v\right)\cap V\left(G\right)|\le 1$ for any $v\in V\left(G_0\right)\setminus V\left(G\right)$, and there exists $w\in V\left(G_0\right)\setminus V\left(G^{\prime }\right)$ such that $|N_{G_0}\left(w\right)\cap V\left(G^{\prime }\right)|\ge 3$, then $|N_{G_0}\left(w\right)\cap (V\left(G^{\prime }\right)\setminus V\left(G\right))|\ge 2$. Assume $P_i$ is a $(v_i,u)$-path for some $v_i\in V\left(G\right)$. Then, $P=v_{1}P1uP2v_2$ is a $(v_1,v_2)$-path and $|N_{G_0}\left(w\right)\cap V(P-\{v_1,v_2\})|\ge 2$.

Let $w_i\in N_{G_0}\left(w\right)\cap V\left(P\right)$ closed to $v_i$. If $|N_G\left(w\right)\cap V\left(P\right)|\ge 3$, then $w{w}_{1}P{v}_1$ and $w{w}_{2}P{v}_2$ are choices of $P_1,P_2$ with fewer vertices, a contradiction. Hence, $|N_{G_0}\left(w\right)\cap V\left(P\right)|=2$ and $N_{G_0}\left(w\right)\cap V\left(G\right)=\left\{w_3\right\}$ for some $w_3\notin \{v_1,v_2\}$. Then, either $w_{1}P{v}_1$, $w_{1}w{w}_3$ or $w_{2}P{v}_2$, $w_{2}w{w}_3$ are candidates of $P_1,P_2$ with fewer vertices, a contradiction. Hence, (D4) is satisfied and the theorem is proved. □

Let $\mathbb{Z}$ be the set of integers, and ${\mathbb{Z}}^2=\{(x_1,x_2)\mid x_1,x_2\in \mathbb{Z}\}$. Then, ${\mathbb{Z}}^2$ is a totally ordered set according to the lexicographic order.

Theorem 5. 

Let ${\mathcal{G}}_3$ be the family of the subdivision of some 3-connected graphs and ${\psi }_3\left(G\right)=\left(\right|V_3\left(G\right)|,-|V\left(G\right)\left|\right)\in {\mathbb{Z}}^2$ for any $G\in {\mathcal{G}}_3$. Then, $({\mathcal{G}}_3,{\psi }_3)$ is a $(3,3)$-extensible system such that every graph G with $\delta \left(G\right)\ge 3$ contains a subgraph $B\in {\mathcal{G}}_3$.

Proof. 

By a theorem of Dirac [17], we see that every graph with minimum degree 3 contains a subdivision of $K_4$, which belongs to ${\mathcal{G}}_3$. It suffices to verify that $(G_3,{\psi }_3)$ is a $(3,3)$-extensible system. By the definition, (D1) and (D2) are clear. It suffices to verify (D3) and (D4). First, we prove the following claims.

Claim 1. For any graph $G_1\supseteq G$ with $G_1\left[V\left(G\right)\right]=G$, if there exists a vertex $v\in V\left(G_1\right)\setminus V\left(G\right)$ and 3 internally disjoint $(v,V_3\left(G\right))$-paths $P_1,P_2,P_3$ such that $|V\left(G_2\right)\setminus V\left(G\right)|$ is as small as possible, where $G_2=G_1\left[V(P_1\cup P_2\cup P_3\cup G)\right]$, then $G_2\in {\mathcal{G}}_3$, $V_3\left(G\right)\subseteq V_3\left(G_2\right)$ and ${\psi }_3\left(G_2\right)>{\psi }_3\left(G\right)$.

By the definition of $G_2$, we see that $V_3\left(G\right)⊊V_3\left(G_2\right)$, and thus ${\psi }_3\left(G_2\right)>{\psi }_3\left(G\right)$. So, it suffices to show that $G_2\in {\mathcal{G}}_3$. Suppose, now, that there exists a vertex cut $\{x_1,x_2\}$ and $C_1,C_2$ are two components of $G_2-\{x_1,x_2\}$ such that $V\left(C_1\right)\cap V_3\left(G_2\right)\ne \varnothing$ and $V_3\left(G\right)\setminus \{x_1,x_2\}\subseteq V\left(C_2\right)$ since G is a subdivision of some 3-connected graph. By the choice of v, we see that $v\in V\left(C_2\right)$. Let $u\in V\left(C_1\right)\cap V_3\left(G_2\right)$. Then, $u\in V\left(P_i\right)\cap V\left(G_1\right)\setminus V_3\left(G\right)$ for some i. Then, there exists an $(x_1,x_2)$-path P whose inner vertices have degree 2 in G such that $u\in V\left(P\right)$ and $V\left(P\right)\setminus \{x_1,x_2\}\subseteq V\left(C_1\right)$. Noting that $v\notin V\left(P\right)$, we see that $x_1,x_2\in V\left(P_i\right)$, and thus $d_{G_2}\left(u\right)=2$, a contradiction. The claim is proved.

Claim 2. $({\mathcal{G}}_3,{\psi }_3)$ satisfies the condition (D3).

Let $G_0$ be the graph defined in (D3). By Claim 1, we may assume that $G_0$ contains at most 2 internally disjoint $(v,V_3\left(G\right))$-paths. It follows that $G_0$ contains a vertex cut $\{x_1,x_2\}$ separating v from $V_3\left(G\right)$. Then, there exists an $(x_1,x_2)$-path P whose inner vertices have degree 2 in G, such that $N_{G_0}\left(v\right)\cap V\left(P\right)|\ge 3$. Let $v_i\in N_{G_0}\left(v\right)\cap V\left(P\right)$ closed to $x_i$ for $i=1,2$. Let $G^{\prime }$ be a graph obtained from G by replacing P with $x_{1}P{v}_{1}vP{x}_2$. Then, $G^{\prime }\in {\mathcal{G}}_3$ and ${\psi }_3\left(G^{\prime }\right)>{\psi }_3\left(G\right)$ since $V_3\left(G^{\prime }\right)=V_3\left(G\right)$ and $|V\left(G^{\prime }\right)|<|V\left(G\right)|$. (D3) is satisfied.

(D4) remains to be verified. By Claim 1, let $G_0$ be the graph such that $G_0\left[V\left(G\right)\right]=G$ and $|N_{G_0}\left(u\right)\cap V\left(G\right)|\le 2$. Let $v\in V_3\left(G_0\right)\setminus V_3\left(G\right)$ and $P_1,P_2,P_3$ be three internally disjoint $(v,V_3\left(G\right))$-paths such that $|V\left(G_0\right)\setminus V\left(G_2\right)|$ is as small as possible, where $G_2=G_0\left[V(P_1\cup P_2\cup P_3\cup G)\right]$. By Claim 1, $G_2\in {\mathcal{G}}_3$, $V_3\left(G_2\right)⊊V_3\left(G\right)$ and ${\psi }_3\left(G_2\right)>{\psi }_3\left(G\right)$. Assume that $P_i$ is a $(v,v_i)$-path for some $v_i\in V_3\left(G\right)$.

Suppose, to the contrary, that (D4) is not true. Then, there exists a vertex $w\in V\left(G_0\right)\setminus V\left(G_2\right)$ such that

$$|N_{G_0}\left(w\right)\cap V\left(G_2\right)|\ge 4 \mathrm{and} |N_{G_0}\left(w\right)\cap V\left(G\right)|\le 2.$$

(2)

We consider the following two cases.

Case 1. There exists i such that $V\left(P_i\right)\cap (V\left(G\right)\setminus V_3\left(G\right))\ne \varnothing$.

In this case, G contains an $(x_1,x_2)$-path P whose inner vertices have degree 2 in G for some $x_1,x_2\in V_3\left(G\right)$ such that $V(P-\{x_1,x_2\})\cap V(P_i-v_i)\ne \varnothing$ for some i. Let Q be an $(x_3,x_4)$-path with minimum length in $G_2\left[V(P_1\cup P_2\cup P_3)\right]$ such that $x_3\in V(P-\{x_1,x_2\})\cap V(P_i-v_i)$ and $x_4\in \{v_1,v_2,v_3\}\setminus \{x_1,x_2\}$. Then, $x_{3}P{x}_1,x_{3}P{x}_2,x_{3}Q{x}_4$ are three internally disjoint $(x_3,V_3\left(G\right))$-paths contained in $G_2$. By the choice of $G_2$, we see that $V\left(G_2\right)=V\left(G\right)\cup V\left(Q\right)$. Without loss of generality, we may assume that $P_1=x_{3}P{x}_1,$$P_2=x_{3}P{x}_2,P_3=x_{3}Q{u}_4$.

Let $P_3^{\prime }\subseteq P_3$ be an $(x_3,x_4^{\prime })$-path with minimum length such that $x_4^{\prime }\in V\left(G\right)$ and $x_4^{\prime }\ne x_3$. Then, $V(P_3^{\prime }-\{x_3,x_4^{\prime }\})=V\left(G_2\right)\setminus V\left(G\right)$. By the choice of $P_3$, we see that $|N_{G_0}\left(w\right)\cap V(P_3^{\prime }-\{x_3,x_4^{\prime }\})|\le 2$, and thus, the inequalities in (2) hold. Then, there exist $y_1,y_2\in N_{G_0}\left(w\right)\cap V(P_3^{\prime }-\{x_3,x_4^{\prime }\})$ and $y_3,y_4\in N_{G_0}\left(w\right)\cap V\left(G\right)$. If $y_3\notin V_3\left(G\right)$, then G contains a path $P^{\prime }\ne P$ with ends in $V_3\left(G\right)$ and inner vertices not in $V_3\left(G\right)$. Hence, there exist $y_3^{\prime }\notin \{x_1,x_2\}$ and a $(y_3,y_3^{\prime })$-path $P_3^{\prime \prime }$ in G with minimum length and disjoint with P. If $y_3\in V_3\left(G\right)$, then let $y_3^{\prime }=y_3$ and $P_3^{\prime \prime }=y_3$. Thus, $P_3^{\prime \prime \prime }=x_3{P}_3^{\prime }{y}_{1}w{y}_3{P}_3^{\prime \prime }{y}_3^{\prime }$ is a candidate of $P_3$ such that $|V\left(P_3^{\prime \prime \prime }\right)\setminus V\left(G\right)|>|V\left(P_3\right)\setminus V\left(G\right)|$ since $G_0$ is bipartite, a contradiction.

Case 2. For each i, $V\left(P_i\right)\cap V\left(G\right)=\left\{v_i\right\}$.

In this case, $V\left(G_2\right)\setminus V\left(G\right)={\bigcup }_{i=1}^{3}V(P_i-v_i)$. By the choice of $P_i$, we see that $|N_{G_0}\left(w\right)\cap V\left(P_i\right)|\le 2$ for $i=1,2,3$. Let $t=|N_{G_0}\left(w\right)\cap V\left(G_2\right)\setminus V\left(G\right)|$. Then, by (2) and by the assumption of (D4), $t\ge 2$, $|N_{G_0}\left(w\right)\cap V(G-\{v_1,v_2,v_3\})|\ge 4-t$, and $G_0\left[V(P_1\cup P_2\cup P_3)\right]$ contains $d:=min\{t,3\}$ disjoint path from $N_{G_0}\left(w\right)\setminus V\left(G\right)$ to $\{v_1,v_2,v_3\}$. Without loss of generality, we may assume that for $1\le i\le d$, $Q_i$ is a $(u_i,v_i)$-path for some $u_i\in N_{G_0}\left(w\right)\setminus V\left(G\right)$ with minimum length such that $Q_i$’s are pairwise disjoint. Without loss of generality, we may assume that $|V\left(Q_1\right)|\le \dots \le |V\left(Q_d\right)|$.

If G contains an $(x_1,x_2)$-path P with ends in $V_3\left(G\right)$ and inner vertices not in $V_3\left(G\right)$ such that there exist $x_3\in N_{G_0}\left(w\right)\cap V(P-\{x_1,x_2\})$, then let Q be an $(x_3,x_4)$-path with minimum length in $G_0[V(P_1\cup P_2\cup P_3)\cup \{w,x_3\}]$ such that $x_4\in \{v_1,v_2,v_3\}\setminus \{x_1,x_2\}$. Then, by the choice of $G_2$, $P_1^{\prime }=x_{3}P{x}_1,P_2^{\prime }=x_{3}P{x}_2,P_3^{\prime }=x_{3}Q{x}_4$ are three internally disjoint $(x_3,V_3\left(G\right))$-paths such that $|N_{G_0}\left(w\right)\cap V\left(P_3^{\prime }\right)|=1$, and then $|V\left(G_2\right)\setminus V\left(G\right)|\ge 2$ since $G_0$ is bipartite and $t\ge 2$. This suggests $|V\left(G_2\right)\setminus V\left(G\right)|>|V(P_1^{\prime }\cup P_2^{\prime }\cup P_3^{\prime })\setminus V\left(G\right)|$, a contradiction to the choice of $P_i$’s. So, we may assume that $N_{G_0}\left(w\right)\cap V\left(G\right)\subseteq V_3\left(G\right)$.

Let $N_{G_0}\left(w\right)\cap V(G-\{v_1,v_2,v_3\})=\{w_1,\dots ,w_s\}$, where $s\ge 4-t$. Then, $w{w}_1,\dots ,$$w{w}_{4-t},Q_1,\dots$, $Q_{t-1}$ are 3 internally disjoint $(w,V_3\left(G\right))$-paths of $G_0$ contained in $G_0[V\left(G_2\right)\cup \left\{w\right\}]$. Noting that $d>t-1$, there exists $w_0\in N_{G_0}\left(w\right)\setminus V(Q_1\cup \dots \cup Q_{t-1})$. Noting that $G_0$ is bipartite, $|V\left(G_2\right)\setminus V(Q_1\cup Q_{t-1})|\ge 2$. This suggests that $|V\left(G_2\right)\setminus V\left(G\right)|>|V(Q_1\cup \dots \cup Q_{t-1})\setminus V\left(G\right)|$, a contradiction to the assumption on $P_i$’s and $G_2$. The proof is complete. □

By Theorems 3–5, we have the following corollary, which confirms Conjecture 2 for 2-connected graphs and 3-connected graphs.

Corollary 2. 

Let $k\le 3$ be a positive integer and $T_0$ be a tree with bipartition $(Z_1,Z_2)$. If G is a k-connected bipartite graph with $\delta \left(G\right)\ge max\left\{\right|Z_1|,|Z_2\left|\right\}+k$, then G contains a k-redundant tree isomorphic to $T_0$.

5. Conclusions

In this paper, we generalize the embedding lemma of arbitrary trees into bipartite graphs (see Lemma 1). As a corollary, we obtain a sufficient condition (Corollary 1) for a bipartite graph to contain an arbitrary tree. Together with Lemma 2, we obtain a crucial embedding lemma of a tree for a bipartite graph (Lemma 3). Then, we propose Conjecture 3 and prove that this implies a k-redundant tree (Theorem 3). Finally, we confirm Conjecture 3 for $k=2$ (Theorem 4) and $k=3$ (Theorem 5). These imply Conjecture 2 for 2-connected graphs and 3-connected graphs (Corollary 2). In fact, the degree condition of our results is slightly weaker than the degree condition of Conjecture 2. Based on these, we believe the following conjecture is also true, which is stronger than Conjecture 2.

Conjecture 4. 

Let k be a positive integer and  $T_0$ be a tree with bipartition $(Z_1,Z_2)$. If G is a k-connected bipartite graph with bipartition $(U_1,U_2)$ such that ${\delta }_G\left(U_i\right)\ge \left|Z_{3-i}\right|+k$ for $i=1,2$, then G contains a k-redundant tree isomorphic to $T_0$.

If the above conjecture is true, then the degree condition is tight. In [8], the authors give the example $K_{k+t-1,k+t-1}$ to state that the minimum degree condition in Conjecture 2 is tight, where $t=max\left\{\right|Z_1|,|Z_2\left|\right\}$. The number of vertex in the example is fixed. We will give an example of Conjecture 4 and Conjecture 2 with an arbitrarily large number of vertices. Let $k,a,b,t$ be positive integers with $t\ge 2$. We shall define a graph $G(k,a,b,t)$ as follows. Let $A_1,\dots ,A_{2t}$, $B_1,\dots ,B_{2t}$, $K_1,\dots ,K_t$ be $5t$ disjoint independent sets such that $|K_1|=\lfloor k/2\rfloor$, $|K_i|=\lceil k/2\rceil$ for $i\ge 2$, $|B_{2i-1}|=a$, $|B_{2i}|=b$ for each i, and

$$|A_{2i-1}|=\left\{\begin{array}{cc}\lfloor k/2\rfloor \hfill & i=1\hfill \\ \lceil k/2\rceil \hfill & i\ge 2\hfill \end{array}\right.,\left|A_{2i}\right|=\left\{\begin{array}{cc}\lceil k/2\rceil \hfill & i=1\hfill \\ \lfloor k/2\rfloor \hfill & i\ge 2\hfill \end{array}\right..$$

Then add all possible edges between $A_{2i-1}\cup B_{2i-1}$ and $A_{2i}\cup B_{2i}$ for $i=1,2,\dots ,t$ and then add all possible edges between $K_i$ and $A_{2i-1}\cup B_{2i-1}$ and between $A_{2i}\cup B_{2i}$ and $K_{i+1}$ for $i=1,2,\dots ,t$, where $K_{t+1}=K_1$. Let $U_1={\bigcup }_{i=1}^t(K_i\cup A_{2i}\cup B_{2i})$ and $U_2={\bigcup }_{i=1}^t(K_{i+1}\cup A_{2i-1}\cup B_{2i-1})$. Then, $G=G(k,a,b,t)$ is a k-connected bipartite graph with bipartition $(U_1,U_2)$. It is easy to verify that ${\delta }_G\left(U_1\right)=k+a$ and ${\delta }_G\left(U_2\right)=k+b$.

Let $T(r,s)$ be a tree with bipartition $(Z_1,Z_2)$ such that $|Z_1|=r$ and $|Z_2|=s$. If $G(k,a,b,t)$ has a redundant tree $T\cong T(a,b+1)$ or $T\cong T(a+1,b)$, then $V\left(T\right)\cap {\bigcup }_{i=1}^t(A_{2i-1}\cup A_{2i}\cup K_i))\ne \varnothing$. If $V\left(T\right)\cap K_j\ne \varnothing$, then $K_1\cup K_j\setminus V\left(T\right)$ is a vertex cut of $G-V\left(T\right)$ with at most $k-1$ vertices, a contradiction. If $V\left(T\right)\cap A_{2j}\ne \varnothing$, then $K_1\cup A_{2i}\setminus V\left(T\right)$ is a vertex cut of $G-V\left(T\right)$ with at most $k-1$ vertices, a contradiction. If $V\left(T\right)\cap A_{2j-1}\ne \varnothing$, then either $K_1\cup A_{2j-1}\setminus V\left(T\right)$ or $K_2\cup A_1\setminus V\left(T\right)$ is a vertex cut of $G(k,a,b,t)-V\left(T\right)$ with at most $k-1$ vertices, a contradiction. This implies that the minimum degree condition of Conjecture 4 is tight.