An Optimization Problem of Distributed Permutation Flowshop Scheduling with an Order Acceptance Strategy in Heterogeneous Factories
Abstract
1. Introduction
2. Related Work
3. Mathematical Model
3.1. Assumptions of a Mathematical Model
- (1)
- There are several distributed factories.
- (2)
- Each factory has one set of flowshop machines.
- (3)
- Each factory has different processing times for orders and statuses.
- (4)
- Pre-emption of orders is not allowed.
- (5)
- The lead time from when an order is completed on the machines of the factories to when it is delivered to the customer is not considered.
3.2. MILP Model
| Parameters & Sets | |
| Set of distributed factories, | |
| Set of operation stage, | |
| Set of orders, | |
| Set of orders and dummy order, | |
| Revenue related to order | |
| Due date related to order | |
| Processing times of production order at stage in distributed factory | |
| Sequence-dependent setup times between orders at stage in factory | |
| Scaling parameter of tardiness costs | |
| Large number | |
| Decision Variables | |
| If order is selected, 1; Otherwise, 0 | |
| If order is produced in factory , 1; Otherwise, 0 | |
| If order is produced immediately after order in factory , 1; Otherwise, 0 | |
| Start time of order at operation stage in factory | |
| Completion time of order at operation stage in factory | |
| Manufacturing completion time of production order | |
| Manufacturing sequence of production order in factory | |
| Tardiness of production order | |
4. Meta-Heuristic Algorithms
4.1. Solution Structure and Decoding Process
4.2. Genetic Algorithm (GA)
| Algorithm 1: Genetic Algorithm |
| While |
| While |
| //Calculate the objective function |
| End While |
| //Conduct the selection procedure |
| While |
| If |
| Randomly select chromosome from |
| //Conduct the crossover operator |
| End If |
| If |
| //Conduct the mutation operator |
| End If |
| End While |
| End While |
4.3. Particle Swarm Optimization (PSO)
| Algorithm 2: The procedure of PSO |
| For |
| For |
| //Calculate the objective function |
| //Update the particle best |
| End For |
| //Update the global best |
| For |
| the position vector of List 1 by following Equation (25) |
| the velocity vector of List 2 by following Equation (29) |
| the position vector of List 1 by following Equation (30) |
| End For |
| End For |
5. Computational Experiments
5.1. Design of Experiments
5.2. Results of Experiments
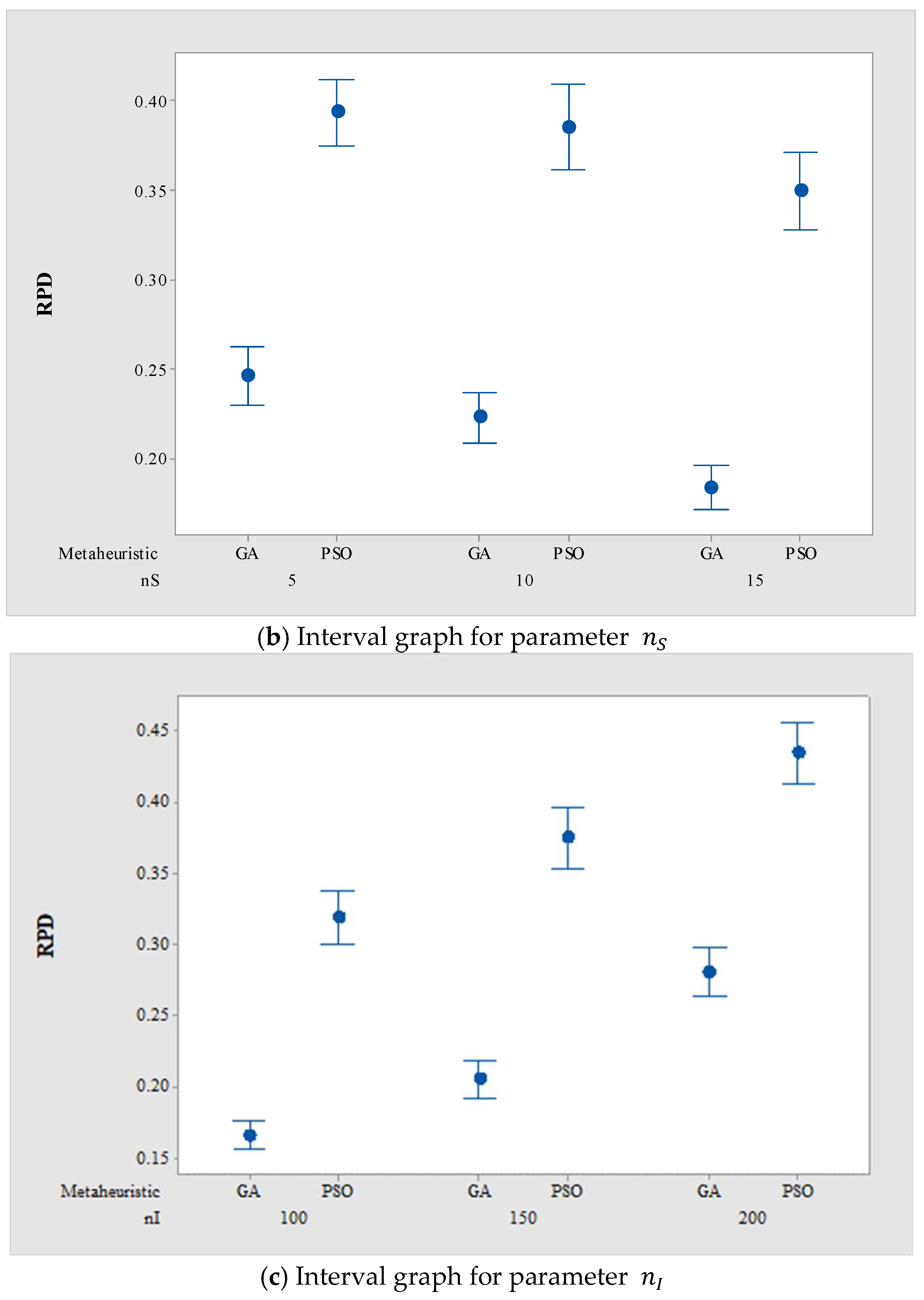
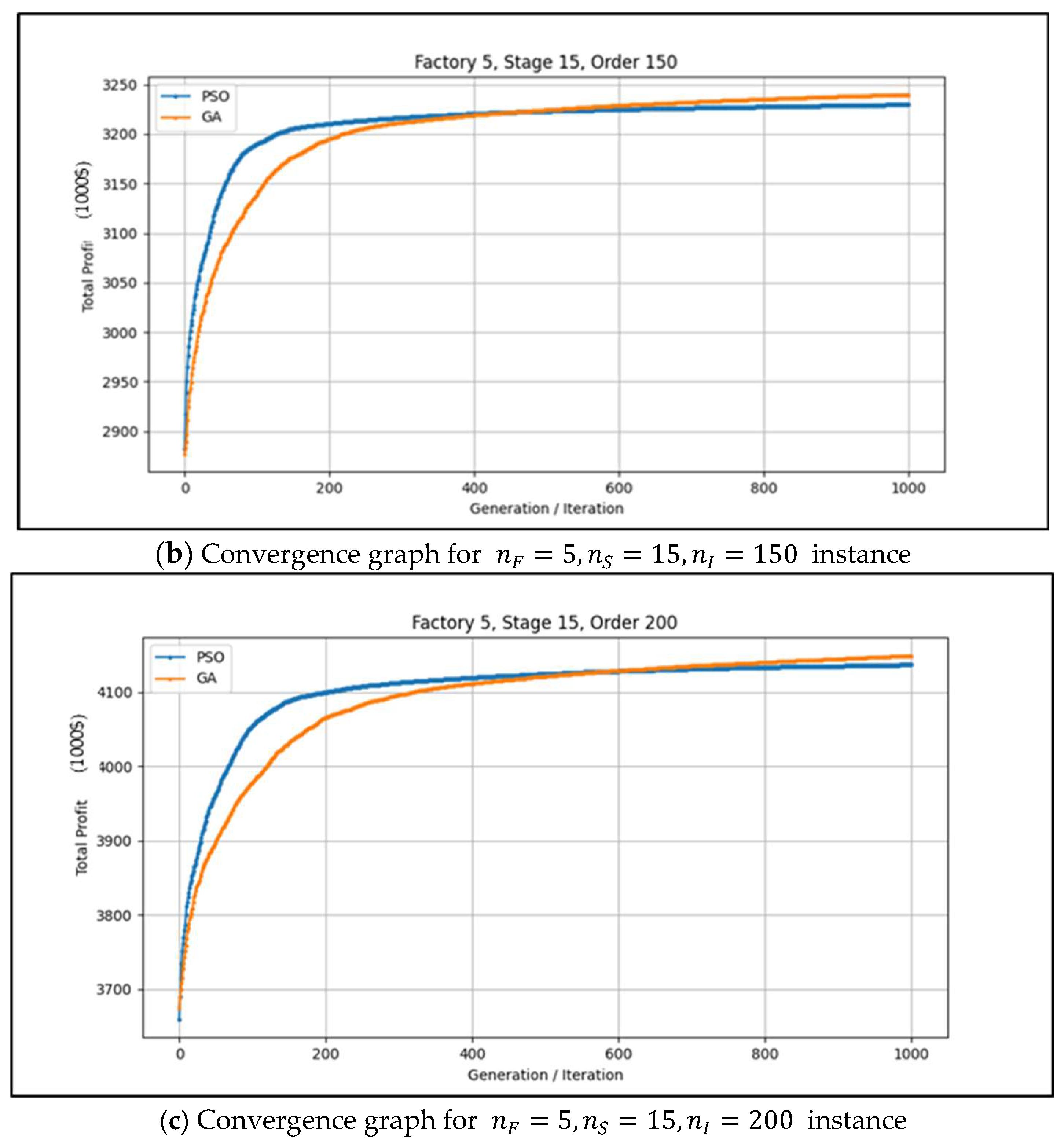
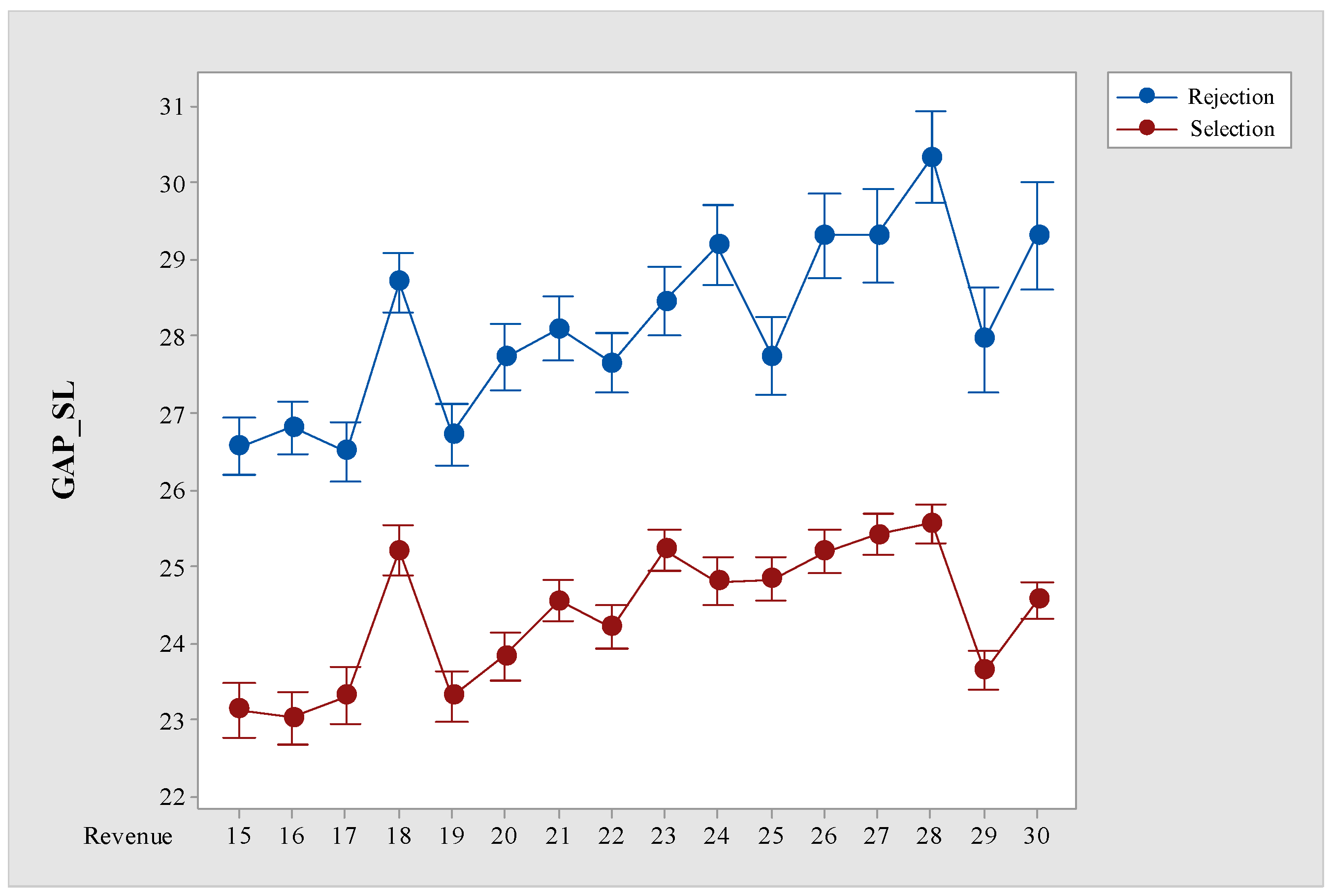
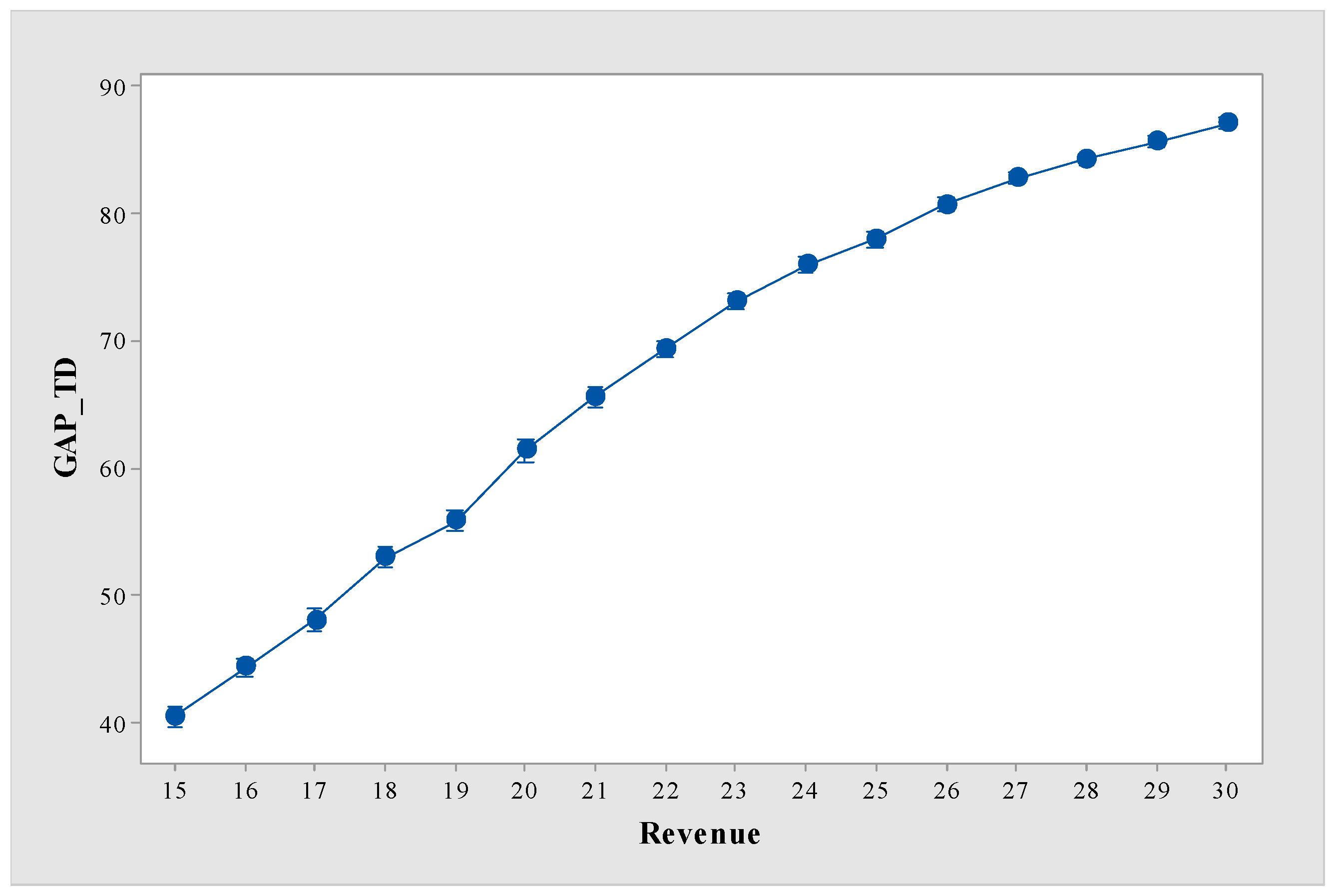
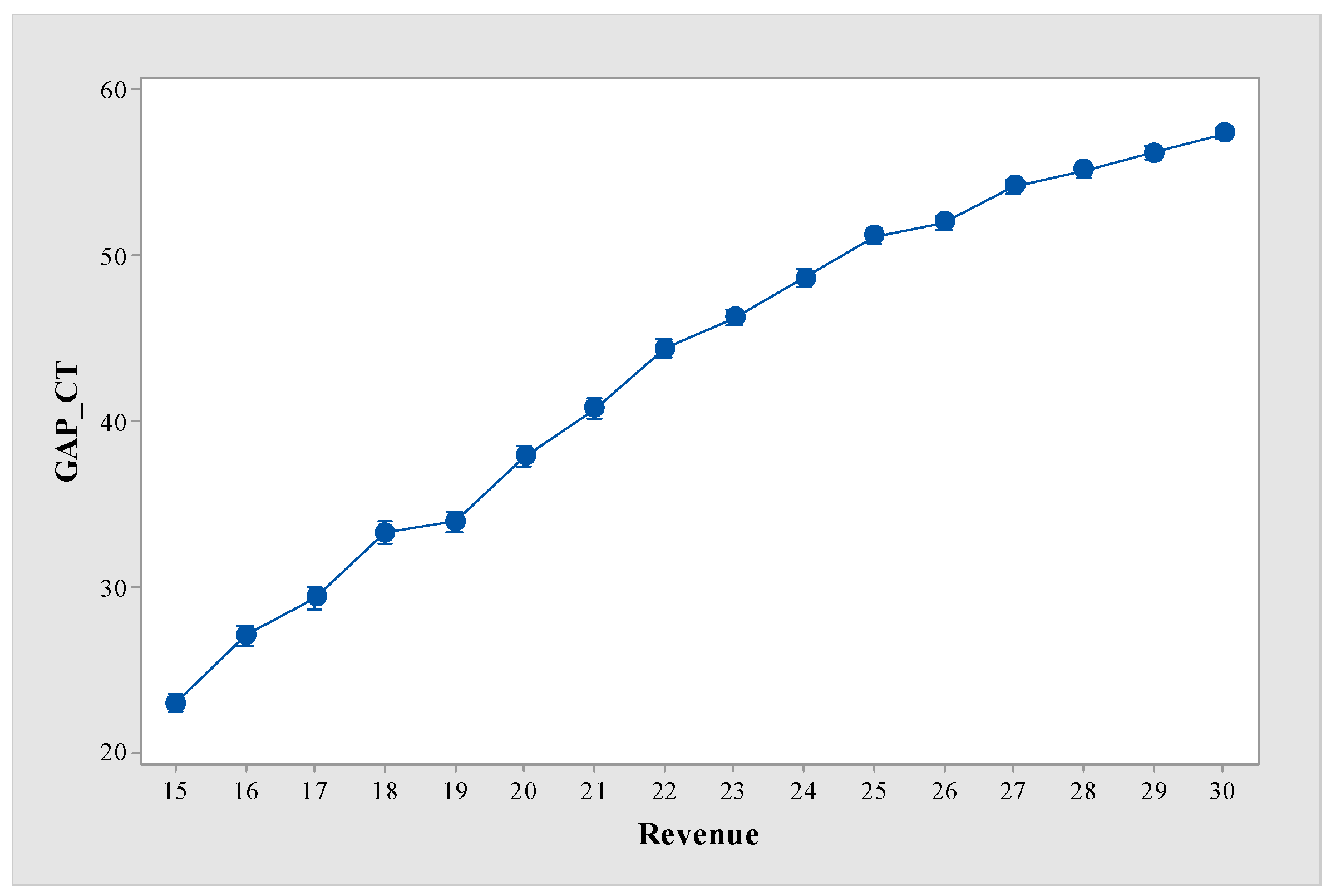
5.3. Results of Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Base Heuristic
| Algorithm A1: Base Heuristic |
| Sort in increasing order based on |
| For |
| For |
| Let as tardiness of order at factory |
| Virtually assign order to factory |
| Calculate |
| End For |
| If |
| Reject order |
| Else |
| Assign order to factory |
| Update factory |
| End If |
| End For |
References
- Zhou, L.; Zhang, L.; Laili, Y.; Zhao, C.; Xiao, Y. Multi-task Scheduling of Distributed 3D Printing Services in Cloud Manufacturing. Int. J. Adv. Manuf. Technol. 2018, 96, 3003–3017. [Google Scholar] [CrossRef]
- Leng, J.; Zhong, Y.; Lin, Z.; Xu, K.; Mourtzis, D.; Zhou, X.; Zheng, P.; Liu, Q.; Zhao, J.L.; Shen, W. Towards Resilience in Industry 5.0: A Decentralized Autonomous Manufacturing Paradigm. J. Manuf. Syst. 2023, 71, 95–114. [Google Scholar] [CrossRef]
- Chang, H.C.; Liu, T.K. Optimisation of Distributed Manufacturing Flexible Job Shop Scheduling by Using Hybrid Genetic Algorithms. J. Intell. Manuf. 2017, 28, 1973–1986. [Google Scholar] [CrossRef]
- De Giovanni, L.; Pezzella, F. An Improved Genetic Algorithm for the Distributed and Flexible Job-shop Scheduling Problem. Eur. J. Oper. Res. 2010, 200, 395–408. [Google Scholar] [CrossRef]
- Shao, W.; Pi, D.; Shao, Z. Optimization of Makespan for the Distributed No-Wait Flow Shop Scheduling Problem with Iterated Greedy Algorithms. Knowl. Based Syst. 2017, 137, 163–181. [Google Scholar] [CrossRef]
- Wang, S.Y.; Wang, L.; Liu, M.; Xu, Y. An Effective Estimation of Distribution Algorithm for Solving the Distributed Permutation Flow-Shop Scheduling Problem. Int. J. Prod. Econ. 2013, 145, 387–396. [Google Scholar] [CrossRef]
- Mönch, L.; Shen, L. Parallel Machine Scheduling with the Total Weighted Delivery Time Performance Measure in Distributed Manufacturing. Comput. Oper. Res. 2021, 127, 105126. [Google Scholar] [CrossRef]
- Lei, D.; Yuan, Y.; Cai, J.; Bai, D. An Imperialist Competitive Algorithm with Memory for Distributed Unrelated Parallel Machines Scheduling. Int. J. Prod. Res. 2020, 58, 597–614. [Google Scholar] [CrossRef]
- Behnamian, J.; Fatemi Ghomi, S.M.T. A Survey of Multi-Factory Scheduling. J. Intell. Manuf. 2016, 27, 231–249. [Google Scholar] [CrossRef]
- Bagheri Rad, N.; Behnamian, J. Recent Trends in Distributed Production Network Scheduling Problem; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Marin-Garcia, J.A.; Garcia-Sabater, J.P.; Miralles, C.; Villalobos, A.R. Profile and Competences of Spanish Industrial Engineers in the European Higher Education Area (EHEA). J. Ind. Eng. Manag. 2008, 1, 269–284. [Google Scholar] [CrossRef][Green Version]
- Renna, P. Coordination Strategies to Support Distributed Production Planning in Production Networks. Eur. J. Ind. Eng. 2015, 9, 366–394. [Google Scholar] [CrossRef]
- Naderi, B.; Ruiz, R. The Distributed Permutation Flowshop Scheduling Problem. Comput. Oper. Res. 2010, 37, 754–768. [Google Scholar] [CrossRef]
- Slotnick, S.A. Order Acceptance and Scheduling: A Taxonomy and Review. Eur. J. Oper. Res. 2011, 212, 1–11. [Google Scholar] [CrossRef]
- Karabulut, K.; Öztop, H.; Kizilay, D.; Tasgetiren, M.F.; Kandiller, L. An Evolution Strategy Approach for the Distributed Permutation Flowshop Scheduling Problem with Sequence-Dependent Setup Times. Comput. Oper. Res. 2022, 142, 105733. [Google Scholar] [CrossRef]
- Huang, J.P.; Pan, Q.K.; Gao, L. An Effective Iterated Greedy Method for the Distributed Permutation Flowshop Scheduling Problem with Sequence-Dependent Setup Times. Swarm Evol. Comput. 2020, 59, 100742. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, X.; Wang, L.; Li, Z. A Memetic Discrete Differential Evolution Algorithm for the Distributed Permutation Flow Shop Scheduling Problem. Complex Intell. Syst. 2022, 8, 141–161. [Google Scholar] [CrossRef]
- Gogos, C. Solving the Distributed Permutation Flow-Shop Scheduling Problem Using Constrained Programming. Appl. Sci. 2023, 13, 12562. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Z. The Distributed Assembly Permutation Flowshop Scheduling Problem with Flexible Assembly and Batch Delivery. Int. J. Prod. Res. 2021, 59, 4053–4071. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Pan, Q.K.; Gao, L.; Miao, Z.H.; Peng, C. A Two-Phase Evolutionary Algorithm for Multi-Objective Distributed Assembly Permutation Flowshop Scheduling Problem. Swarm Evol. Comput. 2022, 74, 101128. [Google Scholar] [CrossRef]
- Pan, Y.; Gao, K.; Li, Z.; Wu, N. Improved Meta-Heuristics for Solving Distributed Lot-Streaming Permutation Flow Shop Scheduling Problems. IEEE Trans. Autom. Sci. Eng. 2023, 20, 361–371. [Google Scholar] [CrossRef]
- Luo, C.; Gong, W.; Li, R.; Lu, C. Problem-Specific Knowledge MOEA/D for Energy-Efficient Scheduling of Distributed Permutation Flow Shop in Heterogeneous Factories. Eng. Appl. Artif. Intell. 2023, 123, 106454. [Google Scholar] [CrossRef]
- Meng, T.; Pan, Q.K. A Distributed Heterogeneous Permutation Flowshop Scheduling Problem with Lot-Streaming and Carryover Sequence-Dependent Setup Time. Swarm Evol. Comput. 2021, 60, 100804. [Google Scholar] [CrossRef]
- Khare, A.; Agrawal, S. Effective Heuristics and Metaheuristics to Minimise Total Tardiness for the Distributed Permutation Flowshop Scheduling Problem. Int. J. Prod. Res. 2021, 59, 7266–7282. [Google Scholar] [CrossRef]
- Lin, Z.; Jing, X.L.; Jia, B.X. An Iterated Greedy Algorithm for Distributed Flowshops with Tardiness and Rejection Costs to Maximize Total Profit. Expert Syst. Appl. 2023, 233, 120830. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhen, T. Improved Jaya Algorithm for Energy-Efficient Distributed Heterogeneous Permutation Flow Shop Scheduling. J. Supercomput. 2025, 81, 434. [Google Scholar] [CrossRef]
- Song, H.; Li, J.; Du, Z.; Yu, X.; Xu, Y.; Zheng, Z.; Li, J. A Q-learning Driven Multi-Objective Evolutionary Algorithm for Worker Fatigue Dual-Resource-Constrained Distributed Hybrid Flow Shop. Comput. Oper. Res. 2025, 175, 106919. [Google Scholar] [CrossRef]
- Zhu, N.; Zhao, F.; Yu, Y.; Wang, L. A Cooperative Learning-Aware Dynamic Hierarchical Hyper-Heuristic for Distributed Heterogeneous Mixed No-Wait Flow-Shop Scheduling. Swarm Evol. Comput. 2024, 90, 101668. [Google Scholar] [CrossRef]
- Perez-Gonzalez, P.; Framinan, J.M. A Review and Classification on Distributed Permutation Flowshop Scheduling Problems. Eur. J. Oper. Res. 2023, 312, 1–21. [Google Scholar] [CrossRef]
- Mraihi, T.; Driss, O.B.; El-Haouzi, H.B. Distributed Permutation Flow Shop Scheduling Problem with Worker Flexibility: Review, Trends and Model Proposition. Expert Syst. Appl. 2023, 238, 121947. [Google Scholar] [CrossRef]
- Kapadia, M.S.; Uzsoy, R.; Starly, B.; Warsing, D.P. A Genetic Algorithm for Order Acceptance and Scheduling in Additive Manufacturing. Int. J. Prod. Res. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Kan, A.R. General Flow-Shop and Job-Shop Problems. In Machine Scheduling Problems; Springer: Boston, MA, USA, 1976; pp. 106–130. [Google Scholar]
- Pan, Q.K.; Tasgetiren, M.F.; Liang, Y.C. A Discrete Particle Swarm Optimization Algorithm for the No-Wait Flowshop Scheduling Problem. Comput. Oper. Res. 2008, 35, 2807–2839. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle Swarm Optimization (PSO). A Tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Cerveira, M.I.F. Heuristics for the Distributed Permutation Flowshop Scheduling Problem with the Weighted Tardiness Objective. 2019. Available online: https://www.proquest.com/openview/109fa27057466f781cfeac17a0b99ee1/1?pq-origsite=gscholar&cbl=2026366&diss=y (accessed on 3 March 2025).
- Ruiz, R.; Stützle, T. An Iterated Greedy Heuristic for the Sequence Dependent Setup Times Flowshop Problem with Makespan and Weighted Tardiness Objectives. Eur. J. Oper. Res. 2008, 187, 1143–1159. [Google Scholar] [CrossRef]
- Molina-Sánchez, L.P.; González-Neira, E.M. GRASP to Minimize Total Weighted Tardiness in a Permutation Flow Shop Environment. Int. J. Ind. Eng. Comput. 2016, 7, 161–176. [Google Scholar] [CrossRef]




| OA | Framework | Setup | Etc. | Method | Objective | ||||
|---|---|---|---|---|---|---|---|---|---|
| Homo | Hetero | Etc. | SD | SI | |||||
| [16] | √ | √ | Mathematical model, IGR | Min. | |||||
| [15] | √ | √ | MILP, CP, ES_en | Min. | |||||
| [17] | √ | MMDE | Min. | ||||||
| [18] | √ | Heuristic, CP | Min. | ||||||
| [19] | √ | Assembly factories | Batch Delivery | Heuristic, VND, IG | Min. DTC | ||||
| [20] | √ | Assembly line | TEA | Min. {TF, TT} | |||||
| [21] | √ | √ | Lot-Streaming | Mathematical model, GA, PSO, ABC, HS, Jaya | Min. | ||||
| [22] | √ | KMOEA/D | Min. {} | ||||||
| [23] | √ | √ | Lot-streaming | MILP, Constructive Heuristic, NEABC | Min. | ||||
| [24] | √ | MILP, HHO, IG | Min. TD | ||||||
| [25] | √ | √ | Deadline | MILP, IG_TR | Max. Total profit | ||||
| [26] | √ | Jaya | Min. {, TEC} | ||||||
| [27] | √ | Worker fatigue | Q-learning driven multi-objective evolutionary algorithm | Min. | |||||
| [28] | √ | √ | No-wait | Hyper-heuristic | Min. | ||||
| This | √ | √ | √ | MILP, GA, PSO | Max. Total profit | ||||
| Small-Sized Instances | Large-Sized Instances | |
|---|---|---|
| 3, 4 | 5, 6, 7 | |
| 3, 4 | 5, 10, 15 | |
| 8, 10, 12 | 100, 150, 200 | |
| (1000 $) | ||
| (min) | ||
| (min) | ||
| (min) | ||
| 0.01 | 0.001 | |
| Fitness Measure | ||
| Ins. | MILP | PSO | GA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RPD | CPU | RPD | CPU | RPD | CPU | |||||
| 1 | 3 | 3 | 8 | 173.00 | 173.00 | 0.38 | 0.30 | 2.01 | 0.00 | 2.57 |
| 2 | 10 | 219.40 | 219.40 | 81.89 | 1.99 | 2.26 | 0.54 | 2.97 | ||
| 3 | 12 | 228.10 | 228.10 | 1800++ | 4.54 | 2.32 | 2.63 | 2.98 | ||
| 4 | 4 | 8 | 181.00 | 181.00 | 0.19 | 0.00 | 2.30 | 0.00 | 2.92 | |
| 5 | 10 | 239.00 | 239.00 | 0.38 | 0.00 | 2.68 | 0.00 | 3.35 | ||
| 6 | 12 | 265.00 | 265.00 | 65.61 | 2.83 | 2.90 | 1.87 | 3.60 | ||
| 7 | 4 | 3 | 8 | 175.00 | 175.00 | 0.47 | 0.00 | 2.09 | 0.00 | 2.74 |
| 8 | 10 | 232.00 | 232.00 | 2.95 | 0.00 | 2.41 | 0.00 | 3.11 | ||
| 9 | 12 | 266.80 | 266.80 | 1800++ | 3.29 | 2.72 | 1.95 | 3.42 | ||
| 10 | 4 | 8 | 184.00 | 184.00 | 0.23 | 0.00 | 2.45 | 0.00 | 3.13 | |
| 11 | 10 | 228.00 | 228.00 | 0.45 | 0.00 | 2.85 | 0.00 | 3.57 | ||
| 12 | 12 | 302.00 | 302.00 | 4.34 | 0.00 | 3.22 | 0.00 | 4.03 | ||
| Mean | 224.44 | 313.09 | 1.08 | 2.52 | 0.58 | 3.20 | ||||
| Ins. | BH | PSO | GA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RPD | CPU | RPD | CPU | RPD | CPU | |||||
| 1 | 5 | 5 | 100 | 2085.28 | 58.54 | <0.01 | 0.43 | 51.16 | 0.18 | 60.14 |
| 2 | 150 | 3117.11 | 73.51 | <0.01 | 0.50 | 76.09 | 0.24 | 88.90 | ||
| 3 | 200 | 4089.50 | 79.56 | <0.01 | 0.52 | 100.32 | 0.31 | 117.30 | ||
| 4 | 10 | 100 | 2141.00 | 52.19 | <0.01 | 0.50 | 88.11 | 0.25 | 99.32 | |
| 5 | 150 | 3199.08 | 66.30 | <0.01 | 0.52 | 130.91 | 0.22 | 147.78 | ||
| 6 | 200 | 4057.96 | 75.97 | <0.01 | 0.67 | 173.42 | 0.34 | 195.25 | ||
| 7 | 15 | 100 | 2110.56 | 41.32 | <0.01 | 0.47 | 124.58 | 0.20 | 138.82 | |
| 8 | 150 | 3247.79 | 63.01 | <0.01 | 0.56 | 184.35 | 0.25 | 206.29 | ||
| 9 | 200 | 4158.53 | 71.23 | <0.01 | 0.51 | 246.16 | 0.21 | 273.49 | ||
| 10 | 6 | 5 | 100 | 2199.86 | 49.42 | <0.01 | 0.33 | 52.12 | 0.19 | 61.29 |
| 11 | 150 | 3094.24 | 67.66 | <0.01 | 0.45 | 77.01 | 0.24 | 90.54 | ||
| 12 | 200 | 4158.09 | 76.40 | <0.01 | 0.41 | 101.81 | 0.29 | 119.55 | ||
| 13 | 10 | 100 | 2134.06 | 38.61 | <0.01 | 0.30 | 88.97 | 0.13 | 100.68 | |
| 14 | 150 | 3265.71 | 60.56 | <0.01 | 0.34 | 132.08 | 0.20 | 149.32 | ||
| 15 | 200 | 4132.82 | 70.42 | <0.01 | 0.41 | 175.08 | 0.29 | 197.79 | ||
| 16 | 15 | 100 | 2285.39 | 30.82 | <0.01 | 0.25 | 124.52 | 0.16 | 140.00 | |
| 17 | 150 | 3263.94 | 54.20 | <0.01 | 0.27 | 186.84 | 0.10 | 208.31 | ||
| 18 | 200 | 4289.71 | 65.40 | <0.01 | 0.43 | 247.83 | 0.28 | 276.32 | ||
| 19 | 7 | 5 | 100 | 2246.76 | 39.55 | <0.01 | 0.19 | 52.83 | 0.10 | 62.43 |
| 20 | 150 | 3267.91 | 61.30 | <0.01 | 0.32 | 78.12 | 0.27 | 92.08 | ||
| 21 | 200 | 4233.85 | 72.09 | <0.01 | 0.39 | 103.20 | 0.40 | 122.14 | ||
| 22 | 10 | 100 | 2301.37 | 28.26 | <0.01 | 0.23 | 89.61 | 0.17 | 101.81 | |
| 23 | 150 | 3244.54 | 54.28 | <0.01 | 0.18 | 133.15 | 0.17 | 151.24 | ||
| 24 | 200 | 4229.25 | 67.08 | <0.01 | 0.33 | 176.52 | 0.24 | 200.70 | ||
| 25 | 15 | 100 | 2230.94 | 22.31 | <0.01 | 0.18 | 126.08 | 0.12 | 141.21 | |
| 26 | 150 | 3301.48 | 45.13 | <0.01 | 0.24 | 186.80 | 0.17 | 210.39 | ||
| 27 | 200 | 4261.60 | 60.05 | <0.01 | 0.24 | 252.75 | 0.16 | 279.27 | ||
| Mean | 3198.09 | 57.23 | <0.01 | 0.38 | 131.87 | 0.22 | 149.35 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.J.; Kim, B.S. An Optimization Problem of Distributed Permutation Flowshop Scheduling with an Order Acceptance Strategy in Heterogeneous Factories. Mathematics 2025, 13, 877. https://doi.org/10.3390/math13050877
Lee SJ, Kim BS. An Optimization Problem of Distributed Permutation Flowshop Scheduling with an Order Acceptance Strategy in Heterogeneous Factories. Mathematics. 2025; 13(5):877. https://doi.org/10.3390/math13050877
Chicago/Turabian StyleLee, Seung Jae, and Byung Soo Kim. 2025. "An Optimization Problem of Distributed Permutation Flowshop Scheduling with an Order Acceptance Strategy in Heterogeneous Factories" Mathematics 13, no. 5: 877. https://doi.org/10.3390/math13050877
APA StyleLee, S. J., & Kim, B. S. (2025). An Optimization Problem of Distributed Permutation Flowshop Scheduling with an Order Acceptance Strategy in Heterogeneous Factories. Mathematics, 13(5), 877. https://doi.org/10.3390/math13050877







