Multirhythmicity, Synchronization, and Noise-Induced Dynamic Diversity in a Discrete Population Model with Competition
Abstract
1. Introduction
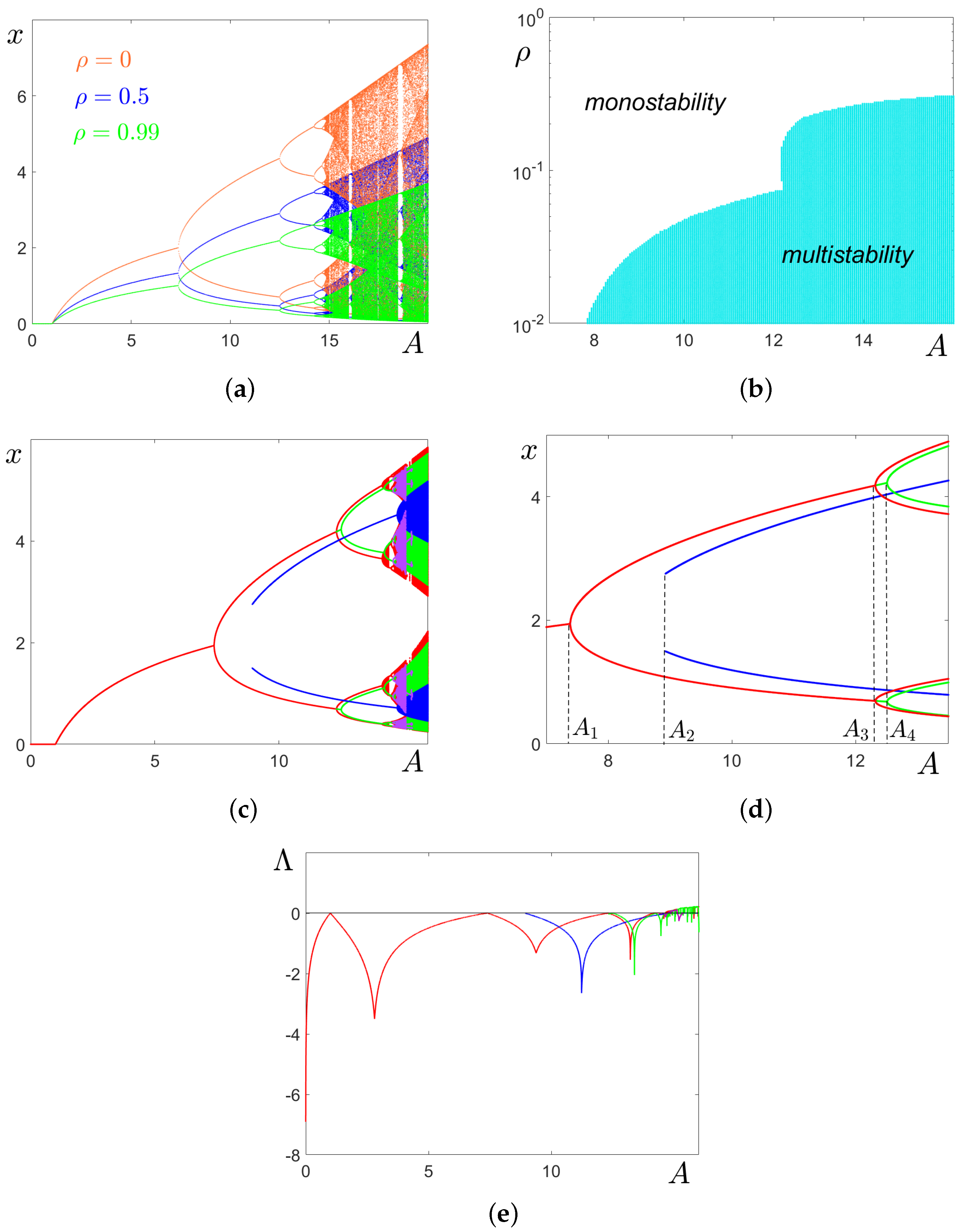
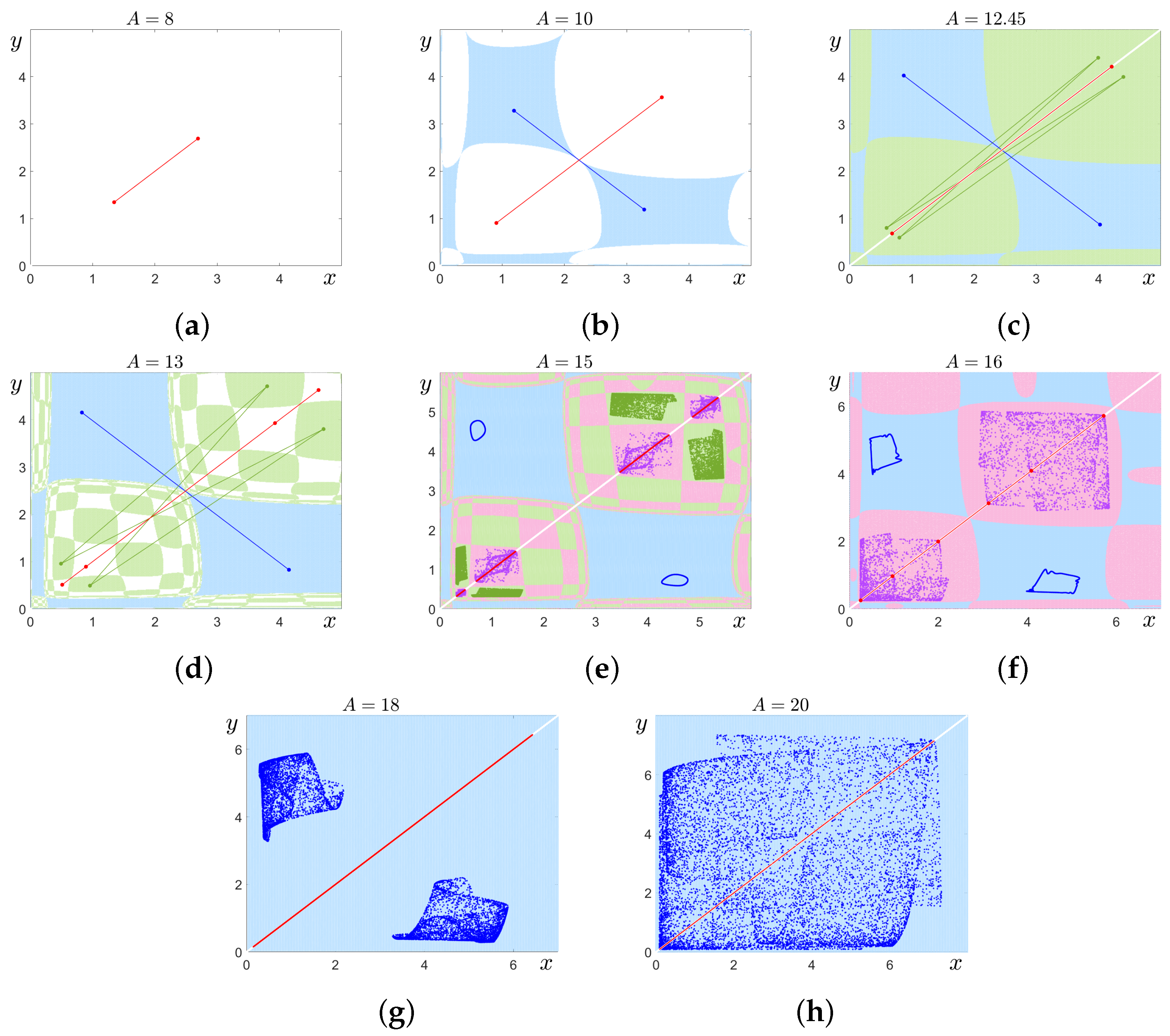
2. Deterministic Model: Multistability, Regular and Chaotic Attractors, and Synchronization
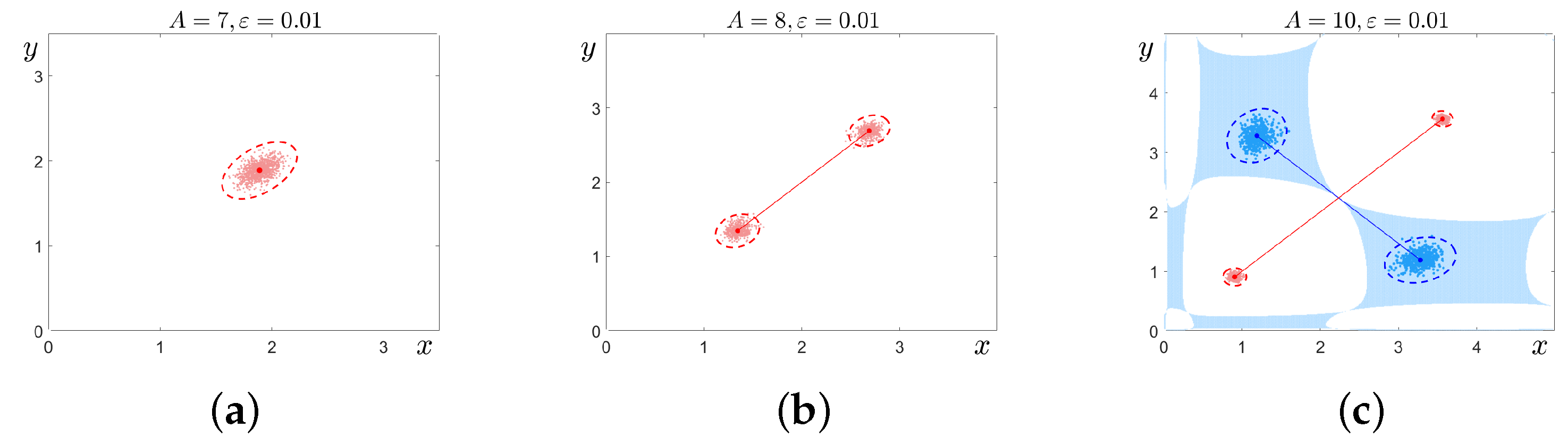
3. Stochastic Model:Analysis of Dispersion of Random States Around Attractors and Noise-Induced Transitions
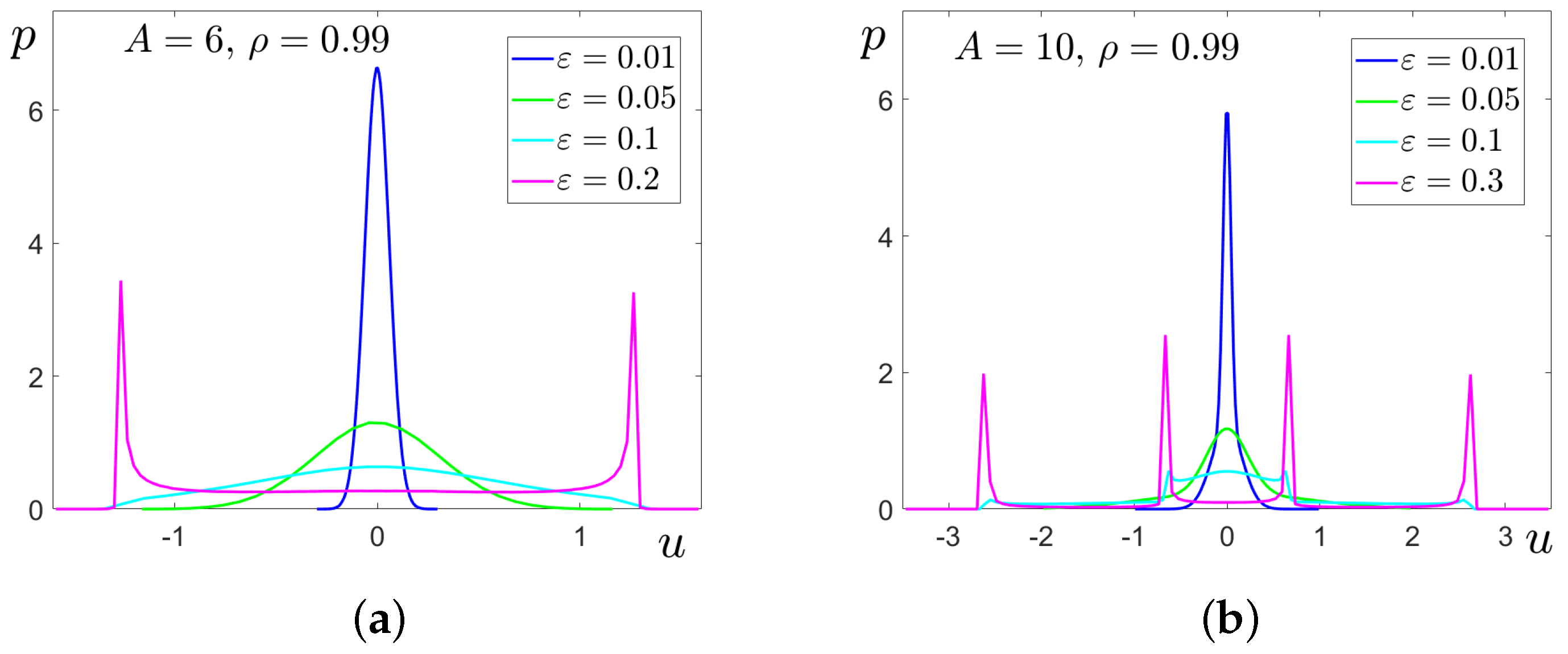
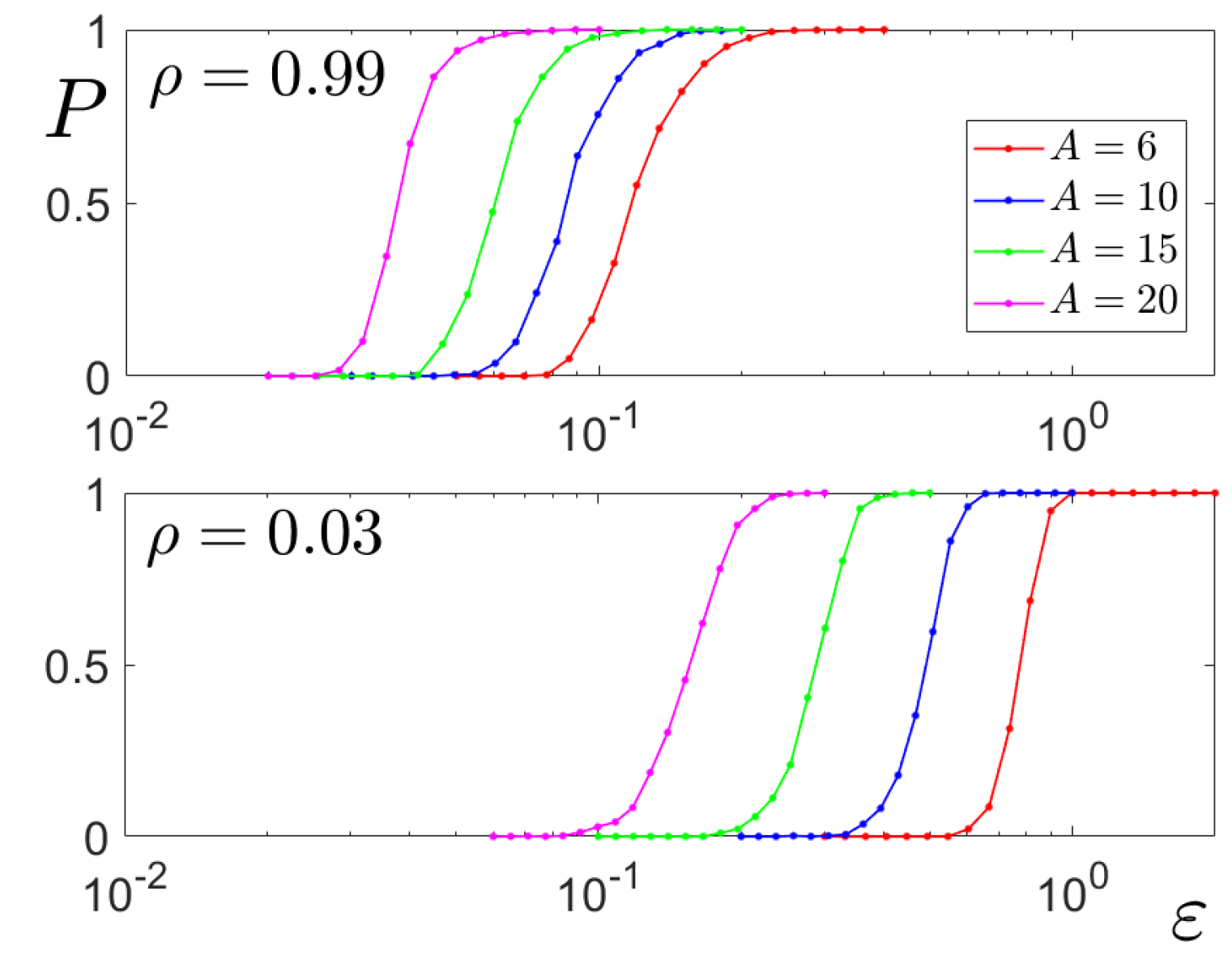
Multistability and Noise-Induced Transitions
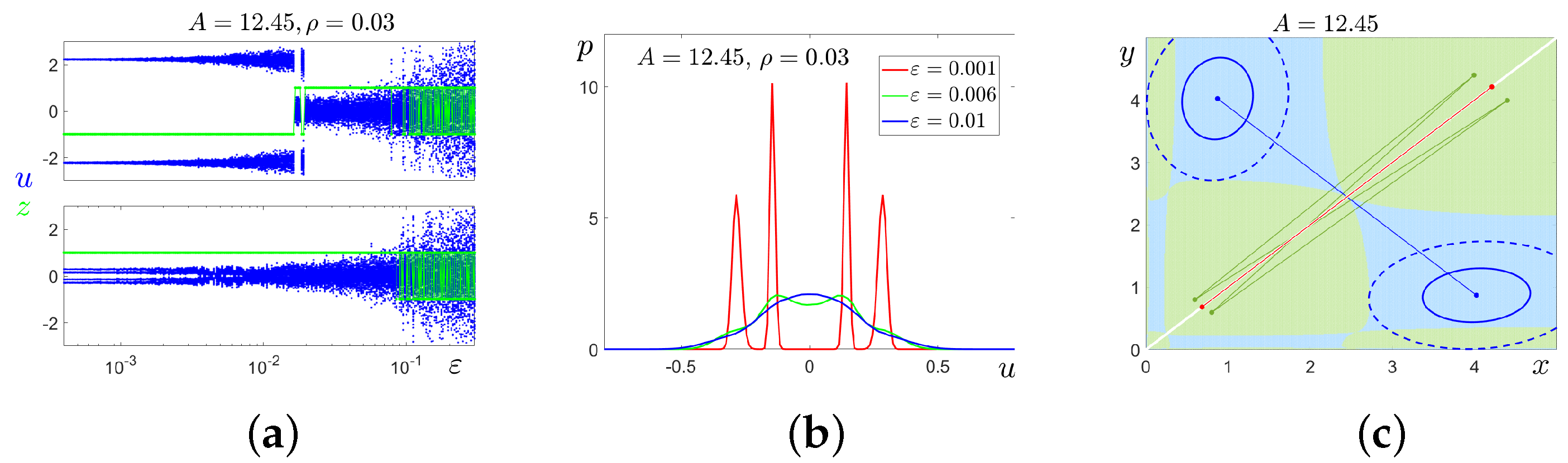
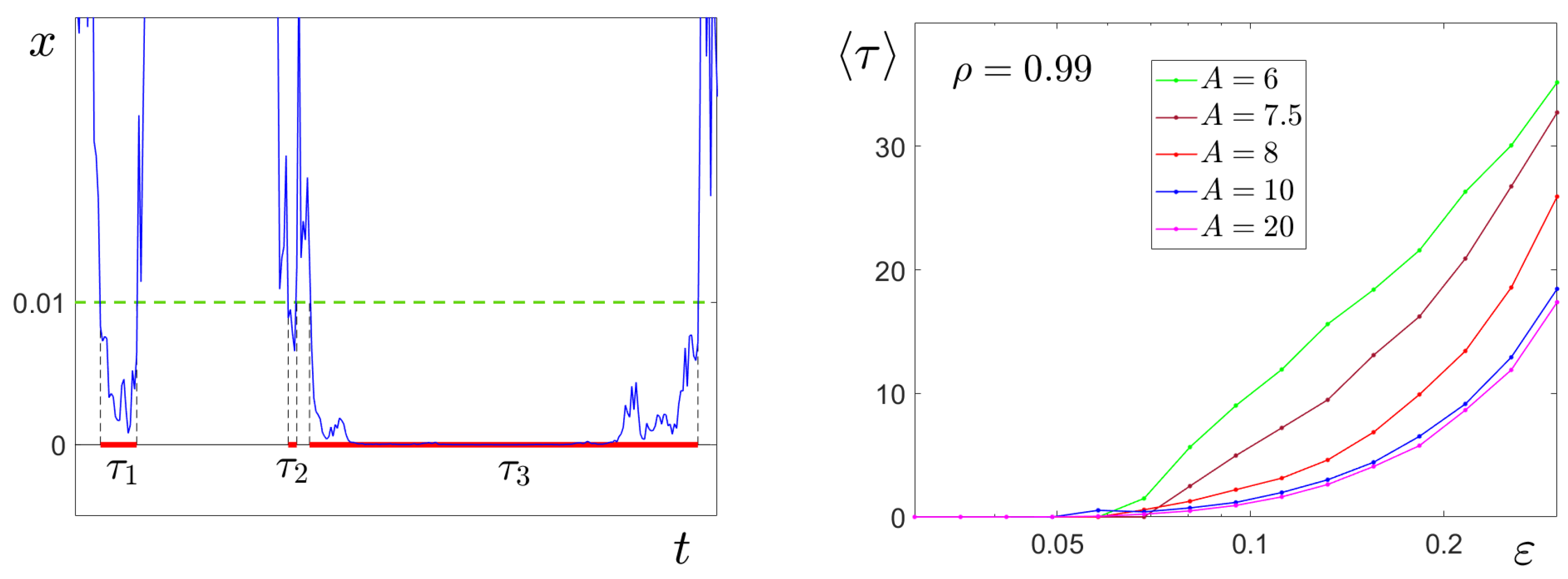
4. Phantom Attractors and Noise-Induced Trigger Regimes
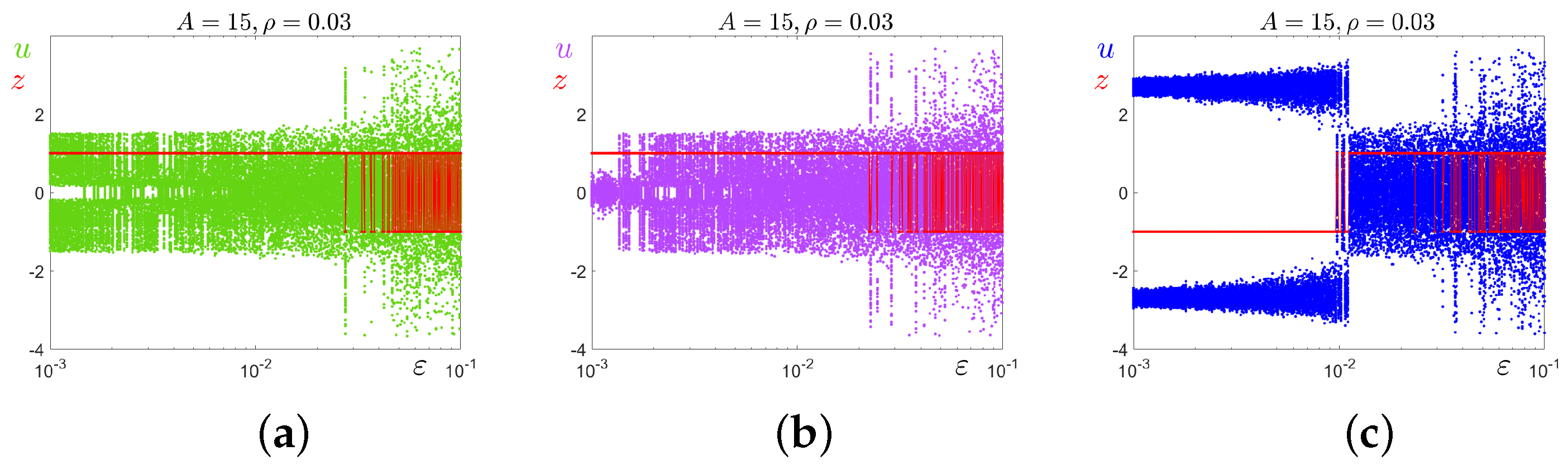
5. Noise-Induced Transitions from Order to Chaos
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hastings, A. Population Biology: Concepts and Models; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Bazykin, A.D. Nonlinear Dynamics of Interacting Populations; World Scientific: Singapore, 1998. [Google Scholar] [CrossRef]
- Turchin, P. Complex Population Dynamics: A Theoretical/Empirical Synthesis; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Shilnikov, L.P.; Shilnikov, A.L.; Turaev, D.V.; Chua, L.O. Methods of Qualitative Theory in Nonlinear Dynamics; World Scientific: Singapore, 1989. [Google Scholar]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Vulpiani, A. Chaos: From Simple Models to Complex Systems; World Scientific: Singapore, 2010. [Google Scholar]
- Bashkirtseva, I.; Ryashko, L. How environmental noise can contract and destroy a persistence zone in population models with Allee effect. Theor. Popul. Biol. 2017, 115, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Naik, P.A.; Eskandari, Z.; Avazzadeh, Z.; Zu, J. Multiple bifurcations of a discrete-time prey–predator model with mixed functional response. Int. J. Bifurc. Chaos 2022, 32, 2250050. [Google Scholar] [CrossRef]
- Belyaev, A.; Bashkirtseva, I.; Ryashko, L. Stochastic variability of regular and chaotic dynamics in 2D metapopulation model. Chaos Solitons Fractals 2021, 151, 111270. [Google Scholar] [CrossRef]
- Kulakov, M.; Neverova, G.; Frisman, E. The Ricker competition model of two species: Dynamic modes and phase multistability. Mathematics 2022, 10, 1076. [Google Scholar] [CrossRef]
- Revutskaya, O.; Neverova, G.; Frisman, E. Discrete-time model of an exploited population with age and sex structures: Instability and the hydra effect. Mathematics 2024, 12, 535. [Google Scholar] [CrossRef]
- Cole, L.C. Competitive exclusion. Science 1960, 132, 348–349. [Google Scholar] [CrossRef]
- Hutchinson, G.E. The paradox of the plankton. Am. Nat. 1961, 95, 137–145. [Google Scholar] [CrossRef]
- Ayala, F. Experimental invalidation of the principle of competitive exclusion. Nature 1969, 224, 1076–1079. [Google Scholar] [CrossRef] [PubMed]
- López-Gómez, J.; Molina-Meyer, M. The competitive exclusion principle versus biodiversity through competitive segregation and further adaptation to spatial heterogeneities. Theor. Popul. Biol. 2006, 69, 94–109. [Google Scholar] [CrossRef]
- Roy, S.; Chattopadhyay, J. Towards a resolution of ‘the paradox of the plankton’: A brief overview of the proposed mechanisms. Ecol. Complex. 2007, 4, 26–33. [Google Scholar] [CrossRef]
- Litchman, E. Resource Competition and the Ecological Success of Phytoplankton. In Evolution of Primary Producers in the Sea; Falkowski, P.G., Knoll, A.H., Eds.; Academic Press: Burlington, NJ, USA, 2007; pp. 351–375. [Google Scholar] [CrossRef]
- Dhondt, A. Interspecific Competition in Birds; Oxford University Press: New York, NY, USA, 2012; p. 296. [Google Scholar]
- Salinas-Ramos, V.B.; Ancillotto, L.; Bosso, L.; Sánchez-Cordero, V.; Russo, D. Interspecific competition in bats: State of knowledge and research challenges. Mammal Rev. 2020, 50, 68–81. [Google Scholar] [CrossRef]
- May, R.M. Biological populations with nonoverlapping generations: Stable points, stable cycles, and chaos. Science 1974, 186, 645–647. [Google Scholar] [CrossRef]
- Luis, R.; Elaydi, S.; Oliveira, H. Stability of a Ricker-type competition model and the competitive exclusion principle. J. Biol. Dyn. 2011, 5, 636–660. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998; p. 323. [Google Scholar]
- Mallet, J. The struggle for existence: How the notion of carrying capacity, K, obscures the links between demography, Darwinian evolution, and speciation. Evol. Ecol. Res. 2012, 14, 627–665. [Google Scholar]
- Chen, S.; Shi, J.; Shuai, Z.; Wu, Y. Global dynamics of a Lotka–Volterra competition patch model. Nonlinearity 2022, 35, 817. [Google Scholar] [CrossRef]
- Boccaletti, S.; Pisarchik, A.N.; del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Huitu, O.; Norrdahl, K.; Korpimäki, E. Competition, predation and interspecific synchrony in cyclic small mammal communities. Ecography 2004, 27, 197–206. [Google Scholar] [CrossRef]
- Greenman, J.V.; Benton, T.G. The impact of environmental fluctuations on structured discrete time population models: Resonance, synchrony and threshold behaviour. Theor. Popul. Biol. 2005, 68, 217–235. [Google Scholar] [CrossRef]
- Rasmussen, N.L.; Rudolf, V.H. Phenological synchronization drives demographic rates of populations. Ecology 2015, 96, 1754–1760. [Google Scholar] [CrossRef]
- Jarillo, J.; Sæther, B.E.; Engen, S.; Cao-García, F.J. Spatial scales of population synchrony in predator-prey systems. Am. Nat. 2020, 195, 216–230. [Google Scholar] [CrossRef]
- Toepfer, J.D.; Sigurdsson, H.; Alyatkin, S.; Lagoudakis, P.G. Lotka-Volterra population dynamics in coherent and tunable oscillators of trapped polariton condensates. Phys. Rev. B 2020, 102, 195428. [Google Scholar] [CrossRef]
- Lande, R.; Engen, S.; Saether, B.E. Stochastic Population Dynamics in Ecology and Conservation; Oxford University Press: Oxford, UK, 2003. [Google Scholar] [CrossRef]
- Ovaskainen, O.; Meerson, B. Stochastic models of population extinction. Trends Ecol. Evol. 2010, 25, 643–652. [Google Scholar] [CrossRef] [PubMed]
- Santra, N.; Mondal, S.; Samanta, G. Complex dynamics of a predator–prey interaction with fear effect in deterministic and fluctuating environments. Mathematics 2022, 10, 3795. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Analysis of stochastic dynamics in a multistable logistic-type epidemiological model. Eur. Phys. J. Spec. Top. 2022, 231, 3563–3575. [Google Scholar] [CrossRef]
- Wang, Q.; Zu, L.; Jiang, D.; O’Regan, D. Study on dynamic behavior of a stochastic predator–prey system with Beddington–DeAngelis functional response and regime switching. Mathematics 2023, 11, 2735. [Google Scholar] [CrossRef]
- Chesson, P.L.; Ellner, S. Invasibility and stochastic boundedness in monotonic competition models. J. Math. Biol. 1989, 27, 117–138. [Google Scholar] [CrossRef]
- Dallas, T.; Melbourne, B.; Hastings, A. Community context and dispersal stochasticity drive variation in spatial spread. J. Anim. Ecol. 2020, 89, 2657–2664. [Google Scholar] [CrossRef]
- Hening, A.; Nguyen, D.H. The competitive exclusion principle in stochastic environments. J. Math. Biol. 2020, 80, 1323–1351. [Google Scholar] [CrossRef]
- Wei, H.; Li, W. Dynamical behaviors of a Lotka–Volterra competition system with the Ornstein–Uhlenbeck process. Math. Biosci. Eng. 2023, 20, 7882–7904. [Google Scholar] [CrossRef]
- Lerch, B.A.; Rudrapatna, A.; Rabi, N.; Wickman, J.; Koffel, T.; Klausmeier, C.A. Connecting local and regional scales with stochastic metacommunity models: Competition, ecological drift, and dispersal. Ecol. Monogr. 2023, 93, e1591. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Q. Asymptotic stability of a stochastic Lotka–Volterra competition model with dispersion and Ornstein–Uhlenbeck process. Appl. Math. Lett. 2024, 157, 109163. [Google Scholar] [CrossRef]
- Shaikhet, L.; Korobeinikov, A. Asymptotic properties of the Lotka–Volterra competition and mutualism model under stochastic perturbations. Math. Med. Biol. A J. IMA 2024, 41, 19–34. [Google Scholar] [CrossRef] [PubMed]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Inoue, J.; Doi, S.; Kumagai, S. Numerical analysis of spectra of the Frobenius-Perron operator of a noisy one-dimensional mapping: Toward a theory of stochastic bifurcations. Phys. Rev. E 2001, 64, 056219. [Google Scholar] [CrossRef] [PubMed]
- Bashkirtseva, I.; Ryashko, L. Stochastic Sensitivity Analysis of Noise-Induced Phenomena in Discrete Systems. In Recent Trends in Chaotic, Nonlinear and Complex Dynamics; World Scientific Series on Nonlinear Science Series B; World Scientific: Singapore, 2021; Chapter 8; pp. 173–192. [Google Scholar] [CrossRef]
- Huang, M.; Yang, A.; Yuan, S.; Zhang, T. Stochastic sensitivity analysis and feedback control of noise-induced transitions in a predator–prey model with anti–predator behavior. Math. Biosci. Eng. 2023, 20, 4219–4242. [Google Scholar] [CrossRef] [PubMed]
- Bashkirtseva, I.; Ryashko, L. How additive noise generates a phantom attractor in a model with cubic nonlinearity. Phys. Lett. A 2016, 380, 3359–3365. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Ryashko, L. Stochastic bifurcations, chaos and phantom attractors in the Langford system with tori. Int. J. Bifurc. Chaos 2020, 30, 2030051. [Google Scholar] [CrossRef]
- Ryashko, L.; Bashkirtseva, I. Noise-induced chaos and generation of phantom attractors in a birhythmic neuron model. Chaos Solitons Fractals 2025, 191, 115841. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1998; p. 600. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryashko, L.; Otman, A.; Bashkirtseva, I. Multirhythmicity, Synchronization, and Noise-Induced Dynamic Diversity in a Discrete Population Model with Competition. Mathematics 2025, 13, 857. https://doi.org/10.3390/math13050857
Ryashko L, Otman A, Bashkirtseva I. Multirhythmicity, Synchronization, and Noise-Induced Dynamic Diversity in a Discrete Population Model with Competition. Mathematics. 2025; 13(5):857. https://doi.org/10.3390/math13050857
Chicago/Turabian StyleRyashko, Lev, Anna Otman, and Irina Bashkirtseva. 2025. "Multirhythmicity, Synchronization, and Noise-Induced Dynamic Diversity in a Discrete Population Model with Competition" Mathematics 13, no. 5: 857. https://doi.org/10.3390/math13050857
APA StyleRyashko, L., Otman, A., & Bashkirtseva, I. (2025). Multirhythmicity, Synchronization, and Noise-Induced Dynamic Diversity in a Discrete Population Model with Competition. Mathematics, 13(5), 857. https://doi.org/10.3390/math13050857







