AE-XGBoost: A Novel Approach for Machine Tool Machining Size Prediction Combining XGBoost, AE and SHAP

Abstract

To achieve intelligent manufacturing and improve the machining quality of machine tools, this paper proposes an interpretable machining size prediction model combining eXtreme Gradient Boosting (XGBoost), autoencoder (AE), and Shapley additive explanation (SHAP) analysis. In this study, XGBoost was used to establish an evaluation system for the actual machining size of computer numerical control (CNC) machine tools. The XGBoost model was combined with SHAP approximation to effectively capture local and global features in the data using autoencoders and transform the preprocessed data into more representative feature vectors. Grey correlation analysis (GRA) and principal component analysis (PCA) were used to reduce the dimensions of the original data features, and the synthetic minority overstimulation technique of the Gaussian noise regression (SMOGN) method was used to deal with the problem of data imbalance. Taking the actual size of the machine tool as the response parameter, based on the size parameters in the milling process of the CNC machine tool, the effectiveness of the model is verified. The experimental results show that the proposed AE-XGBoost model is superior to the traditional XGBoost method, and the prediction accuracy of the model is 7.11% higher than that of the traditional method. The subsequent SHAP analysis reveals the importance and interrelationship of features and provides a reliable decision support system for machine tool processing personnel, helping to improve processing quality and achieve intelligent manufacturing.

1. Introduction

Predicting the quality of the machine tool is the basis and the prerequisite for intelligent machine tool manufacturing and closed-loop control of the machine tool. Therefore, many scholars have carried out in-depth research on the factors affecting machining quality, and analyzed the impact of tools’ geometric parameters, cutting parameters, cutting fluid type, CNC component performance degradation, chatter, dynamic and static characteristics of a tool-works-jig machine tool system, thermal deformation and thermal error and other factors affecting machining quality. Based on directional importance sampling, the Monte Carlo simulation, Zhang et al. [1] proposed a reliability evaluation method for machining accuracy that considered both geometric and vibration errors. Sato et al. [2] developed a nonlinear friction model that takes into account the relationship between friction and vibration and proposed a method to evaluate the impact of tool–chip contact on vibration characteristics; then they evaluated the effects of nonlinear friction and process damping through simulation analysis. Sun et al. [3] used laser texture to make pits on tool surfaces and conducted cutting experiments; the results show that the surface roughness of textured tools is lower than that of non-textured tools, and there is a critical value for the pit diameter on textured tools that will affect the surface roughness of the machined workpiece. Zhang et al. [4] developed an integrated model of the ball screw and cutting process and, based on the proposed model and experimental verification, investigated the effect of harmonics on the surface quality of the final machined part. Liu et al. [5] proposed a robust modeling method based on separated unbiased grey relation analysis, aiming to reduce the collinearity of temperature-sensitive points and select the temperature point with the greatest influence weight, thereby reducing the model accuracy decline caused by fluctuations in temperature-sensitive points. Huang et al. [6] established an integrated model for predicting milling machining accuracy by combining mechanical structure, control system, and cutting force, which significantly improved the reliability of CNC machine tool design by accurately simulating actual machining conditions; at the same time, the correct use of cutting fluid, coupled with the application of external lubrication and cooling methods, is also conducive to improving processing quality, thereby improving the performance of the machine tool [7,8,9].

With the development of technology, neural networks and machine vision technology are applied to predict the machining quality of machine tools. Considering the differences between human-induced faults in a laboratory setting and those encountered in real-world scenarios, Tan et al. [10] introduce a deeply coupled joint distributed adaptive network that enhances the detection of machine tool performance and provides a basis for predictive modeling of machining quality. Liu et al. [11] proposed a tool wear identification method based on analyzing textures generated during machining based on variable-magnifying lenses. Chen et al. [12] proposed a large-scale surface roughness detection method based on machine vision. Shi et al. [13] used wavelet transform to decompose the spindle power signal of the machine tool into feature scale, which was used as an input variable of the support vector machine to predict tool wear and evaluate workpiece machining quality. Song et al. [14] used the deep convolutional neural network model to extract features from the spindle current noise signal and used them as the classification index for four types of milling cutter wear state, thus realizing the monitoring of milling cutter state and workpiece processing quality. Tang et al. [15] developed an online monitoring system for disk milling cutter wear and machining quality prediction by combining current monitoring with the BP neural network and using the GA-BP algorithm to improve the prediction model.

XGBoost [16] is an improved gradient lift tree algorithm that has been widely used in many fields and its effectiveness in solving complex predictive modeling problems has been verified. Qu et al. [17] developed a robust feature recognition model for urban road traffic accidents, which has advantages in identifying key accident features and provides valuable insights for improving traffic safety and developing intelligent transportation systems. Lin et al. [18] established a prediction model of the transverse tensile strength of the self-thrust riveted joint based on the self-thrust riveted dataset of experimental tests and finite element simulation and trained the regression model with the XGBoost algorithm. Dai et al. [19] introduced an enhanced short-term power load forecasting method, which combined the BiLSTM model with an attention mechanism with XGBoost, and with a weighted grey relation projection algorithm for data pre-processing. The accuracy and reliability of the proposed method are verified by predicting the power load in the Singapore and Norway markets. Cao et al. [20] propose an improved XGBoost model that combines a window mechanism and random grid search to enhance short-term regional power load self-prediction and shows better predictive performance and generalization ability on four datasets compared to five alternative models. Han et al. [21] introduce an edge-computing-enabled framework that uses the optimized SMOTE-XGBoost model for unbalanced data quality monitoring in an industrial IoT environment and improves classification accuracy and efficiency during product assembly. Wan et al. [22] used the XGBoost machine learning algorithm to establish a highly accurate mass flow prediction model for refrigerants in electronic expansion valves, which significantly improved the prediction performance, optimized the efficiency of refrigeration systems, and provided effective control strategies. Based on the adaptive self-learning adjustment method, Zhang et al. [23] proposed an improved XGBoost algorithm, which was optimized by the improved bat algorithm to solve the problems of strong coupling and low precision in the existing strip thickness control mathematical model. Chen et al. [24] proposed an optimized XGBoost model based on an improved sparrow search algorithm to predict milling-cutter wear under variable operating conditions. The model integrated a recursive feature elimination algorithm for feature selection and showed high recognition accuracy and prediction performance. Lan [25] uses AE to extract features and reduce dimensions of high-dimensional network traffic data, remove redundant information, and combine with the powerful learning ability of XGBoost to classify and predict the reduced data, which improves detection accuracy. Shan [26] uses AE to reduce noise and extract features from the monitoring data of electric gate valves. XGBoost analyzes features and diagnoses faults, which reflects that AE can deal with data noise and XGBoost can mine potential relationships in data.

In the prediction of tool wear, fault detection, and product quality in machining operations, the main categories usually represent the normal or defect-free machining state. While a few categories indicate the presence of anomalies or defects, these anomalies or defects typically occur much less frequently than canonical states, resulting in an unbalanced data distribution in the collected dataset. For the problem of data imbalance, Chawla et al. [27] put forward the synthetic minority over-sampling technique (SMOTE) to solve the problem of class imbalance in the dataset. They used the SMOTE to improve classifier performance for a few categories in various datasets and compared it with other methods such as under-sampling and changing misclassification loss functions in existing algorithms such as Ripper and naïve Bayes. Khan et al. [28] conducted extensive research on the combination, implementation, and evaluation of ensemble learning methods and data enhancement techniques for solving class imbalance problems, and gained insight into their effectiveness and applicability in various fields.

For the problem of data imbalance in regression tasks, Torgo et al. [29] proposed an improved SMOTE method to synthesize samples to balance the distribution of target variables. Branco et al. [30] introduced a new preprocessing method called SMOGN, which combined under-sampling and two over-sampling techniques to solve the unbalanced regression problem, and evaluated the effectiveness of the proposed method through extensive experimental evaluation of various regression datasets and learning algorithms. Avelino et al. [31] conducted a comprehensive investigation and empirical analysis of resampling strategies for unbalanced regression. They proposed a new taxonomy and validated the effectiveness of various techniques across multiple datasets and learning algorithms while highlighting the impact of dataset characteristics on model performance. To improve the performance of models in regression tasks affected by unbalanced data, some researchers also explored the introduction of neural networks to solve these problems. Nguyen et al. [32] introduced a new approach to integrate a differentiable fuzzy logic system into a generative adversarial network to enhance its regression capabilities. They emphasized that fuzzy logic is effective in improving the stability and performance of generative adversarial networks in regression tasks.

By studying the current mainstream hybrid machine learning (ML) prediction models, Simona et al. [33] used autoencoders in clinical data for various purposes such as dimensionality reduction, denoising, feature extraction, and anomaly detection. XGBoost was trained based on features extracted from AE features. The combination of the two improves the prediction performance and generalization ability and improves the prediction ability of data in clinical data. In terms of soft sensing modeling, the parallel LSTM autoencoder proposed by Ge Zhiqiang [34] extracts dynamic features through the parallel training of data and models. After the original features are merged, XGBoost trains the model based on this to achieve efficient and accurate soft sensing modeling, which improves the prediction performance and robustness. In the field of machine tool processing, Zhao Hongshan et al. [35] used AE and XGBoost for generator fault diagnosis of wind turbines, which not only improved the prediction accuracy but also reduced the computational complexity due to the dimension reduction in AE and improved the overall performance. In practice, the model performance can be optimized by adjusting the structure of AE and XGBoost hyperparameters, such as the convolutional layer of AE and the number of nodes [36], or the learning rate of XGBoost and the maximum depth of the tree to balance the training speed and prediction accuracy.

Summarizing the previous research results of hybrid machine learning, it is found that the data imbalance is not considered enough in the machine tool machining size prediction: there are problems of data redundancy and high complexity, and there is a lack of effective methods to combine feature extraction and model prediction. Therefore, our proposed AE-XGBoost model fills this gap and inherits the autoencoder for feature extraction. XGBoost is used for prediction, SMOGN is used to process the imbalance data, and finally, SHAP is used for interpretation to help engineers intuitively understand the model behavior, so as to better optimize the processing parameters and model size. Various previous hybrid MLs are shown in

Table 1. Summary of multiple hybrid ML models.

Hybrid ML Model	Model Composition	Key of Implementation	Application Scenarios	Advantages and Disadvantages of Performance
XGBoost-LightGBM ensemble model	XGBoost + LightGBM	XGBoost and LightGBM models were initialized using open-source machine learning frameworks, and the respective hyperparameters were adjusted to fuse the predicted values through weighted averages or voting mechanisms.	Industrial process monitoring and forecasting based on large-scale datasets.	Advantages: can handle large-scale data; disadvantages: hyperparameter tuning is more complex and more sensitive to data noise.
Random forest-Adaboost ensemble model	Random forest + AdaBoost	Random forest and AdaBoost models were built in Python with the help of the Scikit-learn library to integrate the prediction output.	Prediction of machining size for small machine tools with high machining accuracy	Advantages: good robustness, can handle high-dimensional data; disadvantages: longer training time on large datasets and poor model interpretation.
CNN-LSTM Mixed model	CNN + LSTM	A deep learning framework was used to construct the CNN part, connect the LSTM layer, and train the model with loss functions such as mean square error.	A machine tool process characterized by a space-time sequence	Advantages: it can effectively capture spatiotemporal characteristics, and has strong modeling ability for complex time series data. Disadvantages: model training requires a large amount of data and computational resources, takes a long time to train, and is prone to overfitting.
Stacking fusion model	Base model + meta-learner	The training and validation sets were divided, and multiple base models were trained. A new dataset was constructed using the prediction results of the validation set to train the meta-learner, and the model parameters of each stage were adjusted.	A variety of machine tool processing scenarios, especially when the processing data sources are diverse and complex features	Advantages: it can integrate the advantages of multiple models to improve prediction performance and generalization ability. Disadvantages: high model complexity, cumbersome training process, and high computational cost.
Blending fusion model	Fusing different models trained on different subsets	Different models were trained with different subsets. The fusion weight was determined according to the performance of the validation set, and the fusion predictive value was weighted.	Machine tool processing scenarios that require rapid construction of prediction models	Advantages: the training speed is relatively fast and the model fusion method is simple. Disadvantages: it is sensitive to data subset division and may lose part of the information.
AE-XGBoost Model	AE + XGBoost	The autoencoder architecture was built by PyTorch or TensorFlow, and the coding features were obtained after pre-training, which were sent to the XGBoost model in Scikit-learn for training and prediction.	Machine tool processing data have high dimension, redundancy, and unobvious features, such as size prediction in complex machine tool processing with multi-process and multi-parameter.	Advantages: autoencoder can effectively perform feature extraction and dimensionality reduction, and remove redundant information and noise, while XGBoost can make efficient and accurate prediction based on the extracted features. The combination of the two can improve the performance and generalization ability of the model, and the requirement for data preprocessing is relatively low. Its uniqueness lies in the combination of unsupervised feature learning (autoencoder) and supervised prediction (XGBoost), which gives full play to the advantages of both, and has better adaptability and accuracy when processing complex machine tool processing data.

below.

The following chapters are as follows. Section 2 is the methodology of this paper, introducing the overall description of the model, the three preprocessing methods, the construction of the AE-XGBoost model, and the visualization and interpretation model of the model results—SHAP analysis model in sequence. In Section 3, the experimental verification is carried out, and the data source, software and hardware configuration, Results and Analysis of Data Screening Processing, Results and Analysis of Prediction of AE-XGBoost and XGBoost, Results and Analysis of feature interpretation based on SHAP analysis, Results, and Analysis of Dimensions Interpretation based on SHAP Analysis are presented in turn; the results are then discussed. Section 4 summarizes the findings and suggests future research directions.

2. AE-XGBoost Model Construction

2.1. Global Model Description

The AE-XGBoost model developed in this paper is short for autoencoder-XGBoost. The advantages of AE and XGBoost are utilized to better process and analyze the machine tool machining dimensional prediction problems. An autoencoder automatically learns important features in the input data and compresses high-dimensional data into a low-dimensional representation. The encoder maps the input data to a low-dimensional latent space, and the decoder reconstructs the original data from the latent space. XGBoost is an efficient gradient-boosting algorithm that performs well in classification and regression tasks. It builds strong learners by integrating multiple weak learners (usually decision trees) that are capable of handling complex nonlinear relationships. Combining AE with the XGBoost model can use AE to learn the intrinsic structure of the data to extract features, better characterize the XGBoost input data size, improve the prediction ability of the error data by using the structural characteristics of the AE error robustness, and also reduce the model’s dependence on specific data distributions by combining the two to achieve better generalization ability.

In addition, the input data for machine tool prediction usually exists in multivariate data, which increases the workload of data collection and the complexity of problem analysis to a certain extent. Therefore, it is necessary to use the principal component analysis, PCA, method to downsize the data to achieve a reduction in indicators to be analyzed while minimizing the loss of information contained in the original indicators; at the same time, it is necessary to combine with the correlation analysis method because if each indicator is analyzed separately, it is easy to blindly downsize the data and lose a large amount of useful information; therefore, combining with the GRA to study the relationship between data dimensions and the resultant prediction to understand the relative strength of the impact of certain residual size factors on the machining size. The imbalance of machine tool size data is also a common problem, so it is necessary to process the data. The core idea of the SMOGN algorithm selected in this paper is to synthesize new minority samples to balance the dataset. For each size data in the minority class, SMOGN will add a certain amount of Gaussian noise to its feature space to add new size data. The initial data are preprocessed by a combination of PCA, GRA, and SMOGN to provide more effective data input for subsequent prediction models.

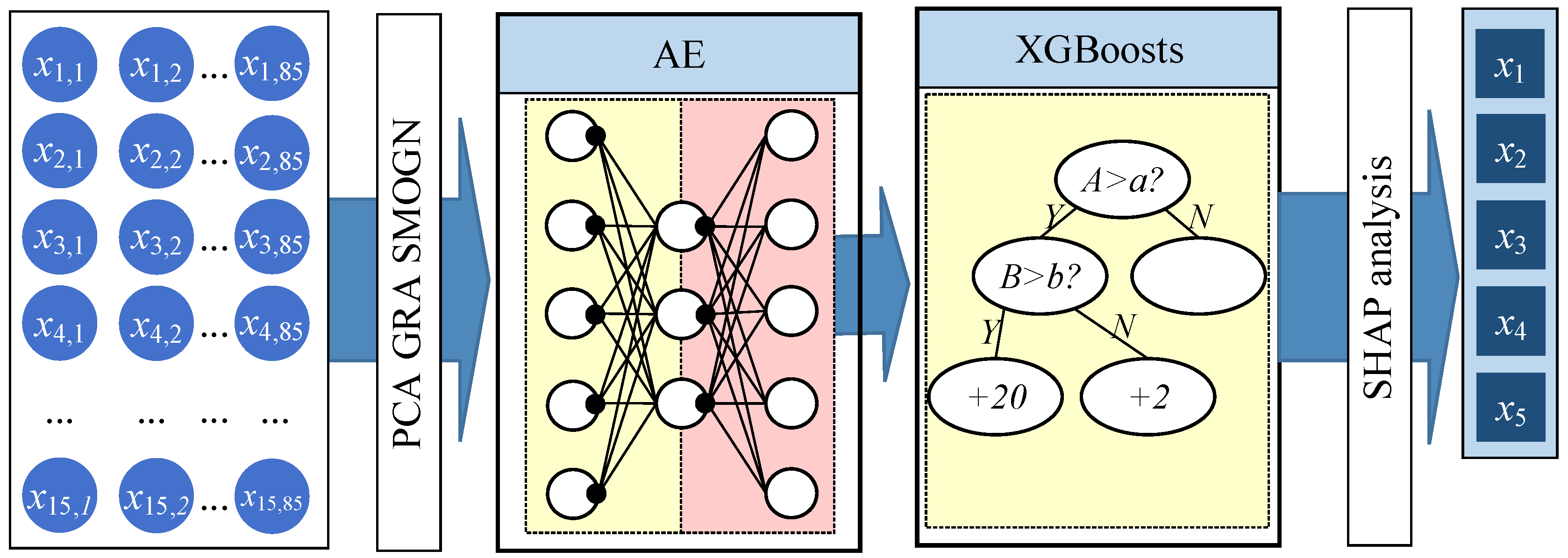
SHAP [37] values are calculated based on Shapley values in cooperative game theory to fairly distribute the contribution of model predictions among the individual features and are used in this model to quantify the contribution of dimensional features to dimensional prediction results and to verify safe ranges for important dimensions. The overall model, as shown in Figure 1, demonstrates how the data flow from input, preprocessing, and between the AE, XGBoost, and SHAP analysis modules, as well as the internal structure and connectivity of each module.

As can be seen in Figure 1, the data related to machine tool processing is used as input to the overall model, including numerical data such as positioning accuracy, repetitive positioning accuracy, clamping rigidity, etc. The size of the input data is 15 × 85, which can be used as a part of the subsequent processing; and then, through the data pre-processing, the data are subjected to PCA dimensionality reduction, GRA correlation analysis, and SMOGN imbalance processing in order; then the data are passed into the self-encoder for feature extraction.

Self-encoder contains an encoder, bottleneck, and decoder; the encoder reduces the input size and compresses the input data into coded form; the bottleneck represents a potential space, which contains all the hidden variables, that is, the smallest features that exist in the space obtained, this is the smallest size of the input data, the minimum number of neurons; the decoder is the inverse of the encoder, which is the role of the realization of data reconstruction, so that the coded representation of the bottleneck layer is as close as possible to the original input data, and verifies the model compression effect.

Subsequently, the potential spatial data of the self-encoder are used as the input features of the XGBoost model, and the combination of the original numerical data and the advanced features extracted by deep learning is passed into the XGBoost prediction module; XGBoost constructs multiple decision trees based on the principle of gradient boosting, and each decision tree learns the patterns in the data by splitting the input features to predict the machining dimensions of the machine tool, and the prediction results of the multiple decision trees are weighted by the weighting of the input features. The prediction results of multiple decision trees are integrated by weighted summation to obtain the final prediction value.

The trained XGBoost model is used to create a SHAP interpreter, which calculates the contribution of each input feature to the model prediction (i.e., SHAP value), which can be used to interpret the model’s prediction, and shows how each feature affects the prediction result and the interactions between the features through the visualization of the feature importance graph and SHAP dependency graph. The model results contain the XGBoost model predictions.

The model results contain the predicted values of the XGBoost model output machine tool dimensions, which can be used for quality control, process optimization, and other applications in real-world production, as well as the interpreted results provided by the SHAP analysis, which help to understand the model’s prediction process by showing which features are critical factors for further optimization of the model and the machining process.

The information flow is as follows: the raw data first enters the PCA block, where principal components are calculated. These components are then passed to the grey correlation analysis (GRA) block. The GRA block outputs a ranked list of features based on their correlation significance, which is then used as input to the autoencoder. The SMOGN method is applied to the original dataset before PCA to address data imbalance issues, ensuring that the subsequent processing steps work on a more representative sample.

2.2. Data Preprocessing Method

Data preprocessing includes three methods, at first, PCA is used for the dimensionality reduction in data, then relational analysis is conducted based on the GRA, and finally, SMOGN is used for unbalanced processing of data. The following describes how to use each method in detail.

A. Data dimensionality reduction based on PCA

PCA is a method for dimensionality reduction in high dimensional feature data, which makes the machine tool processing dimension dataset easier to use and reduces the computation amount of the algorithm. The raw data features are of high dimensionality and vary considerably in the dimension of the influence of different factors during machining on various machine tools, such as positioning accuracy, repeatability, clamping rigidity, machining material, initial heat treatment status of the material, tool structure, tool material, number of cutting edges, cutting edge length, and the amount of free-state oscillation. According to the PCA method, we first set the dataset $X_{n\times m}=[x_1,x_2\cdots ,x_m]$, representing 15 features, $m$ = 15, where each $X$ is an n-dimensional column vector. Decentralization first, and then the average value of each feature is subtracted as follows:

$$X=X-{\displaystyle \frac{1}{m}}{\displaystyle {\sum }_{i=1}^m{x}_i}$$

(1)

Then, the covariance matrix $C={\displaystyle \frac{1}{m}}X{X}^T$, and eigenvalue decomposition of the covariance matrix are calculated to obtain the eigenmatrix, arranged in columns from the largest to the smallest eigenvalues, and the first $k$ columns are taken to form the matrix $P_{n\times k}$, where $k$ is the target dimension, $P$ is equivalent to a coordinate system, and each column in $P$ is a coordinate axis. The data after dimensionality reduction can be obtained by projecting the original data into the $P$ coordinate system. $Y_{k\times m}=P_{n\times k}^T{X}_{n\times m}$ can reduce the dimension of 15-dimensional data to a new space of 5 feature vectors.

B. Data relational processing based on GRA

GRA is a method used to analyze the degree of correlation between factors in a system, and in machine tool dimensional analysis, it is possible to quantify the degree of influence of influencing factors on machining dimensions. GRA can help determine which factors are most closely related to machining dimensions, and it can also be used to screen out key factors efficiently, reducing the complexity of data analysis and making the analysis of machine tool dimensions more efficient and accurate. According to the PCA method, dimensionless processing is carried out on the machine tool dimensions dataset, as shown in the equation below:

$$x_i(k)={\displaystyle \frac{x_i^{\prime }(k)}{\frac{1}{m}{\displaystyle {\sum }_{k=1}^m{x}_i^{\prime }(k)}}}$$

(2)

Then calculate the grey relation coefficient of each factor, as shown in the formula below:

$${\zeta }_i(k)={\displaystyle \frac{{\min }_i{\min }_k\left|x_0(k)-x_i(k)\right|+\rho •{\max }_i{\max }_k\left|x_0(k)-x_i(k)\right|}{\left|x_0(k)-x_i(k)\right|+\rho •{\max }_i{\max }_k\left|x_0(k)-x_i(k)\right|}}$$

(3)

where $x_0(k)$ is the reference column, $k=1,\cdots ,m$. $\rho$ is the resolution coefficient, $\rho$ represents the differentiation coefficient used to control the degree of differentiation, its value is set to 0.5, the smaller the $\rho$, the greater the difference between the relation coefficients, the stronger the differentiation ability.

Then calculate the grey-weighted relation degree, and the mean value of this column is the final score, as shown in the formula below:

$$r_i={\displaystyle \frac{1}{m}}{\displaystyle \sum _{k=1}^m{\zeta }_i(k)}$$

(4)

C. Data imbalance processing based on SMOGN

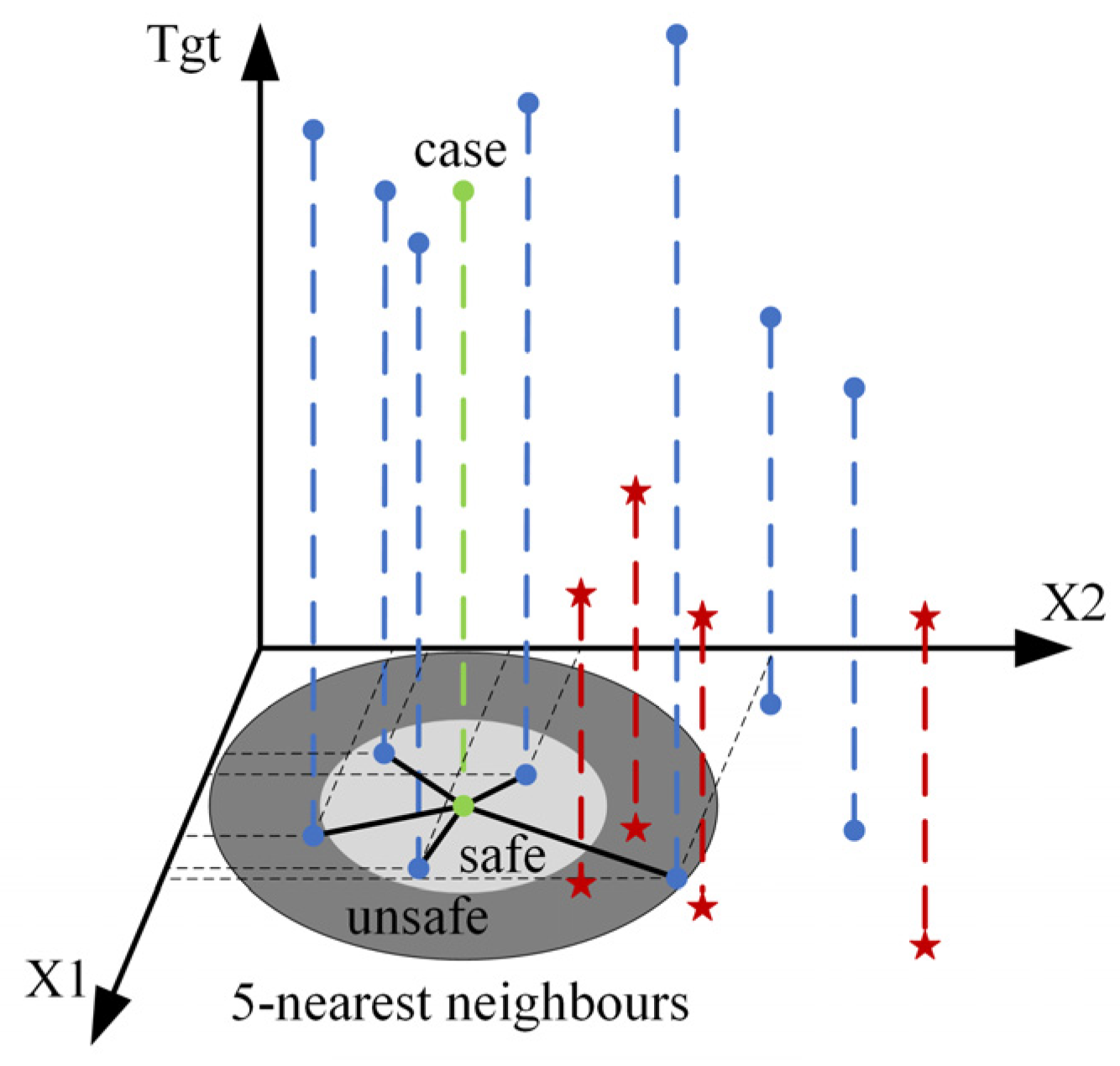
The SMOGN algorithm will also be used to deal with the imbalance of the dataset before constructing the XGBoost model, including interpolating the minority class samples to generate synthetic samples to increase the number of minority class samples. Also, this method reduces the number of large samples in the process of generating new samples. The specific steps of the over-sampling algorithm are as follows: first, the distance between the seed sample and its farthest and nearest neighbor is calculated, and half of this distance is selected as the safety margin. Next, a safe zone for the seed sample is established according to this margin. Samples are classified as “safe” or “unsafe” based on whether the distance between the seed and its neighbors exceeds the safety margin. If the selected neighbor is within the “safe” margin, it is suitable to use the synthetic minority over-sampling technique (SmoteR) policy. Conversely, if the selected neighbor exceeds the “safe” margin, it is considered too far from the interpolation. That means in this case, it is best to introduce Gaussian noise to the seed sample to generate a new sample.

Figure 2 shows a composite example of a seed sample and its 5 closest neighbors. “Tgt” represents the samples showing high relation; the high relation category is represented by the blue dotted line with dots at both ends; the low relation category is represented by the red dotted line with asterisks at both ends; the “case” represents the parameters and dimension results corresponding to a certain processing operation, set as the seed sample; and the horizontal and vertical coordinates represent two different processing parameters. The dark gray “Safe” indicates the area where the data points whose processing dimensions are within the safety margin are distributed, while the light gray “unsafe” indicates the area where the data points whose processing dimensions are within the unsafe margin are located. Different interpolation methods are adopted in the two zones. “Five-nearest neighbors” represent the 5 other data points closest to the seed sample in the data control. The effect is that if the dataset has far more qualified data points than unqualified data points, a few classes of samples can be processed based on the division of the “safe” and “unsafe” zones and the nearest neighbor information. A few class samples are selected in the “unsafe” area, and then new minority class samples are generated by using the information of its nearest neighbors through the over-sampling technology in the SMOGN algorithm to balance the dataset and improve the model’s ability to identify abnormal processing dimensions.

2.3. AE-XGBoost Model

A: AE Structural Foundations

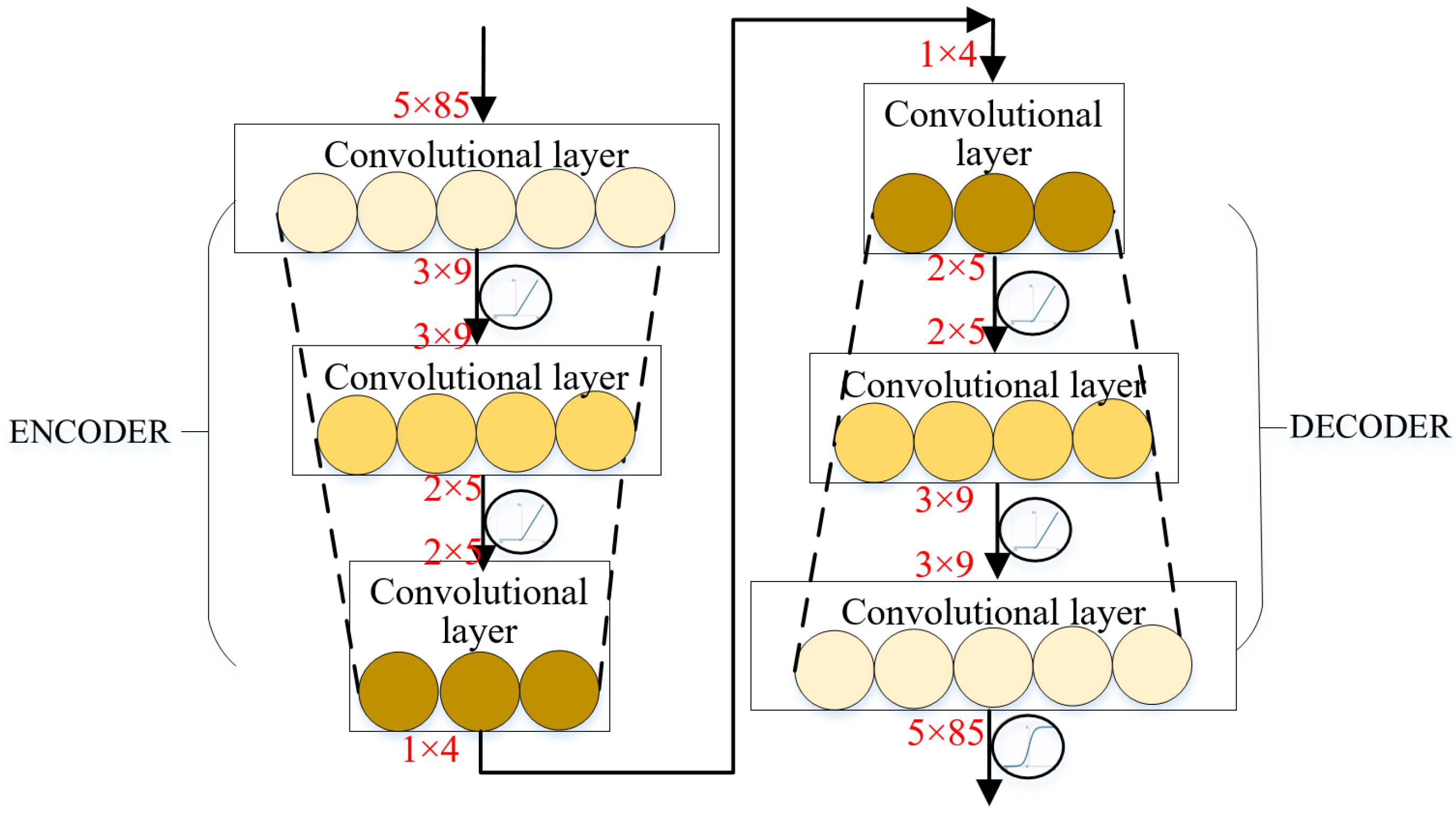
In a machine tool dimension prediction model based on XGBoost, convolutional neural network (CNN), and SHAP analysis, CNN can be used to automatically extract features from machine tool machining data. CNN is a deep learning model that is good at processing data with grid structure, which can automatically learn features in the data through structures such as the convolution layer and pooling layer. The parameter data in the machining process of the machine tool can be used as the input of the CNN. The structure of the CNN usually includes a convolution layer, pooling layer, and fully connected layer, as shown in Figure 3.

Convolution layer: involves feature extraction using multiple convolution checks on input data. Convolution nuclei in the convolution layer slide over the machining parameter data to extract different features using local joins and weight sharing; for example, a convolution kernel may detect some interaction pattern between cutting speed and feed rate, which may be related to changes in machining dimensions.

In the training phase, CNN learns the feature representation in the data and then uses the feature output learned by CNN as input for the XGBoost model.

B: AE-XGBoost Model

XGBoost is an integrated learning algorithm, the basic components are decision trees, which are “weak learners” for classification and regression tasks. Based on the principle of gradient enhancement, each successive tree is constructed to predict the residuals of the previous tree, and there is a sequence between the decision trees that make up XGBoost: the latter will take into account the prediction results of the previous tree, i.e., the deviation of the previous tree. Based on the principle of gradient enhancement, each successive tree is constructed to predict the residuals of the previous tree, and there is a sequence between these decision trees: the generation of the latter decision tree will take into account the prediction results of the previous tree, i.e., the bias of the previous tree will be taken into account so that the training samples of the previous tree that made mistakes in the subsequent tree will be paid more attention to, and then based on the adjusted distribution of the samples to train the next decision tree, and the positive and negative results will be gradually optimized by integrating multiple decision trees. The prediction results are gradually optimized, and the regularization term effectively prevents overfitting and improves the model’s generalization ability. The feature vectors extracted by AE are used as inputs to the XGBoost model to construct an XGBoost-based regression model to predict the machining dimensions of the machine tool. The combination of these individual tree predictions together produces a collective decision for the final prediction. Let us assume that the tree model trained during the $t$ iteration is denoted by $f_t(x_i)$, then the prediction of the sample $i$ after the $t$ iteration, ${{\widehat{y}}_i}^{(t)}$ can be expressed mathematically by (5), as follows:

$${{\widehat{y}}_i}^{(t)}={\displaystyle \sum _{j=1}^t{f}_j\left(x_i\right)={{\widehat{y}}_i}^{(t-1)}+f_t(x_i)}$$

(5)

where $x_i$ is the $i$th data point in the input dataset. Based on the actual value and predicted value, the loss function is obtained as follows (6):

$$L={\displaystyle \sum _{i=1}^{n}l(y_i,{\widehat{y}}_i)}$$

(6)

where the ${\displaystyle \sum _{i=1}^{n}l(y_i,{\widehat{y}}_i)}$ quantifies the difference between the predicted value and the actual value. XGBoost adds regularization terms to the original loss function of the gradient lifting decision tree to improve its performance and prevent overfitting. The improved loss function is expressed in the following Formula (7):

$$obj={\displaystyle \sum _i^{n}l(y_i,{\widehat{y}}_i)+{\displaystyle \sum _{j=1}^J\Omega }}(f_j)$$

(7)

$$\Omega (f_t)=\gamma T+{\displaystyle \frac{1}{2}}\lambda {\displaystyle \sum _{k=1}^T{w}_k^2}$$

(8)

In Formula (8), the $\Omega (f_t)$ is a regularization term, $T$ is the number of leaf nodes, $w$ represents the fraction assigned to leaf nodes, $\gamma$ is used to control the number of leaf nodes and thus affects the complexity of the tree structure, $\lambda$ ensures that the fraction of leaf nodes does not become too large, helping to maintain balance and prevent overfitting.

By substituting Equation (1) into Equation (3) and performing a second-order Taylor expansion of the loss function, it can be derived that the objective function of the $t$-th tree, as shown in Formula (9) as follows:

$$ob{j}^{(t)}={\displaystyle \sum _{i=1}^n[l(y_i,{\widehat{y}}_i^{(t-1)})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)}$$

(9)

where the equation has $g_i={\partial }_{{\widehat{y}}_i^{(t-1)}}l(y_i,{\widehat{y}}^{(t-1)})$, $h_i={\partial }_{{\widehat{y}}^{(t-1)}}^{2}l(y_i,{\widehat{y}}^{(t-1)})$. For a given tree, we can calculate the best value of the objective function by finding the best weight, thus determining the best leaf node, as shown in Formula (10).

$$w_k^{*}=-{\displaystyle \frac{{\displaystyle \sum _{i\in I_k}{g}_i}}{{\displaystyle \sum _{i\in I_k}{h}_i}+\lambda }}$$

(10)

By calculating the gain before and after the segmentation, we can evaluate the quality of the model, as shown in Formula (11).

$$gain={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{{\left({\displaystyle \sum _{i\in I_k}{g}_i}\right)}^2}{{\displaystyle \sum _{i\in I_k}{h}_i}+\lambda }}+{\displaystyle \frac{{\left({\displaystyle \sum _{i\in I_R}{g}_i}\right)}^2}{{\displaystyle \sum _{i\in I_R}{h}_i}+\lambda }}-{\displaystyle \frac{{\left({\displaystyle \sum _{i\in I}{g}_i}\right)}^2}{{\displaystyle \sum _{i\in I}{h}_i}+\lambda }}\right]-\gamma$$

(11)

XGBoost parameters determine the performance of the model. We chose max_depth, n_estimators, learning_rate, colsample_bytree, objective, reg_alpha, and reg_lambda for adjustment. max_depth is used to enhance the complexity of the model, and to capture the relationship in the data in a more detailed way; learning_rate adjusts the weight of the residual fitted by each weak learner, and the fitting effect can be improved by adjusting the number of weak learners; n_estimators represents the number of constructed trees, which is used to improve the accuracy of the model. colsample_bytree represents the proportion of features considered during the splitting process of each tree, helping to manage the complexity of the model. reg_alpha and reg_lambda control L1 and L2 regularization, respectively, to reduce the complexity of the model and prevent overfitting. The objective is used to define the objective function to be optimized by the model, with the parameters set as shown in

Table 2. The values of AE-XGBoost parameters.

Parameters	Optimal Values
max_depth	6
n_estimators	400
learning_rate	0.05
colsample_bytree	0.8
objective	reg: squared error
reg_alpha	0.05
reg_lambda	0.1

.

We define the range of the above parameters. By using grid search cross-validation (GridSearchCV), we systematically traverse the parameter space for a comprehensive combinational search, which evaluates the validity of each parameter combination through cross-validation, ensuring a reliable assessment of its predictive performance. Ultimately, we chose the combination with the highest score to determine the parameters used in the XGBoost model.

C: Model Evaluation Indicators

After completing the AE-XGBoost model dimensional prediction, the dimensional accuracy predicted by the proposed model is compared with the actual dimensional accuracy of the machining process. We selected three commonly used metrics to evaluate the model’s performance: mean absolute error ($X_{MAE}$), mean square error ($X_{MSE}$), and coefficient of determination ($X_{R^2}$) scores. $X_{MAE}$ measures the degree of average absolute deviation between the predicted value and the true value, as shown in Formula (12) as follows:

$$X_{MAE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{t=1}^n\left|y_t-{\widehat{y}}_t\right|}$$

(12)

$X_{MSE}$ focuses on the square of the difference between the predicted value and the true value, so it gives a higher penalty for large errors, as shown in Formula (13) as follows:

$$X_{MSE}={\displaystyle \frac{1}{n}}{{\displaystyle \sum _{t=1}^n\left(y_t-{\widehat{y}}_t\right)}}^2$$

(13)

The $X_{R^2}$ score is an indicator used to assess the goodness of fit of a regression model, it represents the proportion of the total variation in the dependent variable that can be explained by the regression model, as shown in Formula (14), as follows:

$$X_{R^2}=1-{\displaystyle \frac{{\displaystyle \sum _{t=1}^n{\left({\stackrel{⌢}{y}}_t-y_t\right)}^2}}{{\displaystyle \sum _{t=1}^n{\left(\overline{y}-y_t\right)}^2}}}$$

(14)

where $n$ is the number of training data, $y_t$ is the measured machine tool machining dimensions, ${\stackrel{⌢}{y}}_t$ is the predicted machine tool machining values, and $\overline{y}$ is the average of the measured machine tool machining dimensions.

2.4. SHAP Analytical Explanatory Model

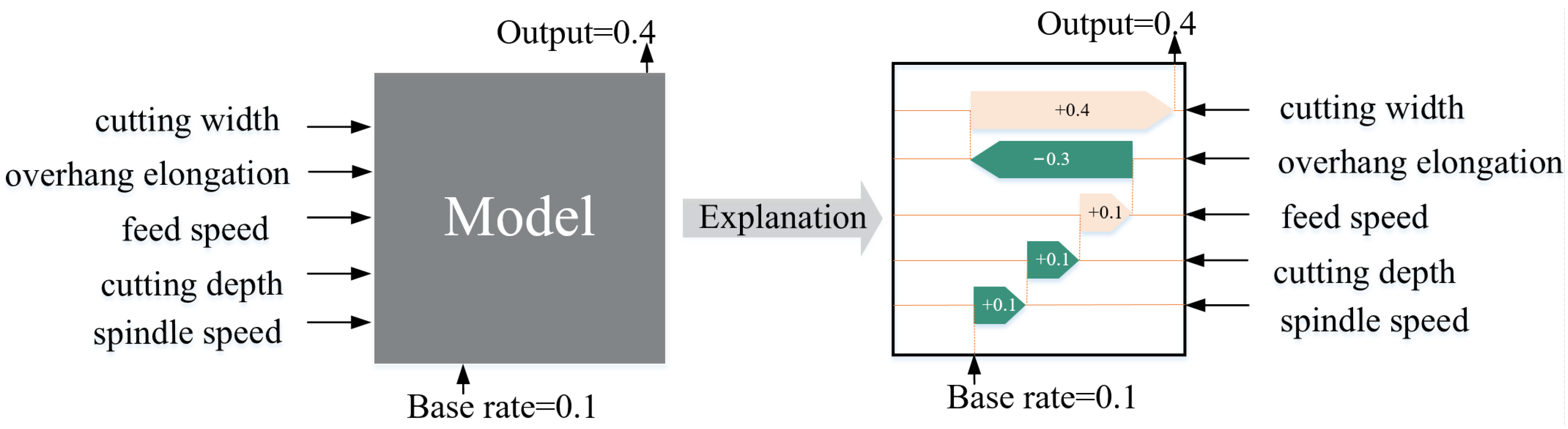
The output of the AE-XGBoost model is used as the input of SHAP analysis, which provides the interpretability of the model prediction. The core idea is to calculate the marginal contribution of the features to the model output, and then interpret the “black-box model” at both global and local levels, and the method is inspired by the Shapley-value-inspired additivity interpretation model. The value-inspired additive explanatory model, the process of the model prediction task is schematically shown in Figure 4.

As seen in Figure 4, first of all, input some known conditions to the model (cutting width, overhang elongation, feed speed, cutting depth, spindle speed), then train the model based on the inputs, Finally, the trained model can output prediction results for this condition (output = 0.4). However, it is impossible to know how the calculation inside the model is performed, and the SHAP model can let us know how these known conditions affect the final prediction results.

For a model with $n$ features, the Shapley value ${\varphi }_i$ of feature $i$ is calculated by considering all possible subsets of features $S\subseteq F$, where $F$ is the set of all features. The specific calculation formula is shown in Formula (15).

$${\varphi }_i=\pm {\displaystyle \sum _{S\subseteq F\backslash \left\{i\right\}}\frac{\left|S\right|!(\left|F\right|-\left|S\right|-1)!}{\left|F\right|!}\left[f_{S\cup \left\{i\right\}}(x_{S\cup \left\{i\right\}})-f_S(x_S)\right]}$$

(15)

where $f_S(x_S)$ is the predicted value of the model on the feature subset $S$, and $\left|S\right|$ represents the number of features in the subset $S$. By iterating over all subsets S that do not contain a feature $i$, the formula calculates the change (i.e., marginal contribution) of the model’s predicted value after adding a feature $i$ to subset $S$, and carries out weighted summation according to the combination of subsets to obtain the Shapley value of feature $i$.

The dimensions of SHAP values directly reflect the importance of features to the model’s prediction results. A SHAP value with a larger absolute value indicates that the feature has a larger impact on the prediction results, while a SHAP value near zero indicates that the feature has a smaller impact. For the prediction of a single sample of machining dimensions, when the machining dimensions of a workpiece are predicted, the SHAP value of the cutting speed is negative, which means that increasing the cutting speed will make the predicted machining dimensions smaller under other conditions. The SHAP value of the tool material is positive, indicating that the use of a high-quality tool material will increase the processing dimensions. Therefore, based on the SHAP value, it is possible to explain how each feature affects the final prediction of the model. By analyzing the SHAP value of the feature and its positivity and negativity, we can find out whether the feature changes the prediction result in a positive or negative direction.

3. Results and Discussion

3.1. Data Preparation

To analyze the factors that affect the dimensional accuracy in CNC milling, this paper starts from the actual CNC milling process. A total quantity of 850 dimensional machining data points were collected, and each data point recorded the corresponding 15 machining size factors, providing a rich data source for model training and validation. These factors include positioning accuracy, repeated positioning accuracy, clamping rigidity, machining material, initial heat treatment state of the material, tool structure, tool material, blade number, overhang elongation, blade length, free state pendulum momentum, spindle speed, feed speed, cutting width and cutting depth, as shown in

Table 3. Influence factors and data source.

Type	Influencing Factor	Data Source
Machine tool	Positioning accuracy	Machine tool
	Repeated positioning accuracy	Machine tool
Jig and fixture	Clamping rigidity	Machining process routine
Processing material	Machining material	Machining process routine
	Initial heat treatment state of the material	Machining process routine
Cutting tool	Tool structure	Tool maintenance center
	Tool material	Tool maintenance center
	Blade number	Tool maintenance center
	Overhang elongation	Tool maintenance center
	Blade length	Tool maintenance center
Cutting tool set	Free-state pendulum momentum	Operational record
Cutting parameters	Spindle speed	Machine tool/CNC program
	Feed speed	Machine tool/CNC program
	Cutting width	Machine tool/CNC program
	Cutting depth	Machine tool/CNC program

.

Table 3 shows 15 different factors affecting dimensional accuracy, divided into six categories according to type, each factor has a specific source.

For the two factors under the “Machine tool category”, “Positioning accuracy” and “Repeated positioning accuracy”, the source of the data is the “Machine tool” itself, and these data reflect the performance of the machine tool in terms of positioning, which has a fundamental influence on the accuracy of the machined dimension.

One factor in the “Jig and fixture” category, “Clamping rigidity”, is derived from the “Machining process routine”, and these parameters affect the fixation of the workpiece in actual machining, which in turn affects the machined dimensions.

Two influencing factors under the category of “Processing material”, “Machining material” and “Repeated positioning accuracy”, data also from the “Machining process routine”, and these information are recorded in the process regulations and used to guide the machining process because different materials and heat treatment states will lead to different deformation behaviors of the material in the cutting process, which affects the machining dimensions.

The five influencing factors under the category of the “Cutting tool”, “Tool structure”, “Tool material”, “Blade number”, “Overhang elongation”, and “Blade length” are provided with data from the “Tool maintenance center”. These parameters are critical to the performance of the tool in the cutting process and they work together to influence the machined dimensions.

One influencing factor under the “Cutting tool set” category is the “Free-state pendulum momentum” data recorded by the operator. These data reflect the mounting accuracy and stability of the toolset, which have a direct impact on machining accuracy.

Four influencing factors under the category of “Cutting parameters” are “Spindle speed”, “Feed speed”, “Cutting width”, and “Cutting depth”, for which data are available from the “machine tool/CNC program”, and for which changes in these parameters directly lead to changes in the machined dimensions. A total of 850 records are included in the comprehensive dataset. Eighty percent of the collected data is used for training and the remaining data is used for testing.

The model is equipped with a 12th-generation Intel(R) Core (TM)i7-12700H processor manufactured by Intel, George Town, Malaysia. The basic processor frequency is 2.70 GHz. The GPU is NVIDIA GeForce RTX3060 manufactured by Gigabyte, New Taipei City, Taiwan, China. The operating system is Windows 11. The programming language used for model training is Python, version 3.10.14. The deep learning framework used is PyTorch, version 2.2.1, and accelerated with cu121.

3.2. Results and Analysis of Data Screening Processing

A. Results and Analysis of Data Screening Processing based on PCA

The dataset contains 15 kinds of data affecting the machining dimensions of machine tools, and whether or not to use the effect of the effect and how much the effect varies, so data screening based on principal component analysis (PCA) and gray correlation analysis (GRA) effectively reduces the dimensionality of the data, filters the key variables, and reveals the relationship between the variables, which provides strong support for the machining of machine tool machining dimension processing.

In the process of various machine tools, some influencing factors remain unchanged, such as positioning accuracy, repeated positioning accuracy, clamping rigidity, machining material, initial heat treatment state of the material, tool structure, tool material, blade number, blade length, and free-state pendulum. Therefore, these constant features were excluded to prevent the generation of misleading results by the model.

PCA projects the original standardized data into the principal component space through eigenvectors to obtain the principal component score of each sample. The contribution rate of the principal components reflects the proportion of the amount of information they contain about the original data. The composite score is a weighted sum of the samples’ scores on each principal component according to the principal component contribution ratio, such that the composite score provides a comprehensive measure of the “importance” of the samples in the principal component space, which is used for tasks such as sample ranking. The formula is shown below.

$${\mathrm{score}}_j={\displaystyle \sum _{j=1}^{num}d{f}_{ij}\times \frac{rat{e}_j}{100}}$$

(16)

where $i$ represents the sample, $j$ represents the principal component, ${\mathrm{score}}_j$ is the composite score of the $j$th principal component, $num$ is the number of principal components, $d{f}_{ij}$ is the score of the $i$th sample on the $j$th principal component, and $rat{e}_j$ is the contribution rate of the $j$th principal component. Because the principal components with a high contribution rate contain more original information, they are more important in the comprehensive evaluation, and their corresponding scores have greater weights. The top five comprehensive evaluation values are actual mass, tool overhang extension, cutting feed rate, cutting spindle speed, cutting width, and depth of cut, and the comprehensive scores are 15.42762416, 5.497486898, −4.643924089, −5.222349954, −5.396497335, respectively.

B. Results and Analysis of Data Screening Processing based on GRA

For the five major factors selected, the GRA algorithm was used to explore the relation between the factors, as shown in the GRA heat map results in Figure 5.

As can be seen in Figure 5, the bluer the color, the higher the relation between factors, and the redder the color, the lower the relation between factors. The relation between various factors is shown in

Table 4. Relation between factors.

	Spindle Speed	Feed Speed	Cutting Width	Cutting Depth	Overhang Elongation
Spindle speed	1	0.74	0.64	0.69	0.67
Feed speed	0.76	1	0.66	0.65	0.65
Cutting width	0.71	0.69	1	1	0.63
Cutting depth	0.73	0.66	0.64	0.66	1
Overhang elongation	0.71	0.66	0.61	0.69	0.69

below.

According to the calculation results of GRA, there are five main influencing factors in the first row and the first column, and the remaining five main influencing factors have a great influence on the GRA value of the machine tool processing dimensions distributed in the range of [0.65, 0.76]. Therefore, overhang elongation, spindle speed, feed speed, cutting width, and cutting depth were selected as the characteristics to predict the machining dimensions.

C. Results and Analysis of Data Screening Processing based on SMOGN

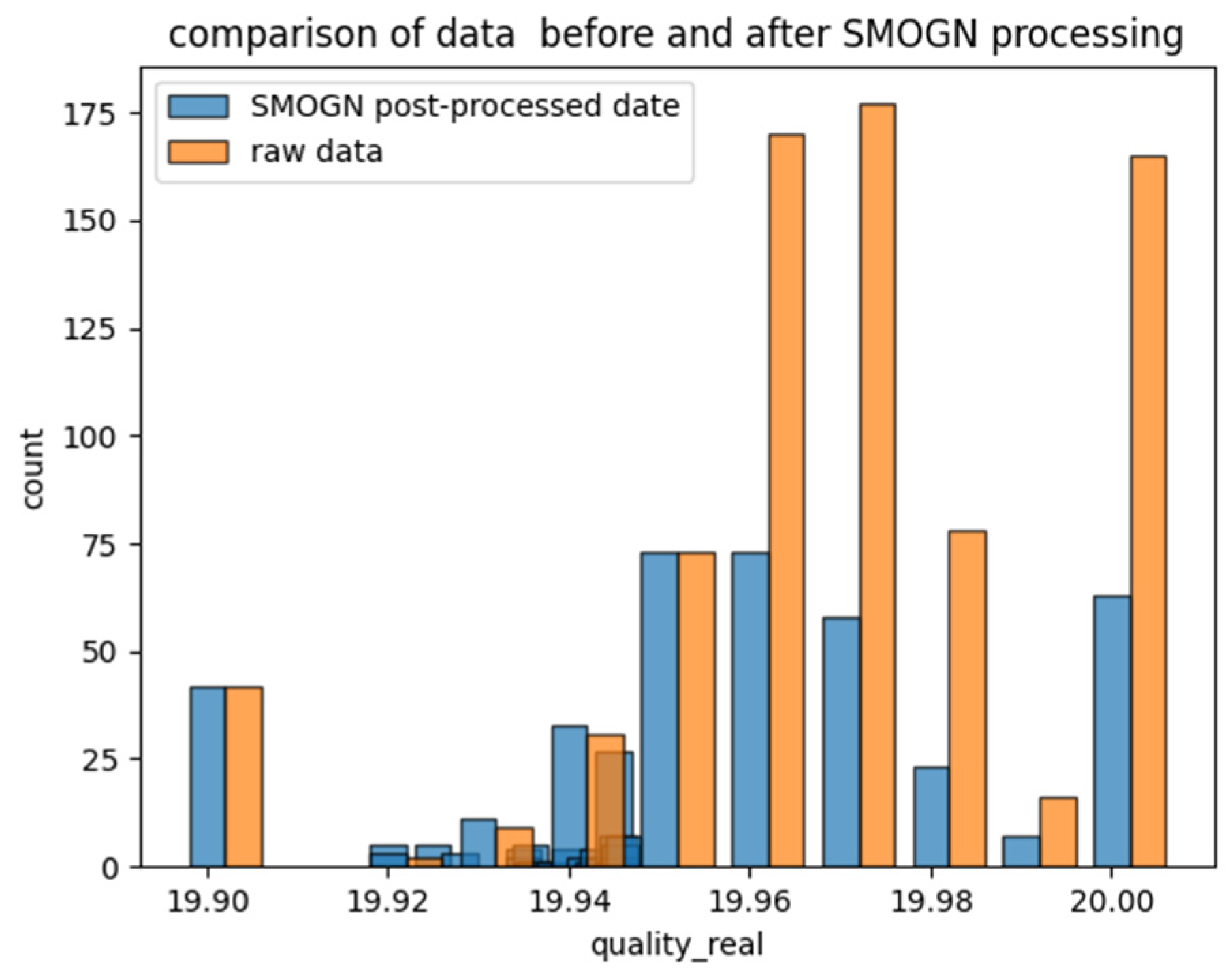
In the unbalanced regression problem, the imbalance in the number of samples may cause the model to perform poorly in predicting samples from fewer categories. To solve this problem, the SMOGN algorithm is used to synthesize the samples to balance the dataset, and the results before and after processing are shown in Figure 6 below, for the size feature of true mass.

The upper histogram in Figure 6 shows that the x-axis represents the value of real quality in the dataset, ranging from 19.90 to 20.00 and the y-axis represents the number of samples corresponding to each quality_real value, with a scale from 0 to 175.

The blue bars represent the pre-processed data and the orange bars represent the SMOGN post-processed data. The blue bars indicate that the number of samples in the original data is higher for the quality_real values of 19.96, and 19.97, which is around 175, while the number of samples for other quality_real values is relatively low. The orange bars show the distribution of the data after SMOGN processing, and it should be noted that the processed data are weakened on distributions with more quality_real samples, e.g., lowering the number of samples around 19.96, 19.97, 19.98, and 20.00, and re-synthesizing to a certain number of samples on distributions with fewer samples, e.g., raising the number of samples around 19.92, 19.93, and 19.94 near to which the sample size was raised.

By comparing the blue and orange bars, it can be seen that the SMOGN processing has an impact on the data distribution, which makes the processed data more spread out and even in the distribution of quality_real values. SMOGN achieves balanced data and avoids the situation where the number of samples is too much or too little for certain values in the original data, which can improve the generalization ability and stability of the model.

3.3. Results and Analysis of Prediction of AE-XGBoost and XGBoost

After training the XGBoost model, we evaluated the performance of the model with test data. The predicted machined dimensions were compared with the measured mass dimensions and the XGBoost model was compared with the AE-XGBoost model based on three evaluation metrics. The results are shown in Figure 7.

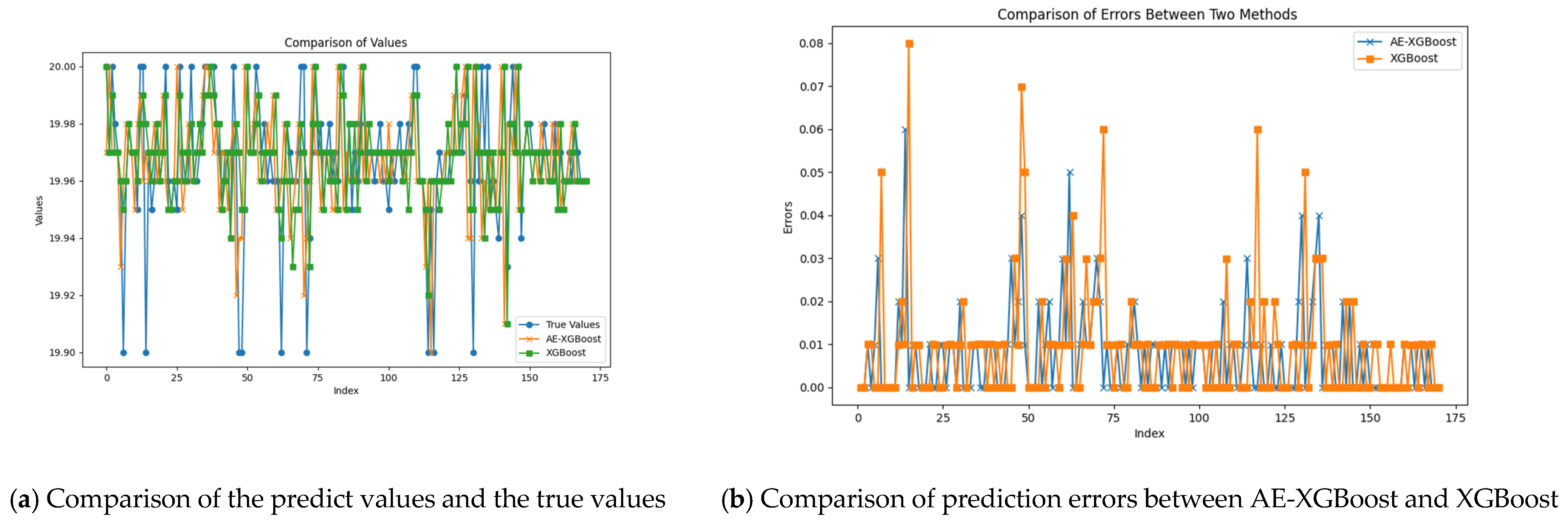
As shown in Figure 7a, the horizontal axis index, ranging from 0 to 80, represents the index of the data points, and the vertical axis values ranging from 19.90 to 20.00 represent the size of the data points; the blue folds in the figure represent the true values, with values ranging from 19.90 to 20.00, and the orange discounts in the figure represent the predicted values from the AE-XGBoost model, with a value range between 19.90 and 19.98; the green discount in the figure represents the value predicted only by the XGBoost model, and the value range is between 19.90 and 20.00. It can be seen in the figure that the predicted value of the AE-XGBoost model is closer to the real value, the value is relatively stable, and it may be closer to the real value around 40, 50, 60, and 70.

According to Figure 7b, the horizontal coordinate is an index, which ranges from 0 to 80, and the vertical coordinate errors, which range from 0 to 0.008, indicate the magnitude of the error value, the blue dash line represents the error predicted by the AE-XGBoost model, and the orange dash line represents the error predicted by the XGBoost model, and it can be seen that the error value of the two methods is between 0 and 0.1, and the overall level shows that the prediction error of AE-XGBoost is significantly lower than the prediction error of XGBoost model, and at certain indexes, e.g., the positions of 20, 50, and 70, the error of the predicted values of AE-XGBoost model is significantly lower than the prediction error of XGBoost model.

To further quantify the differences in the model before and after the improvement, the mean absolute error, mean square error, and coefficient of determination were calculated for both cases, and the results are shown in

Table 5. Evaluation metrics of two methods.

Model	MAE/e-3	MSE/e-4	RMSE/e-2	R2
AE-XGBoost	7.778	1.655	1.286	0.681
XGBoost	9.415	2.696	1.642	0.480

.

The table shows that the MAE, MSE, RMSE, and R² of AE-XGBoost are 7.778 × 10⁻³, 1.655 × 10⁻⁴, 1.286 × 10⁻², and 0.681, respectively, while the evaluation metrics of XGBoost are 9.415 × 10⁻³, 2.696 × 10⁻⁴, 1.642 × 10⁻², and 0.480, respectively. Compared with the XGBoost model, the AE-XGBoost model improves on these three metrics by 17.39%, 38.61%, 21.69%, and 41.88%. It can be clearly seen that the improved AE-XGBoost algorithm has effectively improved the handling of the redundancy and imbalance problems in the initial data.

3.4. Results and Analysis of Feature Interpretation Based on SHAP Analysis

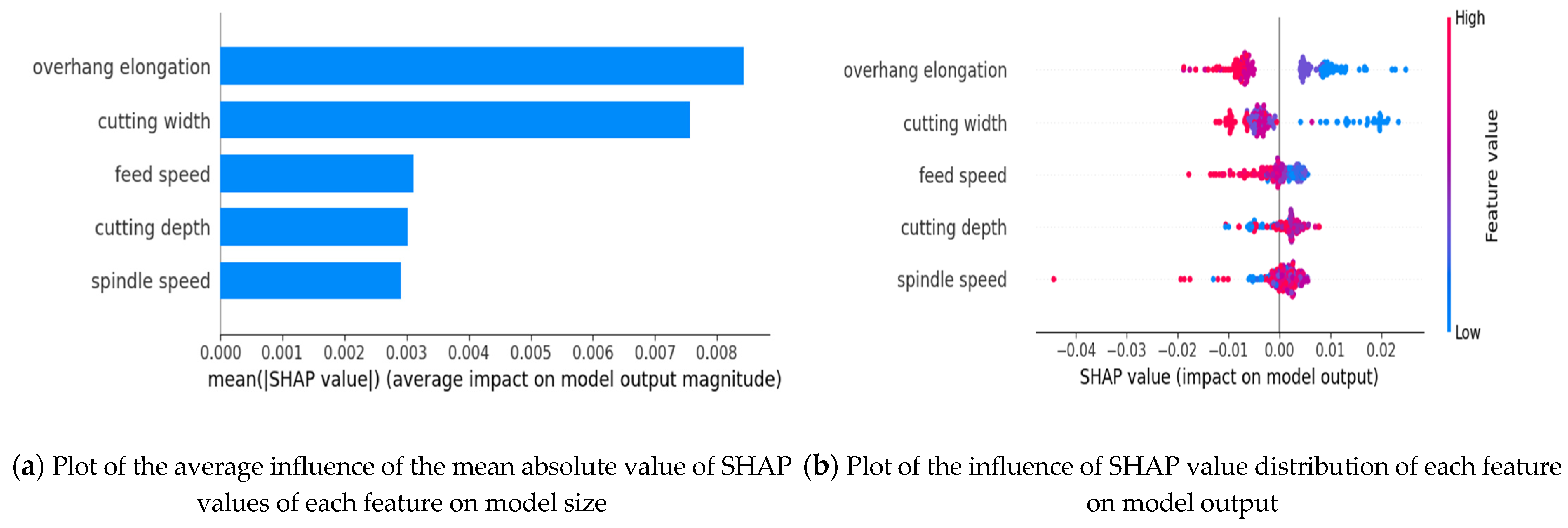
After screening the main influencing factors in the original dataset, SHAP analysis is used to interpret the model. The SHAP value of each feature is calculated, and the important features are listed in descending order of importance. The results are as follows:

The horizontal axis in the bar chart of Figure 8a indicates the magnitude of the average effect ranging from 0 to 0.008, the higher the value, the higher the average effect on the model output magnitude, the vertical axis lists five factors and it can be seen that the overhang elongation and the cutting width are of the highest importance, followed by the feed rate, the depth of cut and the spindle speed.

The horizontal axis in Figure 8b represents the SHAP values ranging from −0.02 to 0.02, and the vertical axis lists five different features: overhang elongation, cutting width, feed speed, cutting depth, spindle speed. The color of the scatter points change from blue to red, with blue representing a lower value of the feature and red representing a higher value of the feature, which shows the effect of different features at different values on the model output.

Obviously, larger eigenvalues of overhang length and cutting width correspond to smaller SHAP values, which indicates that these two eigenvalues are negatively correlated with the machining dimensions.

3.5. Results and Analysis of Dimensions Interpretation Based on SHAP Analysis

Among the results of SHAP interpretation, the two factors of overhanging elongation and cutting width are of the highest importance. The following is a further study on the influence of these two factors on the machining dimensions. The SHAP partial dependence graph and the SHAP dependency graph are used to analyze these two features in more detail, and the results are shown in Figure 9.

According to the SHAP partial dependence in Figure 9a, we observe that when the overhang elongation is 50 or 60, it has a positive impact on the target value, and a smaller value has a greater positive impact. In contrast, when the value is 70 or 80, the overhang elongation has a negative effect on the target value, and the effect remains almost constant as the value increases. According to Figure 9b, we observe that when the cutting width is 2.0, there is a positive effect on the target value. However, when the value is 3.0, 4.0, or 5.0, the cutting width usually has a negative effect on the target value. In addition, as the number increases, the effect on the target value remains almost constant. However, whether the internal coupling of the two factors affects the value of the factor requires further analysis of the SHAP dependence diagram of the suspension length and cutting width. The SHAP dependence results of the two factors are shown in Figure 10.

According to Figure 10, the variation in the influence of suspension elongation on the target value under the same value is attributed to the influence of other characteristics. However, when the overhang elongation is 50 or 60, the increase in the cutting width does not affect its positive effect on the target value. Similarly, when the overhang elongation is 70 or 80, the reduction in the cutting width does not have a negative effect on the target value. This indicates that the coupling relationship between the two features is weak and the parameters can be adjusted independently. The calculation results show that the other three parameters have similar effects on suspension elongation.

3.6. Discussion

We proposed an AE-XGBoost model for predicting machine tool machining dimensions, integrating XGBoost, autoencoder (AE), and SHAP analysis. The experimental results demonstrated the superiority of the AE-XGBoost model over the traditional XGBoost method, with a 7.11% improvement in prediction accuracy. However, a more in-depth discussion of these findings is warranted.

Model Performance and Feature Importance: The improved performance of the AE-XGBoost model can be attributed to its unique architecture. The AE effectively extracts local and global features from the data, reducing noise and redundancy. This pre-processed data is then fed into the XGBoost model, which is known for its ability to handle complex non-linear relationships. The combination allows for a more accurate prediction of machining dimensions. For example, the principal component analysis (PCA) and grey correlation analysis (GRA) pre-processing steps reduce the dimensionality of the data while retaining important information, making the data more suitable for the XGBoost model.

Regarding feature importance, SHAP analysis revealed that overhang elongation and cutting width have the most significant effects on machining dimensions. The negative correlation between the larger values of overhang elongation and cutting width and the machining dimensions, as indicated by the SHAP values, can be explained by the physical processes in machining. A longer overhang elongation may lead to increased tool deflection during machining, causing the actual machining dimensions to deviate from the desired values. Similarly, a wider cutting width may result in greater cutting forces, which can also affect the final dimensions of the machined part. The feed speed, cutting depth, and spindle speed also play important roles, but to a lesser extent.

Comparison with Existing Studies: Compared with previous research in the field of machine tool machining size prediction, our model addresses several limitations. Many existing studies do not adequately consider data imbalance, which can lead to inaccurate predictions. By using the SMOGN method, we were able to balance the dataset and improve the model’s generalization ability. Additionally, the integration of SHAP analysis in our model provides interpretability, which is often lacking in other models. This allows engineers to understand how different features contribute to the prediction results, facilitating the optimization of machining parameters.

Limitations and Future Research: Despite the promising results, our study has some limitations. The dataset used in this study may not cover all possible machining scenarios, which could limit the model’s generalization to other types of machine tools or machining processes. Future research could focus on expanding the dataset to include more diverse machining conditions. Additionally, although the AE-XGBoost model shows good performance, there is still room for improvement. Exploring more advanced feature extraction techniques or optimization algorithms for XGBoost could further enhance the model’s accuracy.

In conclusion, this study provides valuable insights into machine tool machining size prediction. The AE-XGBoost model shows great potential, and the SHAP analysis offers a useful way to interpret the model’s predictions. Future research should aim to overcome the limitations of this study and further improve the performance and generalization of the model.

4. Conclusions and Future Work

4.1. Conclusions

In this study, we proposed an interpretable machining size prediction model that combines XGBoost, autoencoder (AE), and SHAP analysis to address the challenges in machine tool machining size prediction. Our approach aimed to achieve intelligent manufacturing and enhance the machining quality of machine tools.

We began by constructing a comprehensive dataset that incorporated actual machining process parameters, machine parameters, and final machining dimensions. Given the data imbalance commonly encountered in practical engineering scenarios, we employed grey correlation analysis (GRA) and principal component analysis (PCA) to preliminarily screen the features. This not only reduced data redundancy but also retained the most relevant information. Subsequently, the synthetic minority over-sampling technique of gaussian noise regression (SMOGN) was utilized to balance the dataset, ensuring that the model could handle different data distributions effectively.

Before training the XGBoost model, we leveraged the autoencoder network to extract data features. The AE was able to capture both local and global features within the data, transforming the pre-processed data into more representative feature vectors. These features were then fed into the XGBoost model, and its optimal parameters were determined through grid search cross-validation.

The experimental results demonstrated the effectiveness of our proposed AE-XGBoost model. Compared with the traditional XGBoost method, the AE-XGBoost model showed a significant improvement in prediction accuracy. Specifically, it achieved a 7.11% increase in accuracy, with mean absolute error (MAE), mean square error (MSE), and coefficient of determination (R²) values of 1.071 × 10⁻², 2.741 × 10⁻², and 0.570 respectively. These improvements indicated that the AE-XGBoost model was better at handling the redundancy and imbalance problems in the initial data, enabling more accurate predictions of machining dimensions.

We further employed SHAP analysis to rank the feature importance of machining dimensions. Overhang elongation and cutting width were identified as the most significant factors affecting the target variable. Through SHAP partial dependence diagrams and SHAP dependency graphs, we found that an overhang elongation of 50 or 60 had a positive effect on the target, while values of 70 or 80 had a negative effect. For the cutting width, a value of 2.0 had a positive effect, while 3.0, 4.0, and 5.0 had a negative effect. Moreover, the coupling relationship between overhang elongation and cutting width was found to be weak, suggesting that these parameters could be adjusted independently to optimize machining dimensions.

In summary, our research provides a reliable and interpretable model for machine tool machining size prediction. The AE-XGBoost model offers a practical solution for engineers to better understand and control the machining process, ultimately contributing to an improvement in machining quality and the realization of intelligent manufacturing. However, it should be noted that our model still has some limitations. For example, the performance of the model may be affected by the limited diversity of the dataset. Future research directions are discussed in the following section.

4.2. Future Work

Future work could focus on expanding and diversifying datasets and developing new imbalanced data sampling methods, which could help improve model performance under imbalanced data conditions. In addition, more efficient hyperparameter tuning techniques can be explored to further optimize the performance of the XGBoost model. In terms of practical machining applications, this study provides valuable insights for optimizing machining dimensions and adjusting machine parameters, which is helpful in developing more reasonable and effective machining schemes.