Abstract
In response to the limitations of reinforcement learning and Evolutionary Algorithms (EAs) in complex problem-solving, Evolutionary Reinforcement Learning (EvoRL) has emerged as a synergistic solution. This systematic review aims to provide a comprehensive analysis of EvoRL, examining the symbiotic relationship between EAs and reinforcement learning algorithms and identifying critical gaps in relevant application tasks. The review begins by outlining the technological foundations of EvoRL, detailing the complementary relationship between EAs and reinforcement learning algorithms to address the limitations of reinforcement learning, such as parameter sensitivity, sparse rewards, and its susceptibility to local optima. We then delve into the challenges faced by both reinforcement learning and EvoRL, exploring the utility and limitations of EAs in EvoRL. EvoRL itself is constrained by the sampling efficiency and algorithmic complexity, which affect its application in areas like robotic control and large-scale industrial settings. Furthermore, we address significant open issues in the field, such as adversarial robustness, fairness, and ethical considerations. Finally, we propose future directions for EvoRL, emphasizing research avenues that strive to enhance self-adaptation, self-improvement, scalability, interpretability, and so on. To quantify the current state, we analyzed about 100 EvoRL studies, categorizing them based on algorithms, performance metrics, and benchmark tasks. Serving as a comprehensive resource for researchers and practitioners, this systematic review provides insights into the current state of EvoRL and offers a guide for advancing its capabilities in the ever-evolving landscape of artificial intelligence.
Keywords:
evolutionary reinforcement learning; evolutionary algorithms; deep learning; policy search; evolution strategy MSC:
68T07
1. Introduction
Reinforcement learning utilizes agents for autonomous decision-making, focusing on long-term action strategies, particularly effective in tasks like industrial automation and personalized recommendation systems [1,2,3]. However, reinforcement learning faces challenges such as parameter sensitivity and sparse rewards, leading to issues in its learning efficiency and adaptability [4,5]. On the other hand, Evolutionary Algorithms (EAs), inspired by Darwin’s natural selection, excel in solving complex, multi-objective problems in large solution spaces [6,7], showcasing their robust search capabilities in a wide range of optimization tasks.
Hence, Evolutionary Reinforcement Learning (EvoRL), which integrates EAs with reinforcement learning, has been introduced to address the limitations of each method [8]. EvoRL maintains multiple policies within a population and utilizes evolutionary operations like crossover and mutation to refine these policies, enhancing the policy-making process inherent in reinforcement learning. Simultaneously, EvoRL leverages the global search capabilities of EAs for exploring the policy space and optimizing various components like agents and actions. EvoRL’s core mechanism, combining the precision of policy gradients with EAs’ global search, enables effective solutions in complex, high-dimensional environments [9,10]. Additionally, approaches like EGPGs and CERL within EvoRL focus on the collaborative efforts of multiple agents, boosting performance in intricate tasks [11].
EvoRL has been applied in various domains, demonstrating its versatility and effectiveness. For instance, EvoRL enhances the sample efficiency in reinforcement learning, a crucial aspect for practical applications [12,13]. In embodied intelligence, EvoRL fosters complex behavior through the integration of learning and evolution, offering new perspectives in this field [14]. Another significant application of EvoRL lies in quality diversity for neural control, contributing to the advancement of neural network-based control systems [15]. EvoRL’s integration with Deep Reinforcement Learning (DRL) has been instrumental in promoting novelty search, expanding the boundaries of exploration in reinforcement learning [10]. Furthermore, the SUPER-RL approach within EvoRL, which applies genetic soft updates to the actor–critic framework, has been shown to improve the searching efficiency of DRL [16]. Early research highlighted the importance of meta-parameter selection in reinforcement learning, a concept that remains relevant in current EvoRL applications [17]. Lastly, the combination of population diversity from EAs and policy gradient methods from reinforcement learning has led to novel approaches like differentiable quality diversity, further enhancing the gradient approximation capabilities of EvoRL [18].
More specifically, conventional reinforcement learning focuses on obtaining the optimal policy through interactions with the environment. However, it is unstable in high-dimensional and complex environments. EvoRL, by combining reinforcement learning with EAs and taking advantage of global search, not only considers local optimization when searching for optimal policies but also avoids the local optimal problems in reinforcement learning methods. For relatively simple, well-defined tasks, traditional reinforcement learning may be sufficient. However, EvoRL is more effective when faced with complex, dynamic, and high-dimensional environments, especially when a lot of exploration is required.
Recent advances in EvoRL [19,20] have demonstrated significant improvements in both reinforcement learning and EAs. From the perspective of reinforcement learning, EvoRL has been shown to notably enhance the sample efficiency and expand the exploratory capabilities, which are essential in addressing reinforcement learning’s limitations in complex and high-dimensional problem spaces [10,13]. In terms of EAs, the integration with reinforcement learning techniques has resulted in more adaptive and precise evolutionary strategies [16,17]. This review aims to underscore the importance of EvoRL in overcoming the inherent challenges of using reinforcement learning and EAs independently, highlighting its integrated approach in complex problem-solving scenarios.Although EvoRL has shown progress in theory and algorithm design, its practical use faces some challenges. First, the sampling efficiency is a major issue. EvoRL relies on iterative optimization with many samples, making training slow and unsuitable for real-time tasks like robotic control. Second, the algorithm complexity limits its scalability. Optimization in high-dimensional spaces increases the computational costs and slows convergence, especially in large-scale industrial settings. Additionally, EvoRL must address adversarial robustness, fairness, and ethical concerns to ensure reliability and societal acceptance. Thus, this study focuses on three research questions:
- How have previous studies explored the integration of EAs to address the limitations of traditional reinforcement learning?
- What strategies have been proposed in the literature to improve EvoRL’s efficiency and scalability?
- How do existing approaches aim to enhance EvoRL’s robustness in complex environments?
1.1. Contributions
In the field of EvoRL [19,21,22], the surveys [23,24] provide related topics. Ref. [23] categorizes over 45 EvoRL algorithms, primarily developed after 2017, focusing on the integration of EAs with reinforcement learning techniques, which emphasizes the mechanisms of combination rather than the experimental results. Ref. [24] further explores this domain, examining the intersection of EAs and reinforcement learning, and highlights its applications in complex environments. Although these surveys offer valuable insights for EvoRL, they could benefit from incorporating a broader range of perspectives and analytical approaches, ensuring a more diverse understanding of EvoRL’s potential and challenges in future exploration. Specifically, reinforcement learning usually faces issues such as parameter sensitivity and reward sparsity, while EvoRL provides a new way to solve these problems by combining reinforcement learning with EAs, but it also has new challenges such as a low sampling efficiency and high algorithm complexity. Therefore, the core scientific questions of this review are how EvoRL is currently addressing the reinforcement learning challenge, as well as its limitations and potential directions for improvement.
This review makes the following four contributions:
- Multidimensional classification. We have taken a comprehensive look at the EvoRL field, categorizing different approaches and strategies in detail. This detailed classification covers not only EvoRL’s multiple techniques and strategies, such as genetic algorithms and policy gradients, but also their application to complex problem-solving.
- Challenges in EvoRL. We provide an in-depth analysis of the challenges and limitations of current research, including issues encountered by reinforcement learning and EvoRL, and provide their corresponding solutions.
- Constructive open issues. This review presents a summary of emerging topics, including the scalability to high-dimensional spaces, adaptability to dynamic environments, adversarial robustness, ethics, and fairness in EvoRL.
- Promising future directions. We identify key research gaps and propose future directions for EvoRL, highlighting the need for meta-evolutionary strategies, self-adaptation and self-improvement mechanisms, model scalability, interpretability, and explainability, as well as the incorporation of EvoRL within Large Language Models (LLMs).
1.2. Article Organization
This article is organized as follows. Section 3 provides the technical background of EvoRL. In Section 4, we investigate EvoRL algorithms based on the existing literature. Section 5 analyzes the challenges faced by reinforcement learning and EvoRL. In Section 6, we conclude with a discussion on the open issues and future directions in EvoRL. In Section 7, we conclude with a summary of our contributions.
2. Literature Review Methodology
In this study, we applied the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) [25] to systematically collect, filter, and analyze the relevant literature. This study was registered in OSF, registration number 10.17605/OSF.IO/6TKSY. The workflow of the literature selection is shown in Figure 1. To ensure comprehensiveness and reliability, we divided this part into three stages:
- Collection Phase: We established a comprehensive collection strategy that encompassed multiple databases and integrated various keyword combinations.
- Screening Phase: We applied predefined inclusion and exclusion criteria to systematically screen the collected literature. This process involved an initial review of titles and abstracts, followed by a detailed full-text assessment to ensure the selected studies were highly relevant to the research question.
- Analysis Phase: After identifying the eligible studies, we conducted systematic data extraction and quality assessment. Subsequently, we performed qualitative or quantitative analysis on the extracted data to synthesize the findings from existing studies and explore their implications and limitations.
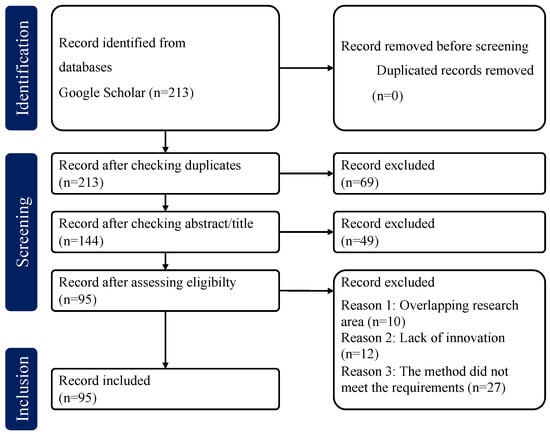
Figure 1.
Literature selection process diagram.
Figure 1.
Literature selection process diagram.
2.1. Collection Phase
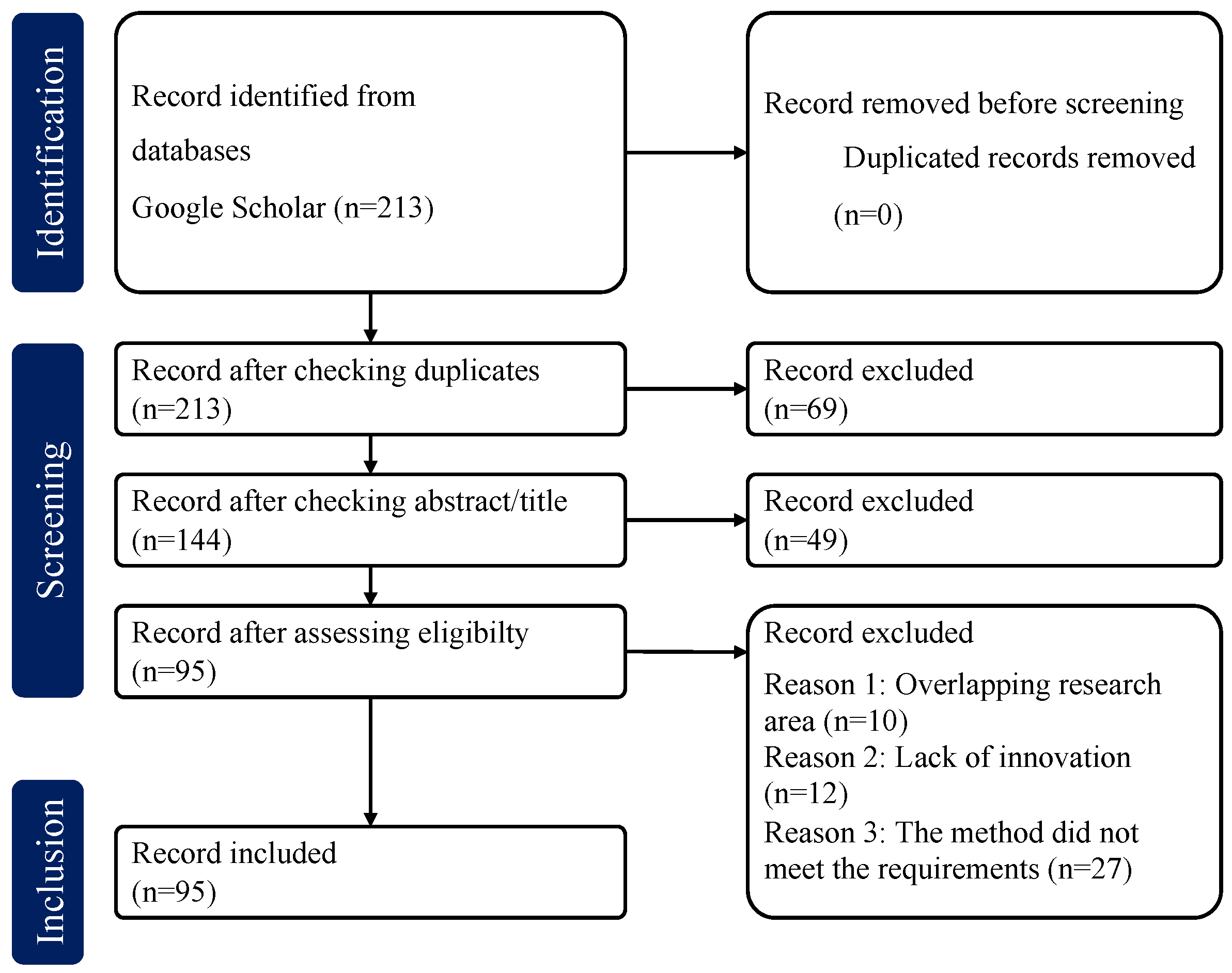
During the literature collection phase, we primarily focused on research related to EvoRL, using Google Scholar as the main database. To ensure comprehensiveness, we compared several existing literature reviews, including [19,21,22], and supplemented these with the articles missing from these reviews [26,27,28]. Ultimately, a total of 213 relevant articles were collected.
The literature screening process followed the guidelines of the PRISMA, aiming to enhance the quality of the literature review and ensure the reproducibility of the research. During the screening process, the following aspects were primarily considered:
- The considered literature spanned from 2000 to 2024, with the search primarily conducted on the Google Scholar database.
- Keywords and their synonyms related to “Evolutionary Reinforcement Learning” were used to ensure the coverage of the core literature in the field (e.g., Evolutionary Strategy, Genetic Algorithm).
- The included literature must have explicitly applied EAs or reinforcement learning methods and demonstrated theoretical or applied innovation.
- Through the removal of duplicate articles and the application of inclusion and exclusion criteria, 213 relevant articles were ultimately obtained.
2.2. Screening Phase
The screening phase involved the evaluation of titles, abstracts, and keywords, with a focus on the relevance of each article to the research topic. In this stage, an initial review of the titles, abstracts, and keywords was conducted for all the collected literature to identify articles highly relevant to the research topic. Through this process, a total of 69 articles were excluded due to irrelevance or duplication, leaving 144 articles for further detailed assessment.
In the subsequent detailed evaluation phase, these articles were subjected to full-text reading. By thoroughly examining the content of the articles, studies that were similar or significantly overlapping in terms of their research field were removed. This process ensured that only studies with unique contributions and innovative findings were retained. Ultimately, after rigorous screening, 49 articles were excluded, and the remaining 95 articles met the inclusion criteria, making them suitable for the in-depth analysis of EvoRL algorithms.
2.3. Analysis Phase
This study conducted a systematic analysis of the EvoRL literature using a multidimensional taxonomy, with implementation pathways comprising the following:
- Categorization of Methodologies: We classified existing methodologies into three reinforcement learning paradigms and five EA implementation mechanisms, revealing the dominant technical integration patterns.
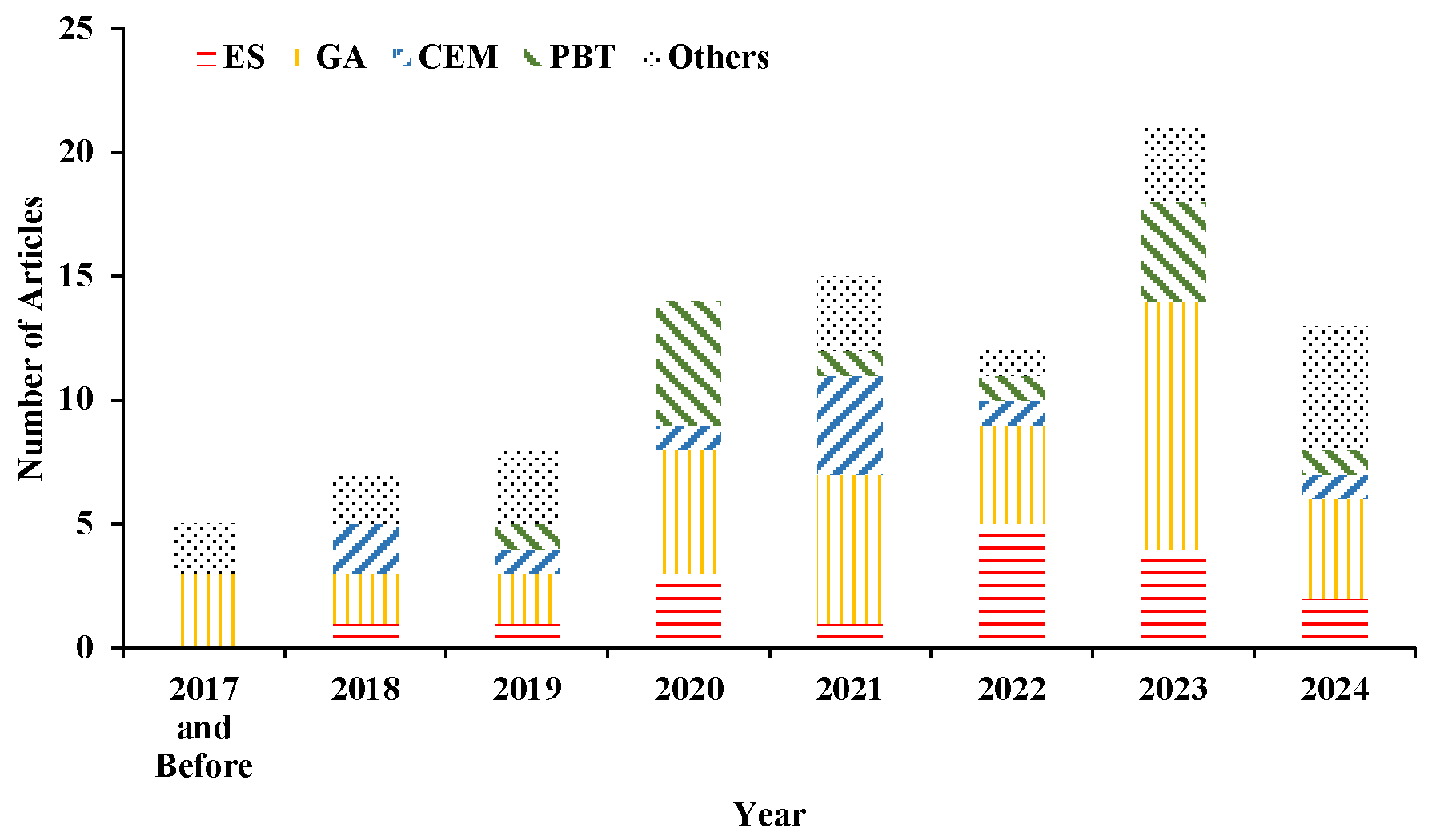
- Chronological Analysis: We constructed the annual publication distribution (Figure 2) to quantitatively visualize the phased evolution of research activity in EvoRL.
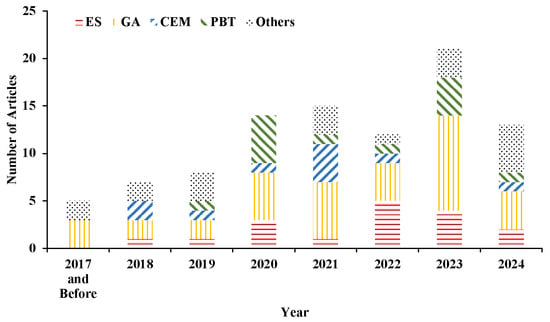 Figure 2. Distribution of year-wise publications (until December 2024) according to different EAs used in EvoRL research. The figure illustrates the number of EvoRL publications utilizing an evolutionary strategy (ES), a genetic algorithm (GA), the cross-entropy method (CEM), population-based training (PBT), and others. The x-axis represents the years, while the y-axis indicates the number of publications. The overall trend suggests a growing research interest in EvoRL, with an increasing number of studies employing evolutionary approaches.
Figure 2. Distribution of year-wise publications (until December 2024) according to different EAs used in EvoRL research. The figure illustrates the number of EvoRL publications utilizing an evolutionary strategy (ES), a genetic algorithm (GA), the cross-entropy method (CEM), population-based training (PBT), and others. The x-axis represents the years, while the y-axis indicates the number of publications. The overall trend suggests a growing research interest in EvoRL, with an increasing number of studies employing evolutionary approaches. - Benchmark Task Clustering: We identified three core testing scenarios (continuous control, multi-task, and multi-objective optimization) through the attribute clustering of benchmark tasks, establishing clear mapping relationships between task characteristics and algorithmic preferences.
- Mainstream Benchmarking Practices: We extracted prevalent comparison algorithms (primarily A2C, SAC, and DDPG) to identify mainstream benchmarking practices in reinforcement learning research.
- Performance Metric Categorization: We systematically categorized performance metrics, emphasizing the cumulative reward, convergence speed, and computational cost, to reflect differentiated assessment requirements across heterogeneous testing environments.
- Comparison with Existing Reviews: We compared our collected literature with prior review studies [19,21,22], confirming that all articles covered in these works were included in our analysis. Additionally, we incorporated more recent publications to ensure the timeliness and comprehensiveness of our study.
3. Background
In the literal sense, EvoRL combines EAs with reinforcement learning. To offer a comprehensive description of EvoRL, this section will provide brief introductions to both EAs and reinforcement learning.
3.1. Reinforcement Learning
As one of the most popular machine learning methods, reinforcement learning has attracted a lot of attention in recent years. It has shown great potential in everything from gaming to autonomous driving. Given that reinforcement learning has been extensively discussed and studied, we will not repeat its basic concepts here, but directly introduce its three main methods.
The value function approach evaluates each state, s, or state–action pair, , by learning a value function, , and guides decision-making according to this [29], which can also be demonstrated as
where denotes the policy under state s. It can also be called a greedy policy [30]. The core concept of this approach is to optimize the value function to predict future rewards.
The policy gradient method directly optimizes the policy itself, aiming to maximize the expected return [1]. This method optimizes the policy by adjusting the policy parameters but not the estimated value function. The policy gradient method provides a formula related to updating the policy parameters using a gradient ascent on the expected return [30]:
where denotes the expected return of the policy, is a trajectory, and represents the cumulative reward after the operating trajectory , while demonstrates the expectation over trajectories sampled from the policy [30].
The actor–critic algorithm is a reinforcement learning technique used for learning optimal policies in unknown environments. Its core concept revolves around guiding the policy improvement of the actor based on the value function estimations provided by the critic [1,29]. In this algorithm, the updating rule of the policy parameter is defined as
where represents the learning rate, denotes the policy, and and are the estimation of the value function under the current state s and the next state , respectively. r is the reward, while represents the discount factor towards future rewards [30].
3.2. Evolutionary Algorithms
EAs do not refer to one specific algorithm, but are a generic term for a series of sub-algorithms that are inspired by natural selection and the principle of genetics. These sub-algorithms solve complex problems by imitating the process of biological evolution. Therefore, EAs can be considered as a general concept that consists of the following five optimization algorithms which utilize the mechanism of biological evolution [31].
Evolutionary strategy was first proposed by Rechenberg [32,33]. Evolutionary strategies optimize candidate solutions by generating populations and applying mutation, recombination, and selection processes, based on principles of biological evolution. There is an adaptive adjustment of the mutation step size in this algorithm, which enables the method to search effectively in the solution space. The following is the core formula of an evolutionary strategy, which is applied to the adjustment of the mutation step size for the dimension:
where and denote the mutation step sizes before and after adjustment, respectively. refers to the adjustment factor, which is derived from the difference between two independent normal distribution random variables, and . This exponentiation of the difference determines whether the step size will increase or decrease. The use of random variations from the normal distribution to adjust the mutation step size introduce stochasticity into the mutation process, effectively mimicking biological mutation, where genetic variations occur at random. This stochastic mutation enables the algorithm to explore new regions of the solution space, potentially escaping local optima and enhancing the exploration capabilities of the algorithm. Evolutionary strategies are particularly well suited for addressing problems in reinforcement learning that involve sparse rewards and policy search due to their robust search capabilities on a large scale [24].
The genetic algorithm is one of the most famous EAs. There are three essential operators, which are selection, mutation, and crossover [22]. The population is also a core concept in the genetic algorithm, where each individual in it represents a potential solution, which will be evaluated through its fitness function [34]. Different from evolutionary strategy, the genetic algorithm focuses on the crossover as the main mechanism of exploration, while evolutionary strategy tends to rely on mutation [32]. The genetic algorithm is usually applied to deal with the problem of hyper-parameter tuning in reinforcement learning.
The cross-entropy method defines an accurate mathematical framework that explores optimal solutions based on advanced simulation theory. It starts by randomizing the issue using a series of probability density functions and solves the associated stochastic problem through adaptive updating [35]. The key concept of the CEM involves the elite solution-based probability density function’s parameter updating and global searching ability enhancement by applying mutation. The following is the core formula of the CEM [36]:
where is a performance function used to evaluate the random variable , denotes a parameterized probability density function, and is a parameter. This equation aims to find a to maximize the logarithmic likelihood expectation when the event happens; is a threshold. That is, a is sought to make it easier for a high-performance event to happen. This is the core idea of the CEM, which is that by minimizing the cross-entropy, the sampling distribution gradually becomes closer to the high-performance region so that high performance is more easily sampled [36]. The CEM offers a robust solution to the challenges of local optima and computational efficiency in reinforcement learning [37].
Differential evolution is one of the most powerful stochastic optimization algorithms. Unlike traditional EAs, differential evolution mutates candidates in the current population by randomly selecting and scaling the differences between distinct candidates. This approach eliminates the need for an independent probability distribution to generate offspring. The core mutation step involves generating variation vectors for the parent candidates:
where is the variation vector, , , and are individual vectors randomly selected from the population, is the scaling factor, and G denotes the current generation. The straightforward implementation of differential evolution makes it an attractive choice, and its ability to enhance the performance of reinforcement learning arises from its efficient global search capabilities using differential vectors and a selection mechanism [38].
Population-based training can be viewed as a type of parallel EA; it optimizes the weights and hyper-parameters of a neural network’s population simultaneously [39]. The algorithm starts by randomly initializing a population of models; each model individual will optimize their weights independently (similarly to mutation) in training iterations. The prepared individual needs to get through two stages, which are “exploit” and “explore”, at the population level. The former is similar to “selection”, that is, replacing the original model weights and hyper-parameters with a better performance model. Actually, it is a parameter transfer inside the population. The latter one is similar to “mutation”, realizing the exploration of the hyper-parameter space by adding noise, which provides diversity for the following training [39]. Due to its characteristics, PBT shows an excellent ability to solve issues of hyper-parametric sensitivity and sparse rewards in reinforcement learning [22,24].
Genetic programming simulates natural selection to generate a mathematical expression. Compared with other EAs, genetic programming has strong flexibility and a strong adaptive ability in optimizing strategy expression, especially suitable for symbolic regression, control strategy optimization, and classification tasks [40].
Swarm Intelligence is an algorithm inspired by biological group behavior. Typical Swarm Intelligence includes Ant Colony Optimization (ACO), particle swarm optimization (PSO), etc. [41]. Differently from GAs, Swarm Intelligence relies on global interactions and information propagation rather than genetic operations. Recently, Swarm Intelligence has demonstrated its utilization potentiality in deep learning and reinforcement learning.
Apart from the algorithms introduced previously, there are several other EAs, e.g., evolutionary computing and random search. Although these algorithms have their own characteristics, they basically share some common principles, like population-based search, iterative optimization, the simulation of natural selection, and genetic mechanisms. Evolutionary computing focuses on the fitness function problem [42], while random search could be used for improving the calculation efficiency of reinforcement learning [43].
4. Methods of Evolutionary Reinforcement Learning
This section aims to provide an in-depth discussion of the core mechanism in EvoRL algorithms, focusing on the EAs (classified sequentially as ESs, GAs, the CEM, PBT, and other EAs) they incorporate. In this section, the components of reinforcement learning and EAs will be described in detail, to analyze their effects on and advancements in the decision-making process. In addition, we will also discuss the evaluation metrics used for assessing EvoRL’s performance and the corresponding benchmarks. An overview of the literature is shown in Table 1. The benchmark tasks are also provided in Table 1. From the perspective of the distribution of benchmark tasks, continuous control is the main application scenario in EvoRL research, covering all EAs. Multi-objective and multi-task optimization are mainly found in GAs and PBT, demonstrating the ability of these methods to optimize multiple goals and generalize tasks. The parameter optimization task also relies heavily on GAs and PBT, leveraging their global search and dynamic tuning capabilities. Discrete Control tasks are few and concentrated in GAs and ESs.

Table 1.
Overview of Evolutionary Reinforcement Learning algorithms with evaluation metrics and benchmarks.
4.1. Evolutionary Strategy
In the expansive field of reinforcement learning, the value function method has always been one of the core research directions, mainly focusing on how to effectively estimate and optimize the expected return under a given policy. Against this background, the natural parameter search mechanism of evolutionary strategy provides a unique approach by simulating the processes of natural selection and heritable variation. This approach has been successfully applied in various real-world scenarios, such as robotic control, automated trading, and industrial process optimization, where traditional gradient-based methods face challenges due to high dimensionality.
Mutation, one of the most essential operations in evolutionary strategy, introduces diversity to the algorithm process by randomly modifying policies or parameters. This operation enables EvoRL to effectively adapt to complex learning environments and avoid falling into local optima. In [44], the authors employed a simple but effective EvoRL algorithm called AEES, which contains two distinct, coexisting mutation strategies. Each of the two strategies is connected with their population subsets. That is, each subset mutates in accordance with one related mutation strategy. AEES applies the cumulative return and convergence rate as evaluation metrics, and the proposed model shows better performance ompared to A2C, SAC, and other DRL methods. Compared to [44], the OHT-ES algorithm in [45] focuses more on adjusting key parameters of the reinforcement learning method through evolutionary strategy, hence improving the adaptability and efficiency of the algorithm. Ref. [45] proves that OHT-ES performs better than traditional DRL (e.g., TD3) in terms of the learning speed.
Differently from the value function, the introduction of evolutionary strategy in the policy gradient method provides a brand new perspective. The idea for the realization of R-R1-ES [46] is distinct from [44]; R-R1-ES put special emphasis on the direct optimization of the policy itself, which applies the Gaussian distribution model and a restart mechanism to update the searching direction, where represents the distribution mean, denotes the mutation strength, and is an n-dimensional covariance matrix at t iterations. The update rule of is given as
where is the changing rate of the covariance matrix, I denotes the unit matrix, and is a vector which represents the primary search direction. The model performs better than NS-ES (Novelty Search–Evolutionary Strategy) according to reward evaluation. The application of evolutionary strategies is anticipated to augment the global search proficiency and yield refined gradient information, through which they can potentially accelerate the convergence towards optimal policy solutions [48].
In addition, the ZOSPI model [50] reveals the potential of combining evolutionary strategy and an actor–critic algorithm. Compared to R-R1-ES [46], ZOSPI chooses to optimize the policy from global and local perspectives, which both exploit the advantages of the global value function and the accuracy of the policy gradient fully. The approach not only improves the sample efficiency but expands the possibility of multi-modal policy learning, creating a novel trajectory for the actor–critic algorithm.
4.2. Genetic Algorithm
Genetic algorithm-based EvoRL methods are different from traditional methods; they focus on applying genetic diversity to the policy search process, which makes the algorithm find an effective and stable policy in a highly complex environment. This characteristic has been particularly beneficial in real-world applications, such as autonomous driving, game AI, and resource management, where the environment is dynamic and highly unpredictable.
One of the valuable contributions of genetic algorithms is the ability to introduce significant diversity in parameters and strategies through crossover operations. This diversity enables the exploration of a broader solution space, which is crucial for finding effective and robust policies in highly complex environments. In [54], the authors introduced an MAERL method that mainly focuses on parameter optimization in the processing industry. The method consists of multi-agent reinforcement learning, Graph Neural Networks (GNNs), and genetic algorithms. The ERLGA [55] method involves the combination of a genetic algorithm and off-policy reinforcement learning, finally reaching a better performance on return than existing methods. Moreover, ref. [59] proposed a MetaPG algorithm to optimize different reinforcement learning targets using multi-objective searching standards and consider individual reinforcement learning targets via the Non-Dominated Sorting Genetic Algorithm II (NSGA-II). MetaPG is able to improve performance and generalization by about and compared to Soft Actor–Critic (SAC) by adjusting the loss function. In addition, ERL-TD [27] similarly utilizes a genetic algorithm-based policy gradient framework but optimizes the learning process by incorporating truncated variance and distillation mutations to enhance the data efficiency and asymptotic performance. Simultaneously, genetic algorithms play a crucial role in fine-tuning the intricacies of policy evolution; ref. [61] developed a PDERL method to solve the scalability issues caused by simple genetic encoding in traditional algorithms. The PDERL method applies the following formula to define the proximal mutation operator:
where Sens represents the sensitivity of the action to weight perturbation, is the size of the action space, denotes the sample size used for calculating the sensitivity, and is the gradient of the policy network to its parameter, , used to evaluate the sensitivity of policy changes to the parameter under state .
In addition, genetic algorithms can be applied to tackle complex reinforcement learning problems that demand extensive interaction with the environment; ref. [62] proposed an SERL which contains a surrogate-assisted controller module. The module combines a genetic algorithm and actor–critic algorithm, where the genetic algorithm here is mainly used for evaluating the fitness of the genetic population. The method applies surrogate models to predict the environmental performance of individuals, which decreases the requirements of direct interaction with the environment and leads to a lower computational cost.
4.3. Cross-Entropy Method
In the field of multiple-EvoRL-method research, the CEM, as a core technique, mainly focuses on selecting elites to update the policy distribution, so that the policy evolves in a better direction. The key concept of CEM-based EvoRL is that it does not rely on complex gradient calculation but processes the iterative optimization of policies by statistical methods.
The CEM-RL [67] is a typical example; it combines the CEM with a policy gradient to balance exploration and exploitation [67]. In [70], the authors proposed an SAC-CEPO method combining the CEM and SAC. More specifically, SAC-CEPO samples the optimal policy distribution iteratively and applies it as the target of policy network updates. The key formula of SAC-CEPO is
where represents the performance of policy , is the expectation under the policy , denotes the discount factor, indicates the reward of action under state , and stands for the model parameter, which is applied to balance the weight between the policy entropy and the rewards.
Not only can the CEM optimize the policy network effectively, but it can also enhance the overall decision quality and algorithmic efficiency through the statistical evolution of the value function. Ref. [65] introduced the QT-OPT method, which applies the CEM to optimize the value function of reinforcement learning. QT-OPT shows a good ability in success rate evaluation compared to existing algorithms. Ref. [66] developed an algorithm that exploits the CEM to seek the optimal action with the maximal Q-value, called GRAC. The combination of EAs and the value function makes GRAC exceed TD3, SAC, and other popular DRL methods in OpenAI Gym’s six continuous control missions.
The CEM also demonstrates a robust capability in guiding population evolution and iteratively optimizing the entire policy space, thereby expanding its application in the field of reinforcement learning. Ref. [68] proposed a PGPS that considers the CEM as its core component. In the PGPS, the CEM is applied to generate the next population based on the current evaluation results to create a higher return (defined as the sum of the instant rewards within a certain number of steps). The PGPS performs better than multiple DRL methods, such as DDPG, PPO, SAC, etc., in several MuJoCo environments.
4.4. Population-Based Training
PBT-based EvoRL shows potential in multiple research fields. The core concept of it is to adjust the parameters and hyper-parameters of the algorithm dynamically in the training process, so that more effective and flexible learning is realized in complicated environments.
Therefore, ref. [4] introduced a parameter control strategy training method for EAs and Swarm Intelligence (SI) algorithms called SBARL. PBT was applied in SBARL to evolve the parameters and hyper-parameters in reinforcement learning; the results of the experiment demonstrate that SBARL performed better than the traditional DRL method TD3. PKAEO [89], an EvoRL algorithm using PBT, evolves both the parameters and policies in reinforcement learning, facilitating more efficient optimization and adaptation. EARL [73] is a framework that combines EAs (more specifically, PBT) and reinforcement learning. The key concept of EARL is that the collaborative work of EAs and reinforcement learning could facilitate the learning and evolving process. Ref. [78] proposed an MERL algorithm that realizes individual and team objectives by combining gradient-less and gradient-based optimizers. Among them, the policy of gradient-based optimizers is added to the regularly evolving population, which enables EAs to leverage skills learned through training in individual-specific rewards to optimize team goals without relying on reward shaping. Besides the policy space, PBT can influence the action space in reinforcement learning, emphasizing the importance of optimizing action decisions. Ref. [74] proposed the EAS-TD3 method, which uses actions selected by the reinforcement learning policy to generate a population and then applies particle swarm optimization to iteratively evolve the population. The key concept of EAS-RL is choosing to optimize the action space but not the policy space; the definition of the loss function in the action space is
where the state and the evolutionary action in this formula are sampled, respectively, from the archive , while denotes the learning parameters in the reinforcement learning policy . The proposed model behaves better than TD3 in MuJoCo environments.
Beyond optimizing parameters and actions, PBT places specific emphasis on automatically adjusting reward functions, e.g., ref. [80] focused on game AI generation. Therefore, they proposed a PBT-based EvoRL method, the EMOGI framework. EMOGI considers the reward function as a part of the candidate objects, realizing the auto-adjustment of the parameters by EAs. EMOGI applies multi-objective optimization to select policies with distinct behaviors to ensure population diversity. The key process of the initialization of EMOGI is to randomly initialize a candidate population consisting of policy parameters and reward weights:
where P denotes the population of candidates; each candidate consists of two parts, the policy parameter and the weight of the reward, . The size of the population is decided by n.
4.5. Other EAs
The preceding chapters covered classical algorithms based on evolutionary strategies, genetic algorithms, the CEM, and PBT, each demonstrating notable results in their respective application scenarios. Additionally, there are other promising EvoRL methods that, while less commonly employed, deserve attention. These include random search-based approaches designed to enhance efficiency by streamlining the search process, genetic programming methods that optimize strategies through the simulation of biological genetic processes, and evolutionary computing algorithms that emphasize the use of the principles of evolutionary theory to improve the learning process.
Random search simplifies the parameter optimization process while maintaining a certain level of exploration ability. This approach can efficiently find solutions in complex tasks. DDQN-RS [84] applies random search to randomly sample individuals from the population using a Gaussian distribution and evaluate their fitness according to the reward obtained from one round of running in the environment. Compared to the Double Deep Q-Network (DDQN), the proposed model performs better than it does in the mission of keeping a vehicle close to the center of a lane for the longest distance.
Compared to the efficient parameter optimization discussed in [84], the genetic programming in [83] demonstrated a capability for the in-depth optimization of computation graphs. In this framework, genetic programming is applied to search in the computation graph space, and these graphs compute the minimal objective function required by the agent. Genetic programming enhances these computation graphs by simulating the evolutionary process of organisms. The proposed model applies the loss function from the Deep Q-Network (DQN) as a key component:
where indicates the Q-value under the current state and action , represents an instant reward, denotes the discount factor, and stands for the maximal expectation of the Q-value under the next state . By applying this loss function, the proposed method focuses more on a more accurate estimation of the Q-value to solve the overestimation issue. Experimental results showed that a DQN modified by genetic programming behaved better than the original DQN in Q-value estimation [83].
Similarly, ref. [85] proposed an EGPRL method that applies genetic programming to search in the computation graph space, finally minimizing the objective function. EGPRL allows agents to operate under multiple environments, including OpenAI Gym’s Classic Control Suite. Experimental results showed that the proposed model possessed a competitive generalization ability and efficiency. Differently from [83] which considers the accurate estimation of the Q-value as its core concept, EGPRL focuses more on the hierarchical structure of memory coding and multi-tasking.
In addition, ECRL [81] applies evolutionary computing to optimize the parameters in reinforcement learning. More specifically, evolutionary computing uses the fitness function to assess each set of parameters, iteratively searching for the optimal solution in the parameter space. Similarly, the RL-RVEA [28] also applies evolutionary computing, combined with the Q-learning from reinforcement learning, to optimize solutions for multi-objective problems by dynamically adjusting reference vectors, effectively enhancing the adaptability and performance of the algorithm.
Additionally, RLHDE [90] utilizes Q-learning to dynamically adjust the mutation strategies in differential evolution. Compared to traditional hybrid EAs, RLHDE demonstrates a better global search capability and convergence speed. It outperforms existing state-of-the-art algorithms on several trajectory optimization benchmark problems provided by ESA-ACT, such as Cassini2 and Messenger-full.
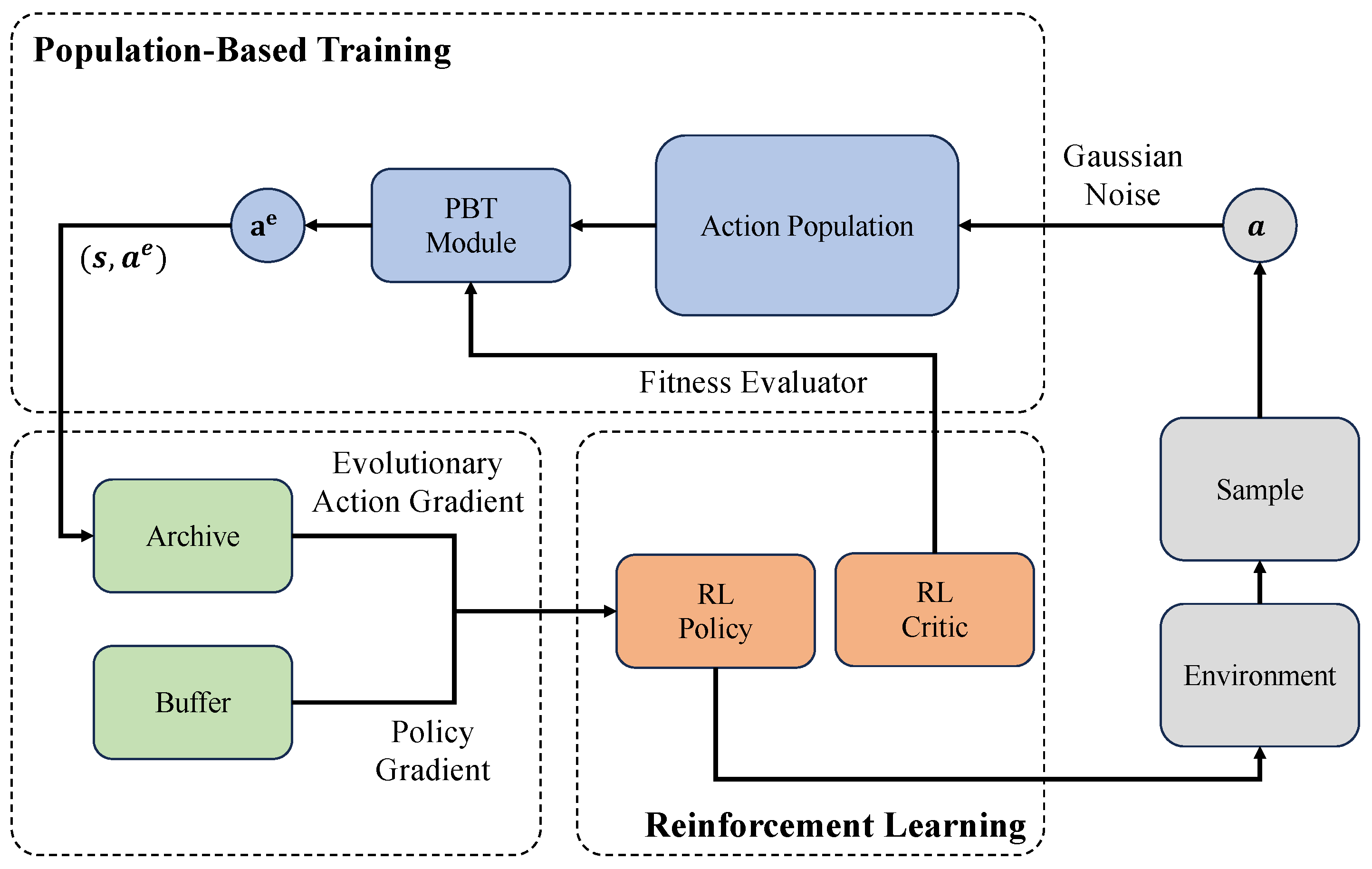
We have discussed the core mechanism of EvoRL in the above contents. EvoRL applies EAs to optimize the decision-making process of reinforcement learning by simulating the principles of natural evolution. In this paper, we primarily emphasize and explore the potential of evolutionary strategy, genetic algorithms, the CEM, and PBT to develop effective and robust strategies in challenging environments. The general workflows of the most frequently used EvoRL methods (i.e., ES-based, GA-based, CEM-based, and PBT-based) are depicted in Figure 3, Figure 4, Figure 5 and Figure 6, respectively. Evolutionary strategy primarily emphasizes the direct optimization of policies and behaviors through the simulation of natural selection and genetic variation. In contrast, the genetic algorithm focuses on searching for effective and stable policies through genetic diversity and crossover operations. The CEM iteratively optimizes strategies through statistical methods, with a particular emphasis on elite selection to guide policy development. PBT demonstrates flexibility in adjusting parameters and hyper-parameters, particularly in the automatic adjustment of reward functions. Genetic programming exhibits deeper complexity in the optimization of computation graphs.
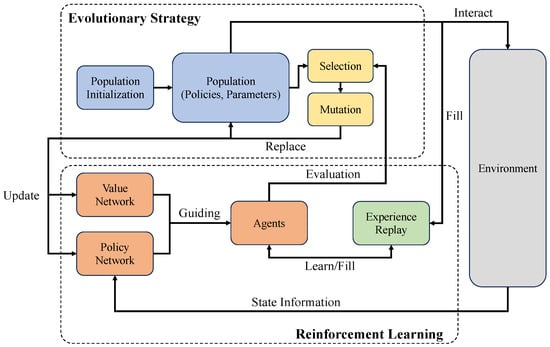
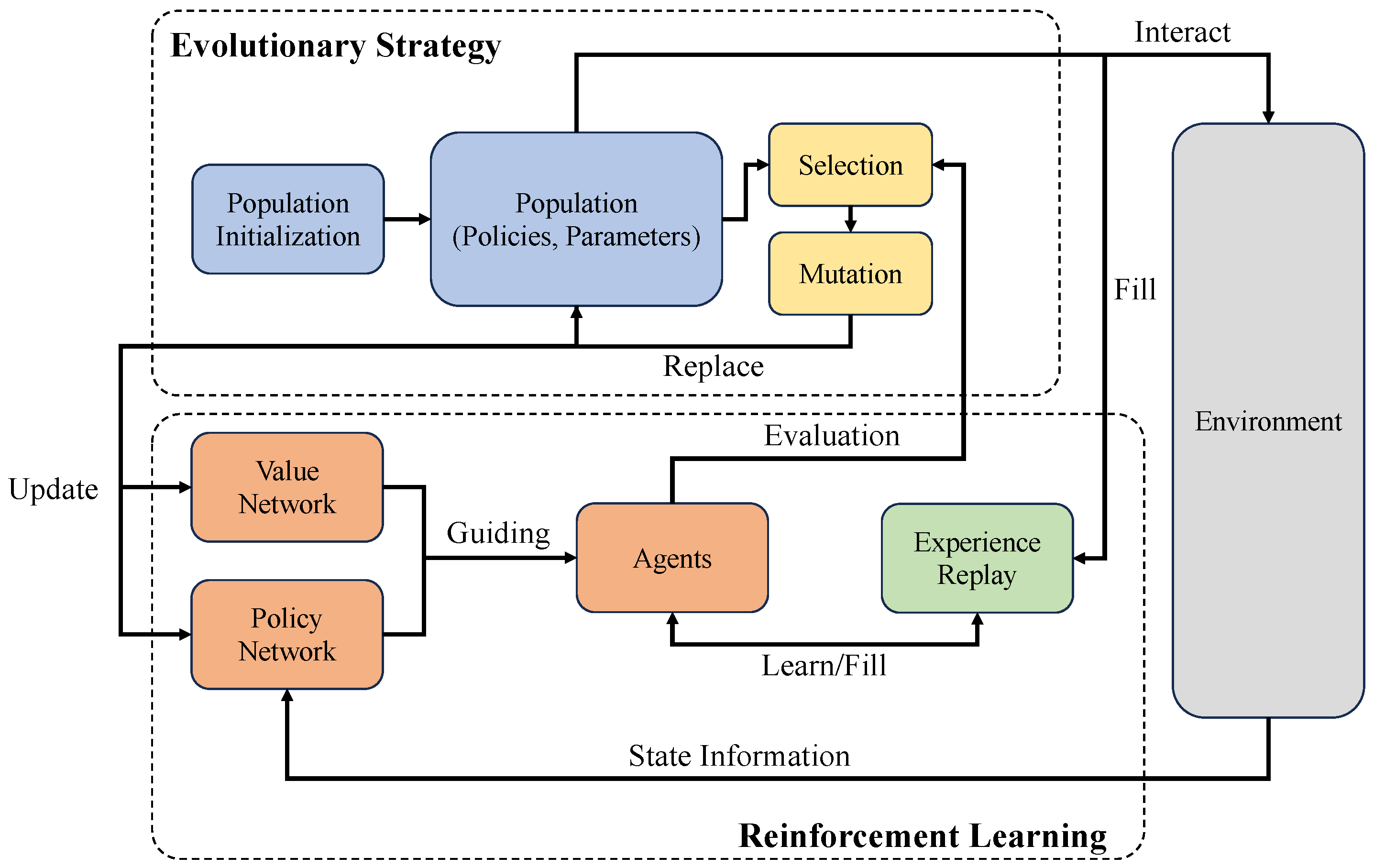
Figure 3.
A general workflow of ES-based EvoRL. The core evolutionary operation here is the mutation, which enhances the diversity of the population [9].
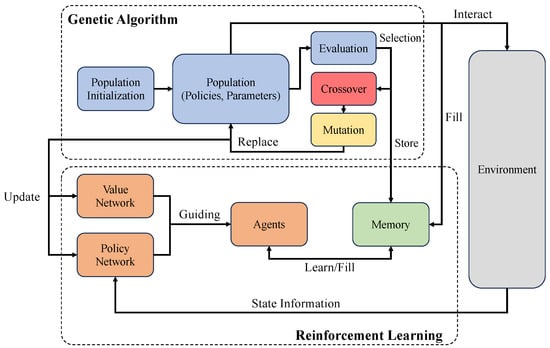
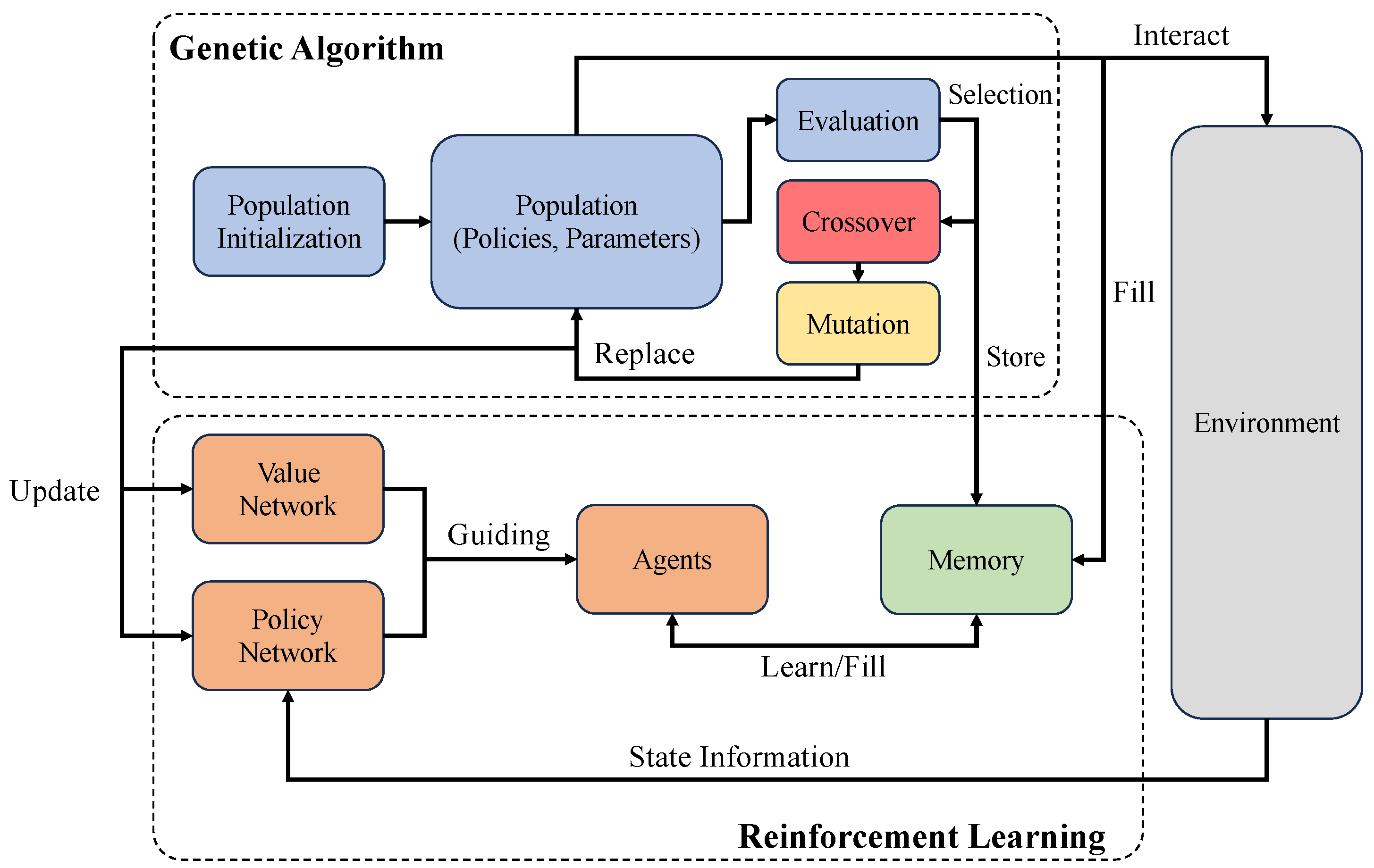
Figure 4.
A general workflow of GA-based EvoRL. The EvoRL retains good genes through a crossover to produce better individuals [16].
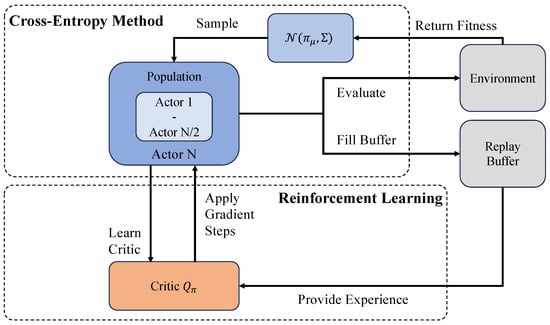
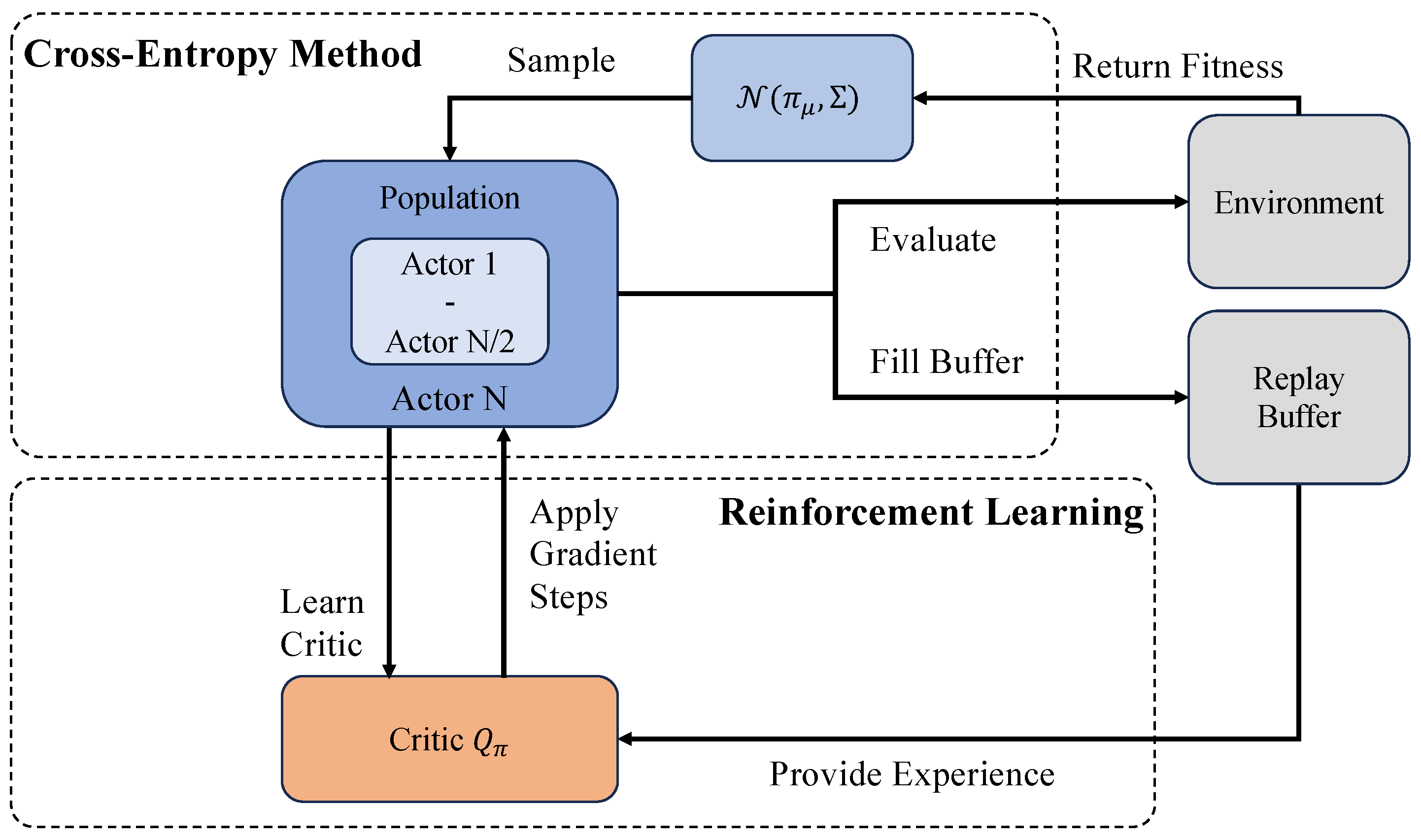
Figure 5.
A general workflow of CEM-based EvoRL. Multiple actors are responsible for sampling actions, evaluating fitness, and refining policies through gradient steps [67].
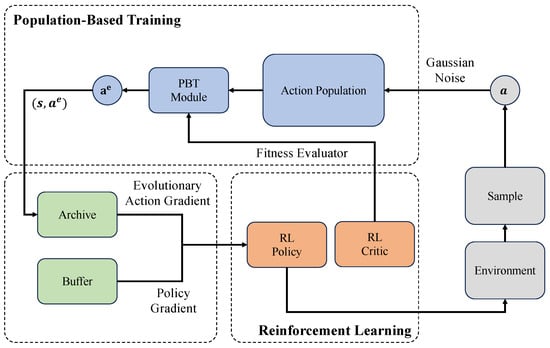
Figure 6.
A general workflow of PBT-based EvoRL, where action populations evolve with the Gaussian noise and are evaluated through reinforcement learning [74].
While these algorithms differ in methods and emphasis, they share a common core objective: to enhance the reinforcement learning process by applying principles from evolutionary theory, thereby improving the performance and adaptability of policies. However, it is crucial to note the distinct mechanisms through which each algorithm contributes to EvoRL. Evolutionary strategy relies heavily on mutation and selection processes to iteratively refine policy parameters, offering a straightforward yet powerful approach to policy optimization. Genetic algorithms, with their crossover and mutation operators, introduce a higher degree of genetic diversity, which can lead to more robust policy solutions but also requires the careful tuning of crossover rates. The CEM’s focus on elite selection ensures that only the best performing policies guide future generations, thus maintaining a high standard of policy quality throughout the learning process. PBT, on the other hand, leverages dynamic parameter adjustments and real-time hyper-parameter tuning, making it particularly adept at responding to changing environments and non-stationary reward functions. Genetic programming extends the evolutionary framework by evolving the structure of policies and computation graphs themselves, thus enabling the discovery of novel policy architectures that might be overlooked by more traditional approaches.
5. Challenges in Evolutionary Reinforcement Learning
In this section, we delve into the challenges encountered when employing reinforcement learning and EAs independently. We specifically analyze how these challenges underscore the importance and advantages of combining reinforcement learning and EAs in EvoRL. While reinforcement learning and EAs each exhibit significant strengths in addressing complex problems, they also have evident limitations. For instance, reinforcement learning commonly faces challenges such as parameter sensitivity, reward sparsity, susceptibility to local optima, multi-task processing difficulties, policy search complexity, and computational efficiency issues. Similarly, when applied in isolation, EAs encounter challenges such as hyper-parameter sensitivity, multi-objective optimization complexities, computational efficiency, and the design of fitness functions. To comprehensively understand these issues, this section is divided into two subsections, addressing the challenges faced when using reinforcement learning and EvoRL individually. Furthermore, we explore how EvoRL, as a holistic approach, overcomes these limitations by integrating the decision optimization capabilities of reinforcement learning with the natural evolutionary simulation of EAs, thereby achieving a more comprehensive, efficient, and adaptive problem-solving methodology.
5.1. Issues Encountered by Reinforcement Learning
When applying reinforcement learning independently, we face many of the problems mentioned above. These challenges limit the scope and efficiency of reinforcement learning in complex environments, suggesting that further methodological innovations and technological advances are needed to overcome these limitations [91]. The EA, as an algorithm that simulates biological evolutionary genetics, can help with reinforcement learning to some extent. An overview of issues encountered by reinforcement learning algorithms and their corresponding solutions is shown in Table 2.

Table 2.
Issues encountered by reinforcement learning and corresponding EA solutions.
5.1.1. Parameter Sensitivity
The performance of reinforcement learning depends heavily on the correct setting of parameters like the learning rate, discount factor, policy network parameters, and reward function parameters. The proper adjustment and optimization of these parameters are crucial for a stable and effective reinforcement learning process. Poor parameter settings can lead to unstable training, slow convergence, or a failure to find effective policies. EAs help tackle these issues by dynamically adjusting the parameters through evolutionary operations. EAs also increase the diversity of the parameter space, making it easier to find the best combination of parameters. This approach ensures that the reinforcement learning system can perform well even in complex and changing environments.
According to [4], the quality of the final results of parameter control methods for metaheuristics with reinforcement learning is highly correlated with the values of these parameters. Therefore, ref. [4] introduced the SBARL method, aiming to dynamically adjust and evolve these parameters while maintaining a static configuration. Specifically, the evaluation of PBT workers in SBARL aligns with their average reward in each training period. The less well-performing workers adopt the parameter settings of the better performing workers as a reference for optimization and evolution. Similarly to SBARL, ref. [42] dynamically selected the optimal local skills to adapt to the varying requirements of a multi-agent environment, effectively addressing the parameter sensitivity issue in reinforcement learning. The proposed MAEDyS [42] not only utilizes policy gradient methods to learn multiple local skills but also enhances the capability to handle parameter sensitivity in complex multi-agent settings through the dynamic selection and optimization of these local skills.
Besides dynamic parameter adjustment, ref. [92] employed a genetic algorithm to directly search and optimize parameters. The approach explores the parameter space through the selection, mutation, and crossover operations of the genetic algorithm, enhancing the diversity of the parameter space. This methodology aids in finding the optimal parameter combination for the proposed method. Ref. [92] presented Polyak-averaging coefficient updates, as shown below:
where and are the parameters of the target Q-network and target policy network, respectively. and denote the parameters of the current Q-network and policy network, and is the Polyak-averaging coefficient, a factor usually close to but greater than zero, used to blend the current and target network parameters.
In addition to dynamic parameter adjustment, NS-MERL [93] relies on novelty search to guide agents to explore a broader state space rather than just optimizing a fixed set of parameters. In addition, NS-MERL combines gradient optimization and evolutionary search to balance individual-level exploration with team-level optimization, improving the learning efficiency and coordination ability in complex tasks.
5.1.2. Sparse Rewards
The sparse reward problem is a significant challenge in reinforcement learning. As highlighted by [5], agents face difficulty obtaining sufficient reward signals to guide an effective learning process when exploring environments with sparse rewards. In such scenarios, the decision-making process of agents may become inefficient due to the lack of immediate feedback, thereby impacting the performance and training speed [5].
To address the issue, ref. [75] exploited the global searching ability of EAs, particularly PBT, to expedite the search process through cooperation and information sharing among multiple agents. More specifically, the proposed model accelerates the learning process by incorporating information on the best strategy, effectively guiding the agent to discover an effective strategy in sparse reward environments.
In addition to expediting the search process, ref. [94] introduced a GEATL method that employs a genetic algorithm to foster policy diversity through exploration in the parameter space. This policy exploration aids the uncovering of solutions effective in sparse reward environments, as it does not depend on frequent or immediate reward feedback.
Similarly, ref. [95] also resolves the sparse reward problem of multi-agent reinforcement learning through improving the diversity of the policy space. Ref. [95] proposed an RACE method which considers each agent as a population and explores new policy space through the crossover and mutation of individuals in the population. The evolutionary operations are able to help reinforcement learning to generate diverse behavior modes. This kind of diversity is quite essential for those effective policies that only appear under certain conditions in a sparse reward environment. Ref. [95] also introduced random perturbation, which is shown as
where and stand for the chosen teams and and depict subsets of the agent indices selected at random. The perturbation function, denoted as P, introduces Gaussian noise to specific parameters or resets them. is utilized to denote the subset of policy representations corresponding to the team characterized by the indices d.
5.1.3. Local Optima
The challenge of local optima is primarily attributed to the vanishing gradient during policy updating, as highlighted by [71]. This issue may hinder the effective exploration of better polices in complex environments. To handle this problem, ref. [71] introduced the DEPRL method, employing the CEM to enhance policy diversity and improve exploration efficiency. This approach shows a significant improvement in continuous control tasks and effectively reduces the risk of getting trapped in local optima.
Similarly, ref. [73] introduced an approach that enhances policy diversity by integrating reinforcement learning and EAs within a unified framework. In the proposed EARL [73], the crucial concept lies in the exchange of information between reinforcement learning agents and EA populations. Reinforcement learning agents acquire diverse exploration experiences from the EA population, while the EA population regularly receives gradient information from reinforcement learning agents. This reciprocal interaction fosters strategy diversity, enhancing the stability and robustness of the algorithm. The formula of the loss function in EARL is shown as
where represents the expectation over the states sampled from a dataset, , and the actions sampled from the policy , given the state .
For the actor–critic algorithm, the diversity of the policy space provided by EAs can improve the sample efficiency and performance. To this end, ref. [96] proposed a G2AC approach that combines gradient-independent and gradient-dependent optimization by integrating genetic algorithms in hidden layers of neural networks. The policy update gradient of G2AC is given as the following formula:
where denotes the expectation under the policy parameterized by , stands for the gradient of the logarithm of the policy , evaluated for a specific state–action pair, , and signifies the advantage function under policy . This approach allows models to diversify their exploration in the solution space and jump around as they find better areas, and G2AC increases the diversity of policies in this way.
5.1.4. Multi-Task Challenges
The multi-task challenges in reinforcement learning arise primarily from the dynamics and complexity of the real world, requiring agents to handle various tasks within distinct environments. As emphasized by [85], agents may need to navigate environments with both discrete and continuous action spaces, often characterized by partial observability. To tackle this issue, ref. [85] proposed the EGPRL method, combining multiple independently adapted agents to realize a synergistic effect among different policies, thereby enhancing the multi-task performance. This is further supported by the Tangled Program Graph (TPG) framework in [85], which leverages hierarchical structures and modular memory to effectively encode and manage environmental information in partially observable settings.
5.1.5. Policy Search
In reinforcement learning, the policy search problem revolves around determining the optimal policy to maximize the cumulative reward for an agent interacting with its environment. A proficient policy search capability is pivotal for efficient learning and preventing potentially sub-optimal or erroneous behavior. As highlighted in [40], conventional reinforcement learning approaches face challenges when confronted with intricate and high-dimensional state spaces. These difficulties can impede the learning process, resulting in subpar strategy quality.
Therefore, ref. [40] proposed a GPRL method which is able to autonomously learn a policy equation. In this method, genetic programming is used to generate the basic algebraic equations that form the reinforcement learning strategy from the pre-existing default state–action trajectory sample. The key to GPRL is that it learns interpretable and moderately complex policy representations from the data in the form of basic algebraic equations.
In a similar vein, genetic programming was applied in a two-stage process in another study [82]. Initially, programs were generated in a simulated environment using genetic programming, serving as candidate solutions for various tasks. Subsequently, these actions, derived from genetic programming, were adapted to the operational characteristics of specific real robots through reinforcement learning, particularly Q-learning. The pivotal aspect of this approach is that programs created by genetic programming provide an effective starting point for reinforcement learning, thereby accelerating and enhancing the process of policy search and adaptation.
Expanding on this concept, another study [86] introduced a genetic programming-based method aimed at automating feature discovery in reinforcement learning. Central to this approach is the use of genetic programming to generate a set of features that significantly enhance the efficiency of reinforcement learning algorithms regarding learning strategies. The key lies in utilizing genetic programming to automatically unearth useful features from an agent’s observations, capturing the intricate non-linear mappings between states and actions. This, in turn, improves both the efficiency and effectiveness of the policy search process [86].
5.1.6. Computational Efficiency
Traditional reinforcement learning methods often grapple with the high cost and inefficiency of calculating the derivative of the optimal target, leading to poor stability and robustness in complex tasks [43]. This challenge is compounded when employing complex neural networks (NNs) as control strategies in most current approaches. These deep NNs, despite their potential for enhanced performance, complicate parameter tuning and computation. In response, ref. [43] introduced FiDi-RL, a novel method that integrates DRL with finite-difference (FiDi) policy search. By combining DDPG and Augmented Random Search (ARS), FiDi-RL enhances ARS’s data efficiency. Empirical results have validated that FiDi-RL not only boosts ARS’s performance and stability but also stands competitively among existing DRL methods.
Complementing this, the CERM-ACER algorithm [97] addresses computational efficiency in reinforcement learning through an EA perspective, blending the CEM with the actor–critic with experiential replay (ACER). This synergistic approach enables policy parameters to make substantial jumps in the parameter space, allowing for more assertive updates per iteration. Consequently, CERM-ACER not only stabilizes the algorithm but also diminishes the necessity for extensive sample collection in complex environments, thus boosting computational efficiency.
Similarly, the CGP algorithm [98] enhances the computational efficiency of Q-learning in continuous action domains. By fusing the CEM with deterministic neural network strategies, CGP employs heuristic sampling for Q function training while simultaneously training a policy network to emulate the CEM. This is mathematically represented by the L2 regression objective:
where denotes the objective function for training the policy network , represents a state in the state space, is the policy generated by the CEM, and is the distribution over states as determined by the CEM policy. This strategy eliminates the need for costly sample iterations during inference, significantly accelerating the inference speed and reducing computational demands. CGP’s efficacy in execution efficiency makes it particularly suited for real-time, compute-sensitive tasks.
In summary, these approaches demonstrate how EAs can revolutionize reinforcement learning’s computational efficiency. Starting from policy generation, these methods adeptly navigate the complexities of reinforcement learning, offering more efficient, stable, and robust solutions.
5.2. Issues Encountered by Evolutionary Reinforcement Learning
Even though EvoRL has solved multiple issues by combining EAs and RL, the shortcomings of EvoRL cannot be ignored. Currently, the problems that need to be fixed are mainly focused on the sample efficiency, algorithm complexity, and different kinds of performance issues. An overview of issues encountered by EvoRL and their corresponding solutions is shown in Table 3.

Table 3.
Issues encountered by evolutionary reinforcement learning.
5.2.1. Sample Efficiency
The sample efficiency typically refers to the effectiveness of an EvoRL algorithm in achieving a certain level of performance with a minimal number of data samples. Algorithms with higher sample efficiency can extract useful information from a relatively small dataset, whereas those with lower sample efficiency require a larger dataset to achieve comparable performance. Consequently, sample efficiency holds significant importance in RL-related domains due to the time and resource consumption involved in acquiring samples through interactions with the environment. In [99], a projection technique was employed to address the challenge of low efficiency in sample transfer across different tasks. Specifically, the transfer of samples from one task to another can rapidly approach zero when the parameter space is sparse, potentially impeding updates to cross-task sample solutions. To maintain consistency in the distance, ref. [99] sampled parameter vectors from the distribution of one task and projected them back to the target distribution of another task.
Furthermore, ref. [74] introduced the EAS-TD3 method, aiming to focus on enhancing the sample utilization efficiency by optimizing action selection. Through evolving actions and adjusting the Q-value, EAS-TD3 significantly improves EvoRL’s ability to learn from limited samples. This approach not only enhances the algorithm’s adaptability to complex environments but also effectively shortens the learning cycle and improves the sample efficiency by making precise use of each sample. The main framework is based on the following proposition:
The core concept of this proposition is that for any state, s, the expectation generated by policy is surpassed by the expectation under the EAS-optimized policy . This indicates that the actions, , optimized through the EAS approach yield a higher expected return than those selected by the original policy, thereby enhancing the sample efficiency and overall learning performance.
5.2.2. Algorithm Complexity
There are numerous parameters and hyper-parameters that need to be selected in EvoRL, such as network parameters [44]. The work by [44] highlights that while EvoRL and its variants perform well in large-scale optimization tasks, they heavily rely on the selection of a large number of diverse parameters, which necessitates extensive computation. Consequently, ref. [44] proposed an AEES approach that divides the population into distinct subsets and assigns different mutation policies to each. During the evaluation stage, this approach amalgamates the entire population, enabling individuals within each subset to compete not only with their own offspring but also with the offspring from other subsets. This method allows the model to both explore and exploit during the evolution process, thereby enhancing the speed of convergence. Compared to DDPG and SAC, AEES demonstrated faster convergence and better scalability for both low- and high-dimensional problems.
In addition, the extensive search space in EvoRL presents significant challenges. Ref. [47] highlighted that the application of NCS (Negatively Correlated Search) directly to reinforcement learning tasks encounters a substantial search space issue. To tackle this, the CCNCS approach was introduced. By effectively decomposing the search space and maintaining parallel exploration, CCNCS achieves efficient learning and optimization. Remarkably, CCNCS demonstrated improved performance with 50% less time consumption in exploring a 1.7 million-dimensional search space. This showcases its capability to efficiently navigate through complex environments, ensuring a balanced exploration and exploitation process.
5.2.3. Performance
Exploring the performance of EvoRL unveils a range of challenges, especially concerning its core attributes. Despite its demonstrated advancements and potential in multiple domains, limitations such as its generalization, adaptation, sparsity, and scalability become apparent upon deeper investigation. These issues impact the effectiveness of EvoRL algorithms and restrict their application in wider and more complex settings.
The generalization issues in EvoRL were discussed by [53]. They highlighted the significance of model transferring across multiple tasks in multi-task EvoRL environments. A common approach involves exploring a vast search space to identify the optimal policy. To address this challenge, ref. [53] introduced the A-MFEA-RL method, which aims to harness the potential synergies among tasks. This is achieved by employing evolutionary computing to tackle multiple optimization tasks simultaneously. At the heart of A-MFEA-RL is the concept of a uniform search space, wherein each candidate solution can be decoded and evaluated as a potential solution for any given task, thereby facilitating the efficient sharing and transfer of knowledge.
Although EvoRL successfully generates diverse experiences for training reinforcement learning agents by evolving a series of actors, enabling it to outperform some advanced reinforcement learning and EA algorithms in unconstrained problems, this approach struggles to balance rewards and constraint violations in constrained environments. Ref. [60] introduced an ECRL algorithm designed to adaptively balance rewards and constraint violations through stochastic ranking and a Lagrange relaxation coefficient:
where and represent the expected cumulative values of rewards and constraints, respectively. is the Lagrange multiplier, and denotes the constraint threshold. Simultaneously, ECRL restricts the policy’s behavior by maintaining a constraint buffer.
Adaptation issues in EvoRL also emerge from the high cost associated with interactions between policies in genetic populations and the real environment, as noted by [62]. These interactions often incur prohibitively high costs and can be impractical. To handle this issue, ref. [62] introduced a novel module, the surrogate-assisted controller (SC), and proposed the SERL method. This method aims to partially substitute the expensive environmental assessment process by incorporating surrogate models into the existing EvoRL framework. Central to this approach is the utilization of an approximate fitness function, derived from a surrogate model, to evaluate the fitness of individuals within a genetic population. This significantly reduces the necessity for direct interactions with the real environment, thus mitigating the adaptation challenges in EvoRL.
In addition, unlike the previous articles focusing on the reward–constraint balance and cost of environment interaction, ref. [46] zeroed in on the mutation adaptability within EvoRL. R-R1-ES tackles this by simplifying CMA-ES for Deep Reinforcement Learning, enhancing mutation strength adaptation with key formulas:
where is the current mutation strength, denotes the cumulative rank rate, and presents a damping parameter that controls the adaption rate.
EvoRL’s sparsity issue is also noteworthy, as [93] identified challenges in discovering complex joint policies due to many policies yielding similar or zero fitness values. The proposed NS-MERL algorithm addresses this by combining a novelty-based fitness function for individual exploration and a sparse fitness function for team performance evaluation. Key to NS-MERL is the introduction of a count-based estimate of state novelty, fostering broader exploration within episodes and enhancing the likelihood of identifying effective joint policies.
EvoRL’s scalability is equally crucial, as addressed by [61], focusing on enhancing GAs for DNN (Deep Neural Network) integration. Traditional GAs have struggled with scalability, largely due to simple genetic encoding and traditional variation operators which, when applied to DNNs, can lead to catastrophic forgetting. PDERL was introduced as a solution [61], characterized by its hierarchical integration of evolution and learning and innovative learning-based variation operators. These operators, unlike traditional ones, meet the functional requirements when applied to directly encoded DNNs, as demonstrated in robot locomotion tasks. Through PDERL, EvoRL’s scalability challenges are significantly mitigated, showcasing improved performance across all tested environments.
6. Open Issues and Future Directions
After a thorough review of EvoRL algorithms, it is evident that their current application does not stand out as a remarkable achievement but rather necessitates further refinement. In this section, we put forward some emerging topics for consideration.
6.1. Open Issues
6.1.1. Scalability to High-Dimensional Spaces
The challenge lies in extending EvoRL methodologies to effectively handle the complex, high-dimensional action and state spaces commonly encountered in real-world applications, such as autonomous vehicles [100], unmanned aerial vehicles [101], and large-scale industrial systems. Overcoming this hurdle entails the development of EvoRL algorithms capable of efficiently exploring and exploiting these expansive spaces while maintaining computational tractability. Furthermore, ensuring the scalability of EvoRL necessitates the implementation of innovative techniques to handle the curse of dimensionality, facilitate effective knowledge transfer [102] across related tasks, and enable the discovery of meaningful solutions amidst the inherent complexity of high-dimensional environments.
6.1.2. Adaptability to Dynamic Environments
The adaptability to dynamic environments stands out as a significant open issue in EvoRL. EvoRL systems usually face challenges in rapidly adjusting their policies to keep pace with changes in the environment, where the optimal strategy may evolve over time. As real-world applications often involve dynamic and uncertain conditions, resolving the challenge of adaptability is essential for making EvoRL systems robust and versatile in handling the complexities of changing environments. To this end, it requires the development of algorithms that can dynamically adapt to shifting conditions. EAs with dynamic parameter adaptation [103], such as Adaptive Evolution Strategies [104], represent one avenue of exploration. These methods allow the algorithm to autonomously adjust parameters based on environmental changes. Additionally, research might delve into the integration of memory mechanisms (e.g., Long Short-Term Memory networks [105]) or continual learning approaches to retain information from past experiences, enabling EvoRL agents to adapt more effectively to evolving scenarios.
6.1.3. Adversarial Robustness in EvoRL
How to ensure that EvoRL agents maintain resilience in the face of intentional perturbations or adversarial interventions is another open issue in EvoRL. Unlike traditional adversarial attacks in DRL, the unique characteristics of EvoRL algorithms introduce a set of challenges that demand tailored solutions [106]. Addressing this issue involves developing algorithms that can evolve policies capable of withstanding adversarial manipulations, ultimately leading to more reliable and secure decision-making in dynamic and uncertain environments. To this end, we may focus on training EvoRL agents with diverse adversarial examples which promote transferable defenses that can withstand perturbations across different environments. In addition, it is worth designing EAs that emphasize safe exploration, aiming to guide the learning process towards policies that are less prone to adversarial manipulation.
6.1.4. Ethics and Fairness
Another open issue in EvoRL that demands attention is the ethics and fairness of the evolved policies. As EvoRL applications become more pervasive, ensuring that the learned policies align with ethical standards and exhibit fairness is crucial. Ethical concerns may arise if the evolved agents exhibit biased behavior or inadvertently learn strategies that have undesirable societal implications. To address this issue, researchers need to explore algorithms that incorporate fairness-aware objectives during the evolutionary process. Techniques inspired by fairness-aware machine learning, such as federated adversarial debiasing [107] or reweighted optimization [108], could be adapted to the EvoRL context. Additionally, integrating human-in-the-loop approaches to validate and guide the evolutionary process may contribute to the development of more ethically aligned policies. As EvoRL continues to impact diverse domains, it will become imperative to develop algorithms that are not only optimized for performance but also adhere to ethical considerations and ensure fairness in decision-making processes.
6.2. Future Directions
6.2.1. Meta-Evolutionary Strategies
Meta-evolutionary strategies involve the evolution of the parameters guiding the evolutionary process or even the evolution of entire learning algorithms. This approach enables EvoRL agents to adapt their behaviors across different tasks and environments, making it inherently more versatile. Techniques inspired by meta-learning, such as the Model-Agnostic Meta-Learning (MAML) algorithm [109], applied to EAs, hold promise for enhancing the ability of agents to generalize knowledge across various tasks. In this integration, MAML helps the agent learn a shared initialization of its parameters that is adaptable to multiple environments with minimal updates. Instead of evolving strategies for each specific task, EvoRL agents using MAML can rapidly adjust their learned parameters to new tasks by using only a few gradient steps. The evolutionary process can then guide the optimization of this shared initialization, improving the agent’s ability to adapt quickly to unseen scenarios. Furthermore, we can integrate mechanisms such as continual learning [110] and episodic memory [111] to further enhance adaptation. Continual learning helps agents to retain and apply knowledge gained from previous tasks without forgetting, while memory networks allow them to store and retrieve relevant information from past experiences when encountering new challenges. Combining these techniques will allow EvoRL agents to not only excel in specific environments but also to generalize and learn efficiently across a wide range of evolving, dynamic scenarios.
6.2.2. Self-Adaptation and Self-Improvement Mechanisms
In the future, EvoRL is likely to witness significant progress in the incorporation of self-adaptation and self-improvement mechanisms, reflecting a paradigm shift towards more autonomous and adaptive learning systems. Self-adaptation refers to an agent’s ability to dynamically adjust its strategies and parameters in response to changes in the environment or its own performance, while self-improvement goes beyond immediate adjustments and focuses on the long-term enhancement of the agent’s capabilities. Researchers are exploring algorithms that enable EvoRL agents to dynamically adjust their strategies and parameters without external intervention. EAs with self-adaptation mechanisms, such as Self-Adaptive Differential Evolution [112] or hybrid differential evolution based on adaptive Q-learning [90], exemplify this trend. These algorithms allow the optimization process to autonomously adapt to the characteristics of the problem at hand, enhancing efficiency and robustness. Additionally, for long-term self-improvement, continual learning techniques [113], such as Elastic Weight Consolidation (EWC) [114], can be integrated. These methods allow EvoRL agents to accumulate knowledge over time without forgetting previous tasks, promoting stability while enhancing the agent’s capacity to adapt to new tasks. This is particularly valuable in real-world environments, such as personalized recommendation systems or long-term autonomous systems, where agents must retain previous learning while adapting to new data. As self-adaptive and self-improving algorithms become integral to the EvoRL landscape, the future holds the promise of more resilient, efficient, and increasingly autonomous learning systems capable of thriving in complex and dynamic environments.
6.2.3. Model Scalability
To achieve scalability in EvoRL, a promising approach is the use of hierarchical models, which allow for the better management of complexity by dividing the problem into multiple levels. For example, in large-scale robotics tasks, a high-level model can focus on managing overall strategies and long-term goals, while low-level models are dedicated to handling more granular actions or immediate decisions. This hierarchical approach enables the EvoRL system to handle larger environments more efficiently, as the complexity is distributed across various levels. However, a significant challenge in this approach is the coordination between different levels, which can introduce inefficiencies in communication and decision-making. This could potentially slow down the evolution process and hinder scalability. A preliminary solution is to use message-passing algorithms [115]. These algorithms facilitate efficient communication between different levels of the hierarchy, ensuring that high-level and low-level models cooperate effectively. For example, the graph-based message-passing technique [116] can be used to allow the high-level model to send strategic updates to the low-level models and vice versa. Additionally, reinforcement learning-based routing protocols [117] could enable the models to adjust their interactions based on the evolving task, ensuring smoother coordination and improving the overall performance.
6.2.4. Heterogeneous Networks and Multi-Agent Systems
As we look ahead, one key area of development involves extending EvoRL methodologies to address the complexities of diverse, heterogeneous environments where agents exhibit varying capabilities, goals, and behaviors. Embracing this heterogeneity requires evolving EvoRL algorithms that can adapt to different agent types, preferences, and constraints, thus enabling the emergence of more robust and adaptive collective behavior [118]. Additionally, the advancement of EvoRL in multi-agent systems will entail exploring algorithms capable of learning strategies for effective coordination and cooperation among diverse agents [119], fostering the evolution of sophisticated group behaviors while considering emergent properties and system-level objectives. To this end, we can leverage Centralized Training with Decentralized Execution (CTDE) [120], which can help agents learn coordination strategies while considering individual constraints. Multi-agent reinforcement learning is particularly useful when agents must collaborate toward a shared goal (e.g., in autonomous systems or smart cities) while balancing competition or conflicting objectives. It also fosters emergent group behaviors, helping to evolve complex cooperation strategies in dynamic environments. This evolution in EvoRL will likely contribute significantly to addressing real-world challenges across domains such as autonomous systems, smart cities, and decentralized networks, paving the way for more resilient, scalable, and adaptable multi-agent ecosystems.
6.2.5. Interpretability and Explainability
The future trajectory of EvoRL is poised to place a heightened emphasis on interpretability and explainability, acknowledging the growing importance of transparent decision-making in artificial intelligence systems. One potential avenue involves the incorporation of symbolic reasoning during the evolutionary process, facilitating the generation of policies that are not only effective but also comprehensible to humans. Hybrid approaches, merging EvoRL with rule-based methods [121], may offer a synergistic solution, ensuring the emergence of policies that align with domain-specific knowledge and are more readily understandable. In addition, to implement dimensionality reduction for policy representations, t-distributed Stochastic Neighbor Embedding (t-SNE) [122] and Principal Component Analysis (PCA) [123] can be applied to map high-dimensional policy data onto a 2D or 3D space. Specifically, PCA can reduce the dimensionality of policy vectors by identifying the most significant principal components, allowing for the visualization of how the policy evolves. t-SNE can then be used to capture local structures, revealing clusters or patterns in policy changes over time. This visualization facilitates an understanding of the learning trajectory, highlighting trends and identifying significant adjustments in the agent’s decision-making process. In EvoRL systems, on the whole, interpretability can help researchers and developers fine-tune EAs and understand how different components contribute to the overall performance, while explainability can help in building trust with users, providing transparency for regulatory compliance, and ensuring that the decisions made by the EvoRL agents are aligned with human values and expectations.
6.2.6. Incorporation in Large Language Models
Incorporating EvoRL within LLMs [124], such as GPT-4 [125], holds tremendous potential. For instance, we can leverage EvoRL to facilitate the evolution and adaptation of language model architectures that can effectively comprehend, generate, and respond to human language. Integrating EvoRL with LLMs could revolutionize training methods by allowing models to learn from both explicit rewards and implicit signals embedded in human interactions. Here, EvoRL can optimize decision-making strategies by utilizing the reinforcement learning framework, while LLMs contribute by providing contextual, emotional, and conversational feedback. A key challenge in this integration is translating human language into reinforcement signals that EvoRL can effectively utilize. To this end, we could design a hybrid model that uses LLMs to produce contextual feedback and then applies a structured translation process to convert that feedback into rewards for EvoRL. Furthermore, the synergy between EvoRL and LLMs may pave the way for novel applications in conversational artificial intelligence, personalized content generation, and context-aware decision-making systems. Specifically, EvoRL can be used to optimize agent strategies, while LLMs can provide multi-modal natural language feedback [126], guiding the agent’s learning process based on user interactions. This synergy could involve using LLMs for generating task-specific language cues or instructions that EvoRL agents can incorporate into their decision-making, improving personalization and context awareness.
7. Conclusions
As an emerging technology, EvoRL holds considerable promise across diverse tasks. In light of this, we present a comprehensive review of various EvoRL algorithms. First, we propose a multidimensional classification of EvoRL algorithms, systematically categorizing them based on the EAs they employ and the corresponding reinforcement learning methods they incorporate. This classification provides a clear structure for understanding the landscape of EvoRL research. Second, we examine the challenges in EvoRL, discussing the limitations of both reinforcement learning and EvoRL. These challenges hinder the performance of EvoRL in certain contexts, yet solutions from the existing literature demonstrate the potential of EvoRL to overcome these issues under specific conditions. Third, we identify constructive open issues in the EvoRL field, including concerns related to adaptability, adversarial robustness, and ethical considerations. These unresolved issues pose obstacles to the widespread adoption of EvoRL in real-world applications. Finally, we put forward promising future directions for EvoRL, emphasizing avenues that can enhance self-adaptation, self-improvement, scalability, and interpretability. These directions offer a roadmap for advancing EvoRL’s capabilities and expanding its application domains. In summary, this review not only outlines the current state of EvoRL but also highlights its challenges and potential future developments, with the aim of improving its performance in an expanding set of scenarios.
Author Contributions
Conceptualization, Y.L. (Yuanguo Lin) and H.C.; methodology, H.C. and G.C.; resources, F.L. and G.C.; validation, L.Z. and Y.L. (Yunxuan Liu); formal analysis, Y.L. (Yunxuan Liu); investigation, Y.L. (Yuanguo Lin); data curation, H.C.; writing—original draft preparation, H.C. and Y.L. (Yuanguo Lin); writing—review and editing, L.Z. and P.W.; visualization, H.C. and P.W.; supervision, H.C.; project administration, Y.L. (Yuanguo Lin); funding acquisition, Y.L. (Yuanguo Lin) and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (No. 61977055), in part by the Xiamen Science and Technology Subsidy Project (No. 2024CXY0306), and in part by the Startup Fund of Jimei University [No. ZQ2024014].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| EA | Evolutionary Algorithm |
| RL | Reinforcement Learning |
| EvoRL | Evolutionary Reinforcement Learning |
| ES | Evolutionary Strategy |
| GA | Genetic Algorithm |
| CEM | Cross-Entropy Method |
| PBT | Population-Based Training |
| DRL | Deep Reinforcement Learning |
| EGPG | Evolution-Guided Policy Gradient |
| CERL | Collaborative Evolutionary Reinforcement Learning |
References
- Lin, Y.; Liu, Y.; Lin, F.; Zou, L.; Wu, P.; Zeng, W.; Chen, H.; Miao, C. A survey on reinforcement learning for recommender systems. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13164–13184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Lin, Y.; Liu, Y.; You, H.; Wu, P.; Lin, F.; Zhou, X. Self-Supervised Reinforcement Learning with dual-reward for knowledge-aware recommendation. Appl. Soft Comput. 2022, 131, 109745. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, L.; Zhang, L.; Ding, Z.; Yin, D.; Tang, J. Deep reinforcement learning for page-wise recommendations. In Proceedings of the 12th ACM Conference on Recommender Systems, Vancouver, BC, Canada, 2–7 October 2018; pp. 95–103. [Google Scholar]
- de Lacerda, M.G.P.; de Lima Neto, F.B.; Ludermir, T.B.; Kuchen, H. Out-of-the-box parameter control for evolutionary and swarm-based algorithms with distributed reinforcement learning. Swarm Intell. 2023, 17, 173–217. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Liu, X. Pns: Population-guided novelty search for reinforcement learning in hard exploration environments. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 5627–5634. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Coello, C.A.C. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Nilsson, O.; Cully, A. Policy gradient assisted map-elites. In Proceedings of the Genetic and Evolutionary Computation Conference, Lisbon, Portugal, 15–19 July 2021; pp. 866–875. [Google Scholar]
- Khadka, S.; Tumer, K. Evolution-guided policy gradient in reinforcement learning. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; Volume 31. [Google Scholar]
- Shi, L.; Li, S.; Zheng, Q.; Yao, M.; Pan, G. Efficient novelty search through deep reinforcement learning. IEEE Access 2020, 8, 128809–128818. [Google Scholar] [CrossRef]
- Khadka, S.; Majumdar, S.; Nassar, T.; Dwiel, Z.; Tumer, E.; Miret, S.; Liu, Y.; Tumer, K. Collaborative evolutionary reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 3341–3350. [Google Scholar]
- Lü, S.; Han, S.; Zhou, W.; Zhang, J. Recruitment-imitation mechanism for evolutionary reinforcement learning. Inf. Sci. 2021, 553, 172–188. [Google Scholar] [CrossRef]
- Franke, J.K.; Köhler, G.; Biedenkapp, A.; Hutter, F. Sample-efficient automated deep reinforcement learning. arXiv 2020, arXiv:2009.01555. [Google Scholar]
- Gupta, A.; Savarese, S.; Ganguli, S.; Fei-Fei, L. Embodied intelligence via learning and evolution. Nat. Commun. 2021, 12, 5721. [Google Scholar] [CrossRef]
- Pierrot, T.; Macé, V.; Cideron, G.; Perrin, N.; Beguir, K.; Sigaud, O. Sample Efficient Quality Diversity for Neural Continuous Control. 2020. Available online: https://openreview.net/forum?id=8FRw857AYba (accessed on 10 February 2025).
- Marchesini, E.; Corsi, D.; Farinelli, A. Genetic soft updates for policy evolution in deep reinforcement learning. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- Eriksson, A.; Capi, G.; Doya, K. Evolution of meta-parameters in reinforcement learning algorithm. In Proceedings of the Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27 October–1 November 2003; Volume 1, pp. 412–417. [Google Scholar]
- Tjanaka, B.; Fontaine, M.C.; Togelius, J.; Nikolaidis, S. Approximating gradients for differentiable quality diversity in reinforcement learning. In Proceedings of the Genetic and Evolutionary Computation Conference, Boston, MA, USA, 9–13 July 2022; pp. 1102–1111. [Google Scholar]
- Majid, A.Y.; Saaybi, S.; Francois-Lavet, V.; Prasad, R.V.; Verhoeven, C. Deep reinforcement learning versus evolution strategies: A comparative survey. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 11939–11957. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, K.; Qian, C. Evolutionary diversity optimization with clustering-based selection for reinforcement learning. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Li, N.; Ma, L.; Yu, G.; Xue, B.; Zhang, M.; Jin, Y. Survey on evolutionary deep learning: Principles, algorithms, applications, and open issues. ACM Comput. Surv. 2023, 56, 1–34. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, X.; Lin, Q.; Ma, L.; Li, J.; Ming, Z.; Chen, J. A survey on Evolutionary Reinforcement Learning algorithms. Neurocomputing 2023, 556, 126628. [Google Scholar] [CrossRef]
- Sigaud, O. Combining evolution and deep reinforcement learning for policy search: A survey. ACM Trans. Evol. Learn. 2023, 3, 1–20. [Google Scholar] [CrossRef]
- Bai, H.; Cheng, R.; Jin, Y. Evolutionary Reinforcement Learning: A Survey. Intell. Comput. 2023, 2, 0025. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Prisma Group. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Int. J. Surg. 2010, 8, 336–341. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, L.; Liu, H.; Li, G. Reducing idleness in financial cloud services via multi-objective evolutionary reinforcement learning based load balancer. Sci. China Inf. Sci. 2024, 67, 120102. [Google Scholar] [CrossRef]
- Lin, Q.; Chen, Y.; Ma, L.; Chen, W.N.; Li, J. ERL-TD: Evolutionary Reinforcement Learning Enhanced with Truncated Variance and Distillation Mutation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 13826–13836. [Google Scholar]
- Liang, P.; Chen, Y.; Sun, Y.; Huang, Y.; Li, W. An information entropy-driven evolutionary algorithm based on reinforcement learning for many-objective optimization. Expert Syst. Appl. 2024, 238, 122164. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, H.; Xia, W.; Lin, F.; Wu, P.; Wang, Z.; Li, Y. A Comprehensive Survey on Deep Learning Techniques in Educational Data Mining. arXiv 2023, arXiv:2309.04761. [Google Scholar]
- Chen, X.; Yao, L.; McAuley, J.; Zhou, G.; Wang, X. A survey of deep reinforcement learning in recommender systems: A systematic review and future directions. arXiv 2021, arXiv:2109.03540. [Google Scholar]
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the 2016 IEEE International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; pp. 261–265. [Google Scholar]
- Hoffmeister, F.; Bäck, T. Genetic algorithms and evolution strategies: Similarities and differences. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 1–3 October 1990; Springer: Berlin/Heidelberg, Germany, 1990; pp. 455–469. [Google Scholar]
- Vent, W. Rechenberg, Ingo, Evolutionsstrategie—Optimierung Technischer Systeme nach Prinzipien der Biologischen Evolution. 170 S. mit 36 Abb. Frommann-Holzboog-Verlag. Stuttgart 1973. Broschiert; Wiley Online Library: Hoboken, NJ, USA, 1975. [Google Scholar]
- Slowik, A.; Kwasnicka, H. Evolutionary algorithms and their applications to engineering problems. Neural Comput. Appl. 2020, 32, 12363–12379. [Google Scholar] [CrossRef]
- Ho, S.L.; Yang, S. The cross-entropy method and its application to inverse problems. IEEE Trans. Magn. 2010, 46, 3401–3404. [Google Scholar] [CrossRef]
- Botev, Z.I.; Kroese, D.P.; Rubinstein, R.Y.; L’Ecuyer, P. The cross-entropy method for optimization. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2013; Volume 31, pp. 35–59. [Google Scholar]
- Huang, K.; Lale, S.; Rosolia, U.; Shi, Y.; Anandkumar, A. CEM-GD: Cross-Entropy Method with Gradient Descent Planner for Model-Based Reinforcement Learning. arXiv 2021, arXiv:2112.07746. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K.; et al. Population based training of neural networks. arXiv 2017, arXiv:1711.09846. [Google Scholar]
- Hein, D.; Udluft, S.; Runkler, T.A. Interpretable policies for reinforcement learning by genetic programming. Eng. Appl. Artif. Intell. 2018, 76, 158–169. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Sachdeva, E.; Khadka, S.; Majumdar, S.; Tumer, K. Maedys: Multiagent evolution via dynamic skill selection. In Proceedings of the Genetic and Evolutionary Computation Conference, Lisbon, Portugal, 15–19 July 2021; pp. 163–171. [Google Scholar]
- Shi, L.; Li, S.; Cao, L.; Yang, L.; Zheng, G.; Pan, G. FiDi-RL: Incorporating Deep Reinforcement Learning with Finite-Difference Policy Search for Efficient Learning of Continuous Control. arXiv 2019, arXiv:1907.00526. [Google Scholar]
- Ajani, O.S.; Mallipeddi, R. Adaptive evolution strategy with ensemble of mutations for reinforcement learning. Knowl.-Based Syst. 2022, 245, 108624. [Google Scholar] [CrossRef]
- Tang, Y.; Choromanski, K. Online hyper-parameter tuning in off-policy learning via evolutionary strategies. arXiv 2020, arXiv:2006.07554. [Google Scholar]
- Chen, Z.; Zhou, Y.; He, X.; Jiang, S. A Restart-based Rank-1 Evolution Strategy for Reinforcement Learning. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019; pp. 2130–2136. [Google Scholar]
- Yang, P.; Zhang, H.; Yu, Y.; Li, M.; Tang, K. Evolutionary reinforcement learning via cooperative coevolutionary negatively correlated search. Swarm Evol. Comput. 2022, 68, 100974. [Google Scholar] [CrossRef]
- Ajani, O.S.; Kumar, A.; Mallipeddi, R. Covariance matrix adaptation evolution strategy based on correlated evolution paths with application to reinforcement learning. Expert Syst. Appl. 2024, 246, 123289. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z.; Huang, K.; Wang, R.; Cheng, G.; Li, T. Evolutionary reinforcement learning algorithm for large-scale multi-agent cooperation and confrontation applications. J. Supercomput. 2024, 80, 2319–2346. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Z.; Song, Y.; Fang, M.; Xiong, J.; Dai, B.; Zhou, B. Zeroth-order supervised policy improvement. arXiv 2020, arXiv:2006.06600. [Google Scholar]
- Houthooft, R.; Chen, Y.; Isola, P.; Stadie, B.; Wolski, F.; Jonathan Ho, O.; Abbeel, P. Evolved policy gradients. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; Volume 31. [Google Scholar]
- Callaghan, A.; Mason, K.; Mannion, P. Evolutionary Strategy Guided Reinforcement Learning via MultiBuffer Communication. arXiv 2023, arXiv:2306.11535. [Google Scholar]
- Martinez, A.D.; Del Ser, J.; Osaba, E.; Herrera, F. Adaptive multifactorial evolutionary optimization for multitask reinforcement learning. IEEE Trans. Evol. Comput. 2021, 26, 233–247. [Google Scholar] [CrossRef]
- Li, W.; He, S.; Mao, X.; Li, B.; Qiu, C.; Yu, J.; Peng, F.; Tan, X. Multi-agent evolution reinforcement learning method for machining parameters optimization based on bootstrap aggregating graph attention network simulated environment. J. Manuf. Syst. 2023, 67, 424–438. [Google Scholar] [CrossRef]
- Zheng, B.; Cheng, R. Rethinking Population-assisted Off-policy Reinforcement Learning. arXiv 2023, arXiv:2305.02949. [Google Scholar]
- Elfwing, S.; Uchibe, E.; Doya, K.; Christensen, H.I. Co-evolution of shaping rewards and meta-parameters in reinforcement learning. Adapt. Behav. 2008, 16, 400–412. [Google Scholar] [CrossRef]
- Zhang, H.; An, T.; Yan, P.; Hu, K.; An, J.; Shi, L.; Zhao, J.; Wang, J. Exploring cooperative evolution with tunable payoff’s loners using reinforcement learning. Chaos Solitons Fractals 2024, 178, 114358. [Google Scholar] [CrossRef]
- Song, Y.; Ou, J.; Pedrycz, W.; Suganthan, P.N.; Wang, X.; Xing, L.; Zhang, Y. Generalized model and deep reinforcement learning-based evolutionary method for multitype satellite observation scheduling. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2576–2589. [Google Scholar] [CrossRef]
- Garau-Luis, J.J.; Miao, Y.; Co-Reyes, J.D.; Parisi, A.; Tan, J.; Real, E.; Faust, A. Multi-objective evolution for generalizable policy gradient algorithms. In Proceedings of the ICLR 2022 Workshop on Generalizable Policy Learning in Physical World, Virtual, 29 April 2022. [Google Scholar]
- Hu, C.; Pei, J.; Liu, J.; Yao, X. Evolving Constrained Reinforcement Learning Policy. arXiv 2023, arXiv:2304.09869. [Google Scholar]
- Bodnar, C.; Day, B.; Lió, P. Proximal distilled evolutionary reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–8 February 2020; Volume 34, pp. 3283–3290. [Google Scholar]
- Wang, Y.; Zhang, T.; Chang, Y.; Wang, X.; Liang, B.; Yuan, B. A surrogate-assisted controller for expensive evolutionary reinforcement learning. Inf. Sci. 2022, 616, 539–557. [Google Scholar] [CrossRef]
- Pierrot, T.; Macé, V.; Chalumeau, F.; Flajolet, A.; Cideron, G.; Beguir, K.; Cully, A.; Sigaud, O.; Perrin-Gilbert, N. Diversity policy gradient for sample efficient quality-diversity optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Boston, MA, USA, 9–13 July 2022; pp. 1075–1083. [Google Scholar]
- Hao, J.; Li, P.; Tang, H.; Zheng, Y.; Fu, X.; Meng, Z. ERL-RE2: Efficient Evolutionary Reinforcement Learning with Shared State Representation and Individual Policy Representation. arXiv 2022, arXiv:2210.17375. [Google Scholar]
- Kalashnikov, D.; Irpan, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnan, M.; Vanhoucke, V.; et al. Qt-opt: Scalable deep reinforcement learning for vision-based robotic manipulation. arXiv 2018, arXiv:1806.10293. [Google Scholar]
- Shao, L.; You, Y.; Yan, M.; Yuan, S.; Sun, Q.; Bohg, J. Grac: Self-guided and self-regularized actor-critic. In Proceedings of the Conference on Robot Learning, PMLR, Auckland, New Zealand, 14–18 December 2022; pp. 267–276. [Google Scholar]
- Pourchot, A.; Sigaud, O. CEM-RL: Combining evolutionary and gradient-based methods for policy search. arXiv 2018, arXiv:1810.01222. [Google Scholar]
- Kim, N.; Baek, H.; Shin, H. PGPS: Coupling Policy Gradient with Population-Based Search. 2020. Available online: https://openreview.net/forum?id=PeT5p3ocagr (accessed on 10 February 2025).
- Zheng, H.; Wei, P.; Jiang, J.; Long, G.; Lu, Q.; Zhang, C. Cooperative heterogeneous deep reinforcement learning. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2020; Volume 33, pp. 17455–17465. [Google Scholar]
- Shi, Z.; Singh, S.P. Soft actor-critic with cross-entropy policy optimization. arXiv 2021, arXiv:2112.11115. [Google Scholar]
- Liu, J.; Feng, L. Diversity evolutionary policy deep reinforcement learning. Comput. Intell. Neurosci. 2021, 2021, 5300189. [Google Scholar] [CrossRef]
- Yu, X.; Hu, Z.; Luo, W.; Xue, Y. Reinforcement learning-based multi-objective differential evolution algorithm for feature selection. Inf. Sci. 2024, 661, 120185. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, K.; Chen, G.D.; Zhang, J.D.; Wang, W.D.; Wang, H.C.; Zhang, L.M.; Yan, X.; Yao, J. Evolutionary-assisted reinforcement learning for reservoir real-time production optimization under uncertainty. Pet. Sci. 2023, 20, 261–276. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, T.; Wei, B.; Liu, Y.; Xu, K.; Li, W. Evolutionary Action Selection for Gradient-Based Policy Learning. In Proceedings of the International Conference on Neural Information Processing, New Orleans, LA, USA, 28 November–9 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 579–590. [Google Scholar]
- Jung, W.; Park, G.; Sung, Y. Population-guided parallel policy search for reinforcement learning. arXiv 2020, arXiv:2001.02907. [Google Scholar]
- Doan, T.; Mazoure, B.; Abdar, M.; Durand, A.; Pineau, J.; Hjelm, R.D. Attraction-repulsion actor-critic for continuous control reinforcement learning. arXiv 2019, arXiv:1909.07543. [Google Scholar]
- Marchesini, E.; Corsi, D.; Farinelli, A. Exploring safer behaviors for deep reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Pomona, CA, USA, 24–28 October 2022; Volume 36, pp. 7701–7709. [Google Scholar]
- Majumdar, S.; Khadka, S.; Miret, S.; McAleer, S.; Tumer, K. Evolutionary reinforcement learning for sample-efficient multiagent coordination. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 6651–6660. [Google Scholar]
- Long, Q.; Zhou, Z.; Gupta, A.; Fang, F.; Wu, Y.; Wang, X. Evolutionary population curriculum for scaling multi-agent reinforcement learning. arXiv 2020, arXiv:2003.10423. [Google Scholar]
- Shen, R.; Zheng, Y.; Hao, J.; Meng, Z.; Chen, Y.; Fan, C.; Liu, Y. Generating Behavior-Diverse Game AIs with Evolutionary Multi-Objective Deep Reinforcement Learning. In Proceedings of the IJCAI, Yokohama, Japan, 11–17 July 2020; pp. 3371–3377. [Google Scholar]
- Fernandez, F.C.; Caarls, W. Parameters tuning and optimization for reinforcement learning algorithms using evolutionary computing. In Proceedings of the 2018 IEEE International Conference on Information Systems and Computer Science (INCISCOS), Quito, Ecuador, 13–15 November 2018; pp. 301–305. [Google Scholar]
- Kamio, S.; Iba, H. Adaptation technique for integrating genetic programming and reinforcement learning for real robots. IEEE Trans. Evol. Comput. 2005, 9, 318–333. [Google Scholar] [CrossRef]
- Co-Reyes, J.D.; Miao, Y.; Peng, D.; Real, E.; Levine, S.; Le, Q.V.; Lee, H.; Faust, A. Evolving reinforcement learning algorithms. arXiv 2021, arXiv:2101.03958. [Google Scholar]
- AbuZekry, A.; Sobh, I.; Hadhoud, M.; Fayek, M. Comparative study of NeuroEvolution algorithms in reinforcement learning for self-driving cars. Eur. J. Eng. Sci. Technol. 2019, 2, 60–71. [Google Scholar] [CrossRef]
- Kelly, S.; Voegerl, T.; Banzhaf, W.; Gondro, C. Evolving hierarchical memory-prediction machines in multi-task reinforcement learning. Genet. Program. Evolvable Mach. 2021, 22, 573–605. [Google Scholar] [CrossRef]
- Girgin, S.; Preux, P. Feature discovery in reinforcement learning using genetic programming. In Proceedings of the European Conference on Genetic Programming, Naples, Italy, 26–28 March 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 218–229. [Google Scholar]
- Zhu, Q.; Wu, X.; Lin, Q.; Chen, W.N. Two-Stage Evolutionary Reinforcement Learning for Enhancing Exploration and Exploitation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 20892–20900. [Google Scholar]
- Wu, X.; Zhu, Q.; Chen, W.N.; Lin, Q.; Li, J.; Coello, C.A.C. Evolutionary Reinforcement Learning with Action Sequence Search for Imperfect Information Games. Inf. Sci. 2024, 676, 120804. [Google Scholar] [CrossRef]
- Zuo, M.; Gong, D.; Wang, Y.; Ye, X.; Zeng, B.; Meng, F. Process knowledge-guided autonomous evolutionary optimization for constrained multiobjective problems. IEEE Trans. Evol. Comput. 2023, 28, 193–207. [Google Scholar] [CrossRef]
- Peng, L.; Yuan, Z.; Dai, G.; Wang, M.; Tang, Z. Reinforcement learning-based hybrid differential evolution for global optimization of interplanetary trajectory design. Swarm Evol. Comput. 2023, 81, 101351. [Google Scholar] [CrossRef]
- Li, Y. Reinforcement learning in practice: Opportunities and challenges. arXiv 2022, arXiv:2202.11296. [Google Scholar]
- Sehgal, A.; La, H.; Louis, S.; Nguyen, H. Deep reinforcement learning using genetic algorithm for parameter optimization. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 596–601. [Google Scholar]
- Aydeniz, A.A.; Loftin, R.; Tumer, K. Novelty seeking multiagent evolutionary reinforcement learning. In Proceedings of the Genetic and Evolutionary Computation Conference, Lisbon, Portugal, 15–19 July 2023; pp. 402–410. [Google Scholar]
- Zhu, S.; Belardinelli, F.; León, B.G. Evolutionary reinforcement learning for sparse rewards. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Lille, France, 10–14 July 2021; pp. 1508–1512. [Google Scholar]
- Li, P.; Hao, J.; Tang, H.; Zheng, Y.; Fu, X. Race: Improve multi-agent reinforcement learning with representation asymmetry and collaborative evolution. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 19490–19503. [Google Scholar]
- Chang, S.; Yang, J.; Choi, J.; Kwak, N. Genetic-gated networks for deep reinforcement learning. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; Volume 31. [Google Scholar]
- Tang, Y. Guiding Evolutionary Strategies with Off-Policy Actor-Critic. In Proceedings of the AAMAS, Online, 3–7 May 2021; pp. 1317–1325. [Google Scholar]
- Simmons-Edler, R.; Eisner, B.; Mitchell, E.; Seung, S.; Lee, D. Q-learning for continuous actions with cross-entropy guided policies. arXiv 2019, arXiv:1903.10605. [Google Scholar]
- Zhang, N.; Gupta, A.; Chen, Z.; Ong, Y.S. Multitask neuroevolution for reinforcement learning with long and short episodes. IEEE Trans. Cogn. Dev. Syst. 2022, 15, 1474–1486. [Google Scholar] [CrossRef]
- Rasouli, A.; Tsotsos, J.K. Autonomous vehicles that interact with pedestrians: A survey of theory and practice. IEEE Trans. Intell. Transp. Syst. 2019, 21, 900–918. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, H.; Zhang, X.; Chang, Z.; Jäntti, R.; Yang, K. Towards Autonomous Multi-UAV Wireless Network: A Survey of Reinforcement Learning-Based Approaches. IEEE Commun. Surv. Tutor. 2023, 25, 3038–3067. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhan, Z.H.; Tan, K.C.; Zhang, J. A meta-knowledge transfer-based differential evolution for multitask optimization. IEEE Trans. Evol. Comput. 2021, 26, 719–734. [Google Scholar] [CrossRef]
- Aleti, A.; Moser, I. A systematic literature review of adaptive parameter control methods for evolutionary algorithms. ACM Comput. Surv. CSUR 2016, 49, 1–35. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Wang, Z.J.; Jin, H.; Zhang, J. Adaptive distributed differential evolution. IEEE Trans. Cybern. 2019, 50, 4633–4647. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Ajao, L.A.; Apeh, S.T. Secure edge computing vulnerabilities in smart cities sustainability using petri net and genetic algorithm-based reinforcement learning. Intell. Syst. Appl. 2023, 18, 200216. [Google Scholar] [CrossRef]
- Hong, J.; Zhu, Z.; Yu, S.; Wang, Z.; Dodge, H.H.; Zhou, J. Federated adversarial debiasing for fair and transferable representations. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 617–627. [Google Scholar]
- Petrović, A.; Nikolić, M.; Radovanović, S.; Delibašić, B.; Jovanović, M. FAIR: Fair adversarial instance re-weighting. Neurocomputing 2022, 476, 14–37. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, NSW, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- De Lange, M.; Aljundi, R.; Masana, M.; Parisot, S.; Jia, X.; Leonardis, A.; Slabaugh, G.; Tuytelaars, T. A continual learning survey: Defying forgetting in classification tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3366–3385. [Google Scholar]
- Liu, J.; Zhang, H.; Yu, T.; Ren, L.; Ni, D.; Yang, Q.; Lu, B.; Zhang, L.; Axmacher, N.; Xue, G. Transformative neural representations support long-term episodic memory. Sci. Adv. 2021, 7, eabg9715. [Google Scholar] [CrossRef]
- Elsayed, S.M.; Sarker, R.A.; Essam, D.L. An improved self-adaptive differential evolution algorithm for optimization problems. IEEE Trans. Ind. Inform. 2012, 9, 89–99. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Su, H.; Zhu, J. A comprehensive survey of continual learning: Theory, method and application. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5362–5383. [Google Scholar] [CrossRef]
- Maschler, B.; Vietz, H.; Jazdi, N.; Weyrich, M. Continual learning of fault prediction for turbofan engines using deep learning with elastic weight consolidation. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; Volume 1, pp. 959–966. [Google Scholar]
- Parmas, P.; Seno, T. Proppo: A message passing framework for customizable and composable learning algorithms. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2022; Volume 35, pp. 29152–29165. [Google Scholar]
- Shi, Q.; Wu, N.; Wang, H.; Ma, X.; Hanzo, L. Factor graph based message passing algorithms for joint phase-noise estimation and decoding in OFDM-IM. IEEE Trans. Commun. 2020, 68, 2906–2921. [Google Scholar] [CrossRef]
- Nazib, R.A.; Moh, S. Reinforcement learning-based routing protocols for vehicular ad hoc networks: A comparative survey. IEEE Access 2021, 9, 27552–27587. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, L.; Yue, D.; Dou, C.; Xie, X.; Chen, L. Coordinated voltage regulation of high renewable-penetrated distribution networks: An evolutionary curriculum-based deep reinforcement learning approach. Int. J. Electr. Power Energy Syst. 2023, 149, 108995. [Google Scholar] [CrossRef]
- Yang, X.; Chen, N.; Zhang, S.; Zhou, X.; Zhang, L.; Qiu, T. An Evolutionary Reinforcement Learning Scheme for IoT Robustness. In Proceedings of the 2023 IEEE 26th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Rio de Janeiro, Brazil, 24–26 May 2023; pp. 756–761. [Google Scholar]
- Ikeda, T.; Shibuya, T. Centralized training with decentralized execution reinforcement learning for cooperative multi-agent systems with communication delay. In Proceedings of the 2022 IEEE 61st Annual Conference of the Society of Instrument and Control Engineers (SICE), Kumamoto, Japan, 6–9 September 2022; pp. 135–140. [Google Scholar]
- Porebski, S. Evaluation of fuzzy membership functions for linguistic rule-based classifier focused on explainability, interpretability and reliability. Expert Syst. Appl. 2022, 199, 117116. [Google Scholar] [CrossRef]
- Belkina, A.C.; Ciccolella, C.O.; Anno, R.; Halpert, R.; Spidlen, J.; Snyder-Cappione, J.E. Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets. Nat. Commun. 2019, 10, 5415. [Google Scholar] [CrossRef]
- Kherif, F.; Latypova, A. Principal component analysis. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 209–225. [Google Scholar]
- Min, B.; Ross, H.; Sulem, E.; Veyseh, A.P.B.; Nguyen, T.H.; Sainz, O.; Agirre, E.; Heintz, I.; Roth, D. Recent advances in natural language processing via large pre-trained language models: A survey. ACM Comput. Surv. 2021, 56, 1–40. [Google Scholar] [CrossRef]
- Chang, E.Y. Examining GPT-4: Capabilities, Implications and Future Directions. In Proceedings of the 10th International Conference on Computational Science and Computational Intelligence, Las Vegas, NV, USA, 13–15 December 2023. [Google Scholar]
- Zhong, S.; Huang, Z.; Wen, W.; Qin, J.; Lin, L. Sur-adapter: Enhancing text-to-image pre-trained diffusion models with large language models. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 567–578. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).