A Comparative Study of Brownian Dynamics Based on the Jerk Equation Against a Stochastic Process Under an External Force Field
Abstract
1. Introduction
2. Brownian Motion Models
2.1. Einstein Model
2.2. Langevin Model
2.3. Chaotic Map-Based Model
2.4. Jerk-Based Model
3. Brownian Motion in a Field of Force
Ornstein–Uhlenbeck Model
- Overdamped .
- Critically damped .
- Underdamped .
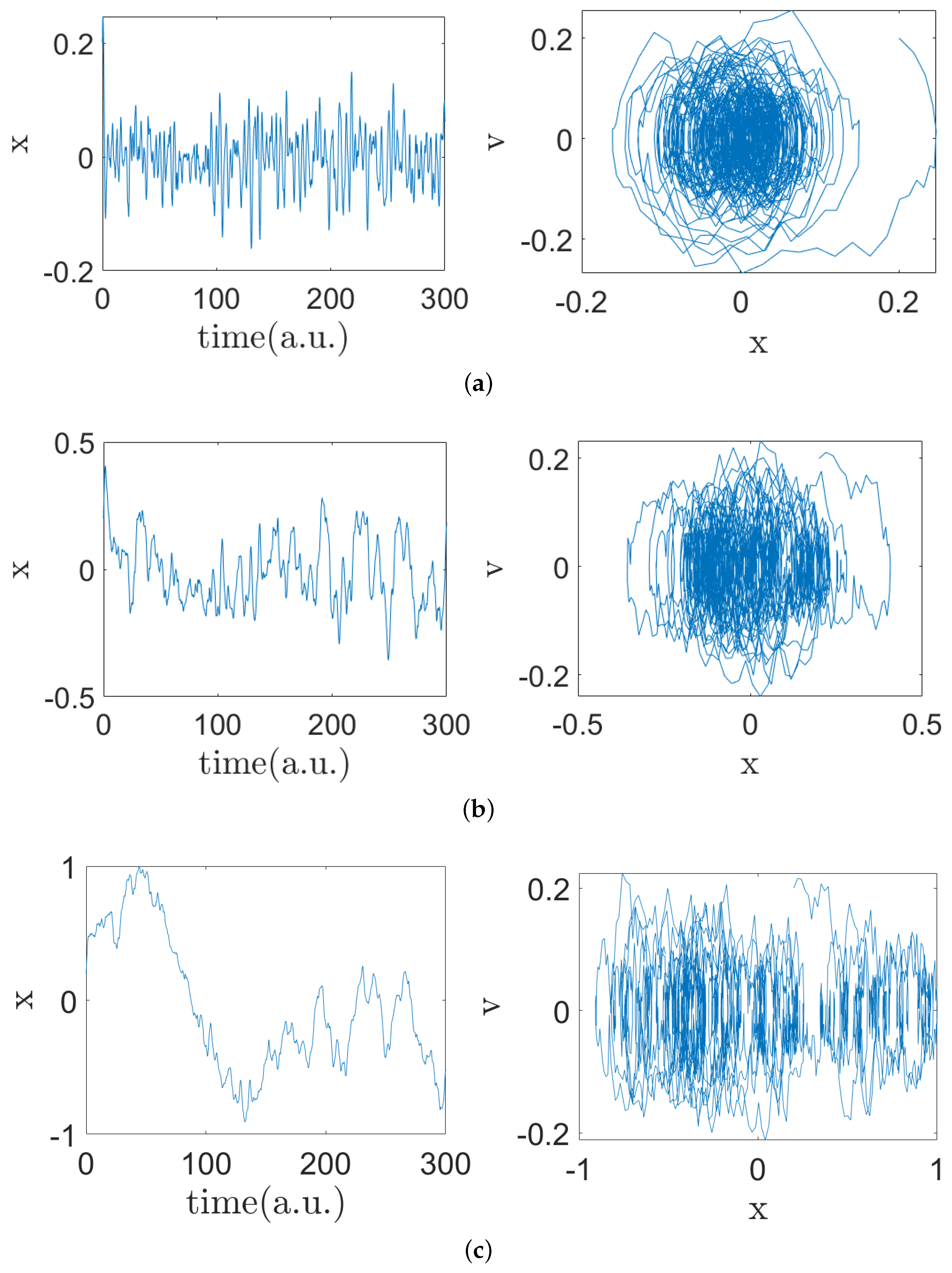
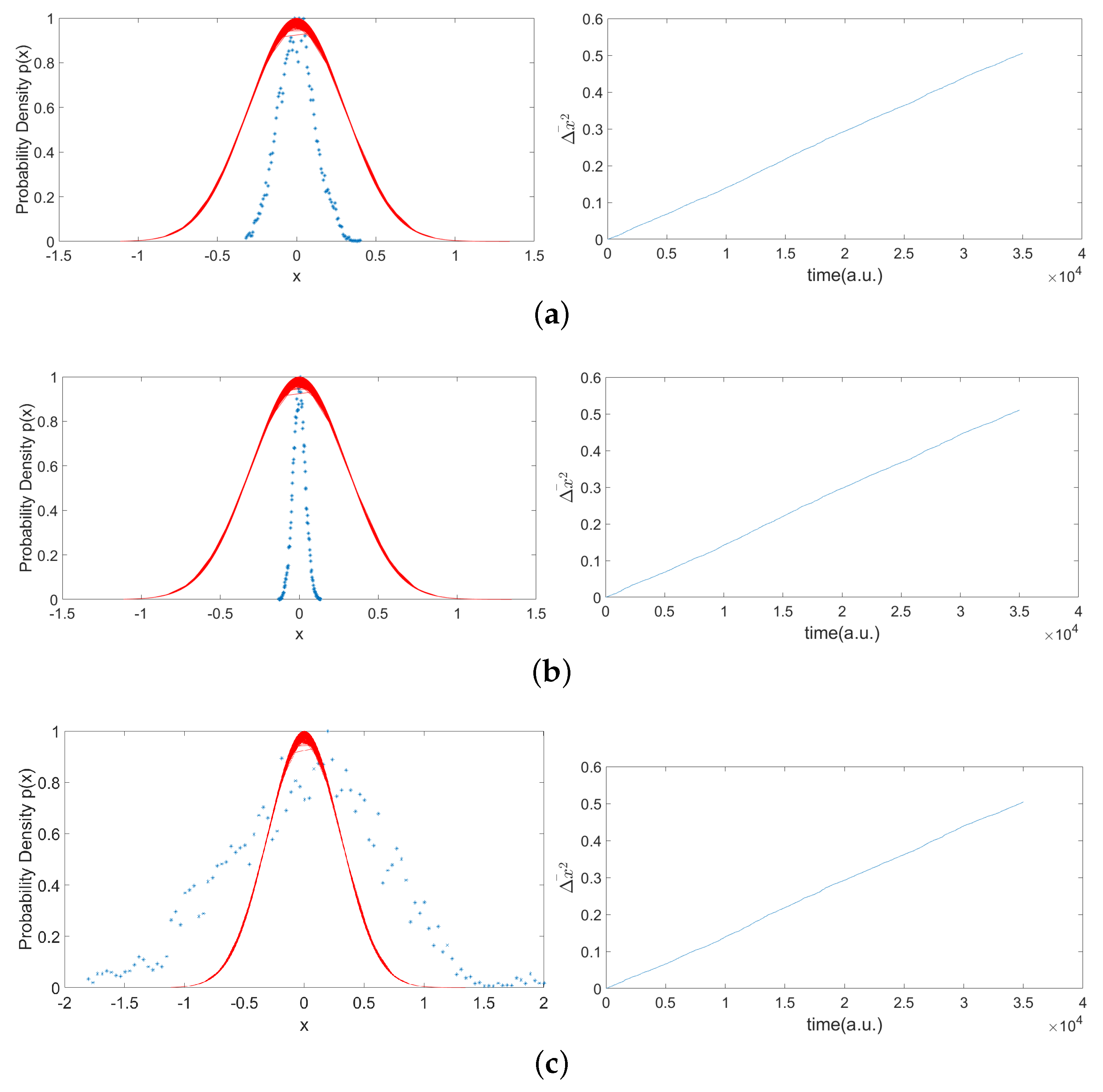
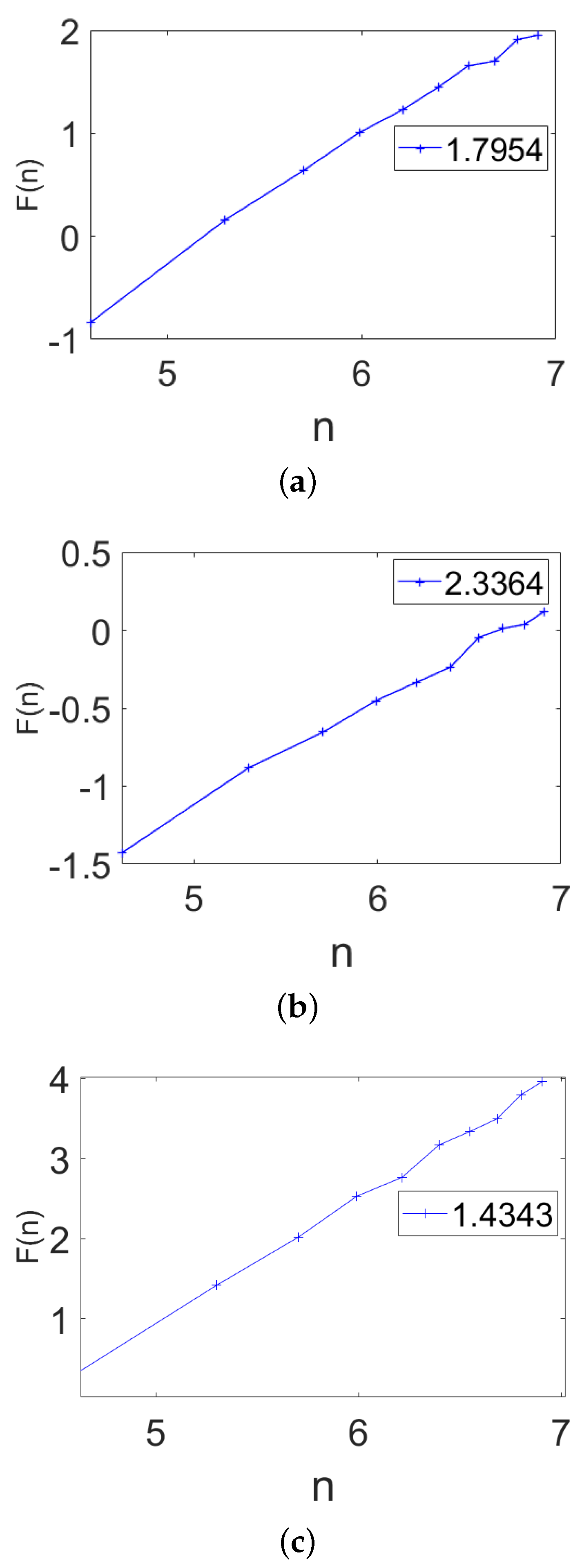
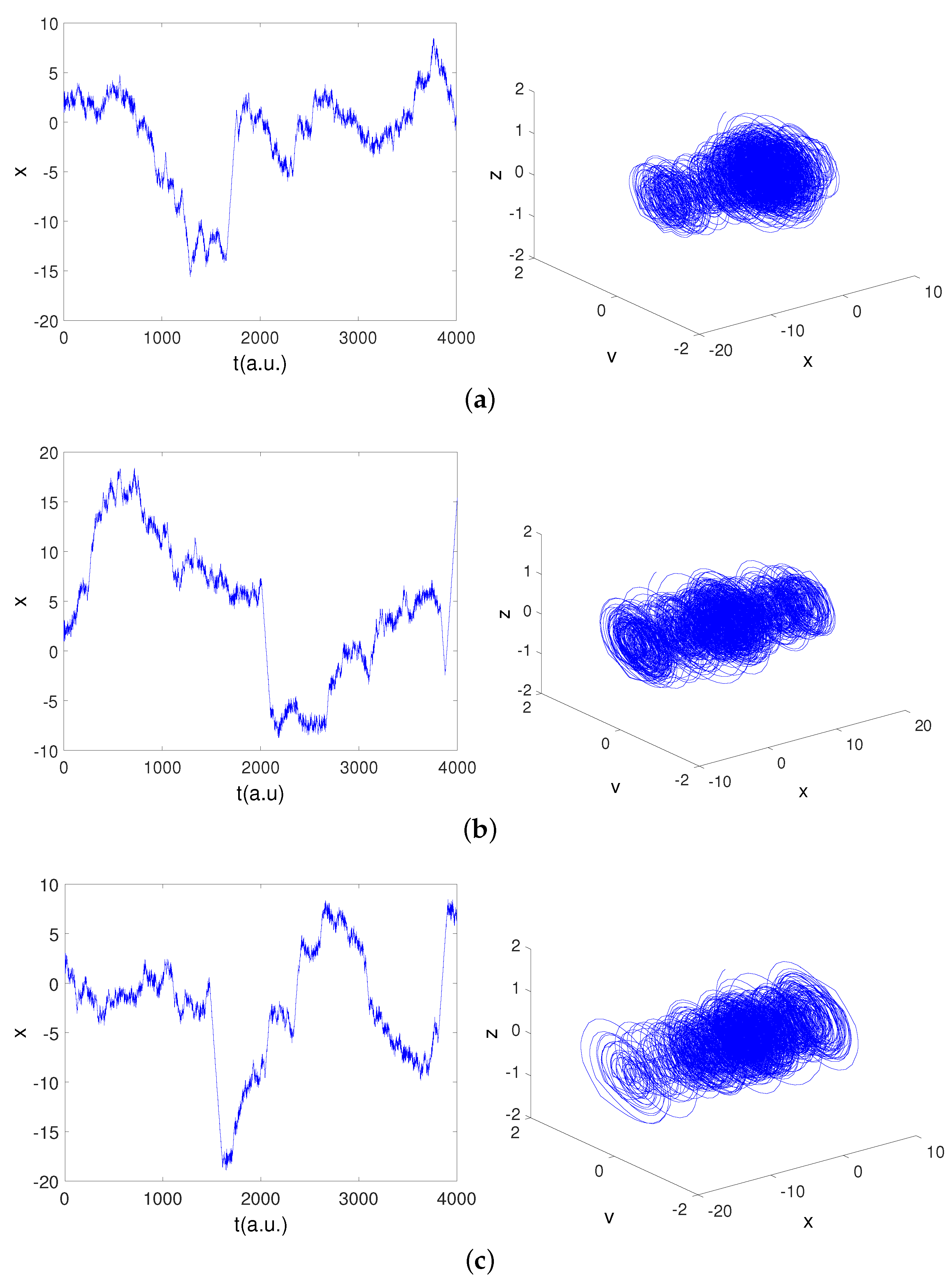
4. Deterministic Model for Brownian Motion in a Force Field
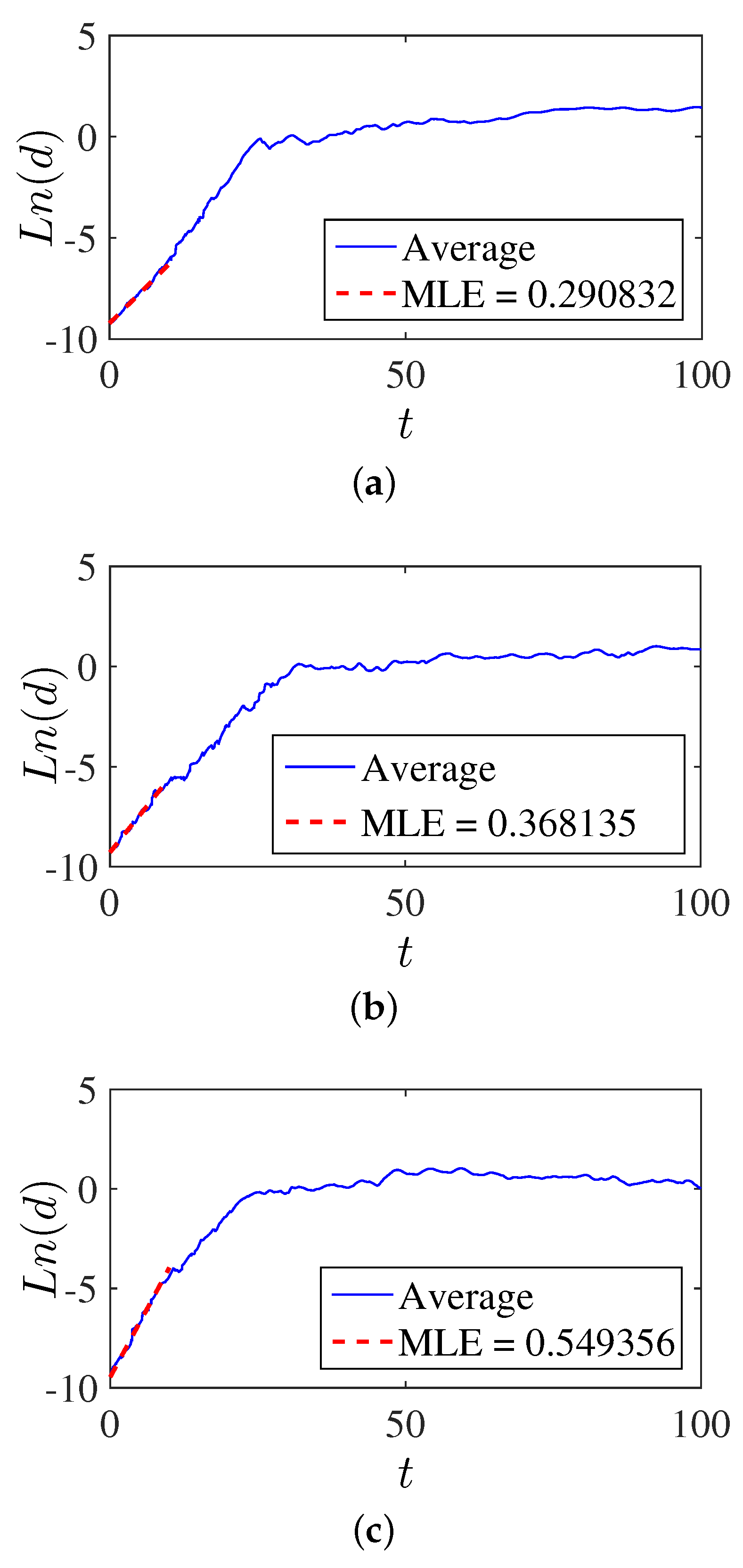
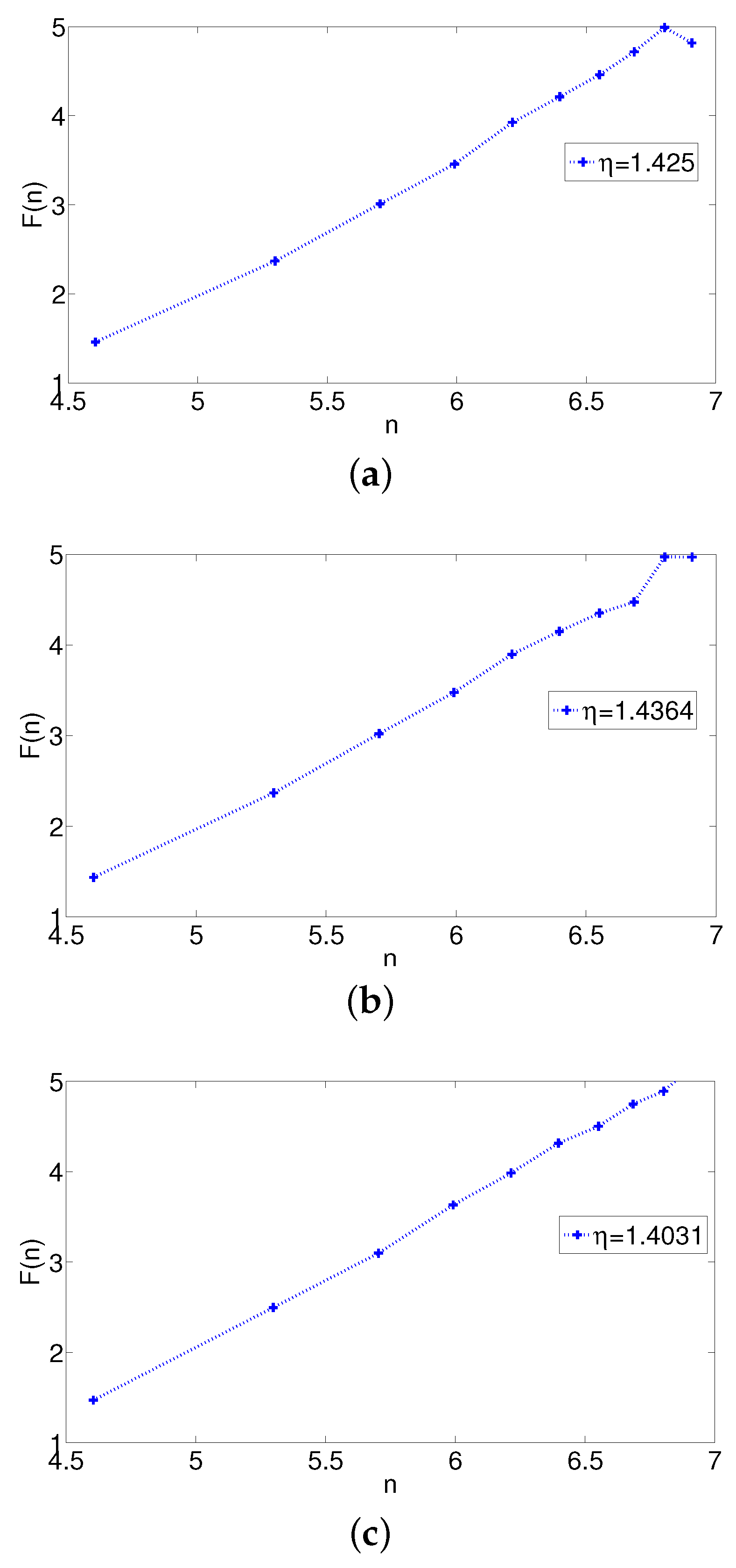
Numerical Results for Brownian Motion in a Harmonic Force Field
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, R. XXVII. A brief account of microscopical observations made in the months of June, July, and August 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. Philos. Mag. 1828, 4, 161–173. [Google Scholar] [CrossRef]
- Bachelier, L. Théorie de la Spéculation. Annales Scientifiques de l′École Normale Supérieure; Gauthier-Villars: Paris, France, 1900; Volume 3, pp. 21–86. [Google Scholar]
- Einstein, A. Investigations on the Theory of the Brownian Movement; Courier Corporation: Chelmsford, MA, USA, 1956. [Google Scholar]
- Nelson, E. Dynamical Theories of Brownian Motion; Princeton University Press: Princeton, NJ, USA, 2020; Volume 106. [Google Scholar]
- Langevin, P. On the theory of Brownian motion. Comptes Rendus L’académie Sci. 1908, 146, 530–533. [Google Scholar]
- Smoluchowski, M. The kinetic theory of Brownian molecular motion and suspensions. Ann. Phys. 1906, 21, 756–780. [Google Scholar] [CrossRef]
- Prigogine, I. Non-Equilibrium Statistical Mechanics; Courier Dover Publications: Mineola, NY, USA, 2017. [Google Scholar]
- Nelson, E. Dynamical Theories of Brownian Motion, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1967; Volume 17. [Google Scholar]
- Serway, R.A.; Jewett, J.W. Física para Ciencias e Ingeniería; Cengage Learning: Boston, MA, USA, 2015; Volume 1, Chapter 21; p. 627. [Google Scholar]
- Gaspard, P.; Briggs, M.; Francis, M.; Sengers, J.; Gammon, R.; Dorfman, J.R.; Calabrese, R. Experimental evidence for microscopic chaos. Nature 1998, 394, 865–868. [Google Scholar] [CrossRef]
- Mackey, M.C.; Tyran-Kamińska, M. Deterministic Brownian motion: The effects of perturbing a dynamical system by a chaotic semi-dynamical system. Phys. Rep. 2006, 422, 167–222. [Google Scholar] [CrossRef]
- Russo, G. Deterministic diffusion of particles. Commun. Pure Appl. Math. 1990, 43, 697–733. [Google Scholar] [CrossRef]
- Ford, G.; Kac, M.; Mazur, P. Statistical mechanics of assemblies of coupled oscillators. J. Math. Phys. 1965, 6, 504–515. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonlinear generalized Langevin equations. J. Stat. Phys. 1973, 9, 215–220. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Path integral approach to quantum Brownian motion. Phys. A Stat. Mech. Its Appl. 1983, 121, 587–616. [Google Scholar] [CrossRef]
- J Evans, D.; P Morriss, G. Statistical Mechanics of Nonequilbrium Liquids; ANU Press: Canberra, Australia, 2007. [Google Scholar]
- Klages, R. Microscopic Chaos, Fractals and Transport in Nonequilibrium Statistical Mechanics; World Scientific: Singapore, 2007; Volume 24. [Google Scholar]
- Gaspard, P. Chaos, scattering and statistical mechanics. Chaos 2005. [Google Scholar]
- Beck, C. Dynamical systems of Langevin type. Phys. A Stat. Mech. Its Appl. 1996, 233, 419–440. [Google Scholar] [CrossRef]
- Schell, M.; Fraser, S.; Kapral, R. Diffusive dynamics in systems with translational symmetry: A one-dimensional-map model. Phys. Rev. A 1982, 26, 504. [Google Scholar] [CrossRef]
- Grossmann, S.; Fujisaka, H. Diffusion in discrete nonlinear dynamical systems. Phys. Rev. A 1982, 26, 1779. [Google Scholar] [CrossRef]
- Hoel, H.; Szepessy, A. Classical Langevin dynamics derived from quantum mechanics. arXiv 2019, arXiv:1906.09858. [Google Scholar] [CrossRef]
- Di Cairano, L. On the derivation of a Nonlinear Generalized Langevin Equation. J. Phys. Commun. 2022, 6, 015002. [Google Scholar] [CrossRef]
- Trefán, G.; Grigolini, P.; West, B.J. Deterministic brownian motion. Phys. Rev. A 1992, 45, 1249. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Jiménez-López, E.; Campos-Cantón, E.; Pisarchik, A.N. An approach to generate deterministic Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2740–2746. [Google Scholar] [CrossRef]
- Gilardi-Velázquez, H.E.; Campos-Cantón, E. Nonclassical point of view of the Brownian motion generation via fractional deterministic model. Int. J. Mod. Phys. C 2018, 29, 1850020. [Google Scholar] [CrossRef]
- Velazquez-Perez, S.; Gilardi-Velazquez, H.; Campos-Canton, E. Analysis of particle settlement characteristics in a one-dimensional deterministic model. Int. J. Mod. Phys. C 2024, 2550024. [Google Scholar] [CrossRef]
- Echenausía-Monroy, J.L.; Campos, E.; Jaimes-Reátegui, R.; García-López, J.H.; Huerta-Cuellar, G. Deterministic Brownian-like Motion: Electronic Approach. Electronics 2022, 11, 2949. [Google Scholar] [CrossRef]
- Velázquez Pérez, S.E.; Campos-Cantón, E.; Huerta Cuellar, G.; Gilardi Velázquez, H.E. Bidimensional Deterministic Model for Diffusion and Settling of Particles. Axioms 2023, 12, 191. [Google Scholar] [CrossRef]
- Nasrin, S.F.; Rajivganthi, C. Dynamical Analysis of a Stochastic Ebola Model with Nonlinear Incidence Functions. J. Nonlinear Sci. 2025, 35, 33. [Google Scholar] [CrossRef]
- Rajivganthi, C.; Rihan, F.A. Global dynamics of a stochastic viral infection model with latently infected cells. Appl. Sci. 2021, 11, 10484. [Google Scholar] [CrossRef]
- Li, T.; Frassu, S.; Viglialoro, G. Combining effects ensuring boundedness in an attraction–repulsion chemotaxis model with production and consumption. Z. Angew. Math. Und Phys. 2023, 74, 109. [Google Scholar] [CrossRef]
- Columbu, A.; Fuentes, R.D.; Frassu, S. Uniform-in-time boundedness in a class of local and nonlocal nonlinear attraction–repulsion chemotaxis models with logistics. Nonlinear Anal. Real World Appl. 2024, 79, 104135. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Gu, Q.; Schiff, E.A.; Grebner, S.; Wang, F.; Schwarz, R. Non-Gaussian transport measurements and the Einstein relation in amorphous silicon. Phys. Rev. Lett. 1996, 76, 3196. [Google Scholar] [CrossRef]
- Amblard, F.; Maggs, A.C.; Yurke, B.; Pargellis, A.N.; Leibler, S. Subdiffusion and anomalous local viscoelasticity in actin networks. Phys. Rev. Lett. 1996, 77, 4470. [Google Scholar] [CrossRef]
- Sciortino, F.; Tartaglia, P. Harmonic dynamics in supercooled liquids: The case of water. Phys. Rev. Lett. 1997, 78, 2385. [Google Scholar] [CrossRef]
- Van Hove, L. Quantum-mechanical perturbations giving rise to a statistical transport equation. Physica 1954, 21, 517–540. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Kou, S.C.; Xie, X.S. Generalized Langevin equation with fractional Gaussian noise: Subdiffusion within a single protein molecule. Phys. Rev. Lett. 2004, 93, 180603. [Google Scholar] [CrossRef] [PubMed]
- Min, W.; Luo, G.; Cherayil, B.J.; Kou, S.; Xie, X.S. Observation of a power-law memory kernel for fluctuations within a single protein molecule. Phys. Rev. Lett. 2005, 94, 198302. [Google Scholar] [CrossRef] [PubMed]
- de la Fraga, L.G.; Ovilla-Martínez, B. Generating pseudo-random numbers with a Brownian system. Integration 2024, 96, 102135. [Google Scholar] [CrossRef]
- Gilardi-Velázquez, H.; Echenausia-Monroy, J.; Escalante-González, R.; Campos, E. Codification of Images Based on Deterministic Brownian Motion. In Proceedings of the Chaotic Modeling and Simulation International Conference, Heraklion, Crete, 13–16 June 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 143–156. [Google Scholar]
- Vinales, A.D.; Desposito, M.A. Anomalous diffusion: Exact solution of the generalized Langevin equation for harmonically bounded particle. Phys. Rev. E 2006, 73, 016111. [Google Scholar] [CrossRef] [PubMed]
- Burov, S.; Barkai, E. Fractional Langevin equation: Overdamped, underdamped, and critical behaviors. Phys. Rev. E 2008, 78, 031112. [Google Scholar] [CrossRef] [PubMed]
- Sevilla, F.J.; Sandoval, M. Smoluchowski diffusion equation for active Brownian swimmers. Phys. Rev. E 2015, 91, 052150. [Google Scholar] [CrossRef] [PubMed]
- Sevilla, F.J.; Rodríguez, R.F.; Gomez-Solano, J.R. Generalized Ornstein-Uhlenbeck model for active motion. Phys. Rev. E 2019, 100, 032123. [Google Scholar] [CrossRef] [PubMed]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [PubMed]
- Sprott, J. Some simple chaotic jerk functions. Am. J. Phys. 1997, 65, 537–543. [Google Scholar] [CrossRef]
- Anzo-Hernández, A.; Gilardi-Velázquez, H.E.; Campos-Cantón, E. On multistability behavior of unstable dissipative systems. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 033613. [Google Scholar] [CrossRef]
- Velazquez, H.E.G.; Canton, E.C. Es el movimiento Browniano un proceso estocástico o determinista? Boletín Soc. Mex. Física 2015, 29, 103–106. [Google Scholar]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Silva, A.; Cassal-Quiroga, B.B.; Escalante-Gonzalez, R.d.J.; Del-Puerto-Flores, J.A.; Gilardi-Velazquez, H.E.; Campos, E. A Comparative Study of Brownian Dynamics Based on the Jerk Equation Against a Stochastic Process Under an External Force Field. Mathematics 2025, 13, 804. https://doi.org/10.3390/math13050804
Ruiz-Silva A, Cassal-Quiroga BB, Escalante-Gonzalez RdJ, Del-Puerto-Flores JA, Gilardi-Velazquez HE, Campos E. A Comparative Study of Brownian Dynamics Based on the Jerk Equation Against a Stochastic Process Under an External Force Field. Mathematics. 2025; 13(5):804. https://doi.org/10.3390/math13050804
Chicago/Turabian StyleRuiz-Silva, Adriana, Bahia Betzavet Cassal-Quiroga, Rodolfo de Jesus Escalante-Gonzalez, José A. Del-Puerto-Flores, Hector Eduardo Gilardi-Velazquez, and Eric Campos. 2025. "A Comparative Study of Brownian Dynamics Based on the Jerk Equation Against a Stochastic Process Under an External Force Field" Mathematics 13, no. 5: 804. https://doi.org/10.3390/math13050804
APA StyleRuiz-Silva, A., Cassal-Quiroga, B. B., Escalante-Gonzalez, R. d. J., Del-Puerto-Flores, J. A., Gilardi-Velazquez, H. E., & Campos, E. (2025). A Comparative Study of Brownian Dynamics Based on the Jerk Equation Against a Stochastic Process Under an External Force Field. Mathematics, 13(5), 804. https://doi.org/10.3390/math13050804






