A Comparative Study of Brownian Dynamics Based on the Jerk Equation Against a Stochastic Process Under an External Force Field

Abstract

Brownian motion has been studied since 1827, leading to numerous important advances in many branches of science and to it being studied primarily as a stochastic dynamical system. In this paper, we present a deterministic model for the Brownian motion for a particle in a constant force field based on the Ornstein–Uhlenbeck model. By adding one degree of freedom, the system evolves into three differential equations. This change in the model is based on the Jerk equation with commutation surfaces and is analyzed in three cases: overdamped, critically damped, and underdamped. The dynamics of the proposed model are compared with classical results using a random process with normal distribution, where despite the absence of a stochastic component, the model preserves key Brownian motion characteristics, which are lost in stochastic models, giving a new perspective to the study of particle dynamics under different force fields. This is validated by a linear average square displacement and a Gaussian distribution of particle displacement in all cases. Furthermore, the correlation properties are examined using detrended fluctuation analysis (DFA) for compared cases, which confirms that the model effectively replicates the essential behaviors of Brownian motion that the classic models lose.

1. Introduction

Brownian motion studies have been developed from Robert Brown’s reflections on the fertilization process of flowers, from which he observed that pollen particles in water have a “rapid oscillatory motion” caused by molecular bombardment [1]. Currently, the idea of Brownian motion is generalized to Brownian agents in systems in which the dynamics of their states have the same statistical properties as Brownian motion.

The study of Brownian motion has been extensive since Robert Brown [1], Louis Bachelier [2], and Albert Einstein [3] proposed the first mathematical description of the Brownian motion of a free particle [4]. Later, Paul Langevin obtained an approximation from Newton’s second law [4]. The model proposed by Langevin [5] is based on a second-order differential equation with a stochastic term, which gives a random character to the movement.

This phenomenon has been studied as a continuous stochastic process in the time characterized by a normal distribution; it can be explained on a molecular scale by a series of collisions in one dimension, in which small particles collide with a larger particle [6], which is believed to be fully described by models based on classical Hamiltonians [7]. In this type of diffusion, the molecules comprising the system adhere to Newton’s laws of motion [8], and their movement is isotropic [9]. This means there are no preferred points or directions; the molecules can move freely in any direction and at any velocity. This isotropic behavior reflects the uniformity of the medium in which the suspended particle is found. It has traditionally been described mathematically as a stochastic process due to its seemingly random nature and the inherent difficulty in precisely predicting the trajectories of the particles.

The idea of deterministic Brownian motion has been discussed in hydrodynamics and chemical reactors with oscillatory behavior, where the movement is completely deterministic and is sometimes referred to as microscopic chaos [10,11]. One of the first publications on the deterministic behavior of particles was presented by Russo in [12], who, by using three different schemes (based on the approximation of the gradient on an irregular mesh, and a finite-element approach), studied its convergence, proposed some applications for the Fokker–Planck equation and other problems of disposing of particles. However, several approaches have been introduced to provide a better understanding. For instance, one approach explores the deep origin of the stochastic nature of a dynamical system. There have been many studies that show how, based on a Hamiltonian (deterministic) description of both the environment and the system, random noise emerges. This occurs when the degrees of freedom of the environment increase as the dynamics of more particles in the medium are considered. However, this approach becomes a computational burden for systems with many particles [13,14,15,16,17,18]. Additionally, diffusion phenomena have been studied using discrete functions constructed from the Langevin equation. However, these systems use independent functions as perturbations to the mapping. Although the time series obtained reflect different diffusion properties, they do not reflect the dynamics of particles in continuous time [14,19,20,21].

Recently, some works have been conducted (e.g., [22,23]) to formalize Zwanzig’s approach and understand how to describe stochastic noise knowing the microscopic details of the environment. Trefán et al. [24] propose modeling Brownian motion from a microscopic process without introducing randomness. The erratic macroscopic movement is shown as a consequence of a filtered process that entails microscopic chaos and produces a Langevin equation for the velocity of the particle, corresponding with the Fokker–Planck equation in the appropriate parameter regime. This makes the Langevin model a generator of deterministic movement; however, the statistical properties of this process differ considerably from the standard assumptions of Gaussian statistics. Huerta-Cuellar et al. [25,26] propose an approach to generate deterministic Brownian movement, adding one degree of freedom to the equation of Langevin and obtaining a third-order model in which the stochastic term is replaced with a new variable defined by a third differential equation (Jerk equation), with which a Gaussian-type probability distribution is generated. The main advantage of this model over models based on stochastic processes lies in the fact that the oscillatory character is a function only of the state variables of the particle itself, as observed in experiments, just as the commutations can describe the distribution of other particles in the medium [27].

In a recent study, Echenausía-Monroy et al. [28] presented a circuit implementation that reproduces Brownian motion based on a fully deterministic set of differential equations, giving the possibility of the results’ reproducibility. In turn, Velázquez-Pérez et al. [27,29] propose a deterministic model for the diffusion and settling of particles in one and two displacement dimensions based on the Jerk equation, with which it is possible to consider different conditions of diffusion in both dimensions and open the option of using Brownian motion for applications in the field of medicine, ecology, etc. [30,31,32,33].

The use of the Langevin equation has been widely discussed and studied [4], but it is common to find physical problems modeled from variations in the Langevin model [34,35,36,37], for example, the Brownian motion of a molecular dipole in a periodic potential [38]. In these cases where other factors are considered in the Langevin equation, it is known as the generalized Langevin equation (GLE) [39]. It has been shown that for the different assumptions derived from the GLE, it is possible to obtain a different behavior. The GLE has been applied to many systems which are characterized by an anomalous diffusion process in which different Memory Kernels are considered. In this sense, S.C. Kou and X. Sunney Xie [40] use fractional Gaussian noise GLE to describe the underdiffusion phenomenon of electron transfer within a protein. Likewise, Wei Min et al. [41] determine, through the GLE, the memory kernel of the fluctuations between the fluorescein–tyrosine pair within a complex protein, as well as for the generation of pseudorandom sequences for cryptography [42,43].

On the other hand, we can also find, in various fields of physics, harmonic motion disturbed by some interaction with an object. Therefore, it is important to analyze the effects associated with the disordered nature of an environment through the study of the dissipation dynamics of a harmonic oscillator immersed in a disordered environment. A. D. Viñales and M. A. Despósito derive the exact solution for the GLE of a particle under the influence of an external harmonic force using Laplace theory [44]. Additionally, S. Burov and E. Barkai describe the dynamics of a harmonic particle through the fractional Langevin equation considering overdamped, underdamped, and critically damped cases, for which they find behaviors different from normal [45]. On the other hand, the Generalized Ornstein–Uhlenbeck model has been used to describe Active Motion [46,47]. It is important to emphasize that in each of the aforementioned works, the dynamic behavior obtained in each case differs from the others, this shows the versatility of the Langevin equation in characterizing different diffusion phenomena. The main objective of this work is to introduce a deterministic dynamic model for the generation of harmonic Brownian motion. Based on Ornstein–Uhlenbeck theory and the Jerk equation, a model is proposed following the methodology presented in [25,26], where the principal advantage of this approach is that the system is autonomous and the particles of the surrounding medium are emulated by switching surfaces. This behavior is characterized by time series analysis via DFA.

2. Brownian Motion Models

At the beginning of the last century, both A. Einstein [3] and M. Smoluchowski [6] raised and successfully described the nature of Brownian motion. With Einstein’s method, Brownian motion is described by the probability $\rho (x,t)$ of finding the particle at position x at time t, which satisfies the macroscopic diffusion equation. A few years later, P. Langevin proposed another method to solve the problem using stochastic differential equations. On the other hand, regarding deterministic Brownian motion, the first model reported in the literature was proposed by Trefán et al. [24] in which they replace the stochastic process in the Langevin equation with chaotic mapping. With this model, they manage to obtain what they call macroscopically Brownian motion; however, this model does not comply with the statistical properties of the phenomenon. Additionally, Huerta-Cuellar et al. [25] propose a deterministic model for the generation of a Brownian motion from the model proposed by Langevin, adding a degree of freedom to the system, thus replacing the stochastic term, related to the fluctuating acceleration, with a third-order differential equation (Jerk equation).

2.1. Einstein Model

During the development of the theory of molecular kinetics, Einstein discovered that it is possible to observe the motion of microscopic suspended particles, which was very similar to Brownian motion [3]. He proposed a probability function $\rho (x,t)$ of finding a Brownian particle at position x at time t, given by

$$\rho (x,t)={\displaystyle \frac{1}{{\left(4\pi Dt\right)}^{1/2}}}{e}^{-{\displaystyle \frac{{\left|x\right|}^2}{4Dt}}},$$

(1)

where D is the diffusion coefficient, which relates an external force to the density of the fluid and its temperature. Thus, considering that the Brownian particle experiences viscous resistance, $mv=6\pi \mu a$, with m representing the mass of the particle, v its speed, r the radius of the particle, and $\mu$ the coefficient of viscosity. It was determined that the diffusion coefficient is of the form

$$D={\displaystyle \frac{kT}{6\pi \mu r}}.$$

(2)

Using the probability density and the diffusion coefficient above, Einstein determined that the mean-squared displacement of a Brownian particle at time $\tau$ is given by

$$\overline{\Delta x^2}={\displaystyle \frac{RT}{N}}{\displaystyle \frac{1}{3\pi \mu r}}\tau ,$$

(3)

where T is the absolute temperature, R is the gas constant, and N is the Avogadro number.

This model determines the nature of the movement of a particle; however, it does not provide a dynamic theory of the phenomenon.

2.2. Langevin Model

First, Langevin postulated that the particle could undergo a frictional force simply by being immersed in a liquid [5]. According to Stokes’ law for a particle of radius r in a medium of viscosity $\eta$, the change in the velocity of the particle in time satisfies

$$\dot{v}=-6\pi \mu rv=-\gamma v.$$

(4)

Later, Langevin proposed adding to the previous equation a stochastic force, called a complementary force, related to the irregularity of the impacts of the fluid molecules. Thus, he postulated the following equation, which is known as the Langevin equation:

$$m\dot{v}=-\gamma v+A_f\left(t\right),$$

(5)

where v is the velocity of the particle, m is its mass, $\gamma >0,$ and the term $A_f\left(t\right)$ represents the fluctuation in acceleration, which provides the stochastic character of the Brownian motion and characterizes a Gaussian process. Therefore, with this model, Langevin determined, in the same way as Einstein, the average squared displacement of the particle, which is given by Equation (3), as well as providing a more general and exact model for the dynamics of a Brownian particle.

2.3. Chaotic Map-Based Model

Regarding deterministic Brownian movement, the first model reported in the literature was proposed by Trefán et al. [24]. They did not derive a microscopic system of equations for this. They considered a deterministic process called “Booster” at the microscopic level, which is chaotic and is related to thermal fluctuations of the Brownian particle; in this sense, the Booster must comply with the characteristic statistical properties of the complementary force of the differential equation (Gaussian distribution). For this model, they started from the Langevin equation and replaced the stochastic process in the equation with the Booster (a chaotic mapping):

$$\begin{array}{ccc}\hfill \dot{x}& =& v,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \dot{v}& =& -\gamma v+{\epsilon }_0\left(t\right),\hfill \end{array}$$

(7)

where ${\epsilon }_0$ is the deterministic force resulting from the chaotic process defined by the mapping:

$${\epsilon }_{n+1}=\alpha \left[{\displaystyle \frac{\eta }{2}}-{\epsilon }_n\right]\left[{\displaystyle \frac{\eta }{2}}+{\epsilon }_n\right]+{\displaystyle \frac{\eta }{2}}.$$

(8)

With this model, they manage to obtain time series with similar behavior, what they call Brownian motion in a macroscopic way. Although this model does not comply with the statistical properties of the phenomenon, it allowed us to see a different way of studying Brownian motion. In other words, Trefán et al. propose a deterministic Brownian motion generator which they present as a discrete system that generates pseudo-random numbers; as already mentioned, the statistical properties of this process differ considerably from the standard assumptions of Gaussian statistics. The main contribution of Trefán et al. is that they confirm that it is possible to generate Brownian dynamics in a deterministic way, without the need to impose statistical assumptions.

2.4. Jerk-Based Model

Huerta-Cuellar et al. [25] introduced another deterministic model for the generation of Brownian motion. Again, it was based on the model proposed by Langevin and added a degree of freedom to the system; this, by replacing the stochastic process, related to the fluctuating acceleration, with a third-order differential equation. In this sense, they obtained an approximation to the generation of Brownian motion in a deterministic way by transforming the model proposed by Langevin into a system of three differential equations. In this model, the stochastic term is replaced by a new variable, z, defined by a third-order differential equation (Jerk equation). This new variable that they proposed acts as the fluctuating acceleration, producing a dynamic of deterministic motion, which is related to changes in velocity and acceleration caused by friction and collisions with other particles in the medium. Therefore, the Jerk-based model is described by the following equations:

$$\begin{array}{ccc}\hfill \dot{x}& =& v,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \dot{v}& =& -\gamma v+z,\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \dot{z}& =& -{\alpha }_{1}x-{\alpha }_{2}v-{\alpha }_{3}z+{\alpha }_4,\hfill \end{array}$$

(11)

where ${\alpha }_1,{\alpha }_2,{\alpha }_3$, and ${\alpha }_4$ are constants defined in [25].

In general, this model provides an approximation to a Gaussian-type probability distribution and a linear square displacement. In this case, a fully continuous model in time is obtained, where the fluctuating acceleration depends on the system´s states.

Additionally, this model reproduces statistical characteristics similar to those of Brownian motion. These include a linear average squared displacement, a Gaussian probability distribution, a power law of “$-2$” for the frequency spectrum, and a power law of “$1.5$” obtained by the detrended fluctuation analysis (DFA), which confirms the Brownian character of the observed movement.

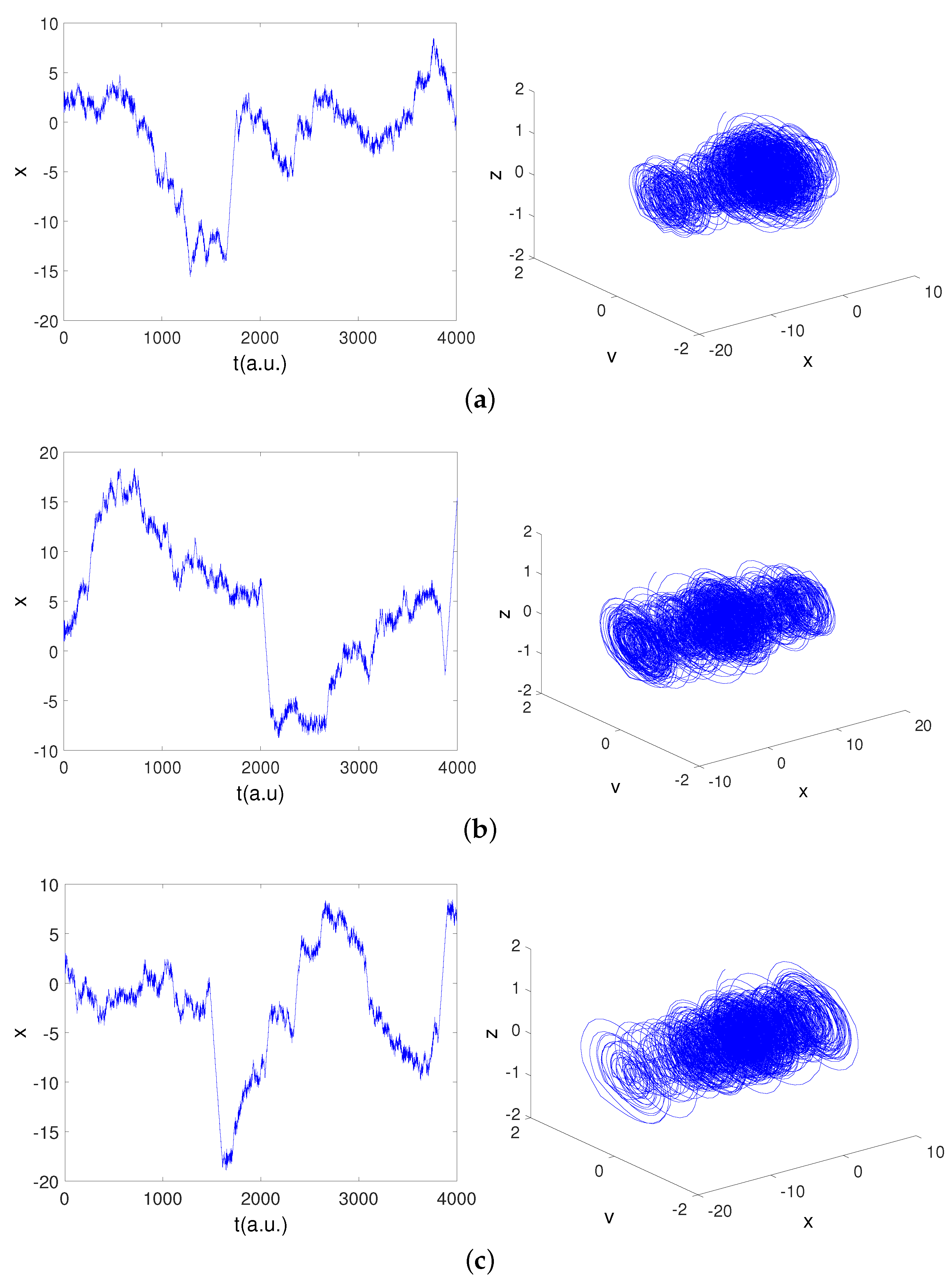
3. Brownian Motion in a Field of Force

Ornstein–Uhlenbeck Model

Suppose a Brownian particle is immersed in an external force field given by $K(x,t)$ in units of acceleration; the Langevin equation within the Ornstein–Uhlenbeck theory is [48]

$$\begin{array}{ccc}dx& =& vdt,\hfill \\ dv& =& K(x,t)dt-\gamma vdt+dB.\hfill \end{array}$$

(12)

In this case, B corresponds to a Wiener process, which is a stochastic process. The first case that can be considered, due to its simplicity, is one in which $K(x,t)$ is a constant. The solution of the aforementioned case and behavior of the system are not significantly affected. This can be seen since the system derivative is zero and the linear operator takes the same form as for a free particle.

Now, consider the case where $K(x,t)$ is linear and independent of t. As an example, S. Burov and E. Barkai [45] described the dynamics of a harmonic particle through the fractional Langevin equation considering overdamped, underdamped, and critically damped cases. Let us consider a one-dimensional harmonic oscillator with angular frequency $\omega$; the Langevin equation in the Ornstein–Uhlenbeck theory is of the form:

$$\begin{array}{ccc}dx& =& vdt,\hfill \\ dv& =& -{\omega }^{2}xdt-\gamma vdt+dB.\hfill \end{array}$$

(13)

As in an oscillator theory harmonic without considering Brownian motion, three cases are distinguished:

• Overdamped $\gamma >2\omega$.
• Critically damped $\gamma =2\omega$.
• Underdamped $\gamma <2\omega$.

Figure 1 displays the particle position versus time considering the same initial condition ${\mathbf{x}}_{\mathbf{0}}={(1.0,0.1)}^T$, $\gamma =1$, and different values for $\omega$. We show only three time series for the $\omega$ values of $\omega \in \{3.0,0.5,0.08\}$ to see the behavior changes on the particle trajectory. Figure 1 shows that as $\omega$ decreases, the displacements of the particle begin to become smaller, as does the decrement in the oscillation frequency; the dynamics of the particle reveal erratic fluctuations around cero and, only for the underdamped case, anisotropic diffusion with a positive effective diffusion coefficient in the x direction, generating a motion with characteristics of a random walk in a dynamic energy landscape and heterogeneous diffusion, which is a characteristic behavior observed in Brownian diffusion. Furthermore, the behavior of the solutions in the $(x,v)$ plane is shown, in which the oscillatory character is observed for the three cases and, very importantly, the speed remains limited and within the same range. It is also important to note that for the overdamped case, the region of oscillation is much smaller compared to the under-damped case.

Figure 2 shows the statistical properties of the time series obtained from the system (13), which are in agreement with the properties reported for the Brownian motion through the Wiener process. Figure 2 shows the probability distributions of the particle in relation to the traditional Brownian motion, the zero-valued Gaussian probability distributions, and the linear growth in the time of the predicted mean square displacement for the (a) overdamped, (b) critically damped, and (c) underdamped cases, in which it can be seen that the probability distributions obtained from the movement generated by the system are bell-shaped, with the underdamped case being the closest to a Gaussian distribution and the overdamped being similar to a Student’s t-distribution. Likewise, it is possible to notice in the probability distributions, in accordance with what was discussed in Figure 1, that the case in which the particle has the highest dispersion coefficient is the underdamped case, in contrast to the critically damped case, in which the standard deviation of the bell is the lowest; with regard to the average square displacement, it maintains the same rate of linear growth in time for the three cases. We approximate a Gaussian bell curve to the data to find a density function that is given by

$$f\left(x\right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}},$$

(14)

where $\mu =0$, and $\sigma$ is set for all cases in $0.5$.

The correlation property of the signals generated by the system (13) is characterized by the detrended fluctuation analysis (DFA) that was developed by Peng [49]. Then, as in the case of a free particle, the DFA technique helps us to guarantee that the proposed system generates Brownian motion, we apply the DFA evaluation method to the time series obtained with the aforementioned parameter values (see Figure 3). The DFA is an important tool for the detection of long-range autocorrelations in non-stationary time series. The DFA is based on random walk theory, which consists of a scaling analysis for which the scaling exponent $\eta \approx 1.5$ defines Brownian noise; having mentioned this, with the calculated exponents, we can only guarantee that the underdamped case (Figure 3c) presents correlations of the Brownian type $\eta =1.4343$, which is also discussed in Figure 1 and Figure 2. For the overdamped $\eta =1.7954$ and critically damped $\eta =2.3364$ cases, it is not possible to describe the type of correlation they present in the series, since values greater than $1.5$ are not characterized in the literature.

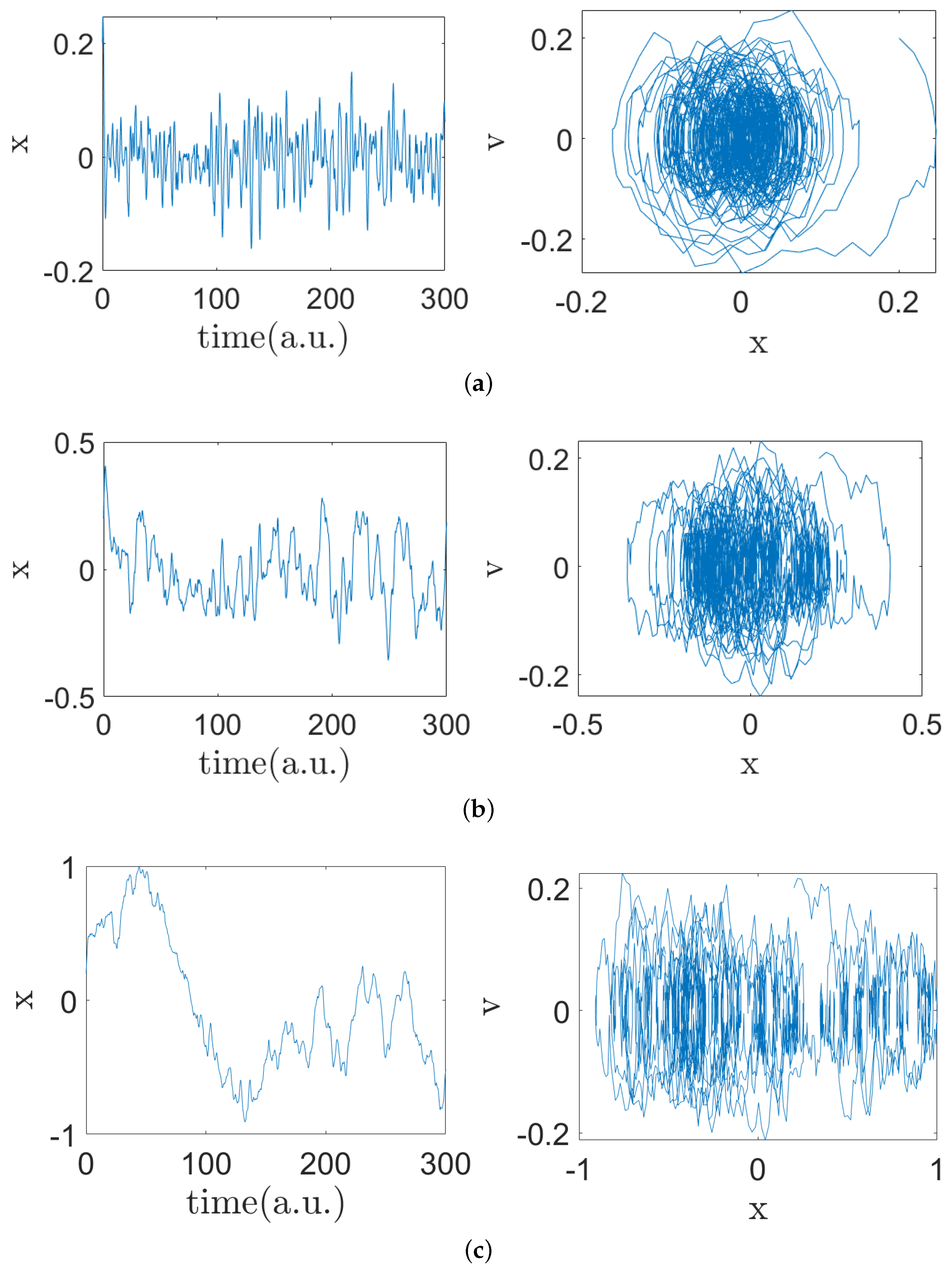
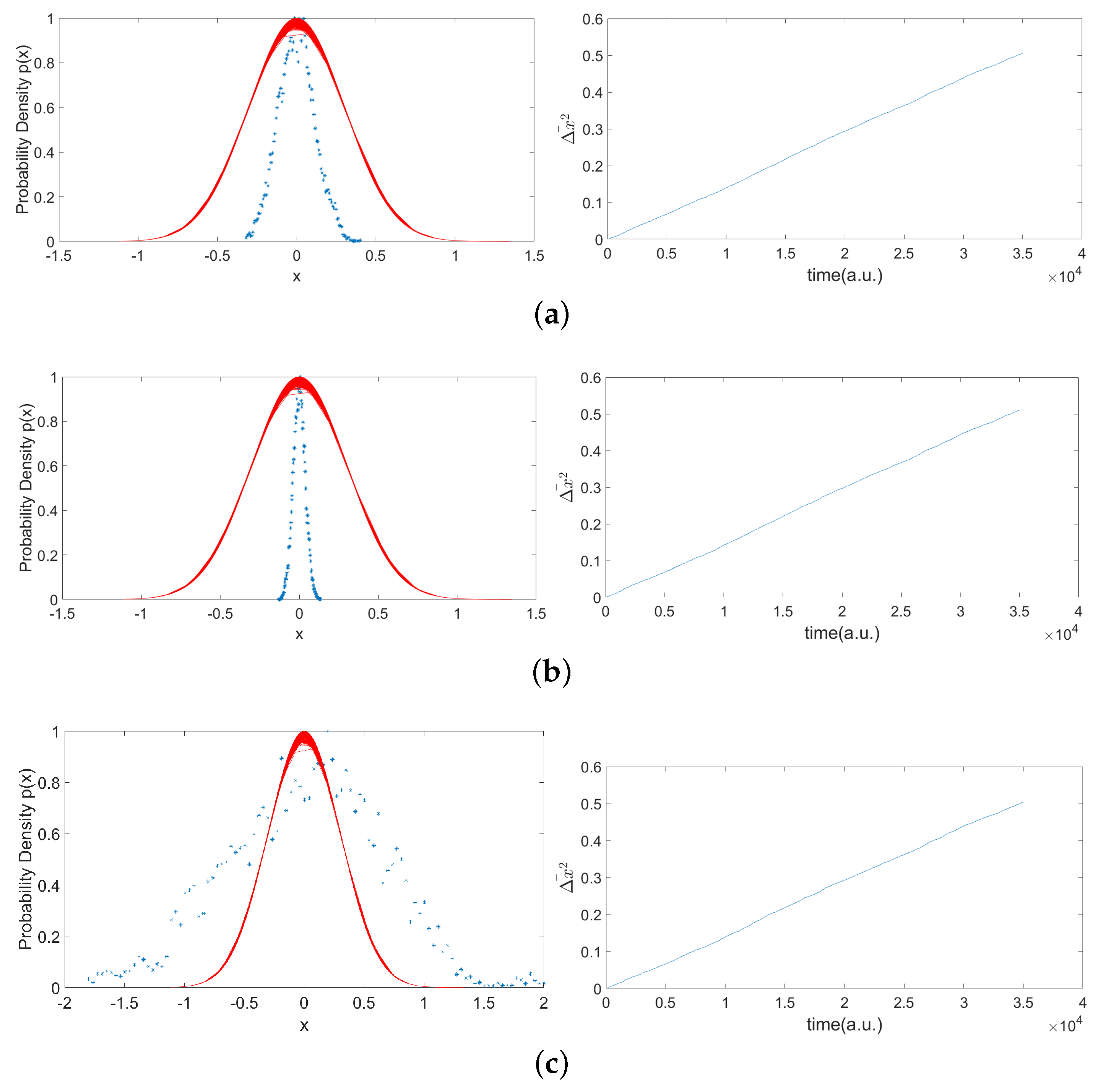
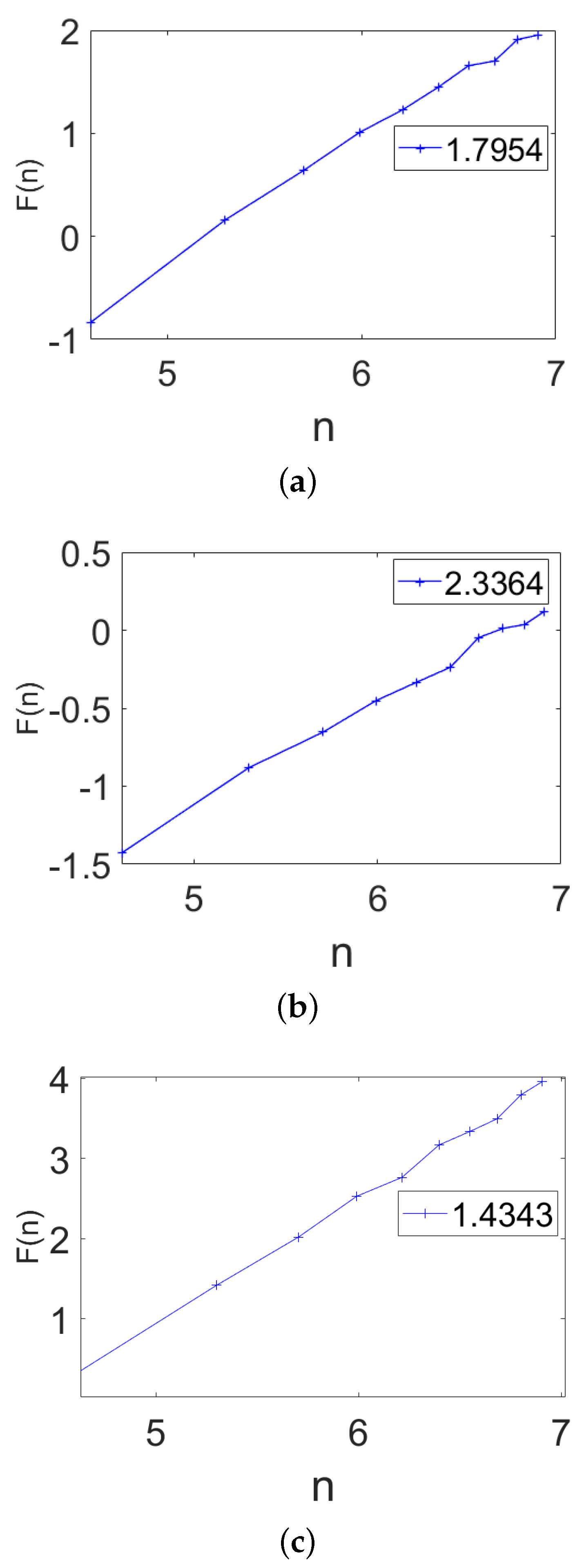
4. Deterministic Model for Brownian Motion in a Force Field

The deterministic Brownian model was developed in the same spirit as that in [25], where they used the Jerk equation to drive the stochastic term. Now, in this case, we start from Equations (12) and (13), driving the Wiener process $\left(dB\right)$ using the Jerk equation. We consider the fluctuating acceleration to be related to a Newtonian Jerk [50], where $F(\ddot{x},\dot{x},x,t)$ and $dF/dt=a_1\ddot{x}+a_2\dot{x}+a_{3}x+a_4$, as shown in [25]; then, this adds one degree of freedom to Equation (13) to obtain a system of three ordinary differential equations:

$$\begin{array}{ccc}\dot{x}& =& v,\hfill \\ \dot{v}& =& -{\omega }^{2}x-\gamma v+z,\hfill \\ \dot{z}& =& {\alpha }_{1}x+{\alpha }_{2}v+{\alpha }_{3}z+{\alpha }_4\left(x\right),\hfill \end{array}$$

(15)

where ${\alpha }_i=1,2,3$ are constants. In this way, the term $\dot{z}$ acts as a fluctuating accelerator that produces a Brownian movement behavior via deterministic dynamics, but in this case, this behavior has the property of dependence on velocity, position, and acceleration due to the Jerk equation involved. The values of ${\alpha }_4$ are defined by the round function:

$${\alpha }_4=C1·Round(x/C2),$$

where $C1=0.9$ and $C2=0.6$ are constants that determine system balance, and round operations limit the movement of the particle generating switching surfaces, which can be related to collisions with other particles in the medium.

Now, to guarantee unstable behavior, we use the linear operator associated with the system (15), whose Jacobian matrix, A, is given by

$$A=\left(\begin{array}{ccc}0& 1& 0\\ -{\omega }^2& -\gamma & 1\\ {\alpha }_1& {\alpha }_2& {\alpha }_3\end{array}\right).$$

(16)

This class of linear systems presents oscillations around equilibria due to stable and unstable manifolds, for which it is necessary to find the parameter values, ${\alpha }_i$, such that the system is dissipative with unstable dynamics. In short, it will be called unstable dissipative system (UDS) type-I, i.e., the sum of associated eigenvalues of A is negative, where one is a negative real number, and the others are complex numbers conjugated with a positive real part (see proposition III.3 of [51]). In particular, we take $\gamma =7\times {10}^{-2}$ and ${\alpha }_i$ values according to those published in [28], ${\alpha }_1=1.5,{\alpha }_2=1.3,{\alpha }_3=0.1$, where the values were obtained by numerical approximation in such a way that the probability of $1/2$ is guaranteed for the free particle to move to the adjacent domain or remain in the same one, and for which the system is UDS type-I, i.e., there exists a dissipative manifold in the one-dimensional system and an unstable two-dimensional manifold.

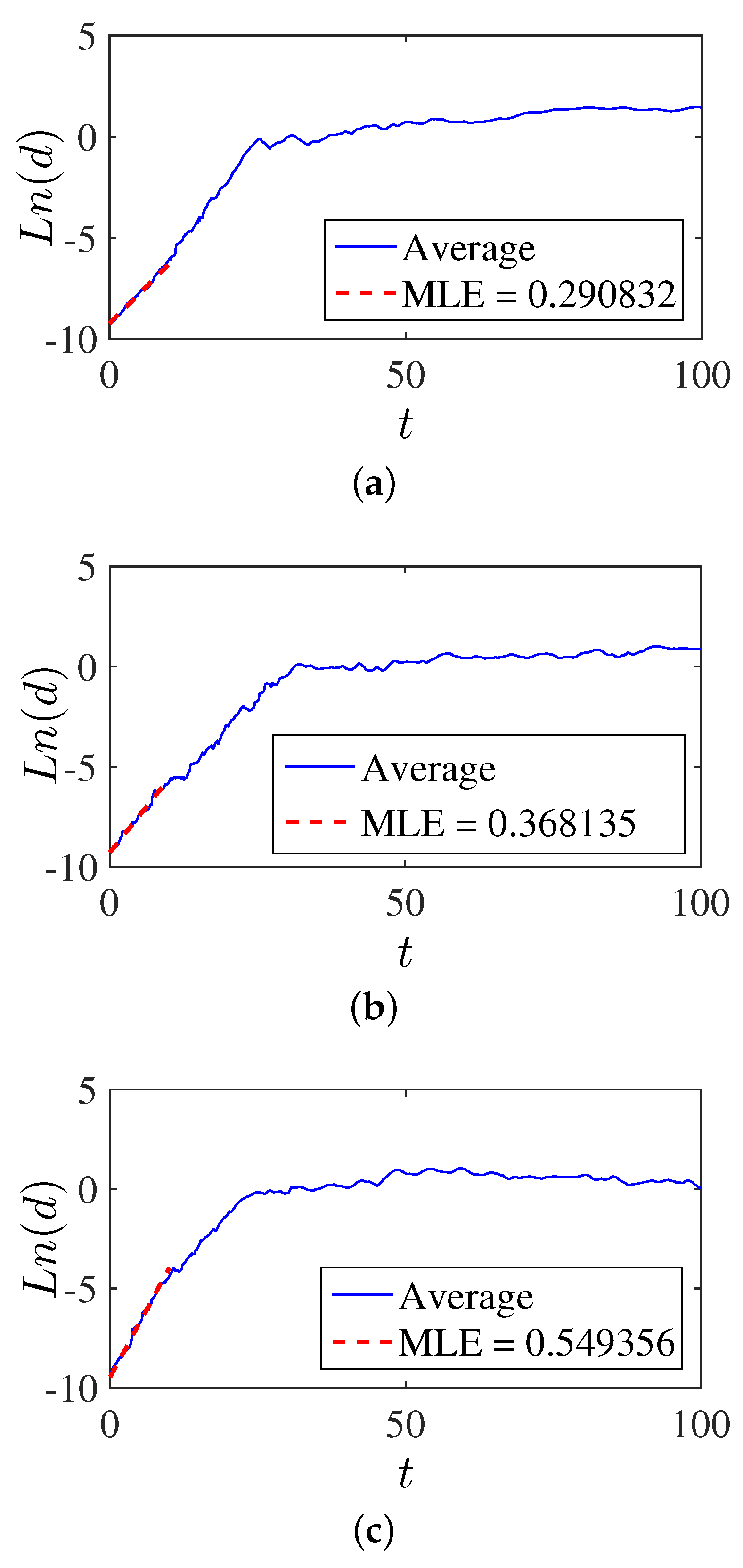
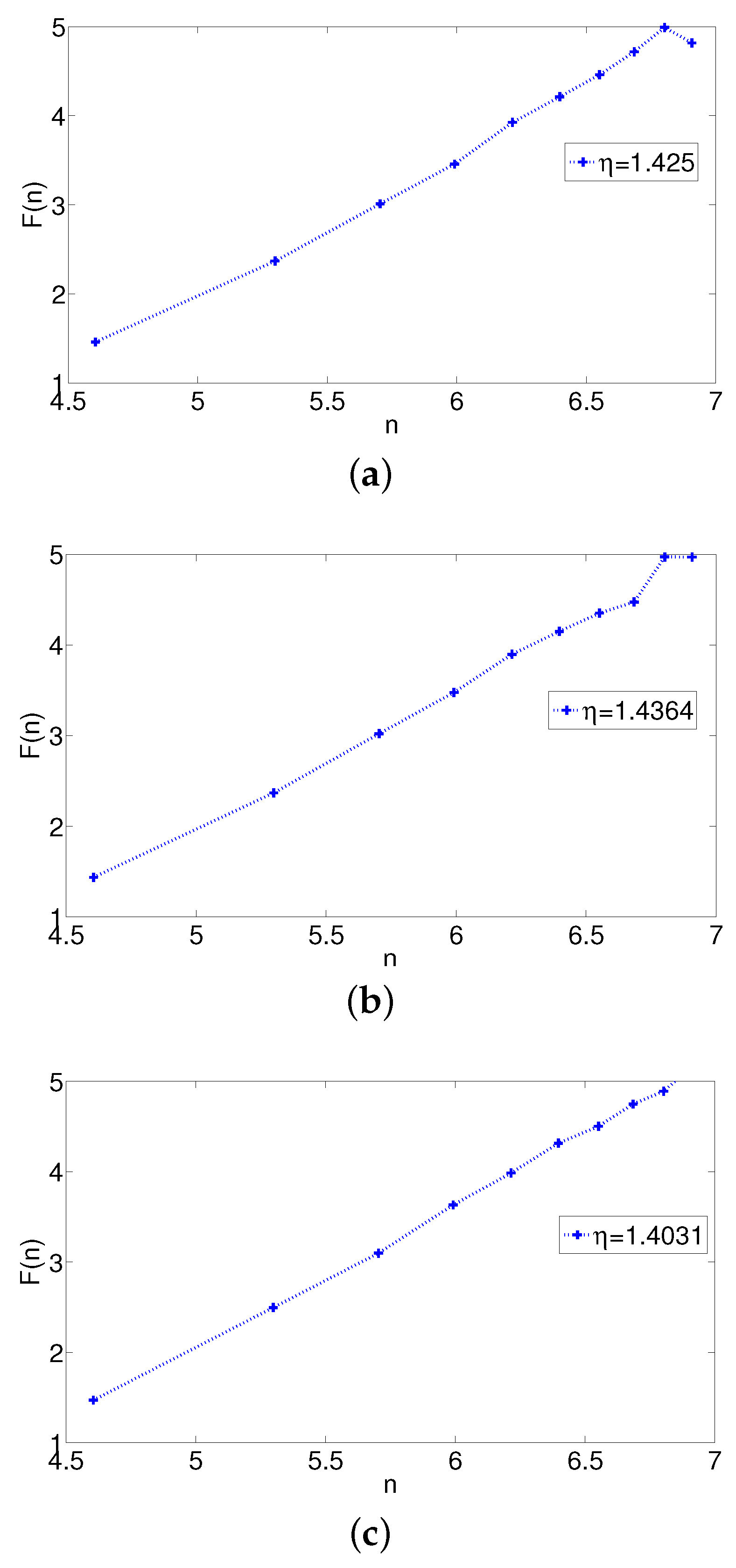
Numerical Results for Brownian Motion in a Harmonic Force Field

Taking into account the parameter values that were defined in the previous section, the numerical solutions obtained for the three cases are shown in Figure 4 for the (a) overdamped ($\omega =3.5\times {10}^{-3}$), (b) critically damped ($\omega =3.5\times {10}^{-2}$), and (c) underdamped ($\omega =3.5\times {10}^{-1}$) cases. Figure 4 shows the time series for the position, and in these images, one can see the characteristic noisy behavior of the Brownian motion as well as the oscillatory behavior associated with the harmonic oscillator. We can also see the solution of the system in the space of states, where it can be seen that the solutions are bounded for velocity and acceleration changes. Furthermore, we can observe that the results obtained are in agreement with the results obtained with stochastic models, in which harmonic behavior prevails over random behavior in the oscillations [48], i.e., in our case, random behavior predominates over harmonic.

Figure 5 shows the statistical properties of the time series obtained from the system (15), which are in agreement with the properties reported for Brownian motion through the Wiener process. Figure 5 shows the probability distributions of the particle in relation to traditional Brownian motion, the zero-valued Gaussian probability distributions, and the linear growth in the time of the predicted mean-square displacement for the (a) overdamped, (b) critically damped, (c) underdamped cases, in which it can be seen that the probability distributions obtained from the movement generated by our system have a good Gaussian approximation. Note that the variable in the three cases takes values in different intervals (Figure 4): $[-15,10]$ for overdamped; $[-10,20]$ for critically damped; $[-20,10]$ for underdamped. We approximate a Gaussian bell curve to the data to find the density function that is given by Equation (14).

The Brownian motion presents divergence in its trajectories. Now, we are interested in finding the divergence in each ((a) overdamped, (b) critically damped, (c) underdamped). As is known, strong divergence is an essential feature in Brownian motion [52] and can be characterized by a positive Lyapunov exponent, which describes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with an initial separation vector ${\delta }_0$ diverge at a rate given by $\lambda$, called the Lyapunov exponent, and can be calculated as follows:

$$\lambda =\underset{t\to \infty }{lim}\underset{|{\delta }_0|\to 0}{lim}{\displaystyle \frac{1}{t}}ln{\displaystyle \frac{\left|\delta \right(t\left)\right|}{|{\delta }_0|}}.$$

(17)

In Figure 6 the maximum Lyapunov exponent obtained, according to [53], of the proposed system is shown to confirm the divergence of the trajectories of the Brownian motion. The maximum Lyapunov exponents obtained for the proposed system (14) for the three cases are as follows: (a) 0.2908 for the overdamped case, where the divergence is less than that of the other cases; (b) 0.3681 for the critically damped case, where the divergence is between that of the overdamped and underdamped cases; and (c) 0.5493 for the underdamped case, where the divergence is greater than that of the other cases. We can infer that in a bounded space, the underdamped case would be ideal if we want to visit the space faster.

Finally, in Figure 7, the scaling law with $\eta =1.425$ for overdamped, $\eta =1.4364$ for critically damped, and $\eta =1.4031$ for underdamped, revealed by the DFA of the proposed system, is shown to confirm the closeness of the Brownian character of the time series [54].

5. Discussion

A dynamical system that exhibits time series with properties of Brownian motion has been presented. This model considers an external force, specifically, a harmonic force field, and the Jerk equation instead of the stochastic process. These changes modify the Ornstein–Uhlenbeck equation by adding one additional degree of freedom, so a three-dimensional model was obtained. The Gaussian probability density distribution was confirmed with numerical simulations. The statistical analysis of the time series obtained with the proposed model displayed typical characteristics of Brownian behavior, such as linear growth of the mean-square displacement, and a Gaussian probability density distribution for displacement. Furthermore, Brownian behavior was confirmed by approximately 1.4 power-law scaling of the fluctuation.

With the results obtained, we could observe that in both models, the stochastic and the Jerk, the harmonic effects affect the response frequency of the system, which agrees with the classical harmonic theory. We were also able to observe, through the correlation analysis, that in the stochastic model, Brownian behavior cannot be guaranteed in the three cases studied, that is, in the overdamped and critically damped cases, the Brownian character is lost. On the contrary, through the approximation based on the Jerk equation, it was observed that regardless of the case that is considered, the Brownian character is preserved.

Based on these results, which were obtained by adding a degree of freedom into the Ornstein–Uhlenbeck model, it can be thought that the methodology presented in this work could be used to construct models under other external forces or behaviors of anomalous diffusion. Additionally, we developed adequate realistic models with real experimental time series in order to obtain the Brownian motion in real systems. In addition, following the electronic approach proposed by [28] to generate Brownian dynamics, the implementation and validation of the system proposed in this work can be carried out.