Dynamic Modeling of Limit Order Book and Market Maker Strategy Optimization Based on Markov Queue Theory
Abstract
1. Introduction
2. Literature Review
3. Construction of a Market Maker Model Based on Markov Processes
3.1. Model Assumptions and Basic Settings
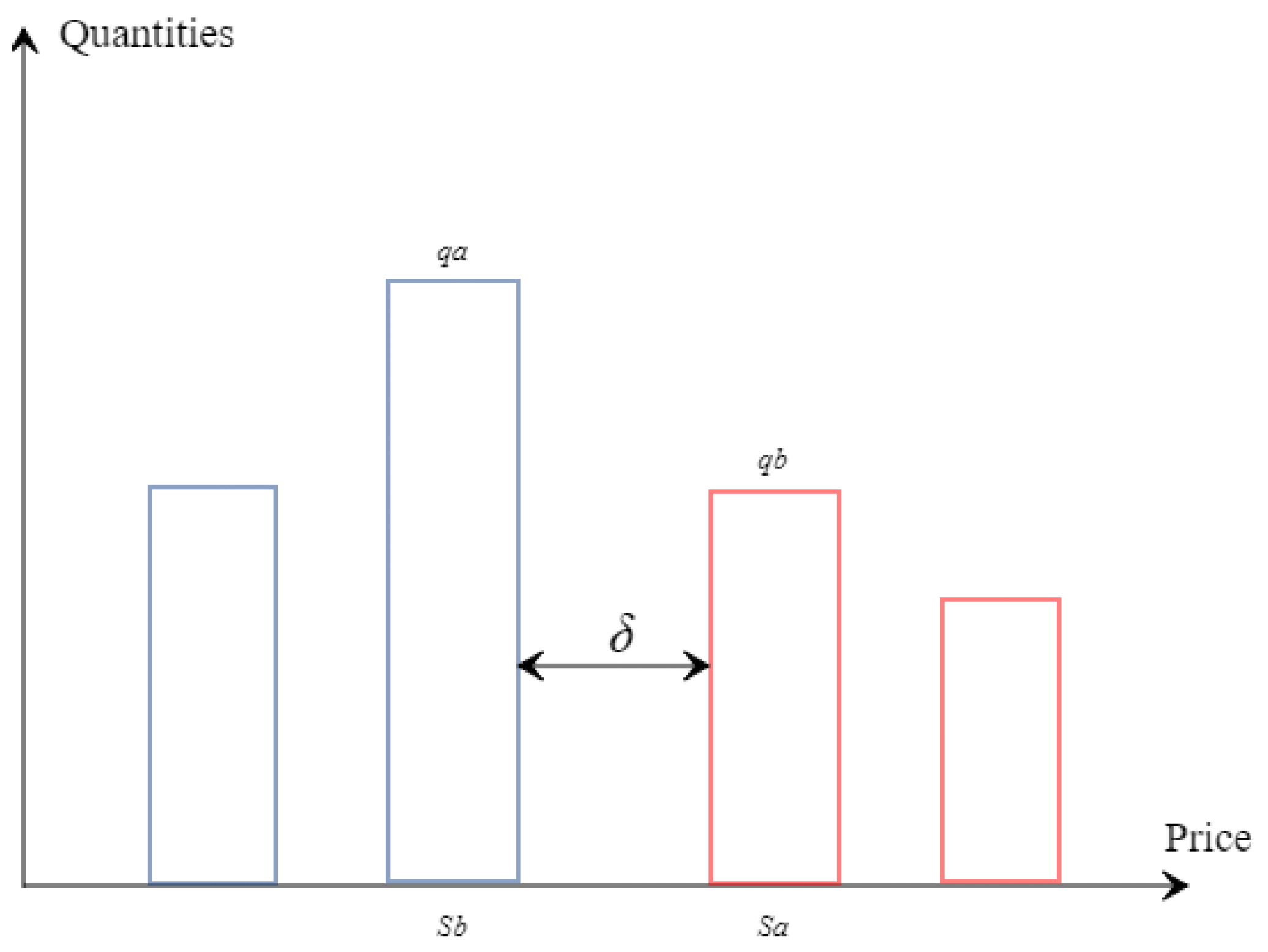
3.1.1. Order Book State
3.1.2. Price Dynamics
3.2. Dynamic Modeling of the Limit Order Book and Characterization of Execution Probability
4. Optimal Market-Making Strategies and Model Solutions
4.1. Optimal Market-Making Strategies
4.2. Establishing the Quasi-Variational Inequality
4.3. Numerical Solution—Finite Difference Method
5. Parameter Estimation and Empirical Analysis
5.1. Data Description and Preprocessing
5.2. Parameter Estimation
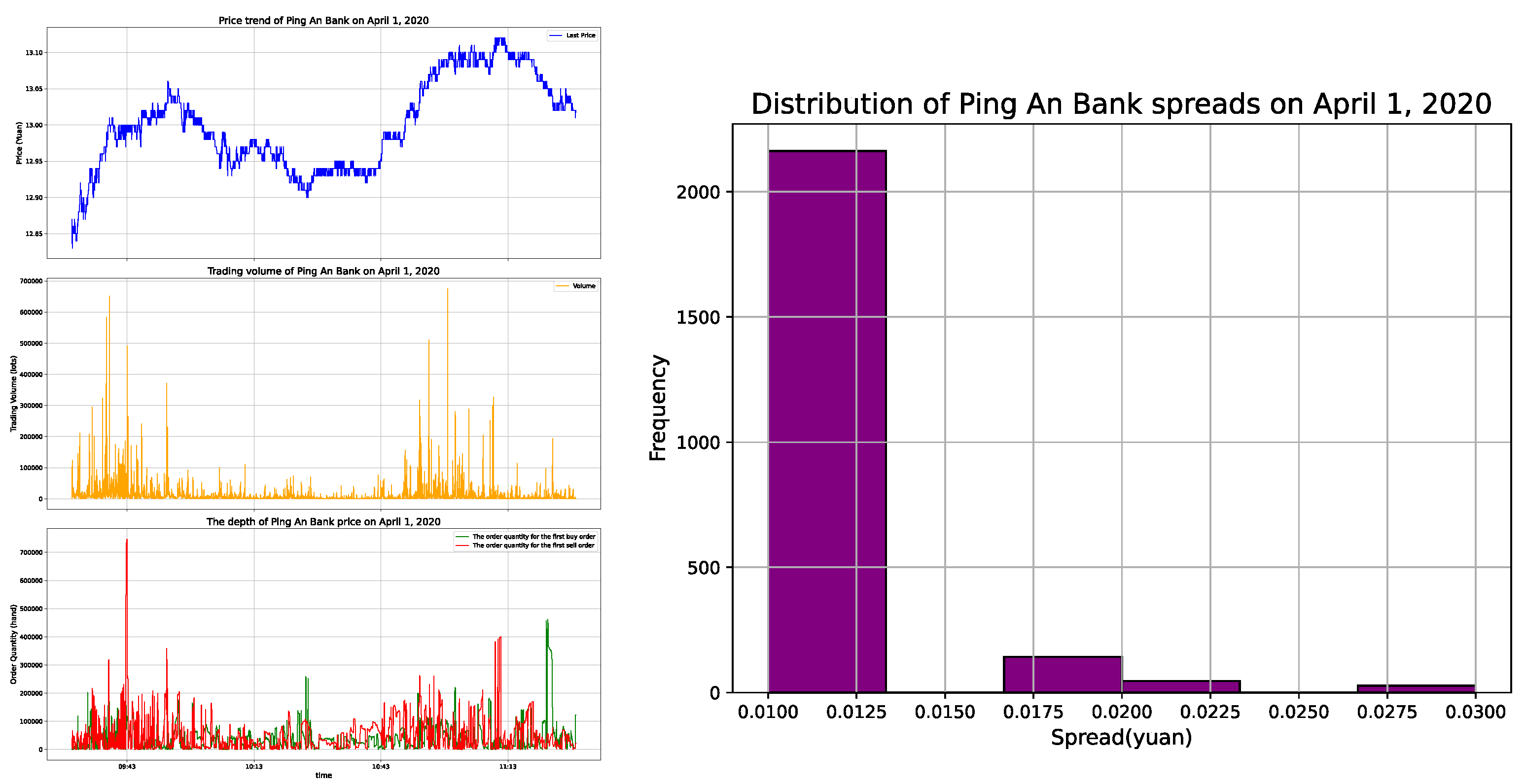
5.2.1. Market Spread Process Parameter Estimation
5.2.2. The State Transition Probability Matrix Estimation
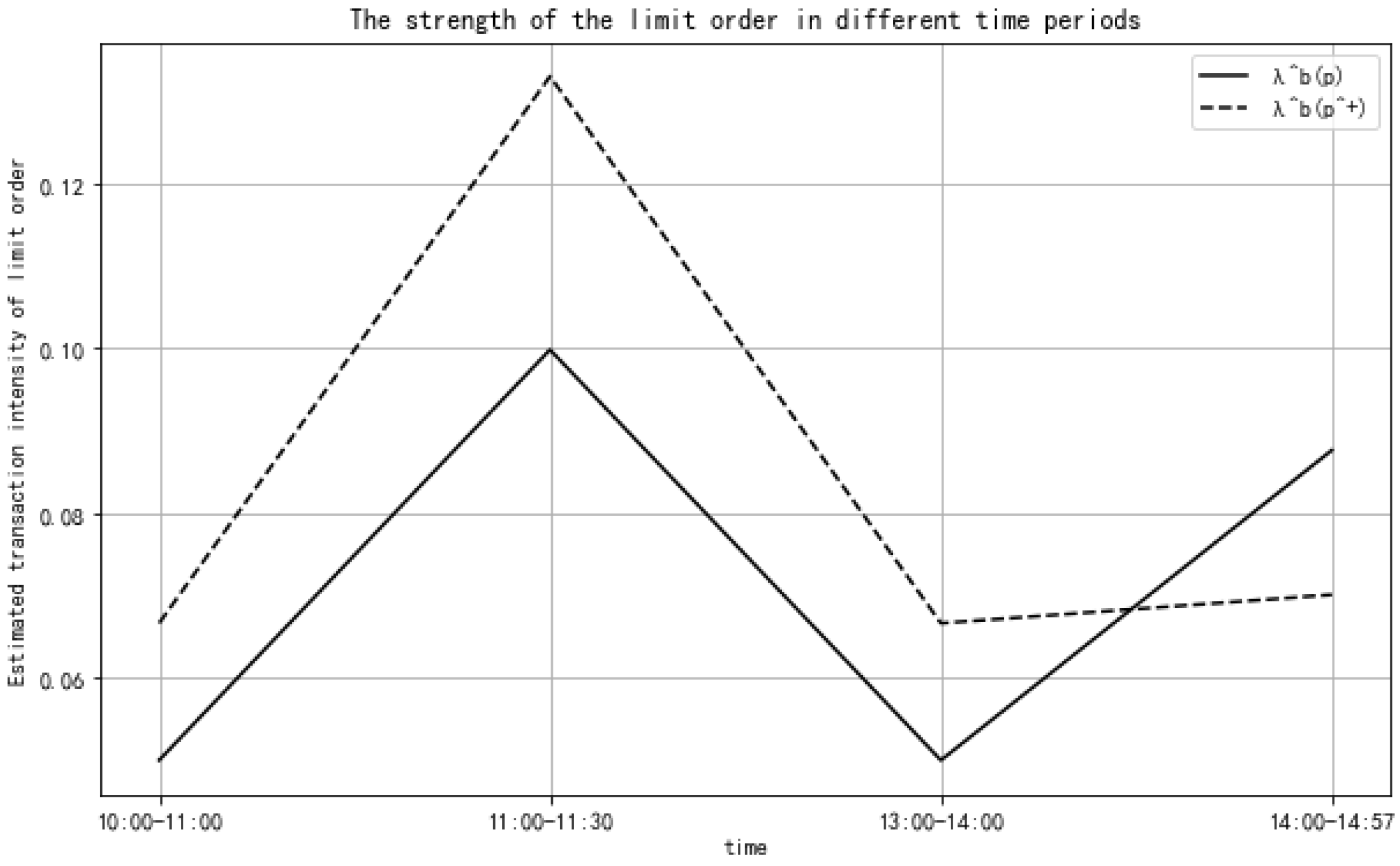
5.2.3. Intensity of Price Spread Changes and Parameter Estimation
5.2.4. One-Dimensional Exponential Hawkes Process Estimation
5.3. Empirical Analysis
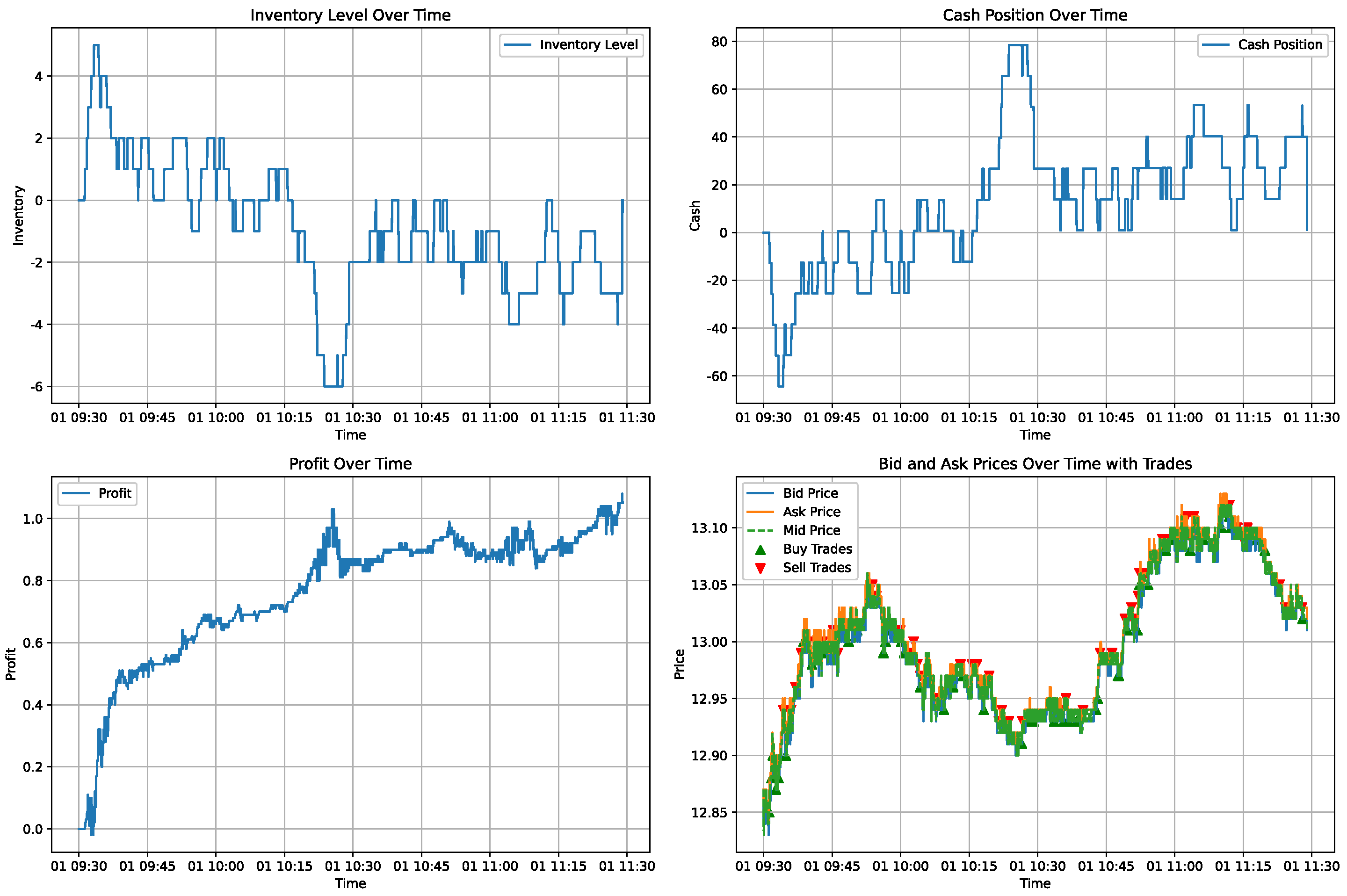
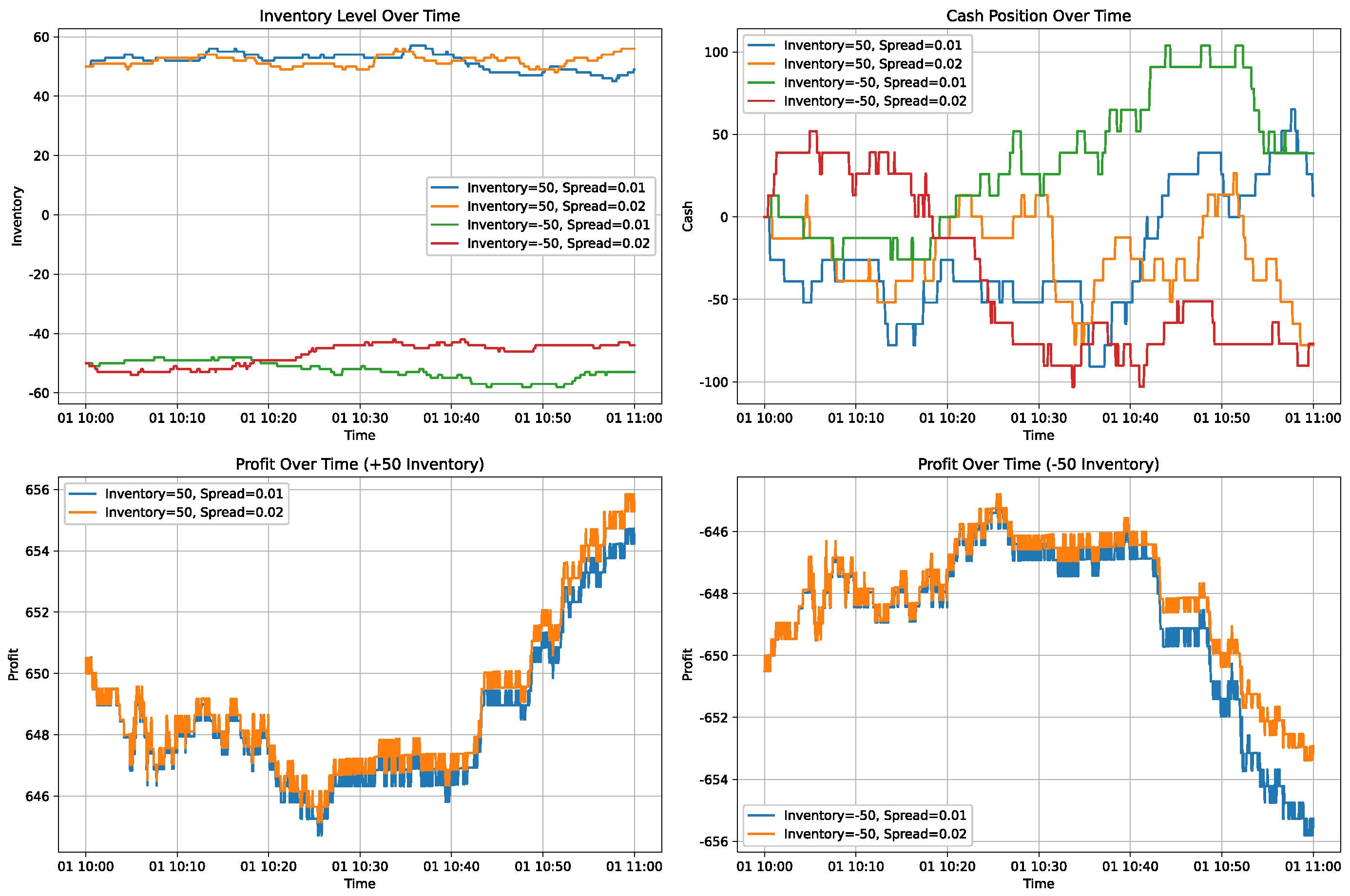
5.3.1. Strategy Validation
- Initial Fund: 100,000 CNY.
- Transaction Cost:
- ▪
- Buying Cost: Set at 0.0001 (0.01%), representing the stamp duty on buy orders.
- ▪
- Selling Cost: Set at 0.0011, including 0.01% stamp duty and 0.1% commission.
- Inventory Threshold: The position limit is determined by the stock’s initial price.
- Spread Threshold: Set at 0.2% of the stock price. When inventory exceeds the threshold, the strategy executes market orders based on the spread to manage the position. Additionally, narrow spreads allow larger market orders for more efficient inventory adjustment. For limit orders, if the spread is within the threshold range, the order is placed at the current best bid or ask price. If the spread exceeds the threshold, the limit order price is incrementally adjusted to capture potential profits from a wider spread (Hollifield et al., 2004) [40].
- End-of-Day Clearance: At the end of each trading day, all positions are liquidated using the closing price to avoid overnight risk.
- Return and Performance Calculation:
- ▪
- Profit: The total trading profit, calculated as ending capital minus initial capital.
- ▪
- Winning Rate: The proportion of profitable trades to total trades.
- ▪
- Stock Return and Strategy Return: This measures the stock price change and overall strategy return to evaluate the relative performance of the strategy.
5.3.2. Market-Wide Analysis
- Intraday Inventory Fluctuations: Song’s study showed that intraday inventory fluctuates around zero, which helps mitigate the risks brought by market price movements. Our simulated trading also showed similar results, with the market maker’s inventory fluctuating around zero, effectively balancing the risks associated with price volatility. This further validates the strategy’s effectiveness in managing intraday inventory.
- Profitability of the Strategy: Song pointed out that placing orders using the strategy could yield considerable profits by the end of the trading day. Our empirical analysis also showed that the strategy performed steadily in different market conditions, particularly in the bull and bear markets, achieving stable profits by the end of the trading day.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Operators and Numerical Methods
Appendix B. Market Maker Strategy Results
| Instrument ID | Buy/Sell Trades | Market Orders | Initial Price | Final Price | Profit | Winning Rate | Stock Return | Strategy Return |
|---|---|---|---|---|---|---|---|---|
| 000027 | 248,995 | 6 | 6.16 | 6.25 | 568.0 | 43.23% | 1.46% | 0.57% |
| 000050 | 235,933 | 36 | 9.2 | 9.71 | −432.0 | 7.20% | 5.54% | −0.43% |
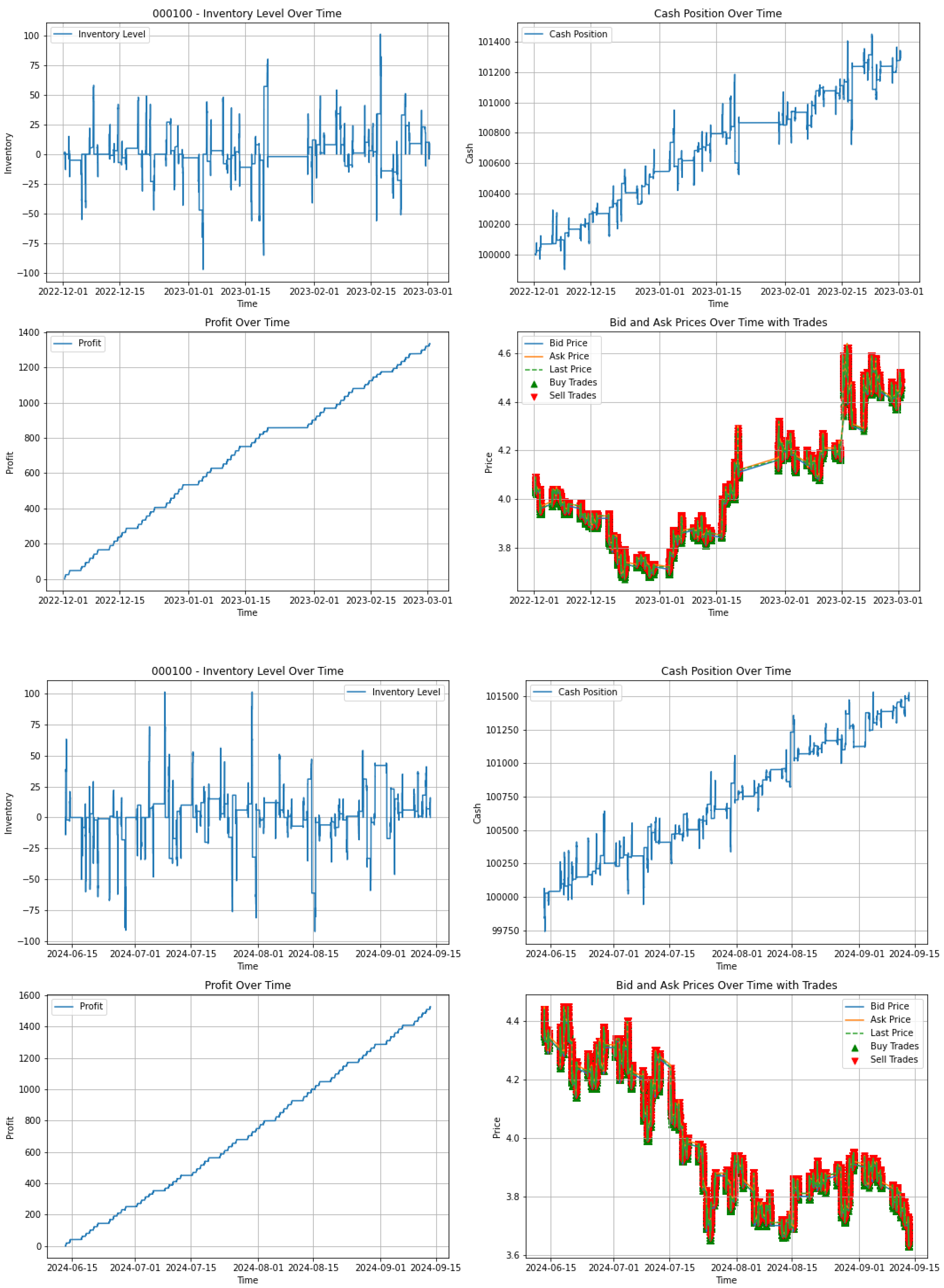
| 000100 | 278,411 | 1 | 4.06 | 4.48 | 1334.9 | 40.86% | 10.34% | 1.33% |
| 000166 | 269,345 | 0 | 4.17 | 4.25 | 1306.2 | 43.06% | 1.92% | 1.31% |
| 000559 | 220,103 | 3 | 5.29 | 5.36 | 757.3 | 43.94% | 1.32% | 0.76% |
| 000591 | 274,477 | 1 | 7.52 | 7.1 | 121.9 | 41.46% | −5.59% | 0.12% |
| 000598 | 234,913 | 1 | 5.1 | 5.15 | 897.0 | 43.77% | 0.98% | 0.90% |
| 000623 | 238,437 | 169 | 15.93 | 15.7 | −2161.6 | 10.24% | −1.44% | −2.16% |
| 000703 | 253,526 | 19 | 7.3 | 8.11 | 54.2 | 42.44% | 11.10% | 0.05% |
| 000776 | 275,615 | 114 | 16.5 | 16.56 | −3048.2 | 11.04% | 0.36% | −3.05% |
| 000785 | 234,094 | 14 | 3.96 | 4.45 | 1058.3 | 43.77% | 12.37% | 1.06% |
| 000883 | 241,464 | 2 | 4.47 | 4.45 | 1112.6 | 44.30% | −0.45% | 1.11% |
| 000958 | 237,321 | 12 | 4.44 | 4.54 | 917.5 | 43.82% | 2.25% | 0.92% |
| 000967 | 223,810 | 11 | 4.94 | 5.43 | 777.7 | 43.32% | 9.92% | 0.78% |
| 000987 | 252,023 | 8 | 6.51 | 6.67 | 362.0 | 42.72% | 2.46% | 0.36% |
| 001227 | 246,551 | 4 | 4.11 | 3.61 | 1282.7 | 45.10% | −12.17% | 1.28% |
| 002252 | 268,804 | 14 | 5.58 | 6.21 | 511.0 | 42.05% | 11.29% | 0.51% |
| 002408 | 222,699 | 13 | 7.5 | 7.19 | 181.8 | 44.03% | −4.13% | 0.18% |
| 002423 | 256,468 | 27 | 7.07 | 7.53 | −129.0 | 41.32% | 6.51% | −0.13% |
| 002429 | 253,460 | 7 | 3.51 | 4.58 | 1235.8 | 43.39% | 30.48% | 1.24% |
| 002500 | 241,403 | 5 | 5.65 | 5.89 | 629.2 | 42.84% | 4.25% | 0.63% |
| 002563 | 232,004 | 8 | 5.1 | 6.02 | 649.0 | 43.04% | 18.04% | 0.65% |
| 002607 | 270,816 | 4 | 5.01 | 5.74 | 599.8 | 40.37% | 14.57% | 0.60% |
| 002608 | 179,394 | 16 | 6.43 | 6.38 | 322.3 | 43.30% | −0.78% | 0.32% |
| 002736 | 242,654 | 7 | 9.24 | 9.86 | −376.5 | 8.10% | 6.71% | −0.38% |
| 002797 | 266,437 | 6 | 6.07 | 6.03 | 616.2 | 42.92% | −0.66% | 0.62% |
| 002926 | 256,978 | 23 | 8.72 | 8.38 | −153.9 | 37.49% | −3.90% | −0.15% |
| 002939 | 259,745 | 12 | 8.83 | 8.75 | −378.0 | 14.00% | −0.91% | −0.38% |
| 300253 | 271,005 | 26 | 8.9 | 10.23 | −1174.6 | 11.38% | 14.94% | −1.17% |
| 300296 | 246,659 | 4 | 5.94 | 6.51 | 544.4 | 43.22% | 9.60% | 0.54% |
| 600000 | 271,997 | 4 | 7.28 | 7.26 | 267.7 | 42.87% | −0.27% | 0.27% |
| 600004 | 276,758 | 120 | 15.1 | 14.31 | −2179.3 | 13.36% | −5.23% | −2.18% |
| 600008 | 278,528 | 0 | 2.91 | 2.98 | 1792.4 | 42.75% | 2.41% | 1.79% |
| 600015 | 271,112 | 2 | 5.27 | 5.25 | 959.6 | 43.00% | −0.38% | 0.96% |
| 600016 | 278,547 | 0 | 3.54 | 3.43 | 1595.8 | 42.83% | −3.11% | 1.60% |
| 600018 | 272,968 | 3 | 5.49 | 5.35 | 920.4 | 42.75% | −2.55% | 0.92% |
| 600019 | 278,633 | 7 | 5.67 | 6.62 | 648.3 | 41.41% | 16.75% | 0.65% |
| 600028 | 279,948 | 0 | 4.55 | 4.74 | 1245.0 | 41.24% | 4.18% | 1.25% |
| 600029 | 278,132 | 7 | 7.68 | 7.9 | −2.9 | 40.37% | 2.86% | 0.00% |
| 600039 | 271,225 | 77 | 11.74 | 13.16 | −1106.8 | 9.99% | 12.10% | −1.11% |
| 600050 | 269,806 | 9 | 4.41 | 5.81 | 809.3 | 39.68% | 31.75% | 0.81% |
| 600056 | 261,436 | 100 | 16.91 | 15.88 | −3485.0 | 10.93% | −6.09% | −3.48% |
| 600061 | 271,972 | 8 | 6.62 | 7.06 | 295.1 | 42.52% | 6.65% | 0.30% |
| 600095 | 265,746 | 18 | 8.15 | 10.43 | −844.0 | 25.02% | 27.98% | −0.84% |
| 600098 | 269,301 | 9 | 5.9 | 5.89 | 746.8 | 42.92% | −0.17% | 0.75% |
| 600104 | 276,732 | 61 | 15.45 | 15.19 | −2271.6 | 8.67% | −1.68% | −2.27% |
| 600109 | 275,736 | 25 | 9.17 | 9.36 | −710.5 | 8.55% | 2.07% | −0.71% |
| 600115 | 276,576 | 1 | 5.42 | 5.47 | 822.2 | 41.67% | 0.92% | 0.82% |
| 600126 | 252,319 | 11 | 4.33 | 4.88 | 1043.2 | 44.39% | 12.70% | 1.04% |
| 600143 | 274,199 | 80 | 10.17 | 10.01 | −785.0 | 7.36% | −1.57% | −0.79% |
| 600155 | 263,266 | 24 | 7.4 | 7.18 | 147.8 | 43.44% | −2.97% | 0.15% |
| 600166 | 278,782 | 7 | 2.73 | 3.56 | 1615.8 | 41.85% | 30.40% | 1.62% |
| 600170 | 276,894 | 1 | 2.81 | 2.71 | 1845.5 | 43.12% | −3.56% | 1.85% |
| 600177 | 243,299 | 1 | 6.5 | 6.58 | 475.5 | 43.94% | 1.23% | 0.48% |
| 600219 | 279,241 | 0 | 3.56 | 3.68 | 1538.8 | 42.38% | 3.37% | 1.54% |
| 600271 | 259,912 | 130 | 11.05 | 12.37 | −1145.4 | 8.57% | 11.95% | −1.15% |
| 600282 | 268,361 | 2 | 3.34 | 4.05 | 1453.3 | 43.34% | 21.26% | 1.45% |
| 600350 | 233,793 | 7 | 5.77 | 5.99 | 623.8 | 43.53% | 3.81% | 0.62% |
| 600352 | 262,242 | 18 | 9.85 | 10.43 | −738.4 | 6.38% | 5.89% | −0.74% |
| 600361 | 212,231 | 67 | 6.72 | 6.44 | 130.5 | 43.48% | −4.17% | 0.13% |
| 600369 | 269,516 | 5 | 4.05 | 4.08 | 1323.0 | 43.74% | 0.74% | 1.32% |
| 600390 | 269,177 | 13 | 5.23 | 5.41 | 783.8 | 42.63% | 3.44% | 0.78% |
| 600399 | 276,053 | 133 | 15.11 | 14.48 | −2278.3 | 12.75% | −4.17% | −2.28% |
| 600415 | 272,184 | 9 | 4.48 | 5.31 | 833.3 | 41.39% | 18.53% | 0.83% |
| 600497 | 277,961 | 13 | 5.37 | 5.58 | 860.2 | 42.10% | 3.91% | 0.86% |
| 600499 | 276,873 | 151 | 16.06 | 16.25 | −2750.6 | 9.51% | 1.18% | −2.75% |
| 600500 | 263,686 | 16 | 7.3 | 7.03 | 240.1 | 42.80% | −3.70% | 0.24% |
| 600515 | 276,845 | 3 | 4.35 | 4.34 | 986.0 | 42.12% | −0.23% | 0.99% |
| 600516 | 273,136 | 12 | 6.49 | 6.72 | 457.2 | 43.37% | 3.54% | 0.46% |
| 600517 | 242,779 | 14 | 5.25 | 5.21 | 803.4 | 44.23% | −0.76% | 0.80% |
| 600528 | 255,070 | 12 | 8.11 | 8.97 | −149.1 | 37.76% | 10.60% | −0.15% |
| 600578 | 257,809 | 6 | 3.51 | 3.33 | 1483.5 | 43.94% | −5.13% | 1.48% |
| 600582 | 274,622 | 5 | 5.45 | 5.44 | 934.6 | 41.82% | −0.18% | 0.93% |
| 600583 | 274,625 | 11 | 5.73 | 6.76 | 432.4 | 40.71% | 17.98% | 0.43% |
| 600637 | 257,811 | 16 | 6.75 | 7.2 | 287.5 | 43.43% | 6.67% | 0.29% |
| 600655 | 260,557 | 10 | 7.38 | 7.85 | 26.2 | 42.31% | 6.37% | 0.03% |
| 600704 | 273,358 | 6 | 4.58 | 4.91 | 1054.4 | 43.08% | 7.21% | 1.05% |
| 600739 | 243,536 | 173 | 13.48 | 13.57 | −1547.3 | 7.90% | 0.67% | −1.55% |
| 600755 | 270,490 | 28 | 7.71 | 8.84 | −50.7 | 39.39% | 14.66% | −0.05% |
| 600808 | 271,900 | 2 | 2.91 | 3.09 | 1698.3 | 43.59% | 6.19% | 1.70% |
| 600816 | 185,272 | 39 | 3.69 | 4 | 778.8 | 45.02% | 8.40% | 0.78% |
| 600820 | 268,422 | 3 | 5.55 | 5.6 | 867.3 | 43.06% | 0.90% | 0.87% |
| 600827 | 257,906 | 193 | 11.46 | 12.17 | −1258.5 | 9.11% | 6.20% | −1.26% |
| 600837 | 276,244 | 8 | 9.08 | 9.25 | −417.7 | 7.50% | 1.87% | −0.42% |
| 600863 | 279,117 | 4 | 3.86 | 3.53 | 1521.4 | 43.19% | −8.55% | 1.52% |
| 600871 | 274,533 | 1 | 2.01 | 2.15 | 2026.3 | 43.27% | 6.97% | 2.03% |
| 600879 | 275,854 | 15 | 6.95 | 7.77 | 149.8 | 42.15% | 11.80% | 0.15% |
| 600901 | 271,499 | 7 | 5.78 | 6.07 | 679.9 | 41.69% | 5.02% | 0.68% |
| 600905 | 279,605 | 0 | 5.82 | 5.65 | 821.3 | 40.41% | −2.92% | 0.82% |
| 600906 | 274,690 | 26 | 8.94 | 8.31 | −407.3 | 23.02% | −7.05% | −0.41% |
| 600909 | 275,763 | 5 | 4.99 | 4.99 | 1022.3 | 42.88% | 0.00% | 1.02% |
| 600919 | 279,218 | 5 | 7.5 | 7.22 | 213.6 | 40.71% | −3.73% | 0.21% |
| 600928 | 250,487 | 3 | 3.58 | 3.55 | 1383.4 | 44.67% | −0.84% | 1.38% |
| 600956 | 245,405 | 171 | 10.82 | 10 | −661.7 | 6.01% | −7.58% | −0.66% |
| 600958 | 277,591 | 14 | 9.16 | 10.37 | −921.1 | 10.43% | 13.21% | −0.92% |
| 600959 | 269,072 | 2 | 3.08 | 3.17 | 1653.6 | 44.35% | 2.92% | 1.65% |
| 600967 | 262,345 | 16 | 8.72 | 9.73 | −339.6 | 14.72% | 11.58% | −0.34% |
| 600968 | 275,637 | 5 | 3.14 | 3.25 | 1639.3 | 43.02% | 3.50% | 1.64% |
| 600977 | 271,495 | 149 | 13.68 | 12.38 | −1835.1 | 10.54% | −9.50% | −1.84% |
| 601000 | 274,504 | 1 | 2.95 | 2.94 | 1762.9 | 43.33% | −0.34% | 1.76% |
| 601006 | 276,383 | 1 | 6.85 | 6.89 | 475.4 | 42.08% | 0.58% | 0.48% |
| 601009 | 276,095 | 54 | 10.4 | 9.93 | −641.0 | 9.47% | −4.52% | −0.64% |
| 601016 | 279,775 | 0 | 4.07 | 3.96 | 1421.6 | 42.32% | −2.70% | 1.42% |
| 601077 | 271,606 | 0 | 3.63 | 3.62 | 1520.1 | 43.97% | −0.28% | 1.52% |
| 601106 | 255,082 | 2 | 3.05 | 3.15 | 1572.1 | 44.79% | 3.28% | 1.57% |
| 601108 | 274,923 | 6 | 7.66 | 7.79 | 50.4 | 42.14% | 1.70% | 0.05% |
| 601111 | 277,863 | 60 | 10.61 | 11.12 | −990.6 | 11.16% | 4.81% | −0.99% |
| 601118 | 255,435 | 11 | 4.46 | 4.65 | 1058.7 | 44.63% | 4.26% | 1.06% |
| 601139 | 262,096 | 21 | 6.98 | 7.15 | 249.7 | 43.34% | 2.44% | 0.25% |
| 601158 | 219,979 | 4 | 5.31 | 5.3 | 787.3 | 44.79% | −0.19% | 0.79% |
| 601162 | 278,776 | 1 | 3.11 | 3.03 | 1713.6 | 42.93% | −2.57% | 1.71% |
| Instrument ID | Buy/Sell Trades | Market Orders | Initial Price | Final Price | Profit | Winning Rate | Stock Return | Strategy Return |
|---|---|---|---|---|---|---|---|---|
| 000027 | 288,338 | 13 | 7.33 | 5.43 | 381.7 | 43.11% | −25.92% | 0.38% |
| 000050 | 291,035 | 23 | 7.54 | 6.38 | 68.7 | 42.02% | −15.38% | 0.07% |
| 000100 | 316,000 | 2 | 4.41 | 3.64 | 1526.7 | 40.72% | −17.46% | 1.53% |
| 000166 | 310,724 | 0 | 4.43 | 4.23 | 1384.0 | 42.39% | −4.51% | 1.38% |
| 000559 | 272,036 | 12 | 4.79 | 4.87 | 1059.7 | 43.82% | 1.67% | 1.06% |
| 000591 | 278,492 | 9 | 4.99 | 4.03 | 1165.9 | 44.14% | −19.24% | 1.17% |
| 000598 | 300,703 | 35 | 7.72 | 6.36 | −83.1 | 41.43% | −17.62% | −0.08% |
| 000623 | 245,520 | 205 | 13.93 | 12.75 | −1664.2 | 6.99% | −8.47% | −1.66% |
| 000703 | 290,218 | 26 | 6.92 | 5.5 | 341.3 | 42.55% | −20.52% | 0.34% |
| 000776 | 302,442 | 99 | 12.51 | 12.34 | −1557.6 | 7.64% | −1.36% | −1.56% |
| 000785 | 267,054 | 8 | 2.72 | 2.28 | 1745.5 | 43.97% | −16.18% | 1.75% |
| 000883 | 297,930 | 19 | 6.03 | 4.53 | 859.1 | 42.58% | −24.88% | 0.86% |
| 000958 | 262,814 | 8 | 3.9 | 3.26 | 1362.7 | 43.75% | −16.41% | 1.36% |
| 000967 | 253,105 | 8 | 4.43 | 3.79 | 1139.8 | 43.71% | −14.45% | 1.14% |
| 000987 | 258,458 | 24 | 5.33 | 4.92 | 825.8 | 44.07% | −7.69% | 0.83% |
| 001227 | 266,938 | 0 | 2.47 | 2.11 | 1893.9 | 45.29% | −14.57% | 1.89% |
| 002252 | 303,497 | 13 | 7.38 | 6.56 | 16 | 41.87% | −11.11% | 0.02% |
| 002408 | 260,904 | 33 | 5.85 | 4.61 | 722 | 43.63% | −21.20% | 0.72% |
| 002423 | 288,163 | 24 | 7.7 | 7.22 | −105 | 43.22% | −6.23% | −0.10% |
| 002429 | 297,095 | 15 | 4.87 | 4.36 | 1087.5 | 42.70% | −10.47% | 1.09% |
| 002500 | 278,693 | 12 | 4.94 | 4.9 | 1052.1 | 43.54% | −0.81% | 1.05% |
| 002563 | 286,940 | 17 | 6.36 | 4.48 | 924.3 | 42.82% | −29.56% | 0.92% |
| 002607 | 291,055 | 4 | 1.91 | 1.85 | 2113.8 | 40.89% | −3.14% | 2.11% |
| 002608 | 268,061 | 17 | 8.06 | 6.49 | 60.2 | 43.23% | −19.48% | 0.06% |
| 002736 | 253,383 | 11 | 9.36 | 8.66 | −290.2 | 16.14% | −7.48% | −0.29% |
| 002797 | 297,355 | 4 | 5.27 | 5.27 | 1009.8 | 43.10% | 0.00% | 1.01% |
| 002926 | 241,404 | 20 | 6.8 | 6.46 | 304.9 | 43.35% | −5.00% | 0.30% |
| 002939 | 273,089 | 20 | 6.98 | 6.87 | 254.3 | 43.15% | −1.58% | 0.25% |
| 300253 | 287,010 | 17 | 6.13 | 5.22 | 626.3 | 42.94% | −14.85% | 0.63% |
| 300296 | 289,871 | 11 | 4.74 | 3.92 | 1134.70 | 43.20% | −17.30% | 1.13% |
| 600000 | 313,255 | 8 | 8.1 | 8.34 | −293.1 | 17.59% | 2.96% | −0.29% |
| 600004 | 279,514 | 142 | 10.09 | 8.59 | −534.9 | 5.79% | −14.87% | −0.53% |
| 600008 | 302,640 | 5 | 2.79 | 2.79 | 1944.50 | 43.17% | 0.00% | 1.94% |
| 600015 | 310,819 | 5 | 6.66 | 6.14 | 576.6 | 41.92% | −7.81% | 0.58% |
| 600016 | 315,637 | 0 | 3.8 | 3.33 | 1725.00 | 41.38% | −12.37% | 1.73% |
| 600018 | 308,979 | 2 | 5.69 | 5.67 | 697.4 | 42.31% | −0.35% | 0.70% |
| 600019 | 314,803 | 3 | 6.75 | 5.58 | 548.6 | 41.07% | −17.33% | 0.55% |
| 600028 | 315,438 | 2 | 6.23 | 6.19 | 518.1 | 40.44% | −0.64% | 0.52% |
| 600029 | 302,297 | 11 | 5.87 | 5.4 | 755.8 | 43.28% | −8.01% | 0.76% |
| 600039 | 297,390 | 17 | 8.39 | 5.47 | 328.8 | 42.38% | −34.80% | 0.33% |
| 600050 | 316,077 | 1 | 4.42 | 4.48 | 1304.90 | 40.47% | 1.36% | 1.30% |
| 600056 | 264,475 | 156 | 10.8 | 9.71 | −772.3 | 5.71% | −10.09% | −0.77% |
| 600061 | 279,294 | 10 | 5.98 | 5.73 | 702 | 43.79% | −4.18% | 0.70% |
| 600095 | 283,078 | 24 | 6.37 | 5.9 | 390.5 | 43.55% | −7.38% | 0.39% |
| 600098 | 283,785 | 29 | 6.76 | 5.46 | 452.7 | 43.39% | −19.23% | 0.45% |
| 600104 | 310,638 | 125 | 14.05 | 11.57 | −2256.1 | 8.67% | −17.65% | −2.26% |
| 600109 | 288,493 | 15 | 7.94 | 7.08 | 23.3 | 43.57% | −10.83% | 0.02% |
| 600115 | 296,388 | 5 | 3.96 | 3.6 | 1479.60 | 43.53% | −9.09% | 1.48% |
| 600126 | 273,234 | 13 | 4.35 | 3.31 | 1340.60 | 43.93% | −23.91% | 1.34% |
| 600143 | 290,984 | 19 | 6.97 | 7.19 | 287.8 | 43.08% | 3.16% | 0.29% |
| 600155 | 284,195 | 24 | 6.45 | 6.06 | 459.7 | 43.59% | −6.05% | 0.46% |
| 600166 | 302,729 | 2 | 2.44 | 2.28 | 2020.30 | 43.64% | −6.56% | 2.02% |
| 600170 | 304,148 | 0 | 2.24 | 1.92 | 2215.70 | 42.78% | −14.29% | 2.22% |
| 600177 | 299,288 | 11 | 7.31 | 6.61 | 252.8 | 42.74% | −9.58% | 0.25% |
| 600219 | 314,864 | 0 | 3.76 | 3.51 | 1646.20 | 41.23% | −6.65% | 1.65% |
| 600271 | 277,074 | 46 | 7.84 | 8.14 | −325.9 | 42.23% | 3.83% | −0.33% |
| 600282 | 305,284 | 7 | 5.02 | 4.04 | 1218.60 | 42.41% | −19.52% | 1.22% |
| 600350 | 289,753 | 17 | 8.93 | 9.3 | −520.6 | 7.64% | 4.14% | −0.52% |
| 600352 | 277,529 | 33 | 8.62 | 9.03 | −369.5 | 6.76% | 4.76% | −0.37% |
| 600361 | 295,873 | 20 | 3.83 | 3.49 | 1280.00 | 42.86% | −8.88% | 1.28% |
| 600369 | 287,723 | 4 | 3.7 | 3.59 | 1484.80 | 43.74% | −2.97% | 1.48% |
| 600390 | 281,077 | 10 | 4.27 | 4.01 | 1307.80 | 44.14% | −6.09% | 1.31% |
| 600399 | 301,223 | 28 | 6 | 5.09 | 638.4 | 43.06% | −15.17% | 0.64% |
| 600415 | 306,867 | 16 | 8.5 | 8.52 | −127.6 | 36.33% | 0.24% | −0.13% |
| 600497 | 310,507 | 14 | 5.57 | 4.59 | 912.7 | 42.51% | −17.59% | 0.91% |
| 600499 | 284,677 | 31 | 9.4 | 7.06 | −97.1 | 35.64% | −24.89% | −0.10% |
| 600500 | 257,907 | 18 | 3.78 | 3.66 | 1277.30 | 44.10% | −3.17% | 1.28% |
| 600515 | 278,333 | 13 | 3.36 | 3.07 | 1560.00 | 44.22% | −8.63% | 1.56% |
| 600516 | 289,534 | 19 | 4.53 | 3.84 | 1249.90 | 43.97% | −15.23% | 1.25% |
| 600517 | 274,913 | 8 | 4.53 | 4.34 | 1214.60 | 43.77% | −4.19% | 1.21% |
| 600528 | 258,277 | 35 | 7.63 | 6.67 | 52.5 | 43.81% | −12.58% | 0.05% |
| 600578 | 295,427 | 14 | 3.35 | 3.03 | 1642.30 | 43.41% | −9.55% | 1.64% |
| 600582 | 308,007 | 15 | 6.97 | 5.22 | 648.6 | 42.10% | −25.11% | 0.65% |
| 600583 | 298,321 | 22 | 6.09 | 4.88 | 779.7 | 42.86% | −19.87% | 0.78% |
| 600637 | 279,367 | 22 | 6.37 | 6.17 | 509.6 | 43.78% | −3.14% | 0.51% |
| 600655 | 265,827 | 12 | 5.65 | 5 | 814.1 | 43.83% | −11.50% | 0.81% |
| 600704 | 298,677 | 7 | 4.64 | 4.03 | 1357.90 | 43.14% | −13.15% | 1.36% |
| 600739 | 268,962 | 42 | 9.29 | 8.01 | −309.7 | 25.97% | −13.78% | −0.31% |
| 600755 | 278,353 | 17 | 8.11 | 5.69 | 360.7 | 43.12% | −29.84% | 0.36% |
| 600808 | 261,699 | 3 | 2.14 | 1.81 | 1931.40 | 44.67% | −15.42% | 1.93% |
| 600816 | 243,533 | 24 | 2.94 | 2.35 | 1548.10 | 44.46% | −20.07% | 1.55% |
| 600820 | 303,435 | 17 | 6.62 | 5.33 | 453.3 | 42.41% | −19.49% | 0.45% |
| 600827 | 251,365 | 27 | 8.08 | 7.27 | −204.4 | 43.17% | −10.02% | −0.20% |
| 600837 | 276,452 | 25 | 8.12 | 8.77 | −444.7 | 11.35% | 8.00% | −0.44% |
| 600863 | 311,623 | 5 | 4.71 | 4.07 | 1336.20 | 42.48% | −13.59% | 1.34% |
| 600871 | 275,491 | 1 | 1.78 | 1.73 | 2116.00 | 43.87% | −2.81% | 2.12% |
| 600879 | 309,224 | 26 | 7.83 | 7.09 | −109.5 | 41.95% | −9.45% | −0.11% |
| 600901 | 309,595 | 9 | 5.22 | 4.29 | 1109.40 | 42.25% | −17.82% | 1.11% |
| 600905 | 315,348 | 2 | 4.61 | 4.07 | 1338.00 | 41.15% | −11.71% | 1.34% |
| 600906 | 274,381 | 22 | 6.21 | 5.75 | 567.6 | 44.01% | −7.41% | 0.57% |
| 600909 | 294,236 | 3 | 4.42 | 4.33 | 1272.70 | 43.31% | −2.04% | 1.27% |
| 600919 | 315,258 | 7 | 7.73 | 7.49 | 54.7 | 40.60% | −3.10% | 0.05% |
| 600925 | 258,467 | 11 | 5.54 | 4.86 | 913.9 | 44.28% | −12.27% | 0.91% |
| 600928 | 271,478 | 4 | 3.34 | 2.96 | 1583.40 | 44.28% | −11.38% | 1.58% |
| 600956 | 262,380 | 23 | 9.04 | 6.59 | −39.9 | 38.50% | −27.10% | −0.04% |
| 600958 | 306,915 | 18 | 8 | 8.43 | −137.7 | 26.57% | 5.37% | −0.14% |
| 600959 | 269,288 | 10 | 2.78 | 2.73 | 1716.60 | 44.27% | −1.80% | 1.72% |
| 600967 | 273,514 | 17 | 7.8 | 6.49 | 99.3 | 43.53% | −16.79% | 0.10% |
| 600968 | 304,787 | 9 | 4.13 | 3.92 | 1440.20 | 42.53% | −5.08% | 1.44% |
| 600977 | 252,991 | 232 | 11.26 | 9.76 | −889.7 | 6.50% | −13.32% | −0.89% |
| 601000 | 305,234 | 13 | 4.18 | 4.81 | 1075.30 | 42.63% | 15.07% | 1.08% |
| 601006 | 314,807 | 0 | 7.23 | 5.93 | 471 | 41.26% | −17.98% | 0.47% |
| 601009 | 311,278 | 108 | 10.12 | 9.91 | −788 | 8.70% | −2.08% | −0.79% |
| 601016 | 298,780 | 4 | 3.18 | 2.65 | 1874.50 | 43.95% | −16.67% | 1.87% |
| 601077 | 311,383 | 2 | 5.08 | 4.78 | 1044.50 | 41.88% | −5.91% | 1.04% |
| 601106 | 253,672 | 4 | 2.4 | 2.28 | 1743.50 | 44.81% | −5.00% | 1.74% |
| 601108 | 297,349 | 12 | 6.93 | 6.42 | 391.3 | 43.33% | −7.36% | 0.39% |
| 601111 | 306,898 | 7 | 7.49 | 6.43 | 275.7 | 42.81% | −14.15% | 0.28% |
| 601118 | 281,091 | 13 | 5.03 | 4.88 | 1077.80 | 43.97% | −2.98% | 1.08% |
| 601139 | 274,328 | 16 | 7.11 | 6.29 | 329 | 43.83% | −11.53% | 0.33% |
| 601158 | 255,587 | 10 | 5.03 | 4.26 | 968.9 | 44.57% | −15.31% | 0.97% |
| 601162 | 299,987 | 0 | 2.37 | 2.97 | 2005.80 | 42.50% | 25.32% | 2.01% |
| 601169 | 314,302 | 5 | 5.67 | 4.91 | 926.7 | 41.25% | −13.40% | 0.93% |
| 601186 | 310,619 | 12 | 8.47 | 6.84 | −132.7 | 27.77% | −19.24% | −0.13% |
Appendix C. Bull Market Full Market Maker Strategy Trends
Appendix D. Bear Market Full Market Maker Strategy Trends
References
- Avellaneda, M.; Stoikov, S. High-frequency trading in a limit order book. Quant. Financ. 2008, 8, 217–224. [Google Scholar] [CrossRef]
- Bauwens, L.; Hautsch, N. Modelling Financial High Frequency Data Using Point Processes; Handbook of Financial Time Series; Springer: Berlin/Heidelberg, Germany, 2009; pp. 953–979. [Google Scholar]
- Abergel, F.; Jedidi, A. A mathematical approach to order book modeling. Int. J. Theor. Appl. Financ. 2013, 16, 1350025. [Google Scholar] [CrossRef]
- Bacry, E.; Delattre, S.; Hoffmann, M.; Muzy, J.F. Modelling microstructure noise with mutually exciting point processes. Quant. Financ. 2013, 13, 65–77. [Google Scholar] [CrossRef]
- Almgren, R.; Chriss, N. Optimal execution of portfolio transactions. J. Risk 2001, 3, 5–40. [Google Scholar] [CrossRef]
- Alfonsi, A.; Fruth, A.; Schied, A. Optimal execution strategies in limit order books with general shape functions. Quant. Financ. 2010, 10, 143–157. [Google Scholar] [CrossRef]
- Sandås, P. Adverse selection and competitive market making: Empirical evidence from a limit order market. Rev. Financ. Stud. 2001, 14, 705–734. [Google Scholar] [CrossRef]
- Ye, J. An Empirical Study on the Formation, Characteristics and Influence of Limit Order Book. Ph.D. Thesis, Fudan University, Shanghai, China, 2011. [Google Scholar]
- Basak, A.; Choudhury, A. Classical and Bayesian inference on traffic intensity of multiserver Markovian queuing system. Commun. Stat.-Simul. Comput. 2023, 52, 2044–2057. [Google Scholar] [CrossRef]
- Engle, R.F.; Lunde, A. Trades and quotes: A bivariate point process. J. Financ. Econ. 2003, 1, 159–188. [Google Scholar] [CrossRef][Green Version]
- Cont, R.; Stoikov, S.; Talreja, R. A stochastic model for order book dynamics. Oper. Res. 2010, 58, 549–563. [Google Scholar] [CrossRef]
- Ho, T.; Stoll, H.R. Optimal dealer pricing under transactions and return uncertainty. J. Financ. Econ. 1981, 9, 47–73. [Google Scholar] [CrossRef]
- Guéant, O.; Lehalle, C.A.; Fernandez-Tapia, J. Dealing with the inventory risk: A solution to the market making problem. Math. Financ. Econ. 2013, 7, 477–507. [Google Scholar] [CrossRef]
- Guilbaud, F.; Pham, H. Optimal high-frequency trading with limit and market orders. Quant. Financ. 2013, 13, 79–94. [Google Scholar] [CrossRef]
- Cartea, Á.; Jaimungal, S.; Ricci, J. Buy low, sell high: A high frequency trading perspective. SIAM J. Financ. Math. 2014, 5, 415–444. [Google Scholar] [CrossRef]
- Bressan, A.; Mazzola, M.; Wei, H. A dynamic model of the limit order book. Discret. Contin. Dyn. Syst.-B 2020, 25, 1015–1041. [Google Scholar] [CrossRef]
- Song, B.; Lin, M.; Tian, Y. Research on Optimal high-frequency market maker strategy based on limit order book. Syst. Eng. Theory Pract. 2018, 38, 16–34. [Google Scholar]
- Li, Z. Optimal Algorithmic Trading Strategy and Empirical Analysis Based on Market Maker Model. Master’s Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Wu, H. Probability Estimation of Limit Order and Its Application in Order Strategy. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2020. [Google Scholar]
- Chi, W. High-Frequency Analysis of Limit Order Transaction Probability and Microstructure in Chinese Stock Market. Ph.D. Thesis, Shanghai University of Finance and Economics, Shanghai, China, 2021. [Google Scholar]
- Zhao, J. Research on Short-Term Stock Price Prediction Based on High-Frequency Order Book. Master’s Thesis, Shanghai University of Finance and Economics, Shanghai, China, 2022. [Google Scholar]
- Stoikov, S.; Sağlam, M. Option market making under inventory risk. Rev. Deriv. Res. 2009, 12, 55–79. [Google Scholar] [CrossRef]
- Øksendal, B.; Agnes, S. Stochastic Control of jump diffusions. In Applied Stochastic Control of Jump Diffusions; Springer International Publishing: Cham, Switzerland, 2019; pp. 93–155. [Google Scholar]
- Herzog, F. Strategic Portfolio Management for Long-Term Investments: An Optimal Control Approach. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2005. [Google Scholar]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Financ. 2001, 1, 223. [Google Scholar] [CrossRef]
- Cont, R.; Kukanov, A.; Stoikov, S. The price impact of order book events. J. Financ. Econom. 2014, 12, 47–88. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Farmer, J.D.; Lillo, F. How markets slowly digest changes in supply and demand. In Handbook of Financial Markets: Dynamics and Evolution; North-Holland: Amsterdam, The Netherlands, 2009; pp. 57–160. [Google Scholar]
- Harris, L.E.; Panchapagesan, V. The information content of the limit order book: Evidence from NYSE specialist trading decisions. J. Financ. Mark. 2005, 8, 25–67. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons. Inc.: New York, NY, USA; London, UK; Sydney, Australia, 1971; Volume II. [Google Scholar]
- Cont, R.; De Larrard, A. Price dynamics in a Markovian limit order market. SIAM J. Financ. Math. 2013, 4, 1–25. [Google Scholar] [CrossRef]
- Lawler, G.F.; Limic, V. Random Walk: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Fodra, P.; Labadie, M. High-frequency market-making with inventory constraints and directional bets. arXiv 2012, arXiv:1206.4810. [Google Scholar]
- Engle, R.F.; Russell, J.R. Autoregressive conditional duration: A new model for irregularly spaced transaction data. Econometrica 1998, 66, 1127–1162. [Google Scholar] [CrossRef]
- Kharroubi, I.; Ma, J.; Pham, H.; Zhang, J. Backward SDEs with constrained jumps and quasi-variational inequalities. Ann. Probab. 2010, 38, 794–840. [Google Scholar] [CrossRef]
- Cohen, J.W.; Boxma, O.J. Boundary Value Problems in Queueing System Analysis; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Bayraktar, E.; Ludkovski, M. Liquidation in limit order books with controlled intensity. Math. Financ. 2014, 24, 627–650. [Google Scholar] [CrossRef]
- Robert, C.Y.; Rosenbaum, M. A new approach for the dynamics of ultra-high-frequency data: The model with uncertainty zones. J. Financ. Econom. 2011, 9, 344–366. [Google Scholar] [CrossRef]
- Ait-Sahalia, Y.; Mykland, P.A.; Zhang, L. How often to sample a continuous-time process in the presence of market microstructure noise. Rev. Financ. Stud. 2005, 18, 351–416. [Google Scholar] [CrossRef]
- Biais, B.; Hillion, P.; Spatt, C. An empirical analysis of the limit order book and the order flow in the Paris Bourse. J. Financ. 1995, 50, 1655–1689. [Google Scholar] [CrossRef]
- Hollifield, B.; Miller, R.A.; Sandås, P. Empirical analysis of limit order markets. Rev. Econ. Stud. 2004, 71, 1027–1063. [Google Scholar] [CrossRef]

| Time Period | ||
|---|---|---|
| 09:30–10:30 | 0.062552 | 0.062481 |
| 10:30–11:30 | 0.124792 | 0.124651 |
| 13:00–14:00 | 0.062552 | 0.062481 |
| 14:00–14:57 | 0.087719 | 0.065789 |
| Spread | ||
|---|---|---|
| 0.01 | 0.312778 | 0.313056 |
| 0.02 | 0.180556 | 0.183333 |
| 0.03 | 0.022222 | 0.025000 |
| 0.05 | 0.000000 | 0.002778 |
| Time Period | Number of Spread Changes | Intensity of Spread Changes λ |
|---|---|---|
| 147 | 0.082 | |
| 104 | 0.029 | |
| 56 | 0.031 | |
| 62 | 0.017 | |
| 72 | 0.02 |
| Inventory | Spread | Buy Order Count | Sell Order Count |
|---|---|---|---|
| 24 | 36 | ||
| 21 | 26 | ||
| 25 | 28 | ||
| 25 | 26 |
| Instrument ID | Market State | Buy/Sell Trades | Market Orders | Initial Price | Final Price | Profit | Winning Rate | Stock Return | Strategy Return |
|---|---|---|---|---|---|---|---|---|---|
| 000958 | Bull | 237,321 | 12 | 4.44 | 4.54 | 917.5 | 43.82% | 2.25% | 0.92% |
| Bear | 262,814 | 8 | 3.9 | 3.26 | 1362.7 | 43.75% | −16.41% | 1.36% | |
| 000166 | Bull | 269,345 | 0 | 4.17 | 4.25 | 1306.2 | 43.06% | 1.92% | 1.31% |
| Bear | 310,724 | 0 | 4.43 | 4.23 | 1384.0 | 42.39% | −4.51% | 1.38% | |
| 000598 | Bull | 234,913 | 1 | 5.1 | 5.15 | 897.0 | 43.77% | 0.98% | 0.90% |
| Bear | 300,703 | 35 | 7.72 | 6.36 | −83.1 | 41.43% | −17.62% | −0.08% | |
| 600008 | Bull | 278,528 | 0 | 2.91 | 2.98 | 1792.4 | 42.75% | 2.41% | 1.79% |
| Bear | 302,640 | 5 | 2.79 | 2.79 | 1944.5 | 43.17% | 0.00% | 1.94% | |
| 600959 | Bull | 269,072 | 2 | 3.08 | 3.17 | 1653.6 | 44.35% | 2.92% | 1.65% |
| Bear | 269,288 | 10 | 2.78 | 2.73 | 1716.6 | 44.27% | −1.80% | 1.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, F.; Liu, Y.; Hu, C.; Liang, S. Dynamic Modeling of Limit Order Book and Market Maker Strategy Optimization Based on Markov Queue Theory. Mathematics 2025, 13, 778. https://doi.org/10.3390/math13050778
Xie F, Liu Y, Hu C, Liang S. Dynamic Modeling of Limit Order Book and Market Maker Strategy Optimization Based on Markov Queue Theory. Mathematics. 2025; 13(5):778. https://doi.org/10.3390/math13050778
Chicago/Turabian StyleXie, Fei, Yang Liu, Changlong Hu, and Shenbao Liang. 2025. "Dynamic Modeling of Limit Order Book and Market Maker Strategy Optimization Based on Markov Queue Theory" Mathematics 13, no. 5: 778. https://doi.org/10.3390/math13050778
APA StyleXie, F., Liu, Y., Hu, C., & Liang, S. (2025). Dynamic Modeling of Limit Order Book and Market Maker Strategy Optimization Based on Markov Queue Theory. Mathematics, 13(5), 778. https://doi.org/10.3390/math13050778




